Для вывода уравнения Бернулли используем известную из механики теорему, касающуюся изменения кинетической энергии. Напомним, что эта теорема читается так: изменение кинетической энергии 2 рассматриваемого тела на некотором его перемещении равно сумме работ всех сил (внешних и внутренних), приложенных к данному телу, на том же перемещении.

Возьмем элементарную струйку потока (рис. 3-20). Выделим сечениями 1-1 и 2-2 некоторый отсек струйки АВ. Обозначим через z 1 и z 2 превыше­ния сечений 1 -1 и 2 -2 над плоскостью сравнения OO, через - площади живых сечений струйки в сечениях 1-1и 2 -2.

Будем считать, что за время отсек АВ струйки переместится в положе­ние А"В" при этом сечение 1-1 струйки переместится на расстояние и сечение 2 -2 струйки - на расстояние . Заметим, что

где и 1 и и 2 - скорости в сечениях 1-1и 2 -2.

Рассуждая, как и в § 3-9, можем показать, что объемы элементарных отсеков струйки АА" и ВВ" равны, т. е.

объем (АА") = объему (ВВ") = (обозначение),

где - расход жидкости для струйки.

Обозначим массу элементарного объема через :

где - плотность жидкости.

Найдем теперь изменение кинетической энергии отсека АВ при переме­щении его в положение А"В" и работу сил, приложенных к этому отсеку, на указанном перемещении.

1°. Изменение кинетической энергии отсека АВ при перемещении его в положение А"В". Обозначим упомянутое изменение кинетической энергии (КЭ) через б (КЭ). Тогда можно написать (см. рис. 3-20):

(КЭ) = КЭ (А"В") - КЭ (АВ) = КЭ (А"В -f ВВ") -

КЭ (АА" + А"В) = КЭ (ВВ") - КЭ (АА"),

или, учитывая (3-55),

Рис. 3-20. К выводу уравнения (3-60)

2°. Работа сил при перемещении отсека АВ в поло­жение А"В". При указанном перемещении получаем работу следующих сил.

1. Работа силы тяжести. Как видно, эффект действия силы тяжести проявился как бы в том, что отсек АА" переместился в положение ВВ" (а отсек А "В остался на месте). Пользуясь такой условной схемой работу силы тяжести (РСТ) получаем в виде

Справедливость (3-57) может быть обоснована и более строго. Разбиваем отсек А"В на элементарные отсеки объемом . Тогда иско­мая работа силы тяжести может быть представлена в виде:

где z", z", z", . . ., z (n) - возвышения над плоскостью 00 граничных сече­ний, выделяющих элементарные объемы .

2. Работа сил гидродинамического давления,
действующего на торцовые сечения1 -1 и 2 -2 отсека
АВ (со стороны окружающей его жидкости). Эта работа

где и - гидродинамические давления соответственно в сечениях 1 -1 и 2-2.

3. Работа внешних сил давления окружающей ж ид кости на боковую поверхность отсека АВ. Эта работа равна нулю, так как силы направлены перпендикулярно к перемещениям жидких частиц, движущихся вдоль боковой поверхности отсека АВ.

4. Работа внутренних сил давления (нормальных сил взаимодействия отдельных частиц жидкости, составляющих объем АВ).

Эти силы являются парными (противоположно направленными) с одинако­выми перемещениями. Сумма работ их равна нулю.

5. Работа внешних и внутренних сил трения равна нулю (силы трения в рассматриваемой нами идеальной жидкости отсут­ствуют).

3°. Окончательный вывод. Используя теорему изменения кинетической энергии, можем написать:

Разделим это выражение на , т. е. отнесем его к еди­нице в е с а того объема жидкости, который проходит за время б/ через живое сечение струйки. При этом полученное уравнение представим в виде

Так как сечения 1-1 и 2 -2 были намечены произвольно, то (3-59) можно переписать также в виде:

Уравнение (3-59) или (3-60) называется уравнением Бернулли. Оно было получено Даниилом Бернулли в 1738 г. Это уравнение относится только к элементарной струйке идеальной жидкости.

Обратим внимание еще на следующее:

1) уравнение Бернулли связывает величины z, р, и;

2) как видно из (3-60), в случае идеальной жидкости сумма трех слагае мых z, , является постоянной величиной вдоль рассматриваемой струйки;

3) если указанная постоянная величина для данной струйки равна A lt то для соседней струйки сумма приведенных трех слагаемых равняется А 2 , причем в" общем случае А 1 ≠ A 2 ;

4) зная для данной струйки постоянную величину А, а также зная для данного сечения струйки из трех величин (z , и, р) какие-либо две величины, мы можем, пользуясь уравнением Бернулли, найти третью неизвестную величину для рассматриваемого сечения струйки.

Уравнение (3-60) можно получить также путем интегрирования дифференциальных урав­нений Эйлера (см. § 3-3) для любой системы объемных сил, действующих на жид­кость и имеющих потенциал (см. § 9-2). Уравнение (3-60) относится к определенной линии тока (точнее: к элементарной струйке, намеченной вдоль определенной линии тока). Это уравнение часто называют интегралом Бернулли.

Более подробное рассмотрение данного вопроса показывает, что уравнение Бернулли (интеграл Бернулли) оказывается справедливым как для безвихревого (потенциального) уста­новившегося движения, так и для вихревого установившегося движения идеальной жидкости, при условии, однако, что на жидкость действуют объемные силы, имеющие потенциал (в част­ности, сила тяжести, которую мы имели в виду выше). При рассмотрении установившегося вихревого движения идеальной жидкости под скоростью и, входящей в уравнение Бернулли, следует понимать (так же как и в случае безвихревого движения) скорость, относящуюся к дей­ствительному векторному полю, отражающему рассматриваемое движение жидкости (к разло­жению движения на три его вида, поясненных в § 3-4, здесь обращаться не следует).

Можно также показать, что в случае: а) без вихревого (потенциального) движения идеальной жидкости и б) объемных сил, действующих на жидкость, имеющих потен­циал, величина А, о которой говорили выше, является одинаковой для всех линий тока, образующих поток: А 1 = А 2 = А 3 = --- В этом случае уравнение (3-60) оказывается справед­ливым для всей области, занятой жидкостью, а не только для определенной линии тока.

Выше были получены дифференциальные уравнения движения идеальной жидкости и уравнение неразрывности движения, образующие замкнутую систему уравнений. Для решения конкретных инженерных задач необходимо уметь находить интегралы этих уравнений.

Прежде чем перейти к интегрированию уравнений движения идеальной жидкости, примем следующие дополнительные условия:

Проекции ускорения массовой силы (в данном случае силы тяжести) примут следующие значения при выбранном; направлении осей координат:

X=0; Y=0; Z=-g.

После преобразования получим:

Деля на g, получим:

Интегрируя это дифференциальное уравнение в полных дифференциалах, придем к следующему результату:

Это уравнение называется уравнением Д. Бернули, оно справедливо при установившемся движении идеальной жидкости.

Для двух произвольных сечений элементарной струйки:

Это и есть уравнение Д. Бернули.

Геометрический и энергетический смысл уравнения

Д. Бернулли

Все члены, входящие в уравнение Д. Бернулли, имеют линейную размерность, поэтому их принято называть высотами. Соответственно общеприняты следующие названия для этих членов:

z - геометрическая или геодезическая высота;

Пьезометрическая высота или высота давления;

– динамический или скоростной напор;

Легко усмотреть следующий геометрический смысл уравнения Д. Бернулли, который заключается в том, что при установившемся движении идеальной жидкости сумма трех высот (геометрической, пьезометрической и скоростной) не меняется вдоль данной элементарной струйки. Это положение наглядно иллюстрируется на рис. 1.

Можно трактовать смысл отдельных членов уравнения

Бернулли иначе. Выше было показано, что сумма

Представляет собой удельную энергию жидкости. В соответствии с этим можно считать, что:

z - есть удельная энергия положения;

Энергия давления;

Есть удельная кинетическая энергия.

Энергетический смысл уравнения Бернулли заключается в том, что при установившемся движении идеальной жидкости сумма удельных энергий положения, давления и кинетической не меняется вдоль данной элементарной струйки .

Рис. 1

Полная удельная энергия (т. е. потенциальная + кинетическая) называется гидродинамическим напором и обозначается . Таким образом, уравнение Бернулли показывает, что при установившемся движении идеальной жидкости для данной струйки гидродинамический напор есть величина постоянная. На графике линия гидродинамического напора изображается горизонтальной линией.

Уравнение Д. Бернулли для элементарной струйки реальной жидкости. Пьезометрический и гидравлический уклоны.

При движении реальной жидкости между соседними струйками возникают силы трения, на преодоление которых затрачивается часть энергии жидкости. Поэтому удельная энергия жидкости в сечении элементарной струйки 2 -2 будет менее удельной энергии жидкости в сечении 1-1 на некоторую величину , которую называют потерянной высотой или потерянной удельной энергией, затрачиваемой на преодоление гидравлических сопротивлений. Аналитически это положение запишется таким образом:

Следовательно, при установившемся движении реальной жид кости сумма четырех высот (геометрической, пьезометриче ской, скоростной и потерянной) или, что то же самое, сумма четырех удельных энергий (положения, давления, кинетической и потерянной) не изменяется вдоль данной элементарной струйки.

Легко изобразить уравнение Бернулли для рассматриваемого случая графически. Для этого следует, выбрав произвольную горизонтальную плоскость сравнения, отложить на ней в каждом сечении высоты ; ; ; и . Концы отрезков z, соединенные плавной кривой, покажут положение оси струйки. Соединяя концы отрезков плавной кривой, получим так называемую пьезометрическую линию. Отложив в каждом сечении вверх от пьезометрической линии отрезки, равные скоростным напорам , и соединив их концы плавной кривой, получим линию гидродинамического напора или, как ее часто называют, гидравлическую линию (рис. 2). Отрезки, равные расстояниям по вертикали от гидравлической линии до горизонтальной плоскости, проходящей над плоскостью сравнения на высоте, равной начальной удельной энергии, представляют собой потери энергии на гидравлические сопротивления на участке от начального до рассматриваемого сечения.

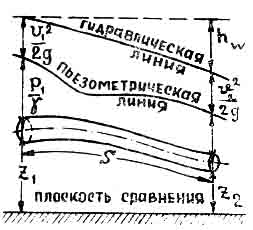
Рис. 2

Падение гидравлической линии на единицу длины элементарной струйки назовем гидравлическим уклоном I :

Гидравлический уклон (рис.3) есть всегда величина положительная, так как полная удельная энергия движущейся части жидкости постепенно уменьшается по мере ее продвижения вдоль элементарной струйки, затрачиваясь на преодоление сил трения, превращаясь в тепловую энергию и рассеиваясь.

Рис. 3

Понятие о плавно изменяющемся (медленно изменяющемся) движении жидкости

В общем случае при установившемся движении поток жидкости можно представить совокупностью элементарных струек, имеющих различные значения углов их расхождения и различные радиусы кривизны. Частный случай дви жения потока, при котором он испытывает слабую деформа цию, так что элементарные струйки остаются параллельными или почти параллельными друг другу (), а радиусы их кривизны принимают весьма большие значения (), называется плавно изменяющимся или медленно изменяющимся движением.

В плоскости живого сечения потока при плавно изме няющемся движении гидродинамические давления распределяются по законам гидростатики, а это значит, что в данном живом сечении удельная потенциальная энергия любой частицы есть величина постоянная:

Уравнение Д. Бернули для потока реальной жидкости.

Условия применимости уравнения Д. Бернули.

Распространим уравнение Бернулли на установившийся поток реальной жидкости. Для этого выберем на слабо деформированном участке потока живое сечение, вблизи которого движение можно считать плавноизменяющимся.

Через это сечение каждой элементарной струйкой за время dt вносится энергия, которая в соответствии с вышеизложенным оказывается равной:

Вынося за скобки вес жидкости, прошедшей через поперечное сечение элементарной струйки за;время dt , равный , перепишем это выражение в следующем виде:

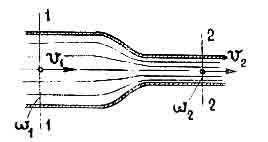
Рис. 4

Найдем полную энергию, проносимую потоком жидкости через живое сечение 1- 1. Для этого необходимо, очевидно, просуммировать полученное выражение по всем струйкам данного живого сечения. Тогда получим:

Таким образом, полная энергия оказывается равной сумме двух интегралов, представляющих собой соответственно потенциальную и кинетическую энергию потока.

Запишем второй интеграл в следующем виде:

Этот интеграл представляет собой, как уже указывалось, кинетическую энергию, проносимую потоком через сечение 1-1 за время dt . Для его вычисления необходимо знать, каким образом распределяются скорости движения частиц жидкости по живому сечению. Если вычислить кинетическую энергию потока в предположении о постоянстве этих скоростей (другими словами, по средней скорости потока в данном живом, сечении ), то получим:

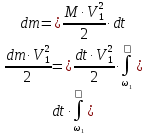
Это выражение по величине всегда меньше, чем действительная кинетическая энергия, вычисленная по действительным скоростям. Обозначим отношение этих двух величин :

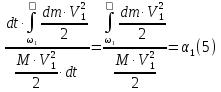
Так как на участке потока между сечениями 1-1 и 2-2 часть энергии потока затрачивается на преодоление гидравлических сопротивлений и необратимо превращается в тепловую энергию, . Очевидно также, что . Разница между этими удельными энергиями выразит потери удельной энергии потока на рассматриваемом участке движения:

После интегрирования и подстановки получим:

Коэффициент называется коэффициентом кинетической энергии потока и представляет собой отношение действитель ной кинетической энергии потока к кинетической энергии, вы численной в предположении, что скорости во всех точках живого сечения равны средней скорости потока. Очевидно, что этот коэффициент всегда больше единицы.

Полученное уравнение и есть уравнение Д. Бернули для установившегося потока реальной жидкости.

Лекция №8.

Гидравлические сопротивления.

Классификация гидравлических сопротивлений и потерь напора.

При движении реальной жидкости часть энергии потока затрачивается на преодоление гидравлических сопротивлений, которые подразделяются на два вида:

1) сопротивления по длине потока;

2) местные сопротивления.

Сопротивлениями по длине потока называются такие сопротивления, которые обусловливаются силами трения и зависят от длины потока.

Местными называются такие сопротивления, которые обусловливаются изменением направления или величины скорости в различных сечениях потока. Эти сопротивления вызываются кранами, задвижками, вентилями на трубах, внезапным расширением или сужением потока и т. д.

Часть энергии потока, которая затрачивается на преодоление гидравлических сопротивлений, называется потерями напора или потерями энергии.

Потери напора также подразделяются на два вида:

1) потери напора по длине потока, которые вызываются гидравлическими сопротивлениями по длине потока (h f );

2) местные потери напора, которые вызываются местными гидравлическими сопротивлениями (h i ). Общие потери напора:

h ω = . (1)

Потери напора существенно зависят от режима движения жидкости.

Ламинарный и турбулентный режимы движения жидкости.

Различают два режима движения жидкости: ламинарный и турбулентный.

При ламинарном режиме движения частицы жидкости движутся отдельными не смешивающимися друг с другом струйками. Примерами ламинарного движения являются: движение грунтовых вод, движение по трубопроводам жидкостей, обладающих большой вязкостью (мазут, нефть и т. д.), движение крови в кровеносных сосудах.

При турбулентном режиме движения отдельные струйки перемешиваются между собой. Турбулентное движение наблюдается в природе значительно чаще, чем ламинарное. Примером турбулентного движения является движение воды в реках, каналах, водопроводных трубах и т.д.

Слово «ламинарный» произошло от латинского слова lamina - пластинка, полоска, слой; слово «турбулентный» произошло от латинского слова turbulentus – беспорядочный.

На существование в природе двух режимов движения жидкости впервые указал выдающийся русский ученый профессор Д. И. Менделеев в 1880 г. в работе «О сопротивлении жидкости и воздухоплавании».

Экспериментальное изучение режимов движения было проведено английским ученым О. Рейнольдсом в 1883 г.

Опыт начинается с пропуска по трубе Д жидкости с малыми скоростями. Одновременно подается краска из бачка С. При этом получается следующая картина (рис. 1б): подкрашенная струйка имеет вид прямой горизонтальной лини, а остальная масса движущейся жидкости остается неокрашенной. Следовательно, в этом случае частицы подкрашенное струйки не перемешиваются с остальной жидкостью, и режим движения жидкости в трубе Д ламинарный.

При постепенном увеличении скорости в трубе Д наступает такой момент, когда подкрашенная струйка исчезает и вся движущаяся жидкость делается равномерно окрашенной. Это свидетельствует о том, что частицы жидкости в потоке перемешиваются, т. е. в трубе Д имеет место турбулентный режим (рис. 1в).

Рис. 1

Скорость, при которой один режим движения переходит в другой, называется критической. Различают две критические скорости: верхнюю критическую скорость V вк , при которой ламинарный режим движения переходит в турбулентный, и нижнюю критическую скорость V нк - при обратном переходе.

На основании экспериментального изучения режимов движения О.Рейнольдc дал критерий для установления того или иного режима движения.

Критерием для определения режима движения жидкости является так называемое число Рейнольдса, которое обозначается через Re и находится по формуле:

Где V – средняя скорость движения потока;

L – характерный геометрический размер живого сечения потока;

– кинематический коэффициент вязкости.

Число Рейнольдса, соответствующее верхней критической скорости, называется верхним критическим числом Рейнольдса и обозначается Re вк , при этом числе Рейнольдса ламинарный режим переходит в турбулентный.

Число Рейнольдса, соответствующее нижней критической скорости, называется нижним критическим числом Рейнольдса и обозначается Re нк ; при этом числе Рейнольдса турбулентный режим переходит в ламинарный.

Для напорного движения в трубопроводах опытами установлены следующие численные значения критического числа Рейнольдса:

Re d (нк) = 2000 2320;

Re d (вк) = 10000 13000.

Реальная жидкость обладает вязкостью, и при ее движении возникают сопротивления движения. Сопротивления движения обусловлены появлением сил внутреннего трения. При движении струйки реальной жидкости механическая энергия, содержащаяся в струйке, вдоль нее будет уменьшаться, так как часть ее будет расходоваться на преодоление сопротивления, .

Эта энергия затрачивается на некоторую необратимую работу, т.е. на работу сил трения, и она переходит в тепло, которое рассеивается.

Чем больше длина струйки, тем больше будут затраты энергии на преодоление сопротивления движения.

Энергия, расходуемая на работу сил трения , - потери механической энергии струйки, переходящие в теплоту. Потери энергии, отнесенные к единице веса жидкости при перемещении ее вдоль элементарной струйки, называются гидравлическими потерями (потерями удельной энергии)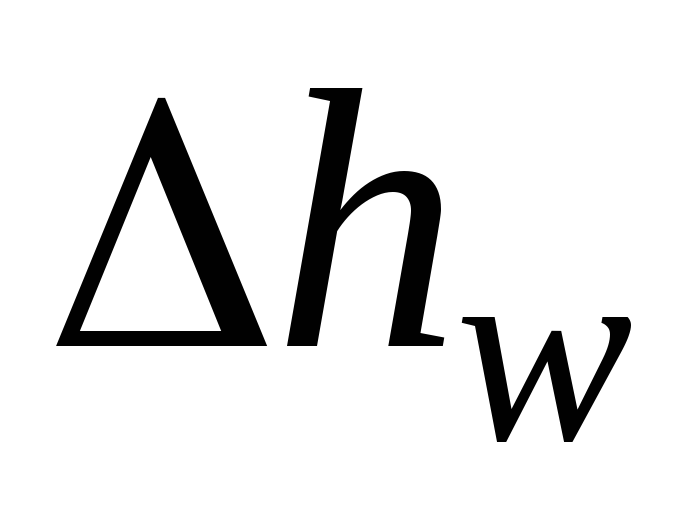

.

Рассмотрим струйку реальной жидкости при установившемся движении (рис. 3.8).

Рис. 3.8. К уравнению Бернулли для струйки реальной жидкости

Полная удельная механическая энергия реальной струйки в ее живых сечениях 1-1 и 2-2 составит

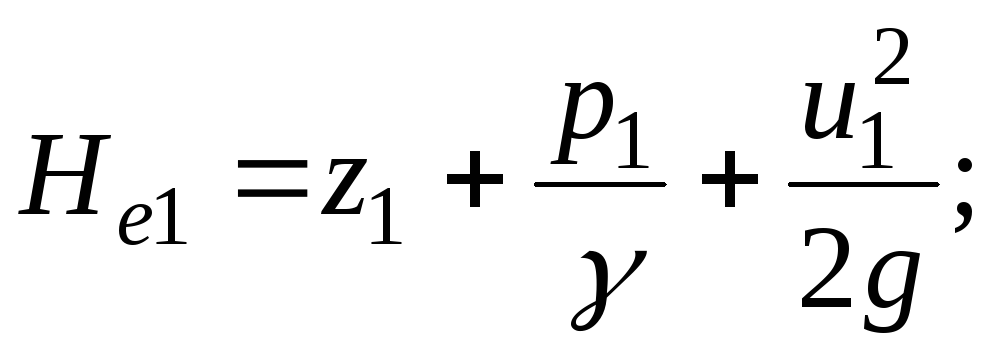
Потери удельной механической энергии, обусловленные трением, на участке живых сечений 1-1 и 2-2

(3.45)

Таким образом, уравнение Бернулли для элементарной струйки реальной жидкости в случае установившегося движения можно представить в виде

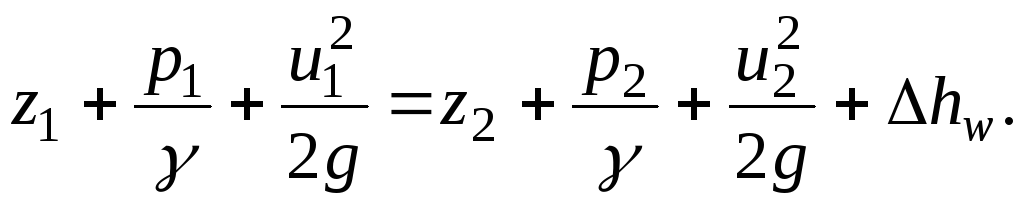(3.47)

Характеристикой движения жидкости является понятие пьезометрического и гидравлического уклонов.

На рис. 3.8 изображены кривые, характеризующие уравнение Бернулли. Линия, проходящая через точки, соответствующие значению пьезометрической высоты в живых сечениях 1-1 и 2-2, является пьезометрической линией .

Пьезометрическим уклоном называется изменение гидростатического напора жидкости вдоль струйки, отнесенное к единице длины. На участке струйки длиной 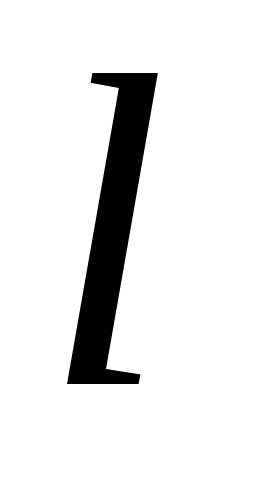между сечениями 1-1 и 2-2 пьезометрический уклон

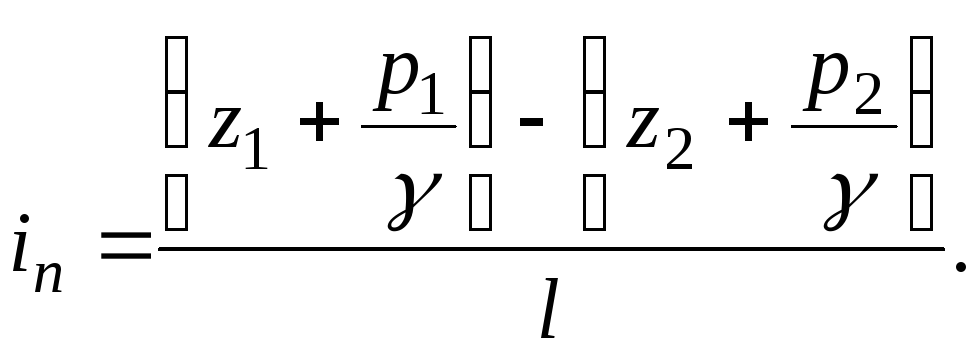(3.48)

Пьезометрический уклон, соответствующий бесконечно малой длине

(при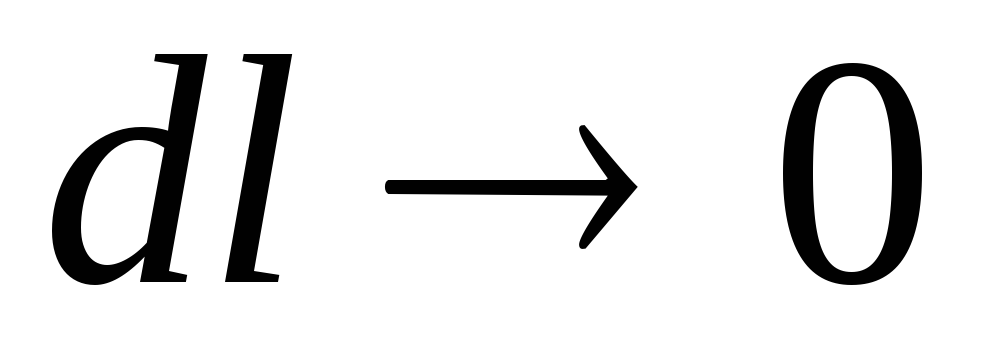

), - уклон в точке:

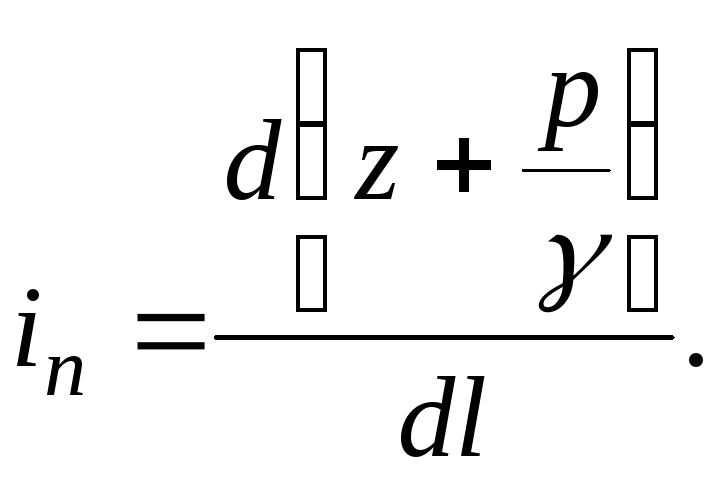(3.49)

Линия, проходящая через точки значений удельных механических энергий в живых сечениях струйки, является напорной линией (линией полного напора). Гидравлическим уклоном называется уменьшение полной удельной механической энергии вдоль струйки, отнесенное к единице длины:

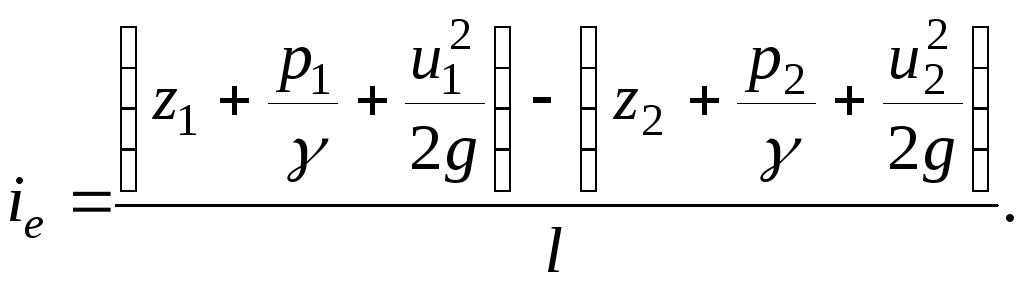(3.50)

При элементарном снижении удельной энергии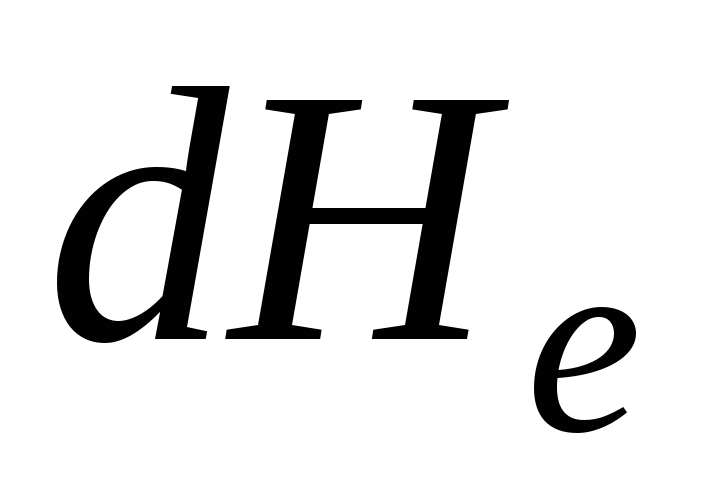

на бесконечно малом участке

гидравлический уклон

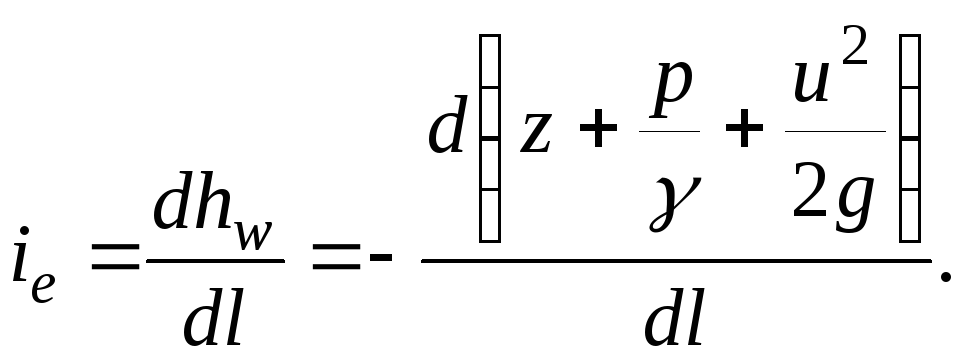(3.51)

Так как кривая полного напора убывает по длине струйки, то знак в выражении (3.51) минус [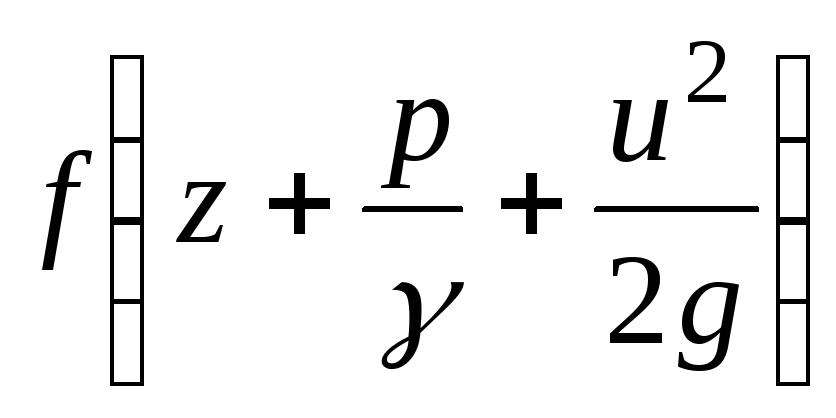

- убывающая функция].

В случае постоянства живых сечений по длине струйки пьезометрическая линия и линия полного напора параллельны.

3.9. Дифференциальные уравнения движения идеальной жидкости (уравнение эйлера)

В пространстве, заполненном движущейся идеальной жидкостью плотностью , выделим элементарный параллелепипед, ребра которого со сторонами

, ,

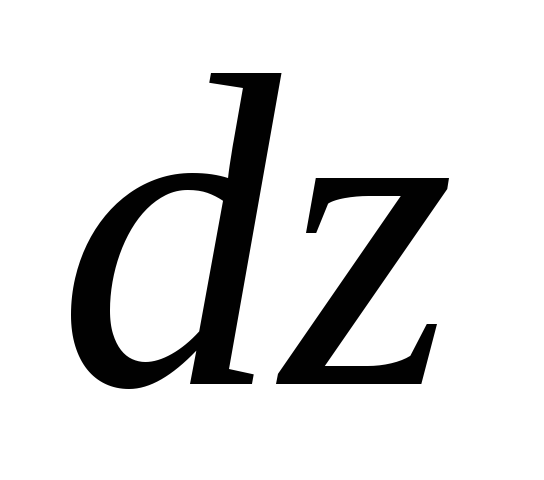параллельны осям координат (рис. 3.9). При движении идеальной жидкости отсутствуют силы внутреннего трения. Элементарный объем, находящийся в параллелепипеде, перемещается с абсолютной скоростью . Составляющие этой скорости по осям координат будут , , .

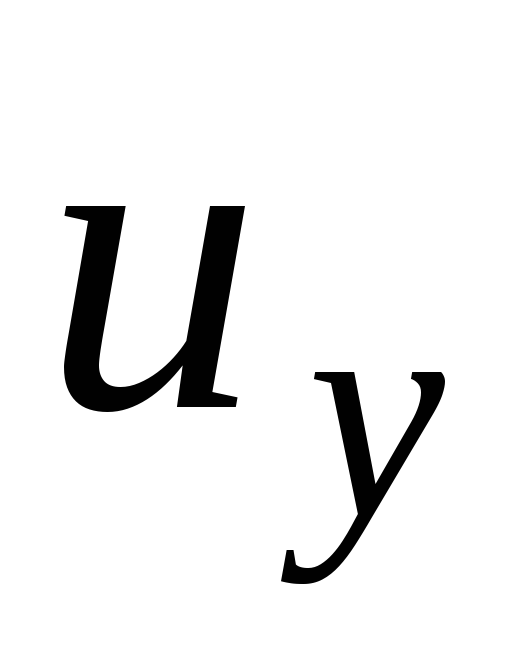На элементарный объем будут действовать массовые и поверхностные силы. Силы трения при движении параллелепипеда равны нулю.

Масса жидкости в элементарном объеме параллелепипеда

(3.52)

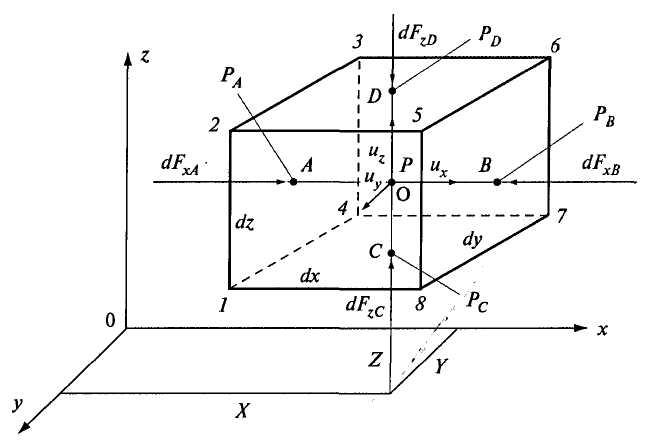
Рис. 3.9. К выводу уравнения движения Эйлера

Проекции массовых сил в направлении координатных осей:

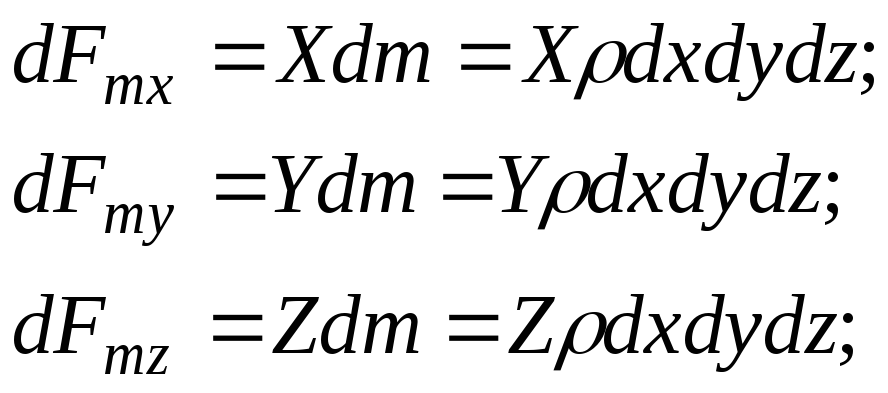(3.53)

где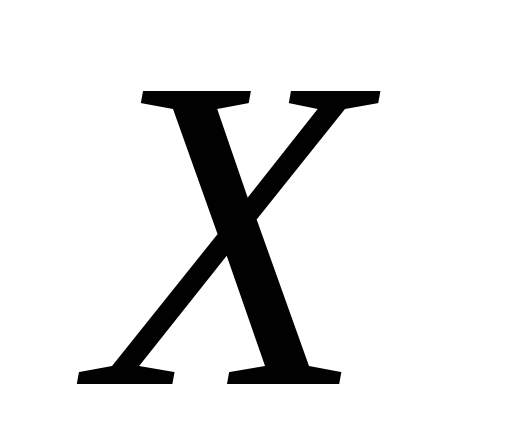

, , - компоненты единичных массовых сил относительно осей , , (проекции ускорения этих сил).

Поверхностные силы определяются давлением, приходящимся на грани параллелепипеда.

Пусть в центре тяжести параллелепипеда (т. О) гидростатическое давление равно 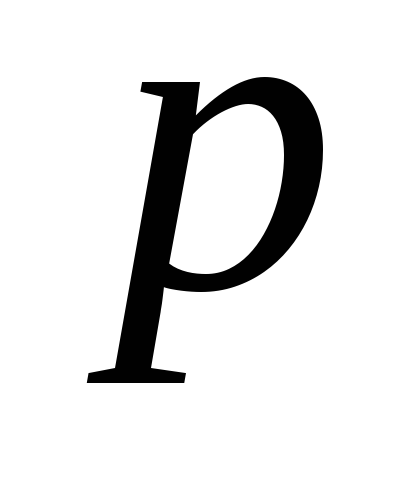, координаты этой точки , , .Скорость движения в этой точке . Составляющие этой скорости по осям координат равны , , .

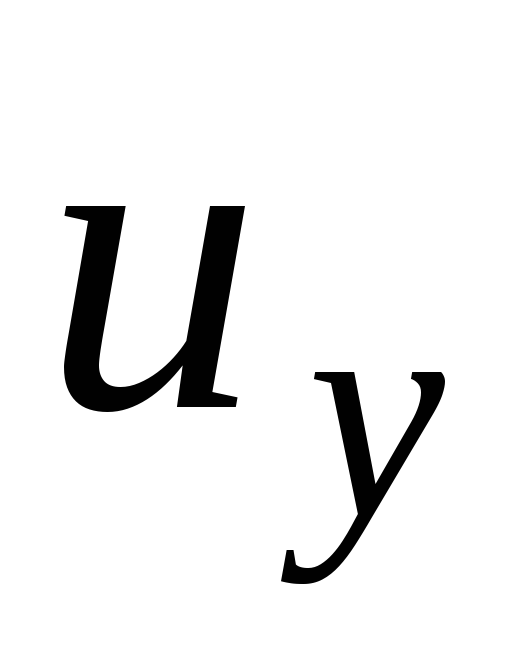Проведем через т. О горизонтальную линию, параллельную оси . Точки пересечения с гранями параллелепипеда А (грань 1234), В (грань 5678). Давление в этих точках по ос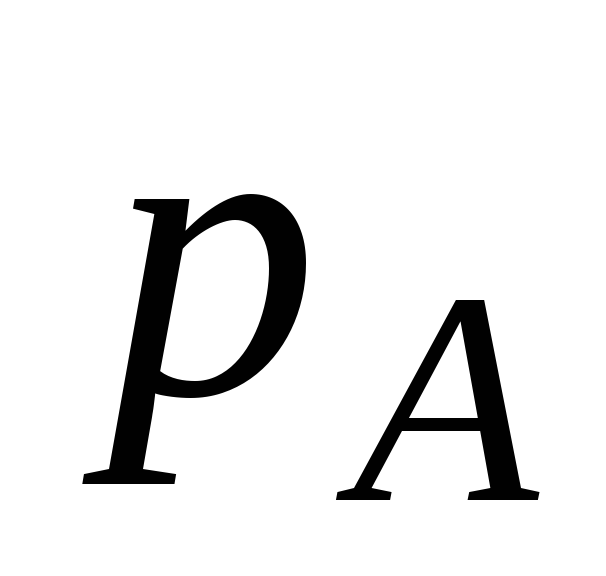и

и

.

В жидкой сплошной среде давление в точке выражается непрерывной сплошной функцией координат расположения точки в пространстве: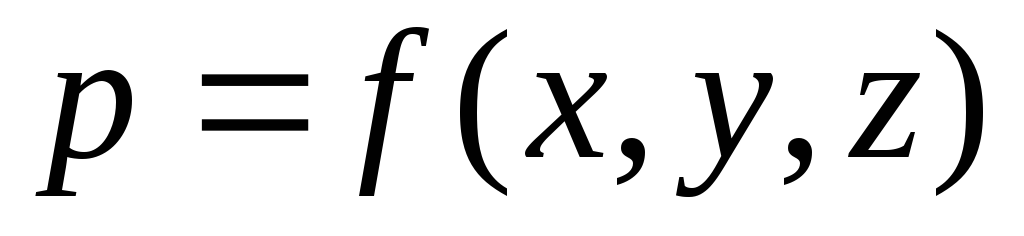

. Гидростатическое давление изменяется непрерывно линейно, и приращение давления на единицу элементарной длины

-

-



-

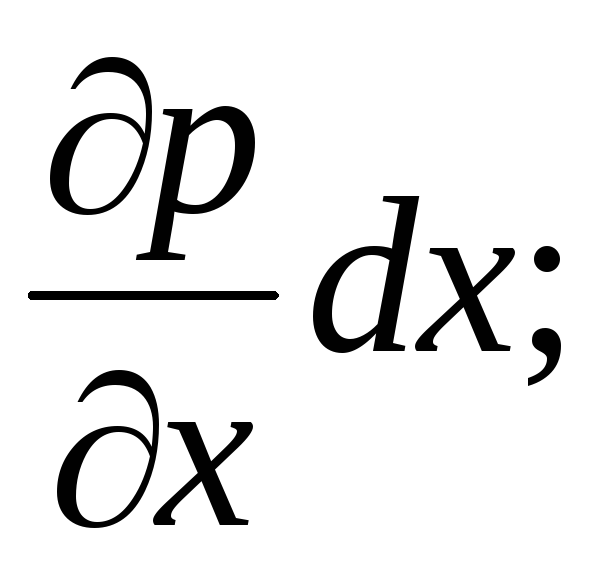
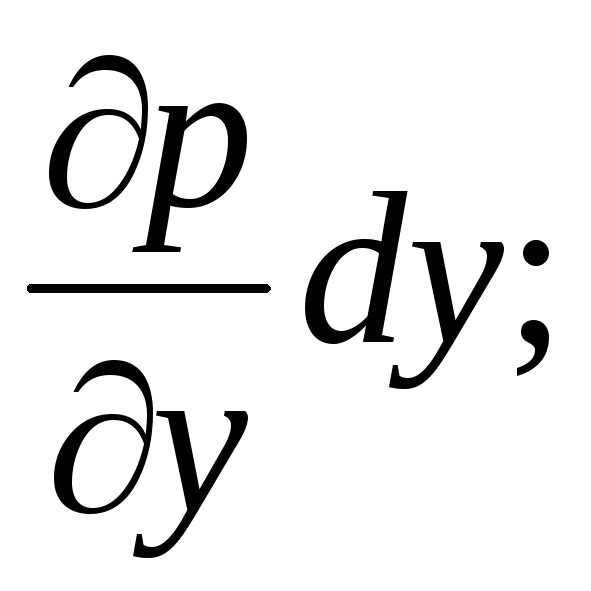
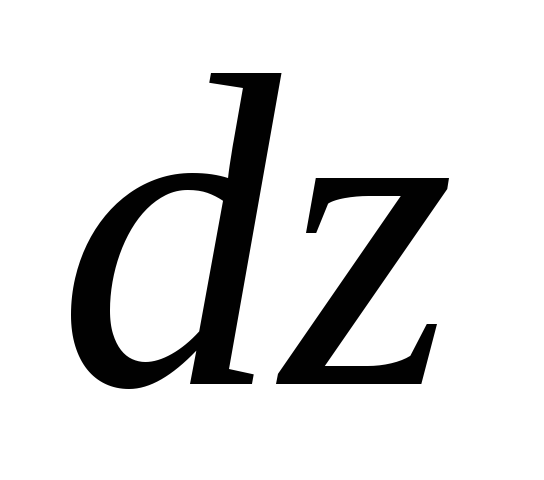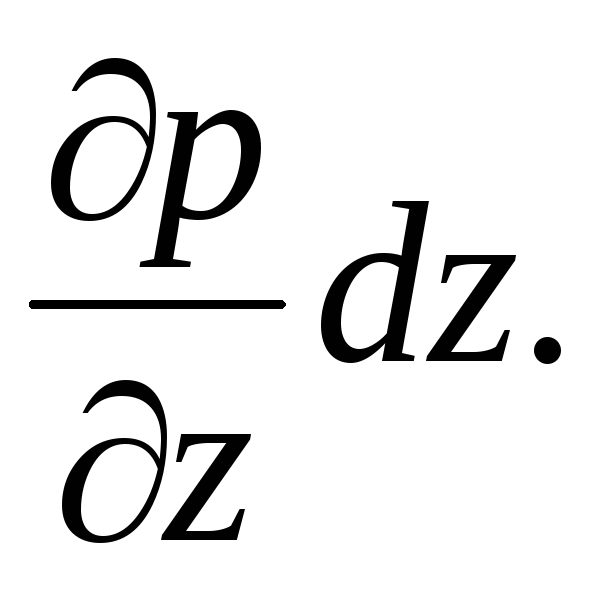
Следовательно, давления в точках А и В будут различаться на величину

.

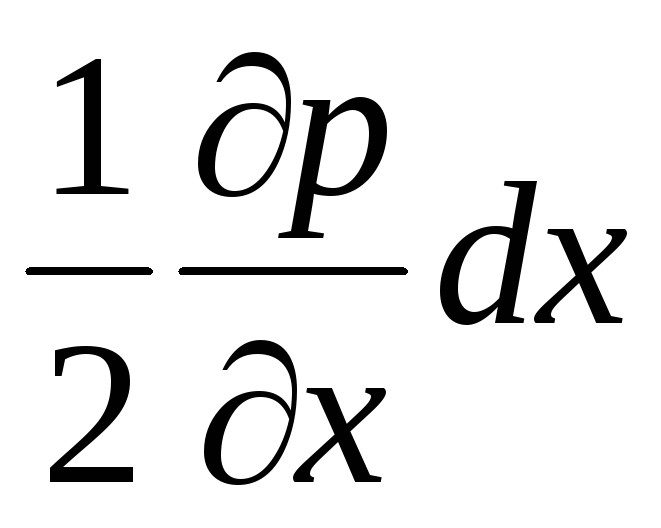Давления в точках А и В выразим в следующем виде:

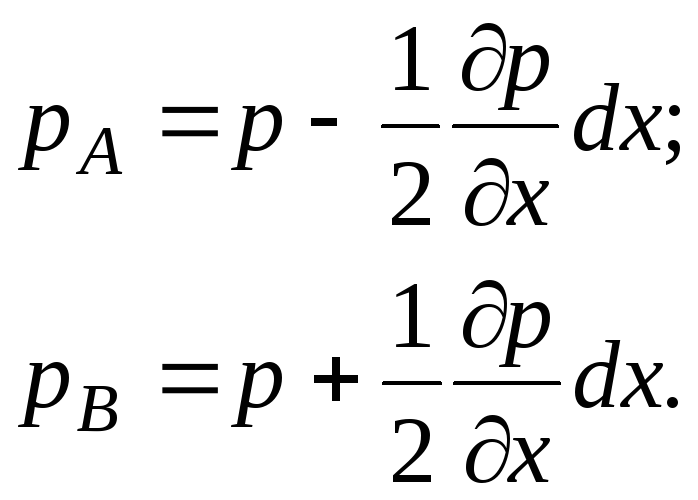(3.54)

Из-за малости площади граней можно считать, что давления

и

являются средними гидростатическими давлениями, действующими на грани 1234 и 5678. Поверхностные силы давления на эти грани по оси равны произведению давления на площади граней:

(3.55)

Аналогично поверхностные силы давления на грани по оси z (грани 1478и 2365):

(3.56)

Также можно определить поверхностные силы на грани по оси .

Рассмотрим равновесие параллелепипеда, находящегося в движущейся жидкости, используя принцип Даламбера .

Согласно принципу Даламбера уравнение движения можно рассматривать как уравнение равновесия, если ввести силы инерции. Полагаем, что параллелепипед массой

перемещается со скоростью , составляющие этой скорости , , .

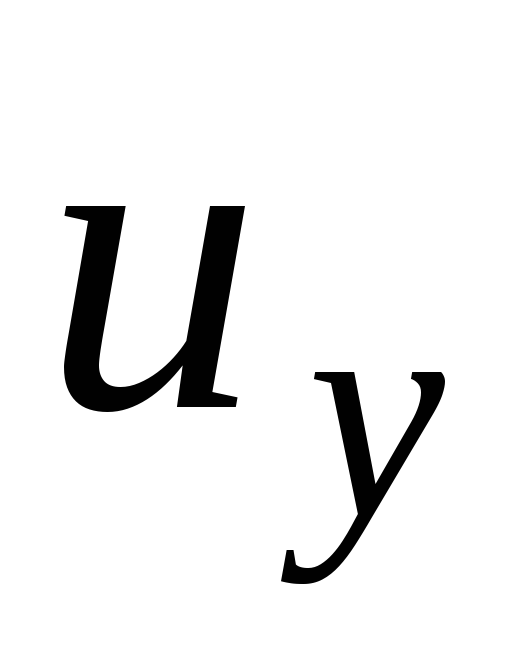Сила инерции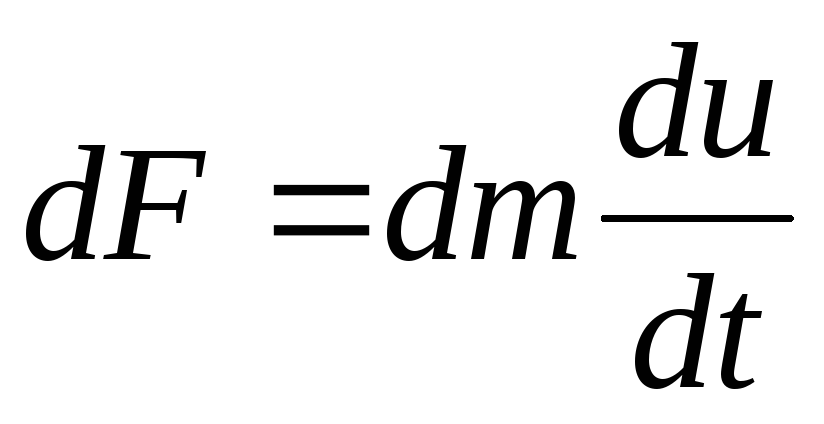

(- ускорение).

Проекции силы инерции на соответствующие координатные оси:

(3.57)

где 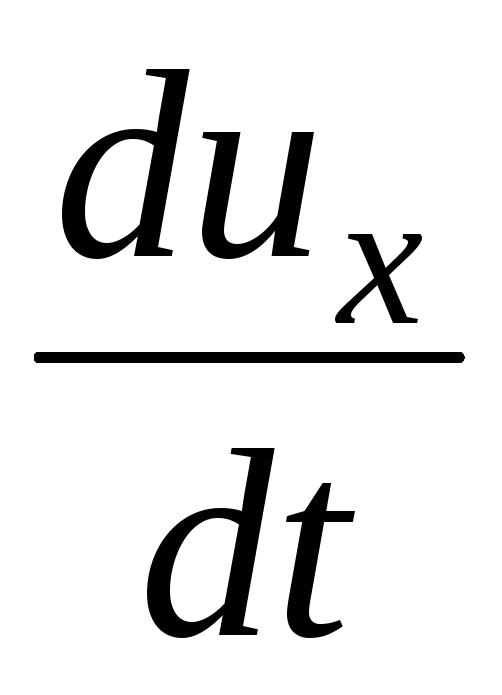,,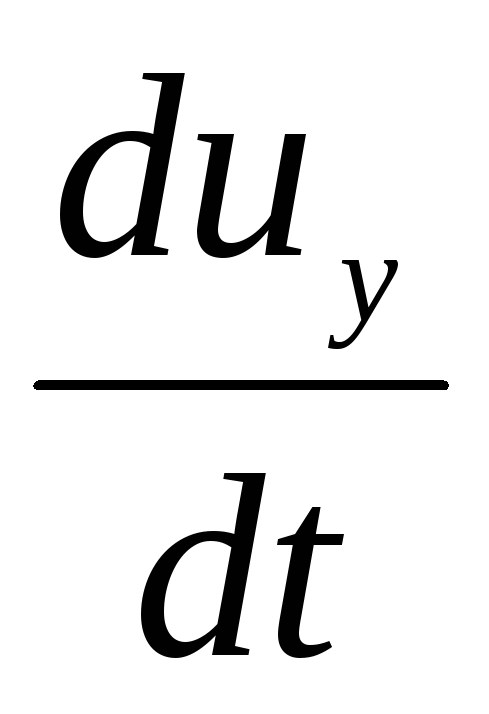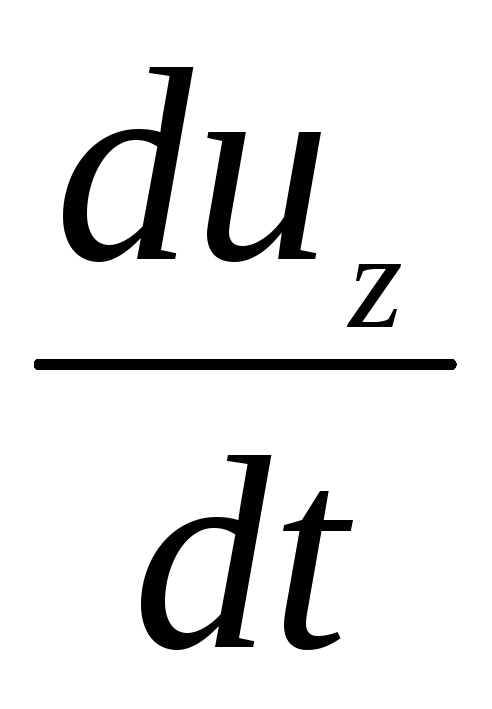- проекции ускорении на оси , , .

Составим уравнение равновесия для сил, действующих на рассматриваемый параллелепипед жидкости, с учетом силы инерции по осям и :

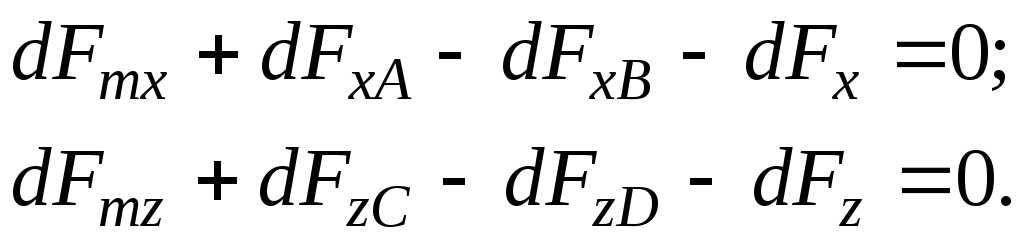(3.58)

Подставляя в (3.58) полученные ранее зависимости (3.53), (3.55), (3.56) и (3.57), получим следующие уравнения

Раскрыв скобки и разделив полученные выше уравнения на

, напишем

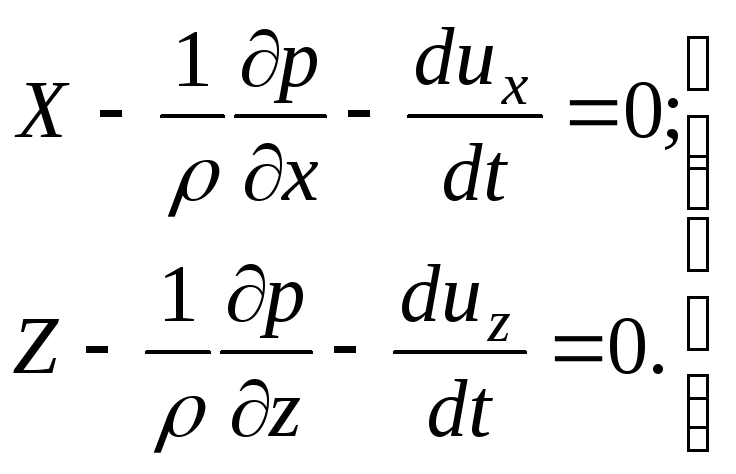(3.59)

Аналогично можно получить уравнение по оси у:

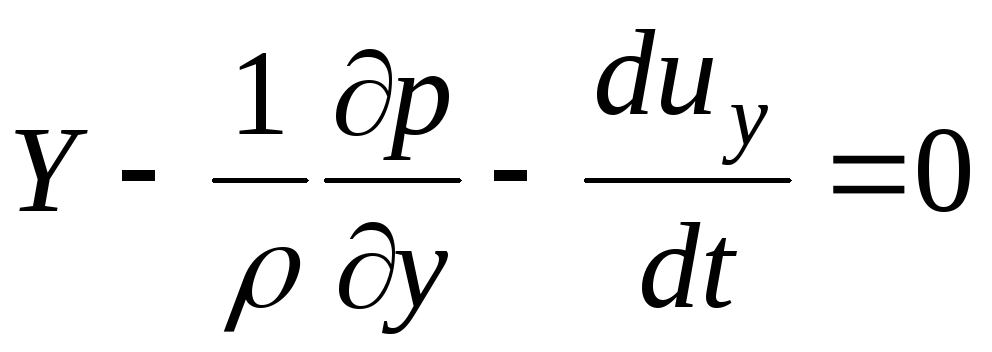(3.60)

Уравнения (3.59) и (3.60) можно записать в виде системы уравнений:

(3.61)

В общем случае величины , , 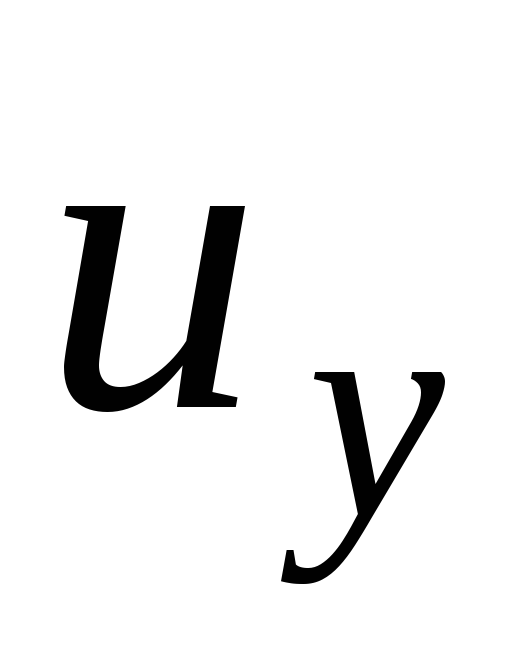являются функцией координат , , , а также времени . Следовательно, полный дифференциал скорости будет

Ускорение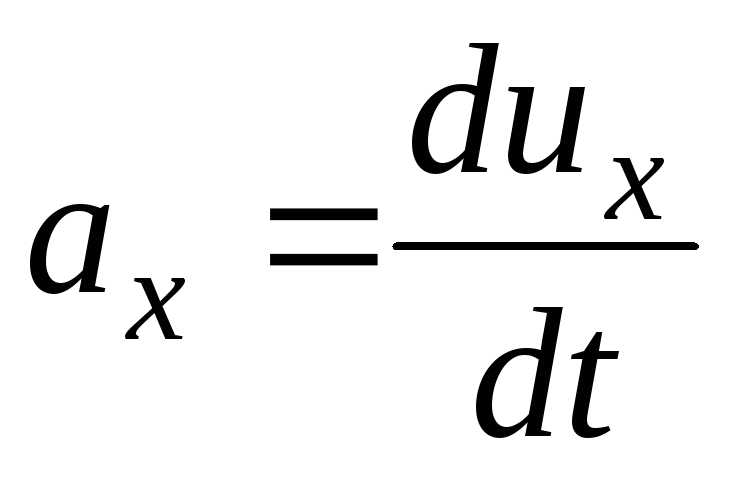

;

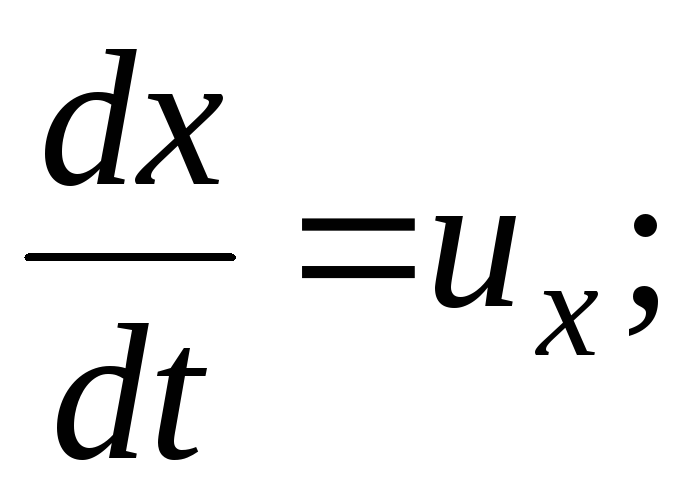
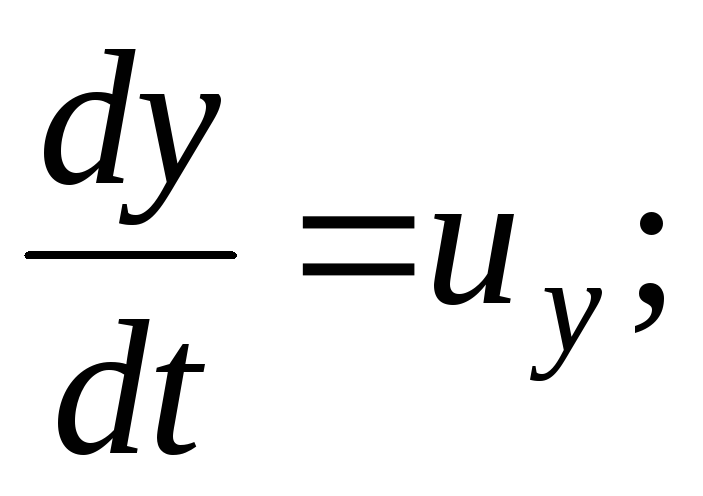
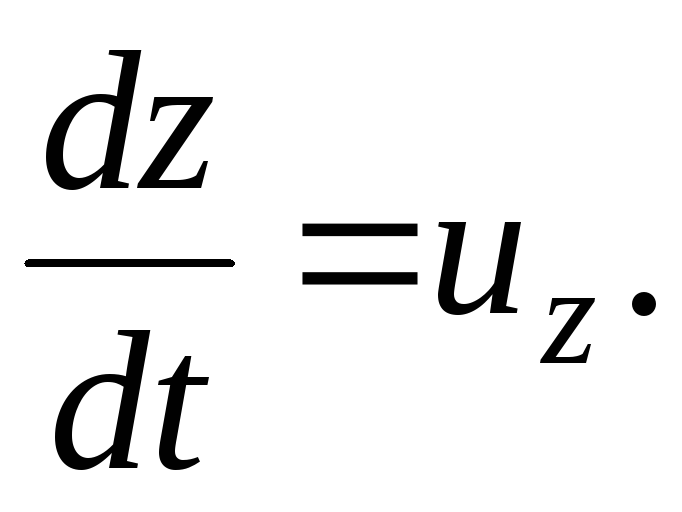
(3.64)

Аналогично можно получить дифференциалы скоростей ,.

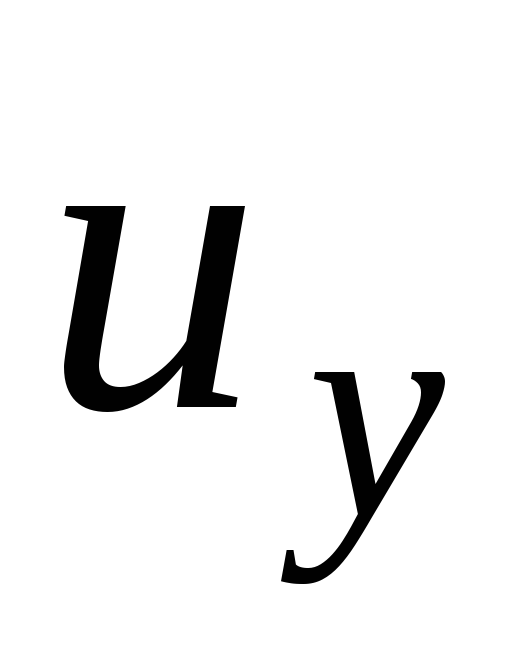После внесения в систему уравнений (3.61) дифференциалов скоросте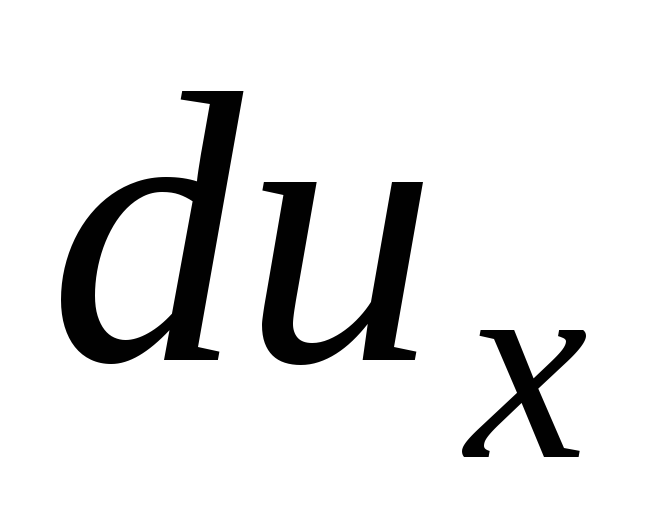й

,

и

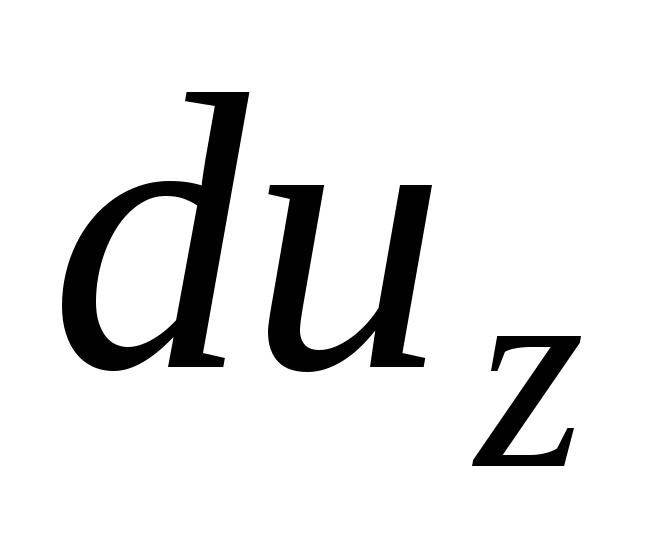она примет вид

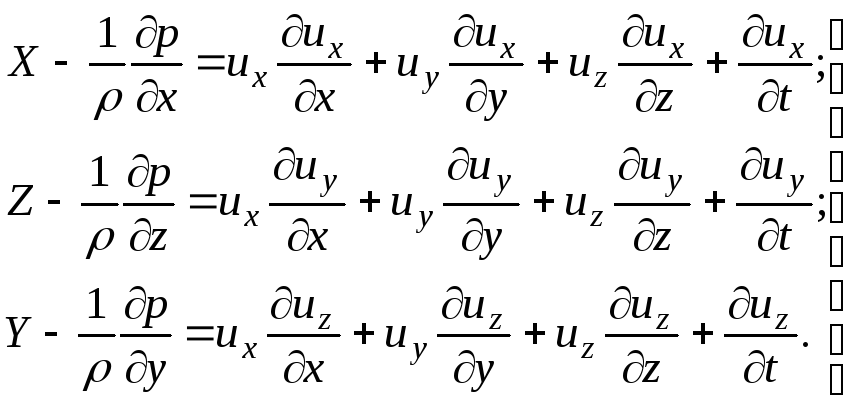(3.65)

В случае установившегося движения

;

;

. (3.66)

Уравнения (3.65) представляют собой дифференциальные уравнения движения идеальной (невязкой) жидкости - уравнения Эйлера . Эти уравнения были получены Эйлером в 1775 г.

Уравнения Эйлера выражают связь между проекциями действующих сил, скоростей, давления и плотности жидкости. Уравнения Эйлера очень важны при изучении движения жидкости.

Для жидкости, находящейся в покое, имеем

Дифференциальные уравнения Эйлера приобретают следующий вид:

(3.67)

Система дифференциальных уравнений является уравнениями равновесия жидкости.

Из уравнения равновесия можно получить основное уравнение гидростатики (2.2) (см. приложение).

Интегрирование уравнения движения Эйлера. Интеграл Бернулли

Рассмотрим установившееся движение идеальной жидкости. Уравнения Эйлера представим в виде (3.61). Умножим первое из уравнений на

, второе - на и третье - на

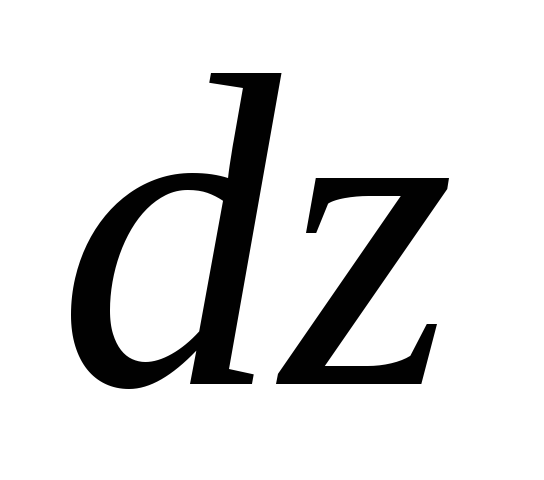, получим

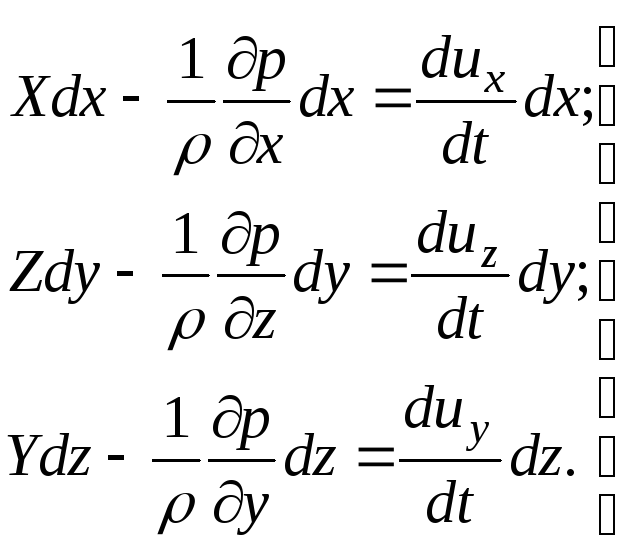(3.68)

Сложим почленно все три уравнения системы:

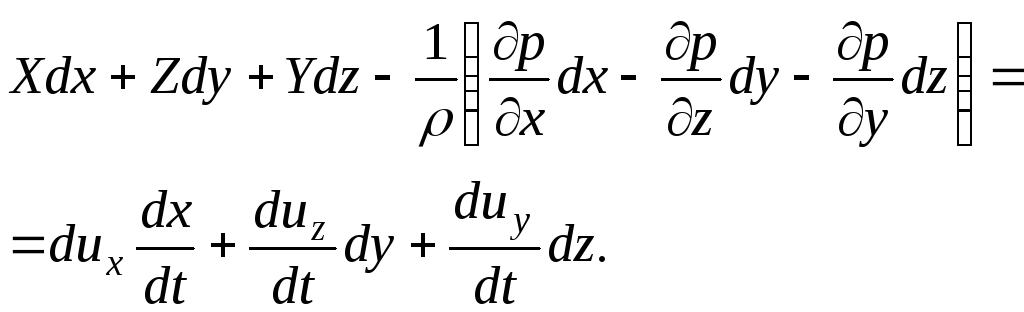(3.69)

Для установившегося движения давление 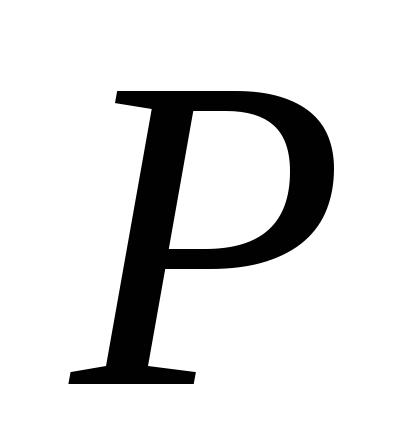в точке является функцией ее координат и не зависит от времени. Поэтому дифференциал давления выражается в частных производных:

.

Так как

;

и

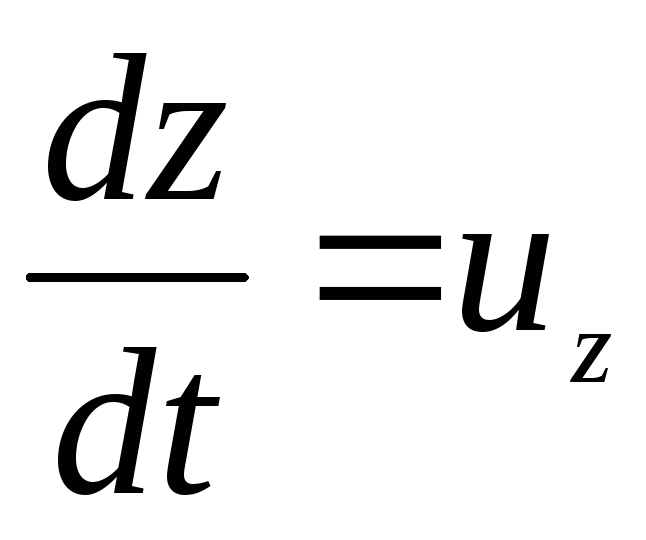, то последний член уравнения (3.69)

кроме того

;

;

.

Следовательно, правая часть уравнения (3.69) примет вид

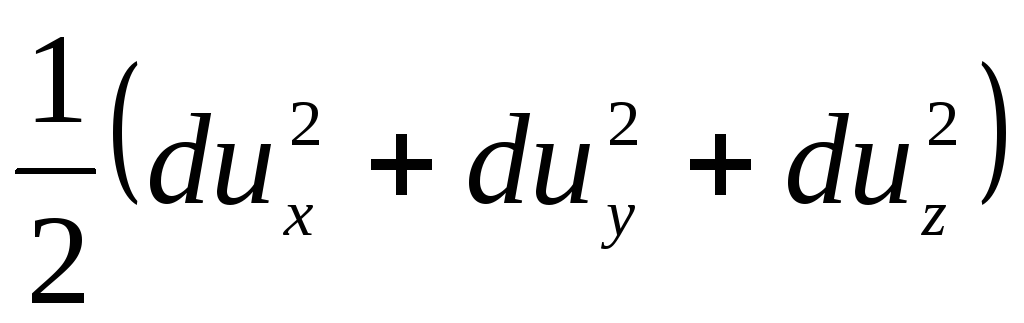. (3.71)

Полная (абсолютная) скорость и выражается через , , :

.

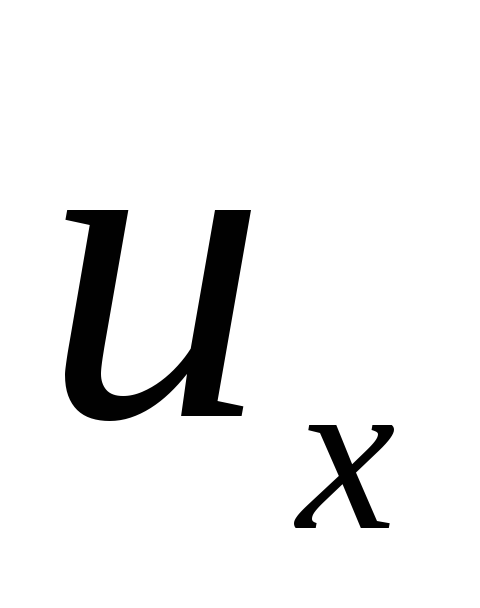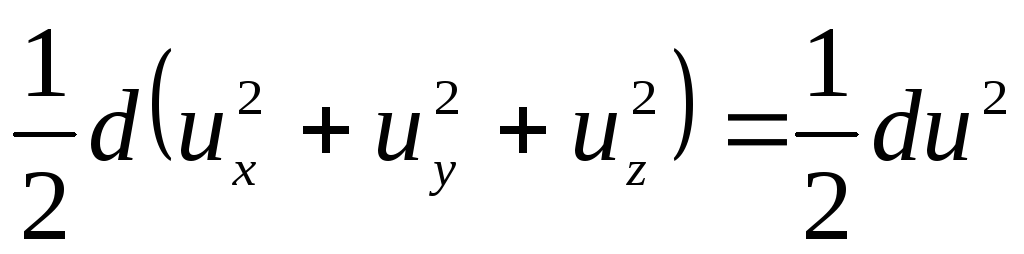. (3.72)

Уравнение (3.69) после преобразования можно переписать в следующем виде:

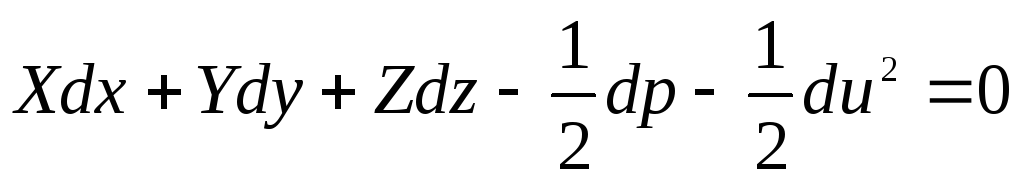. (3.73)

Первые три выражения в этом уравнении является полным дифференциалом силовой (потенциальной) функции:

Таким образом, уравнение (3.74) примет вид

. (3.75)

Проинтегрировав уравнение (3.75), получим

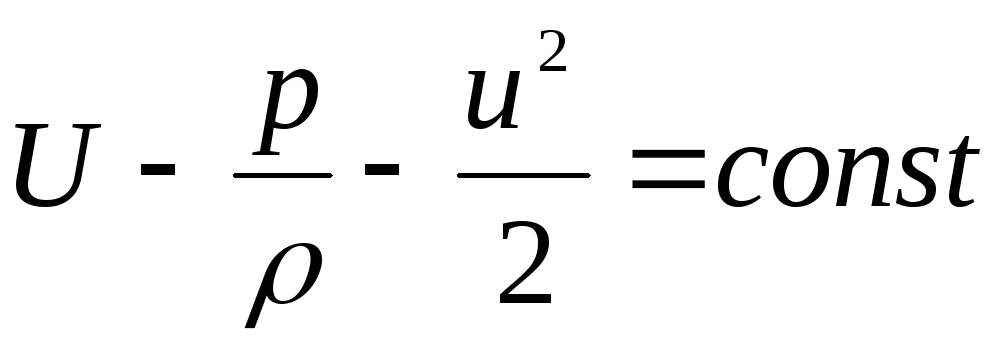. (3.76)

Данное выражение называют интегралом Бернулли-Эйлера.

Полученный трехчлен - уравнения сохраняет неизменное значение вдоль линии тока.

В случае когда движение происходит под действием только одной массовой силы - силы тяжести, то единичные массовые силы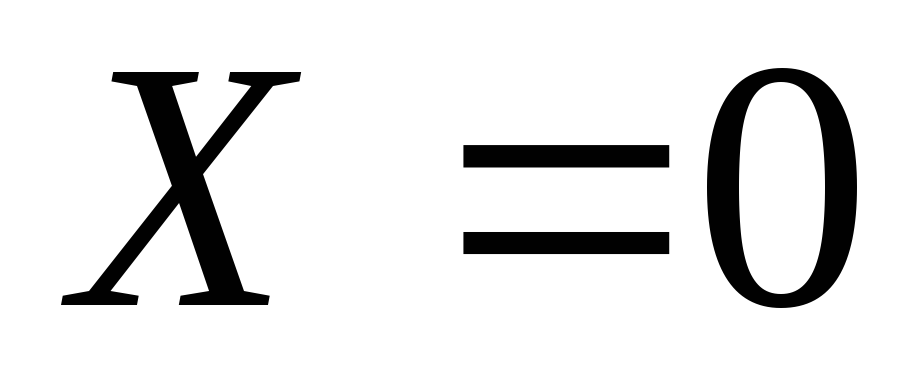

,

,

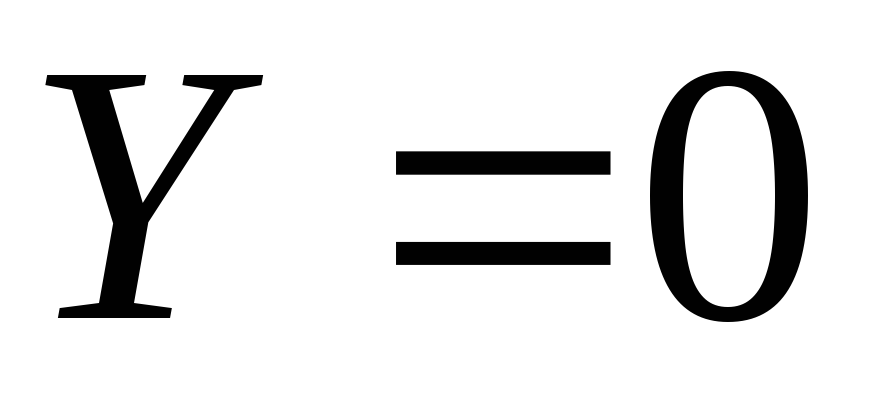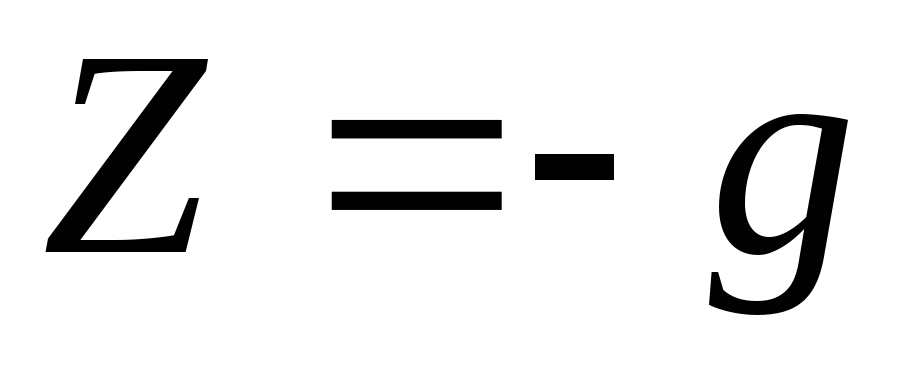(осьнаправлена вертикально вверх). Дифференциал силовой функции

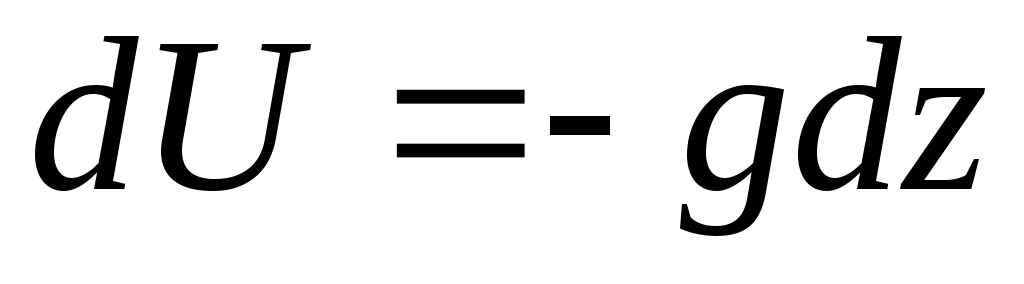. (3.77)

Уравнение (3.75) можно написать в следующем виде:

. (3.78)

Разделим все слагаемые уравнения на ускорение свободного падения , тогда получим

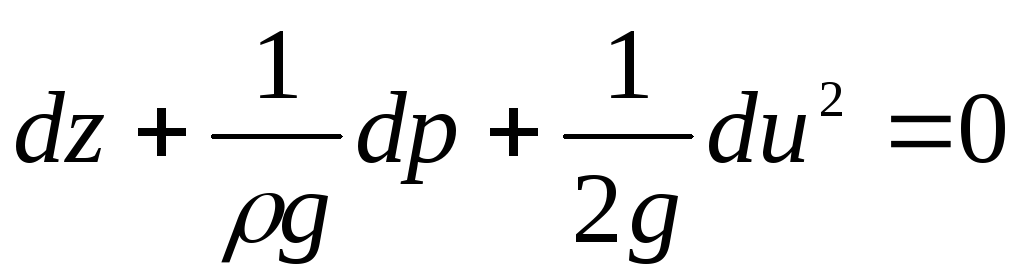. (3 79)

Приращение суммы всех трех членов этого уравнения при перемещении вдоль линии тока равно нулю.

Проинтегрировав дифференциальное уравнение (3.79), получим

. (3.80)

Сумма всех членов вдоль линии тока жидкости - величина постоянная, а следовательно, и вдоль идеальной элементарной струйки она также постоянна.

Уравнение (3.80), полученное с помощью уравнения движения Эйлера, для установившегося движения является уравнением Бернулли. Идентичное уравнение было получено ранее иным путем с использованием теоремы кинетической энергии (3.43).

Уравнение (3.80), записанное для двух живых сечений струйки, приобретает известный ранее вид

.
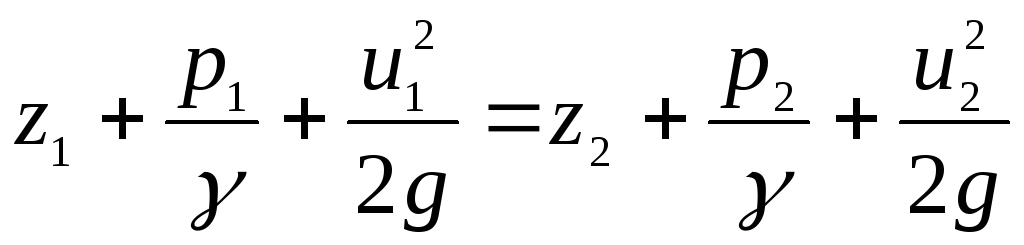