Nehmen wir an, Achilles läuft zehnmal schneller als die Schildkröte und ist ihr tausend Schritte hinterher. In der Zeit, in der Achilles diese Strecke läuft, kriecht die Schildkröte hundert Schritte in die gleiche Richtung. Wenn Achilles hundert Schritte gelaufen ist, kriecht die Schildkröte weitere zehn Schritte und so weiter. Der Prozess wird auf unbestimmte Zeit fortgesetzt, Achilles wird die Schildkröte niemals einholen.
Diese Argumentation wurde zu einem logischen Schock für alle nachfolgenden Generationen. Aristoteles, Diogenes, Kant, Hegel, Gilbert... Alle betrachteten sie auf die eine oder andere Weise als Zenons Aporien. Der Schock war so stark, dass " ... die Diskussionen werden derzeit fortgesetzt, die wissenschaftliche Gemeinschaft hat es noch nicht geschafft, zu einer gemeinsamen Meinung über das Wesen von Paradoxien zu gelangen ... mathematische Analyse, Mengenlehre, neue physikalische und philosophische Ansätze waren an der Untersuchung des Problems beteiligt ; keiner von ihnen wurde zu einer allgemein akzeptierten Lösung des Problems ..."[Wikipedia," Zenos Aporien "]. Jeder versteht, dass er getäuscht wird, aber niemand versteht, was die Täuschung ist.
Aus mathematischer Sicht hat Zenon in seiner Aporie den Übergang vom Wert zu deutlich demonstriert. Dieser Übergang impliziert die Anwendung anstelle von Konstanten. Soweit ich weiß, ist der mathematische Apparat zur Anwendung variabler Maßeinheiten entweder noch nicht entwickelt oder auf Zenos Aporie nicht angewendet worden. Die Anwendung unserer üblichen Logik führt uns in eine Falle. Durch die Trägheit des Denkens wenden wir konstante Zeiteinheiten auf den Kehrwert an. Physikalisch sieht das wie eine Verlangsamung der Zeit aus, bis sie in dem Moment, in dem Achilles die Schildkröte einholt, komplett zum Stillstand kommt. Wenn die Zeit stehen bleibt, kann Achilles die Schildkröte nicht mehr überholen.
Wenn wir die gewohnte Logik umdrehen, ergibt sich alles. Achilles läuft mit konstanter Geschwindigkeit. Jedes nachfolgende Segment seines Weges ist zehnmal kürzer als das vorherige. Dementsprechend ist die Zeit, die für die Überwindung aufgewendet wird, zehnmal kürzer als die vorherige. Wenn wir in dieser Situation den Begriff „Unendlichkeit“ anwenden, dann wäre es richtig zu sagen „Achilles wird die Schildkröte unendlich schnell überholen“.
Wie vermeidet man diese logische Falle? Bleiben Sie in konstanten Zeiteinheiten und wechseln Sie nicht zu reziproken Werten. In Zenos Sprache sieht das so aus:
In der Zeit, die Achilles braucht, um tausend Schritte zu laufen, kriecht die Schildkröte hundert Schritte in die gleiche Richtung. Während des nächsten Zeitintervalls, gleich dem ersten, wird Achilles weitere tausend Schritte laufen und die Schildkröte wird hundert Schritte kriechen. Jetzt ist Achilles der Schildkröte achthundert Schritte voraus.
Dieser Ansatz beschreibt die Realität angemessen ohne logische Paradoxien. Dies ist jedoch keine vollständige Lösung des Problems. Einsteins Aussage über die Unüberwindbarkeit der Lichtgeschwindigkeit ist Zenos Aporie „Achilles und die Schildkröte“ sehr ähnlich. Wir müssen dieses Problem noch untersuchen, überdenken und lösen. Und die Lösung muss nicht in unendlich großen Zahlen, sondern in Maßeinheiten gesucht werden.
Eine weitere interessante Aporie von Zeno erzählt von einem fliegenden Pfeil:
Ein fliegender Pfeil ist bewegungslos, da er zu jedem Zeitpunkt ruht, und da er zu jedem Zeitpunkt ruht, ruht er immer.
In dieser Aporie wird das logische Paradoxon sehr einfach überwunden – es genügt zu verdeutlichen, dass der fliegende Pfeil zu jedem Zeitpunkt an verschiedenen Punkten im Raum ruht, was tatsächlich Bewegung ist. Hier ist noch ein weiterer Punkt zu beachten. Aus einem Foto eines Autos auf der Straße kann weder die Tatsache seiner Bewegung noch die Entfernung zu ihm bestimmt werden. Um die Tatsache der Bewegung des Autos zu bestimmen, werden zwei Fotos benötigt, die vom selben Punkt zu unterschiedlichen Zeitpunkten aufgenommen wurden, aber sie können nicht zur Bestimmung der Entfernung verwendet werden. Um die Entfernung zum Auto zu bestimmen, benötigen Sie zwei Fotos, die gleichzeitig von verschiedenen Punkten im Weltraum aufgenommen wurden, aber Sie können daraus nicht die Tatsache der Bewegung bestimmen (Sie benötigen natürlich noch zusätzliche Daten für Berechnungen, die Trigonometrie hilft Ihnen). . Was ich besonders hervorheben möchte, ist, dass zwei Zeitpunkte und zwei Punkte im Raum zwei verschiedene Dinge sind, die nicht verwechselt werden sollten, da sie unterschiedliche Möglichkeiten der Erforschung bieten.
Mittwoch, 4. Juli 2018
Sehr gut sind die Unterschiede zwischen Menge und Multimenge in Wikipedia beschrieben. Wir schauen.
Wie Sie sehen können, "kann die Menge nicht zwei identische Elemente haben", aber wenn es identische Elemente in der Menge gibt, wird eine solche Menge als "Multimenge" bezeichnet. Vernünftige Wesen werden niemals eine solche Logik der Absurdität verstehen. Dies ist die Ebene sprechender Papageien und abgerichteter Affen, auf der der Verstand dem Wort „vollständig“ abwesend ist. Mathematiker agieren als gewöhnliche Trainer und predigen uns ihre absurden Ideen.
Es war einmal, dass die Ingenieure, die die Brücke gebaut haben, während der Tests der Brücke in einem Boot unter der Brücke waren. Wenn die Brücke einstürzte, starb der mittelmäßige Ingenieur unter den Trümmern seiner Schöpfung. Wenn die Brücke der Belastung standhalten konnte, baute der begabte Ingenieur andere Brücken.
So sehr sich Mathematiker auch hinter dem Satz „wohlgemerkt, ich bin im Haus“ oder vielmehr „Mathematik studiert abstrakte Konzepte“ verstecken, es gibt eine Nabelschnur, die sie untrennbar mit der Realität verbindet. Diese Nabelschnur ist Geld. Wenden wir die mathematische Mengenlehre auf Mathematiker selbst an.
Wir haben sehr gut Mathematik studiert und jetzt sitzen wir an der Kasse und zahlen Gehälter aus. Hier kommt ein Mathematiker auf sein Geld zu uns. Wir zählen ihm den gesamten Betrag vor und legen ihn auf unserem Tisch in verschiedenen Stapeln aus, in die wir Scheine der gleichen Stückelung legen. Dann nehmen wir von jedem Stapel einen Schein und geben dem Mathematiker seinen „mathematischen Gehaltssatz“. Wir erklären die Mathematik, dass er die restlichen Rechnungen nur erhält, wenn er beweist, dass die Menge ohne identische Elemente nicht gleich der Menge mit identischen Elementen ist. Hier beginnt der Spaß.
Zunächst einmal wird die Logik der Abgeordneten funktionieren: "Sie können es auf andere anwenden, aber nicht auf mich!" Außerdem wird zugesichert, dass auf Banknoten derselben Stückelung unterschiedliche Banknotennummern vorhanden sind, was bedeutet, dass sie nicht als identische Elemente angesehen werden können. Nun, wir zählen das Gehalt in Münzen - es gibt keine Zahlen auf den Münzen. Hier erinnert sich der Mathematiker hektisch an die Physik: Verschiedene Münzen haben unterschiedlich viel Schmutz, die Kristallstruktur und Anordnung der Atome für jede Münze ist einzigartig ...
Und jetzt habe ich die interessanteste Frage: Wo ist die Grenze, ab der Elemente einer Multimenge zu Elementen einer Menge werden und umgekehrt? Eine solche Linie gibt es nicht - alles wird von Schamanen entschieden, die Wissenschaft ist hier nicht einmal annähernd.
Schau hier. Wir wählen Fußballstadien mit gleicher Spielfeldfläche aus. Die Fläche der Felder ist gleich, was bedeutet, dass wir eine Multimenge haben. Aber wenn wir die Namen der gleichen Stadien betrachten, bekommen wir viel, weil die Namen unterschiedlich sind. Wie Sie sehen können, ist dieselbe Menge von Elementen gleichzeitig eine Menge und eine Multimenge. Wie richtig? Und hier holt der Mathematiker-Schamane-Schüler ein Trumpf-Ass aus seinem Ärmel und beginnt uns entweder von einem Set oder einem Multiset zu erzählen. Auf jeden Fall wird er uns davon überzeugen, dass er Recht hat.
Um zu verstehen, wie moderne Schamanen mit der Mengentheorie arbeiten und sie an die Realität binden, genügt es, eine Frage zu beantworten: Wie unterscheiden sich die Elemente einer Menge von den Elementen einer anderen Menge? Ich werde es Ihnen zeigen, ohne „als nicht ein Ganzes denkbar“ oder „nicht als ein Ganzes denkbar“.
Sonntag, 18. März 2018
Die Quersumme einer Zahl ist ein Schamanentanz mit Tamburin, der nichts mit Mathematik zu tun hat. Ja, im Mathematikunterricht wird uns beigebracht, die Summe der Ziffern einer Zahl zu finden und zu verwenden, aber dafür sind sie Schamanen, um ihren Nachkommen ihre Fähigkeiten und Weisheit beizubringen, sonst sterben Schamanen einfach aus.
Benötigen Sie einen Nachweis? Öffnen Sie Wikipedia und versuchen Sie, die Seite „Summe der Ziffern einer Zahl“ zu finden. Sie existiert nicht. In der Mathematik gibt es keine Formel, mit der man die Quersumme einer beliebigen Zahl ermitteln kann. Schließlich sind Zahlen grafische Symbole, mit denen wir Zahlen schreiben, und in der Sprache der Mathematik klingt die Aufgabe so: „Finde die Summe von grafischen Symbolen, die eine beliebige Zahl darstellen.“ Mathematiker können dieses Problem nicht lösen, aber Schamanen können es elementar.
Lassen Sie uns herausfinden, was und wie wir tun, um die Summe der Ziffern einer bestimmten Zahl zu finden. Nehmen wir also an, wir haben die Zahl 12345. Was muss getan werden, um die Quersumme dieser Zahl zu finden? Betrachten wir alle Schritte der Reihe nach.
1. Notieren Sie die Nummer auf einem Blatt Papier. Was haben wir getan? Wir haben die Zahl in ein grafisches Zahlensymbol umgewandelt. Dies ist keine mathematische Operation.
2. Wir schneiden ein empfangenes Bild in mehrere Bilder mit separaten Nummern. Das Schneiden eines Bildes ist keine mathematische Operation.
3. Wandeln Sie einzelne Grafikzeichen in Zahlen um. Dies ist keine mathematische Operation.
4. Addieren Sie die resultierenden Zahlen. Das ist jetzt Mathematik.
Die Quersumme der Zahl 12345 ist 15. Dies sind die „Schneide- und Nähkurse“ von Schamanen, die von Mathematikern verwendet werden. Aber das ist noch nicht alles.
Aus mathematischer Sicht spielt es keine Rolle, in welchem Zahlensystem wir die Zahl schreiben. In verschiedenen Zahlensystemen ist die Summe der Ziffern derselben Zahl also unterschiedlich. In der Mathematik wird das Zahlensystem als Index rechts neben der Zahl angegeben. Bei einer großen Zahl von 12345 möchte ich mir nicht den Kopf verdrehen, betrachten Sie die Zahl 26 aus dem Artikel darüber. Lassen Sie uns diese Zahl in binären, oktalen, dezimalen und hexadezimalen Zahlensystemen schreiben. Wir werden nicht jeden Schritt unter die Lupe nehmen, das haben wir bereits getan. Schauen wir uns das Ergebnis an.
Wie Sie sehen können, ist in verschiedenen Zahlensystemen die Summe der Ziffern derselben Zahl unterschiedlich. Dieses Ergebnis hat nichts mit Mathematik zu tun. Es ist genauso, als würde man bei der Bestimmung der Fläche eines Rechtecks in Metern und Zentimetern ganz andere Ergebnisse erhalten.
Die Null sieht in allen Zahlensystemen gleich aus und hat keine Quersumme. Dies ist ein weiteres Argument dafür, dass . Eine Frage an die Mathematiker: Wie bezeichnet man in der Mathematik das, was keine Zahl ist? Was existiert für Mathematiker nur aus Zahlen? Für Schamanen kann ich das zulassen, aber für Wissenschaftler nicht. Realität besteht nicht nur aus Zahlen.
Das erhaltene Ergebnis sollte als Beweis dafür angesehen werden, dass Zahlensysteme Maßeinheiten für Zahlen sind. Schließlich können wir Zahlen mit unterschiedlichen Maßeinheiten nicht vergleichen. Wenn gleiche Handlungen mit unterschiedlichen Maßeinheiten derselben Größe nach dem Vergleich zu unterschiedlichen Ergebnissen führen, dann hat das nichts mit Mathematik zu tun.
Was ist echte Mathematik? Dies ist der Fall, wenn das Ergebnis einer mathematischen Aktion nicht vom Wert der Zahl, der verwendeten Maßeinheit und davon abhängt, wer diese Aktion ausführt.
Autsch! Ist das nicht die Damentoilette?
- Junge Frau! Dies ist ein Labor zum Studium der unbestimmten Heiligkeit der Seelen beim Aufstieg in den Himmel! Nimbus oben und Pfeil nach oben. Welche andere Toilette?
Weiblich ... Ein Heiligenschein oben und ein Pfeil nach unten sind männlich.
Wenn Sie ein solches Designkunstwerk mehrmals täglich vor Augen haben,
Dann ist es nicht verwunderlich, dass Sie plötzlich ein seltsames Symbol in Ihrem Auto finden:
Ich persönlich gebe mir Mühe, bei einer kackenden Person (ein Bild) minus vier Grad zu sehen (Zusammensetzung mehrerer Bilder: Minuszeichen, Zahl vier, Gradbezeichnung). Und ich halte dieses Mädchen nicht für einen Narren, der keine Physik versteht. Sie hat nur ein Bogenstereotyp der Wahrnehmung von grafischen Bildern. Und Mathematiker lehren uns das ständig. Hier ist ein Beispiel.
1A ist nicht "minus vier Grad" oder "ein a". Das ist „pooping man“ oder die Zahl „sechsundzwanzig“ im hexadezimalen Zahlensystem. Wer ständig in diesem Zahlensystem arbeitet, nimmt Zahl und Buchstabe automatisch als ein grafisches Symbol wahr.
Wertetabelle trigonometrischer Funktionen
Notiz. Diese Wertetabelle für trigonometrische Funktionen verwendet das Zeichen √ zur Bezeichnung der Quadratwurzel. Um einen Bruch zu bezeichnen - das Symbol "/".
siehe auch Nützliche Materialien:
Für Bestimmen des Wertes einer trigonometrischen Funktion, finden Sie es am Schnittpunkt der Linie, die die trigonometrische Funktion angibt. Zum Beispiel ein Sinus von 30 Grad - wir suchen eine Spalte mit der Überschrift sin (Sinus) und finden den Schnittpunkt dieser Spalte der Tabelle mit der Zeile "30 Grad". An ihrem Schnittpunkt lesen wir das Ergebnis - eins zweite. Ähnlich finden wir Kosinus 60 Grad, Sinus 60 Grad (auch hier finden wir am Schnittpunkt der sin (Sinus)-Spalte und der 60-Grad-Reihe den Wert sin 60 = √3/2) usw. Auf die gleiche Weise werden die Werte von Sinus, Kosinus und Tangens anderer "beliebter" Winkel gefunden.
Sinus von Pi, Kosinus von Pi, Tangens von Pi und andere Winkel im Bogenmaß
Die folgende Tabelle mit Kosinus, Sinus und Tangens eignet sich auch, um den Wert von trigonometrischen Funktionen zu finden, deren Argument ist in Radiant angegeben. Verwenden Sie dazu die zweite Spalte mit Winkelwerten. Dank dessen können Sie den Wert gängiger Winkel von Grad in Radiant umrechnen. Lassen Sie uns zum Beispiel den 60-Grad-Winkel in der ersten Zeile suchen und seinen Wert im Bogenmaß darunter ablesen. 60 Grad sind gleich π/3 Radianten.
Die Zahl Pi drückt eindeutig die Abhängigkeit des Umfangs eines Kreises vom Gradmaß des Winkels aus. Pi im Bogenmaß entspricht also 180 Grad.
Jede in Pi (Radiant) ausgedrückte Zahl kann leicht in Grad umgewandelt werden, indem die Zahl Pi (π) durch 180 ersetzt wird.
Beispiele:
1. Sinus Pi.
Sünde π = Sünde 180 = 0
Somit ist der Sinus von Pi derselbe wie der Sinus von 180 Grad und gleich Null.
2. Kosinus pi.
cos π = cos 180 = -1
Somit ist der Kosinus von Pi derselbe wie der Kosinus von 180 Grad und gleich minus eins.
3. Tangente pi
tg π = tg 180 = 0
Somit ist der Tangens von Pi derselbe wie der Tangens von 180 Grad und gleich Null.
Tabelle der Sinus-, Cosinus-, Tangens-Werte für Winkel 0 - 360 Grad (häufige Werte)
|
Winkel α (Grad) |
Winkel α (über Pi) |
Sünde (Sinus) |
cos (Kosinus) |
tg (Tangente) |
ctg (Kotangens) |
Sek (Sekante) |
weil (Kosekans) |
| 0 | 0 | 0 | 1 | 0 | - | 1 | - |
| 15 | π/12 | 2 - √3 | 2 + √3 | ||||
| 30 | π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12 | 2 + √3 | 2 - √3 | ||||
| 90 | π/2 | 1 | 0 | - | 0 | - | 1 |
| 105 | 7π/12 |
- |
- 2 - √3 | √3 - 2 | |||
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | - | -1 | - |
| 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/2 | -1 | 0 | - | 0 | - | -1 |
| 360 | 2π | 0 | 1 | 0 | - | 1 | - |
Wenn in der Wertetabelle trigonometrischer Funktionen anstelle des Funktionswerts ein Strich angegeben ist (Tangens (tg) 90 Grad, Kotangens (ctg) 180 Grad), dann für einen bestimmten Wert des Gradmaßes der Winkel, die Funktion hat keinen bestimmten Wert. Wenn kein Bindestrich vorhanden ist, ist die Zelle leer, sodass wir den gewünschten Wert noch nicht eingegeben haben. Wir interessieren uns für die Anfragen, mit denen Benutzer zu uns kommen, und ergänzen die Tabelle mit neuen Werten, obwohl die aktuellen Daten zu den Werten von Cosinus, Sinus und Tangens der häufigsten Winkelwerte ausreichen, um die meisten zu lösen Probleme.
Wertetabelle trigonometrischer Funktionen sin, cos, tg für die gängigsten Winkel
0, 15, 30, 45, 60, 90 ... 360 Grad
(Zahlenwerte „nach Bradis-Tabellen“)
| Winkelwert α (Grad) | Wert des Winkels α im Bogenmaß | Sünde (Sinus) | cos (Kosinus) | tg (Tangente) | ctg (Kotangens) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 |
0,2588 |
0,9659
|
0,2679 |
||
| 30 |
0,5000 |
0,5774 |
|||
| 45 |
0,7071 |
||||
|
0,7660 |
|||||
| 60 |
0,8660 |
0,5000
|
1,7321 |
||
|
7π/18 |
In dem Artikel werden wir vollständig verstehen, wie es aussieht Tabelle der trigonometrischen Werte, Sinus, Kosinus, Tangens und Kotangens. Betrachten Sie den Grundwert trigonometrischer Funktionen aus einem Winkel von 0,30,45,60,90,...,360 Grad. Und sehen wir uns an, wie man diese Tabellen zur Berechnung des Werts trigonometrischer Funktionen verwendet.
Erst überlegen Tabelle von Kosinus, Sinus, Tangens und Kotangens aus einem Winkel von 0, 30, 45, 60, 90, ... Grad. Die Definition dieser Größen ermöglicht es, den Wert der Funktionen von Winkeln von 0 und 90 Grad zu bestimmen:
sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, der Kotangens von 00 ist undefiniert
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, der Tangens von 90 0 ist undefiniert
Nehmen wir rechtwinklige Dreiecke, deren Winkel 30 bis 90 Grad betragen. Wir bekommen:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3
Wir stellen alle erhaltenen Werte im Formular dar trigonometrische Tabelle:
Tabelle von Sinus, Kosinus, Tangens und Kotangens!
Wenn wir die Gussformel verwenden, wird unsere Tabelle erweitert, Werte für Winkel bis zu 360 Grad werden hinzugefügt. Es wird so aussehen:

Basierend auf den Eigenschaften der Periodizität kann die Tabelle auch erweitert werden, wenn wir die Winkel durch 0 0 +360 0 *z .... 330 0 +360 0 *z ersetzen, wobei z eine ganze Zahl ist. In dieser Tabelle ist es möglich, den Wert aller Winkel zu berechnen, die Punkten in einem einzelnen Kreis entsprechen.
Lassen Sie uns deutlich sehen, wie die Tabelle in der Lösung verwendet wird.
Alles ist sehr einfach. Da der benötigte Wert am Schnittpunkt der benötigten Zellen liegt. Nehmen wir zum Beispiel einen Winkel von 60 Grad, in der Tabelle sieht es so aus:

In der Abschlusstabelle der Hauptwerte trigonometrischer Funktionen verfahren wir genauso. Aber in dieser Tabelle ist es möglich, herauszufinden, wie groß die Tangente von einem Winkel von 1020 Grad sein wird, es = -√3 Prüfen wir 1020 0 = 300 0 +360 0 *2. Suchen wir den Tisch.

Bradis-Tisch. Für Sinus, Kosinus, Tangens und Kotangens.
Die Tabellen von Bradys sind in mehrere Teile unterteilt, sie bestehen aus Tabellen von Cosinus und Sinus, Tangens und Kotangens - die in zwei Teile unterteilt sind (tg eines Winkels bis zu 90 Grad und ctg eines kleinen Winkels).
Sinus und Kosinus


Winkel tg von 00 bis 760, Winkel ctg von 140 bis 900.
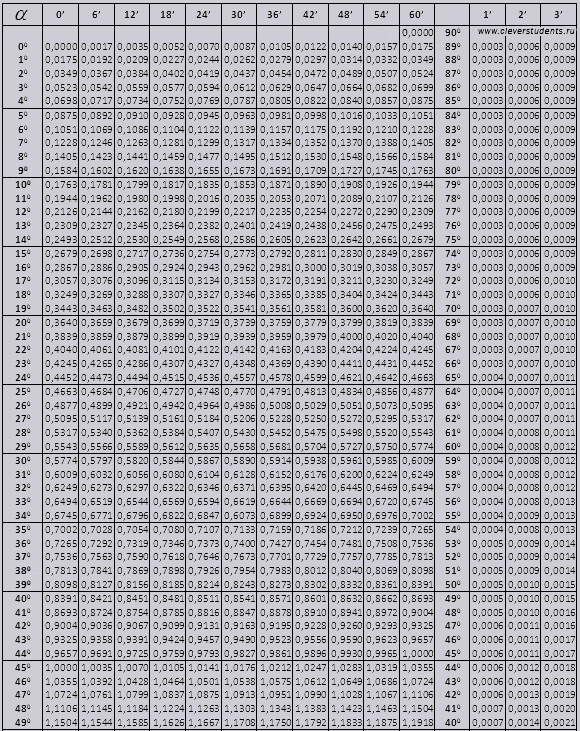

tg bis 900 und ctg kleine Winkel.

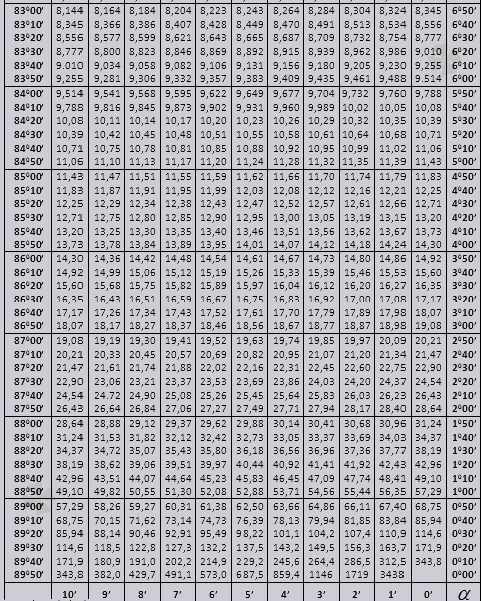
Lassen Sie uns herausfinden, wie man Bradis-Tabellen zur Lösung von Problemen verwendet.
Finden wir die Bezeichnung sin (die Bezeichnung in der Spalte vom linken Rand) 42 Minuten (die Bezeichnung befindet sich in der obersten Zeile). Durch Kreuzen suchen wir eine Bezeichnung, sie ist = 0,3040.
Die Werte der Minuten werden mit einem Intervall von sechs Minuten angezeigt, was ist, wenn der von uns benötigte Wert in dieses Intervall fällt. Nehmen wir 44 Minuten und in der Tabelle sind nur 42. Wir nehmen 42 als Basis und verwenden die zusätzlichen Spalten auf der rechten Seite, nehmen die 2. Korrektur und addieren zu 0,3040 + 0,0006, wir erhalten 0,3046.
Bei sin 47 min nehmen wir 48 min zu Grunde und ziehen davon 1 Korrektur ab, also 0,3057 - 0,0003 = 0,3054
Bei der Berechnung von cos gehen wir ähnlich vor wie bei sin, nur nehmen wir die unterste Zeile der Tabelle zu Grunde. Zum Beispiel cos 20 0 = 0,9397
Werte tg eines Winkels bis zu 90 0 und Kinderbett eines kleinen Winkels sind korrekt und enthalten keine Korrekturen. Finden Sie zum Beispiel tg 78 0 37min = 4,967 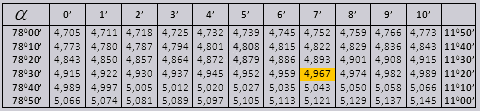
und ctg 20 0 13 min = 25,83 
Nun, hier haben wir die wichtigsten trigonometrischen Tabellen betrachtet. Wir hoffen, dass diese Informationen für Sie äußerst nützlich waren. Ihre Fragen zu den Tischen, falls vorhanden, schreiben Sie unbedingt in die Kommentare!
Hinweis: Wandfender - ein Fenderbrett zum Schutz von Wänden. Folgen Sie dem Link wallless frameless fenders (http://www.spi-polymer.ru/otboyniki/) und erfahren Sie mehr.
Dieser Artikel hat gesammelt Tabellen von Sinus, Kosinus, Tangens und Kotangens. Zuerst geben wir eine Tabelle der Hauptwerte der trigonometrischen Funktionen, dh eine Tabelle der Sinus, Cosinus, Tangenten und Kotangens der Winkel 0, 30, 45, 60, 90, ..., 360 Grad ( 0, π/6, π/4, π/3, π/2, …, 2π Bogenmaß). Danach geben wir eine Tabelle mit Sinus und Kosinus sowie eine Tabelle mit Tangenten und Kotangens von V. M. Bradis und zeigen, wie diese Tabellen verwendet werden, wenn die Werte trigonometrischer Funktionen ermittelt werden.
Seitennavigation.
Sinus-, Kosinus-, Tangens- und Kotangenstabelle für Winkel 0, 30, 45, 60, 90, ... Grad
Referenzliste.
- Algebra: Proz. für 9 Zellen. durchschn. Schule / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Enlightenment, 1990.- 272 S.: Ill.- ISBN 5-09-002727-7
- Bashmakov M.I. Algebra und Beginn der Analysis: Proc. für 10-11 Zellen. durchschn. Schule - 3. Aufl. - M.: Aufklärung, 1993. - 351 S.: Abb. - ISBN 5-09-004617-4.
- Algebra und Beginn der Analyse: Proc. für 10-11 Zellen. Allgemeinbildung Institutionen / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn und andere; Ed. A. N. Kolmogorova.- 14. Aufl.- M.: Enlightenment, 2004.- 384 S.: Abb.- ISBN 5-09-013651-3.
- Gusev V. A., Mordkovich A. G. Mathematik (ein Handbuch für Bewerber an technischen Schulen): Proc. Zulage.- M.; Höher Schule, 1984.-351 S., mit Abb.
- Bradis V.M. Vierstellige mathematische Tabellen: Für die allgemeine Bildung. Lehrbuch Betriebe. - 2. Aufl. - M.: Bustard, 1999.- 96 S.: mit Abb. ISBN 5-7107-2667-2
1. Trigonometrische Funktionen sind elementare Funktionen, deren Argument ist Injektion. Trigonometrische Funktionen beschreiben die Beziehungen zwischen Seiten und spitzen Winkeln in einem rechtwinkligen Dreieck. Die Anwendungsgebiete trigonometrischer Funktionen sind äußerst vielfältig. So lassen sich beispielsweise beliebige periodische Prozesse als Summe trigonometrischer Funktionen (Fourier-Reihen) darstellen. Diese Funktionen treten häufig beim Lösen von Differential- und Funktionsgleichungen auf.
2. Trigonometrische Funktionen umfassen die folgenden 6 Funktionen: Sinus, Kosinus, Tangente,Kotangens, Sekante und Kosekans. Für jede dieser Funktionen gibt es eine inverse trigonometrische Funktion.
3. Es ist bequem, die geometrische Definition trigonometrischer Funktionen mit einzuführen Einheitskreis. Die folgende Abbildung zeigt einen Kreis mit Radius r=1. Auf dem Kreis wird der Punkt M(x,y) markiert. Der Winkel zwischen dem Radiusvektor OM und der positiven Richtung der Ox-Achse ist α.
4. Sinus der Winkel α ist das Verhältnis der Ordinate y des Punktes M(x,y) zum Radius r:
sinα=y/r.
Da r=1 ist, ist der Sinus gleich der Ordinate des Punktes M(x,y).
5. Kosinus der Winkel α ist das Verhältnis der Abszisse x des Punktes M(x,y) zum Radius r:
cosα=x/r
6. Tangente der Winkel α ist das Verhältnis der Ordinate y des Punktes M(x,y) zu seiner Abszisse x:
tanα=y/x,x≠0
7. Kotangens der Winkel α ist das Verhältnis der Abszisse x des Punktes M(x,y) zu seiner Ordinate y:
cotα=x/y,y≠0
8. Sekante Winkel α ist das Verhältnis des Radius r zur Abszisse x des Punktes M(x,y):
secα=r/x=1/x,x≠0
9. Kosekans Winkel α ist das Verhältnis des Radius r zur Ordinate y des Punktes M(x,y):
cscα=r/y=1/y,y≠0
10. Im Einheitskreis der Projektion x, y bilden die Punkte M(x,y) und der Radius r ein rechtwinkliges Dreieck, in dem x,y die Schenkel und r die Hypotenuse sind. Daher werden die obigen Definitionen trigonometrischer Funktionen, angewendet auf ein rechtwinkliges Dreieck, wie folgt formuliert:
Sinus Winkel α ist das Verhältnis des gegenüberliegenden Schenkels zur Hypotenuse.
Kosinus Winkel α ist das Verhältnis des benachbarten Schenkels zur Hypotenuse.
Tangente Winkel α wird das gegenüberliegende Bein zum benachbarten genannt.
Kotangens Winkel α wird das benachbarte Bein zum gegenüberliegenden genannt.
Sekante Winkel α ist das Verhältnis der Hypotenuse zum benachbarten Schenkel.
Kosekans Winkel α ist das Verhältnis der Hypotenuse zum gegenüberliegenden Bein.
11. Sinusfunktionsgraph
y=sinx, Definitionsbereich: x∈R, Definitionsbereich: −1≤sinx≤1
12. Graph der Kosinusfunktion
y=cosx, Wertebereich: x∈R, Wertebereich: −1≤cosx≤1
13. Tangentenfunktionsgraph 14. Graph der Kotangensfunktion 15. Graph der Sekantenfunktion
y=tanx, Definitionsbereich: x∈R,x≠(2k+1)π/2, Definitionsbereich: −∞ 
y=cotx, Definitionsbereich: x∈R,x≠kπ, Definitionsbereich: −∞ 
y=secx, Definitionsbereich: x∈R,x≠(2k+1)π/2, Definitionsbereich: secx∈(−∞,−1]∪∪)
