Multiplikation und Division von Brüchen.

Beachtung!
Es gibt zusätzliche
Material in Sondersektion 555.
Für diejenigen, die stark "nicht sehr ..."
Und für diejenigen, die "sehr viel...")

Diese Operation ist viel schöner als Addition-Subtraktion! Weil es einfacher ist. Ich erinnere Sie daran: Um einen Bruch mit einem Bruch zu multiplizieren, müssen Sie die Zähler (dies wird der Zähler des Ergebnisses sein) und die Nenner (dies wird der Nenner sein) multiplizieren. Also:

Zum Beispiel:

Alles ist sehr einfach. Und bitte nicht nach einem gemeinsamen Nenner suchen! Brauche ich hier nicht...

Um einen Bruch durch einen Bruch zu dividieren, musst du umdrehen zweite(das ist wichtig!) brechen und multiplizieren, also:

Zum Beispiel:

Wenn die Multiplikation oder Division mit ganzen Zahlen und Brüchen abgefangen wird, ist es in Ordnung. Wie bei der Addition machen wir aus einer ganzen Zahl mit einer Einheit im Nenner einen Bruch – und los! Zum Beispiel:

In der High School muss man sich oft mit dreistöckigen (oder sogar vierstöckigen!) Brüchen auseinandersetzen. Zum Beispiel:

Wie bringt man diesen Bruch in eine anständige Form? Ja, ganz einfach! Verwenden Sie die Division durch zwei Punkte:

Aber vergessen Sie nicht die Teilungsreihenfolge! Im Gegensatz zur Multiplikation ist dies hier sehr wichtig! Natürlich werden wir 4:2 oder 2:4 nicht verwechseln. Aber in einem dreistöckigen Bruchteil ist es leicht, einen Fehler zu machen. Bitte beachten Sie zum Beispiel:

Im ersten Fall (Ausdruck links):

Im zweiten (Ausdruck rechts):

Spüre den Unterschied? 4 und 1/9!

Wie ist die Teilungsreihenfolge? Oder Klammern oder (wie hier) die Länge horizontaler Striche. Entwickle ein Auge. Und wenn es keine Klammern oder Bindestriche gibt, wie:

dann dividieren-multiplizieren der Reihe nach von links nach rechts!

Und noch ein sehr einfacher und wichtiger Trick. Bei Aktionen mit Abschlüssen wird es sich für Sie als nützlich erweisen! Teilen wir die Einheit durch einen beliebigen Bruch, zum Beispiel durch 13/15:

Der Schuss ist übergesprungen! Und es passiert immer. Wenn Sie 1 durch einen beliebigen Bruch teilen, ist das Ergebnis derselbe Bruch, nur umgekehrt.

Das sind alle Aktionen mit Brüchen. Die Sache ist recht simpel, gibt aber mehr als genug Fehler. Beachten Sie die praktischen Ratschläge, dann gibt es weniger (Fehler)!

Praktische Tipps:

1. Das Wichtigste bei der Arbeit mit Bruchausdrücken ist Genauigkeit und Aufmerksamkeit! Das sind keine gewöhnlichen Worte, keine guten Wünsche! Dies ist eine dringende Notwendigkeit! Führen Sie alle Berechnungen in der Prüfung als vollwertige Aufgabe mit Konzentration und Klarheit durch. Es ist besser, zwei zusätzliche Zeilen in einen Entwurf zu schreiben, als beim Rechnen im Kopf zu vermasseln.

2. In Beispielen mit verschiedenen Arten von Brüchen - gehen Sie zu gewöhnlichen Brüchen.

3. Wir reduzieren alle Brüche bis zum Anschlag.

4. Wir reduzieren mehrstufige Bruchausdrücke auf gewöhnliche, indem wir die Division durch zwei Punkte verwenden (wir folgen der Divisionsreihenfolge!).

5. Wir teilen die Einheit gedanklich in einen Bruch auf, indem wir einfach den Bruch umdrehen.

Hier sind die Aufgaben, die Sie erledigen müssen. Antworten werden nach allen Aufgaben gegeben. Verwenden Sie die Materialien zu diesem Thema und praktische Ratschläge. Schätzen Sie, wie viele Beispiele Sie richtig lösen könnten. Das erste Mal! Ohne Taschenrechner! Und die richtigen Schlüsse ziehen...

Erinnere dich an die richtige Antwort ab dem zweiten (insbesondere dritten) Mal erhalten - zählt nicht! So ist das harte Leben.

So, im Prüfungsmodus lösen ! Das ist übrigens die Vorbereitung auf die Prüfung. Wir lösen ein Beispiel, wir prüfen, wir lösen folgendes. Wir haben alles entschieden - wir haben noch einmal vom ersten bis zum letzten geprüft. Und nur gemäß schau dir die Antworten an.

Berechnung:

Haben Sie sich entschieden?

Suchen Sie nach Antworten, die zu Ihren passen. Ich habe sie eigens in einem Durcheinander aufgeschrieben, weg von der Versuchung sozusagen ... Hier sind sie, die Antworten, mit Semikolon aufgeschrieben.

0; 17/22; 3/4; 2/5; 1; 25.

Und jetzt ziehen wir Schlüsse. Wenn alles geklappt hat - glücklich für dich! Elementares Rechnen mit Brüchen ist nicht dein Problem! Sie können ernsthaftere Dinge tun. Wenn nicht...

Sie haben also eines von zwei Problemen. Oder beides gleichzeitig.) Unkenntnis und (oder) Unaufmerksamkeit. Aber das lösbar Probleme.

Wenn Ihnen diese Seite gefällt...

Übrigens habe ich noch ein paar interessantere Seiten für Sie.)

Sie können das Lösen von Beispielen üben und Ihr Niveau herausfinden. Testen mit sofortiger Verifizierung. Lernen - mit Interesse!)

Sie können sich mit Funktionen und Ableitungen vertraut machen.

) und der Nenner durch den Nenner (wir erhalten den Nenner des Produkts).

Bruchmultiplikationsformel:

Zum Beispiel:

Bevor Sie mit der Multiplikation von Zählern und Nennern fortfahren, müssen Sie die Möglichkeit einer Bruchkürzung prüfen. Wenn Sie es schaffen, den Bruch zu reduzieren, können Sie leichter weiterrechnen.

Division eines gewöhnlichen Bruchs durch einen Bruch.

Division von Brüchen mit einer natürlichen Zahl.

Es ist nicht so beängstigend, wie es scheint. Wie bei der Addition wandeln wir eine ganze Zahl in einen Bruch mit einer Einheit im Nenner um. Zum Beispiel:

Multiplikation gemischter Brüche.

Regeln zum Multiplizieren von Brüchen (gemischt):

• wandle gemischte Brüche in unechte um;
• multipliziere die Zähler und Nenner von Brüchen;
• wir reduzieren den Bruch;
• Wenn wir einen unechten Bruch erhalten, wandeln wir den unechten Bruch in einen gemischten um.

Beachten Sie! Um einen gemischten Bruch mit einem anderen gemischten Bruch zu multiplizieren, müssen Sie sie zuerst in die Form von unechten Brüchen bringen und dann gemäß der Regel zum Multiplizieren gewöhnlicher Brüche multiplizieren.

Die zweite Möglichkeit, einen Bruch mit einer natürlichen Zahl zu multiplizieren.

Es ist bequemer, die zweite Methode zum Multiplizieren eines gewöhnlichen Bruchs mit einer Zahl zu verwenden.

Beachten Sie! Um einen Bruch mit einer natürlichen Zahl zu multiplizieren, ist es notwendig, den Nenner des Bruchs durch diese Zahl zu dividieren und den Zähler unverändert zu lassen.

Aus dem obigen Beispiel wird deutlich, dass diese Option bequemer zu verwenden ist, wenn der Nenner eines Bruchs ohne Rest durch eine natürliche Zahl dividiert wird.

Mehrstufige Brüche.

In der High School werden oft dreistöckige (oder mehr) Fraktionen gefunden. Beispiel:

Um einen solchen Bruch auf seine übliche Form zu bringen, wird eine Division durch 2 Punkte verwendet:

Beachten Sie! Beim Teilen von Brüchen ist die Reihenfolge der Teilung sehr wichtig. Achtung, hier kommt man leicht durcheinander.

Beachten Sie, Zum Beispiel:

Wenn Sie eins durch einen beliebigen Bruch dividieren, ist das Ergebnis derselbe Bruch, nur umgekehrt:

Praktische Tipps zum Multiplizieren und Dividieren von Brüchen:

1. Das Wichtigste bei der Arbeit mit Bruchausdrücken ist Genauigkeit und Aufmerksamkeit. Führen Sie alle Berechnungen sorgfältig und genau, konzentriert und klar durch. Es ist besser, ein paar zusätzliche Zeilen in einen Entwurf zu schreiben, als sich in den Berechnungen im Kopf zu verirren.

2. Gehen Sie bei Aufgaben mit verschiedenen Arten von Brüchen zur Art der gewöhnlichen Brüche.

3. Wir kürzen alle Brüche, bis eine Kürzung nicht mehr möglich ist.

4. Wir bringen mehrstufige Bruchausdrücke in gewöhnliche Ausdrücke, indem wir die Division durch 2 Punkte verwenden.

5. Wir teilen die Einheit gedanklich in einen Bruch auf, indem wir einfach den Bruch umdrehen.

Wir untersuchen weiterhin Aktionen mit gewöhnlichen Brüchen. Jetzt im Rampenlicht Multiplikation gemeinsamer Brüche. In diesem Artikel geben wir eine Regel zum Multiplizieren gewöhnlicher Brüche an. Betrachten Sie die Anwendung dieser Regel beim Lösen von Beispielen. Wir werden uns auch darauf konzentrieren, einen gewöhnlichen Bruch mit einer natürlichen Zahl zu multiplizieren. Überlegen Sie abschließend, wie die Multiplikation von drei oder mehr Brüchen durchgeführt wird.

Seitennavigation.

Einen gemeinsamen Bruch mit einem gemeinsamen Bruch multiplizieren

Beginnen wir mit der Formulierung Regeln zum Multiplizieren gemeinsamer Brüche: Die Multiplikation eines Bruchs mit einem Bruch ergibt einen Bruch, dessen Zähler gleich dem Produkt der Zähler der multiplizierten Brüche und dessen Nenner gleich dem Produkt der Nenner ist.

Das heißt, die Formel entspricht der Multiplikation gewöhnlicher Brüche a / b und c / d.

Lassen Sie uns ein Beispiel geben, das die Regel der Multiplikation gewöhnlicher Brüche veranschaulicht. Stellen Sie sich ein Quadrat mit einer Seitenlänge von 1 Einheit vor. , während seine Fläche 1 Einheit 2 beträgt. Teilen Sie dieses Quadrat in gleiche Rechtecke mit Seiten 1/4 Einheiten. und 1/8 Einheiten. , während das ursprüngliche Quadrat aus 4 8 = 32 Rechtecken besteht, beträgt die Fläche jedes Rechtecks ​​daher 1/32 der Fläche des ursprünglichen Quadrats, dh sie entspricht 1/32 Einheiten 2. Lassen Sie uns nun einen Teil des ursprünglichen Quadrats übermalen. Alle unsere Maßnahmen spiegeln sich in der folgenden Abbildung wider.

Die Seiten des gefüllten Rechtecks ​​sind 5/8 Einheiten. und 3/4 Einheiten. , was bedeutet, dass seine Fläche gleich dem Produkt der Brüche 5/8 und 3/4 ist, also Einheiten 2. Aber das gefüllte Rechteck besteht aus 15 "kleinen" Rechtecken, also ist seine Fläche 15/32 Einheiten 2 . Somit, . Da 5 3=15 und 8 4=32 , kann die letzte Gleichheit umgeschrieben werden als , was die Formel zum Multiplizieren gewöhnlicher Brüche der Form bestätigt.

Beachten Sie, dass Sie mit Hilfe der stimmhaften Multiplikationsregel sowohl echte als auch unechte Brüche, Brüche mit demselben Nenner und Brüche mit unterschiedlichen Nennern multiplizieren können.

Prüfen Beispiele für die Multiplikation gemeinsamer Brüche.

Multiplizieren Sie den gemeinsamen Bruch 7/11 mit dem gemeinsamen Bruch 9/8.

Das Produkt der Zähler der multiplizierten Brüche 7 und 9 ist 63, und das Produkt der Nenner von 11 und 8 ist 88. Somit ergibt die Multiplikation der gemeinsamen Brüche 7/11 und 9/8 den Bruch 63/88.

Hier ist eine Zusammenfassung der Lösung: .

Wir sollten die Kürzung des resultierenden Bruchs nicht vergessen, wenn als Ergebnis der Multiplikation ein kürzbarer Bruch erhalten wird, und die Auswahl des ganzen Teils aus einem unechten Bruch.

Multipliziere die Brüche 4/15 und 55/6.

Wenden wir die Regel der Multiplikation gewöhnlicher Brüche an: .

Offensichtlich ist der resultierende Bruch reduzierbar (das Zeichen der Teilbarkeit durch 10 erlaubt uns zu behaupten, dass Zähler und Nenner des Bruchs 220/90 einen gemeinsamen Faktor von 10 haben). Lassen Sie uns den Bruch 220/90 reduzieren: GCD(220, 90)=10 und . Es bleibt, den ganzzahligen Teil aus dem resultierenden unechten Bruch auszuwählen: .

Beachten Sie, dass die Bruchkürzung vor der Berechnung der Produkte der Zähler und der Produkte der Nenner der multiplizierten Brüche durchgeführt werden kann, d. h. wenn der Bruch die Form hat. Für diese Zahl werden a, b, c und d durch ihre Primfaktorzerlegungen ersetzt, danach werden die gleichen Faktoren des Zählers und des Nenners gestrichen.

Gehen wir zur Verdeutlichung zurück zum vorherigen Beispiel.

Berechne das Produkt von Brüchen der Form .

Durch die Formel zum Multiplizieren gewöhnlicher Brüche haben wir .

Da 4=2 2 , 55=5 11 , 15=3 5 und 6=2 3 , dann . Nun kürzen wir die gemeinsamen Primfaktoren: .

Es bleibt nur, die Produkte im Zähler und Nenner zu berechnen und dann den ganzzahligen Teil aus dem unechten Bruch auszuwählen: .

Zu beachten ist, dass die Multiplikation von Brüchen durch ein Kommutativgesetz gekennzeichnet ist, d. h. die multiplizierten Brüche können vertauscht werden: .

Einen Bruch mit einer natürlichen Zahl multiplizieren

Beginnen wir mit der Formulierung Regeln für die Multiplikation eines gemeinsamen Bruchs mit einer natürlichen Zahl: Die Multiplikation eines Bruchs mit einer natürlichen Zahl ergibt einen Bruch, dessen Zähler gleich dem Produkt des Zählers des multiplizierten Bruchs mit der natürlichen Zahl ist und dessen Nenner gleich dem Nenner des multiplizierten Bruchs ist.

Mit Hilfe von Buchstaben hat die Regel zum Multiplizieren eines Bruchs a / b mit einer natürlichen Zahl n die Form .

Die Formel folgt aus der Formel zur Multiplikation zweier gewöhnlicher Brüche der Form . Tatsächlich erhalten wir, wenn wir eine natürliche Zahl als Bruch mit dem Nenner 1 darstellen .

Betrachten Sie Beispiele für die Multiplikation eines Bruchs mit einer natürlichen Zahl.

Multipliziere den Bruch 2/27 mit 5.

Die Multiplikation des Zählers 2 mit der Zahl 5 ergibt 10, daher ist aufgrund der Regel, einen Bruch mit einer natürlichen Zahl zu multiplizieren, das Produkt von 2/27 mit 5 gleich dem Bruch 10/27.

Die ganze Lösung lässt sich bequem wie folgt schreiben: .

Bei der Multiplikation eines Bruchs mit einer natürlichen Zahl muss der entstehende Bruch oft gekürzt werden, und wenn er auch falsch ist, dann als gemischte Zahl darstellen.

Multipliziere den Bruch 5/12 mit der Zahl 8.

Nach der Formel zum Multiplizieren eines Bruchs mit einer natürlichen Zahl haben wir . Offensichtlich ist der resultierende Bruch reduzierbar (das Zeichen der Teilbarkeit durch 2 zeigt einen gemeinsamen Teiler 2 von Zähler und Nenner an). Lassen Sie uns den Bruch 40/12 reduzieren: da LCM(40, 12)=4, dann . Es bleibt, den ganzen Teil auszuwählen: .

Hier ist die ganze Lösung: .

Beachten Sie, dass die Reduktion erfolgen könnte, indem Sie die Zahlen im Zähler und Nenner durch ihre Erweiterungen in Primfaktoren ersetzen. In diesem Fall sähe die Lösung so aus:

Zum Abschluss dieses Absatzes stellen wir fest, dass die Multiplikation eines Bruchs mit einer natürlichen Zahl die Kommutativeigenschaft hat, d. h. das Produkt eines Bruchs mit einer natürlichen Zahl ist gleich dem Produkt dieser natürlichen Zahl mit einem Bruch: .

Multipliziere drei oder mehr Brüche

Die Art und Weise, wie wir gewöhnliche Brüche und die Multiplikationsoperation mit ihnen definiert haben, erlaubt uns zu behaupten, dass alle Eigenschaften der Multiplikation natürlicher Zahlen auf die Multiplikation von Brüchen zutreffen.

Die kommutativen und assoziativen Eigenschaften der Multiplikation ermöglichen eine eindeutige Bestimmung Multiplizieren von drei oder mehr Brüchen und natürlichen Zahlen. In diesem Fall geschieht alles analog zur Multiplikation von drei oder mehr natürlichen Zahlen. Insbesondere Brüche und natürliche Zahlen im Produkt können zur Vereinfachung der Berechnung neu angeordnet werden, und wenn keine Klammern vorhanden sind, die die Reihenfolge angeben, in der Aktionen ausgeführt werden, können wir die Klammern selbst auf jede der zulässigen Arten anordnen.

Betrachten Sie Beispiele für die Multiplikation mehrerer Brüche und natürlicher Zahlen.

Multiplizieren Sie drei gemeinsame Brüche 1/20, 12/5, 3/7 und 5/8.

Lassen Sie uns das Produkt schreiben, das wir berechnen müssen . Aufgrund der Regel zum Multiplizieren von Brüchen ist das geschriebene Produkt gleich einem Bruch, dessen Zähler gleich dem Produkt der Zähler aller Brüche ist, und der Nenner ist das Produkt der Nenner: .

Vor der Berechnung der Produkte in Zähler und Nenner empfiehlt es sich, alle Faktoren durch ihre Erweiterungen in Primfaktoren zu ersetzen und zu kürzen (natürlich kann man nach der Multiplikation den Bruch kürzen, aber das erfordert in vielen Fällen viel Rechenaufwand): .

.

Multipliziere fünf Zahlen .

In diesem Produkt ist es praktisch, den Bruch 7/8 mit der Zahl 8 und die Zahl 12 mit dem Bruch 5/36 zu gruppieren, dies vereinfacht die Berechnungen, da bei einer solchen Gruppierung die Reduzierung offensichtlich ist. Wir haben
.

.

Multiplikation von Brüchen

Wir werden die Multiplikation gewöhnlicher Brüche auf mehrere mögliche Arten betrachten.

Einen Bruch mit einem Bruch multiplizieren

Dies ist der einfachste Fall, in dem Sie Folgendes verwenden müssen Regeln zur Multiplikation von Brüchen.

Zu einen Bruch mit einem Bruch multiplizieren, notwendig:

• den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs multiplizieren und ihr Produkt in den Zähler des neuen Bruchs schreiben;
• den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs multiplizieren und ihr Produkt in den Nenner des neuen Bruchs schreiben;

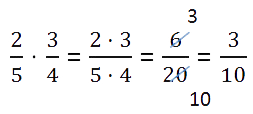
Prüfen Sie vor dem Multiplizieren von Zählern und Nennern, ob sich die Brüche kürzen lassen. Das Kürzen von Brüchen in Berechnungen erleichtert Ihre Berechnungen erheblich.

Einen Bruch mit einer natürlichen Zahl multiplizieren

Zum Bruch mit einer natürlichen Zahl multiplizieren Sie müssen den Zähler des Bruchs mit dieser Zahl multiplizieren und den Nenner des Bruchs unverändert lassen.

Wenn das Ergebnis der Multiplikation ein unechter Bruch ist, vergessen Sie nicht, ihn in eine gemischte Zahl umzuwandeln, dh den ganzen Teil auszuwählen.

Multiplikation gemischter Zahlen

Um gemischte Zahlen zu multiplizieren, musst du sie zuerst in unechte Brüche umwandeln und dann gemäß der Regel zum Multiplizieren gewöhnlicher Brüche multiplizieren.

Eine andere Möglichkeit, einen Bruch mit einer natürlichen Zahl zu multiplizieren

Manchmal ist es bei Berechnungen bequemer, eine andere Methode zum Multiplizieren eines gewöhnlichen Bruchs mit einer Zahl zu verwenden.

Um einen Bruch mit einer natürlichen Zahl zu multiplizieren, musst du den Nenner des Bruchs durch diese Zahl dividieren und den Zähler gleich lassen.

Wie aus dem Beispiel ersichtlich ist, ist es bequemer, diese Version der Regel anzuwenden, wenn der Nenner des Bruchs ohne Rest durch eine natürliche Zahl teilbar ist.

Multiplikation gemischter Zahlen: Regeln, Beispiele, Lösungen.

In diesem Artikel werden wir analysieren Multiplikation gemischter Zahlen. Zuerst werden wir die Regel zum Multiplizieren gemischter Zahlen formulieren und die Anwendung dieser Regel beim Lösen von Beispielen betrachten. Als nächstes werden wir über die Multiplikation einer gemischten Zahl und einer natürlichen Zahl sprechen. Schließlich lernen wir, wie man eine gemischte Zahl und einen gewöhnlichen Bruch multipliziert.

Seitennavigation.

Multiplikation gemischter Zahlen.

Multiplikation gemischter Zahlen kann auf das Multiplizieren gewöhnlicher Brüche reduziert werden. Dazu genügt es, gemischte Zahlen in unechte Brüche umzuwandeln.

Schreiben wir auf Multiplikationsregel für gemischte Zahlen:

• Zunächst müssen die zu multiplizierenden gemischten Zahlen durch unechte Brüche ersetzt werden;
• Zweitens müssen Sie die Regel anwenden, einen Bruch mit einem Bruch zu multiplizieren.

Betrachten Sie Beispiele für die Anwendung dieser Regel, wenn Sie eine gemischte Zahl mit einer gemischten Zahl multiplizieren.

Führe eine Multiplikation mit gemischten Zahlen durch und .

Zunächst stellen wir die multiplizierten gemischten Zahlen als unechte Brüche dar: und . Jetzt können wir die Multiplikation gemischter Zahlen durch die Multiplikation gewöhnlicher Brüche ersetzen: . Wenden wir die Regel der Multiplikation von Brüchen an, erhalten wir . Der resultierende Bruch ist irreduzibel (siehe reduzierbare und irreduzible Brüche), aber er ist falsch (siehe reguläre und unechte Brüche), daher bleibt es, um die endgültige Antwort zu erhalten, den ganzzahligen Teil aus dem unechten Bruch zu extrahieren: .

Lassen Sie uns die gesamte Lösung in einer Zeile schreiben: .

.

Betrachten Sie die Lösung eines anderen Beispiels, um die Fähigkeiten zum Multiplizieren gemischter Zahlen zu festigen.

Führen Sie die Multiplikation durch.

Lustige Zahlen und sind gleich den Brüchen 13/5 bzw. 10/9. Dann . An dieser Stelle ist es an der Zeit, sich an die Bruchreduktion zu erinnern: Wir werden alle Zahlen im Bruch durch ihre Erweiterungen in Primfaktoren ersetzen, und wir werden die Reduktion derselben Faktoren durchführen.

Multiplikation einer gemischten Zahl und einer natürlichen Zahl

Nachdem Sie die gemischte Zahl durch einen unechten Bruch ersetzt haben, Multiplikation einer gemischten Zahl und einer natürlichen Zahl wird auf die Multiplikation eines gewöhnlichen Bruchs und einer natürlichen Zahl reduziert.

Multiplizieren Sie die gemischte Zahl und die natürliche Zahl 45 .

Eine gemischte Zahl ist dann ein Bruch . Lassen Sie uns die Zahlen im resultierenden Bruch durch ihre Erweiterungen in Primfaktoren ersetzen, eine Reduktion vornehmen, wonach wir den ganzzahligen Teil auswählen: .

.

Die Multiplikation einer gemischten Zahl und einer natürlichen Zahl erfolgt manchmal bequem unter Verwendung des Verteilungsgesetzes der Multiplikation in Bezug auf die Addition. In diesem Fall ist das Produkt einer gemischten Zahl und einer natürlichen Zahl gleich der Summe der Produkte des ganzzahligen Teils durch die gegebene natürliche Zahl und des Bruchteils durch die gegebene natürliche Zahl, d. h. .

Berechne das Produkt.

Wir ersetzen die gemischte Zahl durch die Summe der ganzen und gebrochenen Teile, danach wenden wir das Distributivgesetz der Multiplikation an: .

Multiplizieren einer gemischten Zahl und eines gemeinsamen Bruchs Es ist am bequemsten, auf die Multiplikation gewöhnlicher Brüche zu reduzieren, wobei die multiplizierte gemischte Zahl als unechter Bruch dargestellt wird.

Multipliziere die gemischte Zahl mit dem gemeinsamen Bruch 4/15.

Wenn wir die gemischte Zahl durch einen Bruch ersetzen, erhalten wir .

Multiplikation von Bruchzahlen

§ 140. Definitionen. 1) Die Multiplikation einer Bruchzahl mit einer ganzen Zahl ist genauso definiert wie die Multiplikation ganzer Zahlen, nämlich: eine Zahl (Multiplikator) mit einer ganzen Zahl (Multiplikator) zu multiplizieren bedeutet, eine Summe identischer Terme zu bilden, bei der jeder Term gleich dem Multiplikanden und die Anzahl der Terme gleich dem Multiplikator ist.

Mit 5 multiplizieren bedeutet also, die Summe zu finden:
2) Eine Zahl (Multiplikator) mit einem Bruch (Multiplikator) zu multiplizieren bedeutet, diesen Bruchteil des Multiplikanden zu finden.

Wenn wir also einen Bruch einer gegebenen Zahl finden, die wir zuvor betrachtet haben, nennen wir es jetzt Multiplikation mit einem Bruch.

3) Eine Zahl (Multiplikator) mit einer gemischten Zahl (Faktor) zu multiplizieren bedeutet, den Multiplikator zuerst mit der Ganzzahl des Faktors, dann mit dem Bruchteil des Faktors zu multiplizieren und die Ergebnisse dieser beiden Multiplikationen zu addieren.

Zum Beispiel:

Die nach der Multiplikation erhaltene Zahl wird in allen diesen Fällen genannt Arbeit, also genauso wie beim Multiplizieren ganzer Zahlen.

Aus diesen Definitionen wird deutlich, dass die Multiplikation von Bruchzahlen eine immer mögliche und immer eindeutige Handlung ist.

§ 141. Zweckmäßigkeit dieser Definitionen. Um zu verstehen, wie zweckmäßig es ist, die letzten beiden Definitionen der Multiplikation in die Arithmetik einzuführen, nehmen wir folgendes Problem:

Aufgabe. Der Zug fährt bei gleichmäßiger Fahrt 40 km/h; Wie kann man herausfinden, wie viele Kilometer dieser Zug in einer bestimmten Anzahl von Stunden zurücklegt?

Wären wir bei der einen Definition der Multiplikation geblieben, die in der Arithmetik der ganzen Zahlen (Addition gleicher Glieder) angegeben ist, dann hätte unser Problem drei verschiedene Lösungen, nämlich:

Wenn die angegebene Stundenzahl eine ganze Zahl ist (z. B. 5 Stunden), müssen zur Lösung des Problems 40 km mit dieser Stundenzahl multipliziert werden.

Wenn eine bestimmte Anzahl von Stunden als Bruch ausgedrückt wird (z. B. Stunden), müssen Sie den Wert dieses Bruchs aus 40 km ermitteln.

Wenn die angegebene Anzahl von Stunden gemischt ist (z. B. Stunden), müssen 40 km mit einer in der gemischten Zahl enthaltenen ganzen Zahl multipliziert und zum Ergebnis ein solcher Bruchteil von 40 km hinzugefügt werden, wie er in der ist gemischte Zahl.

Die von uns gegebenen Definitionen erlauben es uns, eine allgemeine Antwort auf alle diese möglichen Fälle zu geben:

40 km müssen mit der angegebenen Stundenzahl multipliziert werden, wie hoch diese auch immer sein mag.

Wenn also das Problem in allgemeiner Form wie folgt dargestellt wird:

Ein gleichmäßig fahrender Zug legt v km pro Stunde zurück. Wie viele Kilometer legt der Zug in t Stunden zurück?

dann können wir unabhängig von den Zahlen v und t eine Antwort ausdrücken: Die gewünschte Zahl wird durch die Formel v · t ausgedrückt.

Notiz. Das Finden eines Bruchteils einer gegebenen Zahl bedeutet nach unserer Definition dasselbe wie das Multiplizieren einer gegebenen Zahl mit diesem Bruch; Daher bedeutet beispielsweise das Finden von 5% (dh fünf Hundertstel) einer bestimmten Zahl dasselbe wie das Multiplizieren der angegebenen Zahl mit oder mit; 125% einer gegebenen Zahl zu finden, ist dasselbe wie diese Zahl mit oder mit zu multiplizieren usw.

§ 142. Eine Anmerkung darüber, wann eine Zahl durch Multiplikation zunimmt und wann sie abnimmt.

Bei der Multiplikation mit einem echten Bruch verringert sich die Zahl, bei der Multiplikation mit einem unechten Bruch erhöht sich die Zahl, wenn dieser unechte Bruch größer als eins ist, und bleibt unverändert, wenn er gleich eins ist.
Kommentar. Bei der Multiplikation von Bruchzahlen sowie ganzen Zahlen wird das Produkt gleich Null genommen, wenn einer der Faktoren gleich Null ist, also.

§ 143. Ableitung von Multiplikationsregeln.

1) Einen Bruch mit einer ganzen Zahl multiplizieren. Lassen Sie den Bruch mit 5 multiplizieren. Dies bedeutet, um das 5-fache zu erhöhen. Um einen Bruch um 5 zu erhöhen, genügt es, seinen Zähler um das Fünffache zu erhöhen oder seinen Nenner zu verkleinern (§ 127).

So:
Regel 1. Um einen Bruch mit einer ganzen Zahl zu multiplizieren, müssen Sie den Zähler mit dieser ganzen Zahl multiplizieren und den Nenner gleich lassen; Stattdessen können Sie auch den Nenner des Bruchs durch die angegebene ganze Zahl dividieren (wenn möglich) und den Zähler gleich lassen.

Kommentar. Das Produkt aus einem Bruch und seinem Nenner ist gleich seinem Zähler.

So:
Regel 2. Um eine ganze Zahl mit einem Bruch zu multiplizieren, müssen Sie die ganze Zahl mit dem Zähler des Bruchs multiplizieren und dieses Produkt zum Zähler machen und den Nenner des gegebenen Bruchs als Nenner signieren.
Regel 3. Um einen Bruch mit einem Bruch zu multiplizieren, musst du den Zähler mit dem Zähler und den Nenner mit dem Nenner multiplizieren und das erste Produkt zum Zähler und das zweite zum Nenner des Produkts machen.

Kommentar. Diese Regel lässt sich auch auf die Multiplikation eines Bruchs mit einer ganzen Zahl und einer ganzen Zahl mit einem Bruch anwenden, wenn wir nur die ganze Zahl als Bruch mit dem Nenner Eins betrachten. So:

Somit sind die drei nun genannten Regeln in einer enthalten, die sich allgemein wie folgt ausdrücken lässt:
4) Multiplikation gemischter Zahlen.

Regel 4. Um gemischte Zahlen zu multiplizieren, musst du sie in unechte Brüche umwandeln und dann gemäß den Regeln für die Multiplikation von Brüchen multiplizieren. Zum Beispiel:
§ 144. Herabsetzung der Multiplikation. Beim Multiplizieren von Brüchen sollte, wenn möglich, vorab gekürzt werden, wie die folgenden Beispiele zeigen:

Eine solche Kürzung ist möglich, weil sich der Wert eines Bruchs nicht ändert, wenn Zähler und Nenner gleich oft gekürzt werden.

§ 145. Produktänderung bei Faktoränderung. Wenn sich die Faktoren ändern, ändert sich das Produkt von Bruchzahlen genauso wie das Produkt von ganzen Zahlen (§ 53), nämlich: Wenn Sie einen beliebigen Faktor mehrmals erhöhen (oder verringern), dann wird das Produkt erhöht (oder verringert) um den gleichen Betrag.

Also, wenn im Beispiel:
Um mehrere Brüche zu multiplizieren, muss man ihre Zähler untereinander und die Nenner untereinander multiplizieren und das erste Produkt zum Zähler und das zweite zum Nenner des Produkts machen.

Kommentar. Diese Regel kann auch auf solche Produkte angewendet werden, bei denen einige Teiler der Zahl ganzzahlig oder gemischt sind, wenn wir nur die ganze Zahl als Bruch mit dem Nenner eins betrachten und gemischte Zahlen in unechte Brüche umwandeln. Zum Beispiel:
§ 147. Grundeigenschaften der Multiplikation. Zur Multiplikation von Bruchzahlen gehören auch jene Eigenschaften der Multiplikation, die wir für ganze Zahlen angegeben haben (§ 56, 57, 59). Lassen Sie uns diese Eigenschaften spezifizieren.

1) Das Produkt ändert sich nicht, wenn die Orte der Faktoren geändert werden.

Zum Beispiel:

In der Tat ist nach der Regel des vorherigen Absatzes das erste Produkt gleich dem Bruch und das zweite gleich dem Bruch. Aber diese Brüche sind gleich, weil sich ihre Terme nur in der Reihenfolge der ganzzahligen Faktoren unterscheiden und das Produkt ganzer Zahlen sich nicht ändert, wenn die Stellen der Faktoren wechseln.

2) Das Produkt ändert sich nicht, wenn irgendeine Gruppe von Faktoren durch ihr Produkt ersetzt wird.

Zum Beispiel:

Die Ergebnisse sind die gleichen.

Aus dieser Eigenschaft der Multiplikation kann man folgende Schlussfolgerung ableiten:

Um eine Zahl mit einem Produkt zu multiplizieren, können Sie diese Zahl mit dem ersten Faktor multiplizieren, die resultierende Zahl mit dem zweiten multiplizieren und so weiter.

Zum Beispiel:
3) Das Distributivgesetz der Multiplikation (in Bezug auf die Addition). Um die Summe mit einer Zahl zu multiplizieren, kannst du jeden Term separat mit dieser Zahl multiplizieren und die Ergebnisse addieren.

Dieses Gesetz ist von uns (§ 59) auf ganze Zahlen angewendet erklärt worden. Sie bleibt unverändert für Bruchzahlen gültig.

Zeigen wir in der Tat, dass die Gleichheit

(a + b + c + .)m = am + bm + cm + .

(das Verteilungsgesetz der Multiplikation in Bezug auf die Addition) bleibt auch dann gültig, wenn die Buchstaben Bruchzahlen bedeuten. Betrachten wir drei Fälle.

1) Nehmen wir zunächst an, dass der Faktor m eine ganze Zahl ist, zum Beispiel m = 3 (a, b, c sind beliebige Zahlen). Nach der Definition der Multiplikation mit einer ganzen Zahl kann man schreiben (der Einfachheit halber auf drei Terme beschränkt):

(a + b + c) * 3 = (a + b + c) + (a + b + c) + (a + b + c).

Aufgrund des assoziativen Additionsgesetzes können wir alle Klammern auf der rechten Seite weglassen; Wenn wir das kommutative Additionsgesetz und dann wieder das Kombinationsgesetz anwenden, können wir die rechte Seite offensichtlich wie folgt umschreiben:

(a + a + a) + (b + b + b) + (c + c + c).

(a + b + c) * 3 = a * 3 + b * 3 + c * 3.

Damit ist das Distributivgesetz in diesem Fall bestätigt.

Division eines Bruchs durch eine natürliche Zahl

Abschnitte: Mathematik

T Klassenart: ONZ (Entdeckung neuen Wissens - nach der Technologie der Aktivitätsmethode des Unterrichts).

1. Methoden zur Division eines Bruchs durch eine natürliche Zahl herleiten;
2. Um die Fähigkeit zu bilden, die Division eines Bruchs durch eine natürliche Zahl durchzuführen;
3. Wiederholen und konsolidieren Sie die Division von Brüchen;
4. Trainieren Sie die Fähigkeit, Brüche zu kürzen, Probleme zu analysieren und zu lösen.

Ausrüstungsdemomaterial:

1. Aufgaben zur Wissensaktualisierung:

2. Probeaufgabe (Einzelaufgabe).

1. Division durchführen:

2. Führen Sie die Division durch, ohne die gesamte Rechenkette auszuführen: .

• Wenn du einen Bruch durch eine natürliche Zahl dividierst, kannst du den Nenner mit dieser Zahl multiplizieren und den Zähler gleich lassen.

• Wenn der Zähler durch eine natürliche Zahl teilbar ist, können Sie beim Teilen eines Bruchs durch diese Zahl den Zähler durch die Zahl teilen und den Nenner gleich lassen.

I. Motivation (Selbstbestimmung) für Lernaktivitäten.

1. Die Verwirklichung der Anforderungen an den Schüler seitens der Bildungsaktivitäten organisieren („Muss“);
2. Organisieren Sie die Aktivitäten der Schüler, um einen thematischen Rahmen zu schaffen („Ich kann“);
3. Bedingungen schaffen, damit der Schüler ein inneres Bedürfnis nach Inklusion in Bildungsaktivitäten hat („Ich will“).

Organisation des Bildungsprozesses in Stufe I.

Hallo! Ich freue mich, Sie alle im Matheunterricht zu sehen. Ich hoffe, es beruht auf Gegenseitigkeit.

Leute, welche neuen Erkenntnisse habt ihr in der letzten Lektion erworben? (Brüche dividieren).

Recht. Was hilft dir beim Dividieren von Brüchen? (Regel, Eigenschaften).

Wo brauchen wir dieses Wissen? (In Beispielen, Gleichungen, Aufgaben).

Gut erledigt! In der letzten Stunde hast du dich gut geschlagen. Sie möchten heute selbst neues Wissen entdecken? (Ja).

Dann geh! Und das Motto des Unterrichts lautet: „Mathematik lernt man nicht, indem man zuschaut, wie es der Nachbar macht!“.

II. Aktualisierung des Wissens und Fixierung einer individuellen Schwierigkeit in einer Probehandlung.

1. Die Aktualisierung der untersuchten Handlungsmethoden zu organisieren, die ausreicht, um neues Wissen aufzubauen. Fixieren Sie diese Methoden verbal (in der Sprache) und symbolisch (Standard) und verallgemeinern Sie sie;
2. Organisieren Sie die Aktualisierung von mentalen Operationen und kognitiven Prozessen, die ausreichen, um neues Wissen aufzubauen;
3. Motivation für eine Probeklage und deren eigenständige Durchführung und Begründung;
4. Eine individuelle Aufgabe für eine Schnupperaktion stellen und analysieren, um neue Bildungsinhalte zu identifizieren;
5. Organisieren Sie die Festlegung des Bildungsziels und des Unterrichtsthemas;
6. Organisation der Durchführung einer Probeaktion und Behebung der Schwierigkeit;
7. Organisieren Sie eine Analyse der erhaltenen Antworten und erfassen Sie individuelle Schwierigkeiten, eine Probemaßnahme durchzuführen oder zu rechtfertigen.

Organisation des Bildungsprozesses auf Stufe II.

Frontal mit Tablets (Einzeltafeln).

1. Ausdrücke vergleichen:

(Diese Ausdrücke sind gleich)

Welche interessanten Dinge sind Ihnen aufgefallen? (Der Zähler und Nenner des Dividenden, der Zähler und Nenner des Divisors in jedem Ausdruck werden um die gleiche Anzahl von Malen erhöht. Daher werden die Dividenden und Divisoren in den Ausdrücken durch Brüche dargestellt, die einander gleich sind).

Finde die Bedeutung des Ausdrucks und schreibe sie auf die Tafel. (2)

Wie schreibt man diese Zahl als Bruch?

Wie haben Sie die Teilungsaktion durchgeführt? (Kinder sprechen die Regel aus, der Lehrer hängt Buchstaben an die Tafel)

2. Berechnen und notieren Sie nur die Ergebnisse:

3. Addieren Sie Ihre Ergebnisse und schreiben Sie Ihre Antwort auf. (2)

Wie heißt die Nummer aus Aufgabe 3? (Natürlich)

Glaubst du, du kannst einen Bruch durch eine natürliche Zahl teilen? (Ja, wir werden es versuchen)

Versuche dies.

4. Individuelle (Probe-)Aufgabe.

Führen Sie die Division durch: (nur Beispiel a)

Nach welcher Regel hast du geteilt? (Nach der Regel, einen Bruch durch einen Bruch zu teilen)

Und jetzt teilen Sie den Bruch auf einfachere Weise durch eine natürliche Zahl, ohne die gesamte Rechenkette durchzuführen: (Beispiel b). Ich gebe Ihnen dafür 3 Sekunden.

Wer hat die Aufgabe nicht in 3 Sekunden erledigt?

Wer hat es gemacht? (Es gibt keine solchen)

Wieso den? (Wir kennen den Weg nicht)

Was hast du bekommen? (Schwierigkeit)

Was denkst du, werden wir im Unterricht machen? (Brüche durch natürliche Zahlen dividieren)

Richtig, öffnen Sie Ihre Notizbücher und schreiben Sie das Thema der Lektion "Teilen eines Bruchs durch eine natürliche Zahl" auf.

Warum klingt dieses Thema neu, wenn Sie bereits wissen, wie man Brüche dividiert? (Brauche einen neuen Weg)

Recht. Heute werden wir eine Technik etablieren, die die Division eines Bruchs durch eine natürliche Zahl vereinfacht.

III. Identifizierung des Ortes und der Ursache der Schwierigkeit.

1. Organisieren Sie die Wiederherstellung abgeschlossener Operationen und fixieren Sie (verbal und symbolisch) den Ort - Schritt, Operation, an dem die Schwierigkeit aufgetreten ist;
2. Die Korrelation der Aktionen der Schüler mit der verwendeten Methode (Algorithmus) und die Fixierung der Ursache der Schwierigkeit in externer Sprache zu organisieren - jene spezifischen Kenntnisse, Fähigkeiten oder Fähigkeiten, die nicht ausreichen, um das anfängliche Problem dieser Art zu lösen.

Organisation des Bildungsprozesses auf Stufe III.

Welche Aufgabe mussten Sie erledigen? (Teile einen Bruch durch eine natürliche Zahl, ohne die ganze Rechenkette zu durchlaufen)

Was hat Ihnen Schwierigkeiten bereitet? (Konnte in kurzer Zeit nicht schnell gelöst werden)

Was ist das Ziel unseres Unterrichts? (Finden Sie einen schnellen Weg, einen Bruch durch eine natürliche Zahl zu dividieren)

Was wird Ihnen helfen? (Bereits bekannte Regel zur Division von Brüchen)

IV. Bau des Projekts eines Ausgangs aus Schwierigkeiten.

1. Klärung des Zwecks des Projekts;
2. Methodenwahl (Klärung);
3. Definition von Fonds (Algorithmus);
4. Erstellen Sie einen Plan, um das Ziel zu erreichen.

Organisation des Bildungsprozesses auf Stufe IV.

Kommen wir zurück zum Testfall. Hast du gesagt, dass du nach der Bruchregel dividiert hast? (Ja)

Dazu eine natürliche Zahl durch einen Bruch ersetzen? (Ja)

Welche(n) Schritt(e) können Sie Ihrer Meinung nach überspringen?

(Die Lösungskette ist auf dem Brett offen:

Analysieren und ein Fazit ziehen. (Schritt 1)

Wenn es keine Antwort gibt, fassen wir die Fragen zusammen:

Wo ist der natürliche Teiler geblieben? (zum Nenner)

Hat sich der Zähler geändert? (Nein)

Welcher Schritt kann also "weggelassen" werden? (Schritt 1)

• Multipliziere den Nenner eines Bruchs mit einer natürlichen Zahl.
• Der Zähler ändert sich nicht.
• Wir bekommen einen neuen Bruch.

V. Umsetzung des errichteten Projekts.

1. Organisieren Sie die kommunikative Interaktion, um das konstruierte Projekt umzusetzen, das darauf abzielt, das fehlende Wissen zu erwerben;
2. Organisieren Sie die Fixierung der konstruierten Handlungsweise in Sprache und Zeichen (mit Hilfe eines Standards);
3. Organisieren Sie die Lösung des ursprünglichen Problems und notieren Sie die Überwindung der Schwierigkeit;
4. Organisieren Sie eine Klärung der Allgemeinheit des neuen Wissens.

Organisation des Bildungsprozesses auf Stufe V.

Führen Sie den Testfall jetzt schnell auf die neue Weise aus.

Können Sie die Aufgabe jetzt schnell erledigen? (Ja)

Erklären Sie, wie Sie es gemacht haben? (Kinder sprechen)

Das bedeutet, dass wir neue Erkenntnisse erhalten haben: die Regel zum Teilen eines Bruchs durch eine natürliche Zahl.

Gut erledigt! Sagen Sie es zu zweit.

Dann spricht ein Schüler zur Klasse. Wir fixieren den Regelalgorithmus mündlich und in Form eines Standards an der Tafel.

Geben Sie nun die Buchstabenbezeichnungen ein und schreiben Sie die Formel für unsere Regel auf.

Der Schüler schreibt an die Tafel und spricht die Regel aus: Wenn Sie einen Bruch durch eine natürliche Zahl teilen, können Sie den Nenner mit dieser Zahl multiplizieren und den Zähler gleich lassen.

(Jeder schreibt die Formel in Hefte).

Analysieren Sie nun noch einmal die Lösungskette der Versuchsaufgabe und achten Sie dabei besonders auf die Antwort. Was haben Sie gemacht? (Der Zähler des Bruchs 15 wurde durch die Zahl 3 geteilt (gekürzt))

Was ist das für eine Nummer? (Natürlich, Divisor)

Wie sonst kann man also einen Bruch durch eine natürliche Zahl dividieren? (Überprüfen Sie: Wenn der Zähler eines Bruchs durch diese natürliche Zahl teilbar ist, können Sie den Zähler durch diese Zahl teilen, das Ergebnis in den Zähler des neuen Bruchs schreiben und den Nenner gleich lassen.)

Schreiben Sie diese Methode in Form einer Formel. (Der Schüler schreibt die Regel an die Tafel. Alle schreiben die Formel in Hefte.)

Kommen wir zurück zur ersten Methode. Kann es verwendet werden, wenn a:n? (Ja, das ist der allgemeine Weg)

Und wann ist die zweite Methode bequem anzuwenden? (Wenn der Zähler eines Bruchs ohne Rest durch eine natürliche Zahl teilbar ist)

VI. Primäre Konsolidierung mit Aussprache in der externen Sprache.

1. Organisation der Aneignung einer neuen Handlungsweise durch Kinder bei der Lösung typischer Probleme mit ihrer Aussprache in der Außensprache (frontal, zu zweit oder in Gruppen).

Organisation des Bildungsprozesses auf Stufe VI.

Neu rechnen:

• Nr. 363 (a; d) - an der Tafel auftreten und die Regel aussprechen.
• Nr. 363 (d; f) - paarweise mit einem Scheck auf dem Muster.

VII. Eigenständiges Arbeiten mit Selbsttest nach Norm.

1. Eigenständige Aufgabenerfüllung der Studierenden für eine neue Handlungsweise zu organisieren;
2. Selbsttest anhand des Vergleichs mit der Norm organisieren;
3. Organisieren Sie auf der Grundlage der Ergebnisse der unabhängigen Arbeit eine Reflexion über die Assimilation einer neuen Handlungsweise.

Organisation des Bildungsprozesses auf Stufe VII.

Neu rechnen:

Die Schüler überprüfen den Standard, notieren die Korrektheit der Leistung. Fehlerursachen werden analysiert und Fehler behoben.

Der Lehrer fragt die Schüler, die Fehler gemacht haben, was ist der Grund?

In dieser Phase ist es wichtig, dass jeder Schüler seine Arbeit selbstständig überprüft.

Betrachten Sie vor der Lösung von Aufgabe 8) ein Beispiel aus dem Lehrbuch:

IX. Reflexion der Lernaktivitäten im Unterricht.

1. Organisieren Sie die Fixierung neuer Inhalte, die in der Lektion gelernt wurden;
2. Organisieren Sie eine reflektierende Analyse der Bildungsaktivitäten im Hinblick auf die Erfüllung der den Schülern bekannten Anforderungen.
3. Organisieren Sie die Bewertung der eigenen Aktivitäten der Schüler im Unterricht;
4. Organisieren Sie die Fixierung ungelöster Schwierigkeiten im Unterricht als Richtung für zukünftige Lernaktivitäten;
5. Diskussionen organisieren und Hausaufgaben aufzeichnen.

Organisation des Bildungsprozesses auf Stufe IX.

Leute, welche neuen Erkenntnisse habt ihr heute entdeckt? (Wir haben gelernt, auf einfache Weise einen Bruch durch eine natürliche Zahl zu dividieren)

Formulieren Sie einen allgemeinen Weg. (Man sagt)

Auf welche Weise und in welchen Fällen können Sie es noch verwenden? (Man sagt)

Was ist der Vorteil der neuen Methode?

Haben wir unser Unterrichtsziel erreicht? (Ja)

Welches Wissen haben Sie genutzt, um das Ziel zu erreichen? (Man sagt)

Ist es Ihnen gelungen?

Was waren die Schwierigkeiten?

§ 87. Addition von Brüchen.

Das Addieren von Brüchen hat viele Ähnlichkeiten mit dem Addieren ganzer Zahlen. Die Addition von Brüchen ist eine Aktion, die darin besteht, dass mehrere gegebene Zahlen (Begriffe) zu einer Zahl (Summe) kombiniert werden, die alle Einheiten und Brüche von Einheiten von Begriffen enthält.

Wir betrachten der Reihe nach drei Fälle:

1. Addition von Brüchen mit gleichem Nenner.
2. Addition von Brüchen mit unterschiedlichen Nennern.
3. Addition von gemischten Zahlen.

1. Addition von Brüchen mit gleichem Nenner.

Betrachten Sie ein Beispiel: 1 / 5 + 2 / 5 .

Nehmen Sie das Segment AB (Abb. 17), nehmen Sie es als Einheit und teilen Sie es in 5 gleiche Teile, dann entspricht der Teil AC dieses Segments 1/5 des Segments AB und der Teil desselben Segments CD entspricht 2/5 AB.

Aus der Zeichnung ist ersichtlich, dass, wenn wir das Segment AD nehmen, es gleich 3/5 AB ist; aber das Segment AD ist genau die Summe der Segmente AC und CD. Wir können also schreiben:

1 / 5 + 2 / 5 = 3 / 5

Wenn wir diese Terme und den resultierenden Betrag betrachten, sehen wir, dass der Zähler der Summe durch Addition der Zähler der Terme erhalten wurde und der Nenner unverändert blieb.

Daraus erhalten wir folgende Regel: Um Brüche mit demselben Nenner zu addieren, müssen Sie ihre Zähler addieren und denselben Nenner belassen.

Betrachten Sie ein Beispiel:

2. Addition von Brüchen mit unterschiedlichen Nennern.

Addieren wir Brüche: 3/4 + 3/8 Zuerst müssen sie auf den kleinsten gemeinsamen Nenner gebracht werden:

Das Zwischenglied 6/8 + 3/8 hätte nicht geschrieben werden können; Wir haben es hier für mehr Klarheit geschrieben.

Um also Brüche mit unterschiedlichen Nennern zu addieren, musst du sie zuerst auf den kleinsten gemeinsamen Nenner bringen, ihre Zähler addieren und den gemeinsamen Nenner vorzeichenen.

Betrachten Sie ein Beispiel (wir schreiben zusätzliche Faktoren über die entsprechenden Brüche):

3. Addition von gemischten Zahlen.

Addieren wir die Zahlen: 2 3 / 8 + 3 5 / 6.

Bringen wir zunächst die Bruchteile unserer Zahlen auf einen gemeinsamen Nenner und schreiben sie noch einmal um:

Fügen Sie nun der Reihe nach die ganzzahligen und gebrochenen Teile hinzu:

§ 88. Subtraktion von Brüchen.

Die Subtraktion von Brüchen wird genauso definiert wie die Subtraktion von ganzen Zahlen. Dies ist eine Aktion, bei der aus der Summe von zwei Termen und einem von ihnen ein weiterer Term gefunden wird. Betrachten wir der Reihe nach drei Fälle:

1. Subtraktion von Brüchen mit gleichem Nenner.
2. Subtraktion von Brüchen mit unterschiedlichen Nennern.
3. Subtraktion gemischter Zahlen.

1. Subtraktion von Brüchen mit gleichem Nenner.

Betrachten Sie ein Beispiel:

13 / 15 - 4 / 15

Nehmen wir das Segment AB (Abb. 18), nehmen es als Einheit und teilen es in 15 gleiche Teile; dann entspricht der AC-Teil dieses Segments 1/15 von AB, und der AD-Teil desselben Segments entspricht 13/15 AB. Lassen Sie uns ein weiteres Segment ED beiseite legen, gleich 4/15 AB.

Wir müssen 4/15 von 13/15 subtrahieren. In der Zeichnung bedeutet dies, dass das Segment ED vom Segment AD subtrahiert werden muss. Infolgedessen bleibt das Segment AE bestehen, was 9/15 des Segments AB entspricht. Wir können also schreiben:

Das von uns gemachte Beispiel zeigt, dass der Zähler der Differenz durch Subtraktion der Zähler erhalten wurde und der Nenner gleich blieb.

Um also Brüche mit gleichem Nenner zu subtrahieren, musst du den Zähler des Subtrahenten vom Zähler des Minuends subtrahieren und den gleichen Nenner belassen.

2. Subtraktion von Brüchen mit unterschiedlichen Nennern.

Beispiel. 3/4 - 5/8

Lassen Sie uns diese Brüche zunächst auf den kleinsten gemeinsamen Nenner bringen:

Der Zwischenlink 6 / 8 - 5 / 8 wird hier aus Gründen der Übersichtlichkeit geschrieben, kann aber in Zukunft übersprungen werden.

Um also einen Bruch von einem Bruch zu subtrahieren, musst du sie zuerst auf den kleinsten gemeinsamen Nenner bringen, dann den Zähler des Subtrahenten vom Zähler des Minuends subtrahieren und den gemeinsamen Nenner unter ihrer Differenz signieren.

Betrachten Sie ein Beispiel:

3. Subtraktion gemischter Zahlen.

Beispiel. 10 3 / 4 - 7 2 / 3 .

Bringen wir die Nachkommastellen von Minuend und Subtrahend auf den kleinsten gemeinsamen Nenner:

Wir subtrahieren ein Ganzes von einem Ganzen und einen Bruch von einem Bruch. Aber es gibt Fälle, in denen der Bruchteil des Subtrahends größer ist als der Bruchteil des Minuends. In solchen Fällen müssen Sie eine Einheit aus dem ganzzahligen Teil des reduzierten Teils nehmen, sie in die Teile aufteilen, in denen der Bruchteil ausgedrückt wird, und zum Bruchteil des reduzierten Teils hinzufügen. Und dann wird die Subtraktion auf die gleiche Weise wie im vorherigen Beispiel durchgeführt:

§ 89. Multiplikation von Brüchen.

Beim Studium der Multiplikation von Brüchen werden wir die folgenden Fragen berücksichtigen:

1. Einen Bruch mit einer ganzen Zahl multiplizieren.
2. Finden eines Bruchteils einer gegebenen Zahl.
3. Multiplikation einer ganzen Zahl mit einem Bruch.
4. Einen Bruch mit einem Bruch multiplizieren.
5. Multiplikation gemischter Zahlen.
6. Das Konzept des Interesses.
7. Finden von Prozentsätzen einer gegebenen Zahl. Betrachten wir sie der Reihe nach.

1. Einen Bruch mit einer ganzen Zahl multiplizieren.

Das Multiplizieren eines Bruchs mit einer ganzen Zahl hat dieselbe Bedeutung wie das Multiplizieren einer ganzen Zahl mit einer ganzen Zahl. Einen Bruch (Multiplikand) mit einer ganzen Zahl (Multiplikator) zu multiplizieren bedeutet, die Summe identischer Terme zu bilden, wobei jeder Term gleich dem Multiplikanden und die Anzahl der Terme gleich dem Multiplikator ist.

Wenn Sie also 1/9 mit 7 multiplizieren müssen, können Sie dies folgendermaßen tun:

Wir haben das Ergebnis leicht erhalten, da die Aktion auf das Addieren von Brüchen mit demselben Nenner reduziert wurde. Somit,

Die Betrachtung dieser Aktion zeigt, dass das Multiplizieren eines Bruchs mit einer Ganzzahl dem Erhöhen dieses Bruchs so oft entspricht, wie es Einheiten in der Ganzzahl gibt. Und da die Erhöhung des Bruchs entweder durch Erhöhen seines Zählers erreicht wird

oder indem man seinen Nenner verringert , dann können wir entweder den Zähler mit der ganzen Zahl multiplizieren oder den Nenner durch sie dividieren, falls eine solche Division möglich ist.

Von hier erhalten wir die Regel:

Um einen Bruch mit einer Ganzzahl zu multiplizieren, müssen Sie den Zähler mit dieser Ganzzahl multiplizieren und den Nenner gleich lassen oder, wenn möglich, den Nenner durch diese Zahl teilen, wobei der Zähler unverändert bleibt.

Beim Multiplizieren sind Abkürzungen möglich, zum Beispiel:

2. Finden eines Bruchteils einer gegebenen Zahl. Es gibt viele Aufgaben, bei denen Sie einen Teil einer gegebenen Zahl finden oder berechnen müssen. Der Unterschied zwischen diesen Aufgaben und anderen besteht darin, dass sie die Anzahl einiger Objekte oder Maßeinheiten angeben und Sie einen Teil dieser Nummer finden müssen, der hier auch durch einen bestimmten Bruch angegeben wird. Um das Verständnis zu erleichtern, werden wir zunächst Beispiele für solche Probleme geben und dann die Methode zu ihrer Lösung vorstellen.

Aufgabe 1. Ich hatte 60 Rubel; 1/3 dieses Geldes habe ich für den Kauf von Büchern ausgegeben. Wie viel haben die Bücher gekostet?

Aufgabe 2. Der Zug muss die Strecke zwischen den Städten A und B zurücklegen, die 300 km entspricht. 2/3 dieser Strecke hat er bereits zurückgelegt. Wie viele Kilometer sind das?

Aufgabe 3. Es gibt 400 Häuser im Dorf, 3/4 davon sind aus Backstein, der Rest aus Holz. Wie viele Backsteinhäuser gibt es?

Hier sind einige der vielen Probleme, mit denen wir uns befassen müssen, um einen Bruchteil einer gegebenen Zahl zu finden. Sie werden normalerweise Probleme zum Finden eines Bruchteils einer gegebenen Zahl genannt.

Lösung des Problems 1. Ab 60 Rubel. Ich habe 1/3 für Bücher ausgegeben; Um also die Kosten für Bücher zu ermitteln, müssen Sie die Zahl 60 durch 3 teilen:

Problemlösung 2. Die Bedeutung des Problems ist, dass Sie 2 / 3 von 300 km finden müssen. Berechnen Sie das erste 1/3 von 300; Dies wird erreicht, indem 300 km durch 3 geteilt werden:

300: 3 = 100 (das ist 1/3 von 300).

Um zwei Drittel von 300 zu finden, müssen Sie den resultierenden Quotienten verdoppeln, also mit 2 multiplizieren:

100 x 2 = 200 (das sind 2/3 von 300).

Lösung des Problems 3. Hier müssen Sie die Anzahl der Backsteinhäuser bestimmen, die 3/4 von 400 ausmachen. Lassen Sie uns zuerst 1/4 von 400 finden,

400: 4 = 100 (das ist 1/4 von 400).

Um drei Viertel von 400 zu berechnen, muss der resultierende Quotient verdreifacht, also mit 3 multipliziert werden:

100 x 3 = 300 (das sind 3/4 von 400).

Basierend auf der Lösung dieser Probleme können wir die folgende Regel ableiten:

Um den Wert eines Bruchs einer gegebenen Zahl zu finden, musst du diese Zahl durch den Nenner des Bruchs dividieren und den resultierenden Quotienten mit seinem Zähler multiplizieren.

3. Multiplikation einer ganzen Zahl mit einem Bruch.

Zuvor (§ 26) wurde festgelegt, dass die Multiplikation ganzer Zahlen als Addition identischer Terme zu verstehen ist (5 x 4 \u003d 5 + 5 + 5 + 5 \u003d 20). In diesem Absatz (Absatz 1) wurde festgelegt, dass die Multiplikation eines Bruchs mit einer ganzen Zahl bedeutet, dass die Summe identischer Terme gleich diesem Bruch ist.

In beiden Fällen bestand die Multiplikation darin, die Summe identischer Terme zu finden.

Jetzt gehen wir dazu über, eine ganze Zahl mit einem Bruch zu multiplizieren. Hier werden wir zum Beispiel auf eine solche Multiplikation treffen: 9 2 / 3. Es ist ziemlich offensichtlich, dass die vorherige Definition der Multiplikation auf diesen Fall nicht zutrifft. Das zeigt sich daran, dass wir eine solche Multiplikation nicht durch Addition gleicher Zahlen ersetzen können.

Aus diesem Grund werden wir die Multiplikation neu definieren müssen, d.h. mit anderen Worten die Frage beantworten müssen, was unter einer Multiplikation mit einem Bruch zu verstehen ist, wie diese Aktion zu verstehen ist.

Die Bedeutung der Multiplikation einer ganzen Zahl mit einem Bruch ergibt sich aus der folgenden Definition: eine ganze Zahl (Multiplikator) mit einem Bruch (Multiplikator) zu multiplizieren bedeutet, diesen Bruchteil des Multiplikators zu finden.

Das Multiplizieren von 9 mit 2/3 bedeutet nämlich, 2/3 von neun Einheiten zu finden. Im vorherigen Absatz wurden solche Probleme gelöst; Es ist also leicht herauszufinden, dass wir am Ende 6 haben.

Aber jetzt stellt sich eine interessante und wichtige Frage: Warum werden scheinbar unterschiedliche Aktionen wie das Finden der Summe gleicher Zahlen und das Finden des Bruchs einer Zahl in der Arithmetik mit demselben Wort „Multiplikation“ bezeichnet?

Dies geschieht, weil die vorherige Aktion (mehrfaches Wiederholen der Zahl mit Begriffen) und die neue Aktion (Finden des Bruchs einer Zahl) eine Antwort auf homogene Fragen geben. Das heißt, wir gehen hier von den Überlegungen aus, dass homogene Fragestellungen bzw. Aufgaben durch ein und dieselbe Handlung gelöst werden.

Um dies zu verstehen, betrachten Sie das folgende Problem: „1 m Stoff kostet 50 Rubel. Wie viel kosten 4 m eines solchen Stoffes?

Dieses Problem wird gelöst, indem die Anzahl der Rubel (50) mit der Anzahl der Meter (4) multipliziert wird, d. H. 50 x 4 = 200 (Rubel).

Nehmen wir das gleiche Problem, aber darin wird die Stoffmenge als Bruchzahl ausgedrückt: „1 m Stoff kostet 50 Rubel. Wie viel kosten 3/4 m eines solchen Stoffes?

Dieses Problem muss auch gelöst werden, indem die Anzahl der Rubel (50) mit der Anzahl der Meter (3/4) multipliziert wird.

Sie können die darin enthaltenen Zahlen auch mehrmals ändern, ohne die Bedeutung der Aufgabe zu ändern, z. B. 9/10 m oder 2 3/10 m usw.

Da diese Probleme den gleichen Inhalt haben und sich nur in Zahlen unterscheiden, nennen wir die Aktionen, die zu ihrer Lösung verwendet werden, das gleiche Wort - Multiplikation.

Wie wird eine ganze Zahl mit einem Bruch multipliziert?

Nehmen wir die Zahlen aus dem letzten Problem:

Gemäß der Definition müssen wir 3 / 4 von 50 finden. Zuerst finden wir 1 / 4 von 50 und dann 3 / 4.

1/4 von 50 ist 50/4;

3/4 von 50 ist .

Somit.

Betrachten Sie ein anderes Beispiel: 12 5 / 8 = ?

1/8 von 12 ist 12/8,

5/8 der Zahl 12 ist .

Somit,

Von hier erhalten wir die Regel:

Um eine ganze Zahl mit einem Bruch zu multiplizieren, müssen Sie die ganze Zahl mit dem Zähler des Bruchs multiplizieren und dieses Produkt zum Zähler machen und den Nenner des gegebenen Bruchs als Nenner signieren.

Wir schreiben diese Regel mit Buchstaben:

Um diese Regel ganz klar zu machen, sei daran erinnert, dass ein Bruch als Quotient betrachtet werden kann. Daher ist es sinnvoll, die gefundene Regel mit der in § 38 aufgestellten Regel zum Multiplizieren einer Zahl mit einem Quotienten zu vergleichen

Es muss daran erinnert werden, dass Sie vor der Multiplikation (wenn möglich) Folgendes tun sollten: Schnitte, Zum Beispiel:

4. Einen Bruch mit einem Bruch multiplizieren. Das Multiplizieren eines Bruchs mit einem Bruch hat dieselbe Bedeutung wie das Multiplizieren einer Ganzzahl mit einem Bruch, dh wenn Sie einen Bruch mit einem Bruch multiplizieren, müssen Sie den Bruch im Multiplikator aus dem ersten Bruch (Multiplikator) finden.

Das Multiplizieren von 3/4 mit 1/2 (halb) bedeutet nämlich, die Hälfte von 3/4 zu finden.

Wie multipliziert man einen Bruch mit einem Bruch?

Nehmen wir ein Beispiel: 3/4 mal 5/7. Das bedeutet, dass Sie 5/7 aus 3/4 finden müssen. Finden Sie zuerst 1/7 von 3/4 und dann 5/7

1/7 von 3/4 würde so ausgedrückt werden:

5 / 7 Zahlen 3 / 4 werden wie folgt ausgedrückt:

Auf diese Weise,

Ein weiteres Beispiel: 5/8 mal 4/9.

1/9 von 5/8 ist ,

4/9 Zahlen 5/8 sind .

Auf diese Weise,

Aus diesen Beispielen lässt sich folgende Regel ableiten:

Um einen Bruch mit einem Bruch zu multiplizieren, musst du den Zähler mit dem Zähler und den Nenner mit dem Nenner multiplizieren und das erste Produkt zum Zähler und das zweite Produkt zum Nenner des Produkts machen.

Diese Regel lässt sich allgemein wie folgt schreiben:

Beim Multiplizieren müssen (wenn möglich) Abstriche gemacht werden. Betrachten Sie Beispiele:

5. Multiplikation gemischter Zahlen. Da gemischte Zahlen leicht durch unechte Brüche ersetzt werden können, macht man sich diesen Umstand meist bei der Multiplikation gemischter Zahlen zunutze. Das bedeutet, dass in den Fällen, in denen der Multiplikand oder der Multiplikator oder beide Faktoren als gemischte Zahlen ausgedrückt werden, diese durch unechte Brüche ersetzt werden. Multiplizieren Sie zum Beispiel gemischte Zahlen: 2 1/2 und 3 1/5. Wir verwandeln jeden von ihnen in einen unechten Bruch und multiplizieren dann die resultierenden Brüche gemäß der Regel, einen Bruch mit einem Bruch zu multiplizieren:

Regel. Um gemischte Zahlen zu multiplizieren, musst du sie zuerst in unechte Brüche umwandeln und dann gemäß der Regel der Multiplikation eines Bruchs mit einem Bruch multiplizieren.

Notiz. Wenn einer der Faktoren eine ganze Zahl ist, kann die Multiplikation nach dem Verteilungsgesetz wie folgt durchgeführt werden:

6. Das Konzept des Interesses. Beim Lösen von Problemen und bei verschiedenen praktischen Berechnungen verwenden wir alle Arten von Brüchen. Aber man muss bedenken, dass viele Größen keine, sondern für sie natürliche Unterteilungen zulassen. Zum Beispiel können Sie ein Hundertstel (1/100) eines Rubels nehmen, es wird ein Penny sein, zwei Hundertstel sind 2 Kopeken, drei Hundertstel sind 3 Kopeken. Sie können 1/10 des Rubels nehmen, es sind "10 Kopeken oder ein Cent. Sie können ein Viertel des Rubels nehmen, d. H. 25 Kopeken, einen halben Rubel, d. H. 50 Kopeken (fünfzig Kopeken). Aber sie ziehen praktisch an Nehmen Sie zum Beispiel nicht 2/7 Rubel, da der Rubel nicht in Siebtel unterteilt ist.

Die Maßeinheit für das Gewicht, also das Kilogramm, erlaubt zunächst dezimale Unterteilungen, zum Beispiel 1/10 kg oder 100 g, und solche Bruchteile eines Kilogramms wie 1/6, 1/11, 1/ 13 sind ungewöhnlich.

Im Allgemeinen sind unsere (metrischen) Maße dezimal und erlauben dezimale Unterteilungen.

Es ist jedoch zu beachten, dass es in den unterschiedlichsten Fällen äußerst sinnvoll und bequem ist, die gleiche (einheitliche) Methode zur Unterteilung von Größen zu verwenden. Langjährige Erfahrung hat gezeigt, dass eine solche gut begründete Teilung die „Hundertstel“-Teilung ist. Betrachten wir einige Beispiele, die sich auf die unterschiedlichsten Bereiche menschlicher Praxis beziehen.

1. Der Buchpreis ist um 12/100 des vorherigen Preises gesunken.

Beispiel. Der vorherige Preis des Buches beträgt 10 Rubel. Sie ging um 1 Rubel zurück. 20 Kop.

2. Sparkassen zahlen im Laufe des Jahres 2/100 des eingezahlten Betrags an Sparer aus.

Beispiel. 500 Rubel werden in die Kasse gesteckt, die Einnahmen aus diesem Betrag für das Jahr betragen 10 Rubel.

3. Die Zahl der Absolventen einer Schule betrug 5/100 der Gesamtzahl der Studenten.

BEISPIEL Nur 1.200 Schüler besuchten die Schule, 60 von ihnen absolvierten die Schule.

Das Hundertstel einer Zahl wird Prozent genannt..

Das Wort „Prozent“ ist der lateinischen Sprache entlehnt und seine Wurzel „cent“ bedeutet hundert. Zusammen mit der Präposition (pro centum) bedeutet dieses Wort „für hundert“. Die Bedeutung dieses Ausdrucks ergibt sich aus der Tatsache, dass Zinsen im alten Rom zunächst das Geld waren, das der Schuldner „für jeden Hunderter“ an den Verleiher zahlte. Das Wort "Cent" ist in so bekannten Wörtern zu hören: Zentner (einhundert Kilogramm), Zentimeter (sie sagen Zentimeter).

Anstatt beispielsweise zu sagen, dass das Werk im vergangenen Monat 1/100 aller von ihm hergestellten Produkte produziert hat, sagen wir Folgendes: Das Werk hat im vergangenen Monat ein Prozent der Ausschussware produziert. Anstatt zu sagen: Das Werk produzierte 4/100 Produkte mehr als der festgelegte Plan, werden wir sagen: Das Werk übertraf den Plan um 4 Prozent.

Die obigen Beispiele können anders ausgedrückt werden:

1. Der Preis für Bücher ist um 12 Prozent des vorherigen Preises gesunken.

2. Sparkassen zahlen Einlegern jährlich 2 Prozent des angelegten Sparbetrags aus.

3. Die Zahl der Absolventen einer Schule betrug 5 Prozent der Zahl aller Schüler der Schule.

Um den Buchstaben zu verkürzen, ist es üblich, anstelle des Wortes "Prozent" das %-Zeichen zu schreiben.

Es muss jedoch beachtet werden, dass das %-Zeichen normalerweise nicht in Berechnungen geschrieben wird, es kann in die Problemstellung und in das Endergebnis geschrieben werden. Wenn Sie Berechnungen durchführen, müssen Sie mit diesem Symbol einen Bruch mit einem Nenner von 100 anstelle einer ganzen Zahl schreiben.

Sie müssen in der Lage sein, eine ganze Zahl mit dem angegebenen Symbol durch einen Bruch mit einem Nenner von 100 zu ersetzen:

Umgekehrt müssen Sie sich daran gewöhnen, anstelle eines Bruchs mit dem Nenner 100 eine ganze Zahl mit dem angegebenen Symbol zu schreiben:

7. Finden von Prozentsätzen einer gegebenen Zahl.

Aufgabe 1. Die Schule erhielt 200 Kubikmeter. m Brennholz, wobei Birkenholz 30 % ausmacht. Wie viel Birkenholz war da?

Die Bedeutung dieses Problems ist, dass Birkenbrennholz nur ein Teil des Brennholzes war, das an die Schule geliefert wurde, und dieser Teil wird als Bruchteil von 30 / 100 ausgedrückt. Wir stehen also vor der Aufgabe, einen Bruchteil einer Zahl zu finden. Um es zu lösen, müssen wir 200 mit 30 / 100 multiplizieren (Aufgaben zum Finden des Bruchs einer Zahl werden gelöst, indem eine Zahl mit einem Bruch multipliziert wird.).

Also 30% von 200 sind gleich 60.

Der bei dieser Aufgabe auftretende Bruch 30 / 100 kann um 10 reduziert werden. Es wäre möglich, diese Reduktion von Anfang an durchzuführen; die Lösung des Problems würde sich nicht ändern.

Aufgabe 2. Im Lager waren 300 Kinder unterschiedlichen Alters. Kinder im Alter von 11 Jahren machten 21 % aus, Kinder im Alter von 12 Jahren 61 % und schließlich 13-Jährige 18 %. Wie viele Kinder jeden Alters waren im Lager?

Bei dieser Aufgabe müssen Sie drei Berechnungen durchführen, dh nacheinander die Anzahl der Kinder im Alter von 11 Jahren, dann 12 Jahren und schließlich 13 Jahren ermitteln.

Hier muss also dreimal ein Bruchteil einer Zahl gefunden werden. Machen wir das:

1) Wie viele Kinder waren 11 Jahre alt?

2) Wie viele Kinder waren 12 Jahre alt?

3) Wie viele Kinder waren 13 Jahre alt?

Nach Lösung der Aufgabe ist es sinnvoll, die gefundenen Zahlen zu addieren; Ihre Summe sollte 300 sein:

63 + 183 + 54 = 300

Beachten Sie auch, dass die Summe der in der Problembedingung angegebenen Prozentsätze 100 beträgt:

21% + 61% + 18% = 100%

Dies deutet darauf hin, dass die Gesamtzahl der Kinder im Lager mit 100 % angenommen wurde.

3 a da cha 3. Der Arbeiter erhielt 1.200 Rubel pro Monat. Davon gab er 65 % für Lebensmittel aus, 6 % für Wohnung und Heizung, 4 % für Gas, Strom und Radio, 10 % für Kulturbedarf und 15 % sparte er. Wie viel Geld wurde für die in der Aufgabe angegebenen Bedürfnisse ausgegeben?

Um dieses Problem zu lösen, musst du fünfmal einen Bruchteil der Zahl 1.200 finden.

1) Wie viel Geld wird für Lebensmittel ausgegeben? Die Aufgabe besagt, dass dieser Aufwand 65 % aller Einnahmen ausmacht, also 65/100 der Zahl 1200. Machen wir die Rechnung:

2) Wie viel Geld wurde für eine Wohnung mit Heizung bezahlt? Wenn wir wie die vorherige argumentieren, kommen wir zu folgender Rechnung:

3) Wie viel Geld haben Sie für Gas, Strom und Radio bezahlt?

4) Wie viel Geld wird für kulturelle Zwecke ausgegeben?

5) Wie viel Geld hat der Arbeiter gespart?

Zur Überprüfung ist es sinnvoll, die in diesen 5 Fragen gefundenen Zahlen zu addieren. Der Betrag sollte 1.200 Rubel betragen. Alle Einnahmen werden als 100 % angenommen, was leicht zu überprüfen ist, indem man die Prozentsätze addiert, die in der Bedingung des Problems angegeben sind.

Wir haben drei Probleme gelöst. Trotz der Tatsache, dass es bei diesen Aufgaben um verschiedene Dinge ging (Lieferung von Brennholz für die Schule, Anzahl der Kinder unterschiedlichen Alters, Ausgaben des Arbeiters), wurden sie auf die gleiche Weise gelöst. Dies geschah, weil bei allen Aufgaben ein paar Prozent der angegebenen Zahlen gefunden werden mussten.

§ 90. Teilung von Brüchen.

Beim Studium der Division von Brüchen werden wir die folgenden Fragen berücksichtigen:

1. Teilen Sie eine ganze Zahl durch eine ganze Zahl.
2. Division eines Bruchs durch eine ganze Zahl
3. Division einer ganzen Zahl durch einen Bruch.
4. Division eines Bruchs durch einen Bruch.
5. Division gemischter Zahlen.
6. Finden einer Zahl in Anbetracht ihres Bruchs.
7. Finden einer Zahl anhand ihres Prozentsatzes.

Betrachten wir sie der Reihe nach.

1. Teilen Sie eine ganze Zahl durch eine ganze Zahl.

Wie im Abschnitt über ganze Zahlen angedeutet, ist die Division die Handlung, die darin besteht, dass bei gegebenem Produkt zweier Faktoren (dem Dividenden) und einem dieser Faktoren (dem Divisor) ein weiterer Faktor gefunden wird.

Die Division einer ganzen Zahl durch eine ganze Zahl haben wir in der Abteilung für ganze Zahlen betrachtet. Wir trafen dort auf zwei Fälle von Division: Division ohne Rest oder "ganz" (150: 10 = 15) und Division mit Rest (100: 9 = 11 und 1 im Rest). Wir können daher sagen, dass im Bereich der ganzen Zahlen eine exakte Division nicht immer möglich ist, da der Dividende nicht immer das Produkt aus dem Divisor und der ganzen Zahl ist. Nach der Einführung der Multiplikation mit einem Bruch können wir jeden Fall der Division ganzer Zahlen als möglich betrachten (nur die Division durch Null ist ausgeschlossen).

Zum Beispiel bedeutet das Teilen von 7 durch 12, eine Zahl zu finden, deren Produkt mal 12 7 wäre. Diese Zahl ist der Bruch 7/12, weil 7/12 12 = 7. Ein weiteres Beispiel: 14: 25 = 14/25, weil 14/25 25 = 14.

Um also eine ganze Zahl durch eine ganze Zahl zu teilen, müssen Sie einen Bruch bilden, dessen Zähler gleich dem Dividenden ist und dessen Nenner der Divisor ist.

2. Division eines Bruchs durch eine ganze Zahl.

Teilen Sie den Bruch 6 / 7 durch 3. Gemäß der oben gegebenen Definition der Division haben wir hier das Produkt (6 / 7) und einen der Faktoren (3); Es ist erforderlich, einen solchen zweiten Faktor zu finden, der, wenn er mit 3 multipliziert wird, das gegebene Produkt 6 / 7 ergeben würde. Offensichtlich sollte es dreimal kleiner sein als dieses Produkt. Das bedeutet, dass die vor uns gestellte Aufgabe darin bestand, den Bruch 6 / 7 um das Dreifache zu verkleinern.

Wir wissen bereits, dass die Kürzung eines Bruchs entweder durch Verringerung seines Zählers oder durch Erhöhen seines Nenners erfolgen kann. Daher kann man schreiben:

In diesem Fall ist der Zähler 6 durch 3 teilbar, also sollte der Zähler um das Dreifache reduziert werden.

Nehmen wir ein anderes Beispiel: 5 / 8 geteilt durch 2. Hier ist der Zähler 5 nicht durch 2 teilbar, was bedeutet, dass der Nenner mit dieser Zahl multipliziert werden muss:

Darauf aufbauend können wir die Regel aufstellen: Um einen Bruch durch eine ganze Zahl zu dividieren, musst du den Zähler des Bruchs durch diese ganze Zahl dividieren(wenn möglich), den gleichen Nenner belassen, oder den Nenner des Bruchs mit dieser Zahl multiplizieren und den gleichen Zähler belassen.

3. Division einer ganzen Zahl durch einen Bruch.

Es sei erforderlich, 5 durch 1 / 2 zu dividieren, d.h. eine Zahl zu finden, die nach Multiplikation mit 1 / 2 das Produkt 5 ergibt. Offensichtlich muss diese Zahl größer als 5 sein, da 1 / 2 ein echter Bruch ist, und wenn eine Zahl mit einem echten Bruch multipliziert wird, muss das Produkt kleiner als der Multiplikand sein. Um es klarer zu machen, schreiben wir unsere Aktionen wie folgt: 5: 1 / 2 = X , also x 1 / 2 \u003d 5.

Wir müssen eine solche Zahl finden X , was, wenn es mit 1/2 multipliziert wird, 5 ergeben würde. Da das Multiplizieren einer bestimmten Zahl mit 1/2 bedeutet, 1/2 dieser Zahl zu finden, also 1/2 der unbekannten Zahl X ist 5 und die ganze Zahl X doppelt so viel, d. H. 5 2 \u003d 10.

Also 5: 1 / 2 = 5 2 = 10

Lass uns das Prüfen:

Betrachten wir ein weiteres Beispiel. Es sei erforderlich, 6 durch 2/3 zu teilen. Versuchen wir zunächst, anhand der Zeichnung (Abb. 19) das gewünschte Ergebnis zu finden.

Abb.19

Zeichne ein Segment AB, gleich 6 von einigen Einheiten, und teile jede Einheit in 3 gleiche Teile. In jeder Einheit sind drei Drittel (3 / 3) im gesamten Abschnitt AB 6-mal größer, d.h. E. 18/3. Wir verbinden mit Hilfe von kleinen Klammern 18 erhaltene Segmente von 2; Es wird nur 9 Segmente geben. Das bedeutet, dass der Bruch 2/3 9 mal in b Einheiten enthalten ist, oder anders ausgedrückt, der Bruch 2/3 ist 9 mal kleiner als 6 ganzzahlige Einheiten. Somit,

Wie erhält man dieses Ergebnis ohne eine Zeichnung, die nur Berechnungen verwendet? Wir argumentieren wie folgt: Es ist erforderlich, 6 durch 2 / 3 zu teilen, d.h. es ist erforderlich, die Frage zu beantworten, wie oft 2 / 3 in 6 enthalten ist. Lassen Sie uns zuerst herausfinden: wie oft ist 1 / 3 in 6 enthalten? In einer ganzen Einheit - 3 Drittel und in 6 Einheiten - 6 mal mehr, d. H. 18 Drittel; Um diese Zahl zu finden, müssen wir 6 mit 3 multiplizieren. Also ist 1/3 18-mal in b-Einheiten enthalten und 2/3 ist nicht 18-mal, sondern halb so oft in b enthalten, also 18: 2 = 9. Daher haben wir bei der Division von 6 durch 2 / 3 Folgendes getan:

Von hier aus erhalten wir die Regel zum Teilen einer ganzen Zahl durch einen Bruch. Um eine ganze Zahl durch einen Bruch zu dividieren, müssen Sie diese ganze Zahl mit dem Nenner des gegebenen Bruchs multiplizieren und dieses Produkt zum Zähler machen, indem Sie es durch den Zähler des gegebenen Bruchs dividieren.

Wir schreiben die Regel mit Buchstaben:

Um diese Regel ganz klar zu machen, sei daran erinnert, dass ein Bruch als Quotient betrachtet werden kann. Daher ist es sinnvoll, die gefundene Regel mit der in § 38 aufgestellten Regel zum Teilen einer Zahl durch einen Quotienten zu vergleichen. Beachten Sie, dass dort dieselbe Formel erhalten wurde.

Beim Teilen sind Abkürzungen möglich, zum Beispiel:

4. Division eines Bruchs durch einen Bruch.

Es sei erforderlich, 3/4 durch 3/8 zu teilen. Was bezeichnet die Zahl, die als Ergebnis der Teilung erhalten wird? Es wird die Frage beantworten, wie oft der Bruch 3/8 im Bruch 3/4 enthalten ist. Um dieses Problem zu verstehen, machen wir eine Zeichnung (Abb. 20).

Nehmen Sie das Segment AB, nehmen Sie es als Einheit, teilen Sie es in 4 gleiche Teile und markieren Sie 3 solcher Teile. Das Segment AC entspricht 3/4 des Segments AB. Lassen Sie uns nun jedes der vier Anfangssegmente halbieren, dann wird das Segment AB in 8 gleiche Teile geteilt und jeder dieser Teile wird gleich 1/8 des Segments AB sein. Wir verbinden 3 solcher Segmente mit Bögen, dann ist jedes der Segmente AD und DC gleich 3/8 des Segments AB. Die Zeichnung zeigt, dass das Segment gleich 3/8 genau zweimal in dem Segment gleich 3/4 enthalten ist; Das Ergebnis der Division kann also wie folgt geschrieben werden:

3 / 4: 3 / 8 = 2

Betrachten wir ein weiteres Beispiel. Es sei erforderlich, 15/16 durch 3/32 zu teilen:

Wir können so argumentieren: Wir müssen eine Zahl finden, die nach Multiplikation mit 3 / 32 ein Produkt von 15 / 16 ergibt. Schreiben wir die Berechnungen wie folgt:

15 / 16: 3 / 32 = X

3 / 32 X = 15 / 16

3/32 unbekannte Nummer X bilden 15 / 16

1/32 unbekannte Zahl X ist ,

32 / 32 Zahlen X bilden .

Somit,

Um also einen Bruch durch einen Bruch zu dividieren, müssen Sie den Zähler des ersten Bruchs mit dem Nenner des zweiten multiplizieren und den Nenner des ersten Bruchs mit dem Zähler des zweiten multiplizieren und das erste Produkt zum Zähler und dem machen zweitens der Nenner.

Schreiben wir die Regel mit Buchstaben:

Beim Teilen sind Abkürzungen möglich, zum Beispiel:

5. Division gemischter Zahlen.

Beim Teilen von gemischten Zahlen müssen sie zuerst in unechte Brüche umgewandelt werden, und dann sollten die resultierenden Brüche gemäß den Regeln zum Teilen von Bruchzahlen geteilt werden. Betrachten Sie ein Beispiel:

Gemischte Zahlen in unechte Brüche umwandeln:

Jetzt teilen wir uns auf:

Um also gemischte Zahlen zu dividieren, musst du sie in unechte Brüche umwandeln und dann gemäß der Regel zum Dividieren von Brüchen dividieren.

6. Finden einer Zahl in Anbetracht ihres Bruchs.

Unter den verschiedenen Aufgaben zu Brüchen gibt es manchmal solche, bei denen der Wert eines Bruchteils einer unbekannten Zahl angegeben ist und es erforderlich ist, diese Zahl zu finden. Diese Art von Problem ist umgekehrt zu dem Problem, einen Bruchteil einer gegebenen Zahl zu finden; dort wurde eine Zahl angegeben und es musste ein Bruchteil dieser Zahl gefunden werden, hier wird ein Bruchteil einer Zahl angegeben und es ist erforderlich, diese Zahl selbst zu finden. Diese Idee wird noch deutlicher, wenn wir uns der Lösung dieser Art von Problemen zuwenden.

Aufgabe 1. Am ersten Tag verglasten Glaser 50 Fenster, was 1 / 3 aller Fenster des gebauten Hauses entspricht. Wie viele Fenster hat dieses Haus?

Entscheidung. Die Aufgabe besagt, dass 50 verglaste Fenster 1/3 aller Fenster des Hauses ausmachen, was bedeutet, dass es insgesamt dreimal mehr Fenster gibt, d.h.

Das Haus hatte 150 Fenster.

Aufgabe 2. Der Laden verkaufte 1.500 kg Mehl, das sind 3/8 des gesamten Mehlbestands im Laden. Was war der anfängliche Mehlvorrat des Ladens?

Entscheidung. Aus der Problemstellung ist ersichtlich, dass die verkauften 1.500 kg Mehl 3/8 des Gesamtbestandes ausmachen; das bedeutet, dass 1/8 dieses Bestands dreimal weniger ist, d.h. um ihn zu berechnen, müssen Sie 1500 um das Dreifache reduzieren:

1.500 : 3 = 500 (das ist 1/8 der Aktie).

Offensichtlich wird der gesamte Bestand 8-mal größer sein. Somit,

500 8 \u003d 4.000 (kg).

Der anfängliche Vorrat an Mehl im Lager betrug 4.000 kg.

Aus der Betrachtung dieses Problems kann die folgende Regel abgeleitet werden.

Um eine Zahl durch einen bestimmten Wert ihres Bruchs zu finden, reicht es aus, diesen Wert durch den Zähler des Bruchs zu dividieren und das Ergebnis mit dem Nenner des Bruchs zu multiplizieren.

Wir haben zwei Probleme beim Auffinden einer Zahl in Anbetracht ihres Bruchs gelöst. Solche Probleme werden, wie besonders gut aus dem letzten zu sehen ist, durch zwei Aktionen gelöst: Division (wenn ein Teil gefunden wird) und Multiplikation (wenn die ganze Zahl gefunden wird).

Nachdem wir jedoch die Division von Brüchen studiert haben, können die obigen Probleme in einer Aktion gelöst werden, nämlich: Division durch einen Bruch.

Die letzte Aufgabe kann beispielsweise in einer Aktion wie folgt gelöst werden:

In Zukunft werden wir das Problem lösen, eine Zahl durch ihren Bruch in einer Aktion zu finden - Division.

7. Finden einer Zahl anhand ihres Prozentsatzes.

Bei diesen Aufgaben müssen Sie eine Zahl finden und einige Prozent dieser Zahl kennen.

Aufgabe 1. Anfang dieses Jahres bekam ich von der Sparkasse 60 Rubel. Einkommen aus dem Betrag, den ich vor einem Jahr gespart habe. Wie viel Geld habe ich bei der Sparkasse angelegt? (Kassen geben Einlegern 2 % des Einkommens pro Jahr.)

Der Sinn des Problems ist, dass ein bestimmter Geldbetrag von mir in eine Sparkasse gelegt wurde und dort ein Jahr lag. Nach einem Jahr erhielt ich von ihr 60 Rubel. Einkommen, das sind 2/100 des Geldes, das ich eingezahlt habe. Wie viel Geld habe ich eingezahlt?

Wenn wir also den Teil dieses Geldes kennen, der auf zwei Arten ausgedrückt wird (in Rubel und in Bruchteilen), müssen wir den gesamten, noch unbekannten Betrag finden. Dies ist ein gewöhnliches Problem, eine Zahl zu finden, wenn ihr Bruch gegeben ist. Folgende Aufgaben werden durch Teilung gelöst:

Also wurden 3.000 Rubel in die Sparkasse gesteckt.

Aufgabe 2. In zwei Wochen erfüllten die Fischer den Monatsplan zu 64 %, nachdem sie 512 Tonnen Fisch zubereitet hatten. Was war ihr Plan?

Aus dem Zustand des Problems ist bekannt, dass die Fischer einen Teil des Plans abgeschlossen haben. Dieser Teil entspricht 512 Tonnen, was 64 % des Plans entspricht. Wie viele Tonnen Fisch laut Plan geerntet werden müssen, wissen wir nicht. Die Lösung des Problems besteht darin, diese Nummer zu finden.

Solche Aufgaben werden gelöst durch Teilen:

Laut Plan müssen Sie also 800 Tonnen Fisch zubereiten.

Aufgabe 3. Der Zug fuhr von Riga nach Moskau. Als er den 276. Kilometer passierte, fragte einer der Passagiere den vorbeifahrenden Schaffner, wie viel von der Strecke sie bereits zurückgelegt hätten. Darauf antwortete der Schaffner: „Wir haben bereits 30 % der gesamten Fahrt zurückgelegt.“ Wie weit ist es von Riga nach Moskau?

Aus dem Zustand des Problems ist ersichtlich, dass 30 % der Strecke von Riga nach Moskau 276 km lang sind. Wir müssen die gesamte Entfernung zwischen diesen Städten finden, d. h. für diesen Teil das Ganze finden:

§ 91. Reziproke Zahlen. Division durch Multiplikation ersetzen.

Nehmen Sie den Bruch 2/3 und ordnen Sie den Zähler an die Stelle des Nenners, wir erhalten 3/2. Wir haben einen Bruchteil, den Kehrwert von diesem.

Um den Kehrwert eines gegebenen Bruchs zu erhalten, musst du seinen Zähler an die Stelle des Nenners setzen und den Nenner an die Stelle des Zählers. Auf diese Weise können wir einen Bruch erhalten, der der Kehrwert eines beliebigen Bruchs ist. Zum Beispiel:

3/4, umgekehrt 4/3; 5/6, umgekehrt 6/5

Man nennt zwei Brüche, die die Eigenschaft haben, dass der Zähler des ersten der Nenner des zweiten und der Nenner des ersten der Zähler des zweiten ist gegenseitig invers.

Lassen Sie uns nun darüber nachdenken, welcher Bruch der Kehrwert von 1/2 sein wird. Offensichtlich wird es 2 / 1 oder nur 2 sein. Wenn wir nach dem Kehrwert davon suchen, haben wir eine ganze Zahl erhalten. Und dieser Fall ist kein Einzelfall; im Gegenteil, für alle Brüche mit einem Zähler von 1 (eins) sind die Kehrwerte ganze Zahlen, zum Beispiel:

1 / 3, umgekehrt 3; 1/5, rückwärts 5

Da wir beim Finden von Reziproken auch auf ganze Zahlen gestoßen sind, sprechen wir in Zukunft nicht mehr von Reziproken, sondern von Reziproken.

Lass uns herausfinden, wie man den Kehrwert einer ganzen Zahl schreibt. Bei Brüchen wird dies einfach gelöst: Sie müssen den Nenner an die Stelle des Zählers setzen. Auf die gleiche Weise können Sie den Kehrwert einer ganzen Zahl erhalten, da jede ganze Zahl einen Nenner von 1 haben kann. Der Kehrwert von 7 ist also 1 / 7, weil 7 \u003d 7 / 1; für die Zahl 10 ist das Gegenteil 1 / 10, da 10 = 10 / 1

Diese Idee kann man auch anders ausdrücken: Den Kehrwert einer gegebenen Zahl erhält man, indem man eins durch die gegebene Zahl dividiert. Diese Aussage gilt nicht nur für ganze Zahlen, sondern auch für Brüche. In der Tat, wenn Sie eine Zahl schreiben möchten, die der Kehrwert des Bruchs 5 / 9 ist, dann können wir 1 nehmen und durch 5 / 9 teilen, d.h.

Lassen Sie uns nun auf einen hinweisen Eigentum gegenseitig reziproke Zahlen, die uns nützlich sein werden: das Produkt reziproker Zahlen ist gleich eins. Tatsächlich:

Unter Verwendung dieser Eigenschaft können wir Kehrwerte auf folgende Weise finden. Finden wir den Kehrwert von 8.

Bezeichnen wir es mit dem Buchstaben X , dann 8 X = 1, also X = 1/8 . Lassen Sie uns eine andere Zahl finden, die Umkehrung von 7/12, bezeichnen Sie sie mit einem Buchstaben X , dann 7 / 12 X = 1, also X = 1:7/12 bzw X = 12 / 7 .

Wir haben hier den Begriff der reziproken Zahlen eingeführt, um die Informationen über die Division von Brüchen etwas zu ergänzen.

Wenn wir die Zahl 6 durch 3 / 5 teilen, gehen wir wie folgt vor:

Achten Sie besonders auf den Ausdruck und vergleichen Sie ihn mit dem gegebenen: .

Wenn wir den Ausdruck getrennt nehmen, ohne Verbindung mit dem vorherigen, dann ist es unmöglich, die Frage zu lösen, woher er kommt: von der Division von 6 durch 3/5 oder von der Multiplikation von 6 mit 5/3. In beiden Fällen ist das Ergebnis das gleiche. Also können wir sagen dass die Division einer Zahl durch eine andere durch die Multiplikation des Dividenden mit dem Kehrwert des Divisors ersetzt werden kann.

Die Beispiele, die wir unten geben, bestätigen diese Schlussfolgerung voll und ganz.

Dezimale Multiplikation erfolgt in drei Stufen.

Dezimalzahlen werden in eine Spalte geschrieben und als gewöhnliche Zahlen multipliziert.

Wir zählen die Anzahl der Dezimalstellen für die erste Dezimalstelle und die zweite. Wir fügen ihre Nummer hinzu.

In dem erhaltenen Ergebnis zählen wir von rechts nach links so viele Ziffern, wie sich im obigen Absatz herausgestellt haben, und setzen ein Komma.

Wie man Dezimalzahlen multipliziert

Wir schreiben Dezimalbrüche in eine Spalte und multiplizieren sie als natürliche Zahlen, wobei wir die Kommas ignorieren. Das heißt, wir betrachten 3,11 als 311 und 0,01 als 1.

Erhalten 311 . Nun zählen wir für beide Brüche die Anzahl der Vorzeichen (Ziffern) nach dem Komma. Die erste Dezimalstelle hat zwei Ziffern und die zweite zwei. Gesamtzahl der Ziffern nach Kommas:

Wir zählen von rechts nach links 4 Zeichen (Zahlen) der resultierenden Zahl. Das Ergebnis enthält weniger Stellen, als Sie mit einem Komma trennen müssen. In diesem Fall benötigen Sie links Ordnen Sie die fehlende Anzahl von Nullen zu.

Uns fehlt eine Ziffer, also ordnen wir links eine Null zu.

Beim Multiplizieren eines beliebigen Dezimalbruchs am 10.; 100; 1000 usw. Der Dezimalpunkt rückt um so viele Stellen nach rechts, wie Nullen nach der Eins stehen.

• 70,1 10 = 701
• 0,023 100 = 2,3
• 5,6 1000 = 5600

Um eine Dezimalzahl mit 0,1 zu multiplizieren; 0,01; 0,001 usw. muss in diesem Bruch das Komma um so viele Stellen nach links verschoben werden, wie Nullen vor der Einheit stehen.

Wir zählen null ganze Zahlen!

• 12 0,1 = 1,2
• 0,05 0,1 = 0,005
• 1,256 0,01 = 0,012 56

Multiplikation von Brüchen

Wir werden die Multiplikation gewöhnlicher Brüche auf mehrere mögliche Arten betrachten.

Einen Bruch mit einem Bruch multiplizieren

Dies ist der einfachste Fall, in dem Sie Folgendes verwenden müssen Regeln zur Multiplikation von Brüchen.

Zu einen Bruch mit einem Bruch multiplizieren, notwendig:

• den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs multiplizieren und ihr Produkt in den Zähler des neuen Bruchs schreiben;
• den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs multiplizieren und ihr Produkt in den Nenner des neuen Bruchs schreiben;

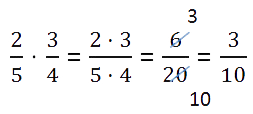
Prüfen Sie vor dem Multiplizieren von Zählern und Nennern, ob sich die Brüche kürzen lassen. Das Kürzen von Brüchen in Berechnungen erleichtert Ihre Berechnungen erheblich.

Einen Bruch mit einer natürlichen Zahl multiplizieren

Zum Bruch mit einer natürlichen Zahl multiplizieren Sie müssen den Zähler des Bruchs mit dieser Zahl multiplizieren und den Nenner des Bruchs unverändert lassen.

Wenn das Ergebnis der Multiplikation ein unechter Bruch ist, vergessen Sie nicht, ihn in eine gemischte Zahl umzuwandeln, dh den ganzen Teil auszuwählen.

Multiplikation gemischter Zahlen

Um gemischte Zahlen zu multiplizieren, musst du sie zuerst in unechte Brüche umwandeln und dann gemäß der Regel zum Multiplizieren gewöhnlicher Brüche multiplizieren.

Eine andere Möglichkeit, einen Bruch mit einer natürlichen Zahl zu multiplizieren

Manchmal ist es bei Berechnungen bequemer, eine andere Methode zum Multiplizieren eines gewöhnlichen Bruchs mit einer Zahl zu verwenden.

Um einen Bruch mit einer natürlichen Zahl zu multiplizieren, musst du den Nenner des Bruchs durch diese Zahl dividieren und den Zähler gleich lassen.

Wie aus dem Beispiel ersichtlich ist, ist es bequemer, diese Version der Regel anzuwenden, wenn der Nenner des Bruchs ohne Rest durch eine natürliche Zahl teilbar ist.

Wie man einen Bruch mit einer ganzzahligen Regel multipliziert

ICH. Um einen Dezimalbruch mit einer natürlichen Zahl zu multiplizieren, müssen Sie ihn mit dieser Zahl multiplizieren, das Komma ignorieren, und im resultierenden Produkt so viele Ziffern rechts trennen, wie es nach dem Dezimalkomma im angegebenen Bruch gab.

Beispiele. Multiplikation durchführen: 1) 1,25 7; 2) 0,345 8; 3) 2.391 14.

Entscheidung.

II. Um einen Dezimalbruch mit einem anderen zu multiplizieren, müssen Sie die Multiplikation durchführen, die Kommas ignorieren, und im resultierenden Ergebnis so viele Ziffern rechts mit einem Komma trennen, wie in beiden Faktoren zusammen nach den Kommas stehen.

Beispiele. Multiplikation durchführen: 1) 18,2 0,09; 2) 3,2 0,065; 3) 0,54 12,3.

Entscheidung.

III. Um eine Dezimalzahl mit 10, 100, 1000 usw. zu multiplizieren, müssen Sie den Dezimalpunkt um 1, 2, 3 usw. Stellen nach rechts verschieben.

Beispiele. Multiplikation durchführen: 1) 3,25 10; 2) 0,637 100; 3) 4.307 1000; 4) 2,04 1000; 5) 0,00031 10000.

Entscheidung.

IV. Um eine Dezimalzahl mit 0,1 zu multiplizieren; 0,01; 0,001 usw. müssen Sie das Komma um 1, 2, 3 usw. Ziffern nach links verschieben.

Beispiele. Multiplikation durchführen: 1) 28,3 0,1; 2) 324,7 0,01; 3) 6,85 0,01; 4) 6179,5 0,001; 5) 92,1 0,0001.

www.mathematics-repetition.com

Multiplikation von Dezimalbrüchen, Regeln, Beispiele, Lösungen.

Wir wenden uns dem Studium der nächsten Aktion mit Dezimalbrüchen zu, jetzt werden wir umfassend darüber nachdenken Dezimalzahlen multiplizieren. Lassen Sie uns zunächst die allgemeinen Prinzipien der Multiplikation von Dezimalbrüchen besprechen. Lassen Sie uns danach mit der Multiplikation eines Dezimalbruchs mit einem Dezimalbruch fortfahren, zeigen Sie, wie die Multiplikation von Dezimalbrüchen mit einer Spalte durchgeführt wird, und betrachten Sie die Lösungen von Beispielen. Als nächstes analysieren wir die Multiplikation von Dezimalbrüchen mit natürlichen Zahlen, insbesondere mit 10, 100 usw. Lassen Sie uns abschließend über die Multiplikation von Dezimalbrüchen mit gewöhnlichen Brüchen und gemischten Zahlen sprechen.

Sagen wir gleich, dass wir in diesem Artikel nur über die Multiplikation positiver Dezimalbrüche sprechen werden (siehe positive und negative Zahlen). Die restlichen Fälle werden in den Artikeln Multiplikation rationaler Zahlen und analysiert Multiplikation reeller Zahlen.

Seitennavigation.

Allgemeine Prinzipien zum Multiplizieren von Dezimalzahlen

Lassen Sie uns die allgemeinen Prinzipien besprechen, die bei der Multiplikation mit Dezimalbrüchen befolgt werden sollten.

Da nachfolgende Dezimalzahlen und unendliche periodische Brüche die Dezimalform von gemeinsamen Brüchen sind, ist das Multiplizieren solcher Dezimalzahlen im Wesentlichen das Multiplizieren von gemeinsamen Brüchen. Mit anderen Worten, Multiplikation der letzten Dezimalstellen, Multiplikation von letzten und periodischen Dezimalbrüchen, und auch periodische Dezimalzahlen multiplizieren Kommt darauf an, gewöhnliche Brüche zu multiplizieren, nachdem Dezimalbrüche in gewöhnliche Brüche umgewandelt wurden.

Betrachten Sie Beispiele für die Anwendung des stimmhaften Prinzips der Multiplikation von Dezimalbrüchen.

Führen Sie die Multiplikation der Dezimalstellen 1,5 und 0,75 durch.

Ersetzen wir die multiplizierten Dezimalbrüche durch die entsprechenden gewöhnlichen Brüche. Da 1,5=15/10 und 0,75=75/100, dann. Sie können den Bruch kürzen und dann den ganzen Teil aus dem unechten Bruch auswählen, und es ist bequemer, den resultierenden gewöhnlichen Bruch 1 125/1 000 als Dezimalbruch 1,125 zu schreiben.

Es ist zu beachten, dass es praktisch ist, die letzten Dezimalbrüche in einer Spalte zu multiplizieren. Wir werden im nächsten Absatz über diese Methode zum Multiplizieren von Dezimalbrüchen sprechen.

Betrachten Sie ein Beispiel für die Multiplikation periodischer Dezimalbrüche.

Berechne das Produkt der periodischen Dezimalzahlen 0,(3) und 2,(36) .

Lassen Sie uns periodische Dezimalbrüche in gewöhnliche Brüche umwandeln:

Dann. Sie können den resultierenden gewöhnlichen Bruch in einen Dezimalbruch umwandeln:

Wenn es unter den multiplizierten Dezimalbrüchen unendliche nicht periodische Brüche gibt, sollten alle multiplizierten Brüche, einschließlich endlicher und periodischer, auf eine bestimmte Ziffer aufgerundet werden (siehe Zahlen runden) und führen Sie dann die Multiplikation der nach dem Runden erhaltenen letzten Dezimalbrüche durch.

Multiplizieren Sie die Dezimalstellen 5,382… und 0,2.

Zuerst runden wir einen unendlichen nichtperiodischen Dezimalbruch ab, es kann auf Hundertstel gerundet werden, wir haben 5,382 ... ≈5,38. Der letzte Dezimalbruch 0,2 muss nicht auf Hundertstel gerundet werden. Also 5,382… 0,2≈5,38 0,2. Es bleibt das Produkt der letzten Dezimalbrüche zu berechnen: 5,38 0,2 \u003d 538 / 100 2 / 10 \u003d 1.076/1.000 \u003d 1,076.

Multiplikation von Dezimalbrüchen mit einer Spalte

Die Multiplikation endlicher Dezimalbrüche kann mit einer Spalte durchgeführt werden, ähnlich wie die Multiplikation mit einer Spalte mit natürlichen Zahlen.

Lassen Sie uns formulieren Multiplikationsregel für Dezimalbrüche. Um Dezimalbrüche mit einer Spalte zu multiplizieren, benötigen Sie:

• Ignorieren Sie Kommas und führen Sie eine Multiplikation gemäß allen Regeln der Multiplikation mit einer Spalte natürlicher Zahlen durch.
• bei der resultierenden Zahl rechts so viele Stellen mit einem Dezimalpunkt trennen, wie es in beiden Faktoren zusammen Nachkommastellen gibt, und wenn das Produkt nicht genügend Stellen hat, dann muss links die erforderliche Anzahl Nullen hinzugefügt werden.

Betrachten Sie Beispiele für die Multiplikation von Dezimalbrüchen mit einer Spalte.

Multiplizieren Sie die Dezimalstellen 63,37 und 0,12.

Führen wir die Multiplikation von Dezimalbrüchen mit einer Spalte durch. Zuerst multiplizieren wir die Zahlen und ignorieren die Kommas:

Es bleibt, ein Komma in das resultierende Produkt zu setzen. Sie muss rechts 4 Stellen trennen, da die Faktoren vier Dezimalstellen haben (zwei beim Bruch 3,37 und zwei beim Bruch 0,12). Da sind genug Zahlen drin, also musst du links keine Nullen hinzufügen. Beenden wir den Rekord:

Als Ergebnis haben wir 3,37 0,12 = 7,6044.

Berechnen Sie das Produkt der Dezimalstellen 3,2601 und 0,0254 .

Nachdem wir die Multiplikation mit einer Spalte ohne Berücksichtigung von Kommas durchgeführt haben, erhalten wir folgendes Bild:

Jetzt müssen Sie im Produkt 8 Ziffern rechts mit einem Komma trennen, da die Gesamtzahl der Dezimalstellen der multiplizierten Brüche acht beträgt. Das Produkt hat aber nur 7 Ziffern, daher müssen Sie links so viele Nullen zuweisen, dass 8 Ziffern durch ein Komma getrennt werden können. In unserem Fall müssen wir zwei Nullen zuweisen:

Damit ist die Multiplikation von Dezimalbrüchen mit einer Spalte abgeschlossen.

Multiplizieren von Dezimalzahlen mit 0,1, 0,01 usw.

Ziemlich oft müssen Sie Dezimalzahlen mit 0,1, 0,01 und so weiter multiplizieren. Daher ist es ratsam, eine Regel für die Multiplikation eines Dezimalbruchs mit diesen Zahlen zu formulieren, die sich aus den oben diskutierten Prinzipien der Multiplikation von Dezimalbrüchen ergibt.

So, Multiplizieren einer gegebenen Dezimalzahl mit 0,1, 0,01, 0,001 und so weiter gibt einen Bruch an, der aus dem ursprünglichen erhalten wird, wenn in seiner Eingabe das Komma um 1, 2, 3 usw. Ziffern nach links verschoben wird und wenn nicht genügend Ziffern vorhanden sind, um das Komma zu verschieben, müssen Sie um die erforderliche Anzahl von Nullen auf der linken Seite hinzuzufügen.

Um beispielsweise den Dezimalbruch 54,34 mit 0,1 zu multiplizieren, müssen Sie den Dezimalpunkt im Bruch 54,34 um 1 Ziffer nach links verschieben, und Sie erhalten den Bruch 5,434, dh 54,34 0,1 \u003d 5,434. Nehmen wir ein anderes Beispiel. Multipliziere den Dezimalbruch 9,3 mit 0,0001. Dazu müssen wir das Komma im multiplizierten Dezimalbruch 9,3 um 4 Stellen nach links verschieben, aber der Datensatz des Bruchs 9,3 enthält nicht so viele Zeichen. Daher müssen wir so viele Nullen in den Datensatz des Bruchs 9,3 auf der linken Seite einfügen, dass wir das Komma leicht auf 4 Ziffern übertragen können, wir haben 9,3 0,0001 \u003d 0,00093.

Beachten Sie, dass die angekündigte Regel zum Multiplizieren eines Dezimalbruchs mit 0,1, 0,01, ... auch für unendliche Dezimalbrüche gilt. Zum Beispiel 0,(18) 0,01=0,00(18) oder 93,938… 0,1=9,3938… .

Multiplikation einer Dezimalzahl mit einer natürlichen Zahl

Im Kern Dezimalzahlen mit natürlichen Zahlen multiplizieren unterscheidet sich nicht von der Multiplikation einer Dezimalzahl mit einer Dezimalzahl.

Es ist am bequemsten, einen endlichen Dezimalbruch mit einer natürlichen Zahl mit einer Spalte zu multiplizieren, während Sie die Regeln für die Multiplikation mit einer Spalte von Dezimalbrüchen befolgen sollten, die in einem der vorherigen Absätze besprochen wurden.

Berechnen Sie das Produkt 15 2.27 .

Führen wir die Multiplikation einer natürlichen Zahl mit einem Dezimalbruch in einer Spalte durch:

Beim Multiplizieren eines periodischen Dezimalbruchs mit einer natürlichen Zahl sollte der periodische Bruch durch einen gewöhnlichen Bruch ersetzt werden.

Multipliziere den Dezimalbruch 0,(42) mit der natürlichen Zahl 22.

Lassen Sie uns zuerst die periodische Dezimalzahl in einen gewöhnlichen Bruch umwandeln:

Jetzt machen wir die Multiplikation: . Dieses Dezimalergebnis ist 9,(3) .

Und wenn Sie einen unendlichen nicht periodischen Dezimalbruch mit einer natürlichen Zahl multiplizieren, müssen Sie zuerst abrunden.

Machen Sie die Multiplikation 4 2,145….

Wenn wir den ursprünglichen unendlichen Dezimalbruch auf Hundertstel aufrunden, kommen wir zur Multiplikation einer natürlichen Zahl und eines letzten Dezimalbruchs. Wir haben 4 2,145…≈4 2,15=8,60.

Multiplizieren einer Dezimalzahl mit 10, 100, ...

Nicht selten müssen Sie Dezimalbrüche mit 10, 100, ... multiplizieren. Daher ist es ratsam, sich ausführlich mit diesen Fällen zu befassen.

Lassen Sie uns sprechen Regel zum Multiplizieren einer Dezimalzahl mit 10, 100, 1.000 usw. Wenn Sie einen Dezimalbruch in seinem Eintrag mit 10, 100, ... multiplizieren, müssen Sie das Komma um 1, 2, 3, ... Stellen nach rechts verschieben und die zusätzlichen Nullen links verwerfen; Wenn der Datensatz des multiplizierten Bruchs nicht genügend Ziffern enthält, um das Komma zu übertragen, müssen Sie rechts die erforderliche Anzahl von Nullen hinzufügen.

Multipliziere die Dezimalzahl 0,0783 mit 100.

Lassen Sie uns den Bruch 0,0783 zwei Ziffern nach rechts in den Datensatz übertragen, und wir erhalten 007,83. Wenn wir links zwei Nullen weglassen, erhalten wir den Dezimalbruch 7,38. Also 0,0783 100 = 7,83.

Multipliziere den Dezimalbruch 0,02 mit 10.000.

Um 0,02 mit 10.000 zu multiplizieren, müssen wir das Komma um 4 Ziffern nach rechts verschieben. Offensichtlich gibt es in der Aufzeichnung des Bruchs 0,02 nicht genügend Ziffern, um das Komma auf 4 Ziffern zu übertragen, also fügen wir rechts ein paar Nullen hinzu, damit das Komma übertragen werden kann. In unserem Beispiel reicht es, drei Nullen hinzuzufügen, wir haben 0,02000. Nach dem Verschieben des Kommas erhalten wir den Eintrag 00200.0 . Wenn wir die Nullen links weglassen, haben wir die Zahl 200,0, die gleich der natürlichen Zahl 200 ist, die das Ergebnis der Multiplikation des Dezimalbruchs 0,02 mit 10.000 ist.

Die genannte Regel gilt auch für die Multiplikation von unendlichen Dezimalbrüchen mit 10, 100, ... Bei der Multiplikation von periodischen Dezimalbrüchen müssen Sie auf die Periode des Bruches achten, der das Ergebnis der Multiplikation ist.

Multiplizieren Sie die periodische Dezimalzahl 5,32(672) mit 1000 .

Vor der Multiplikation schreiben wir einen periodischen Dezimalbruch als 5,32672672672 ..., damit können wir Fehler vermeiden. Jetzt verschieben wir das Komma um 3 Ziffern nach rechts, wir haben 5 326.726726 .... Somit erhält man nach der Multiplikation einen periodischen Dezimalbruch 5 326, (726) .

5,32(672) 1000=5326,(726) .

Bei der Multiplikation unendlicher nichtperiodischer Brüche mit 10, 100, ... müssen Sie den unendlichen Bruch zunächst auf eine bestimmte Ziffer runden und dann die Multiplikation durchführen.

Multiplizieren einer Dezimalzahl mit einem gemeinsamen Bruch oder einer gemischten Zahl

Um einen endlichen Dezimalbruch oder einen unendlich periodischen Dezimalbruch mit einem gewöhnlichen Bruch oder einer gemischten Zahl zu multiplizieren, müssen Sie den Dezimalbruch als gewöhnlichen Bruch darstellen und dann die Multiplikation durchführen.

Multipliziere den Dezimalbruch 0,4 mit der gemischten Zahl.

Da 0,4=4/10=2/5 und dann. Die resultierende Zahl kann als periodischer Dezimalbruch 1,5(3) geschrieben werden.

Beim Multiplizieren eines unendlichen nicht periodischen Dezimalbruchs mit einem gemeinsamen Bruch oder einer gemischten Zahl sollte der gemeinsame Bruch oder die gemischte Zahl durch einen Dezimalbruch ersetzt werden, dann die multiplizierten Brüche runden und die Berechnung abschließen.

Seit 2/3 \u003d 0,6666 ... also. Nachdem wir die multiplizierten Brüche auf Tausendstel gerundet haben, erhalten wir das Produkt aus zwei letzten Dezimalbrüchen 3,568 und 0,667. Machen wir die Multiplikation in einer Spalte:

Das erhaltene Ergebnis sollte auf Tausendstel gerundet werden, da die multiplizierten Brüche mit einer Genauigkeit von Tausendsteln genommen wurden, haben wir 2,379856≈2,380.

www.cleverstudents.ru

Multiplikation gewöhnlicher Brüche: Regeln, Beispiele, Lösungen.

Wir untersuchen weiterhin Aktionen mit gewöhnlichen Brüchen. Jetzt im Rampenlicht Multiplikation gemeinsamer Brüche. In diesem Artikel geben wir eine Regel zum Multiplizieren gewöhnlicher Brüche an. Betrachten Sie die Anwendung dieser Regel beim Lösen von Beispielen. Wir werden uns auch darauf konzentrieren, einen gewöhnlichen Bruch mit einer natürlichen Zahl zu multiplizieren. Überlegen Sie abschließend, wie die Multiplikation von drei oder mehr Brüchen durchgeführt wird.

Seitennavigation.

Einen gemeinsamen Bruch mit einem gemeinsamen Bruch multiplizieren

Beginnen wir mit der Formulierung Regeln zum Multiplizieren gemeinsamer Brüche: Die Multiplikation eines Bruchs mit einem Bruch ergibt einen Bruch, dessen Zähler gleich dem Produkt der Zähler der multiplizierten Brüche und dessen Nenner gleich dem Produkt der Nenner ist.

Das heißt, die Formel entspricht der Multiplikation gewöhnlicher Brüche a / b und c / d.

Lassen Sie uns ein Beispiel geben, das die Regel der Multiplikation gewöhnlicher Brüche veranschaulicht. Stellen Sie sich ein Quadrat mit einer Seitenlänge von 1 Einheit vor. , während seine Fläche 1 Einheit 2 beträgt. Teilen Sie dieses Quadrat in gleiche Rechtecke mit Seiten 1/4 Einheiten. und 1/8 Einheiten. , während das ursprüngliche Quadrat aus 4 8 = 32 Rechtecken besteht, beträgt die Fläche jedes Rechtecks ​​daher 1/32 der Fläche des ursprünglichen Quadrats, dh sie entspricht 1/32 Einheiten 2. Lassen Sie uns nun einen Teil des ursprünglichen Quadrats übermalen. Alle unsere Maßnahmen spiegeln sich in der folgenden Abbildung wider.

Die Seiten des gefüllten Rechtecks ​​sind 5/8 Einheiten. und 3/4 Einheiten. , was bedeutet, dass seine Fläche gleich dem Produkt der Brüche 5/8 und 3/4 ist, also Einheiten 2. Aber das gefüllte Rechteck besteht aus 15 "kleinen" Rechtecken, also ist seine Fläche 15/32 Einheiten 2 . Somit, . Da 5 3=15 und 8 4=32 , kann die letzte Gleichheit umgeschrieben werden als , was die Formel zum Multiplizieren gewöhnlicher Brüche der Form bestätigt.

Beachten Sie, dass Sie mit Hilfe der stimmhaften Multiplikationsregel sowohl echte als auch unechte Brüche, Brüche mit demselben Nenner und Brüche mit unterschiedlichen Nennern multiplizieren können.

Prüfen Beispiele für die Multiplikation gemeinsamer Brüche.

Multiplizieren Sie den gemeinsamen Bruch 7/11 mit dem gemeinsamen Bruch 9/8.

Das Produkt der Zähler der multiplizierten Brüche 7 und 9 ist 63, und das Produkt der Nenner von 11 und 8 ist 88. Somit ergibt die Multiplikation der gemeinsamen Brüche 7/11 und 9/8 den Bruch 63/88.

Hier ist eine Zusammenfassung der Lösung: .

Wir sollten die Kürzung des resultierenden Bruchs nicht vergessen, wenn als Ergebnis der Multiplikation ein kürzbarer Bruch erhalten wird, und die Auswahl des ganzen Teils aus einem unechten Bruch.

Multipliziere die Brüche 4/15 und 55/6.

Wenden wir die Regel der Multiplikation gewöhnlicher Brüche an: .

Offensichtlich ist der resultierende Bruch reduzierbar (das Zeichen der Teilbarkeit durch 10 erlaubt uns zu behaupten, dass Zähler und Nenner des Bruchs 220/90 einen gemeinsamen Faktor von 10 haben). Lassen Sie uns den Bruch 220/90 reduzieren: GCD(220, 90)=10 und . Es bleibt, den ganzzahligen Teil aus dem resultierenden unechten Bruch auszuwählen: .

Beachten Sie, dass die Bruchkürzung vor der Berechnung der Produkte der Zähler und der Produkte der Nenner der multiplizierten Brüche durchgeführt werden kann, d. h. wenn der Bruch die Form hat. Für diese Zahl werden a, b, c und d durch ihre Primfaktorzerlegungen ersetzt, danach werden die gleichen Faktoren des Zählers und des Nenners gestrichen.

Gehen wir zur Verdeutlichung zurück zum vorherigen Beispiel.

Berechne das Produkt von Brüchen der Form .

Durch die Formel zum Multiplizieren gewöhnlicher Brüche haben wir .

Da 4=2 2 , 55=5 11 , 15=3 5 und 6=2 3 , dann . Nun kürzen wir die gemeinsamen Primfaktoren: .

Es bleibt nur, die Produkte im Zähler und Nenner zu berechnen und dann den ganzzahligen Teil aus dem unechten Bruch auszuwählen: .

Zu beachten ist, dass die Multiplikation von Brüchen durch ein Kommutativgesetz gekennzeichnet ist, d. h. die multiplizierten Brüche können vertauscht werden: .

Einen Bruch mit einer natürlichen Zahl multiplizieren

Beginnen wir mit der Formulierung Regeln für die Multiplikation eines gemeinsamen Bruchs mit einer natürlichen Zahl: Die Multiplikation eines Bruchs mit einer natürlichen Zahl ergibt einen Bruch, dessen Zähler gleich dem Produkt des Zählers des multiplizierten Bruchs mit der natürlichen Zahl ist und dessen Nenner gleich dem Nenner des multiplizierten Bruchs ist.

Mit Hilfe von Buchstaben hat die Regel zum Multiplizieren eines Bruchs a / b mit einer natürlichen Zahl n die Form .

Die Formel folgt aus der Formel zur Multiplikation zweier gewöhnlicher Brüche der Form . Tatsächlich erhalten wir, wenn wir eine natürliche Zahl als Bruch mit dem Nenner 1 darstellen .

Betrachten Sie Beispiele für die Multiplikation eines Bruchs mit einer natürlichen Zahl.

Multipliziere den Bruch 2/27 mit 5.

Die Multiplikation des Zählers 2 mit der Zahl 5 ergibt 10, daher ist aufgrund der Regel, einen Bruch mit einer natürlichen Zahl zu multiplizieren, das Produkt von 2/27 mit 5 gleich dem Bruch 10/27.

Die ganze Lösung lässt sich bequem wie folgt schreiben: .

Bei der Multiplikation eines Bruchs mit einer natürlichen Zahl muss der entstehende Bruch oft gekürzt werden, und wenn er auch falsch ist, dann als gemischte Zahl darstellen.

Multipliziere den Bruch 5/12 mit der Zahl 8.

Nach der Formel zum Multiplizieren eines Bruchs mit einer natürlichen Zahl haben wir . Offensichtlich ist der resultierende Bruch reduzierbar (das Zeichen der Teilbarkeit durch 2 zeigt einen gemeinsamen Teiler 2 von Zähler und Nenner an). Lassen Sie uns den Bruch 40/12 reduzieren: da LCM(40, 12)=4, dann . Es bleibt, den ganzen Teil auszuwählen: .

Hier ist die ganze Lösung: .

Beachten Sie, dass die Reduktion erfolgen könnte, indem Sie die Zahlen im Zähler und Nenner durch ihre Erweiterungen in Primfaktoren ersetzen. In diesem Fall sähe die Lösung so aus:

Zum Abschluss dieses Absatzes stellen wir fest, dass die Multiplikation eines Bruchs mit einer natürlichen Zahl die Kommutativeigenschaft hat, d. h. das Produkt eines Bruchs mit einer natürlichen Zahl ist gleich dem Produkt dieser natürlichen Zahl mit einem Bruch: .

Multipliziere drei oder mehr Brüche

Die Art und Weise, wie wir gewöhnliche Brüche und die Multiplikationsoperation mit ihnen definiert haben, erlaubt uns zu behaupten, dass alle Eigenschaften der Multiplikation natürlicher Zahlen auf die Multiplikation von Brüchen zutreffen.

Die kommutativen und assoziativen Eigenschaften der Multiplikation ermöglichen eine eindeutige Bestimmung Multiplizieren von drei oder mehr Brüchen und natürlichen Zahlen. In diesem Fall geschieht alles analog zur Multiplikation von drei oder mehr natürlichen Zahlen. Insbesondere Brüche und natürliche Zahlen im Produkt können zur Vereinfachung der Berechnung neu angeordnet werden, und wenn keine Klammern vorhanden sind, die die Reihenfolge angeben, in der Aktionen ausgeführt werden, können wir die Klammern selbst auf jede der zulässigen Arten anordnen.

Betrachten Sie Beispiele für die Multiplikation mehrerer Brüche und natürlicher Zahlen.

Multiplizieren Sie drei gemeinsame Brüche 1/20, 12/5, 3/7 und 5/8.

Lassen Sie uns das Produkt schreiben, das wir berechnen müssen . Aufgrund der Regel zum Multiplizieren von Brüchen ist das geschriebene Produkt gleich einem Bruch, dessen Zähler gleich dem Produkt der Zähler aller Brüche ist, und der Nenner ist das Produkt der Nenner: .

Vor der Berechnung der Produkte in Zähler und Nenner empfiehlt es sich, alle Faktoren durch ihre Erweiterungen in Primfaktoren zu ersetzen und zu kürzen (natürlich kann man nach der Multiplikation den Bruch kürzen, aber das erfordert in vielen Fällen viel Rechenaufwand): .

.

Multipliziere fünf Zahlen .

In diesem Produkt ist es praktisch, den Bruch 7/8 mit der Zahl 8 und die Zahl 12 mit dem Bruch 5/36 zu gruppieren, dies vereinfacht die Berechnungen, da bei einer solchen Gruppierung die Reduzierung offensichtlich ist. Wir haben
.

.

www.cleverstudents.ru

Beliebt:

• Bei Antragstellung beim Amtsgericht Liebe Besucherinnen und Besucher der Seite! Abteilung des Bundesfinanzministeriums für St. Petersburg (Interdistrict IFTS of Russia No. 10 for St. Petersburg) TIN der Steuerbehörde Kontonummer des Begünstigten NORD-WEST […]
• Berechnung der staatlichen Abgabe zur Kürzung des Unterhaltsbetrags Die Gerichte halten an folgender Position fest: Die staatliche Abgabe berechnet sich aus dem Betrag, um den der Unterhaltsbetrag gekürzt wird (aus dem Forderungswert). Ein Beispiel für die Berechnung der Höhe der staatlichen Gerichtspflicht bei [...]
• Division von Dezimalbrüchen, Regeln, Beispiele, Lösungen. Wir studieren weiterhin Aktionen mit Dezimalbrüchen, es ist Zeit, über die Division von Dezimalbrüchen zu sprechen. Beginnen wir mit den allgemeinen Prinzipien der Dezimaldivision. Weiter […]
• Artikel 333.19 der Abgabenordnung der Russischen Föderation. Höhe der staatlichen Gebühr in Fällen, die vom Obersten Gericht der Russischen Föderation, den Gerichten der allgemeinen Gerichtsbarkeit und den Friedensrichtern ST 333.19 der Abgabenordnung der Russischen Föderation geprüft werden. 1. In Fällen vor dem Obersten Gerichtshof […]
• Musterverordnung über die (autorisierte) Kommission für Sozialversicherung N 556a „Musterverordnung über die (autorisierte) Kommission für Sozialversicherung“ GENEHMIGT vom Vorsitzenden der Sozialversicherungskasse der Russischen Föderation […]
• Die Details für die Zahlung der staatlichen Abgaben der Streitkräfte der Russischen Föderation sowie des Schiedsgerichts Moskau und des Schiedsgerichts des Moskauer Bezirks haben sich geändert Neue Bankverbindung für die Zahlung der staatlichen Abgaben in Fällen, die im Obersten Gericht geprüft werden Gericht der Russischen Föderation, das Schiedsgericht der Stadt Moskau und […]
• Ein Bohrreservoir ist ein Gestein mit hoher Porosität und Permeabilität, das förderbare Mengen an Öl und Gas enthält. Die Hauptklassifizierungsmerkmale des Reservoirs sind die Bedingungen der Filtration und Akkumulation in […]
• Unsere Gruppe in VK Holen Sie sich einen Rabatt auf das Training. Beeilen Sie sich, um einen Rabatt von 1000 Rubel zu erhalten! Anmeldung in einer Fahrschule Füllen Sie dieses Formular aus, wir werden uns mit Ihnen in Verbindung setzen und Sie zum Unterricht einladen. Willkommen zurück! 1. Warnzeichen Warnung […]