Erwarteter Wert. mathematische Erwartung diskrete Zufallsvariable X, die eine endliche Anzahl von Werten annimmt Xich mit Wahrscheinlichkeiten Rich, heißt die Summe:

mathematische Erwartung stetige Zufallsvariable X heißt das Integral des Produkts seiner Werte X auf der Wahrf(x):

(6b)

Unechtes Integral (6 b) wird als absolut konvergent angenommen (andernfalls sagen wir, dass der Erwartungswert M(X) existiert nicht). Die mathematische Erwartung charakterisiert mittlere Bedeutung zufällige Variable X. Seine Dimension stimmt mit der Dimension einer Zufallsvariablen überein.

Eigenschaften der mathematischen Erwartung:

Streuung. Streuung zufällige Variable X Nummer heißt:

Die Streuung ist Streucharakteristik Werte einer Zufallsvariablen X relativ zu seinem Durchschnittswert M(X). Die Dimension der Varianz ist gleich der quadrierten Dimension der Zufallsvariablen. Basierend auf den Definitionen von Varianz (8) und mathematischem Erwartungswert (5) für eine diskrete Zufallsvariable und (6) für eine kontinuierliche Zufallsvariable erhalten wir ähnliche Ausdrücke für die Varianz:

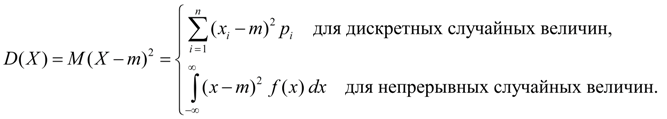(9)

Hier m = M(X).

Dispersionseigenschaften:

Standardabweichung:

(11)

Da die Dimension der Standardabweichung dieselbe ist wie die einer Zufallsvariablen, wird sie häufiger als die Varianz als Streuungsmaß verwendet.

Verteilungsmomente. Die Konzepte des mathematischen Erwartungswerts und der Varianz sind Spezialfälle eines allgemeineren Konzepts für die numerischen Eigenschaften von Zufallsvariablen - Verteilungsmomente. Die Verteilungsmomente einer Zufallsvariablen werden als mathematische Erwartungen einiger einfacher Funktionen einer Zufallsvariablen eingeführt. Also der Moment der Bestellung k relativ zum Punkt X 0 heißt Erwartung M(X–X 0 )k. Momente relativ zum Ursprung X= 0 aufgerufen werden erste Momente und sind gekennzeichnet:

(12)

Das Anfangsmoment der ersten Ordnung ist das Verteilungszentrum der betrachteten Zufallsvariablen:

(13)

Momente relativ zum Verteilzentrum X= m namens zentrale Momente und sind gekennzeichnet:

(14)

Aus (7) folgt, dass das zentrale Moment erster Ordnung immer gleich Null ist:

Die zentralen Momente hängen nicht von der Herkunft der Werte der Zufallsvariablen ab, da bei einer Verschiebung um einen konstanten Wert Mit sein Verteilungsschwerpunkt ist um den gleichen Wert verschoben Mit, und die Abweichung vom Mittelpunkt ändert sich nicht: X – m = (X – Mit) – (m – Mit).
Nun ist das offensichtlich Streuung- Das zentrales Moment zweiter Ordnung:

Asymmetrie. Zentrales Moment der dritten Ordnung:

(17)

dient der Auswertung Verteilungsschiefe. Wenn die Verteilung symmetrisch um den Punkt ist X= m, dann ist das zentrale Moment dritter Ordnung gleich Null (sowie alle zentralen Momente ungerader Ordnung). Wenn also das zentrale Moment dritter Ordnung von Null verschieden ist, kann die Verteilung nicht symmetrisch sein. Die Größe der Asymmetrie wird unter Verwendung eines Dimensionslosen geschätzt Asymmetriekoeffizient:

(18)

Das Vorzeichen des Asymmetriekoeffizienten (18) zeigt rechtsseitige oder linksseitige Asymmetrie an (Abb. 2).

Reis. 2. Arten der Asymmetrie von Verteilungen.

Überschuss. Zentrales Moment der vierten Ordnung:

(19)

dient der Auswertung der sog Kurtosis, der den Grad der Steilheit (Spitzigkeit) der Verteilungskurve in der Nähe des Verteilungszentrums in Bezug auf die Normalverteilungskurve bestimmt. Da für eine Normalverteilung die als Kurtosis angenommene Menge ist:

(20)

Auf Abb. 3 zeigt Beispiele von Verteilungskurven mit unterschiedlichen Werten der Kurtosis. Für eine Normalverteilung E= 0. Kurven mit stärkeren Spitzen als normal haben eine positive Kurtosis, und Kurven mit flacheren Spitzen haben eine negative Kurtosis.

Reis. 3. Verteilungskurven mit unterschiedlicher Steilheit (Kurtosis).

Momente höherer Ordnung werden in technischen Anwendungen der mathematischen Statistik normalerweise nicht verwendet.

Mode diskret Zufallsvariable ist ihr wahrscheinlichster Wert. Mode kontinuierlich eine Zufallsvariable ist ihr Wert, bei dem die Wahrscheinlichkeitsdichte maximal ist (Abb. 2). Hat die Verteilungskurve ein Maximum, so heißt die Verteilung unimodal. Wenn die Verteilungskurve mehr als ein Maximum hat, wird die Verteilung aufgerufen polymodal. Manchmal gibt es Verteilungen, deren Kurven kein Maximum, sondern ein Minimum haben. Solche Distributionen werden aufgerufen antimodal. Im allgemeinen Fall stimmen Modus und mathematischer Erwartungswert einer Zufallsvariablen nicht überein. Im Einzelfall, z modal, d.h. mit einem Modus, einer symmetrischen Verteilung, und vorausgesetzt, dass es eine mathematische Erwartung gibt, fällt letztere mit dem Modus und dem Symmetriezentrum der Verteilung zusammen.

Median zufällige Variable X ist seine Bedeutung Mir, für die Gleichheit gilt: d.h. es ist ebenso wahrscheinlich, dass die Zufallsvariable X wird weniger oder mehr sein Mir. Geometrisch Median ist die Abszisse des Punktes, an dem die Fläche unter der Verteilungskurve halbiert wird (Abb. 2). Bei einer symmetrischen Modalverteilung sind Median, Modus und Mittelwert gleich.

Modus ist der wahrscheinlichste Wert einer Zufallsvariablen. Bei einer symmetrischen Verteilung bezüglich des Mittelwerts stimmt der Modus mit der mathematischen Erwartung überein. Wenn sich die Werte der Zufallsvariablen nicht wiederholen, gibt es keinen Modus.

Der Punkt auf der x-Achse, der dem Maximum der Verteilungsdichtekurve entspricht, wird Modus genannt, d. h. der Modus ist der wahrscheinlichste Wert der Zufallsvariablen. Der Modus ist jedoch nicht für alle Distributionen vorhanden. Ein Beispiel ist die Gleichverteilung. In diesem Fall ist die Definition des Verteilzentrums als Verkehrsträger nicht möglich. Mode wird normalerweise als Mo bezeichnet.

Es gibt Konzepte von Modus und Median einer Zufallsvariablen.

Es ist offensichtlich, dass im Fall eines symmetrischen Medians der Modus und der mathematische Erwartungswert übereinstimmen.

Aufgrund der Tatsache, dass der Modus nicht auf Einzelmessungen basiert, sondern auf einer großen Menge an Beobachtungen, kann er nicht als Zufallsvariable betrachtet werden. Das Ausmaß des Modus wird nicht durch verschiedene Arten von Arbeitsverzögerungen und den Verlust seiner normalen Raten beeinflusst.

Manchmal werden bei der Analyse empirischer Verteilungen die Konzepte des Modus und des Medians der Verteilung verwendet: "... Der Modus ist der wahrscheinlichste Wert einer Zufallsvariablen,

Eine erweiterte probabilistische Interpretation des Lotteriephänomens ist das Konzept einer probabilistischen Verteilung einer Zufallsvariablen. Es wird verwendet, um die Wahrscheinlichkeiten zu bestimmen, dass eine Zufallsvariable den einen oder anderen ihrer möglichen Werte annimmt. Bezeichne mit y die Zufallsvariable und mit y ihre möglichen Werte. Dann für eine diskrete Zufallsvariable , die mögliche Werte Y, y2, US, annehmen kann. .., yn Eine bequeme Form der Wahrscheinlichkeitsverteilung sollte die Abhängigkeit P(y = y) betrachtet werden, die üblicherweise als Wahrscheinlichkeitsreihe, n-Verteilungsreihe bezeichnet wird. In der Praxis werden für eine operative verallgemeinerte Einschätzung der Wahrscheinlichkeitsverteilung von Risikowerten häufig die sogenannten numerischen und andere Merkmale der Verteilung von Zufallsergebnissen verwendet: mathematischer Erwartungswert, Varianz, Standardabweichung, Variationskoeffizient, Modus, Median, usw. (siehe zum Beispiel und andere .). Mit anderen Worten, für eine schnelle und ganzheitliche Wahrnehmung sucht der Unternehmer (oder einfach Sie

Basierend auf den Daten des staatlichen Statistikausschusses der UdSSR über die Verteilung der Bevölkerung nach dem gesamten Pro-Kopf-Einkommen werden wir versuchen, die Indikatoren des Durchschnitts-, Median- und Modaleinkommens zu vergleichen (Tabelle 1). Die Tabelle zeigt, dass das Durchschnittseinkommen in absoluten Zahlen das Median- und Modaleinkommen übersteigt und sein Wachstum hauptsächlich auf eine Zunahme des Anteils der Personen mit hohem Einkommen zurückzuführen ist, dh die Verwendung des Dführt zu einer erheblichen Überschätzung des Einkommensniveaus des Großteils der Bevölkerung und verbirgt weitgehend den Prozess ihrer Differenzierung. Die Werte des Modaleinkommens tendieren zu den unteren Verteilungsgruppen und weichen vom Medianeinkommen nach unten ab. Der Treffer einer Mode in dem einen oder anderen Intervall ist jedoch oft zufälliger Natur, eine eher kleine Änderung in der Verteilung - und die Mode befindet sich bereits im benachbarten Intervall. Beispielsweise lag 1989 das häufigste Einkommensniveau zwischen 100 und 125 Rubel (16,1% der Bevölkerung erhielten ein solches Einkommen), aber aufgrund geringfügiger Einkommensverschiebungen in den Jahren 1989-1990 stellte sich heraus, dass das häufigste Intervall war das folgende Intervall (125-150 Rubel): , und der Wert der Mode selbst stieg um 15,6 Rubel. Darüber hinaus kann der Anteil der Bevölkerung am modalen Einkommensintervall andere Anteile geringfügig übersteigen.

Um das Verteilungszentrum einer logarithmisch normalen Zufallsvariablen a zu charakterisieren, kann man neben dem bereits berechneten mathematischen Erwartungswert Ma den Modus verwenden

Modus - Mode. Der wahrscheinlichste Wert einer Zufallsvariablen.

MODE - Konzept

Neben der mathematischen Erwartung und Streuung werden in der Wahrscheinlichkeitstheorie eine Reihe numerischer Merkmale verwendet, die bestimmte Merkmale der Verteilung widerspiegeln.

Definition. Modus Mo(X) einer Zufallsvariablen X ist ihr wahrscheinlichster Wert(Wofür die Wahrscheinlichkeit r r oder Wahrscheinlichkeitsdichte

Erreicht die Wahrscheinlichkeit oder Wahrscheinlichkeitsdichte nicht an einem, sondern an mehreren Punkten ein Maximum, spricht man von einer Verteilung polymodal(Abb. 3.13).

Mode Moos), bei der die Wahrscheinlichkeit R ( oder die Wahrscheinlichkeitsdichte (p(x) erreicht ein globales Maximum) heißt wahrscheinlichster Wert Zufallsvariable (in Abb. 3.13 diese Mo(X)2).

Definition. Der Median Me(X) einer kontinuierlichen Zufallsvariablen X ist ihr Wert, wofür

jene. die Wahrscheinlichkeit, dass die Zufallsvariable X nimmt einen Wert an, der kleiner als der Median ist Pelz) oder größer als es, gleich und gleich 1/2. Geometrisch vertikale Linie X = Pelz) durch einen Punkt mit einer Abszisse gleich Pelz), teilt die Fläche der Abbildung der Verteilungskurve in zwei gleiche Teile (Abb. 3.14). Offensichtlich an der Stelle X = Pelz) die Verteilungsfunktion ist gleich 1/2, d.h. P(Me(X))= 1/2 (Abb. 3.15).

Beachten Sie eine wichtige Eigenschaft des Medians einer Zufallsvariablen: die mathematische Erwartung des Betrags der Abweichung der Zufallsvariablen X vom konstanten Wert C ist dann minimal, wenn diese Konstante C gleich dem Median Me(X) = m ist, d.h.

(Die Eigenschaft ähnelt der Eigenschaft (3.10") der Minimalität des mittleren Quadrats der Abweichung einer Zufallsvariablen von ihrer mathematischen Erwartung).

O Beispiel 3.15. Finden Sie Modus, Median und Mittelwert einer Zufallsvariablen Xs Wahrscheinlichkeitsdichte φ(x) = 3x 2 für xx.

Entscheidung. Die Verteilungskurve ist in Abb. 1 dargestellt. 3.16. Offensichtlich ist die Wahrscheinlichkeitsdichte φ(x) bei maximal X= Mo(X) = 1.

Median Pelz) = b wir finden aus Bedingung (3.28):

wo

Der mathematische Erwartungswert wird nach der Formel (3.25) berechnet:

Gegenseitige Anordnung von Punkten M(X) > Me(X) und Moos) in aufsteigender Reihenfolge der Abszisse ist in Abb. 1 gezeigt. 3.16. ?

Neben den oben erwähnten numerischen Merkmalen wird das Konzept der Quantile und Prozentpunkte verwendet, um eine Zufallsvariable zu beschreiben.

Definition. Niveauquantil y-Quantil )

heißt ein solcher Wert x q einer Zufallsvariablen , bei dem seine Verteilungsfunktion einen Wert gleich annimmt sterben.

Einige Quantile haben einen besonderen Namen erhalten. Offensichtlich das oben Median Zufallsvariable ist das 0,5-Niveau-Quantil, d.h. Ich (X) \u003d x 05. Die Quantile dg 0 2 5 und x 075 werden entsprechend benannt niedriger und oberes QuartilK

Eng verwandt mit dem Konzept eines Quantils ist das Konzept Prozentpunkt. Unter YuOuHo-noi-Punkt impliziertes Quantil x x (( , jene. ein solcher Wert einer Zufallsvariablen x, unter welchen

0 Beispiel 3.16. Finden Sie gemäß Beispiel 3.15 das Quantil x 03 und 30 % zufälliger variabler Punkt x.

Entscheidung. Nach Formel (3.23) die Verteilungsfunktion

Das Quantil r 0 z finden wir aus Gleichung (3.29), d.h. x$ 3 \u003d 0,3, von wo aus L "oz -0,67. Finden Sie den 30%-Punkt der Zufallsvariablen x, oder Quantil x 0 7, aus der Gleichung x $ 7 = 0,7, woher x 0 7 "0,89. ?

Unter den numerischen Merkmalen einer Zufallsvariablen sind die Momente - Anfangs- und Zentralmoment - von besonderer Bedeutung.

Definition. Startmomentk-ter Ordnung einer Zufallsvariablen X ist der mathematische Erwartungswert der k-ten Potenz dieser Variablen :

Definition. Zentraler Punktk-te Ordnung einer Zufallsvariablen X ist die mathematische Erwartung des k-ten Grades der Abweichung der Zufallsvariablen X von ihrer mathematischen Erwartung:

Formeln zur Berechnung der Momente für diskrete Zufallsvariablen (mit den Werten x 1 mit Wahrscheinlichkeiten p,) und kontinuierlich (mit Wahrscheinlichkeitsdichte cp(x)) sind in Tabelle angegeben. 3.1.

Tabelle 3.1

Es ist leicht zu sehen, wann k = 1 erster Anfangsmoment der Zufallsvariablen X ist seine mathematische Erwartung, d.h. h x \u003d M [X) \u003d a, beim zu= 2 das zweite zentrale Moment ist die Dispersion, d.h. p2 = T)(X).

Die zentralen Momente p A können in Bezug auf die Anfangsmomente unter Verwendung der Formeln ausgedrückt werden:

usw.

Zum Beispiel c3 \u003d M (X-a) * \u003d M (X * -ZaX 2 + Za 2 X-a-\u003e) \u003d M (X *) ~ -ZaM (X 2) + Za 2 M (X) ~ a3 \u003d y 3 -Zy ^ + Zy (y, -y ^ \u003d y 3 - Zy ^ + 2y ^ (bei der Ableitung haben wir das berücksichtigt a = M(X)= V, - nicht zufälliger Wert). ?

Wie oben erwähnt, die mathematische Erwartung M(X), oder das erste Anfangsmoment, charakterisiert den Durchschnittswert oder die Position, das Verteilungszentrum einer Zufallsvariablen X auf dem Zahlenstrahl; Streuung OH), oder das zweite zentrale Moment p 2 , - s t s - Verteilungsstreuung X verhältnismäßig M(X). Momente höherer Ordnung dienen der genaueren Beschreibung der Verteilung.

Dritter zentraler Moment p 3 dient zur Charakterisierung der Asymmetrie der Verteilung (Schiefe). Es hat die Dimension eines Würfels einer Zufallsvariablen. Um einen dimensionslosen Wert zu erhalten, wird er durch etwa 3 geteilt, wobei a die Standardabweichung der Zufallsvariablen ist x. Erhaltener Wert SONDERN namens Asymmetriekoeffizient einer Zufallsvariablen.

Wenn die Verteilung bezüglich der mathematischen Erwartung symmetrisch ist, dann ist der Schiefekoeffizient A = 0.

Auf Abb. 3.17 zeigt zwei Verteilungskurven: I und II. Kurve I hat eine positive (rechtsseitige) Asymmetrie (L > 0), und Kurve II hat eine negative (linksseitige) (L

Vierter zentraler Moment p 4 dient zur Charakterisierung der Steilheit (Peak of the Top oder Flat Top - Post) der Verteilung.

Mode- der Wert in der Gruppe von Beobachtungen, der am häufigsten auftritt

Mo \u003d X Mo + h Mo * (f Mo - f Mo-1) : ((f Mo - f Mo-1) + (f Mo - f Mo + 1)),

hier ist X Mo die linke Grenze des modalen Intervalls, h Mo ist die Länge des modalen Intervalls, f Mo-1 ist die Frequenz des prämodalen Intervalls, f Mo ist die Frequenz des modalen Intervalls, f Mo+1 ist die Häufigkeit des postmodalen Intervalls.

Der Modus einer absolut kontinuierlichen Verteilung ist jeder Punkt des lokalen Maximums der Verteilungsdichte. Bei diskreten Verteilungen ist ein Modus ein beliebiger Wert a i , dessen Wahrscheinlichkeit p i größer ist als die Wahrscheinlichkeiten benachbarter Werte

Median stetige Zufallsvariable X sein Wert Me heißt ein solcher, für den es gleich wahrscheinlich ist, ob die Zufallsvariable kleiner oder größer ausfallen wird Mir, d.h.

M e \u003d (n + 1) / 2 P(X < Me) = P(X > Mir)

Gleichmäßig verteilt NEU

Gleichmäßige Verteilung. Eine stetige Zufallsvariable heißt auf der Strecke () gleichverteilt, wenn ihre Verteilungsdichtefunktion (Abb. 1.6, a) sieht aus wie:

Bezeichnung: - SW wird einheitlich verteilt auf .

Dementsprechend ist die Verteilungsfunktion auf dem Segment (Abb. 1.6, b):

Reis. 1.6. Funktionen einer Zufallsvariablen gleichmäßig verteilt auf [ a,b]: a– Wahrscheinlichkeitsdichten f(x); b– Ausschüttungen F(x)

Der mathematische Erwartungswert und die Varianz dieses RV werden durch die Ausdrücke bestimmt:

Aufgrund der Symmetrie der Dichtefunktion fällt sie mit dem Median zusammen. Mode hat keine einheitliche Verteilung

Beispiel 4 Die Wartezeit auf eine Antwort auf einen Anruf ist eine Zufallsvariable, die einem Gleichverteilungsgesetz im Bereich von 0 bis 2 Minuten gehorcht. Finden Sie die integralen und differentiellen Verteilungsfunktionen dieser Zufallsvariablen.

27. Normalgesetz der Wahrscheinlichkeitsverteilung

Eine kontinuierliche Zufallsvariable x hat eine Normalverteilung mit Parametern: m,s > 0, wenn die Wahrdie Form hat:

wobei: m die mathematische Erwartung ist, s die Standardabweichung ist.

Die Normalverteilung wird nach dem deutschen Mathematiker Gauß auch Gaußsche Verteilung genannt. Die Tatsache, dass eine Zufallsvariable normalverteilt ist mit Parametern: m, , wird wie folgt bezeichnet: N (m, s), wobei: m=a=M[X];

Nicht selten wird in Formeln der mathematische Erwartungswert mit bezeichnet a . Ist eine Zufallsvariable nach dem Gesetz N(0,1) verteilt, so spricht man von einem normierten oder standardisierten Normalwert. Die Verteilungsfunktion dafür hat die Form:

Das Diagramm der Dichte der Normalverteilung, die als Normalkurve oder Gaußsche Kurve bezeichnet wird, ist in Abb. 5.4 dargestellt.

Reis. 5.4. Normalverteilungsdichte

Eigenschaften eine Zufallsvariable mit einem Normalverteilungsgesetz.

1. Wenn , dann um die Wahrscheinlichkeit zu finden, dass dieser Wert in ein gegebenes Intervall fällt ( x 1; x 2) wird die Formel verwendet:

2. Die Wahrscheinlichkeit, dass die Abweichung einer Zufallsvariablen von ihrer mathematischen Erwartung den Wert (als Absolutwert) nicht überschreitet, ist gleich:

3. „Drei-Sigma-Regel“. Handelt es sich um eine Zufallsvariable, dann ist es praktisch sicher, dass ihre Werte im Intervall () enthalten sind. (Die Wahrscheinlichkeit, diese Grenzen zu überschreiten, beträgt 0,0027.) Die Regel ermöglicht es, bei Kenntnis der Parameter ( und ), das Intervall praktischer Werte einer Zufallsvariablen ungefähr zu bestimmen.

Exponentialverteilung

Eine Zufallsvariable X hat eine Exponentialverteilung mit einem Parameter, wenn ihre Dichte die Form hat

Durch Integrieren der Dichte erhalten wir die Exponentialverteilungsfunktion:

Hauptmerkmale der Exponentialverteilung:

Dichtediagramme und Funktionen der resultierenden Exponentialverteilung