Weißt du, wie ein regelmäßiges Sechseck aussieht?
Diese Frage wurde nicht zufällig gestellt. Die meisten Schüler der 11. Klasse kennen die Antwort darauf nicht.

Ein regelmäßiges Sechseck ist eines, in dem alle Seiten gleich sind und alle Winkel ebenfalls gleich sind..

Eiserne Nuss. Schneeflocke. Eine Wabenzelle, in der Bienen leben. Benzol-Molekül. Was haben diese Objekte gemeinsam? - Die Tatsache, dass sie alle eine regelmäßige sechseckige Form haben.

Viele Schulkinder sind verloren, wenn sie Aufgaben für ein regelmäßiges Sechseck sehen, und sie glauben, dass einige spezielle Formeln benötigt werden, um sie zu lösen. Ist es so?

Zeichne die Diagonalen eines regelmäßigen Sechsecks. Wir haben sechs gleichseitige Dreiecke.

Wir wissen, dass die Fläche eines gleichseitigen Dreiecks ist.

Dann ist die Fläche eines regelmäßigen Sechsecks sechsmal größer.

Wo ist die Seite eines regelmäßigen Sechsecks.

Bitte beachten Sie, dass in einem regelmäßigen Sechseck der Abstand von seiner Mitte zu jedem der Eckpunkte gleich und gleich der Seite des regelmäßigen Sechsecks ist.

Das bedeutet, dass der Radius eines um ein regelmäßiges Sechseck umschriebenen Kreises gleich seiner Seite ist.
Der Radius eines Kreises, der in ein regelmäßiges Sechseck eingeschrieben ist, ist leicht zu finden.
Er ist gleich.
Jetzt können Sie problemlos alle USE-Probleme lösen, bei denen ein regelmäßiges Sechseck erscheint.

Finde den Radius eines Kreises, der in ein regelmäßiges Sechseck mit Seitenlänge eingeschrieben ist.

Der Radius eines solchen Kreises ist .

Antworten: .

Welche Seite hat ein regelmäßiges Sechseck, das einem Kreis mit Radius 6 einbeschrieben ist?

Wir wissen, dass die Seite eines regelmäßigen Sechsecks gleich dem Radius des umschriebenen Kreises ist.

Die bekannteste Figur mit mehr als vier Ecken ist das regelmäßige Sechseck. In der Geometrie wird es oft bei Problemen verwendet. Und genau das haben Waben im Leben im Schnitt.

Wie unterscheidet es sich von falsch?

Erstens ist ein Sechseck eine Figur mit 6 Ecken. Zweitens kann es konvex oder konkav sein. Der erste unterscheidet sich dadurch, dass vier Eckpunkte auf einer Seite einer geraden Linie liegen, die durch die anderen beiden gezogen wird.

Drittens zeichnet sich ein regelmäßiges Sechseck dadurch aus, dass alle seine Seiten gleich sind. Darüber hinaus hat auch jede Ecke der Figur den gleichen Wert. Um die Summe aller Winkel zu bestimmen, müssen Sie die Formel verwenden: 180º * (n - 2). Hier ist n die Anzahl der Eckpunkte der Figur, also 6. Eine einfache Rechnung ergibt einen Wert von 720º. Jeder Winkel beträgt also 120 Grad.

Bei alltäglichen Aktivitäten findet sich ein regelmäßiges Sechseck in einer Schneeflocke und einer Nuss. Chemiker sehen es sogar im Benzolmolekül.

Welche Eigenschaften müssen Sie kennen, wenn Sie Probleme lösen?

Zu dem oben Gesagten ist hinzuzufügen:

• die durch die Mitte gezogenen Diagonalen der Figur teilen sie in sechs gleichseitige Dreiecke;
• die Seite eines regelmäßigen Sechsecks hat einen Wert, der mit dem Radius des umschriebenen Kreises um ihn herum übereinstimmt;
• Mit einer solchen Figur ist es möglich, die Ebene zu füllen, und zwischen ihnen gibt es keine Lücken und keine Überlappungen.

Notation eingeführt

Traditionell wird die Seite einer regelmäßigen geometrischen Figur mit dem lateinischen Buchstaben „a“ bezeichnet. Um Probleme zu lösen, werden auch Fläche und Umfang benötigt, dies sind S bzw. P. Ein Kreis wird in ein regelmäßiges Sechseck einbeschrieben oder um es herum umschrieben. Dann werden Werte für ihre Radien eingegeben. Sie werden jeweils mit den Buchstaben r und R bezeichnet.

In einigen Formeln erscheinen ein Innenwinkel, ein Halbumfang und ein Apothem (das eine Senkrechte zur Mitte einer beliebigen Seite von der Mitte des Polygons ist). Für sie werden Buchstaben verwendet: α, p, m.

Formeln, die eine Figur beschreiben

Um den Radius eines einbeschriebenen Kreises zu berechnen, benötigen Sie Folgendes: r= (a * √3) / 2 und r = m. Das heißt, die gleiche Formel gilt für das Apothem.

Da der Umfang eines Sechsecks die Summe aller Seiten ist, wird er wie folgt bestimmt: P = 6 * a. Da die Seite gleich dem Radius des umschriebenen Kreises ist, gibt es für den Umfang eine solche Formel für ein regelmäßiges Sechseck: P \u003d 6 * R. Aus der für den Radius des einbeschriebenen Kreises angegebenen Beziehung zwischen a und r wird abgeleitet. Dann nimmt die Formel folgende Form an: Р = 4 r * √3.

Für die Fläche eines regelmäßigen Sechsecks könnte dies praktisch sein: S = p * r = (a 2 * 3 √3) / 2.

Aufgaben

Nr. 1. Zustand. Es gibt ein regelmäßiges sechseckiges Prisma mit einer Kantenlänge von 4 cm, in das ein Zylinder eingeschrieben ist, dessen Volumen bestimmt werden muss.

Entscheidung. Das Volumen eines Zylinders ist definiert als das Produkt aus Grundfläche und Höhe. Letztere fällt mit der Kante des Prismas zusammen. Und es ist gleich der Seite eines regelmäßigen Sechsecks. Das heißt, die Höhe des Zylinders beträgt ebenfalls 4 cm.

Um die Fläche seiner Basis herauszufinden, müssen Sie den Radius des Kreises berechnen, der in das Sechseck eingeschrieben ist. Die Formel dafür ist oben abgebildet. Also r = 2√3 (cm). Dann die Fläche des Kreises: S \u003d π * r 2 \u003d 3,14 * (2√3) 2 \u003d 37,68 (cm 2).

Antworten. V \u003d 150,72 cm 3.

Nr. 2. Zustand. Berechnen Sie den Radius eines Kreises, der einem regelmäßigen Sechseck einbeschrieben ist. Es ist bekannt, dass seine Seite √3 cm lang ist. Welchen Umfang wird er haben?

Entscheidung. Diese Aufgabe erfordert die Verwendung von zwei der obigen Formeln. Darüber hinaus müssen sie ohne Änderung angewendet werden, ersetzen Sie einfach den Wert der Seite und berechnen Sie.

Der Radius des einbeschriebenen Kreises ergibt sich also zu 1,5 cm Für den Umfang erweist sich folgender Wert als richtig: 6√3 cm.

Antworten. r = 1,5 cm, Р = 6√3 cm.

Nr. 3. Zustand. Der Radius des umschriebenen Kreises beträgt 6 cm. Welchen Wert hat in diesem Fall die Seite eines regelmäßigen Sechsecks?

Entscheidung. Aus der Formel für den Radius eines Kreises, der einem Sechseck einbeschrieben ist, erhält man leicht diejenige, nach der die Seite berechnet werden muss. Es ist klar, dass der Radius mit zwei multipliziert und durch die Wurzel aus drei dividiert wird. Es ist notwendig, die Irrationalität im Nenner loszuwerden. Daher hat das Ergebnis der Aktionen die folgende Form: (12 √3) / (√3 * √3), dh 4√3.

Antworten. a = 4√3 cm.

Weißt du, wie ein regelmäßiges Sechseck aussieht?
Diese Frage wurde nicht zufällig gestellt. Die meisten Schüler der 11. Klasse kennen die Antwort darauf nicht.

Ein regelmäßiges Sechseck ist eines, in dem alle Seiten gleich sind und alle Winkel ebenfalls gleich sind..

Eiserne Nuss. Schneeflocke. Eine Wabenzelle, in der Bienen leben. Benzol-Molekül. Was haben diese Objekte gemeinsam? - Die Tatsache, dass sie alle eine regelmäßige sechseckige Form haben.

Viele Schulkinder sind verloren, wenn sie Aufgaben für ein regelmäßiges Sechseck sehen, und sie glauben, dass einige spezielle Formeln benötigt werden, um sie zu lösen. Ist es so?

Zeichne die Diagonalen eines regelmäßigen Sechsecks. Wir haben sechs gleichseitige Dreiecke.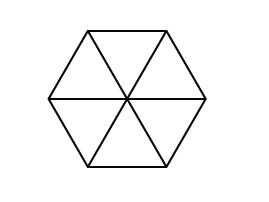

Wir wissen, dass die Fläche eines gleichseitigen Dreiecks ist.

Dann ist die Fläche eines regelmäßigen Sechsecks sechsmal größer.

Wo ist die Seite eines regelmäßigen Sechsecks.

Bitte beachten Sie, dass in einem regelmäßigen Sechseck der Abstand von seiner Mitte zu jedem der Eckpunkte gleich und gleich der Seite des regelmäßigen Sechsecks ist.

Das bedeutet, dass der Radius eines um ein regelmäßiges Sechseck umschriebenen Kreises gleich seiner Seite ist.
Der Radius eines Kreises, der in ein regelmäßiges Sechseck eingeschrieben ist, ist leicht zu finden.
Er ist gleich.
Jetzt können Sie problemlos alle USE-Probleme lösen, bei denen ein regelmäßiges Sechseck erscheint.

Finde den Radius eines Kreises, der in ein regelmäßiges Sechseck mit Seitenlänge eingeschrieben ist.

Der Radius eines solchen Kreises ist .

Antworten: .

Welche Seite hat ein regelmäßiges Sechseck, das einem Kreis mit Radius 6 einbeschrieben ist?

Wir wissen, dass die Seite eines regelmäßigen Sechsecks gleich dem Radius des umschriebenen Kreises ist.

Gibt es einen Bleistift in Ihrer Nähe? Schauen Sie sich seinen Abschnitt an - es ist ein regelmäßiges Sechseck oder, wie es auch genannt wird, ein Sechseck. Der Querschnitt einer Nuss, ein sechseckiges Schachfeld, einige komplexe Kohlenstoffmoleküle (z. B. Graphit), eine Schneeflocke, eine Wabe und andere Objekte haben ebenfalls diese Form. Kürzlich wurde ein gigantisches regelmäßiges Sechseck entdeckt. Ist es nicht seltsam, dass die Natur Strukturen dieser besonderen Form so oft für ihre Kreationen verwendet? Lasst uns genauer hinschauen.

Ein regelmäßiges Sechseck ist ein Polygon mit sechs gleichen Seiten und gleichen Winkeln. Aus dem Schulunterricht wissen wir, dass es folgende Eigenschaften hat:

• Die Länge seiner Seiten entspricht dem Radius des umschriebenen Kreises. Diese Eigenschaft hat allerdings nur ein regelmäßiges Sechseck.
• Die Winkel sind einander gleich und die Größe beträgt jeweils 120 °.
• Der Umfang eines Sechsecks kann mit der Formel Р=6*R ermittelt werden, wenn der Radius des umschriebenen Kreises bekannt ist, oder Р=4*√(3)*r, wenn der Kreis darin einbeschrieben ist. R und r sind die Radien der umschriebenen und einbeschriebenen Kreise.
• Die von einem regelmäßigen Sechseck eingenommene Fläche wird wie folgt bestimmt: S=(3*√(3)*R 2)/2. Wenn der Radius unbekannt ist, ersetzen wir ihn durch die Länge einer der Seiten - wie Sie wissen, entspricht dies der Länge des Radius des umschriebenen Kreises.

Das regelmäßige Sechseck hat ein interessantes Merkmal, aufgrund dessen es in der Natur so weit verbreitet ist - es kann jede Oberfläche der Ebene ohne Überlappungen und Lücken ausfüllen. Es gibt sogar das sogenannte Pal-Lemma, wonach ein regelmäßiges Sechseck, dessen Seite gleich 1/√(3) ist, ein universeller Reifen ist, das heißt, es kann jede Menge mit einem Durchmesser von einer Einheit überdecken.

Betrachten Sie nun die Konstruktion eines regelmäßigen Sechsecks. Es gibt mehrere Möglichkeiten, von denen die einfachste die Verwendung eines Kompasses, Bleistifts und Lineals beinhaltet. Zuerst zeichnen wir mit einem Zirkel einen beliebigen Kreis, dann machen wir einen Punkt an einer beliebigen Stelle auf diesem Kreis. Ohne die Lösung des Kompasses zu ändern, setzen wir die Spitze an diesen Punkt, markieren die nächste Kerbe auf dem Kreis und fahren so fort, bis wir alle 6 Punkte erhalten. Jetzt müssen sie nur noch mit geraden Segmenten miteinander verbunden werden, und die gewünschte Figur wird sich herausstellen.

In der Praxis gibt es Zeiten, in denen Sie ein großes Sechseck zeichnen müssen. An einer zweistöckigen Gipskartondecke müssen Sie beispielsweise um den Befestigungspunkt des zentralen Kronleuchters herum sechs kleine Lampen auf der unteren Ebene installieren. Es wird sehr, sehr schwierig sein, einen Kompass dieser Größe zu finden. Wie ist in diesem Fall vorzugehen? Wie zeichnet man einen großen Kreis? Sehr einfach. Sie müssen einen starken Faden der gewünschten Länge nehmen und eines seiner Enden gegenüber dem Bleistift binden. Jetzt muss nur noch ein Helfer gefunden werden, der das zweite Ende des Fadens an der richtigen Stelle an die Decke drückt. Natürlich sind in diesem Fall kleinere Fehler möglich, die aber einem Außenstehenden kaum auffallen werden.

Konstruktion eines regelmäßigen Sechsecks, das einem Kreis einbeschrieben ist. Die Konstruktion eines Sechsecks basiert darauf, dass seine Seite gleich dem Radius des umschriebenen Kreises ist. Zum Bauen reicht es daher aus, den Kreis in sechs gleiche Teile zu teilen und die gefundenen Punkte miteinander zu verbinden (Abb. 60, a).

Ein regelmäßiges Sechseck kann mit einem T-Winkel und einem 30X60°-Winkel konstruiert werden. Um diese Konstruktion durchzuführen, nehmen wir den horizontalen Durchmesser des Kreises als Winkelhalbierende der Winkel 1 und 4 (Abb. 60, b), bauen die Seiten 1-6, 4-3, 4-5 und 7-2, danach bauen wir Zeichne die Seiten 5-6 und 3-2.

Konstruktion eines gleichseitigen Dreiecks, das einem Kreis einbeschrieben ist. Die Eckpunkte eines solchen Dreiecks können mit einem Kompass und einem Quadrat mit Winkeln von 30 und 60 ° oder nur einem Kompass konstruiert werden.

Betrachten Sie zwei Möglichkeiten, ein gleichseitiges Dreieck zu konstruieren, das einem Kreis einbeschrieben ist.

Erster Weg(Abb. 61, a) basiert auf der Tatsache, dass alle drei Winkel des Dreiecks 7, 2, 3 jeweils 60 ° enthalten und die durch Punkt 7 gezogene Vertikale sowohl die Höhe als auch die Winkelhalbierende von Winkel 1 ist. Da die Winkel 0-1- 2 ist gleich 30°, um dann die Seite zu finden

1-2 reicht es, einen Winkel von 30° an Punkt 1 und Seite 0-1 aufzubauen. Stellen Sie dazu das T-Quadrat und das Quadrat wie in der Abbildung gezeigt ein und zeichnen Sie eine Linie 1-2, die eine der Seiten des gewünschten Dreiecks sein wird. Um Seite 2-3 zu bauen, stellen Sie das T-Quadrat auf die Position, die durch die gestrichelten Linien angezeigt wird, und ziehen Sie eine gerade Linie durch Punkt 2, die den dritten Eckpunkt des Dreiecks definiert.

Zweiter Weg basiert auf der Tatsache, dass, wenn Sie ein regelmäßiges Sechseck bauen, das in einen Kreis eingeschrieben ist, und dann seine Eckpunkte durch eins verbinden, Sie ein gleichseitiges Dreieck erhalten.

Um ein Dreieck zu konstruieren (Abb. 61, b), markieren wir einen Scheitelpunkt 1 auf dem Durchmesser und zeichnen eine diametrale Linie 1-4. Ferner beschreiben wir von Punkt 4 mit einem Radius gleich D / 2 den Bogen, bis er sich mit dem Kreis an den Punkten 3 und 2 schneidet. Die resultierenden Punkte sind zwei andere Eckpunkte des gewünschten Dreiecks.

Konstruktion eines in einen Kreis einbeschriebenen Quadrats. Diese Konstruktion kann mit einem Winkel und einem Zirkel durchgeführt werden.

Die erste Methode beruht darauf, dass sich die Diagonalen des Quadrats im Mittelpunkt des umschriebenen Kreises schneiden und in einem Winkel von 45° zu dessen Achsen geneigt sind. Darauf aufbauend installieren wir einen T-Winkel und einen Winkel mit Winkeln von 45 °, wie in Abb. 62, a, und markieren Sie die Punkte 1 und 3. Weiter zeichnen wir durch diese Punkte die horizontalen Seiten des Quadrats 4-1 und 3-2 mit Hilfe eines T-Quadrats. Dann zeichnen wir mit einem T-Quadrat entlang des Beins des Quadrats die vertikalen Seiten des Quadrats 1-2 und 4-3.

Die zweite Methode basiert auf der Tatsache, dass die Eckpunkte des Quadrats die Kreisbögen halbieren, die zwischen den Enden des Durchmessers eingeschlossen sind (Abb. 62, b). Wir markieren die Punkte A, B und C an den Enden zweier zueinander senkrechter Durchmesser und beschreiben von ihnen mit einem Radius y die Bögen, bis sie sich schneiden.

Außerdem zeichnen wir durch die Schnittpunkte der Bögen Hilfslinien, die in der Figur mit durchgezogenen Linien markiert sind. Ihre Schnittpunkte mit dem Kreis definieren die Eckpunkte 1 und 3; 4 und 2. Die Eckpunkte des auf diese Weise erhaltenen gewünschten Quadrats werden miteinander in Reihe geschaltet.

Konstruktion eines regelmäßigen Fünfecks, das in einen Kreis eingeschrieben ist.

Um ein regelmäßiges Fünfeck in einen Kreis einzuschreiben (Abb. 63), führen wir die folgenden Konstruktionen aus.

Wir markieren Punkt 1 auf dem Kreis und nehmen ihn als eine der Ecken des Fünfecks. Segment AO halbieren. Dazu beschreiben wir mit dem Radius AO von Punkt A den Bogen, bis er den Kreis an den Punkten M und B schneidet. Wenn wir diese Punkte mit einer Geraden verbinden, erhalten wir Punkt K, den wir dann mit Punkt 1 verbinden. Mit ein Radius gleich dem Segment A7, wir beschreiben den Bogen vom Punkt K bis zum Schnittpunkt mit der diametralen Linie AO ​​am Punkt H. Wenn wir Punkt 1 mit Punkt H verbinden, erhalten wir die Seite des Fünfecks. Dann finden wir mit einer Kompassöffnung gleich dem Segment 1H, nachdem wir den Bogen von Scheitelpunkt 1 bis zum Schnittpunkt mit dem Kreis beschrieben haben, die Scheitelpunkte 2 und 5. Nachdem wir Serifen aus den Scheitelpunkten 2 und 5 mit der gleichen Kompassöffnung gemacht haben, erhalten wir die verbleibende Eckpunkte 3 und 4. Wir verbinden die gefundenen Punkte der Reihe nach miteinander.

Konstruktion eines regelmäßigen Fünfecks mit gegebener Seite.

Um ein regelmäßiges Fünfeck entlang seiner gegebenen Seite zu konstruieren (Abb. 64), teilen wir die Strecke AB in sechs gleiche Teile. Von den Punkten A und B mit dem Radius AB beschreiben wir Bögen, deren Schnittpunkt den Punkt K ergibt. Durch diesen Punkt und die Teilung 3 auf der Linie AB ziehen wir eine vertikale Linie.

Wir erhalten den Punkt 1-Eckpunkt des Fünfecks. Dann beschreiben wir mit einem Radius gleich AB von Punkt 1 den Bogen bis zum Schnittpunkt mit den zuvor von den Punkten A und B gezeichneten Bögen. Die Schnittpunkte der Bögen bestimmen die Eckpunkte des Fünfecks 2 und 5. Wir verbinden das Gefundene Eckpunkte in Reihe zueinander.

Konstruktion eines regelmäßigen Siebenecks, das in einen Kreis eingeschrieben ist.

Gegeben sei ein Kreis vom Durchmesser D; Sie müssen ein regelmäßiges Siebeneck hineinschreiben (Abb. 65). Teilen Sie den vertikalen Durchmesser des Kreises in sieben gleiche Teile. Von Punkt 7 mit einem Radius gleich dem Durchmesser des Kreises D beschreiben wir den Bogen, bis er sich mit der Fortsetzung des horizontalen Durchmessers bei Punkt F schneidet. Punkt F wird als Pol des Polygons bezeichnet. Wenn wir den Punkt VII als einen der Eckpunkte des Siebenecks nehmen, zeichnen wir Strahlen vom Pol F durch gleichmäßige Teilungen des vertikalen Durchmessers, deren Schnittpunkt mit dem Kreis die Eckpunkte VI, V und IV des Siebenecks bestimmt. Um die Eckpunkte / - // - /// von den Punkten IV, V und VI zu erhalten, zeichnen wir horizontale Linien, bis sie sich mit dem Kreis schneiden. Wir verbinden die gefundenen Knoten in Reihe miteinander. Das Siebeneck kann konstruiert werden, indem Strahlen vom F-Pol und durch ungerade Teilungen des vertikalen Durchmessers gezogen werden.

Das obige Verfahren eignet sich zum Konstruieren regelmäßiger Polygone mit einer beliebigen Anzahl von Seiten.

Die Teilung eines Kreises in beliebig viele gleiche Teile kann auch mit den Daten in Tabelle erfolgen. 2, die die Koeffizienten zeigt, die es ermöglichen, die Abmessungen der Seiten von regelmäßig einbeschriebenen Polygonen zu bestimmen.