Решение неравенств онлайн
Перед тем как решать неравенства, необходимо хорошо усвоить как решаются уравнения .
Не важно каким является неравенство – строгим () или нестрогим (≤, ≥), первым делом приступают к решению уравнения, заменив знак неравенства на равенство (=).
Поясним что означает решить неравенство?
После изучения уравнений в голове у школьника складывается следующая картина: нужно найти такие значения переменной, при которых обе части уравнения принимают одинаковые значения. Другими словами, найти все точки, в которых выполняется равенство. Всё правильно!
Когда говорят о неравенствах, имеют в виду нахождение интервалов (отрезков), на которых выполняется неравенство. Если в неравенстве две переменные, то решением будут уже не интервалы, а какие-то площади на плоскости. Догадайтесь сами, что будет решением неравенства от трех переменных?
Как решать неравенства?
Универсальным способом решения неравенств считают метод интервалов (он же метод промежутков), который заключается в определении всех интервалов, в границах которых будет выполняться заданное неравенство.
Не вдаваясь в тип неравенства, в данном случае это не суть, требуется решить соответствующее уравнение и определить его корни с последующим обозначением этих решений на числовой оси.
Как правильно записывать решение неравенства?
Когда вы определили интервалы решений неравенства, нужно грамотно выписать само решение. Есть важный нюанс – входят ли границы интервалов в решение?
Тут всё просто. Если решение уравнения удовлетворяет ОДЗ и неравенство является нестрогим, то граница интервала входит в решение неравенства. В противном случае – нет.
Рассматривая каждый интервал, решением неравенства может оказаться сам интервал, либо полуинтервал (когда одна из его границ удовлетворяет неравенству), либо отрезок – интервал вместе с его границами.
Важный момент
Не думайте, что решением неравенства могут быть только интервалы, полуинтервалы и отрезки. Нет, в решение могут входить и отдельно взятые точки.
Например, у неравенства |x|≤0 всего одно решение – это точка 0.
А у неравенства |x|
Для чего нужен калькулятор неравенств?
Калькулятор неравенств выдает правильный итоговый ответ. При этом в большинстве случаев приводится иллюстрация числовой оси или плоскости. Видно, входят ли границы интервалов в решение или нет – точки отображаются закрашенными или проколотыми.
Благодаря онлайн калькулятору неравенств можно проверить правильно ли вы нашли корни уравнения, отметили их на числовой оси и проверили на интервалах (и границах) выполнение условия неравенства?
Если ваш ответ расходится с ответом калькулятора, то однозначно нужно перепроверить свое решение и выявить допущенную ошибку.
Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 6 является 6, модулем числа -6 тоже является 6.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |6|, |х |, |а | и т.д.
(Подробнее - в разделе «Модуль числа»).
Уравнения с модулем.
Пример 1 . Решить уравнение |10 х - 5| = 15.
Решение .
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
10х
- 5 = 15
10х
- 5 = -15
Решаем:
10х
= 15 + 5 = 20
10х
= -15 + 5 = -10
х
= 20: 10
х
= -10: 10
х
= 2
х
= -1
Ответ : х 1 = 2, х 2 = -1.
Пример 2 . Решить уравнение |2 х + 1| = х + 2.
Решение .
Поскольку модуль - число неотрицательное, то х + 2 ≥ 0. Соответственно:
х ≥ -2.
Составляем два уравнения:
2х
+ 1 = х
+ 2
2х
+ 1 = -(х
+ 2)
Решаем:
2х
+ 1 = х
+ 2
2х
+ 1 = -х
- 2
2х
- х
= 2 - 1
2х
+ х
= -2 - 1
х
= 1
х
= -1
Оба числа больше -2. Значит, оба являются корнями уравнения.
Ответ : х 1 = -1, х 2 = 1.
Пример 3
. Решить уравнение
|х
+ 3| - 1
————— = 4
х
- 1
Решение .
Уравнение имеет смысл, если знаменатель не равен нулю - значит, если х ≠ 1. Учтем это условие. Наше первое действие простое - не просто освобождаемся от дроби, а преобрахуем ее так, чтобы получить модуль в чистом виде:
|х + 3| - 1 = 4 · (х - 1),
|х + 3| - 1 = 4х - 4,
|х + 3| = 4х - 4 + 1,
|х + 3| = 4х - 3.
Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.
Модуль числа есть неотрицательное число - то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:
4х - 3 ≥ 0
4х ≥ 3
х ≥ 3/4
Таким образом, у нас появилось второе условие: корень уравнения должен быть не меньше 3/4.
В соответствии с правилом, составляем совокупность двух уравнений и решаем их:
х
+ 3 = 4х
- 3
х
+ 3 = -(4х
- 3)
х
+ 3 = 4х
- 3
х
+ 3 = -4х
+ 3
х
- 4х
= -3 - 3
х
+ 4х
= 3 - 3
х
= 2
х
= 0
Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.
У нас было два условия: корень уравнения не может быть равен 1, и он должен быть не меньше 3/4. То есть х ≠ 1, х ≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов - число 2. Значит, только оно и является корнем исходного уравнения.
Ответ : х = 2.
Неравенства с модулем.
Пример 1 . Решить неравенство | х - 3| < 4
Решение .
Правило модуля гласит:
|а | = а , если а ≥ 0.
|а | = -а , если а < 0.
Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая: х - 3 ≥ 0 и х - 3 < 0.
1) При х
- 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:
х
- 3 < 4.
2) При х - 3 < 0 в исходном неравенстве надо поставить знак минус перед всем подмодульным выражением:
-(х - 3) < 4.
Раскрыв скобки, получаем:
-х + 3 < 4.
Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:
х
- 3 ≥ 0
х
- 3 < 4
х
- 3 < 0
-х
+ 3 < 4
Решим их:
х
≥ 3
х
< 7
х
< 3
х
> -1
Итак, у нас в ответе объединение двух множеств:
3 ≤ х < 7 U -1 < х < 3.
Определяем наименьшее и наибольшее значения. Это -1 и 7. При этом х
больше -1, но меньше 7.
Кроме того, х
≥ 3. Значит, решением неравенства является все множество чисел от -1 до 7, исключая эти крайние числа.
Ответ : -1 < х < 7.
Или: х ∈ (-1; 7).
Дополнения .
1) Есть более простой и короткий способ решения нашего неравенства - графический. Для этого надо нарисовать горизонтальную ось (рис.1).
Выражение |х - 3| < 4 означает, что расстояние от точки х до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа - к точке 7. Таким образом, точки х мы просто увидели, не вычисляя их.
При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:
1 < х < 7.
2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:
4 < х - 3 < 4.
Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число -4 являются границами решения неравенства.
4 + 3 < х < 4 + 3
1 < х < 7.
Пример 2 . Решить неравенство | х - 2| ≥ 5
Решение .
Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны -3 и больше или равны 7. А значит, мы уже получили ответ.
Ответ : -3 ≥ х ≥ 7.
Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:
5 ≥ х - 2 ≥ 5
5 + 2 ≥ х ≥ 5 + 2
Ответ тот же: -3 ≥ х ≥ 7.
Или: х ∈ [-3; 7]
Пример решен.
Пример 3 . Решить неравенство 6 х 2 - | х | - 2 ≤ 0
Решение .
Число х может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х ≥ 0 и х < 0. При х ≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:
6х 2 - х - 2 ≤ 0.
Теперь о втором случае: если х < 0. Модулем отрицательного числа является это же число с противоположным знаком. То есть пишем число под модулем с обратным знаком и опять же освобождаемся от знака модуля:
6х 2 - (-х ) - 2 ≤ 0.
Раскрываем скобки:
6х 2 + х - 2 ≤ 0.
Таким образом, мы получили две системы уравнений:
6х
2 - х
- 2 ≤ 0
х
≥ 0
6х
2 + х
- 2 ≤ 0
х
< 0
Надо решить неравенства в системах - а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.
Начнем с первого:
6х 2 - х - 2 = 0.
Как решается квадратное уравнение - см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:
х 1 = -1/2, х 2 = 2/3.
Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от -1/2 до 2/3. Пишем объединение решений при х
≥ 0:
[-1/2; 2/3].
Теперь решим второе квадратное уравнение:
6х 2 + х - 2 = 0.
Его корни:
х 1 = -2/3, х 2 = 1/2.
Вывод: при х < 0 корнями исходного неравенства являются также все числа от -2/3 до 1/2.
Объединим два ответа и получим итоговый ответ: решением является все множество чисел от -2/3 до 2/3, включая и эти крайние числа.
Ответ : -2/3 ≤ х ≤ 2/3.
Или: х ∈ [-2/3; 2/3].
РАССМОТРЕНО
Педагогическим советом МОУ
«Зашижемская СОШ»
Протокол № 1
СОГЛАСОВАНО
Заместитель директора по УВР
_______ /Сидоркина Р.Л./
УТВЕРЖДАЮ
Директор школы:
А.П.Конаков
Приказ №63
Решение уравнений и неравенств с модулем
Исследовательская работа
Программу составила:
учитель математики высшей
Сидоркина Р.Л.
с.Зашижемье, 2014 г.
Оглавление
Введение…………………………………………………………………3
Простейшие уравнения и неравенства с модулем……………………5
Графическое решение уравнений и неравенств с модулем………….8
Иные способы решения уравнений и неравенств с модулем……......10
Заключение ……………………………………………………………..16
Список литературы………………………………………………………18
Введение
Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел.
Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы и на ЕГЭ. И поэтому для нас стало важно изучить некоторые аспекты этой темы.
Главной целью в нашей работе является изучение различных методов решения уравнений и неравенств с модулями.
Данная цель должна быть достигнута при решении следующих задач :
Изучить определение и некоторые свойства модуля.
Освоить решение простейших уравнений и неравенств с модулем через равносильные переходы
Рассмотреть различные методы решения уравнений и неравенств с модулем.
Объектом исследования являются некоторые типы уравнений и неравенств с модулем.
Предмет исследования – различные методы решения уравнений и неравенств с модулем, а именно: графический способ, метод геометрической интерпретации, использование тождества , применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель,метод раскрытия модулей.
В ходе исследования применялись такие методы, как изучение литературы по данному вопросу и практический метод.
В ходе работы мы исследовал такие источники, как:
1. «Большая математическая энциклопедия» для школьников и студентов;
Математика. ЕГЭ – 2011-2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
Энциклопедия «Я познаю мир» Математика;
;
Простейшие уравнения и неравенства с модулем
К простейшим уравнениям мы будем относить уравнения, решаемые одним из нижеприведенных равносильных переходов: 
Примеры решения простейших уравнений.
Пример 1
Решим уравнение 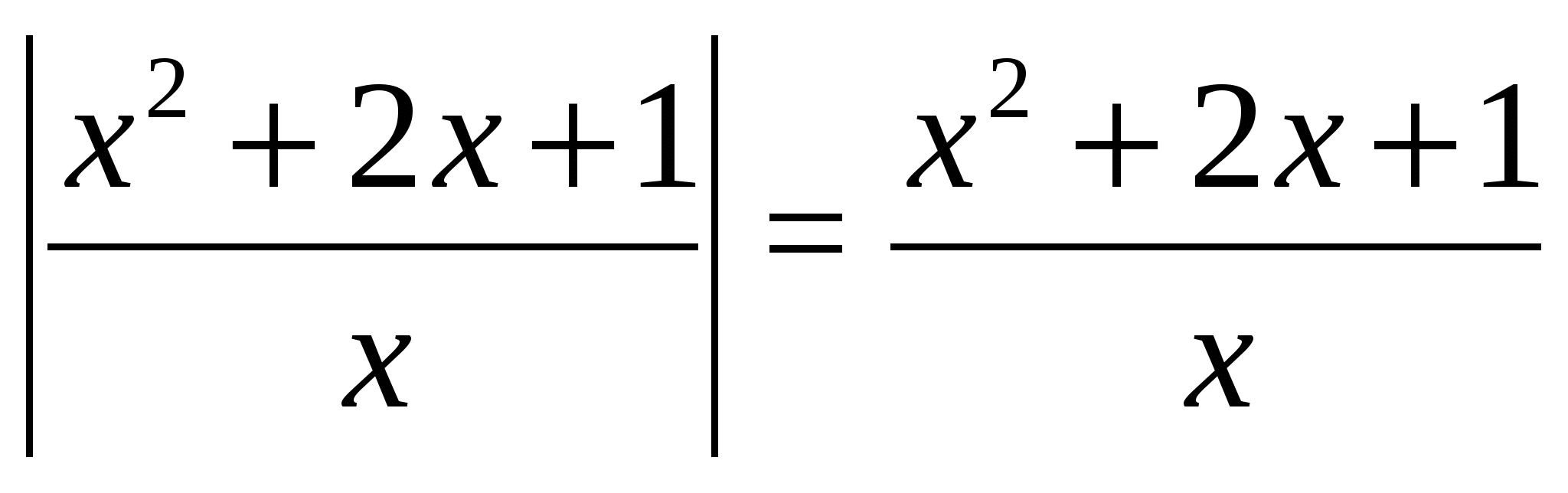 .
.
Решение.
Ответ.
 .
.
Пример 2 Решим уравнение .
Решение.
Ответ.
 .
.
Пример 3
Решим уравнение 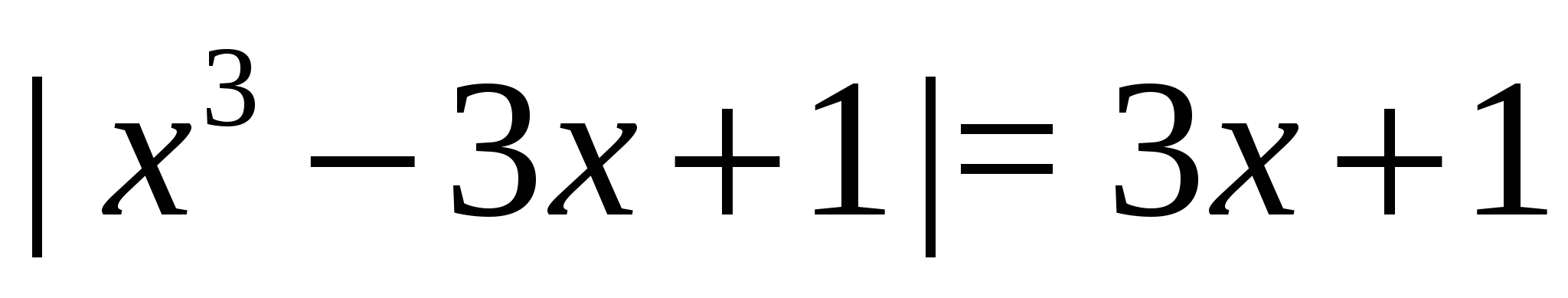 .
.
Решение.

Ответ.
 .
.
Ряд уравнений решается с использованием следующей теоремы.
Теорема.4 Сумма модулей равна алгебраической сумме подмодульнх величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму.
Пример 5 Решить уравнение
Решение.
Так как , то мы имеем равенство вида , где  ,
,  . Поэтому исходное уравнение равносильно системе:
. Поэтому исходное уравнение равносильно системе:


Ответ.
 .
.
Примеры решения простейших неравенств.
Пример 6
Решим неравенство 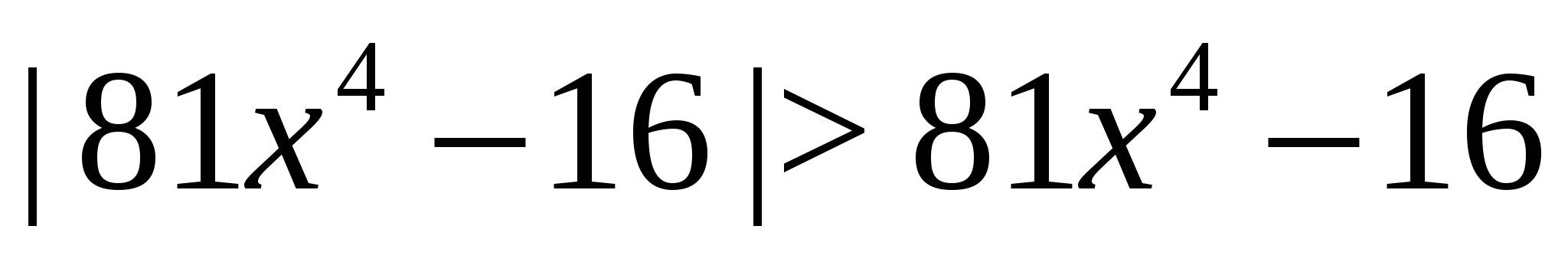 .
.
Решение.
Ответ.
 .
.
Пример 7
Решим неравенство  .
.
Решение.
Ответ.
 .
.
Как ни странно, но 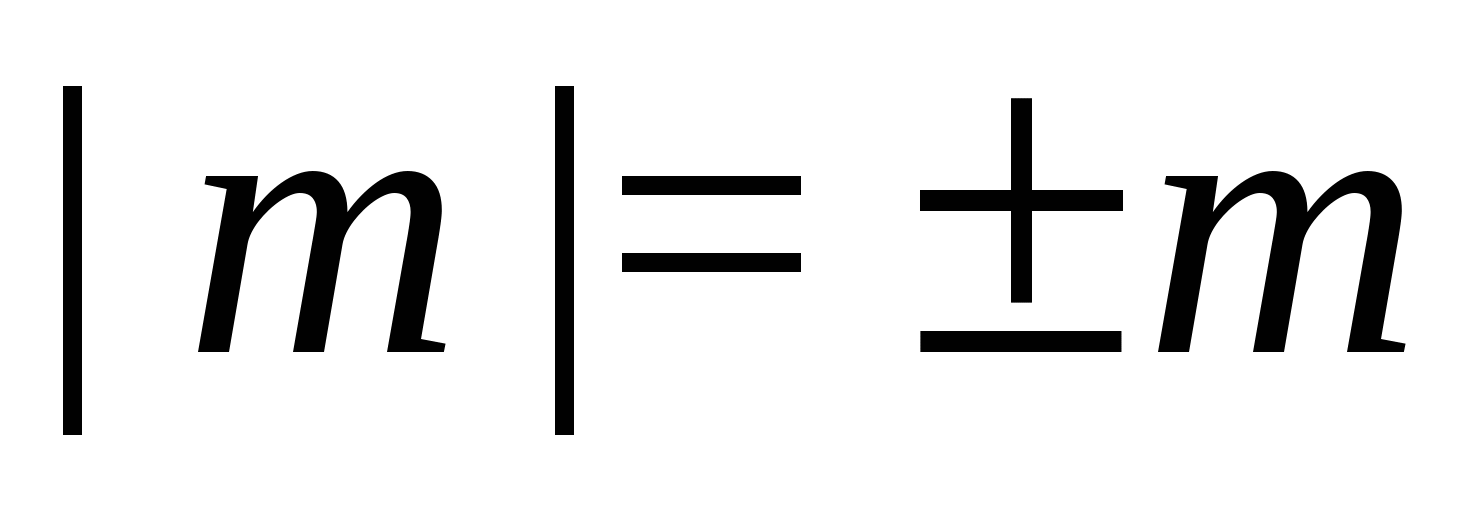 достаточно, чтобы избавиться от знака модуля в любых неравенствах.
достаточно, чтобы избавиться от знака модуля в любых неравенствах.
Пример 8 Решить неравенство

Решение.



Ответ.
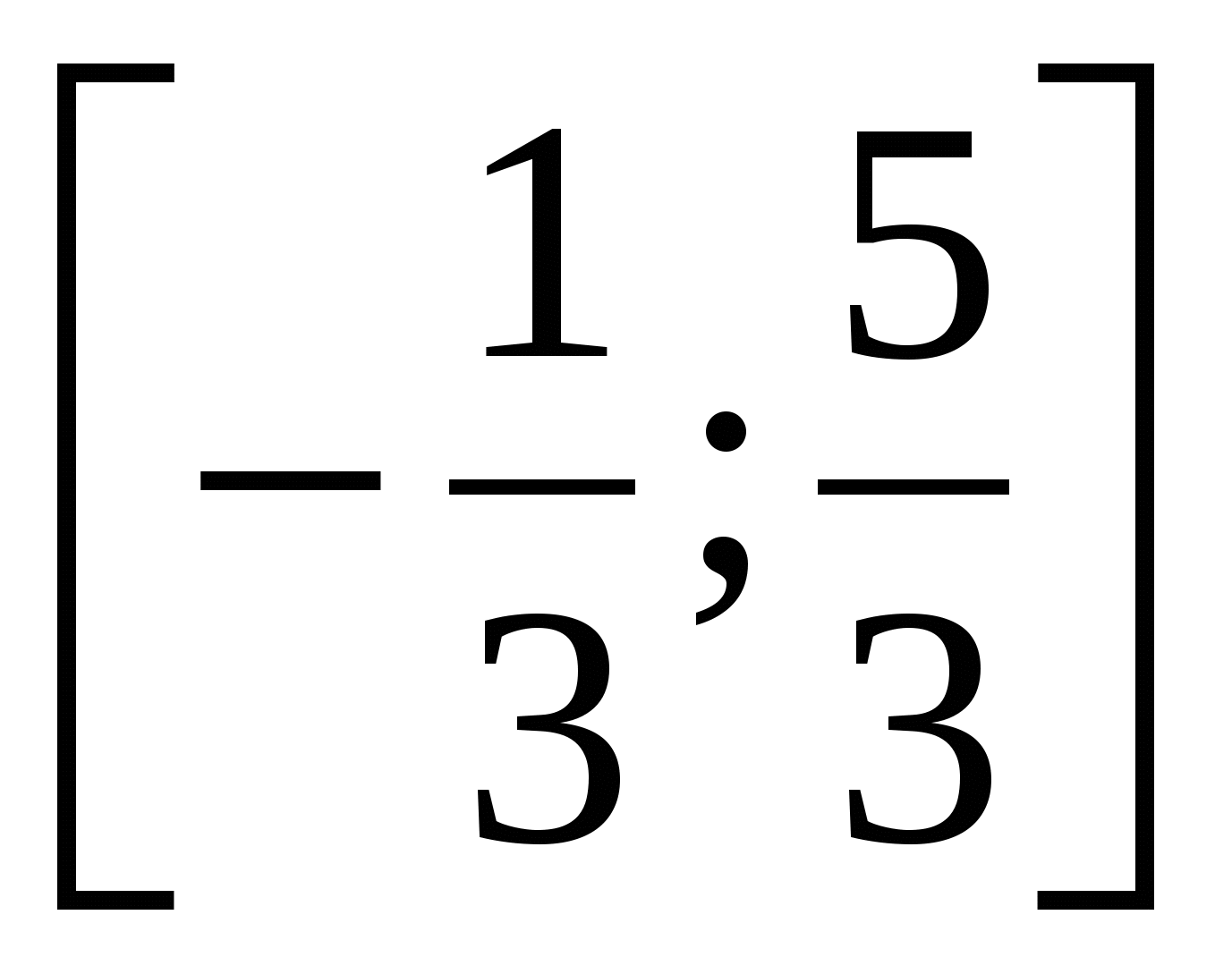 .
.
3. Графическое решение уравнений и неравенств с модулем
Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры).
Пример 9 (С5, ЕГЭ - 2010)
C
5. Для каждого значения
a
укажите число решений уравнения 
Решение.
Построим график функции
 . Для этого выделим полный квадрат:
. Для этого выделим полный квадрат:
Число точек пересечения графика функции у =
 с горизонтальными прямыми у = а равно числу решений уравнения.
с горизонтальными прямыми у = а равно числу решений уравнения.
О твет:
если
твет:
если  < 0, то решений нет; если а= 0, то два решения, если
< 0, то решений нет; если а= 0, то два решения, если  0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения.
0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения.
Иные способы решения уравнений и неравенств с модулем
Метод раскрытия модулей
Метод раскрытия модулей рассмотрим на примере:
Пример 10 Решить уравнение
Решение. Это уравнение содержит более одного модуля.
Метод решения уравнений, содержащих переменные под знаком двух и более модулей, состоит в следующем.
1. Найти значения переменной, при которых каждый из модулей обращается в нуль: 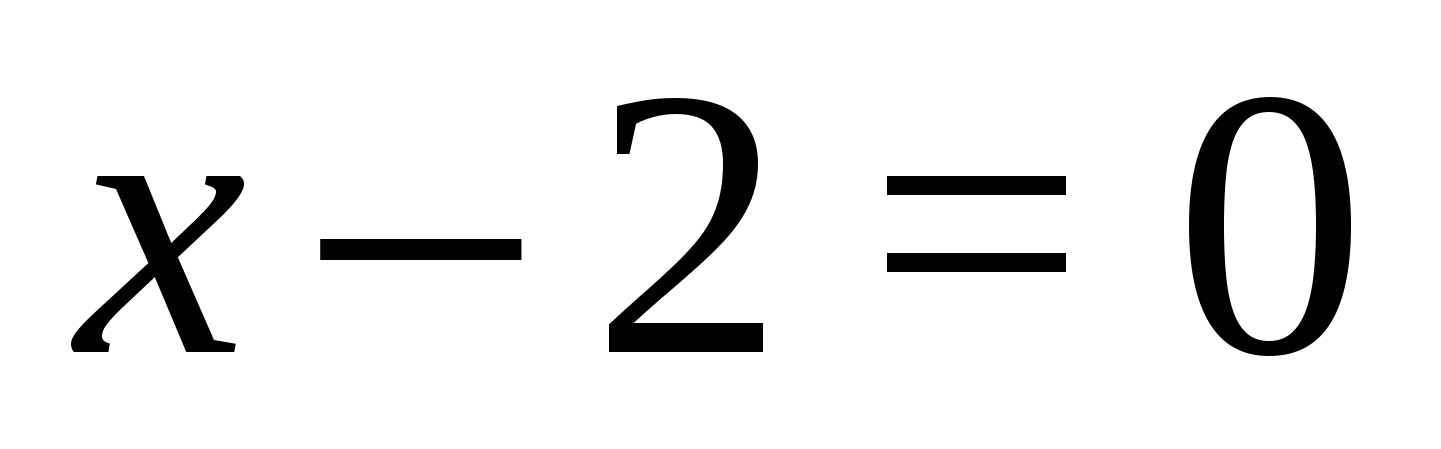 ,
,  ;
;  ,
,  ;
;  ,
,  .
.
2. Отметить эти точки на числовой прямой.
3. Рассматриваем уравнение на каждом из промежутков и устанавливаем знак выражений, которые находятся под модулями.
1) При  или
или 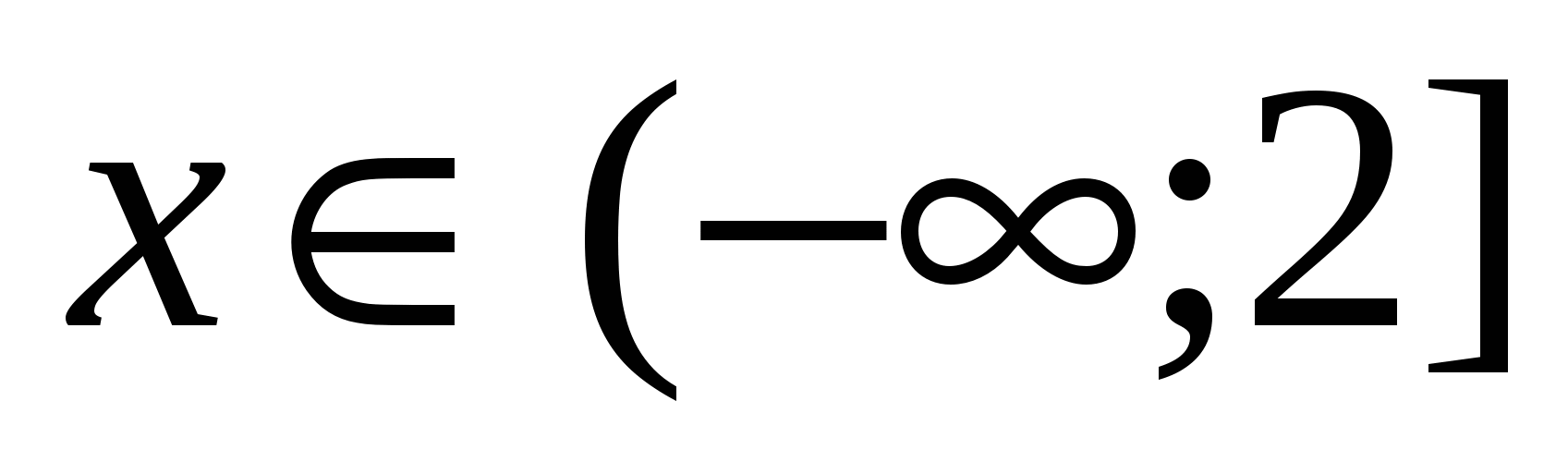 . Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение
. Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение  из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех
из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех  из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях
из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях  из этого промежутка выражение будет положительным.
из этого промежутка выражение будет положительным.
Возьмем значение  из промежутка
из промежутка 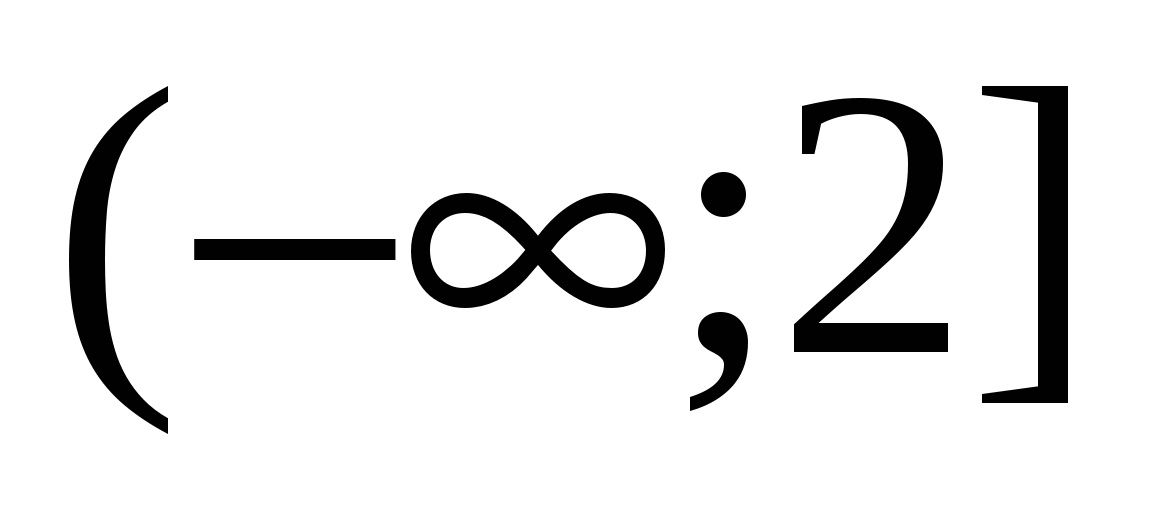 и подставим его значение в выражение
и подставим его значение в выражение 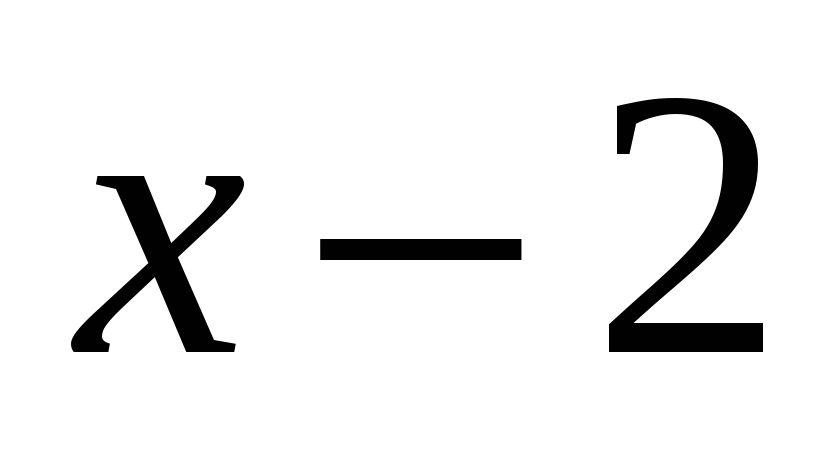 , получаем
, получаем  , значит на этом промежутке
, значит на этом промежутке 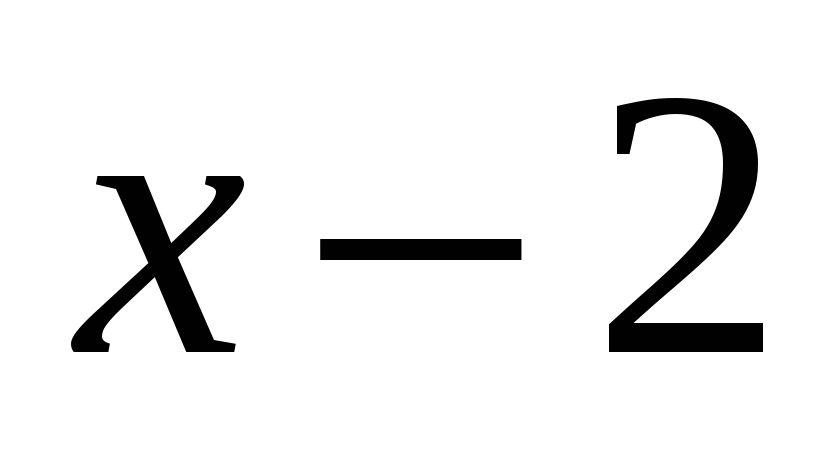 отрицательно, а следовательно ``выйдет"" из под модуля со знаком ``минус"", получим:
отрицательно, а следовательно ``выйдет"" из под модуля со знаком ``минус"", получим:  .
.
При этом значении  , выражение
, выражение  получит значение
получит значение  , значит, оно на промежутке
, значит, оно на промежутке 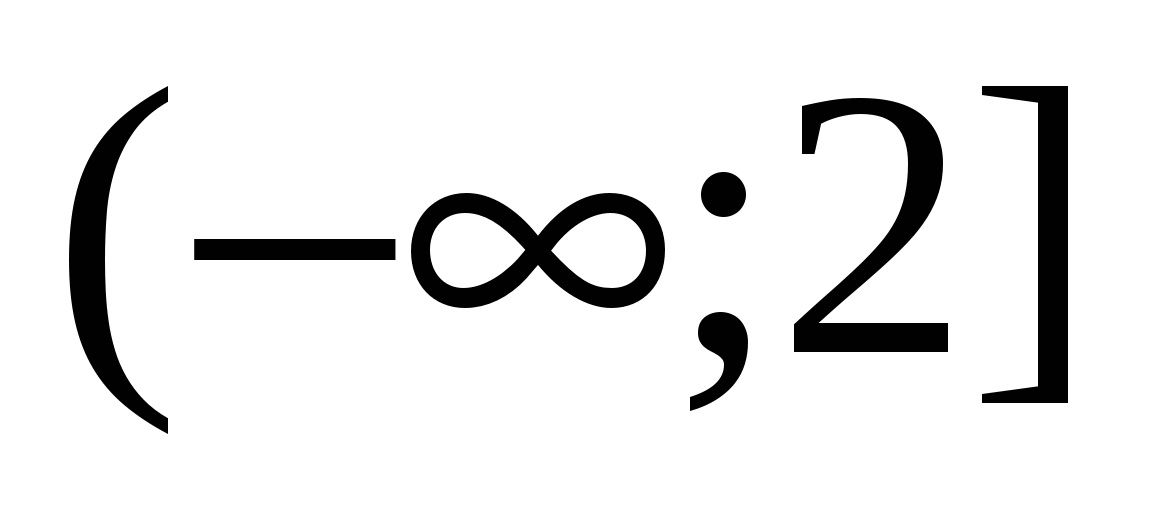 также принимает отрицательные значения и ``выйдет"" из модуля со знаком ``минус"", получим:
также принимает отрицательные значения и ``выйдет"" из модуля со знаком ``минус"", получим:  .
.
Выражение  получит значение
получит значение  и «выйдет» из под модуля со знаком ``минус"":
и «выйдет» из под модуля со знаком ``минус"":  .
.
Уравнение на этом промежутке получится таким: , решая его, находим:  .
.
Выясняем, входит ли это значение в промежуток 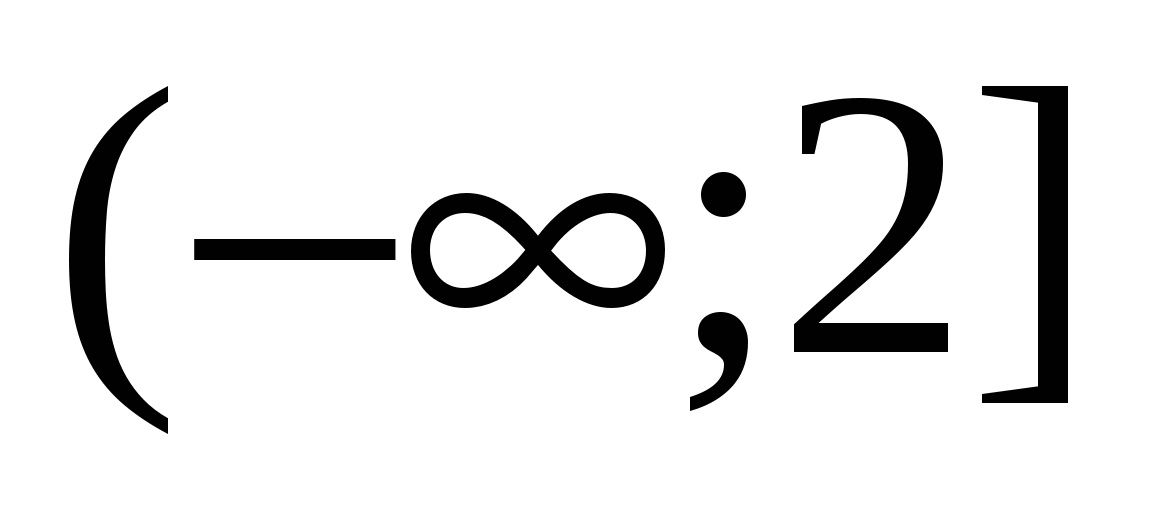 . Оказывается входит, значит
. Оказывается входит, значит  является корнем уравнения.
является корнем уравнения.
2) При  . Выбираем любое значение
. Выбираем любое значение  из этого промежутка. Пусть
из этого промежутка. Пусть  . Определяем знак каждого из выражений под модулем при этом значении
. Определяем знак каждого из выражений под модулем при этом значении  . Оказывается, что выражение
. Оказывается, что выражение 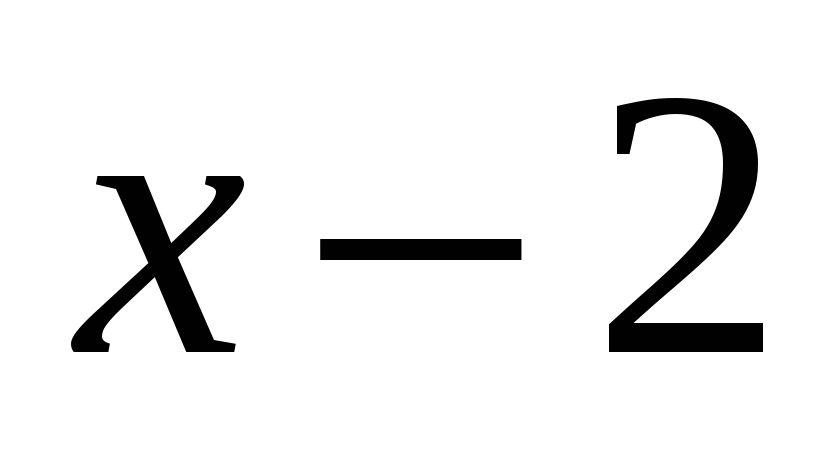 положительно, а два других отрицательны.
положительно, а два других отрицательны.
Уравнение на этом промежутке примет вид: . Решая его, находим  . Это значение не входит в промежуток
. Это значение не входит в промежуток 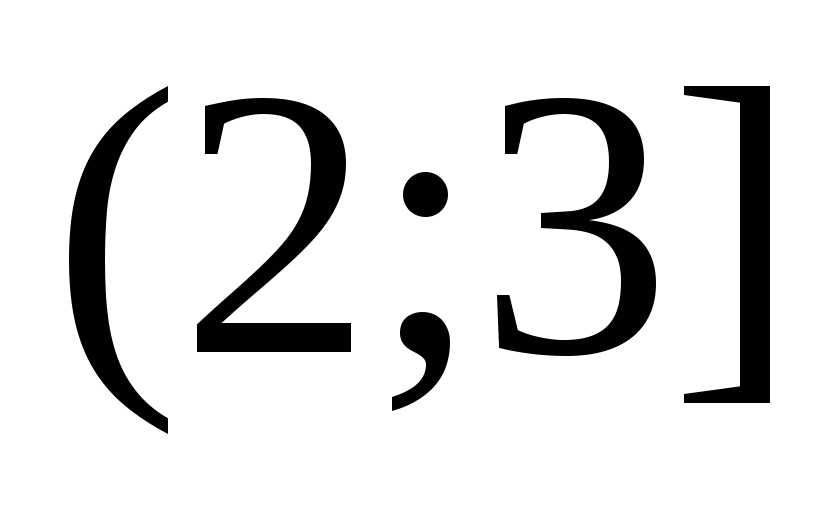 , а значит, не является корнем уравнения.
, а значит, не является корнем уравнения.
3) При  . Выбираем произвольное значение
. Выбираем произвольное значение  из этого промежутка, скажем,
из этого промежутка, скажем,  и подставляем в каждое из выражений. Находим, что выражения
и подставляем в каждое из выражений. Находим, что выражения 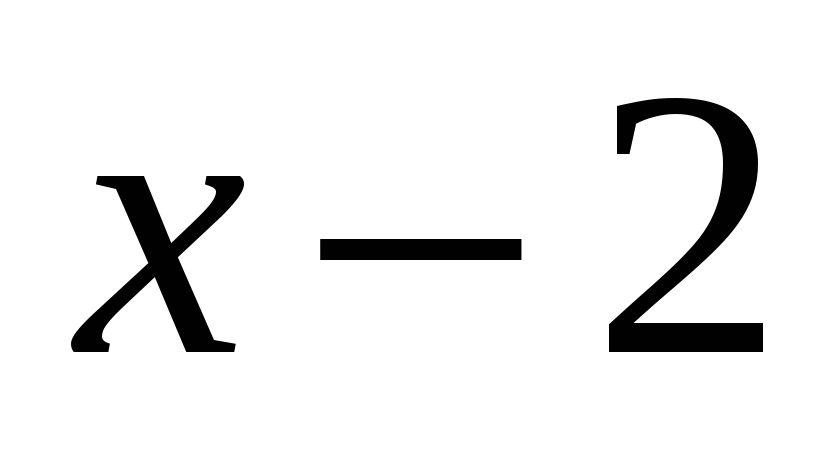 и
и  положительны, а
положительны, а  - отрицательно. Получим следующее уравнение: .
- отрицательно. Получим следующее уравнение: .
После преобразования, получим:  , а значит, уравнение не имеет корней на этом промежутке.
, а значит, уравнение не имеет корней на этом промежутке.
4) При 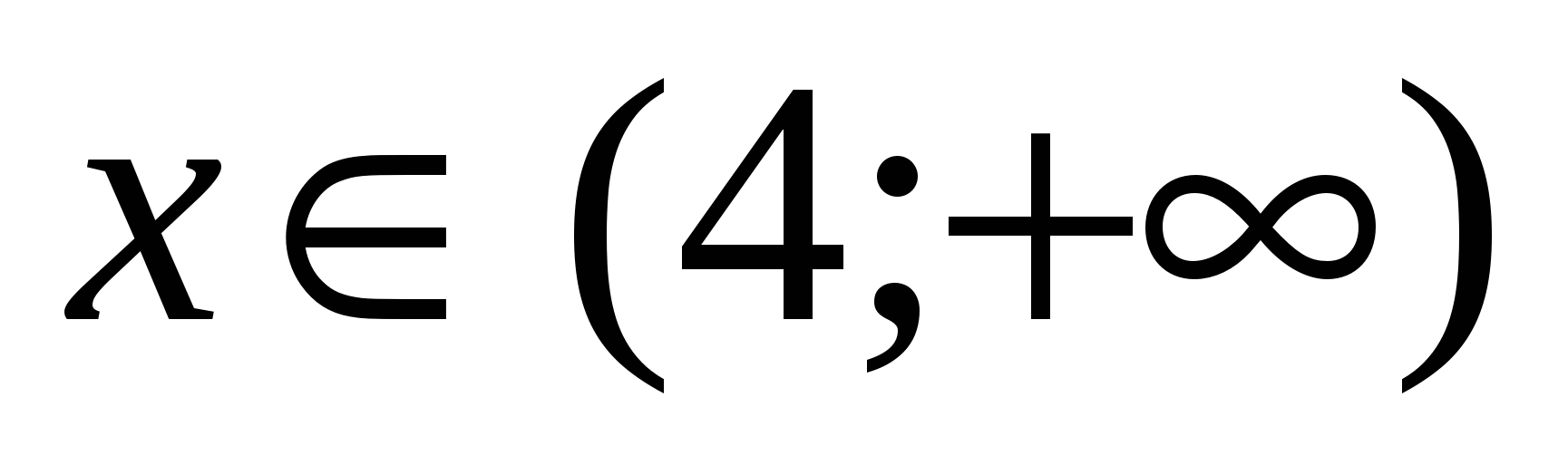 . Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение: ,
. Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение: ,  ,
, 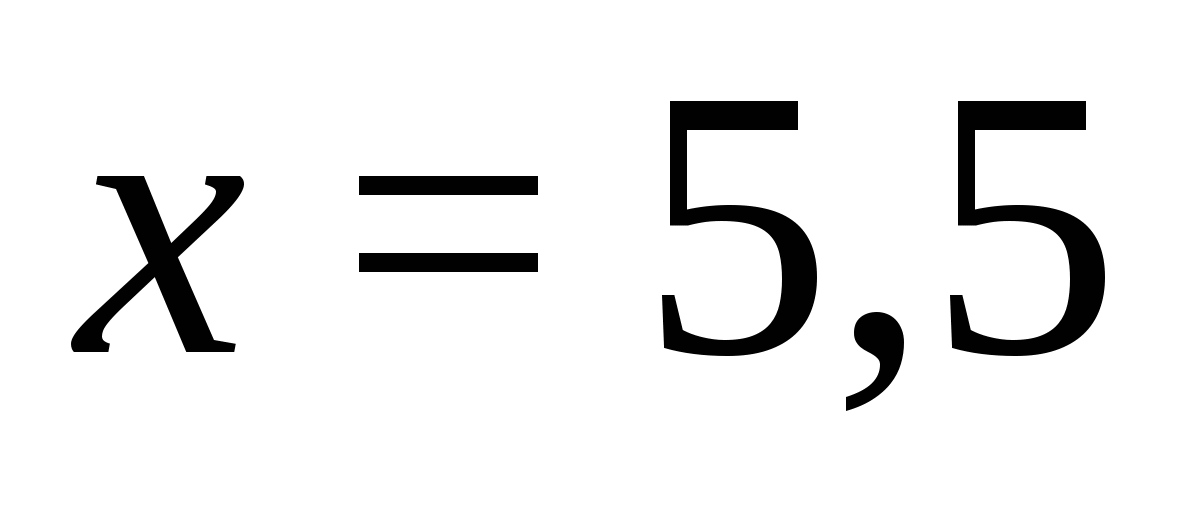 которое входит в промежуток и является корнем уравнения.
которое входит в промежуток и является корнем уравнения.
Ответ.
 ,
, 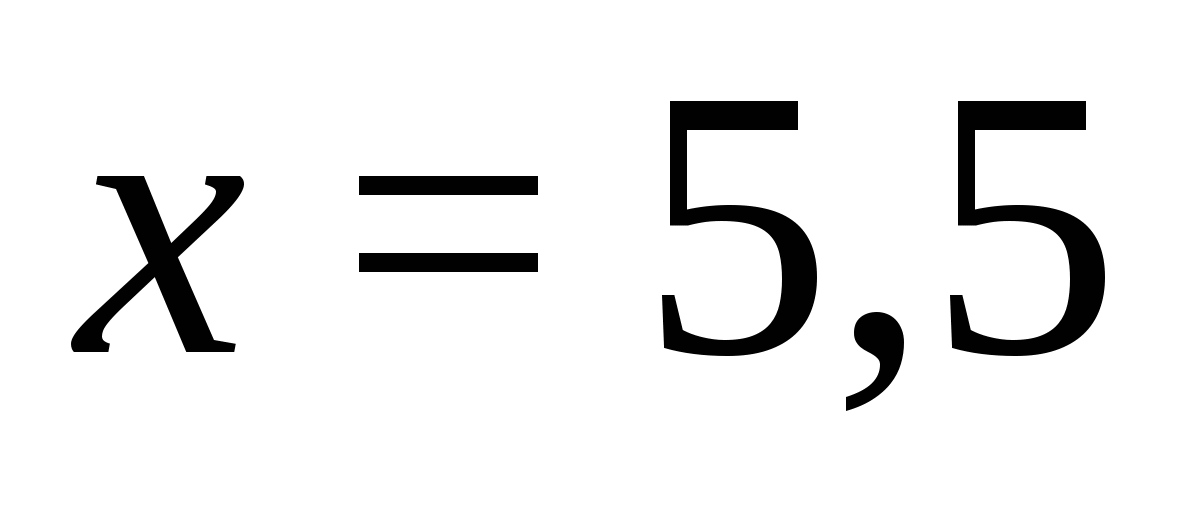 .
.
Решение уравнений содержащих модули неотрицательных выражений
Пример 11 Чему равна сумма корней уравнения (корень, если он один) уравнения

Решение. Рассмотрим выражение
 и преобразуем его к виду
и преобразуем его к виду 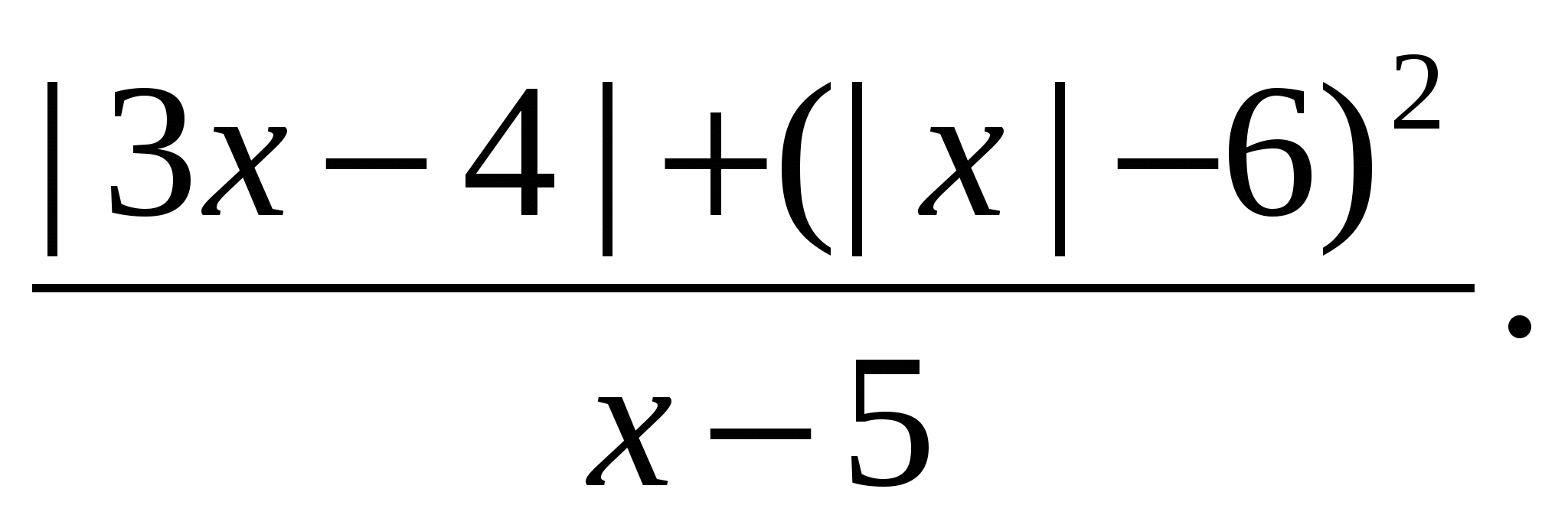
Очевидно, что числитель дроби при любых значениях переменной является положительным числом. Значит дробное выражение положительно, если  (т.к.
(т.к.  ). Преобразуем полученное выражение, при условии
). Преобразуем полученное выражение, при условии  . Получим уравнение, равносильное исходному:
. Получим уравнение, равносильное исходному:

Ответ.
 .
.
Пример 12 Решить уравнение
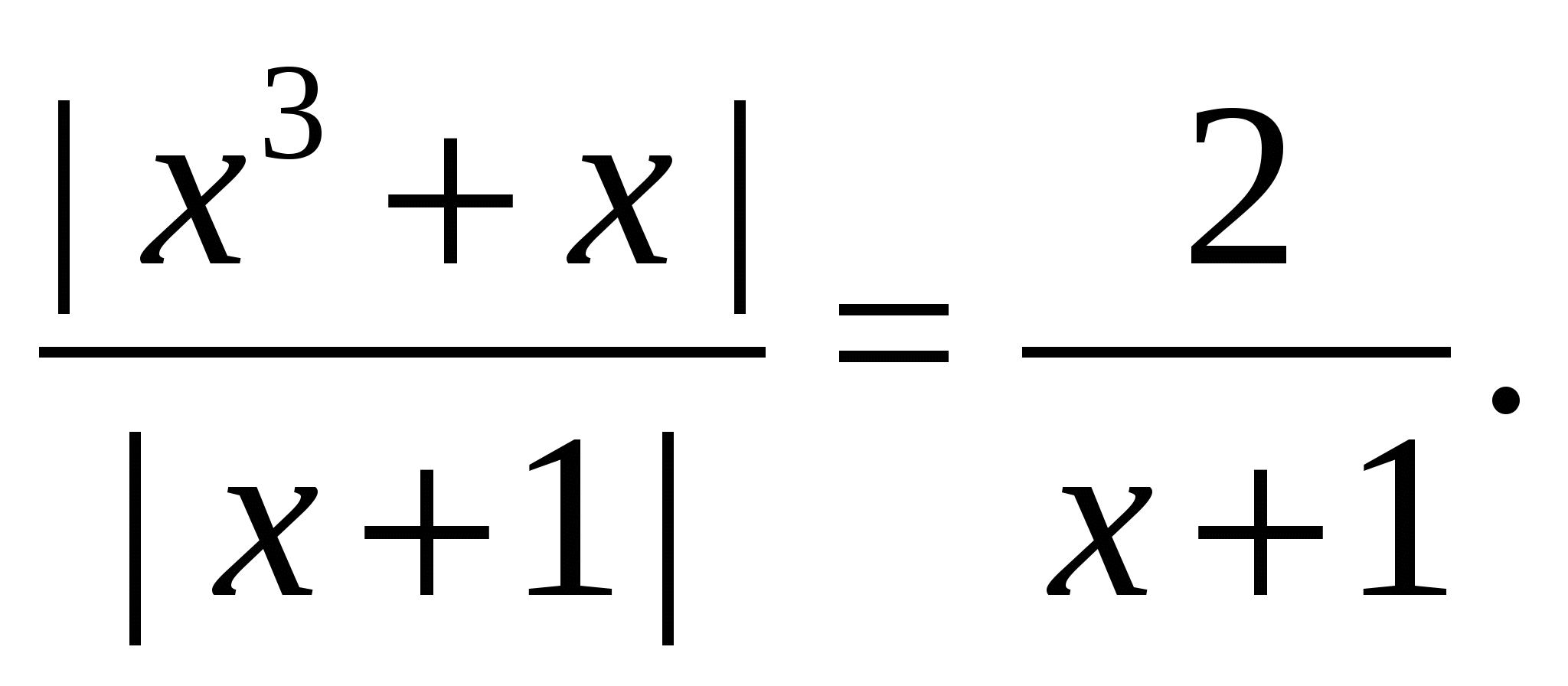
Решение.
Поскольку левая часть уравнения неотрицательна, при всех допустимых значениях переменной, на множестве корней уравнения правая его часть тоже должна быть неотрицательной, отсюда условие  , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение
, на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение 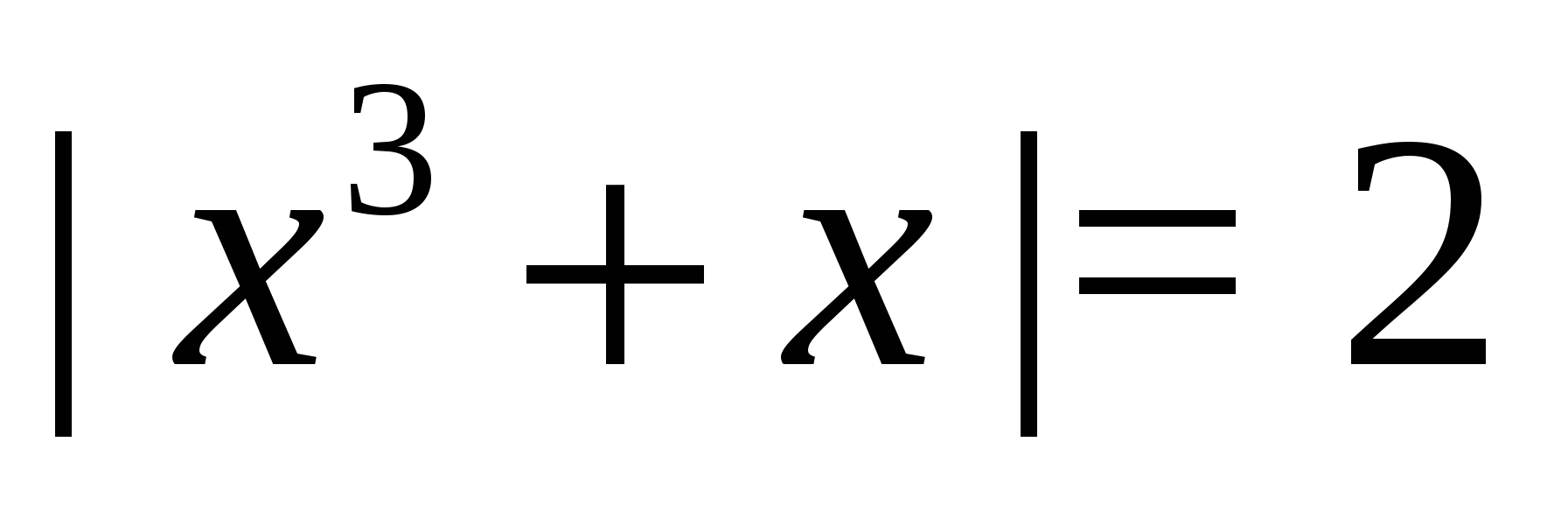 . Решая его и учитывая ограничение
. Решая его и учитывая ограничение  , получаем
, получаем
Ответ.
 .
.
Решение уравнений с использованием геометрической интерпретации
Геометрический смысл выражения  - длина отрезка координатной оси, соединяющего точки с абсциссами
- длина отрезка координатной оси, соединяющего точки с абсциссами  и
и  . Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.
. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.
Пример 13
Решим уравнение  .
.
Решение.
Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой  до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка
до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка  обладают требуемым свойством, а точки, расположенные вне этого отрезка, - нет.
обладают требуемым свойством, а точки, расположенные вне этого отрезка, - нет.
Ответ.
 .
.
Пример 14
Решить неравенство  .
.
Решение.
Изобразим на координатной прямой точки, сумма расстояний от которых до точек  и
и  в точности равна
в точности равна  . Это все точки отрезка
. Это все точки отрезка  . Для всех чисел вне данного отрезка сумма расстояний будет больше двух.
. Для всех чисел вне данного отрезка сумма расстояний будет больше двух.
Ответ.
 .
.
Пример (С3, ЕГЭ - 2010)15 Решить уравнение

Решение.
Дважды применяя тождество  , получим уравнение
, получим уравнение

решением которого является интервал  .
.
Ответ.
 .
.
Пример (С3, ЕГЭ - 2011)16 17 Решить уравнение
Решение. .
Ответ.
 .
.
Применение теоремы о знаках при решении уравнений
Сформулируем теорему, удобную при решении неравенств, относительно произведений или частных разности модулей:
Теорема 18
Знак разности модулей двух выражений совпадает со знаком разности квадратов этих выражений.
не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Вычисляя, например,  , получаем, что функция принимает только положительные значения.
, получаем, что функция принимает только положительные значения.
Ответ.
 .
.
Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих выражений. Это позволяет, последовательно перебирая эти промежутки, одновременно избавляться от всех модулей и решать обычное уравнение или неравенство (проверяя при этом, что найденный ответ входит в данный промежуток).
Решение уравнений домножением на положительный множитель
Заключение.
Подводя итог нашей работы, можно сказать следующее.
Целью работы было изучение различных методов решения уравнений и неравенств с модулями.
Рассмотрены некоторые разновидности простейших уравнений и неравенств с модулем, решаемых с помощью равносильных переходов,а также теоремы о сумме модулей; графический способ решения уравнений. Нужно сказать, что в школьном курсе математики именно эти методы решения наиболее часто используются. Графический метод особо актуален при решении задач C 5 из контрольно-измерительных материалов ЕГЭ.
Далее мы изучили на нескольких примерах иные способы решения уравнений и неравенств с модулями, а именно: метод раскрытия модулей; решение уравнений, содержащих модули неотрицательных выражений; решение уравнений с использованием геометрической интерпретации; с использованием тождества  ; применение теоремы о знаках; решение уравнений переходом к следствию, домножением на положительный множитель,а также решение неравенств методом интервалов.
; применение теоремы о знаках; решение уравнений переходом к следствию, домножением на положительный множитель,а также решение неравенств методом интервалов.
Таким образом, в ходе исследования мы пришли к следующим выводам.
Наиболее универсальными и применимыми к наибольшему количеству задач мы считаем метод раскрытия модулей, графический метод и метод интервалов. Это убеждение возникло в результате решения большого числа задач из контрольно-измерительных материалов ЕГЭ, предметных чемпионатов, олимпиадных задач, а также изучение литературы по данному вопросу. Также очень важным мы считаем знание и применение тождества  , так как оно используется не только при решении уравнений и неравенств, но и для преобразования многих выражений с радикалами. Остальные методы решения, которые мы рассмотрели, безусловно, представляют большой интерес в плане расширения математического кругозора и общего математического развития. Поэтому мы планируем использовать их для подготовки к государственной итоговой аттестации в форме ЕГЭ и подготовке к обучению в высшем учебном заведении.
, так как оно используется не только при решении уравнений и неравенств, но и для преобразования многих выражений с радикалами. Остальные методы решения, которые мы рассмотрели, безусловно, представляют большой интерес в плане расширения математического кругозора и общего математического развития. Поэтому мы планируем использовать их для подготовки к государственной итоговой аттестации в форме ЕГЭ и подготовке к обучению в высшем учебном заведении.
Список используемой литературы.
«Большая математическая энциклопедия» для школьников и студентов;
Математика. ЕГЭ – 2011, 2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
М.Я. Выгодский. Справочник по элементарной математике
«Новейший справочник школьника»;
Энциклопедия «Я познаю мир. Математика»;
;
Математика является символом мудрости науки ,
образцом научной строгости и простоты ,
эталоном совершенства и красоты в науке.
Российский философ, профессор А.В. Волошинов
Неравенства с модулем
Наиболее сложно решаемыми задачами школьной математики являются неравенства , содержащие переменные под знаком модуля. Для успешного решения таких неравенств необходимо хорошо знать свойства модуля и иметь навыки их использования.
Основные понятия и свойства
Модуль (абсолютная величина) действительного числа обозначается и определяется следующим образом:
К простым свойствам модуля относятся следующие соотношения:
И .
Отметим , что последние два свойства справедливы для любой четной степени.
Кроме того , если , где , то и
Более сложные свойства модуля , которые можно эффективно использовать при решении уравнений и неравенств с модулями , формулируются посредством следующих теорем:
Теорема 1. Для любых аналитических функций и справедливо неравенство .
Теорема 2. Равенство равносильно неравенству .
Теорема 3. Равенство равносильно неравенству .
Наиболее распространенными в школьной математике неравенствами , содержащие неизвестные переменные под знаком модуля , являются неравенства вида и , где некоторая положительная константа.
Теорема 4. Неравенство равносильно двойному неравенству , а решение неравенства сводится к решению совокупности неравенств и .
Данная теорема является частным случаем теорем 6 и 7.
Более сложными неравенствами , содержащие модуль, являются неравенства вида , и .
Методы решения таких неравенств можно сформулировать посредством следующих трех теорем.
Теорема 5. Неравенство равносильно совокупности двух систем неравенств
И (1)
Доказательство. Так как , то
Отсюда вытекает справедливость (1).
Теорема 6. Неравенство равносильно системе неравенств
Доказательство. Так как , то из неравенства следует , что . При таком условии неравенство и при этом вторая система неравенств (1) окажется несовместной.
Теорема доказана.
Теорема 7. Неравенство равносильно совокупности одного неравенства и двух систем неравенств
И (3)
Доказательство. Поскольку , то неравенство всегда выполняется , если .
Пусть , тогда неравенство будет равносильно неравенству , из которого вытекает совокупность двух неравенств и .
Теорема доказана.
Рассмотрим типовые примеры решения задач на тему «Неравенства , содержащие переменные под знаком модуля».
Решение неравенств с модулем
Наиболее простым методом решения неравенств с модулем является метод , основанный на раскрытии модулей. Этот метод является универсальным , однако в общем случае его применение может привести к весьма громоздким вычислениям. Поэтому учащиеся должны знать и другие (более эффективные) методы и приемы решения таких неравенств. В частности , необходимо иметь навыки применения теорем , приведенных в настоящей статье.
Пример 1. Решить неравенство
. (4)
Решение. Неравенство (4) будем решать «классическим» методом – методом раскрытия модулей. С этой целью разобьем числовую ось точками и на интервалы и рассмотрим три случая.
1. Если , то , , , и неравенство (4) принимает вид или .
Так как здесь рассматривается случай , то является решением неравенства (4).
2. Если , то из неравенства (4) получаем или . Так как пересечение интервалов и является пустым , то на рассматриваемом интервале решений неравенства (4) нет.
3. Если , то неравенство (4) принимает вид или . Очевидно , что также является решением неравенства (4).
Ответ: , .
Пример 2. Решить неравенство .
Решение. Положим , что . Так как , то заданное неравенство принимает вид или . Поскольку , то и отсюда следует или .
Однако , поэтому или .
Пример 3. Решить неравенство
. (5)
Решение. Так как , то неравенство (5) равносильно неравенствам или . Отсюда , согласно теореме 4 , имеем совокупность неравенств и .
Ответ: , .
Пример 4. Решить неравенство
. (6)
Решение. Обозначим . Тогда из неравенства (6) получаем неравенства , , или .
Отсюда , используя метод интервалов , получаем . Так как , то здесь имеем систему неравенств
Решением первого неравенства системы (7) является объединение двух интервалов и , а решением второго неравенства – двойное неравенство . Отсюда следует , что решение системы неравенств (7) представляет собой объединение двух интервалов и .
Ответ: ,
Пример 5. Решить неравенство
. (8)
Решение. Преобразуем неравенство (8) следующим образом:
Или .
Применяя метод интервалов , получаем решение неравенства (8).
Ответ: .
Примечание. Если в условии теоремы 5 положить и , то получим .
Пример 6. Решить неравенство
. (9)
Решение. Из неравенства (9) следует . Преобразуем неравенство (9) следующим образом:
Или
Так как , то или .
Ответ: .
Пример 7. Решить неравенство
. (10)
Решение. Так как и , то или .
В этой связи и неравенство (10) принимает вид
Или
. (11)
Отсюда следует, что или . Так как , то и из неравенства (11) вытекает или .
Ответ: .
Примечание. Если к левой части неравенства (10) применить теорему 1 , то получим . Отсюда и из неравенства (10) следует , что или . Так как , то неравенство (10) принимает вид или .
Пример 8. Решить неравенство
. (12)
Решение. Так как , то и из неравенства (12) следует или . Однако , поэтому или . Отсюда получаем или .
Ответ: .
Пример 9. Решить неравенство
. (13)
Решение. Согласно теореме 7 решением неравенства (13) являются или .
Пусть теперь . В таком случае и неравенство (13) принимает вид или .
Если объединить интервалы и , то получим решение неравенства (13) вида .
Пример 10. Решить неравенство
. (14)
Решение. Перепишем неравенство (14) в равносильном виде: . Если к левой части данного неравенства применить теорему 1, то получим неравенство .
Отсюда и из теоремы 1 следует , что неравенство (14) выполняется для любых значений .
Ответ: любое число.
Пример 11. Решить неравенство
. (15)
Решение. Применяя теорему 1 к левой части неравенства (15) , получаем . Отсюда и из неравенства (15) вытекает уравнение , которое имеет вид .
Согласно теореме 3 , уравнение равносильно неравенству . Отсюда получаем .
Пример 12. Решить неравенство
. (16)
Решение . Из неравенства (16), согласно теореме 4, получаем систему неравенств
При решении неравенства воспользуемся теоремой 6 и получим систему неравенств из которой следует .
Рассмотрим неравенство . Согласно теореме 7 , получаем совокупность неравенств и . Второе неравенство совокупности справедливо для любого действительного .
Следовательно , решением неравенства (16) являются .
Пример 13. Решить неравенство
. (17)
Решение. Согласно теореме 1 можно записать
(18)
Принимая во внимание неравенство (17), делаем вывод о том, что оба неравенства (18) обращаются в равенства, т.е. имеет место система уравнений
По теореме 3 данная система уравнений равносильна системе неравенств
или
Пример 14. Решить неравенство
. (19)
Решение. Так как , то . Умножим обе части неравенства (19) на выражение , которое для любых значений принимает только положительные значения. Тогда получим неравенство, которое равносильно неравенству (19), вида
Отсюда получаем или , где . Так как и , то решением неравенства (19) являются и .
Ответ: , .
Для более глубокого изучения методов решения неравенств с модулем можно посоветовать обратиться к учебным пособиям , приведенных в списке рекомендованной литературы.
1. Сборник задач по математике для поступающих во втузы / Под ред. М.И. Сканави. – М.: Мир и Образование , 2013. – 608 с.
2. Супрун В.П. Математика для старшеклассников: методы решения и доказательства неравенств. – М.: Ленанд / URSS , 2018. – 264 с.
3. Супрун В.П. Математика для старшеклассников: нестандартные методы решения задач. – М.: КД «Либроком» / URSS , 2017. – 296 с.
Остались вопросы?
Чтобы получить помощь репетитора – зарегистрируйтесь .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
