The solution of the trigonometric equation consists of two stages: equation transformation to get it simple type (see above) and solutionobtained simplest trigonometric equation. There are seven basic methods for solving trigonometric equations.
1. Algebraic method.
(variable substitution and substitution method).
2. Factorization.
EXAMPLE 1. Solve the equation: sin x+ cos x = 1 .
Solution. Move all terms of the equation to the left:
Sin x+ cos x – 1 = 0 ,
Let us transform and factorize the expression in
Left side of the equation:

Example 2. Solve the equation: cos 2 x+ sin x cos x = 1.
SOLUTION cos 2 x+ sin x cos x– sin 2 x– cos 2 x = 0 ,
Sin x cos x– sin 2 x = 0 ,
Sin x(cos x– sin x ) = 0 ,
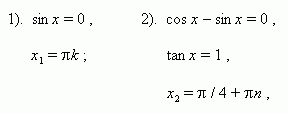
Example 3. Solve the equation: cos 2 x– cos 8 x+ cos 6 x = 1.
SOLUTION cos 2 x+ cos 6 x= 1 + cos8 x,
2 cos 4 x cos 2 x= 2 cos² 4 x ,
Cos 4 x · (cos 2 x– cos 4 x) = 0 ,
Cos 4 x 2 sin 3 x sin x = 0 ,
1). cos 4 x= 0 , 2). sin 3 x= 0 , 3). sin x = 0 ,
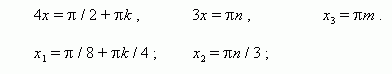
3. Bringing to uniform equation.The equation called homogeneous from relatively sin And cos , If all of it terms of the same degree with respect to sin And cos the same angle. To solve a homogeneous equation, you need: A) move all its members to the left side; b) put all common factors out of brackets; V) equate all factors and brackets to zero; G) parentheses set to zero give homogeneous equation of lesser degree, which should be divided by cos(or sin) in the senior degree; d) solve the resulting algebraic equation with respect totan . sin 2 x+ 4 sin x cos x+ 5 cos 2 x = 2. Solution: 3sin 2 x+ 4 sin x cos x+ 5 cos 2 x= 2 sin 2 x+ 2 cos 2 x , Sin 2 x+ 4 sin x cos x+ 3 cos 2 x = 0 , Tan 2 x+ 4tan x + 3 = 0 , from here y 2 + 4y +3 = 0 , The roots of this equation are:y 1 = - 1, y 2 = - 3, hence 1) tan x= –1, 2) tan x = –3, |
4. Transition to half corner.
Let's look at this method with an example:
EXAMPLE Solve Equation: 3 sin x– 5cos x = 7.
Solution: 6 sin ( x/ 2) cos ( x/ 2) – 5 cos² ( x/ 2) + 5 sin² ( x/ 2) =
7 sin² ( x/ 2) + 7 cos² ( x/ 2) ,
2 sin² ( x/ 2) – 6 sin ( x/ 2) cos ( x/ 2) + 12 cos² ( x/ 2) = 0 ,
tan²( x/ 2) – 3 tan ( x/ 2) + 6 = 0 ,
. . . . . . . . . .
5. Introduction of an auxiliary angle.
Consider an equation of the form:
a sin x + b cos x = c ,
Where a, b, c– coefficients;x- unknown.
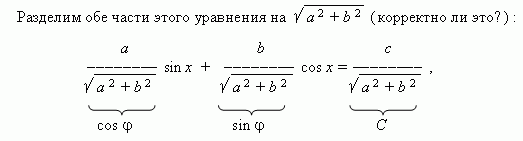
Now the coefficients of the equation have the properties of sine and cosine, namely: module (absolute value) of each of which no more than 1 and the sum of their squares is 1. Then one can designate them respectively How cos and sin (here - so-called auxiliary angle), Andour equation is
Subject:"Methods for solving trigonometric equations".
Lesson Objectives:
educational:
To form skills to distinguish types of trigonometric equations;
Deepening understanding of methods for solving trigonometric equations;
educational:
Education of cognitive interest in the educational process;
Formation of the ability to analyze the task;
developing:
To form the skill to analyze the situation with the subsequent choice of the most rational way out of it.
Equipment: poster with basic trigonometric formulas, computer, projector, screen.
Let's start the lesson by repeating the basic technique for solving any equation: reducing it to a standard form. Through transformations, linear equations are reduced to the form ax \u003d b, square ones to the form ax2+bx +c=0. In the case of trigonometric equations, it is necessary to reduce them to the simplest, of the form: sinx \u003d a, cosx \u003d a, tgx \u003d a, which can be easily solved.
First of all, of course, for this it is necessary to use the basic trigonometric formulas that are presented on the poster: addition formulas, double angle formulas, lowering the multiplicity of an equation. We already know how to solve such equations. Let's repeat some of them:
At the same time, there are equations, the solution of which requires knowledge of some special techniques.
The topic of our lesson is the consideration of these techniques and the systematization of methods for solving trigonometric equations.
Methods for solving trigonometric equations.
1. Transformation to a quadratic equation with respect to some trigonometric function, followed by a change of variable.
We will consider each of the listed methods with examples, but we will dwell on the last two in more detail, since we have already used the first two in solving equations.
1. Transformation to a quadratic equation with respect to any trigonometric function.
2. Solution of equations by the factorization method.
3. Solution of homogeneous equations.
Homogeneous equations of the first and second degree are called equations of the form:
respectively (a ≠ 0, b ≠ 0, c ≠ 0).
When solving homogeneous equations, both parts of the equation are divided term by term by cosx for (1) of the equation and by cos 2 x for (2). Such a division is possible, since sinx and cosx are not equal to zero at the same time - they vanish at different points. Consider examples of solving homogeneous equations of the first and second degree.
Remember this equation: when considering the next method - the introduction of an auxiliary argument, we will solve it in a different way.
4. Introduction of an auxiliary argument.
Consider the equation already solved by the previous method:
As you can see, the same result is obtained.
Let's look at another example:
In the examples considered, it was generally clear what the original equation needs to be divided into in order to introduce an auxiliary argument. But it may happen that it is not obvious which divisor to choose. There is a special technique for this, which we will now consider in a general way. Let an equation be given.
Methods for solving trigonometric equations Contents
- Variable replacement method
- Factorization method
- Homogeneous trigonometric equations
- Using trigonometric formulas:
- Addition formulas
- Cast formulas
- Double Argument Formulas
By replacing t = sinx or t = cosx, where t∈ [−1;1] the solution of the original equation is reduced to the solution of a quadratic or other algebraic equation.
See examples 1 - 3
Sometimes a universal trigonometric substitution is used: t = tg
Example 1 Example 2 Example 3 Factoring method
The essence of this method is that the product of several factors is equal to zero if at least one of them is equal to zero, while the others do not lose their meaning:
f(x) g(x) h(x) … = 0⟺ f(x) = 0 or g(x) = 0 or h(x) = 0
etc. provided that each of the factors exists
See examples 4 - 5
Example 4 Example 5 Homogeneous trigonometric equations An equation of the form a sin x + b cos x = 0 is called a homogeneous trigonometric equation of the first degree.
a sin x + b cos x = 0
Comment.
Dividing by cos x is valid because solutions to the equation cos x = 0 are not solutions to the equation a sin x + b cos x = 0.
a sin x b cos x 0
a tg x + b = 0
tg x = -
Homogeneous trigonometric equations
a sin2x + b sin x cos x + c cos2x = 0
An equation of the form a sin2x + b sin x cos x + c cos2x = 0 is called a homogeneous trigonometric equation of the second degree.
a tg2x + b tg x + c = 0
a sin2x b sin x cos x c cos2x 0
Comment. If in this equation a \u003d 0 or c \u003d 0, then the equation is solved by the decomposition method
for multipliers.
Example 6
Example 8 Example 9 Example 10 Example 11 1. Addition formulas:
sin(x + y) = sinx cozy + cosx siny
cos (x + y) = cosx cozy − sinx siny
tgx + tgy
tg(x + y) =
1 − tgx tgy
sin(x − y) = sinx cozy + cosx siny
cos(x − y) = cosx cozy + sinx siny
tgx − tgy
tg (x − y) =
1 + tgx tgy
сtgx сtgy − 1
ctg (x + y) =
сtgу + с tgх
ctgx ctgy + 1
сtg (x − y) =
сtgу − с tgх
Example 12 Example 13 Using Trigonometric Formulas 2. Casting formulas:
horse rule
In the good old days, there lived an absent-minded mathematician who, when looking for an answer, change or not change the name of a function ( sinus on cosine), looked at his smart horse, and she nodded her head along the coordinate axis, which belonged to the point corresponding to the first term of the argument π/ 2 + α or π + α .
If the horse nodded its head along the axis OU, then the mathematician considered that the answer was received "yes, change" if along the axis OH, That "no, don't change".
Using trigonometric formulas 3. Double argument formulas:
sin2x = 2sinx cosx
cos2x = cos2x – sin2x
cos2x = 2cos2x - 1
cos2x = 1 – 2sin2x
1-tg2x
ctg 2x =
ctg2x - 1
Example 14 Using trigonometric formulas 4. Degree reduction formulas:
5. Half angle formulas:
Using trigonometric formulas 6. Sum and difference formulas: Using trigonometric formulas 7. Product formulas: Mnemonic rule “Trigonometry in the palm of your hand”
Very often it is required to know by heart the meanings cos, sin, tg, ctg for angles 0°, 30°, 45°, 60°, 90°.
But if suddenly any value is forgotten, then you can use the rule of the hand.
Rule: If you draw lines through the little finger and thumb,
then they will intersect at a point called the “lunar hillock”.
An angle of 90° is formed. The little finger line forms an angle of 0°.
Having drawn the rays from the “lunar hillock” through the ring, middle, index fingers, we obtain angles of 30 °, 45 °, 60 °, respectively.
Substituting instead of n: 0, 1, 2, 3, 4, we get the values sin, for angles 0°, 30°, 45°, 60°, 90°.
For cos counting is in reverse order.
You can order a detailed solution to your problem !!!
An equality containing an unknown under the sign of a trigonometric function (`sin x, cos x, tg x` or `ctg x`) is called a trigonometric equation, and we will consider their formulas further.
The simplest equations are `sin x=a, cos x=a, tg x=a, ctg x=a`, where `x` is the angle to be found, `a` is any number. Let's write the root formulas for each of them.
1. Equation `sin x=a`.
For `|a|>1` it has no solutions.
With `|a| \leq 1` has an infinite number of solutions.
Root formula: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Equation `cos x=a`
For `|a|>1` - as in the case of the sine, there are no solutions among real numbers.
With `|a| \leq 1` has an infinite number of solutions.
Root formula: `x=\pm arccos a + 2\pi n, n \in Z`

Special cases for sine and cosine in graphs. 
3. Equation `tg x=a`
Has an infinite number of solutions for any values of `a`.
Root formula: `x=arctg a + \pi n, n \in Z`

4. Equation `ctg x=a`
It also has an infinite number of solutions for any values of `a`.
Root formula: `x=arcctg a + \pi n, n \in Z`

Formulas for the roots of trigonometric equations in the table
For sinus:  For cosine:
For cosine:  For tangent and cotangent:
For tangent and cotangent:  Formulas for solving equations containing inverse trigonometric functions:
Formulas for solving equations containing inverse trigonometric functions:

Methods for solving trigonometric equations
The solution of any trigonometric equation consists of two stages:
- using to convert it to the simplest;
- solve the resulting simple equation using the above formulas for the roots and tables.
Let's consider the main methods of solution using examples.
algebraic method.
In this method, the replacement of a variable and its substitution into equality is done.
Example. Solve the equation: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
make a replacement: `cos(x+\frac \pi 6)=y`, then `2y^2-3y+1=0`,
we find the roots: `y_1=1, y_2=1/2`, from which two cases follow:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.
Answer: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Factorization.
Example. Solve the equation: `sin x+cos x=1`.
Solution. Move to the left all terms of equality: `sin x+cos x-1=0`. Using , we transform and factorize the left side:
`sin x - 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.
Answer: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Reduction to a homogeneous equation
First, you need to bring this trigonometric equation to one of two forms:
`a sin x+b cos x=0` (homogeneous equation of the first degree) or `a sin^2 x + b sin x cos x +c cos^2 x=0` (homogeneous equation of the second degree).
Then split both parts by `cos x \ne 0` for the first case, and by `cos^2 x \ne 0` for the second. We get equations for `tg x`: `a tg x+b=0` and `a tg^2 x + b tg x +c =0`, which must be solved using known methods.
Example. Solve the equation: `2 sin^2 x+sin x cos x - cos^2 x=1`.
Solution. Let's write the right side as `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x - cos^2 x -` ` sin^2 x - cos^2 x=0`
`sin^2 x+sin x cos x - 2 cos^2 x=0`.
This is a homogeneous trigonometric equation of the second degree, dividing its left and right sides by `cos^2 x \ne 0`, we get:
`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) - \frac(2 cos^2 x)(cos^2 x)=0`
`tg^2 x+tg x - 2=0`. Let's introduce the replacement `tg x=t`, as a result `t^2 + t - 2=0`. The roots of this equation are `t_1=-2` and `t_2=1`. Then:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Answer. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Go to Half Corner
Example. Solve the equation: `11 sin x - 2 cos x = 10`.
Solution. Applying the double angle formulas, the result is: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2 +10 cos^2 x/2`
`4 tg^2 x/2 - 11 tg x/2 +6=0`
Applying the algebraic method described above, we obtain:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Answer. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Introduction of an auxiliary angle
In the trigonometric equation `a sin x + b cos x =c`, where a,b,c are coefficients and x is a variable, we divide both parts by `sqrt (a^2+b^2)`:
`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2 +b^2))`.
The coefficients on the left side have the properties of sine and cosine, namely, the sum of their squares is equal to 1 and their modulus is not greater than 1. Denote them as follows: `\frac a(sqrt (a^2+b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2))=C`, then:
`cos \varphi sin x + sin \varphi cos x =C`.
Let's take a closer look at the following example:
Example. Solve the equation: `3 sin x+4 cos x=2`.
Solution. Dividing both sides of the equation by `sqrt (3^2+4^2)`, we get:
`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`
`3/5 sin x+4/5 cos x=2/5`.
Denote `3/5 = cos \varphi` , `4/5=sin \varphi`. Since `sin \varphi>0`, `cos \varphi>0`, we take `\varphi=arcsin 4/5` as an auxiliary angle. Then we write our equality in the form:
`cos \varphi sin x+sin \varphi cos x=2/5`
Applying the formula for the sum of angles for the sine, we write our equality in the following form:
`sin(x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Answer. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Fractional-rational trigonometric equations
These are equalities with fractions, in the numerators and denominators of which there are trigonometric functions.
Example. Solve the equation. `\frac (sin x)(1+cos x)=1-cos x`.
Solution. Multiply and divide the right side of the equation by `(1+cos x)`. As a result, we get:
`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`
`\frac (sin x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`
`\frac (sin x-sin^2 x)(1+cos x)=0`
Given that the denominator cannot be zero, we get `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Equate the numerator of the fraction to zero: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Then `sin x=0` or `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Given that ` x \ne \pi+2\pi n, n \in Z`, the solutions are `x=2\pi n, n \in Z` and `x=\pi /2+2\pi n` , `n \in Z`.
Answer. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Trigonometry, and trigonometric equations in particular, are used in almost all areas of geometry, physics, and engineering. The study begins in the 10th grade, there are always tasks for the exam, so try to remember all the formulas of trigonometric equations - they will definitely come in handy for you!
However, you don’t even need to memorize them, the main thing is to understand the essence, and be able to deduce. It's not as difficult as it seems. See for yourself by watching the video.
