500-luvulla eKr. antiikin kreikkalainen filosofi Zeno Elealainen muotoili kuuluisat aporiat, joista kuuluisin on aporia "Achilles ja kilpikonna". Tältä se kuulostaa:

Oletetaan, että Akhilleus juoksee kymmenen kertaa nopeammin kuin kilpikonna ja on tuhat askelta sen takana. Sinä aikana, jona Akhilleus juoksee tämän matkan, kilpikonna ryömi sata askelta samaan suuntaan. Kun Akhilleus on juossut sata askelta, kilpikonna ryömii vielä kymmenen askelta ja niin edelleen. Prosessi jatkuu loputtomiin, Akhilleus ei koskaan saavuta kilpikonnaa.

Tästä päättelystä tuli looginen shokki kaikille seuraaville sukupolville. Aristoteles, Diogenes, Kant, Hegel, Gilbert... Heitä kaikkia, tavalla tai toisella, katsottiin Zenonin aporiaksi. Järkytys oli niin voimakas, että " ... keskustelut jatkuvat tälläkin hetkellä, tiedeyhteisö ei ole vielä päässyt yhteisymmärrykseen paradoksien olemuksesta ... matemaattista analyysiä, joukkoteoriaa, uusia fysikaalisia ja filosofisia lähestymistapoja on otettu mukaan asian tutkimiseen ; mikään niistä ei tullut yleisesti hyväksyttyä ratkaisua ongelmaan ..."[Wikipedia," Zenon Aporias "]. Kaikki ymmärtävät, että heitä huijataan, mutta kukaan ei ymmärrä, mikä petos on.

Matematiikan näkökulmasta Zeno osoitti aporiassaan selvästi siirtymisen arvosta toiseen. Tämä siirtymä edellyttää soveltamista vakioiden sijaan. Ymmärtääkseni matemaattista laitteistoa muuttuvien mittayksiköiden soveltamiseksi ei ole vielä kehitetty tai sitä ei ole sovellettu Zenon aporiaan. Tavallisen logiikkamme soveltaminen johtaa meidät ansaan. Me, ajattelun inertialla, sovellamme käänteisarvoon vakioaikayksiköitä. Fyysisestä näkökulmasta tämä näyttää ajan hidastumiselta, kunnes se pysähtyy kokonaan sillä hetkellä, kun Akhilleus saavuttaa kilpikonnan. Jos aika pysähtyy, Akhilleus ei voi enää ohittaa kilpikonnaa.

Jos käännämme logiikkaa, johon olemme tottuneet, kaikki loksahtaa paikoilleen. Akhilleus juoksee tasaisella nopeudella. Jokainen sen polun seuraava osa on kymmenen kertaa lyhyempi kuin edellinen. Näin ollen sen voittamiseen käytetty aika on kymmenen kertaa vähemmän kuin edellinen. Jos käytämme "äärettömyyden" käsitettä tässä tilanteessa, olisi oikein sanoa "Achilles ohittaa äärettömän nopeasti kilpikonnan".

Kuinka välttää tämä looginen ansa? Pysy vakioissa aikayksiköissä äläkä vaihda käänteisarvoihin. Zenon kielellä se näyttää tältä:

Kun Akhilleus juoksee tuhat askelta, kilpikonna ryömii sata askelta samaan suuntaan. Seuraavan aikavälin aikana, joka on yhtä suuri kuin ensimmäinen, Akhilleus juoksee toiset tuhat askelta ja kilpikonna ryömi sata askelta. Nyt Akhilleus on kahdeksansataa askelta kilpikonnan edellä.

Tämä lähestymistapa kuvaa todellisuutta riittävästi ilman loogisia paradokseja. Mutta tämä ei ole täydellinen ratkaisu ongelmaan. Einsteinin lausunto valonnopeuden ylitsepääsemättömyydestä on hyvin samanlainen kuin Zenon aporia "Achilles ja kilpikonna". Meidän on vielä tutkittava, pohdittava ja ratkaistava tämä ongelma. Ja ratkaisua ei tarvitse etsiä äärettömän suurista luvuista, vaan mittayksiköistä.

Toinen Zenonin mielenkiintoinen aporia kertoo lentävästä nuolesta:

Lentävä nuoli on liikkumaton, koska se on joka hetki levossa, ja koska se on levossa joka hetki, se on aina levossa.

Tässä aporiassa looginen paradoksi voitetaan hyvin yksinkertaisesti - riittää selventämään, että lentävä nuoli on joka hetki levossa avaruuden eri pisteissä, mikä itse asiassa on liikettä. Tässä on huomioitava toinen seikka. Yhdestä valokuvasta tiellä olevasta autosta on mahdotonta määrittää sen liikkeen tosiasiaa tai etäisyyttä siihen. Auton liikkeen tosiasian selvittämiseksi tarvitaan kaksi valokuvaa, jotka on otettu samasta pisteestä eri ajankohtina, mutta niitä ei voida käyttää etäisyyden määrittämiseen. Etäisyyden määrittämiseksi autoon tarvitset kaksi valokuvaa, jotka on otettu avaruuden eri pisteistä samanaikaisesti, mutta et voi määrittää niistä liikkeen tosiasiaa (tietenkin tarvitset edelleen lisätietoja laskelmia varten, trigonometria auttaa sinua) . Haluan erityisesti korostaa, että kaksi pistettä ajassa ja kaksi pistettä avaruudessa ovat kaksi eri asiaa, joita ei pidä sekoittaa, koska ne tarjoavat erilaisia ​​mahdollisuuksia tutkimiseen.

Keskiviikkona 4.7.2018

Erot setin ja multisetin välillä on kuvattu hyvin Wikipediassa. Me katsomme.

Kuten näet, "joukossa ei voi olla kahta identtistä elementtiä", mutta jos joukossa on identtisiä elementtejä, tällaista joukkoa kutsutaan "multisiksi". Järkevät olennot eivät koskaan ymmärrä tällaista absurdin logiikkaa. Tämä on puhuvien papukaijojen ja koulutettujen apinoiden taso, jossa mieli puuttuu sanasta "täysin". Matemaatikot toimivat tavallisina kouluttajina ja saarnaavat meille absurdeja ideoitaan.

Kerran sillan rakentaneet insinöörit olivat sillan alla veneessä sillan kokeiden aikana. Jos silta romahti, keskinkertainen insinööri kuoli luomansa raunioiden alle. Jos silta kesti kuormituksen, lahjakas insinööri rakensi muita siltoja.

Riippumatta siitä, kuinka matemaatikot piiloutuvat lauseen "huomaa minua, olen kotona" tai pikemminkin "matematiikka tutkii abstrakteja käsitteitä" taakse, on olemassa yksi napanuora, joka yhdistää ne erottamattomasti todellisuuteen. Tämä napanuora on rahaa. Sovelletaan matemaattista joukkoteoriaa matemaatikoihin itseensä.

Opiskelimme matematiikkaa erittäin hyvin ja nyt istumme kassalla ja maksamme palkkoja. Täällä matemaatikko tulee meille rahoilleen. Laskemme hänelle koko summan ja levitämme sen pöydällemme eri pinoihin, joihin laitamme samanarvoisia seteleitä. Sitten otamme yhden laskun jokaisesta pinosta ja annamme matemaatikolle hänen "matemaattisen palkkasarjansa". Selitämme matematiikan, että hän saa loput laskut vasta kun hän osoittaa, että joukko ilman identtisiä elementtejä ei ole sama kuin joukko, jossa on identtisiä elementtejä. Tästä hauskuus alkaa.

Ensinnäkin kansanedustajien logiikka toimii: "se voi soveltaa muihin, mutta ei minuun!" Lisäksi aletaan varmistua siitä, että samanarvoisissa seteleissä on eri setelinumeroita, joten niitä ei voida pitää identtisinä elementteinä. No, me laskemme palkan kolikoissa - kolikoissa ei ole numeroita. Täällä matemaatikko muistelee kiihkeästi fysiikkaa: eri kolikoissa on eri määrä likaa, kunkin kolikon kiderakenne ja atomien järjestely on ainutlaatuinen ...

Ja nyt minulla on mielenkiintoisin kysymys: missä on raja, jonka jälkeen monijoukon elementit muuttuvat joukon elementeiksi ja päinvastoin? Tällaista linjaa ei ole olemassa - shamaanit päättävät kaikesta, tiede ei ole edes lähellä.

Kuulehan. Valitsemme jalkapallostadionit, joilla on sama kenttäalue. Kenttien pinta-ala on sama, mikä tarkoittaa, että meillä on multiset. Mutta jos otamme huomioon samojen stadionien nimet, saamme paljon, koska nimet ovat erilaisia. Kuten näet, sama elementtijoukko on samanaikaisesti sekä joukko että monijoukko. Kuinka oikein? Ja tässä matemaatikko-shamaani-shuller ottaa valttiässän hihastaan ​​ja alkaa kertoa meille joko setistä tai multisetistä. Joka tapauksessa hän saa meidät vakuuttuneeksi siitä, että hän on oikeassa.

Ymmärtääksemme, kuinka nykyaikaiset shamaanit toimivat joukkoteorian kanssa ja sitovat sen todellisuuteen, riittää, kun vastaat yhteen kysymykseen: kuinka yhden joukon elementit eroavat toisen joukon elementeistä? Näytän sinulle ilman mitään "ei ole ajateltavissa yhtenä kokonaisuutena" tai "ei ajateltavissa yhtenä kokonaisuutena".

sunnuntaina 18. maaliskuuta 2018

Luvun numeroiden summa on shamaanien tanssi tamburiinilla, jolla ei ole mitään tekemistä matematiikan kanssa. Kyllä, matematiikan tunneilla meitä opetetaan etsimään luvun numeroiden summa ja käyttämään sitä, mutta he ovat shamaaneja sitä varten, opettaakseen jälkeläisilleen heidän taitojaan ja viisauttaan, muuten shamaanit yksinkertaisesti kuolevat sukupuuttoon.

Tarvitsetko todisteita? Avaa Wikipedia ja yritä löytää "Luvun numeroiden summa" -sivu. Häntä ei ole olemassa. Matematiikassa ei ole kaavaa, jolla voit löytää minkä tahansa luvun numeroiden summan. Loppujen lopuksi luvut ovat graafisia symboleja, joilla kirjoitamme numeroita, ja matematiikan kielellä tehtävä kuulostaa tältä: "Etsi mitä tahansa numeroa edustavien graafisten symbolien summa." Matemaatikot eivät voi ratkaista tätä ongelmaa, mutta shamaanit voivat tehdä sen alkeellisesti.

Selvitetään mitä ja miten teemme löytääksemme tietyn luvun numeroiden summan. Ja niin, oletetaan, että meillä on numero 12345. Mitä on tehtävä tämän luvun numeroiden summan löytämiseksi? Harkitsemme kaikkia vaiheita järjestyksessä.

1. Kirjoita numero paperille. Mitä me olemme tehneet? Olemme muuntaneet numeron numerograafiseksi symboliksi. Tämä ei ole matemaattinen operaatio.

2. Leikkaamme yhden vastaanotetun kuvan useiksi kuviksi, joissa oli erilliset numerot. Kuvan leikkaaminen ei ole matemaattinen operaatio.

3. Muunna yksittäiset graafiset merkit numeroiksi. Tämä ei ole matemaattinen operaatio.

4. Laske yhteen saadut luvut. Nyt se on matematiikkaa.

Numeron 12345 numeroiden summa on 15. Nämä ovat matemaatikoiden käyttämiä shamaanien "leikkaus- ja ompelukursseja". Mutta siinä ei vielä kaikki.

Matematiikan kannalta ei ole väliä kumpaan lukujärjestelmään numero kirjoitetaan. Joten eri numerojärjestelmissä saman numeron numeroiden summa on erilainen. Matematiikassa numerojärjestelmä ilmoitetaan alaindeksinä luvun oikealla puolella. Suurella luvulla 12345 en halua huijata päätäni, harkitse artikkelin numeroa 26. Kirjoitetaan tämä luku binääri-, oktaali-, desimaali- ja heksadesimaalilukujärjestelmiin. Emme harkitse jokaista askelta mikroskoopin alla, olemme jo tehneet sen. Katsotaanpa tulosta.

Kuten näet, eri numerojärjestelmissä saman numeron numeroiden summa on erilainen. Tällä tuloksella ei ole mitään tekemistä matematiikan kanssa. Aivan kuin suorakulmion alueen löytäminen metreinä ja senttimetreinä antaisi täysin erilaisia ​​tuloksia.

Nolla kaikissa numerojärjestelmissä näyttää samalta, eikä siinä ole numeroiden summaa. Tämä on toinen argumentti sen tosiasian puolesta, että . Kysymys matemaatikoille: miten matematiikassa ilmaistaan ​​sitä, mikä ei ole luku? Mitä matemaatikoille ei ole olemassa mitään muuta kuin numeroita? Shamaaneille voin sallia tämän, mutta tiedemiehille en. Todellisuus ei ole vain numeroita.

Saatua tulosta tulee pitää todisteena siitä, että lukujärjestelmät ovat lukujen mittayksiköitä. Emmehän voi verrata lukuja eri mittayksiköihin. Jos samat toiminnot saman suuren eri mittayksiköillä johtavat eri tuloksiin niiden vertailun jälkeen, niin tällä ei ole mitään tekemistä matematiikan kanssa.

Mitä on oikea matematiikka? Tällöin matemaattisen toiminnon tulos ei riipu luvun arvosta, käytetystä mittayksiköstä ja siitä, kuka tämän toiminnon suorittaa.

Ovessa kyltti Avaa oven ja sanoo:

Auts! Eikö tämä ole naisten vessa?
- Nuori nainen! Tämä on laboratorio, jossa tutkitaan sielujen loputonta pyhyyttä taivaaseen nousemisen yhteydessä! Nimbus päällä ja nuoli ylös. Mikä muu wc?

Naaras... Halo päällä ja nuoli alas on miespuolinen.

Jos sinulla on tällainen taideteos, joka vilkkuu silmiesi edessä useita kertoja päivässä,

Sitten ei ole yllättävää, että löydät yhtäkkiä oudon kuvakkeen autostasi:

Itse yritän itselleni nähdä miinus neljä astetta kakkaavassa ihmisessä (yksi kuva) (usean kuvan kokoonpano: miinusmerkki, numero neljä, asteen merkintä). Enkä pidä tätä tyttöä typeränä, joka ei tunne fysiikkaa. Hänellä on vain stereotypia graafisten kuvien käsityksestä. Ja matemaatikot opettavat meille tätä koko ajan. Tässä on esimerkki.

1A ei ole "miinus neljä astetta" tai "yksi a". Tämä on "kakkava mies" tai luku "kaksikymmentäkuusi" heksadesimaalilukujärjestelmässä. Ne ihmiset, jotka työskentelevät jatkuvasti tässä numerojärjestelmässä, näkevät numeron ja kirjaimen automaattisesti yhtenä graafisena symbolina.

Trigonometristen funktioiden arvojen taulukko

Huomautus. Tämä trigonometristen funktioiden arvotaulukko käyttää √-merkkiä neliöjuuren merkitsemiseen. Murto-osan merkitsemiseksi - symboli "/".

Katso myös hyödyllisiä materiaaleja:

varten trigonometrisen funktion arvon määrittäminen, etsi se trigonometrisen funktion osoittavan viivan leikkauspisteestä. Esimerkiksi 30 asteen sini - etsimme saraketta, jonka otsikko on sin (sini) ja löydämme taulukon tämän sarakkeen leikkauspisteen rivillä "30 astetta", niiden leikkauspisteestä luemme tuloksen - yksi toinen. Samoin löydämme kosini 60 astetta, sini 60 astetta (jälleen sini (sini) -sarakkeen ja 60 asteen rivin leikkauspisteestä löydämme arvon sin 60 = √3/2) jne. Samalla tavalla löydetään muiden "suosittujen" kulmien sinien, kosinien ja tangenttien arvot.

Pi:n sini, pi:n kosini, pi:n tangentti ja muut kulmat radiaaneina

Alla oleva kosinien, sinien ja tangenttien taulukko soveltuu myös sellaisten trigonometristen funktioiden arvon löytämiseen, joiden argumentti on radiaaneina annettuna. Käytä tätä varten toista kulma-arvojen saraketta. Tämän ansiosta voit muuntaa suosittujen kulmien arvon asteina radiaaneiksi. Etsitään esimerkiksi 60 asteen kulma ensimmäiseltä riviltä ja luetaan sen arvo radiaaneina sen alta. 60 astetta on yhtä suuri kuin π/3 radiaania.

Luku pi ilmaisee yksiselitteisesti ympyrän kehän riippuvuuden kulman astemittasta. Pi radiaanit on siis 180 astetta.

Mikä tahansa pi:nä (radiaani) ilmaistu luku voidaan helposti muuntaa asteina korvaamalla luku pi (π) luvulla 180.

Esimerkkejä:
1. sine pi.
sin π = sin 180 = 0
siis pi:n sini on sama kuin 180 asteen sini ja on yhtä suuri kuin nolla.

2. kosini pi.
cos π = cos 180 = -1
näin ollen pi:n kosini on sama kuin 180 asteen kosini ja yhtä suuri kuin miinus yksi.

3. Tangentti pi
tg π = tg 180 = 0
siten pi:n tangentti on sama kuin 180 asteen tangentti ja on yhtä suuri kuin nolla.

Taulukko sini-, kosini- ja tangenttiarvoista kulmille 0 - 360 astetta (yleiset arvot)

kulma α (astetta)	kulma α radiaaneina (pi:n kautta)	synti (sinus)	cos (kosini)	tg (tangentti)	ctg (kotangentti)	sek (sekantti)	syy (kosekantti)
0	0	0	1	0	-	1	-
15	π/12			2 - √3	2 + √3
30	π/6	1/2	√3/2	1/√3	√3	2/√3	2
45	π/4	√2/2	√2/2	1	1	√2	√2
60	π/3	√3/2	1/2	√3	1/√3	2	2/√3
75	5π/12			2 + √3	2 - √3
90	π/2	1	0	-	0	-	1
105	7π/12		-	- 2 - √3	√3 - 2
120	2π/3	√3/2	-1/2	-√3	-√3/3
135	3π/4	√2/2	-√2/2	-1	-1	-√2	√2
150	5π/6	1/2	-√3/2	-√3/3	-√3
180	π	0	-1	0	-	-1	-
210	7π/6	-1/2	-√3/2	√3/3	√3
240	4π/3	-√3/2	-1/2	√3	√3/3
270	3π/2	-1	0	-	0	-	-1
360	2π	0	1	0	-	1	-

Jos trigonometristen funktioiden arvotaulukossa on funktion arvon sijasta viiva (tangentti (tg) 90 astetta, kotangentti (ctg) 180 astetta), niin tietylle arvolle astemitta kulma, funktiolla ei ole tarkkaa arvoa. Jos viivaa ei ole, solu on tyhjä, joten emme ole vielä syöttäneet haluttua arvoa. Olemme kiinnostuneita siitä, mitä pyyntöjä käyttäjät tulevat meille ja täydennämme taulukkoa uusilla arvoilla huolimatta siitä, että nykyinen tieto yleisimpien kulma-arvojen kosinien, sinien ja tangenttien arvoista riittää ratkaisemaan useimmat ongelmia.

Taulukko trigonometristen funktioiden sin, cos, tg arvoista suosituimmille kulmille
0, 15, 30, 45, 60, 90 ... 360 astetta
(lukuarvot "Bradis-taulukoiden mukaan")

kulman arvo α (astetta)	kulman α arvo radiaaneina	synti (sini)	cos (kosini)	tg (tangentti)	ctg (kotangentti)
0	0
15		0,2588	0,9659	0,2679
30		0,5000		0,5774
45		0,7071
		0,7660
60		0,8660	0,5000	1,7321
	7π/18

Artikkelissa ymmärrämme täysin, miltä se näyttää trigonometristen arvojen taulukko, sini, kosini, tangentti ja kotangentti. Tarkastellaan trigonometristen funktioiden perusarvoa kulmasta 0,30,45,60,90,...,360 astetta. Ja katsotaanpa, kuinka näitä taulukoita käytetään laskettaessa trigonometristen funktioiden arvoa.
Ensin harkitse kosinin, sinin, tangentin ja kotangentin taulukko 0, 30, 45, 60, 90,... asteen kulmasta. Näiden suureiden määrittely mahdollistaa 0 ja 90 asteen kulmien funktioiden arvon määrittämisen:

sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, 00:n kotangentti on määrittelemätön
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0:n tangentti on määrittelemätön

Jos otamme suorakulmaiset kolmiot, joiden kulmat ovat 30 - 90 astetta. Saamme:

sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √ 2/2, cos 45 0 = √ 2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 = √3, ctg 60 0 = √3/3

Esitämme kaikki saadut arvot muodossa trigonometrinen taulukko:

Sinien, kosinien, tangenttien ja kotangenttien taulukko!

Jos käytämme valukaavaa, taulukkomme kasvaa, arvot kulmille lisätään jopa 360 astetta. Se näyttää tältä:

Myös jaksollisuuden ominaisuuksien perusteella taulukkoa voidaan suurentaa korvaamalla kulmat 0 0 +360 0 *z .... 330 0 +360 0 *z, jossa z on kokonaisluku. Tässä taulukossa on mahdollista laskea kaikkien yhden ympyrän pisteitä vastaavien kulmien arvo.

Katsotaanpa selkeästi, kuinka taulukkoa käytetään ratkaisussa.
Kaikki on hyvin yksinkertaista. Koska tarvitsemamme arvo on tarvitsemiemme solujen leikkauspisteessä. Otetaan esimerkiksi 60 asteen kulman cos, taulukossa se näyttää tältä:

Trigonometristen funktioiden pääarvojen lopullisessa taulukossa toimimme samalla tavalla. Mutta tästä taulukosta on mahdollista saada selville kuinka suuri tangentti on 1020 asteen kulmasta, se = -√3 Tarkastetaan 1020 0 = 300 0 +360 0 *2. Etsitään pöytä.

Bradis pöytä. Sinille, kosinille, tangentille ja kotangentille.

Bradysin taulukot on jaettu useisiin osiin, ne koostuvat kosini- ja sinitaulukoista, tangentista ja kotangentista - joka on jaettu kahteen osaan (90 asteen kulman tg ja pienten kulmien ctg).

Sini ja kosini

kulma tg välillä 00 - 760, kulma ctg välillä 140 - 900.

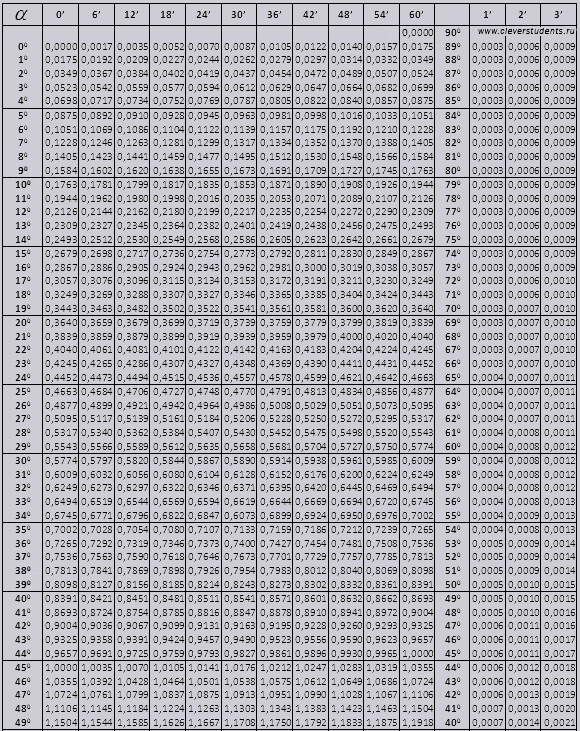
tg jopa 900 ja ctg pienet kulmat.

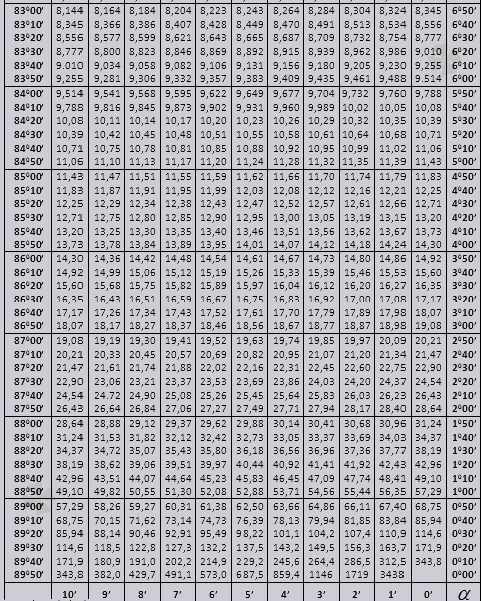
Selvitetään kuinka käyttää Bradis-taulukoita ongelmien ratkaisemiseen.

Etsitään nimitys sin (nimitys sarakkeessa vasemmasta reunasta) 42 minuuttia (nimitys on ylärivillä). Ylittämällä etsimme nimitystä, se on = 0,3040.

Minuuttiarvot ilmoitetaan kuuden minuutin välein, entä jos tarvitsemamme arvo osuu tähän väliin. Otetaan 44 minuuttia, ja taulukossa on vain 42. Otetaan 42 pohjaksi ja käytetään lisäsarakkeita oikealla puolella, otetaan 2. korjaus ja lisätään 0.3040 + 0.0006 saamme 0.3046.

Kun sin 47 min, otamme perustaksi 48 min ja vähennämme siitä 1 korjauksen, eli 0,3057 - 0,0003 = 0,3054

Cosia laskettaessa toimimme samalla tavalla kuin sin, vain otamme pohjaksi taulukon alimman rivin. Esimerkiksi cos 20 0 = 0,9397

Kulman arvot tg 90 0 asti ja pienen kulman cot ovat oikein, eikä niissä ole korjauksia. Etsi esimerkiksi tg 78 0 37 min = 4,967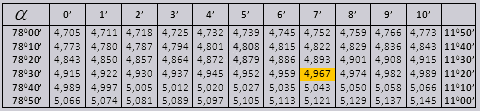


ja ctg 20 0 13 min = 25,83

No, tässä olemme tarkastelleet tärkeimpiä trigonometrisiä taulukoita. Toivomme, että nämä tiedot olivat erittäin hyödyllisiä sinulle. Kysymyksesi pöydistä, jos niitä on, muista kirjoittaa kommentteihin!

Huomautus: Seinälokasuojat - lokasuojalevy seinien suojaamiseen. Seuraa linkkiä seinättömät kehyksettömät lokasuojat (http://www.spi-polymer.ru/otboyniki/) ja lue lisää.

Tämä artikkeli on kerännyt sinien, kosinien, tangenttien ja kotangenttien taulukot. Ensin annamme taulukon trigonometristen funktioiden pääarvoista eli taulukon kulmien sinistä, kosineista, tangenteista ja kotangenteista 0, 30, 45, 60, 90, ..., 360 astetta ( 0, π/6, π/4, π/3, π/2, …, 2π radiaani). Sen jälkeen annamme taulukon sinistä ja kosineista sekä V. M. Bradisin tangenttien ja kotangenttien taulukon ja näytämme, kuinka näitä taulukoita käytetään etsittäessä trigonometristen funktioiden arvoja.

Sivulla navigointi.

Taulukko sinistä, kosineista, tangenteista ja kotangenteista kulmille 0, 30, 45, 60, 90, ... astetta

Bibliografia.

• Algebra: Proc. 9 solulle. keskim. koulu / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Enlightenment, 1990.- 272 s.: Ill.- ISBN 5-09-002727-7
• Bashmakov M.I. Algebra ja analyysin alku: Proc. 10-11 solulle. keskim. koulu - 3. painos - M.: Enlightenment, 1993. - 351 s.: ill. - ISBN 5-09-004617-4.
• Algebra ja analyysin alku: Proc. 10-11 solulle. Yleissivistävä koulutus instituutiot / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn ja muut; Ed. A. N. Kolmogorova.- 14. painos- M.: Enlightenment, 2004.- 384 s.: ill.- ISBN 5-09-013651-3.
• Gusev V. A., Mordkovich A. G. Matematiikka (käsikirja teknisiin kouluihin hakijoille): Proc. korvaus.- M.; Korkeampi koulu, 1984.-351 s., ill.
• Bradis V.M. Nelinumeroiset matemaattiset taulukot: Yleissivistävälle koulutukselle. oppikirja laitokset. - 2. painos - M.: Bustard, 1999.- 96 s.: ill. ISBN 5-7107-2667-2

1. Trigonometriset funktiot ovat alkeisfunktioita, joiden argumentti on injektio. Trigonometriset funktiot kuvaavat suoran kolmion sivujen ja terävien kulmien välisiä suhteita. Trigonometristen funktioiden käyttöalueet ovat erittäin monipuoliset. Joten esimerkiksi mikä tahansa jaksollinen prosessi voidaan esittää trigonometristen funktioiden summana (Fourier-sarja). Nämä funktiot tulevat usein esiin, kun ratkaistaan ​​differentiaali- ja funktionaalisia yhtälöitä.

2. Trigonometriset funktiot sisältävät seuraavat 6 funktiota: sinus, kosini, tangentti,kotangentti, sekantti ja kosekantti. Jokaiselle näistä funktioista on käänteinen trigonometrinen funktio.

3. Trigonometristen funktioiden geometrinen määritelmä on kätevä esitellä käyttämällä yksikköympyrä. Alla olevassa kuvassa on ympyrä, jonka säde r=1. Piste M(x,y) on merkitty ympyrään. Sädevektorin OM ja Ox-akselin positiivisen suunnan välinen kulma on α.

4. sinus kulma α on pisteen M(x,y) ordinaatin y suhde säteeseen r:
sinα=y/r.
Koska r=1, niin sini on yhtä suuri kuin pisteen M(x,y) ordinaatt.

5. kosini kulma α on pisteen M(x,y) abskissan x suhde säteeseen r:
cosα=x/r

6. tangentti kulma α on pisteen M(x,y) ordinaatan y suhde sen abskissaan x:
tanα=y/x,x≠0

7. Kotangentti kulma α on pisteen M(x,y) abskissan x suhde sen ordinaataan y:
cotα=x/y,y≠0

8. Sekantti kulma α on säteen r suhde pisteen M(x,y) abskissaan x:
secα=r/x=1/x,x≠0

9. Kosekantti kulma α on säteen r suhde pisteen M(x,y) ordinaataan y:
cscα=r/y=1/y,y≠0

10. Projektion x, y yksikköympyrässä pisteet M(x,y) ja säde r muodostavat suorakulmaisen kolmion, jossa x,y ovat haarat ja r hypotenuusa. Siksi yllä olevat trigonometristen funktioiden määritelmät suorakulmaiseen kolmioon sovellettuina muotoillaan seuraavasti:
sinus kulma α on vastakkaisen jalan suhde hypotenuusaan.
kosini kulma α on viereisen jalan suhde hypotenuusaan.
tangentti Kulmaa α kutsutaan viereisen haaran vastakkaiseksi haaraksi.
Kotangentti kulmaa α kutsutaan vastakohdan viereiseksi haaraksi.
Sekantti kulma α on hypotenuusan suhde viereiseen jalkaan.
Kosekantti kulma α on hypotenuusan suhde vastakkaiseen jalkaan.

11. sinifunktiokaavio
y=sinx, alue: x∈R, alue: −1≤sinx≤1

12. Kosinifunktion kuvaaja
y=cosx, verkkotunnus: x∈R, alue: −1≤cosx≤1

13. tangenttifunktiokaavio
y=tanx, alue: x∈R,x≠(2k+1)π/2, verkkoalue: −∞

14. Kotangenttifunktion kuvaaja
y=cotx, verkkoalue: x∈R,x≠kπ, verkkoalue: −∞

15. Sekanttifunktion kaavio
y=secx, verkkotunnus: x∈R,x≠(2k+1)π/2, verkkoalue: secx∈(−∞,−1]∪∪)