Ellipsi on pisteiden sijainti tasossa, etäisyyksien summa jokaisesta niistä kahteen annettuun pisteeseen F_1, ja F_2 on vakioarvo (2a), suurempi kuin näiden pisteiden välinen etäisyys (2c) (kuva 1). 3,36, a). Tämä geometrinen määritelmä ilmaisee ellipsin polttopiste.
Ellipsin polttopiste
Pisteitä F_1 ja F_2 kutsutaan ellipsin polttopisteiksi, niiden välinen etäisyys 2c=F_1F_2 on polttoväli, janan F_1F_2 keskipiste O on ellipsin keskipiste, numero 2a on ellipsin pääakselin pituus. ellipsi (vastaavasti luku a on ellipsin pääpuoliakseli). Janaja F_1M ja F_2M, jotka yhdistävät mielivaltaisen ellipsin pisteen M sen polttopisteisiin, kutsutaan pisteen M polttosäteiksi. Janaa, joka yhdistää kaksi ellipsin pistettä, kutsutaan ellipsin jänteeksi.
Suhdetta e=\frac(c)(a) kutsutaan ellipsin epäkeskisyydeksi. Määritelmästä (2a>2c) seuraa, että 0\leqslant e<1 . При e=0 , т.е. при c=0 , фокусы F_1 и F_2 , а также центр O совпадают, и эллипс является окружностью радиуса a (рис.3.36,6).
Ellipsin geometrinen määritelmä, joka ilmaisee sen polttovälin, vastaa sen analyyttistä määritelmää - ellipsin kanonisen yhtälön antama viiva:
Todellakin, otetaan käyttöön suorakaiteen muotoinen koordinaattijärjestelmä (Kuva 3.36, c). Ellipsin keskipiste O otetaan koordinaattijärjestelmän origoksi; polttopisteiden (polttoakseli tai ellipsin ensimmäinen akseli) läpi kulkeva suora viiva otetaan abskissa-akseliksi (sillä oleva positiivinen suunta pisteestä F_1 pisteeseen F_2); polttoakseliin nähden kohtisuorassa ellipsin keskipisteen (ellipsin toinen akseli) läpi kulkeva suora viiva otetaan y-akseliksi (y-akselin suunta valitaan siten, että suorakaiteen muotoinen koordinaattijärjestelmä Oxy on oikea ).
Muotoilkaamme ellipsin yhtälö käyttämällä sen geometristä määritelmää, joka ilmaisee polttopisteen ominaisuuden. Valitussa koordinaattijärjestelmässä määritämme polttopisteiden koordinaatit F_1(-c,0),~F_2(c,0). Mielivaltaiselle pisteelle M(x,y), joka kuuluu ellipsiin, meillä on:
\vline\,\overrightarrow(F_1M)\,\vline\,+\vline\,\overrightarrow(F_2M)\,\vline\,=2a.
Kirjoittamalla tämä yhtäläisyys koordinaattimuotoon, saamme:
\sqrt((x+c)^2+y^2)+\sqrt((x-c)^2+y^2)=2a.
Siirrämme toisen radikaalin oikealle puolelle, neliöimme yhtälön molemmat puolet ja annamme vastaavat termit:
(x+c)^2+y^2=4a^2-4a\sqrt((x-c)^2+y^2)+(x-c)^2+y^2~\nuoli vasenoikealle ~4a\sqrt((x-c) )^2+y^2)=4a^2-4cx.
Jakamalla 4:llä, neliöimme yhtälön molemmat puolet:
A^2(x-c)^2+a^2y^2=a^4-2a^2cx+c^2x^2~\nuoli oikealle~ (a^2-c^2)^2x^2+a^2y^ 2=a^2(a^2-c^2).
Merkitsee b=\sqrt(a^2-c^2)>0, saamme b^2x^2+a^2y^2=a^2b^2. Jakamalla molemmat osat luvulla a^2b^2\ne0, pääsemme ellipsin kanoniseen yhtälöön:
\frac(x^2)(a^2)+\frac(y^2)(b^2)=1.
Siksi valittu koordinaattijärjestelmä on kanoninen.
Jos ellipsin polttopisteet ovat samat, niin ellipsi on ympyrä (kuva 3.36.6), koska a=b. Tässä tapauksessa mikä tahansa suorakaiteen muotoinen koordinaattijärjestelmä, jonka origo on pisteessä O\equiv F_1\equiv F_2, ja yhtälö x^2+y^2=a^2 on ympyrän yhtälö, jonka keskipiste on O ja säde a .
Taaksepäin päättelemällä voidaan osoittaa, että kaikki pisteet, joiden koordinaatit täyttävät yhtälön (3.49), ja vain ne, kuuluvat pisteen lokukseen, jota kutsutaan ellipsiksi. Toisin sanoen ellipsin analyyttinen määritelmä vastaa sen geometrista määritelmää, joka ilmaisee ellipsin polttoominaisuuden.
Ellipsin hakemistoominaisuus
Ellipsin suuntaviivat ovat kaksi suoraa, jotka kulkevat yhdensuuntaisesti kanonisen koordinaatiston y-akselin kanssa samalla etäisyydellä \frac(a^2)(c) siitä. Kun c=0 , kun ellipsi on ympyrä, ei ole suuntaviivoja (voimme olettaa, että suuntaviivat poistetaan äärettömästi).
Ellipsi, jonka epäkeskisyys on 0
Todellakin esimerkiksi tarkennukselle F_2 ja suunnalle d_2 (kuva 3.37.6) ehto \frac(r_2)(\rho_2)=e voidaan kirjoittaa koordinaattimuotoon:
\sqrt((x-c)^2+y^2)=e\cdot\!\left(\frac(a^2)(c)-x\oikea)
Irrationaalisuudesta eroon pääseminen ja korvaaminen e=\frac(c)(a),~a^2-c^2=b^2, päästään ellipsin kanoniseen yhtälöön (3.49). Samanlainen päättely voidaan tehdä myös tarkennukselle F_1 ja suuntaviivalle d_1\colon\frac(r_1)(\rho_1)=e.
Ellipsiyhtälö napakoordinaateissa
Ellipsiyhtälö napakoordinaatistossa F_1r\varphi (kuva 3.37,c ja 3.37(2)) on muotoa
R=\frac(p)(1-e\cdot\cos\varphi)
missä p=\frac(b^2)(a) on ellipsin polttoparametri.
Itse asiassa valitaan ellipsin vasen polttopiste F_1 napakoordinaattijärjestelmän napaksi ja säde F_1F_2 napa-akseliksi (kuva 3.37, c). Sitten mielivaltaiselle pisteelle M(r,\varphi) on ellipsin geometrisen määritelmän (fokusointiominaisuuden) mukaan r+MF_2=2a . Ilmoitetaan pisteiden M(r,\varphi) ja F_2(2c,0) välinen etäisyys (katso huomautuksen 2.8 kohta 2):
\begin(tasattu)F_2M&=\sqrt((2c)^2+r^2-2\cdot(2c)\cdot r\cos(\varphi-0))=\\ &=\sqrt(r^2- 4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2).\end(tasattu)
Siksi koordinaattimuodossa ellipsin yhtälöllä F_1M+F_2M=2a on muoto
R+\sqrt(r^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2)=2\cdot a.
Eristämme radikaalin, neliöimme yhtälön molemmat puolet, jaamme 4:llä ja annamme vastaavat termit:
R^2-4\cdot c\cdot r\cdot\cos\varphi+4\cdot c^2~\Leftrightarrow~a\cdot\!\left(1-\frac(c)(a)\cdot\cos \varphi\right)\!\cdot r=a^2-c^2.
Ilmaisemme napasäteen r ja teemme korvauksen e=\frac(c)(a),~b^2=a^2-c^2,~p=\frac(b^2)(a):
R=\frac(a^2-c^2)(a\cdot(1-e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(b^2)(a\cdot(1) -e\cdot\cos\varphi)) \quad \Leftrightarrow \quad r=\frac(p)(1-e\cdot\cos\varphi),
Q.E.D.
Ellipsiyhtälön kertoimien geometrinen merkitys
Etsitään ellipsin leikkauspisteet (ks. kuva 3.37, a) koordinaattiakseleiden (zllips-pisteiden) kanssa. Korvaamalla yhtälöön y=0, löydämme ellipsin leikkauspisteet abskissa-akselin kanssa (polttoakselin kanssa): x=\pm a . Siksi ellipsin sisällä olevan polttoakselin segmentin pituus on yhtä suuri kuin 2a. Kuten edellä todettiin, tätä segmenttiä kutsutaan ellipsin pääakseliksi ja numero a on ellipsin pääpuoliakseli. Korvaamalla x=0 saadaan y=\pm b . Siksi ellipsin toisen akselin segmentin pituus ellipsin sisällä on 2b. Tätä segmenttiä kutsutaan ellipsin sivuakseliksi ja lukua b kutsutaan ellipsin pieneksi puoliakseliksi.
Todella, b=\sqrt(a^2-c^2)\leqslant\sqrt(a^2)=a, ja yhtälö b=a saadaan vain tapauksessa c=0 kun ellipsi on ympyrä. Asenne k=\frac(b)(a)\leqslant1 kutsutaan ellipsin supistumistekijäksi.
Huomautuksia 3.9
1. Suorat x=\pm a,~y=\pm b rajoittavat koordinaattitasolla pääsuorakulmiota, jonka sisällä ellipsi sijaitsee (ks. kuva 3.37, a).
2. Ellipsi voidaan määritellä seuraavasti pisteiden paikka, joka saadaan supistamalla ympyrä sen halkaisijaan.
Todellakin, olkoon suorakulmaisessa koordinaattijärjestelmässä Oxy ympyräyhtälö muotoa x^2+y^2=a^2 . Pakattuna x-akseliin kertoimella 0 \begin(cases)x"=x,\\y"=k\cdot y.\end(cases) Korvaamalla x=x" ja y=\frac(1)(k)y" ympyrän yhtälöön, saadaan yhtälö pisteen M(x) kuvan M"(x",y") koordinaateille ,y): (x")^2+(\left(\frac(1)(k)\cdot y"\oikea)\^2=a^2 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{k^2\cdot a^2}=1 \quad \Leftrightarrow \quad \frac{(x")^2}{a^2}+\frac{(y")^2}{b^2}=1,
!} koska b=k\cdot a . Tämä on ellipsin kanoninen yhtälö. 3. (kanonisen koordinaattijärjestelmän) koordinaattiakselit ovat ellipsin symmetria-akseleita (jota kutsutaan ellipsin pääakseleiksi), ja sen keskipiste on symmetriakeskus. Todellakin, jos piste M(x,y) kuuluu ellipsiin . silloin pisteet M"(x,-y) ja M""(-x,y) , jotka ovat symmetriset pisteen M suhteen koordinaattiakseleiden suhteen, kuuluvat myös samaan ellipsiin. 4. Ellipsin yhtälöstä napakoordinaatistossa r=\frac(p)(1-e\cos\varphi)(katso kuva 3.37, c), polttoparametrin geometrinen merkitys selkiytyy - tämä on puolet polttoakseliin nähden kohtisuorassa sen fokuksen läpi kulkevan ellipsin jänteen pituudesta ( r = p at \varphi=\frac(\pi)(2)). 5. Epäkeskisyys e kuvaa ellipsin muotoa, eli ellipsin ja ympyrän välistä eroa. Mitä suurempi e, sitä pitkänomaisempi ellipsi on, ja mitä lähempänä e on nollaa, sitä lähempänä ellipsi on ympyrää (kuva 3.38, a). Todellakin, kun otetaan huomioon, että e=\frac(c)(a) ja c^2=a^2-b^2 , saamme E^2=\frac(c^2)(a^2)=\frac(a^2-b^2)(a^2)=1-(\left(\frac(a)(b)\right )\^2=1-k^2,
!} missä k on ellipsin supistumiskerroin, 0 6. Yhtälö \frac(x^2)(a^2)+\frac(y^2)(b^2)=1 a
7. Yhtälö \frac((x-x_0)^2)(a^2)+\frac((y-y_0)^2)(b^2)=1,~a\geqslant b määrittää pisteen O "(x_0, y_0) keskipisteen ellipsin, jonka akselit ovat yhdensuuntaiset koordinaattiakseleiden kanssa (kuva 3.38, c). Tämä yhtälö pelkistetään kanoniseksi rinnakkaismuunnolla (3.36). Jos a=b=R yhtälö (x-x_0)^2+(y-y_0)^2=R^2 kuvaa ympyrää, jonka säde on R ja jonka keskipiste on piste O"(x_0,y_0) . Ellipsin parametrinen yhtälö kanonisessa koordinaattijärjestelmässä on muoto \begin(cases)x=a\cdot\cos(t),\\ y=b\cdot\sin(t),\end(cases)0\leqslant t<2\pi.
Todellakin, korvaamalla nämä lausekkeet yhtälöllä (3.49), saamme trigonometrisen perusidentiteetin \cos^2t+\sin^2t=1 . Esimerkki 3.20. piirrä ellipsi \frac(x^2)(2^2)+\frac(y^2)(1^2)=1 kanonisessa koordinaattijärjestelmässä Oxy . Etsi puoliakselit, polttoväli, epäkeskisyys, kuvasuhde, polttoparametri, suuntayhtälöt. Päätös. Vertaamalla annettua yhtälöä kanoniseen yhtälöön määritetään puoliakselit: a=2 - pääpuoliakseli, b=1 - ellipsin pieni puoliakseli. Rakennamme pääsuorakulmion, jonka sivut 2a=4,~2b=2 on keskitetty origoon (kuva 3.39). Ottaen huomioon ellipsin symmetria, sovitamme sen pääsuorakulmioon. Tarvittaessa määritämme joidenkin ellipsin pisteiden koordinaatit. Esimerkiksi korvaamalla ellipsiyhtälöön x=1, saamme \frac(1^2)(2^2)+\frac(y^2)(1^2)=1 \quad \Leftrightarrow \quad y^2=\frac(3)(4) \quad \Leftrightarrow \ quad y=\pm\frac(\sqrt(3))(2). Siksi pisteet, joissa on koordinaatit \left(1;\,\frac(\sqrt(3))(2)\right)\!,~\left(1;\,-\frac(\sqrt(3))(2)\oikea)- kuuluvat ellipsiin. Laske puristussuhde k=\frac(b)(a)=\frac(1)(2); polttoväli 2c=2\sqrt(a^2-b^2)=2\sqrt(2^2-1^2)=2\sqrt(3); epäkeskisyys e=\frac(c)(a)=\frac(\sqrt(3))(2); polttoparametri p=\frac(b^2)(a)=\frac(1^2)(2)=\frac(1)(2). Muodostamme suuntayhtälöt: x=\pm\frac(a^2)(c)~\Leftrightarrow~x=\pm\frac(4)(\sqrt(3)). Määritelmä. Ellipsi on tason pisteiden paikka, jonka kunkin etäisyyden summa tämän tason kahdesta annetusta pisteestä, nimeltään polttopiste, on vakioarvo (edellyttäen, että tämä arvo on suurempi kuin polttopisteiden välinen etäisyys). Merkitään polttopisteitä niiden välisen etäisyyden kautta - kautta , ja vakioarvo, joka on yhtä suuri kuin etäisyyksien summa ellipsin kustakin pisteestä polttopisteeseen, kautta (ehdon mukaan). Muodostetaan karteesinen koordinaattijärjestelmä siten, että polttopisteet ovat abskissa-akselilla ja koordinaattien origo osuu janan keskikohtaan (kuva 44). Tällöin tarkennuksilla on seuraavat koordinaatit: vasen tarkennus ja oikea tarkennus. Johdetaan ellipsin yhtälö valitsemassamme koordinaattijärjestelmässä. Tarkastellaan tätä varten mielivaltaista ellipsin pistettä. Ellipsin määritelmän mukaan etäisyyksien summa tästä pisteestä polttopisteeseen on: Käyttämällä kahden pisteen välisen etäisyyden kaavaa saamme siis Tämän yhtälön yksinkertaistamiseksi kirjoitamme sen muotoon Sitten yhtälön molempien puolten neliöinti antaa tai ilmeisten yksinkertaistamisen jälkeen: Nyt taas neliöimme yhtälön molemmat puolet, minkä jälkeen meillä on: tai identtisten muunnosten jälkeen: Koska ellipsin määritelmän ehdon mukaan , niin on positiivinen luku. Esittelemme merkinnän Sitten yhtälö saa seuraavan muodon: Ellipsin määritelmän mukaan minkä tahansa sen pisteen koordinaatit täyttävät yhtälön (26). Mutta yhtälö (29) on yhtälön (26) seuraus. Siksi se myös täyttää minkä tahansa ellipsin pisteen koordinaatit. Voidaan osoittaa, että niiden pisteiden koordinaatit, jotka eivät ole ellipsillä, eivät täytä yhtälöä (29). Siten yhtälö (29) on ellipsin yhtälö. Sitä kutsutaan ellipsin kanoniseksi yhtälöksi. Perustetaan ellipsin muoto sen kanonisen yhtälön avulla. Ensinnäkin huomaa, että tämä yhtälö sisältää vain x:n ja y:n parilliset potenssit. Tämä tarkoittaa, että jos jokin piste kuuluu ellipsiin, se sisältää myös pisteen, joka on symmetrinen abskissa-akselin ympärillä olevan pisteen kanssa, ja pisteen, joka on symmetrinen y-akselin ympärillä olevan pisteen kanssa. Ellipsillä on siis kaksi keskenään kohtisuoraa symmetria-akselia, jotka valitsemassamme koordinaattijärjestelmässä osuvat yhteen koordinaattiakseleiden kanssa. Ellipsin symmetriaakseleita kutsutaan ellipsin akseleiksi ja niiden leikkauspistettä - ellipsin keskipisteeksi. Akselia, jolla ellipsin polttopisteet sijaitsevat (tässä tapauksessa abskissa-akseli), kutsutaan polttoakseliksi. Määritetään ensin ellipsin muoto ensimmäisellä neljänneksellä. Tätä varten ratkaisemme yhtälön (28) y:n suhteen: On selvää, että tässä, koska y ottaa imaginaariset arvot arvolle . Nollasta a:ksi kasvaessa y pienenee b:stä 0:aan. Ensimmäisellä neljänneksellä oleva ellipsin osa on kaari, jota rajoittavat pisteet B (0; b) ja joka sijaitsee koordinaattiakseleilla (kuva 45). Käyttämällä nyt ellipsin symmetriaa, päättelemme, että ellipsillä on kuvan 1 mukainen muoto. 45. Ellipsin ja akseleiden leikkauspisteitä kutsutaan ellipsin pisteiksi. Ellipsin symmetriasta seuraa, että ellipsillä on kärkien lisäksi kaksi muuta kärkeä (ks. kuva 45). Ellipsin segmenttejä ja yhdistäviä vastakkaisia pisteitä sekä niiden pituuksia kutsutaan vastaavasti ellipsin pää- ja sivuakseliksi. Lukuja a ja b kutsutaan vastaavasti ellipsin suureksi ja pieneksi puoliakseliksi. Polttopisteiden välisen puolen etäisyyden suhdetta ellipsin puolipääakseliin kutsutaan ellipsin epäkeskisyydeksi ja sitä merkitään yleensä kirjaimella: Koska , Silloin ellipsin epäkeskisyys on pienempi kuin yksi: Epäkeskisyys luonnehtii ellipsin muotoa. Kaavasta (28) todellakin seuraa, että tästä voidaan nähdä, että mitä pienempi ellipsin epäkeskisyys on, sitä vähemmän sen pieni puoliakseli b eroaa suuresta puoliakselista a, eli mitä vähemmän ellipsi on pidennetty (polttopistettä pitkin) akseli). Rajoitavassa tapauksessa, kun saat ympyrän, jonka säde on a: , tai . Samaan aikaan ellipsin polttopisteet ikään kuin sulautuvat yhteen pisteeseen - ympyrän keskipisteeseen. Ympyrän epäkeskisyys on nolla: Yhteys ellipsin ja ympyrän välillä voidaan määrittää toisesta näkökulmasta. Osoitetaan, että ellipsiä, jonka puoliakselit ovat a ja b, voidaan pitää säteittäisen a ympyrän projektiona. Tarkastellaan kahta tasoa P ja Q, jotka muodostavat keskenään sellaisen kulman a, joille (kuva 46). Tehdään P-tasoon koordinaattijärjestelmä ja Q-tasoon - Oxy-järjestelmä, jolla on yhteinen origo O ja yhteinen abskissa-akseli, joka osuu yhteen tasojen leikkauslinjan kanssa. Tarkastellaan tasossa P ympyrää keskitetty alkupisteeseen ja säteeseen a. Olkoon ympyrän mielivaltaisesti valittu piste, sen projektio Q-tasolle ja pisteen M projektio Ox-akselille. Osoitetaan, että piste sijaitsee ellipsillä, jonka puoliakselit ovat a ja b. 11.1. Peruskonseptit Tarkastellaan toisen asteen yhtälöiden määrittelemiä viivoja nykyisten koordinaattien suhteen Yhtälön kertoimet ovat reaalilukuja, mutta sen mukaan vähintään yksi luvuista A, B tai C on eri kuin nolla. Tällaisia viivoja kutsutaan toisen asteen viivoiksi (käyriksi). Alla selvitetään, että yhtälö (11.1) määrittelee ympyrän, ellipsin, hyperbolin tai paraabelin tasossa. Ennen kuin jatkamme tähän väitteeseen, tutkikaamme lueteltujen käyrien ominaisuuksia. 11.2. Ympyrä Sitten ehdosta saadaan yhtälö Yhtälö (11.2) täyttyy minkä tahansa pisteen koordinaateista annetulla ympyrällä, eikä sitä tyydytä yhdenkään pisteen koordinaatit, joka ei ole ympyrällä. Kutsutaan yhtälöä (11.2). ympyrän kanoninen yhtälö Erityisesti olettaen ja , Saamme yhtälö ympyrän keskitetty alkuperä Ympyräyhtälö (11.2) saa yksinkertaisten muunnosten jälkeen muotoa . Kun tätä yhtälöä verrataan toisen kertaluvun käyrän yleiseen yhtälöön (11.1), on helppo nähdä, että ympyräyhtälölle täyttyy kaksi ehtoa: 1) kertoimet kohdissa x 2 ja y 2 ovat keskenään yhtä suuret; 2) ei ole jäsentä, joka sisältää nykyisten koordinaattien xy-tulon. Tarkastellaan käänteistä ongelmaa. Asettamalla yhtälöön (11.1) arvot ja saamme Muunnetaan tämä yhtälö: Tästä seuraa, että yhtälö (11.3) määrittää ympyrän ehdon alla Jos Sen tyydyttävät yhden pisteen koordinaatit Jos 11.3. Ellipsi Ellipsin kanoninen yhtälö Ellipsi
on tason kaikkien pisteiden joukko, etäisyyksien summa jokaisesta niistä tämän tason kahteen annettuun pisteeseen, ns. temppuja
, on vakioarvo, joka on suurempi kuin polttopisteiden välinen etäisyys. Ellipsin yhtälön johtamiseksi valitsemme koordinaattijärjestelmän siten, että polttopisteet F1 ja F2 sijaitsevat akselilla , ja alkupiste on sama kuin segmentin keskipiste F 1 F 2. Tällöin polttopisteillä on seuraavat koordinaatit: ja . Antaa olla mielivaltainen piste ellipsi. Sitten ellipsin määritelmän mukaan, ts. Tämä on itse asiassa ellipsin yhtälö. Muunnamme yhtälön (11.5) yksinkertaisempaan muotoon seuraavasti: Kuten a>kanssa, sitten. Laitetaanpa Sitten viimeinen yhtälö saa muodon tai Voidaan todistaa, että yhtälö (11.7) on ekvivalentti alkuperäisen yhtälön kanssa. Sitä kutsutaan ellipsin kanoninen yhtälö
. Ellipsi on toisen asteen käyrä. Ellipsin muodon tutkimus sen yhtälön mukaan Perustetaan ellipsin muoto sen kanonisen yhtälön avulla. 1. Yhtälö (11.7) sisältää x:n ja y:n vain parillisina potenssiin, joten jos piste kuuluu ellipsiin, niin siihen kuuluvat myös pisteet ,,. Tästä seuraa, että ellipsi on symmetrinen suhteessa akseleihin ja , sekä suhteessa kohtaan , jota kutsutaan ellipsin keskustaksi. 3. Yhtälöstä (11.7) seuraa, että yksikään vasemman puolen termi ei ylitä yhtä, ts. on epätasa-arvoa ja tai ja . Siksi kaikki ellipsin pisteet sijaitsevat suorien viivojen muodostaman suorakulmion sisällä. 4. Yhtälössä (11.7) ei-negatiivisten termien summa ja on yhtä suuri kuin yksi. Näin ollen, kun yksi termi kasvaa, toinen pienenee, eli jos se kasvaa, niin se pienenee ja päinvastoin. Siitä, mitä on sanottu, seuraa, että ellipsillä on kuvan 1 mukainen muoto. 50 (soikea suljettu käyrä). Lisää ellipsistä Ellipsin muoto riippuu suhteesta. Kun ellipsi muuttuu ympyräksi, ellipsiyhtälö (11.7) saa muodon . Ellipsin muodon ominaisuutena suhdetta käytetään useammin. Polttopisteiden välisen etäisyyden puolen suhdetta ellipsin puolipääakseliin kutsutaan ellipsin epäkeskisyydeksi ja o6o merkitään kirjaimella ε ("epsilon"): 0 kanssa<ε< 1, так как 0<с<а. С учетом равенства (11.6) формулу
(11.8) можно переписать в виде Tämä osoittaa, että mitä pienempi ellipsin epäkeskisyys on, sitä vähemmän litistynyt ellipsi on; jos laitamme ε = 0, niin ellipsi muuttuu ympyräksi. On olemassa kaavoja Suoria viivoja kutsutaan Tasa-arvosta (11.6) seuraa, että . Jos , niin yhtälö (11.7) määrittää ellipsin, jonka pääakseli on Oy-akselilla ja sivuakseli Ox-akselilla (ks. kuva 52). Tällaisen ellipsin fokukset ovat kohdissa ja , Missä 11.4. Hyperbeli Hyperbolin kanoninen yhtälö Hyperbolia
kutsutaan tason kaikkien pisteiden joukoksi, jonka moduuli etäisyyksien erosta kustakin tämän tason kahteen tiettyyn pisteeseen, ns. temppuja
, on vakioarvo, pienempi kuin polttopisteiden välinen etäisyys. Hyperboliyhtälön johtamiseksi valitsemme koordinaattijärjestelmän siten, että polttopisteet F1 ja F2 sijaitsevat akselilla , ja alkupiste osui yhteen segmentin keskipisteen kanssa F 1 F 2(katso kuva 53). Sitten polttopisteillä on koordinaatit ja Antaa olla mielivaltainen hyperbolin piste. Sitten hyperbelin määritelmän mukaan Hyperbola on toisen kertaluvun rivi. Hyperbolin muodon tutkiminen yhtälön mukaan Perustetaan hyperbolin muoto käyttämällä sen kakonista yhtälöä. 1. Yhtälö (11.9) sisältää x:n ja y:n vain parillisissa potenssiissa. Siksi hyperbola on symmetrinen akseleiden ja , samoin kuin pisteen suhteen, jota ns. hyperbolan keskusta.
2. Etsi hyperbolin leikkauspisteet koordinaattiakseleiden kanssa. Asettamalla yhtälön (11.9) löydämme kaksi hyperabelin ja akselin leikkauspistettä: ja . Laittamalla (11.9) saamme , joka ei voi olla. Siksi hyperbola ei leikkaa y-akselia. Pisteitä ja kutsutaan
huiput
hyperbolit ja segmentti todellinen akseli
, Jana - todellinen puoliakseli
hyperbolia. Pisteitä yhdistävää janaa kutsutaan
kuvitteellinen akseli
, numero b - kuvitteellinen akseli
. Suorakulmio sivuilla 2a ja 2b nimeltään hyperbelin pääsuorakulmio
. 3. Yhtälöstä (11.9) seuraa, että minuutti ei ole pienempi kuin yksi, eli se tai . Tämä tarkoittaa, että hyperbelin pisteet sijaitsevat suoran oikealla puolella (hyperbolin oikea haara) ja suoran vasemmalla puolella (hyperbolin vasen haara). 4. Hyperbolin yhtälöstä (11.9) voidaan nähdä, että kun se kasvaa, niin se myös kasvaa. Tämä johtuu siitä, että erotus pitää vakioarvon yhtä suurena kuin yksi. Sanomasta seuraa, että hyperbolilla on kuvan 54 mukainen muoto (käyrä, joka koostuu kahdesta rajoittamattomasta haarasta). Hyperbolan asymptootit
Suoraa L kutsutaan asymptootiksi Osoitetaan, että hyperbolalla on kaksi asymptoottia: Koska suorat (11.11) ja hyperboli (11.9) ovat symmetrisiä koordinaattiakseleiden suhteen, riittää, että huomioidaan vain ne pisteet osoitetuista suorista, jotka sijaitsevat ensimmäisessä kvadrantissa. Otetaan suora piste N, jolla on sama abskissa x kuin hyperbelin pisteellä Kuten näet, kun x kasvaa, murto-osan nimittäjä kasvaa; osoittaja on vakioarvo. Siksi segmentin pituus Kun muodostetaan hyperbolia (11.9), on suositeltavaa rakentaa ensin hyperbolin pääsuorakulmio (katso kuva 57), piirtää tämän suorakulmion vastakkaisten kärkien kautta kulkevat viivat - hyperbelin asymptootit ja merkitä kärjet ja , hyperbola . Tasasivuisen hyperbolin yhtälö. joiden asymptootit ovat koordinaattiakselit Tasasivuisen hyperbolin asymptooteilla on yhtälöt ja ne ovat siksi koordinaattikulmien puolittajia. Tarkastellaan tämän hyperbelin yhtälöä uudessa koordinaattijärjestelmässä (katso kuva 58), joka saadaan vanhasta koordinaattiakseleita kiertämällä kulman verran. Käytämme kaavoja koordinaattiakselien kiertoon: Korvaamme x:n ja y:n arvot yhtälössä (11.12): Tasasivuisen hyperbolin yhtälö, jonka akselit Ox ja Oy ovat asymptootteja, on muotoa . Lisää hyperbolista epäkeskisyys
hyperbola (11.9) on polttopisteiden välisen etäisyyden suhde hyperabelin todellisen akselin arvoon, jota merkitään ε:lla: Koska hyperbelille , hyperbelin epäkeskisyys on suurempi kuin yksi: . Epäkeskisyys luonnehtii hyperbolin muotoa. Tasa-arvosta (11.10) todellakin seuraa, että ts. ja Tästä voidaan nähdä, että mitä pienempi hyperbolin epäkeskisyys on, sitä pienempi on sen puoliakselien suhde, mikä tarkoittaa, että mitä enemmän sen pääsuorakulmio laajenee. Tasasivuisen hyperbolin epäkeskisyys on . Todella, Polttopisteen säteet Suoria viivoja kutsutaan hyperbelin suuntaviivoiksi. Koska hyperbolille ε > 1, niin . Tämä tarkoittaa, että oikea suuntaviiva sijaitsee hyperbolan keskipisteen ja oikean kärjen välissä, vasen suuntaviiva on keskustan ja vasemman kärjen välissä. Hyperbolin suuntaviivat ovat samat kuin ellipsin suuntaviivat. Yhtälön määrittelemä käyrä on myös hyperboli, jonka reaaliakseli 2b sijaitsee Oy-akselilla ja imaginaariakseli 2 a- Ox-akselilla. Kuvassa 59 se on esitetty katkoviivana. Ilmeisesti hyperboloilla ja on yhteisiä asymptootteja. Tällaisia hyperboleja kutsutaan konjugaateiksi. 11.5. Paraabeli Kanoninen paraabeliyhtälö Paraabeli on joukko tason kaikkia pisteitä, joista jokainen on yhtä kaukana tietystä pisteestä, jota kutsutaan polttopisteeksi, ja tietystä suorasta, jota kutsutaan suuntaviivaksi. Etäisyyttä fokuksesta F suuntaviivaan kutsutaan paraabelin parametriksi ja sitä merkitään p (p > 0). 1. Yhtälössä (11.13) muuttuja y sisältyy parilliseen asteeseen, mikä tarkoittaa, että paraabeli on symmetrinen Ox-akselin suhteen; x-akseli on paraabelin symmetria-akseli. 2. Koska ρ > 0, (11.13) seuraa, että . Siksi paraabeli sijaitsee y-akselin oikealla puolella. 3. Kun meillä on y \u003d 0. Siksi paraabeli kulkee origon kautta. 4. Kun x:ää kasvaa rajattomasti, myös moduuli y kasvaa loputtomasti. Paraabelilla on kuvan 61 mukainen muoto (muoto). Pistettä O (0; 0) kutsutaan paraabelin kärjeksi, janaa FM \u003d r pisteen M polttosäteeksi. Yhtälöt , , ( p>0) määrittelevät myös paraabelit, ne näkyvät kuvassa 62 On helppo osoittaa, että neliötrinomin kuvaaja, jossa , B ja C ovat mitä tahansa reaalilukuja, on paraabeli edellä olevan määritelmänsä mukaisesti. 11.6. Toisen asteen rivien yleinen yhtälö Toisen kertaluvun käyrien yhtälöt, joissa symmetria-akselit ovat yhdensuuntaiset koordinaattiakseleiden kanssa Etsitään ensin yhtälö ellipsistä, jonka keskipiste on piste, jonka symmetria-akselit ovat yhdensuuntaiset koordinaattiakseleiden Ox ja Oy kanssa ja puoliakselit vastaavasti ovat a ja b. Laitetaan ellipsin O 1 keskelle uuden koordinaattijärjestelmän origo, jonka akselit ja puoliakselit a ja b(katso kuva 64): Ja lopuksi, kuvassa 65 esitetyillä paraboleilla on vastaavat yhtälöt. Yhtälö Ellipsin, hyperabelin, paraabelin ja ympyrän yhtälöt muunnoksien jälkeen (avaavat sulut, siirrät yhtälön kaikkia termejä yhteen suuntaan, tuovat samanlaisia termejä, tuovat kertoimille uuden merkinnän) voidaan kirjoittaa käyttämällä yhtä yhtälöä lomake jossa kertoimet A ja C eivät ole yhtä aikaa nolla. Herää kysymys: määrittääkö jokin muotoa (11.14) oleva yhtälö jonkin toisen kertaluvun käyristä (ympyrä, ellipsi, hyperbola, paraabeli)? Vastaus saadaan seuraavalla lauseella. Lause 11.2. Yhtälö (11.14) määrittää aina: joko ympyrän (jos A = C) tai ellipsin (jos A C > 0), tai hyperbolin (jos A C< 0), либо
параболу (при А×С= 0). При этом возможны случаи вырождения: для эллипса (окружности)
- в точку или мнимый эллипс (окружность), для гиперболы - в пару пересекающихся
прямых, для параболы - в пару параллельных прямых. Toisen kertaluvun yleinen yhtälö Tarkastellaan nyt toisen asteen yleistä yhtälöä kahdella tuntemattomalla: Se eroaa yhtälöstä (11.14) sillä, että siinä on termi koordinaattien tulon (B¹ 0) kanssa. Kiertämällä koordinaattiakseleita kulmalla a, tämä yhtälö voidaan muuntaa siten, että termi koordinaattien tulolla puuttuu siitä. Kaavojen käyttö akseleiden kääntämiseen Ilmaistaan vanhat koordinaatit uusilla: Valitsemme kulman a niin, että kerroin kohdassa x "y" häviää, eli niin, että yhtälö Siten, kun akseleita kierretään kulman a läpi, joka täyttää ehdon (11.17), yhtälö (11.15) pelkistyy yhtälöksi (11.14). Johtopäätös: toisen kertaluvun yleinen yhtälö (11.15) määrittelee tasolla (lukuun ottamatta rappeutumis- ja rappeutumistapauksia) seuraavat käyrät: ympyrä, ellipsi, hyperbola, paraabeli. Huomaa: Jos A = C, yhtälö (11.17) menettää merkityksensä. Tässä tapauksessa cos2α = 0 (katso (11.16)), sitten 2α = 90°, eli α = 45°. Joten, kun A = C, koordinaattijärjestelmää tulisi kiertää 45 °. Toisen asteen käyrät tasossa kutsutaan yhtälöiden määrittelemiä suoria, joissa muuttujan koordinaatit x ja y sisältyvät toiseen asteeseen. Näitä ovat ellipsi, hyperbola ja paraabeli. Toisen asteen käyräyhtälön yleinen muoto on seuraava: missä A B C D E F- numerot ja vähintään yksi kertoimista A, B, C ei ole nolla. Toisen kertaluvun käyrien tehtäviä ratkaistaessa otetaan useimmiten huomioon ellipsin, hyperbelin ja paraabelin kanoniset yhtälöt. Niille on helppo siirtyä yleisistä yhtälöistä, esimerkki 1 ellipsien tehtävistä on omistettu tälle. Ellipsin määritelmä. Ellipsi on joukko tason kaikkia pisteitä, joiden pisteiden etäisyyksien summa, jota kutsutaan polttopisteiksi, on vakio ja suurempi kuin polttopisteiden välinen etäisyys. Kohteet on merkitty alla olevan kuvan mukaisesti. Ellipsin kanoninen yhtälö on: missä a ja b (a > b) - puoliakselien pituudet, eli puolet koordinaattiakseleiden ellipsin leikkaamien segmenttien pituuksista. Ellipsin polttopisteiden läpi kulkeva suora on sen symmetria-akseli. Toinen ellipsin symmetria-akseli on suora viiva, joka kulkee segmentin keskikohdan läpi kohtisuorassa tätä segmenttiä vastaan. Piste O näiden viivojen leikkauspiste toimii ellipsin symmetriakeskuksena tai yksinkertaisesti ellipsin keskipisteenä. Ellipsin abskissa-akseli leikkaa pisteissä ( a, O) ja (- a, O), ja y-akseli on pisteissä ( b, O) ja (- b, O). Näitä neljää pistettä kutsutaan ellipsin kärjeksi. Ellipsin kärkien välistä segmenttiä abskissa-akselilla kutsutaan sen pääakseliksi ja ordinaattisella akselilla - sivuakseliksi. Niiden segmenttejä ylhäältä ellipsin keskustaan kutsutaan puoliakseleiksi. Jos a = b, niin ellipsin yhtälö saa muodon . Tämä on sädeympyrän yhtälö a, ja ympyrä on ellipsin erikoistapaus. Ellipsi voidaan saada sädeympyrästä a, jos puristat sen sisään a/b kertaa akselia pitkin Oy
. Esimerkki 1 Tarkista, onko yleisen yhtälön antama viiva Päätös. Teemme muunnoksia yleisestä yhtälöstä. Käytämme vapaan termin siirtoa oikealle, yhtälön termi-jakoa samalla luvulla ja murtolukujen vähentämistä: Vastaus. Tuloksena oleva yhtälö on ellipsin kanoninen yhtälö. Siksi tämä viiva on ellipsi. Esimerkki 2 Kirjoita ellipsin kanoninen yhtälö, jos sen puoliakselit ovat 5 ja 4. Päätös. Tarkastellaan ellipsin ja substituutin kanonisen yhtälön kaavaa: puolipääakseli on a= 5, pieni puoliakseli on b= 4. Saamme ellipsin kanonisen yhtälön: Pisteet ja merkitty vihreällä pääakselilla, missä nimeltään temppuja. nimeltään epäkeskisyys ellipsi. Asenne b/a luonnehtii ellipsin "litteyttä". Mitä pienempi tämä suhde, sitä enemmän ellipsi ulottuu pääakselia pitkin. Ellipsin venymäaste ilmaistaan kuitenkin useammin epäkeskisyydellä, jonka kaava on annettu yllä. Eri ellipseille epäkeskisyys vaihtelee välillä 0 - 1, jääden aina alle yhden. Esimerkki 3 Kirjoita ellipsin kanoninen yhtälö, jos polttopisteiden välinen etäisyys on 8 ja pääakseli on 10. Päätös. Teemme yksinkertaiset johtopäätökset: Jos pääakseli on 10, niin sen puolisko eli puoliakseli a = 5
, Jos polttopisteiden välinen etäisyys on 8, niin luku c tarkennuskoordinaateista on 4. Korvaa ja laske: Tuloksena on ellipsin kanoninen yhtälö: Esimerkki 4 Kirjoita ellipsin kanoninen yhtälö, jos sen pääakseli on 26 ja epäkeskisyys on . Päätös. Kuten sekä pääakselin koosta että epäkeskisyysyhtälöstä seuraa, ellipsin pääpuoliakseli a= 13. Epäkeskisyysyhtälöstä ilmaisemme luvun c, tarvitaan pienen puoliakselin pituuden laskemiseen: Laskemme pienemmän puoliakselin pituuden neliön: Muodostamme ellipsin kanonisen yhtälön: Esimerkki 5 Määritä kanonisen yhtälön antaman ellipsin polttopisteet. Päätös. Pitää löytää numero c, joka määrittää ellipsin polttopisteiden ensimmäiset koordinaatit: Saamme ellipsin fokukset: Esimerkki 6 Ellipsin polttopisteet sijaitsevat akselilla Härkä symmetrinen alkuperän suhteen. Kirjoita ellipsin kanoninen yhtälö, jos: 1) polttopisteiden välinen etäisyys on 30 ja pääakseli on 34 2) sivuakseli on 24 ja yksi tarkennuksista on pisteessä (-5; 0) 3) epäkeskisyys, ja yksi polttopisteistä on pisteessä (6; 0) Jos - mielivaltainen ellipsin piste (merkitty vihreällä piirustuksessa ellipsin oikeassa yläkulmassa) ja - etäisyydet tähän pisteeseen polttopisteistä, etäisyyksien kaavat ovat seuraavat: Jokaiselle ellipsiin kuuluvalle pisteelle etäisyyksien summa polttopisteistä on vakioarvo, joka on yhtä suuri kuin 2 a. Yhtälöillä määritellyt suorat nimeltään ohjaajat ellipsi (piirustuksessa - punaiset viivat reunoja pitkin). Yllä olevista kahdesta yhtälöstä seuraa, että mille tahansa ellipsin pisteelle missä ja ovat etäisyydet tämän pisteen Directrixes ja . Esimerkki 7 Annettu ellipsi. Kirjoita yhtälö sen suuntaviivoja varten. Päätös. Tarkastellaan suuntayhtälöä ja todetaan, että ellipsin epäkeskisyys on löydettävä, eli . Kaikki tiedot tätä varten ovat. Laskemme: Saamme ellipsin suuntaviivan yhtälön: Esimerkki 8 Kirjoita ellipsin kanoninen yhtälö, jos sen polttopisteet ovat pisteitä ja suuntaviivat viivoja.Ellipsin parametrinen yhtälö
ActiveX-komponentit on otettava käyttöön, jotta voit tehdä laskelmia!
Toisen asteen yksinkertaisin käyrä on ympyrä. Muista, että pisteeseen keskitetty ympyrä, jonka säde on R, on joukko tason kaikkia pisteitä Μ, jotka täyttävät ehdon . Olkoon suorakaiteen muotoisen koordinaatiston pisteen koordinaatit x 0, y 0 a - mielivaltainen ympyrän piste (katso kuva 48).
(11.2)
.
(11.4)
. Sen keskipiste on pisteessä 
, ja säde
.
, niin yhtälöllä (11.3) on muoto
.
. Tässä tapauksessa he sanovat: "ympyrä on rappeutunut pisteeksi" (säde on nolla).
, niin yhtälö (11.4) ja siten vastaava yhtälö (11.3) ei määritä mitään suoraa, koska yhtälön (11.4) oikea puoli on negatiivinen ja vasen puoli ei ole negatiivinen (sanotaan "kuvitteellinen ympyrä").
Merkitse fokuksia F1 ja F2, niiden välinen etäisyys kohdassa 2 c, ja etäisyyksien summa ellipsin mielivaltaisesta pisteestä polttopisteeseen - 2:een a(katso kuva 49). Määritelmän mukaan 2 a > 2c, eli a
> c.
(11.6)
(11.7)
2. Etsi ellipsin ja koordinaattiakselien leikkauspisteet. Laittamalla , löydämme kaksi pistettä ja , joissa akseli leikkaa ellipsin (katso kuva 50). Asettamalla yhtälön (11.7) löydämme ellipsin ja akselin leikkauspisteet: ja . pisteitä A 1 ,
A2 , B1, B2 nimeltään ellipsin kärjet. Segmentit A 1 A2 ja B1 B2, sekä niiden pituudet 2 a ja 2 b kutsutaan vastaavasti suur- ja sivuakselit ellipsi. Numerot a ja b kutsutaan isoksi ja pieneksi. akselin akselit ellipsi.
Olkoon M(x; y) mielivaltainen ellipsin piste, jonka polttopisteet ovat F 1 ja F 2 (katso kuva 51). Segmenttien F 1 M=r 1 ja F 2 M = r 2 pituuksia kutsutaan pisteen M polttosäteiksi. Ilmeisesti
Lause 11.1. Jos on etäisyys mielivaltaisesta ellipsin pisteestä johonkin kohdistukseen, d on etäisyys samasta pisteestä tätä kohdistusta vastaavaan suuntaviivaan, niin suhde on vakioarvo, joka on yhtä suuri kuin ellipsin epäkeskisyys:
.
Merkitse fokuksia F1 ja F2 niiden välinen etäisyys 2s, ja etäisyyseron moduuli hyperbolin kustakin pisteestä polttopisteisiin 2a. A-priory 2a < 2s, eli a < c.
tai ts. yksinkertaistamisen jälkeen, kuten tehtiin ellipsiyhtälön johdossa, saadaan
hyperbelin kanoninen yhtälö
(11.9)
(11.10)
rajoittamattoman käyrän K, jos etäisyys d käyrän K pisteestä M tähän suoraan pyrkii nollaan, kun piste M liikkuu käyrää K pitkin määräämättömästi origosta. Kuva 55 havainnollistaa asymptootin käsitettä: viiva L on asymptootti käyrälle K.
(11.11)
(katso kuva 56) ja löydä ero ΜN suoran ja hyperbolin haaran välillä:
ΜN on yleensä nolla. Koska ΜN on suurempi kuin pisteen Μ ja suoran välinen etäisyys d, niin d pyrkii vielä enemmän nollaan. Siten viivat ovat hyperbelin (11.9) asymptootteja.
Hyperbolaa (11.9) kutsutaan tasasivuiseksi, jos sen puoliakselit ovat yhtä suuret (). Sen kanoninen yhtälö
(11.12)
.
ja 
sillä hyperbelin oikean haaran pisteillä on muoto ja , ja vasemmalle - 
ja 
.
Paraabeliyhtälön johtamiseksi valitsemme Oxy-koordinaatiston siten, että Oxy-akseli kulkee polttopisteen F läpi kohtisuoraan suuntaviivaan nähden suunnasta F-suuntaan ja origo O sijaitsee keskipisteen ja suuntaviivan välissä. (katso kuva 60). Valitussa järjestelmässä kohdistuksella F on koordinaatit ja suuntayhtälön muoto on , tai .
Kanonisen yhtälön antama ellipsi
, ellipsi.
.
.
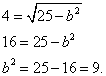
Jatkamme ellipsin ongelmien ratkaisemista yhdessä
,
.
