Tarkastellaan kolmea sädettä a, b, c, jotka lähtevät samasta pisteestä eivätkä ole samassa tasossa. Kolmikulmainen kulma (abc) on kuvio, joka koostuu "kolmesta tasaisesta kulmasta (ab), (bc) ja (ac) (kuva 2). Näitä kulmia kutsutaan kolmikulmaisen kulman pinnoiksi, ja niiden sivut ovat reunoja, Tasaisten kulmien yhteistä kärkeä kutsutaan Kolmikulmaisen kulman pintojen muodostamia kaksitahoisia kulmia kutsutaan kolmiulotteisen kulman dihedrikulmiksi.

Monitahoisen kulman käsite määritellään samalla tavalla (kuva 3).

Polyhedron

Stereometriassa tutkitaan avaruuden hahmoja, joita kutsutaan kappaleiksi. Visuaalisesti (geometrinen) kappale tulee kuvitella osana tilaa, jonka miehittää fyysinen kappale ja jota rajaa pinta.

Monitahoinen on kappale, jonka pinta koostuu äärellisestä määrästä litteitä polygoneja (kuva 4). Monitahoista kutsutaan kuperaksi, jos se sijaitsee jokaisen pinnallaan olevan tasaisen monikulmion tason toisella puolella. Tällaisen tason ja kuperan monitahoisen pinnan yhteistä osaa kutsutaan kasvoksi. Kuperan polyhedronin pinnat ovat litteitä kuperaa monikulmiota. Pintojen sivuja kutsutaan monitahoisen reunuksiksi ja huippuja monitahoisen kärjeksi.

Selvitetään, mitä sanottiin tutun kuution esimerkissä (kuva 5). Kuutio on kupera monitahoinen. Sen pinta koostuu kuudesta ruudusta: ABCD, BEFC, .... Ne ovat sen kasvot. Kuution reunat ovat näiden neliöiden sivut: AB, BC, BE,.... Kuution kärjet ovat neliöiden kärjet: A, B, C, D, E, .... Kuutiossa on kuusi pintaa, kaksitoista reunaa ja kahdeksan kärkeä.

Yksinkertaisimmat polyhedrat - prismat ja pyramidit, jotka ovat tutkimuksemme pääkohde - annamme määritelmät, jotka pohjimmiltaan eivät käytä kehon käsitettä. Ne määritellään geometrisiksi kuvioiksi, joissa on kaikki niihin kuuluvat avaruuden pisteet. Geometrisen kappaleen käsite ja sen pinta yleisessä tapauksessa annetaan myöhemmin.

MONIKEDRISET KULMAT

Monitahoinen kulma on monikulmion spatiaalinen analogi. Muista, että tasossa oleva monikulmio on kuvio, joka muodostuu yksinkertaisesta suljetusta katkoviivasta ja sen rajoittamasta sisäisestä alueesta. Käsittelemme avaruudessa olevaa sädettä tason pisteen analogina ja tasaista kulmaa avaruudessa tason segmentin analogina. Tällöin yksinkertaisen suljetun katkoviivan analogi tasossa on pinta, jonka muodostaa äärellinen tasokulmien joukkoA 1 SA 2 , A 2 SA 3 , …, A n -1 SA n, A n SA 1 yhteisellä topallaS (Kuva 1), jossa vierekkäisillä kulmilla ei ole yhteisiä pisteitä, paitsi yhteisen säteen pisteitä, ja ei-naapurikulmilla ei ole yhteisiä pisteitä yhteistä kärkeä lukuun ottamatta. Kuvaa, joka muodostuu määritellystä pinnasta ja yhdestä kahdesta sen rajoittamasta avaruuden osasta, kutsutaan monitahoinen kulma. yhteinen toppiSnimeltään kokous monipuolinen kulma. SäteetSA 1 , …, SA nnimeltään kylkiluut monitahoinen kulma ja itse litteät kulmatA 1 SA 2 , A 2 SA 3 , …, A n -1 SA n, A n SA 1 – kasvot monipuolinen kulma. Monitahoinen kulma on merkitty kirjaimillaSA 1 … A n, joka osoittaa kärjen ja pisteet sen reunoilla. Pintojen lukumäärästä riippuen monitahoisia kulmia kutsutaan kolmiedrisiksi, tetraedrisiksi, viisiedrisiksi (kuva 2) jne.

Monitahoista kulmaa kutsutaan kupera, jos se on kupera kuvio, ts. sisältää yhdessä minkä tahansa kahden pisteensä kanssa liitoskohdan Jana. Kuvassa 2 kolmio- ja tetraedrikulmat ovat kuperat, mutta viisitahdiset eivät ole.
Harkitse joitain kolmioiden ominaisuuksia ja vastaavia kolmiokulmien ominaisuuksia.
Kiinteistö 1(Kolmioiden epätasa-arvo). Kolmion kumpikin sivu on pienempi kuin kahden muun sivun summa.
Samanlainen ominaisuus kolmikulmaisille kulmille on seuraava ominaisuus.
Kiinteistö 1". Jokainen kolmikulmaisen kulman tasainen kulma on pienempi kuin sen kahden muun litteän kulman summa.
Todiste. Harkitse kolmikulmaista kulmaa SABC . Olkoon suurin sen litteistä kulmista kulma ASC. Sitten eriarvoisuudet

ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .

Epätasa-arvo on siis vielä todistettava ASC< ASB+ BSC.
Laitetaan se reunaan ASC kulma ASD, yhtä kuin ASB , ja kohta B valita niin SB = SD(Kuva 3). Sitten kolmiot ASB Ja ASD ovat yhtä suuret (kahdella sivulla ja niiden välinen kulma) ja siksi AB = AD. Käytetään kolmion epäyhtälöä AC< AB + BC . Vähentäminen molemmista osista AD=AB, saamme epätasa-arvon DC< BC. Kolmioissa DSC Ja BSC yksi puoli yhteinen SC), SD = SB Ja DC< BC. Tässä tapauksessa suurempi kulma on suurempaa sivua vastapäätä ja siksi DSC< BSC . Lisäämällä tämän epätasa-arvon molemmille puolille kulma ASD , yhtä suuri ASB, saamme vaaditun epäyhtälön ASC< ASB+ BSC.

Seuraus 1.Kolmikulmaisen kulman tasokulmien summa on pienempi kuin 360° .
Todiste. Antaa SABC on annettu kolmikulmainen kulma. Tarkastellaan kolmiokulmaa, jossa on kärki A, muodostavat kasvot ABS, ACS ja kulma BAC. Todistetun ominaisuuden perusteella meillä on epätasa-arvo BAC< BAS+ CAS. Samoin kolmikulmaisille kulmille, joissa on kärkipisteitä B Ja KANSSA on epätasa-arvoa: ABS< ABS+ CBS, ACB< ACS+ BCS. Lisätään nämä epäyhtälöt ja otetaan huomioon, että kolmion kulmien summa ABC vastaa 180° , saamme 180 ° < BAS+CAS+ ABS+CBS+BCS+ ACS= 180 ° - ASB+ 180°- BSC+180° - ASC. Siten, ASB + BSC + ASC< 360 ° .
Seuraus 2.Kuperan monitahoisen kulman tasokulmien summa on pienempi kuin 360.
Todistus on samanlainen kuin edellinen.
Seuraus 3.Kolmiokulman dihedraalisten kulmien summa on suurempi kuin 180° .
Todiste. Antaa SABC- kolmikulmainen kulma. Valitaan kohta P sen sisällä ja pudota kohtisuorat siitä PA 1 , PB 1 , PC 1 reunassa (kuva 4).

tasaiset kulmat B 1 PC 1 , A 1 PC 1 , A 1 PB 1 täydentää vastaavia dihedraalisia kulmia rivoilla SA, SB, SC 180 asti° . Siksi näiden dihedraalisten kulmien summa on 540° - ( B 1 PC 1 +A 1 PC 1 + A 1 PB 1 ). Ottaen huomioon, että kolmiokolmikon tasokulmien summa, jossa on kärki P kulma alle 360° , saadaan, että alkuperäisen kolmiokulman kaksikulmaisten kulmien summa on suurempi kuin 180° .
Kiinteistö 2.Kolmion puolittajat leikkaavat yhdessä pisteessä.
Kiinteistö 2". Kolmiokulman kaksitahoisten kulmien puolittaiset tasot leikkaavat yhtä suoraa pitkin.
Todistus on samanlainen kuin lentokoneen tapauksessa. Nimittäin anna SABC- kolmikulmainen kulma. Dihedraalisen kulman puolittaistaso SA on kulman GMT, joka on yhtä kaukana sen pinnasta ASC Ja ASB. Samoin dihedraalisen kulman puolittajataso SB on kulman GMT, joka on yhtä kaukana sen pinnasta BSA Ja BSC . Heidän leikkauslinjansa NIIN on yhtä kaukana kolmikulmaisen kulman kaikista pinnoista ja siksi kaksikulmaisen kulman puolittaistaso kulkee sen läpi SC .
Kiinteistö 3.Kolmion sivujen kohtisuorat puolittajat leikkaavat yhdessä pisteessä.
Kiinteistö 3".Kolmikulmaisen kulman pintojen puolittajien läpi kulkevat ja näihin pintoihin nähden kohtisuorassa olevat tasot leikkaavat yhtä suoraa pitkin.
Todistus on samanlainen kuin edellisen ominaisuuden todistus.
Kiinteistö 4.Kolmion mediaanit leikkaavat yhdessä pisteessä.
Kiinteistö 4".Kolmikulmaisen kulman reunojen läpi kulkevat tasot ja vastakkaisten pintojen puolittajat leikkaavat yhtä suoraa pitkin.
Todiste. Harkitse kolmikulmaista kulmaa SABC, SA = SB = SC(Kuva 5). Sitten puolittajat SA 1 , SB 1 , SC 1 kulmat BSC, ASC, ASB ovat vastaavien kolmioiden mediaanit. Siksi AA 1 , BB 1 , CC 1 - kolmion mediaanit ABC. Antaa O on niiden leikkauspiste. Suoraan NIIN sisältyy kaikkiin kolmeen tarkasteltuun tasoon ja on siksi niiden leikkausviiva.

Kiinteistö 5.Kolmion korkeudet leikkaavat yhdessä pisteessä.
Kiinteistö 5". Tasot, jotka kulkevat kolmikulmaisen kulman reunojen läpi ja ovat kohtisuorassa vastakkaisiin pintoihin nähden, leikkaavat yhtä suoraa pitkin.
Todiste. Tarkastellaan kolmiokulmaa, jossa on kärki S ja kylkiluut a, b, c. Merkitse a 1 , b 1 , c 1 – pintojen leikkausviivat tasojen kanssa, jotka kulkevat vastaavien reunojen läpi ja ovat kohtisuorassa näihin pintoihin nähden (kuva 6). Korjaa kohta C reunalla c ja pudota kohtisuorat siitä CA 1 Ja CB 1 suoraan a 1 ja b 1 . Merkitse A Ja B linjan risteyksiä CA 1 ja CB 1 suoran kanssa a Ja b. Sitten SA 1 on projektio AA 1 partaalle BSC. Koska eKr kohtisuorassa SA 1 , silloin se on kohtisuorassa ja AA 1 . Samoin AC kohtisuorassa BB 1 . Täten, AA 1 ja BB 1 ovat kolmion korkeudet ABC. Antaa O on niiden leikkauspiste. Tasot kulkevat suorien viivojen kautta a Ja a 1 , b Ja b 1 kohtisuorassa tasoon nähden ABC ja siten niiden leikkausviiva NIIN kohtisuorassa ABC. tarkoittaa, NIIN kohtisuorassa AB. Toisella puolella, CO kohtisuorassa AB. Siksi kone kulkee reunan läpi c Ja NIIN on kohtisuorassa vastakkaiselle puolelle.
Ominaisuus 6 (sinilause). Kolmiossa ABC puolueiden kanssa a, b, c vastaavasti meillä on tasa-arvo a : synti A=b: synti B=c: synti C.
Kiinteistö 6". Olkoon a, b, g - kolmikulmaisen kulman tasaiset kulmat, a, b, c ovat niiden vastakkaiset dihedraaliset kulmat. Sitten sin a : synti a= synti b : synti b= sin g : synti c.
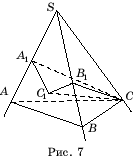
Todiste. Antaa SABC- kolmikulmainen kulma. Pudotus pisteestä C kohtisuorassa CC 1 lentokoneeseen ASB ja kohtisuorassa CA 1 reunalla SA(Kuva 7). Sitten kulma CA 1 C 1 on dihedraalisen kulman lineaarinen kulma a. Siksi CC 1 = CA 1 synti a = SC synti b synti a. Samoin on osoitettu, että CC 1 = CB 1 synti b = SC synti syntiä b. Siksi tasa-arvo synti b synti a = synti a synti b ja siksi tasa-arvosynti a: synti a= sinb : synti b. Samalla tavalla todistamme, että tasa-arvo tekee syntiä b: synti b= sin g : synti c.

Kiinteistö 7.Jos ympyrä voidaan kirjoittaa kuperaan nelikulmioon, niin vastakkaisten sivujen summat ovat yhtä suuret.
Kiinteistö 7". Jos pallo voidaan kirjoittaa kuperaan tetraedrikulmaan, niin vastakkaisten tasokulmien summat ovat yhtä suuret.

Kirjallisuus
1. Hadamard J. Alkeinen geometria. Osa II. Stereometria. – M.: Uchpedgiz, 1938.
2. Perepelkin D.I. Perusgeometrian kurssi. Osa II. Geometria avaruudessa. - M.-L.: Gostekhizdat, 1949.
3. Alkeismatematiikan tietosanakirja. Kirja IV. Geometria. - M.; 1963.
4. Smirnova I.M. Monitahoisten maailmassa. – M.: Enlightenment, 1995.

Dihedraalinen kulma on kuvio, joka muodostuu kahdesta puolitasosta, joita rajoittaa yhteinen suora. Puolitasoja kutsutaan kasvoiksi ja niitä rajoittavaa suoraa kutsutaan dihedraalisen kulman reunaksi.

Kuvassa 142 on dihedraalinen kulma, jonka reuna on a ja kasvot a ja (3.

Taso, joka on kohtisuorassa kaksitahoisen kulman reunaan nähden, leikkaa sen pinnat kahta puoliviivaa pitkin. Näiden puoliviivojen muodostamaa kulmaa kutsutaan dihedraalisen kulman lineaarikulmaksi. Dihedraalisen kulman mitta otetaan vastaavan lineaarikulman mittana. Jos kaksitahoisen kulman reunan a pisteen A kautta piirretään tähän reunaan nähden kohtisuorassa oleva taso y, niin se leikkaa tasot a ja (3 puoliviivoja pitkin (kuva 142); annetun dihedralin lineaarikulma kulma Tämän lineaarisen kulman astemitta on kaksitahoisen kulman astemitta. Dihedraalisen kulman mittaaminen ei riipu lineaarisen kulman valinnasta.

Kolmikulmainen kulma on kuvio, joka koostuu kolmesta litteästä kulmasta (kuva 143). Näitä kulmia kutsutaan kolmikulmaisen kulman pinnoiksi ja niiden sivuja reunoksi. Tasaisten kulmien yhteistä kärkeä kutsutaan kolmikulmaisen kulman kärjeksi. Pintojen ja niiden jatkeiden muodostamia kaksitahoisia kulmia kutsutaan kolmiulotteisen kulman dihedrikulmiksi.

Samoin monitahoisen kulman käsite määritellään litteistä kulmista koostuvaksi kuvioksi (kuva 144). Monitahoisen kulman osalta pintojen, reunojen ja dihedraalisten kulmien käsitteet määritellään samalla tavalla kuin kolmiokulmalle.

Monitahoinen on kappale, jonka pinta koostuu äärellisestä määrästä litteitä polygoneja (kuva 145).

Monitahoista kutsutaan kuperaksi, jos se sijaitsee pinnallaan kunkin polygonin tason toisella puolella (kuva 145, a, b). Tällaisen tason ja kuperan monitahoisen pinnan yhteistä osaa kutsutaan kasvoksi. Kuperan polyhedronin pinnat ovat kuperia polygoneja. Pintojen sivuja kutsutaan monitahoisen reunuksiksi ja huippuja monitahoisen kärjeksi.

Määritelmät. Otetaan useita kulmia (kuva 37): ASB, BSC, CSD, jotka sarjassa vierekkäin sijaitsevat samassa tasossa yhteisen kärjen S ympärillä.

Kierretään kulmatasoa ASB yhteisen puolen SB ympäri siten, että tämä taso muodostaa jonkinlaisen dihedraalisen kulman tason BSC kanssa. Sitten, muuttamatta tuloksena olevaa dihedraalikulmaa, käännämme sitä suoran SC ympäri siten, että BSC-taso muodostaa jonkin verran dihedraalikulmaa CSD-tason kanssa. Jatketaan tätä peräkkäistä kiertoa jokaisen yhteisen puolen ympäri. Jos tässä tapauksessa SF:n viimeinen puoli yhdistetään SA:n ensimmäiseen sivuun, muodostuu kuvio (kuva 38), joka on ns. monitahoinen kulma. Kulmat ASB, BSC,... kutsutaan tasaiset kulmat tai kasvot, niiden sivuja SA, SB, ... kutsutaan kylkiluut, ja yhteinen kärki S- kokous monipuolinen kulma.

Jokainen reuna on myös jonkin dihedraalisen kulman reuna; siksi monitahoisessa kulmassa on yhtä monta dihedraalikulmaa ja yhtä monta tasokulmaa kuin siinä on kaikkia reunoja. Pienin määrä kasvoja monitahoisessa kulmassa on kolme; tätä kulmaa kutsutaan kolmikantainen. Kulmia voi olla nelisivuisia, viisisivuisia jne.

Monitahoinen kulma merkitään joko yhdellä kärkeen sijoitetulla kirjaimella S tai kirjainsarjalla SABCDE, joista ensimmäinen merkitsee kärkeä ja muut reunat siinä järjestyksessä, jossa ne sijaitsevat.

Monitahoista kulmaa kutsutaan kuperaksi, jos se kaikki sijaitsee toisella puolella sen jokaisen pinnan tasoa, joka on rajattomasti pidennetty. Tällainen on esimerkiksi kuvassa 38 esitetty kulma. Päinvastoin, piirustuksen 39 kulmaa ei voida kutsua kuperaksi, koska se sijaitsee ASB-pinnan tai BSC-pinnan molemmilla puolilla.

Jos monitahoisen kulman kaikki pinnat leikkaavat taso, muodostuu monikulmio osaan ( abcde ). Kuperassa monikulmiossa tämä monikulmio on myös kupera.

Otamme huomioon vain kuperat monitahoiset kulmat.

Lause. Kolmikulmaisessa kulmassa kukin tasainen kulma on pienempi kuin kahden muun tasaisen kulman summa.

Olkoon kolmikulmaisessa kulmassa SABC (kuva 40) suurin litteistä kulmista kulma ASC.

Piirretään kulma ASD tähän kulmaan, joka on yhtä suuri kuin kulma ASB, ja piirretään suora AC, joka leikkaa SD jossain pisteessä D. Laitetaan SB = SD. Yhdistämällä B:n A:n ja C:n kanssa saadaan \(\Delta\)ABC, jossa

AD+DC< АВ + ВС.

Kolmiot ASD ja ASB ovat yhteneväisiä, koska ne sisältävät saman kulman yhtäläisten sivujen välillä: joten AD = AB. Siksi, jos hylkäämme johdetun epäyhtälön yhtäläiset termit AD ja AB, saamme tuon DC:n< ВС.

Nyt huomaamme, että kolmioiden SCD ja SCB kaksi sivua on yhtä kuin toisen kaksi sivua, ja kolmannet sivut eivät ole yhtä suuret; tässä tapauksessa suurempi kulma on vastapäätä suurempaa näistä sivuista; tarkoittaa,

∠CSD< ∠ CSВ.

Lisäämällä kulma ASD tämän epäyhtälön vasemmalle puolelle ja kulma ASB, joka on yhtä suuri oikealle puolelle, saadaan epäyhtälö, joka oli todistettava:

∠ASC< ∠ CSB + ∠ ASB.

Olemme osoittaneet, että jopa suurin tasainen kulma on pienempi kuin kahden muun kulman summa. Lause on siis todistettu.

Seuraus. Vähennä kulman ASB tai kulman CSB viimeisen epäyhtälön molemmista osista; saamme:

∠ASC - ∠ASB< ∠ CSB;

∠ASC - ∠CSB< ∠ ASB.

Ottaen huomioon nämä epäyhtälöt oikealta vasemmalle ja ottaen huomioon, että kulma ASC suurimmana kolmesta kulmasta on suurempi kuin kahden muun kulman erotus, päätämme, että kolmikulmaisessa kulmassa jokainen tasokulma on suurempi kuin kahden muun kulman erotus.

Lause. Kuperassa monitahoisessa kulmassa kaikkien tasokulmien summa on pienempi kuin 4d (360°) .

Leikkaamme kuperan kulman SABCDE pinnat (kuva 41) jonkin tason kanssa; tästä osassa saadaan kupera n-gon ABCDE.

Soveltamalla aiemmin todistettua lausetta jokaiseen kolmikulmaiseen kulmaan, jonka kärjet ovat pisteissä A, B, C, D ja E, paholim:

∠ABC< ∠ABS + ∠SВC, ∠BCD < ∠BCS + ∠SCD и т. д.

Lisätään kaikki nämä epäyhtälöt termiltä. Sitten vasemmalla puolella saadaan monikulmion ABCDE kaikkien kulmien summa, joka on yhtä suuri kuin 2 dn - 4d , ja oikealla - kolmioiden ABS, SBC jne. kulmien summa, paitsi ne kulmat, jotka ovat kärjessä S. Merkitään näiden viimeisten kulmien summa kirjaimella X , saamme lisäyksen jälkeen:

2dn - 4d < 2dn - x .

Koska eroissa 2 dn - 4d ja 2 dn - x minuendit ovat samat, niin jotta ensimmäinen ero olisi pienempi kuin toinen, on välttämätöntä, että aliosa 4 d oli enemmän kuin vähennetty X ; tarkoittaa 4 d > X , eli X < 4d .

Yksinkertaisimmat kolmikulmaisten kulmien yhtäläisyyden tapaukset

Lauseet. Kolmikulmaiset kulmat ovat yhtä suuret, jos niillä on:

1) yhtä suurella kaksikulmaisella kulmalla, joka on kahden vastaavasti samansuuruisen ja tasaisin välein olevan tasokulman välissä, tai

2) yhtä tasokulmaa pitkin, joka on kahden vastaavasti samansuuruisen ja tasaisin välimatkan päässä olevan dihedraalisen kulman välissä.

1) Olkoot S ja S 1 kaksi kolmikulmaista kulmaa (kuva 42), joissa ∠ASB = ∠A 1 S 1 B 1 , ∠ASC = ∠A 1 S 1 C 1 (ja nämä yhtä suuret kulmat sijaitsevat tasaisesti) ja dihedraali kulma AS on yhtä suuri kuin dihedraalikulma A 1 S 1 .

Upotetaan kulma S 1 kulmaan S niin, että pisteet S 1 ja S, suorat S 1 A 1 ja SA sekä tasot A 1 S 1 B 1 ja ASB yhtyvät. Sitten reuna S 1 B 1 kulkee SB:tä pitkin (kulmien A 1 S 1 B 1 ja ASB yhtäläisyyden vuoksi), taso A 1 S 1 C 1 kulkee ASC:tä pitkin (dihedraalisten kulmien yhtäläisyyden vuoksi), ja reuna S 1 C 1 kulkee reunaa SC pitkin (kulmien A 1 S 1 C 1 ja ASC yhtäläisyyden vuoksi). Siten kolmikulmaiset kulmat yhdistetään kaikilla niiden reunoilla, ts. he ovat tasa-arvoisia.

2) Toinen kriteeri, kuten ensimmäinen, todistetaan upottamalla.

Symmetriset monitahoiset kulmat

Kuten tiedät, pystykulmat ovat yhtä suuria suorien viivojen tai tasojen muodostamissa kulmissa. Katsotaan pitääkö tämä väite totta monitahoisille kulmille.

Jatketaan (kuva 43) kaikki kulman SABCDE reunat kärjen S yli, sitten muodostuu toinen monitahoinen kulma SA 1 B 1 C 1 D 1 E 1, joka voidaan ns. pystysuora ensimmäisen kulman suhteen. On helppo nähdä, että molemmilla kulmilla on samat taso- ja dihedraaliset kulmat, mutta molemmat ovat käänteisessä järjestyksessä. Todellakin, jos kuvittelemme tarkkailijan, joka katsoo monitahoisen kulman ulkopuolelta sen kärkeen, niin reunat SA, SB, SC, SD, SE näyttävät hänestä olevan vastapäivään, kun hän katsoo kulmaa SA. 1 B 1 C 1 D 1 E 1 , hän näkee reunat SA 1 , SВ 1 , ... sijaitsevat myötäpäivään.

Monitahoisia kulmia, joissa on vastaavasti yhtä suuri taso- ja dihedraalikulma, mutta jotka sijaitsevat päinvastaisessa järjestyksessä, ei voi yhdistää lainkaan upotuksen yhteydessä; eli ne eivät ole tasa-arvoisia. Tällaisia ​​kulmia kutsutaan symmetrinen(suhteessa ylimpään S). Alla käsitellään lisää kuvioiden symmetriasta avaruudessa.

Muut materiaalit

№1 Päivämäärä 5.9.14

Aihe geometria

Luokka 11

Oppitunnin aihe: Monitahoisen kulman käsite. kolmiokulma.

Oppitunnin tavoitteet:

ottaa käyttöön käsitteet: "kolmikulmat", "monitahoiset kulmat", "polyedri";

perehdyttää opiskelijat kolmi- ja monitahokulman elementteihin, monitahoiseen kulmaan sekä kuperan monitahoisen kulman määritelmiin ja monitahoisen kulman litteiden kulmien ominaisuuksiin;

jatkaa työskentelyä tilaesitysten ja tilamielikuvituksen sekä opiskelijoiden loogisen ajattelun kehittämiseksi.

Oppitunnin tyyppi: uuden materiaalin oppiminen

TUTKIEN AIKANA

1. Organisatorinen hetki.

Oppilaiden tervehtiminen, luokan valmiuden tarkistaminen oppitunnille, oppilaiden huomion järjestäminen, oppitunnin yleisten tavoitteiden ja sen suunnitelman paljastaminen.

2. Uusien käsitteiden ja toimintatapojen muodostaminen.

Tehtävät: Varmistaa, että opiskelijat ymmärtävät, ymmärtävät ja muistavat opiskelumateriaalin ulkoa. Varmistaa, että opiskelija hallitsee opitun materiaalin kopiointimenetelmät, edistää omaksuttavien käsitteiden, lakien, sääntöjen ja kaavojen filosofista ymmärtämistä. Selvittää opiskelijoiden opiskelun aineiston oikeellisuus ja tietoisuus, tunnistaa puutteet perusymmärryksessä, suorittaa korjaus. Varmistaa, että opiskelijat korreloivat subjektiivisen kokemuksensa tieteellisen tiedon merkkeihin.

Olkoon kolme sädettä annettuA, b Jas s yhteinen lähtökohtaNOIN (Kuva 1.1). Nämä kolme sädettä eivät välttämättä ole samassa tasossa. Kuvassa 1.2 säteetb JaKanssa makaa lentokoneessaR, sädeA ei makaa tällä tasolla.

SäteetA, b JaKanssa parit määrittelevät kolme tasaista kulmaa, jotka erotetaan kaarilla (Kuva 1.3).

Tarkastellaan kuvaa, joka koostuu kolmesta yllä mainitusta kulmasta ja näiden litteiden kulmien rajaamasta avaruuden osasta. Tätä tilahahmoa kutsutaankolmikulmainen kulma (Kuva 2).

SäteetA, b ja kanssa nimeltäänkolmikulmaisen kulman reunat, ja kulmat: = AOC, = AOB,

= BOC , kolmiokulman rajoittaminen, - senkasvot. Nämä kulmat muodostuvatkolmikantinen pinta. PisteNOIN nimeltäänkolmiokulman kärki. Kolmikulmainen kulma voidaan merkitä seuraavasti: OABC

Tutkittuaan huolellisesti kaikki kuvassa 3 esitetyt monitahoiset kulmat, voimme päätellä, että jokaisella monitahoisella kulmalla on sama määrä reunoja ja pintoja:

4 pintaa ja yksi kärki;

viisisivuisessa kulmassa on 5 reunaa, 5 pintaa ja yksi kärki;

• 
  kuusikulmaisessa kulmassa on 6 reunaa, 6 pintaa ja yksi kärki jne.

Monitahoiset kulmat ovat kupera Ja ei-kupera.

Kuvittele, että otimme neljä sädettä, joilla on yhteinen alkuperä, kuten kuvassa 4. Tässä tapauksessa saimmeei-kupera monitahoinen kulma.

Määritelmä 1. Monitahoista kulmaa kutsutaan kuperaksi kulmaksi,jos hänsijaitsee kunkin sen pinnan tason toisella puolella.

Toisin sanoen kupera monitahoinen kulma voidaan aina sijoittaa millä tahansa pinnallaan johonkin tasoon. Voit nähdä, että kuvan 4 tapauksessa tämä ei aina ole mahdollista. Kuvassa 4 esitetty tetraedrikulma on ei-kupera.

Huomaa, että jos sanomme opetusohjelmassamme "monitahoinen kulma", tarkoitamme, että se on kupera. Jos tarkasteltu monitahoinen kulma on ei-kupera, tästä keskustellaan erikseen.

Monitahoisen kulman tasokulmien ominaisuudet

Lause 1.Jokainen kolmikulmaisen kulman tasainen kulma on pienempi kuin kahden muun tasaisen kulman summa.

Lause 2.Kuperan monitahoisen kulman kaikkien tasokulmien arvojen summa on pienempi kuin 360°.

3. Sovellus. Taitojen ja kykyjen muodostuminen.

Tavoitteet: Varmistaa, että opiskelijat soveltavat SW:ssä tarvitsemiaan tietoja ja toimintatapoja, luoda edellytykset opiskelijoille tunnistaa yksilöllisiä tapoja soveltaa oppimaansa.

6. Lavatiedot kotitehtävistä.

Tavoitteet: Varmistaa, että opiskelijat ymmärtävät läksyjen tarkoituksen, sisällön ja menetelmät.

§ 1(1.1, 1.2) s. 4, nro 9.

7. Oppitunnin yhteenveto.

Tavoite: Antaa laadullinen arvio luokan ja yksittäisten opiskelijoiden työstä.

8. Heijastusvaihe.

Tehtävät: Aloita opiskelijoiden reflektio toiminnan itsearviointiin. Varmistaa, että opiskelijat oppivat itsesääntelyn ja yhteistyön periaatteet.

Keskustelu aiheesta:

Mitä mielenkiintoista pidit oppitunnilla?

Mikä on epäselvää?

Mihin opettajan tulee kiinnittää huomiota seuraavalla oppitunnilla?

Miten arvioisit työsi luokassa?