Tujuan Pelajaran:

Untuk membentuk pengetahuan, keterampilan, dan kemampuan penerapan yang efektif dari metode interval umum, berdasarkan sifat fungsi kontinu;

Merumuskan algoritme tindakan yang mengarah ke transformasi yang setara;

Ajari diri Anda untuk menerapkannya saat memecahkan ketidaksetaraan;

Untuk melakukan transfer pengetahuan, keterampilan, dan kemampuan ke kondisi baru.

Pendidikan: sistematisasi, konsolidasi, generalisasi pengetahuan, keterampilan dan kemampuan.

Pendidikan: pendidikan tentang perlunya argumentasi, akurasi, kemandirian yang konsisten.

Mengembangkan: pengembangan logika matematika, pembentukan gaya berpikir matematis (pembedahan yang jelas dari jalannya penalaran), minat kognitif.

1) Pendahuluan, menetapkan tujuan dan sasaran pelajaran - 2 menit.

2) Memeriksa pekerjaan rumah - 2 menit. (kerja frontal, pengendalian diri).

3) Pembuktian matematis dari tahapan pemecahan pertidaksamaan dengan metode interval - 4 menit (jawaban siswa disiapkan).

4) Pengulangan sifat-sifat pertidaksamaan - 2 menit.

5) Persiapan asimilasi (studi) materi pendidikan baru melalui pengulangan dan pemutakhiran pengetahuan dasar - 5 menit. (pekerjaan frontal, jawaban atas pertanyaan, situasi masalah).

6) Metode interval umum untuk menyelesaikan pertidaksamaan, pemahaman awal - 13 menit. (solusi kolektif ketidaksetaraan dengan metode interval: di papan tulis dan di buku catatan).

7) Informasi tentang pekerjaan rumah, instruksi untuk melakukannya - 1 menit.

8) Konsolidasi pengetahuan baru - 15 menit. (pekerjaan independen - opsi 1).

9) Menyimpulkan pelajaran, refleksi - 1 menit.

1) Pendahuluan, menetapkan tujuan dan sasaran pelajaran. (cerita guru)

1) Perlunya penerapan yang lebih luas dari metode interval di sekolah ditentukan oleh ideologi seluruh proses pengajaran matematika. Intinya adalah bahwa garis fungsional (salah satu yang utama dalam studi dasar-dasar matematika) menerima dukungan teknologi yang kuat. Metode interval didasarkan pada karakteristik penting ketergantungan fungsional seperti nol dari suatu fungsi, interval dari tanda konstan dan monotonisitasnya. Kemudian asal fungsional persamaan dan pertidaksamaan, serta metode penyelesaiannya, menjadi lebih jelas. Kategori-kategori kontinuitas suatu fungsi, perilaku grafiknya di sekitar titik-titik diskontinuitas tak hingga, teorema-teorema pada akar, keteguhan tanda, titik-titik ekstrem dan tipe-tipenya menjadi lebih visual. Dan semua ini secara organik terhubung menjadi satu kesatuan fungsional.

Di sisi lain, geometrisasi objek studi yang digunakan juga sangat berharga, yaitu. visual, kiasan menyajikan semua alat matematika yang digunakan ketergantungan fungsional.

Prinsip dasar yang mendasari metode interval:

• pendekatan fungsional (umum);
• ketergantungan pada geometrisasi sifat fungsional;
• visualisasi penelitian.

Ini mengarah pada keunggulan metode berikut dibandingkan dengan metode lain yang digunakan dalam jenis tugas yang sama: kesederhanaan dan kecepatan mencapai tujuan; visibilitas (dan kemampuan untuk mengontrol atau memeriksa ulang); ekonomi dalam sumber daya komputasi dan waktu; luasnya cakupan seluruh situasi, pembentukan dan pengembangan keterampilan berpikir dan analisis umum, serta keterampilan yang terkait dengan ini untuk menarik kesimpulan logis.

2) Memeriksa pekerjaan rumah.(Slide nomor 4)

3) Sebuah cerita tentang metode interval untuk memecahkan ketidaksetaraan. (Jawaban siswa).

Pembuktian matematis dari solusi pertidaksamaan dengan metode interval.

1) Pertimbangkan pertidaksamaan: (x-2)(x-3)>0. (slide nomor 5)

Anda dapat menyelesaikannya seperti ini: Produk (hasil bagi) dari dua faktor adalah positif jika dan hanya jika kedua faktor memiliki tanda yang sama, yaitu. ketimpangan setara dengan kombinasi dua sistem: (slide nomor 6)

Dari sistem pertama kita mendapatkan x >3, dari sistem kedua x< 2.

Solusinya adalah gabungan dari solusi dari dua sistem.

Menjawab:

Metode grafik (nomor slide 7)

Metode lain adalah metode interval(slide nomor 8).

Idenya adalah sebagai berikut.

Pada garis nyata, tandai nol (akar) dari polinomial (x-2)(x-3) berdiri

di sisi kiri pertidaksamaan, mis. nomor 2 dan 3.

Ketika x >3 (di sebelah kanan akar yang lebih besar), maka (x-2)(x-3)>0, karena setiap faktor positif.

Jika Anda bergerak sepanjang sumbu dalam arah negatif, maka ketika Anda melewati titik x=3, faktor (x-3) akan berubah tanda. Pada perkalian (x-2) (x-3) akan muncul satu faktor negatif, akibatnya (x-2) (x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

Sekarang mudah untuk menuliskan solusi pertidaksamaan:

Kesimpulan: produk dapat berubah tanda hanya jika melewati titik x=2 dan x=3

dan, oleh karena itu, mempertahankan tanda pada setiap interval yang diperoleh.

Dalam contoh sederhana ini, mudah untuk memahami ide metode interval, tetapi tidak menunjukkan keuntungan yang nyata.

Rasionalitas metode interval, kekuatannya, kami akan mempertimbangkan contoh berikut (slide No. 9, 10,11, 12))

2) Selesaikan pertidaksamaan (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) (x-10)>0.

Untuk menyelesaikan pertidaksamaan ini dengan menggunakan sekumpulan sistem, kita harus mempertimbangkan sekumpulan 512 sistem dengan 10 pertidaksamaan di setiap sistem.

Mari kita gunakan metode interval. Kami menandai nol dari polinomial pada garis nyata. Pada interval x>10, polinomial akan positif, karena setiap faktor positif. Ketika melewati setiap akar berikutnya, polinomial akan berubah tanda, karena faktor negatif tambahan akan muncul dalam produk. Sekarang mudah untuk menulis solusi pertidaksamaan menggunakan pergantian tanda.

Keuntungan dari metode interval.

• kesederhanaan dan kecepatan mencapai tujuan;
• visibilitas (dan kemampuan untuk mengontrol atau memeriksa ulang);
• pengurangan yang signifikan dalam jumlah pekerjaan komputasi dan waktu;
• luasnya cakupan seluruh situasi;
• pembentukan dan pengembangan keterampilan berpikir dan analisis secara umum, serta keterampilan terkait untuk menarik kesimpulan yang logis.

Komentar. Sangat mudah untuk menyelesaikan ketidaksetaraan, yang sisi kirinya difaktorkan, karena tidak sulit untuk menemukan nol (akar).

Tugas: Selesaikan pertidaksamaan menggunakan metode interval (x+3) 3 (x-4) 2 (x-5)>0(Slide 13)

4) Pengulangan sifat-sifat pertidaksamaan.

a) Pertanyaan: Pertidaksamaan apa yang disebut ekuivalen?

(Dua pertidaksamaan disebut ekuivalen jika solusi apa pun untuk pertidaksamaan pertama adalah solusi untuk pertidaksamaan kedua dan, sebaliknya, solusi apa pun untuk pertidaksamaan kedua adalah solusi untuk yang pertama).

Atau: dua pertidaksamaan dikatakan ekuivalen jika himpunan penyelesaiannya sama.

Slide 14. Pengulangan sifat-sifat pertidaksamaan.

Slide 15. Jawab pertanyaan dan jelaskan.

Apakah ketidaksetaraan sama?

1) 4x-5<0 и 4х<5

2) -2x+5>0 dan 2x-5<0

3) -3x 2 +5x-7>0 dan 3x 2 -5x+7<0

4) (x+1)>0 dan (x 2 +5x+10)(x+1)>0

5) Karya frontal lisan dalam persiapan asimilasi (studi) materi pendidikan baru melalui pengulangan dan pemutakhiran pengetahuan dasar.

Slide 16. Definisi fungsi kontinu di suatu titik.

Slide 17. Properti fungsi kontinu.

Slide 18. Temukan kesenjangan kontinuitas.

Slide 19. Temukan kesalahannya.

Slide 20. Selesaikan pertidaksamaan secara lisan,
menggunakan grafik.

Slide 21, 22. Mengganti pertidaksamaan dengan kondisi ekuivalen.

Selesaikan pertidaksamaan

Pertidaksamaan ini ekuivalen dengan kondisi f(x) < 0 menghitung

Oleh karena itu, kita perlu mencari semua nilai x yang kondisinya f(x) < 0.

6) Metode interval umum untuk menyelesaikan pertidaksamaan, pemahaman awal - 10 menit. (solusi kolektif ketidaksetaraan dengan metode interval: di papan tulis dan di buku catatan).

geser 23. Algoritma. Metode umum untuk memecahkan ketidaksetaraan.

Solusi pertidaksamaan f(x)>0, f(x) > 0, f(x)<0, f(x)< 0 dengan metode interval. (Skema)

Slide 24 dan 25. Memecahkan pertidaksamaan dengan algoritma. (Komentar untuk semua poin dari algoritma).

geser 26. Ilustrasi grafis dari solusi ketidaksetaraan ini.

Slide 27. Selesaikan pertidaksamaan di papan tulis dan di buku catatan .

Slide 28. Ilustrasi grafis dari solusi pertidaksamaan ini.

Slide 29. Selesaikan pertidaksamaan di papan tulis dan di buku catatan

Slide 30. Ilustrasi grafis dari solusi pertidaksamaan ini.

Slide 31, 32. Selesaikan pertidaksamaan secara lisan, sesuai gambar

7) Informasi tentang pekerjaan rumah.(Pecahkan dengan metode interval pilihan nomor 2)

8) Konsolidasi pengetahuan baru (pekerjaan mandiri, opsi No. 1).

9) Menyimpulkan pelajaran, pengendalian diri pada solusi yang sudah jadi (slide 33, 34, 35), pengulangan algoritma metode interval umum dan penerapannya.

10) Analisis asimilasi materi dan minat siswa terhadap topik. Metode ini bersifat universal dalam menyelesaikan pertidaksamaan apa pun, termasuk rasional, modulo, irasional, eksponensial, logaritma, karena metode interval mereduksi solusi pertidaksamaan menjadi penyelesaian persamaan, mencari domain dan nilai fungsi pada suatu titik tidak menyebabkan kesulitan. Tetapi saya harus memberikan contoh ketidaksetaraan di mana penggunaan metode ini tidak dibenarkan, di mana lebih rasional untuk menerapkan metode lain untuk menyelesaikan ketidaksetaraan.

Presentasi “Penerapan kontinuitas dalam penyelesaian pertidaksamaan”. (35 slide)

Definisi 4. Suatu fungsi disebut kontinu pada segmen jika kontinu di setiap titik segmen ini (di titik a kontinu di sebelah kanan, yaitu, dan di titik b kontinu di sebelah kiri, yaitu).

Semua fungsi dasar dasar kontinu dalam domain definisinya.

Sifat-sifat fungsi kontinu pada segmen:

• 1) Jika suatu fungsi kontinu pada suatu segmen, maka fungsi tersebut terbatas pada segmen ini (teorema Weierstrass pertama).
• 2) Jika suatu fungsi kontinu pada suatu segmen, maka pada segmen ini fungsi tersebut mencapai nilai minimum dan nilai maksimumnya (teorema Weierstrass kedua) (lihat Gambar 2).
• 3) Jika suatu fungsi kontinu pada suatu segmen dan mengambil nilai dari tanda yang berbeda pada ujung-ujungnya, maka setidaknya ada satu titik di dalam segmen sedemikian rupa sehingga (teorema Bolzano-Cauchy).

Breakpoint fungsi dan klasifikasinya

segmen titik kontinuitas fungsi

Titik-titik di mana kondisi kontinuitas tidak terpenuhi disebut titik diskontinuitas fungsi ini. Jika adalah titik diskontinuitas suatu fungsi, maka setidaknya salah satu dari tiga kondisi kontinuitas fungsi yang ditentukan dalam Definisi 1, 2 tidak terpenuhi di dalamnya, yaitu:

1) Fungsi didefinisikan di sekitar titik, tetapi tidak didefinisikan pada titik itu sendiri. Jadi fungsi yang dipertimbangkan dalam contoh 2 a) memiliki jeda pada suatu titik, karena tidak didefinisikan pada titik ini.

2) Fungsi didefinisikan pada suatu titik dan lingkungannya, ada batas satu sisi dan, tetapi mereka tidak sama satu sama lain: . Misalnya, fungsi dari contoh 2 b) didefinisikan pada suatu titik dan lingkungannya, tetapi, karena, a.

3) Fungsi didefinisikan di titik dan sekitarnya, ada batas satu sisi dan, mereka sama satu sama lain, tetapi tidak sama dengan nilai fungsi di titik: . Misalnya, fungsi. Berikut adalah break point: pada titik ini fungsi didefinisikan, ada batas satu sisi dan sama satu sama lain, tetapi, yaitu .

Fungsi breakpoint diklasifikasikan sebagai berikut.

Definisi 5. Suatu titik disebut titik diskontinuitas jenis pertama dari suatu fungsi jika ada batas-batas yang terbatas dan pada titik ini, tetapi mereka tidak sama satu sama lain: . Besaran tersebut kemudian disebut loncatan fungsi di titik tersebut.

Definisi 6 . Suatu titik disebut titik diskontinuitas yang dapat dilepas dari suatu fungsi jika pada titik ini ada batas yang terbatas dan, mereka sama satu sama lain: , tetapi fungsi itu sendiri tidak terdefinisi pada titik tersebut, atau terdefinisi, tetapi.

Definisi 7. Suatu titik disebut titik diskontinuitas fungsi jenis kedua jika pada titik ini paling sedikit salah satu batas satu sisi (atau) tidak ada atau sama dengan tak hingga.

Contoh 3. Temukan break point dari fungsi berikut dan tentukan jenisnya: a) b)

Keputusan. a) Fungsi didefinisikan dan kontinu pada interval u, karena pada setiap interval ini diberikan oleh fungsi dasar kontinu. Oleh karena itu, titik putus fungsi yang diberikan hanya dapat berupa titik di mana fungsi tersebut mengubah tugas analitiknya, mis. poin i. Mari kita cari batas satu sisi dari fungsi di titik:

Karena batas satu sisi ada dan terbatas, tetapi tidak sama satu sama lain, titik tersebut adalah titik diskontinuitas jenis pertama. Lompatan fungsi:

Untuk titik yang kita temukan.

Kontinuitas suatu fungsi pada suatu interval

Nama parameter	Berarti
Subjek artikel:	Kontinuitas suatu fungsi pada suatu interval
Rubrik (kategori tematik)	Matematika

Definisi. Suatu fungsi disebut kontinu pada suatu interval jika fungsi tersebut kontinu di setiap titik interval ini.

Jika fungsi didefinisikan untuk X=sebuah dan dimana f(X) = f(sebuah),

lalu mereka mengatakan itu f(X) pada intinya dan terus menerus di sebelah kanan. Demikian pula, jika f(X) = f(b), maka kita mengatakan bahwa pada titik b fungsi ini kiri terus menerus.

Definisi. Fungsi tersebut biasanya disebut kontinu pada interval [ sebuah, b], jika kontinu pada setiap titiknya (pada titik sebuah kontinu di sebelah kanan, pada suatu titik b kontinu di sebelah kiri).

nilai tertinggi fungsi pada = f(x) pada segmen [ sebuah, b f(x 1) itu f(x) £ f(x 1) untuk semua orang X Î [ sebuah, b].

Nilai terendah fungsi pada = f(x) pada segmen [ sebuah, b] adalah kebiasaan untuk menyebut seperti itu nilainya f(x 2) itu f(x) ³ f(x 2) untuk semua orang X Î [ sebuah, b].

Fungsi yang kontinu pada suatu interval memiliki sejumlah sifat penting, yang dinyatakan oleh teorema berikut.

Teorema 3.3.1. Sebuah fungsi kontinu pada segmen [ sebuah, b], mencapai nilai minimumnya m dan nilai terbesar M, yaitu, ada poin seperti itu x 1 dan x 2 dari segmen ini, yang f(x 1) = m, f(x 2) = M.

Teorema ini memiliki arti geometris sederhana (lihat Gambar 2).

Teorema 3.3.2. Jika fungsinya pada = f(x) kontinu pada selang [ sebuah, b] dan mengambil nilai yang tidak sama pada ujungnya f(sebuah) = A, f(b) = B, A B, maka berapapun bilangan C antara A dan B ada titik dengan Î [ sebuah, b] seperti yang f(dengan) = C

Arti geometris dari teorema diilustrasikan pada Gambar.3. Garis lurus apa saja pada= C, dimana A< C < B (или A >C > B), memotong grafik fungsi pada = f(x).

Konsekuensi. Jika fungsi kontinu pada suatu segmen dan mengambil nilai dari tanda yang berbeda pada ujungnya, maka setidaknya ada satu titik pada segmen ini di mana fungsi tersebut hilang.

Arti geometris dari konsekuensi diilustrasikan pada Gbr.4.

Pertanyaan untuk pengendalian diri

1. Fungsi apa yang disebut kontinu di suatu titik?

2. Berikan satu lagi definisi ekuivalen melalui peningkatan fungsi dan argumen.

3. Apa yang dapat dikatakan tentang jumlah, selisih, hasil kali, dan hasil bagi dua fungsi kontinu?

4. Untuk nilai argumen apa seluruh fungsi rasional dan pecahan-rasional kontinu?

5. Kapan suatu fungsi kompleks kontinu di suatu titik?

6. Apa yang biasa disebut titik putus fungsi?

7. Titik apa yang disebut titik diskontinuitas jenis pertama?

8. Nilai apa yang biasa disebut fungsi lompat?

9. Jelaskan konsep "titik putus yang dapat dilepas". Berikan contoh.

10. Titik apa yang disebut titik diskontinuitas jenis kedua? Berikan contoh.

11. Jelaskan konsep: ""kontinuitas pada interval"", ""kontinuitas di sebelah kanan"", ""kontinuitas di sebelah kiri"", ""kontinuitas pada segmen"".

12. Tentukan nilai fungsi terbesar dan terkecil.

13. Merumuskan teorema tentang hubungan kontinuitas pada suatu ruas dengan nilai fungsi terbesar dan terkecil. Jelaskan dengan gambar.

14. Merumuskan teorema tentang hubungan antara kontinuitas fungsi pada suatu ruas dengan ruas nilai fungsi. Ilustrasikan makna geometrisnya pada gambar.

15. Berikan konsekuensi dari teorema di atas dan interpretasi geometrisnya.

KULIAH 4

Topik kuliah: turunan fungsi

Rencana kuliah: Konsep turunan, makna geometris dan fisiknya. Aturan dasar diferensiasi. Turunan dari fungsi kompleks. Beberapa aplikasi turunan.

4.1. Konsep turunan, makna geometris dan fisiknya

Pertimbangkan fungsinya pada = f(x) ditentukan dalam interval ] sebuah, b[. Biarlah XÎ ] sebuah, b[ dan X Î ] sebuah, b[, maka fungsi bertambah pada titik X 0 dinyatakan dengan rumus D pada = f(x 0+D X) – f(x 0).

Definisi. Turunan dari fungsi y = f(x) pada intinya X 0 biasanya disebut batas rasio kenaikan fungsi ini terhadap kenaikan argumen ketika yang terakhir cenderung nol:

f'(x 0) = atau y"(x 0) =.

Arti geometris dari turunan: turunan fungsi ini di suatu titik sama dengan garis singgung sudut antara sumbu Ox dan garis singgung grafik fungsi ini pada titik yang bersesuaian (lihat Gambar 1):

f"(x 0) = tan a.

Definisi. Jika fungsi f(x) didefinisikan pada interval [ a, b], kontinu di setiap titik interval ( a, b), pada titik sebuah kontinu di sebelah kanan, pada suatu titik b kontinu di sebelah kiri, maka kita mengatakan bahwa fungsi f(x) kontinu pada segmen [a, b].

Dengan kata lain, fungsi f(x) kontinu pada selang [ a, b] jika tiga kondisi terpenuhi:

1) "x 0 Î( a, b): f(x) = f(x 0);

2) f(x) = f(sebuah);

3) f(x) = f(b).

Untuk fungsi yang kontinu pada suatu interval, kami mempertimbangkan beberapa properti, yang kami rumuskan dalam bentuk teorema berikut tanpa bukti.

Teorema 1. Jika fungsi f(x) kontinu pada selang [ a, b], kemudian mencapai nilai terkecil dan terbesarnya pada segmen ini.

Teorema ini menyatakan (Gbr. 1.15) bahwa pada interval [ a, b] ada titik seperti itu x 1 itu f(x 1) £ f(x) untuk apa saja x dari [ a, b] dan bahwa ada benarnya x 2 (x 2 [ a, b]) seperti yang " xÎ[ a, b] (f(x 2) f(x)).

Berarti f(x 1) adalah yang terbesar untuk fungsi yang diberikan pada [ a, b], sebuah f(x 2) - yang terkecil. Menunjukkan: f(x 1) = M, f(x 2) =m. Sejak f(x) pertidaksamaan berikut berlaku: " xÎ[ a, b] m£ f(x) £ M, maka kita memperoleh akibat wajar berikut dari Teorema 1.

Konsekuensi. Jika fungsi f(x) kontinu pada suatu segmen, maka dibatasi pada segmen ini.

Teorema 2. Jika fungsi f(x) kontinu pada selang [ a, b] dan mengambil nilai tanda yang berbeda di ujung segmen, maka ada titik interior x 0 segmen [ a, b], di mana fungsi berubah menjadi 0, mis. $ x 0 Î ( a, b) (f(x 0) = 0).

Teorema ini menyatakan bahwa grafik fungsi y=f(x), kontinu pada segmen [ a, b], melintasi sumbu Sapi setidaknya sekali jika nilainya f(sebuah) dan f(b) memiliki tanda yang berlawanan. Jadi, (Gbr. 1.16) f(sebuah) > 0, f(b) < 0 и функция f(x) menghilang di titik x 1 , x 2 , x 3 .

Teorema 3. Biarkan fungsinya f(x) kontinu pada selang [ a, b], f(sebuah) = A, f(b) = B dan A¹ B. (Gbr. 1.17). Kemudian untuk nomor berapa pun C, menyimpulkan antara angka A dan B, ada titik interior seperti itu x 0 segmen [ a, b], Apa f(x 0) = C.

Konsekuensi. Jika fungsi f(x) kontinu pada selang [ a, b], m- nilai terkecil f(x), M- nilai terbesar dari fungsi f(x) pada segmen [ a, b], maka fungsi tersebut mengambil (setidaknya sekali) nilai apa pun m di antara m dan M, dan oleh karena itu segmen [ m, M] adalah himpunan semua nilai fungsi f(x) pada segmen [ a, b].

Perhatikan bahwa jika fungsi kontinu pada interval ( a, b) atau memiliki interval [ a, b] dari titik diskontinuitas, maka Teorema 1, 2, 3 tidak lagi benar untuk fungsi tersebut.

Sebagai kesimpulan, pertimbangkan teorema tentang keberadaan fungsi terbalik.

Ingatlah bahwa interval adalah segmen, interval, atau setengah interval terbatas atau tak terbatas.

Teorema 4. Biarlah f(x) kontinu pada interval X, bertambah (atau berkurang) sebesar X dan memiliki rentang nilai kamu. Kemudian untuk fungsi y=f(x) ada fungsi terbalik x= j(kamu) ditentukan pada interval kamu, terus menerus dan meningkat (atau menurun) pada kamu dengan banyak arti X.

Komentar. Biarkan fungsinya x= j(kamu) adalah kebalikan dari fungsi f(x). Karena argumen biasanya dilambangkan dengan x, dan fungsi melalui kamu, maka kita tulis fungsi inversnya sebagai y=j(x).

Contoh 1. Fungsi y=x 2 (Gbr. 1.8, a) di set X= jika kontinu di semua titik internal segmen ini, dan di ujungnya, mis. di titik-titik sebuah dan b, berturut-turut kontinu di kanan dan kiri.

Teorema 1. Sebuah fungsi kontinu pada segmen [ sebuah, b], setidaknya pada satu titik segmen ini mengambil nilai terbesar dan setidaknya pada satu titik - terkecil.

Teorema menyatakan bahwa jika fungsi y = f(x) kontinu pada segmen [ sebuah, b], maka setidaknya ada satu titik x 1 Î [ sebuah, b] sehingga nilai fungsi f(x) pada titik ini akan menjadi yang terbesar dari semua nilainya di segmen ini: f(x1) f(x). Demikian pula, ada poin seperti itu x2, di mana nilai fungsi akan menjadi yang terkecil dari semua nilai pada segmen: f(x 1) f(x).

Jelas bahwa mungkin ada beberapa titik seperti itu, misalnya, gambar menunjukkan bahwa fungsi f(x) mengambil nilai terkecil di dua titik x2 dan x 2 ".

Komentar. Pernyataan teorema dapat menjadi salah jika kita mempertimbangkan nilai fungsi pada interval ( sebuah, b). Memang, jika kita mempertimbangkan fungsinya y=x pada (0, 2), maka kontinu pada interval ini, tetapi tidak mencapai nilai maksimum atau minimum di dalamnya: ia mencapai nilai-nilai ini di ujung interval, tetapi ujungnya bukan milik kita wilayah.

Juga, teorema tidak lagi benar untuk fungsi diskontinu. Berikan contoh.

Konsekuensi. Jika fungsi f(x) terus menerus pada [ sebuah, b], maka dibatasi pada interval ini.

Teorema 2. Biarkan fungsinya y = f(x) kontinu pada interval [ sebuah, b] dan mengambil nilai tanda yang berbeda di ujung segmen ini, maka setidaknya ada satu titik di dalam segmen x=C, di mana fungsi menghilang: f(C)= 0, dimana< C< b

Teorema ini memiliki arti geometris sederhana: jika titik-titik dari grafik fungsi kontinu y = f(x), sesuai dengan ujung segmen [ sebuah, b] terletak pada sisi yang berlawanan dari sumbu Sapi, maka grafik ini setidaknya pada satu titik segmen memotong sumbu Sapi. Fungsi terputus mungkin tidak memiliki properti ini.

Teorema ini mengakui generalisasi berikut.

Teorema 3 (teorema tentang nilai-nilai antara). Biarkan fungsinya y = f(x) kontinu pada interval [ sebuah, b] dan f(a) = A, f(b) = B. Kemudian untuk nomor berapa pun C di antara A dan B, ada titik seperti itu di dalam segmen ini CÎ [ sebuah, b], Apa f(c) = C.

Teorema ini secara geometris jelas. Perhatikan grafik fungsi y = f(x). Biarlah f(a) = A, f(b) = B. Lalu garis apa saja y=C, di mana C- nomor berapa pun di antara A dan B, memotong grafik fungsi setidaknya di satu titik. Absis titik potong akan menjadi nilai itu x=C, di mana f(c) = C.

Dengan demikian, fungsi kontinu, yang berpindah dari satu nilainya ke nilai lainnya, tentu melewati semua nilai antara. Secara khusus:

Konsekuensi. Jika fungsi y = f(x) kontinu pada beberapa interval dan mengambil nilai terbesar dan terkecil, maka pada interval ini dibutuhkan, setidaknya sekali, nilai apa pun antara nilai terkecil dan terbesarnya.

DERIVATIF DAN APLIKASINYA. DEFINISI DERIVATIF

Mari kita memiliki beberapa fungsi y=f(x), didefinisikan pada beberapa interval. Untuk setiap nilai argumen x dari interval ini fungsi y=f(x) memiliki arti tertentu.

Pertimbangkan dua nilai argumen: inisial x 0 dan baru x.

Perbedaan x–x 0 disebut kenaikan argumen x pada intinya x 0 dan dilambangkan x. Dengan demikian, x = x – x 0 (kenaikan argumen bisa positif atau negatif). Dari persamaan ini dapat disimpulkan bahwa x=x 0 +Δx, yaitu nilai awal variabel telah menerima beberapa kenaikan. Kemudian, jika pada intinya x 0 nilai fungsi tadi f(x 0 ), kemudian di titik baru x fungsi akan mengambil nilai f(x) = f(x 0 +∆x).

Perbedaan Y y 0 = f(x) – f(x 0 ) ditelepon peningkatan fungsi y = f(x) pada intinya x 0 dan dilambangkan dengan simbol y. Dengan demikian,

y = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Biasanya nilai awal argumen x 0 dianggap tetap dan nilai baru x- variabel. Kemudian kamu 0 = f(x 0 ) ternyata konstan dan y = f(x)- variabel. kenaikan y dan x juga akan menjadi variabel dan rumus (1) menunjukkan bahwa hari adalah fungsi dari variabel x.

Tulis rasio kenaikan fungsi dengan kenaikan argumen

Mari kita cari limit dari relasi ini di x→0. Jika limit ini ada, maka disebut turunan dari fungsi ini. f(x) pada intinya x 0 dan menunjukkan f "(x 0). Jadi,

turunan fungsi ini y = f(x) pada intinya x 0 disebut limit dari rasio kenaikan fungsi kamu dengan kenaikan argumen x ketika yang terakhir secara sewenang-wenang cenderung nol.

Perhatikan bahwa untuk fungsi yang sama turunan pada titik yang berbeda x dapat mengambil nilai yang berbeda, yaitu turunan dapat dianggap sebagai fungsi dari argumen x. Fungsi ini dilambangkan f "(x)

Turunan dilambangkan dengan simbol f "(x), y", . Nilai spesifik dari turunan di x = dilambangkan f "(sebuah) atau kamu "| x=a.

Operasi mencari turunan dari suatu fungsi f(x) disebut diferensiasi fungsi ini.

Untuk langsung menemukan turunan menurut definisi, Anda dapat menerapkan yang berikut ini aturan praktis:

Contoh.

MAKNA MEKANIK DARI TURUNAN

Diketahui dari fisika bahwa hukum gerak beraturan memiliki bentuk s = v t, di mana s- jalur yang ditempuh hingga titik waktu t, v adalah kecepatan gerak seragam.

Namun, sejak sebagian besar gerakan yang terjadi di alam tidak merata, maka dalam kasus umum, kecepatan, dan, akibatnya, jarak s akan tergantung pada waktu t, yaitu akan menjadi fungsi waktu.

Jadi, biarkan titik material bergerak dalam garis lurus dalam satu arah sesuai dengan hukum s=s(t).

Catat momen dalam waktu t 0 . Pada titik ini, titik telah melewati jalan s=s(t 0 ). Mari kita tentukan kecepatannya v titik materi pada waktu t 0 .

Untuk melakukan ini, pertimbangkan beberapa saat lain waktu t 0 + Δ t. Ini sesuai dengan jarak yang ditempuh s =s(t 0 + Δ t). Maka untuk selang waktu t titik telah menempuh lintasan s =s(t 0 + Δ t)–s(t).

Mari kita pertimbangkan hubungannya. Ini disebut kecepatan rata-rata dalam selang waktu t. Kecepatan rata-rata tidak dapat secara akurat mengkarakterisasi kecepatan pergerakan suatu titik pada saat ini t 0 (karena gerakannya tidak merata). Untuk lebih akurat mengungkapkan kecepatan sebenarnya ini menggunakan kecepatan rata-rata, Anda perlu mengambil interval waktu yang lebih kecil t.

Jadi, kecepatan gerakan pada waktu tertentu t 0 (kecepatan sesaat) adalah batas kecepatan rata-rata dalam selang waktu dari t 0 sampai t 0 +Δ t kapan t→0:

,

itu. kecepatan gerakan tidak rata adalah turunan dari jarak yang ditempuh terhadap waktu.

MAKNA GEOMETRI TURUNAN

Mari kita pertama memperkenalkan definisi garis singgung kurva pada titik tertentu.

Biarkan kita memiliki kurva dan titik tetap di atasnya M 0(lihat gambar). Pertimbangkan hal lain M kurva ini dan menggambar garis potong M 0 M. Jika titik M mulai bergerak sepanjang kurva, dan titik M 0 tetap diam, garis potong berubah posisinya. Jika, dengan pendekatan tak terbatas dari titik M kurva ke titik M 0 di sisi mana pun, garis potong cenderung mengambil posisi garis lurus tertentu M 0 T, maka garis lurus M 0 T disebut garis singgung kurva di titik tertentu M 0.

Itu., garis singgung ke kurva di titik tertentu M 0 disebut posisi batas garis potong M 0 M kapan intinya M cenderung sepanjang kurva ke suatu titik M 0.

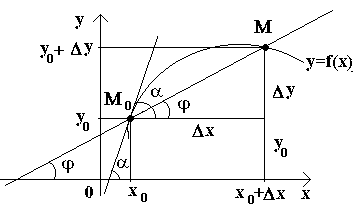
Pertimbangkan sekarang fungsi kontinu y=f(x) dan kurva yang sesuai dengan fungsi ini. Untuk beberapa nilai X 0 fungsi mengambil nilai y0=f(x0). Nilai-nilai ini x 0 dan kamu 0 pada kurva sesuai dengan titik M 0 (x 0; y 0). Mari berargumentasi x0 kenaikan X. Nilai baru dari argumen sesuai dengan nilai fungsi yang bertambah kamu 0 +Δ y=f(x 0 –Δ x). Kami mendapat poin M(x 0+Δ x; y 0+Δ y). Mari kita menggambar garis potong M 0 M dan dilambangkan dengan sudut yang dibentuk oleh garis potong dengan arah sumbu positif Sapi. Mari kita buat hubungan dan perhatikan bahwa .

Jika sekarang x→0, maka, karena kontinuitas fungsi pada→0, dan karena itu intinya M, bergerak sepanjang kurva, mendekati titik tanpa batas M 0. Kemudian garis potong M 0 M akan cenderung mengambil posisi garis singgung kurva di titik M 0, dan sudut →α di x→0, di mana menunjukkan sudut antara garis singgung dan arah positif sumbu Sapi. Karena fungsi tg terus menerus bergantung pada di /2, maka di →α tg → tg dan, oleh karena itu, kemiringan garis singgungnya adalah:

itu. f"(x)= tgα .

Jadi, secara geometris y "(x 0) mewakili kemiringan garis singgung ke grafik fungsi ini di titik x0, yaitu untuk nilai argumen yang diberikan x, turunannya sama dengan garis singgung sudut yang dibentuk oleh garis singgung grafik fungsi f(x) pada titik yang sesuai M 0 (x; y) dengan arah sumbu positif Sapi.

Contoh. Tentukan kemiringan garis singgung kurva y = x 2 pada titik M(-1; 1).

Kita telah melihat bahwa ( x 2)" = 2X. Tetapi kemiringan garis singgung kurva adalah tg = kamu"| x=-1 = - 2.

DIFERENSIBILITAS FUNGSI. KONTINUITAS FUNGSI YANG BERBEDA

Fungsi y=f(x) ditelepon dapat dibedakan dalam beberapa kasus x 0 jika memiliki turunan tertentu pada titik ini, mis. jika limit dari relasi tersebut ada dan berhingga.

Jika suatu fungsi terdiferensialkan pada setiap titik dari suatu ruas [ sebuah; b] atau selang ( sebuah; b), kemudian mereka mengatakan bahwa itu dapat dibedakan pada segmen [ sebuah; b] atau, masing-masing, dalam interval ( sebuah; b).

Teorema berikut ini valid, yang menetapkan hubungan antara fungsi terdiferensiasi dan fungsi kontinu.

Dalil. Jika fungsi y=f(x) terdiferensiasi di beberapa titik x0, maka kontinu pada titik ini.

Dengan demikian, diferensiasi suatu fungsi menyiratkan kontinuitasnya.

Bukti. Jika sebuah , kemudian

,

di mana adalah nilai yang sangat kecil, yaitu kuantitas cenderung nol pada x→0. Tapi kemudian

Δ kamu=f "(x0) Δ x+αΔ x=> Δ kamu→0 di x→0, yaitu f(x) – f(x0)→0 at x→x 0 , yang berarti bahwa fungsi f(x) terus menerus pada titik x 0 . Q.E.D.

Jadi, pada titik-titik diskontinuitas, fungsi tersebut tidak dapat memiliki turunan. Pernyataan kebalikannya tidak benar: ada fungsi kontinu yang tidak terdiferensiasi di beberapa titik (yaitu, mereka tidak memiliki turunan di titik-titik ini).

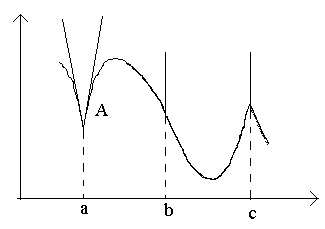
Perhatikan titik-titik pada gambar a, b, c.

Pada intinya sebuah di x→0 relasi tidak memiliki limit (karena limit satu sisi berbeda untuk x→0–0 dan x→0+0). Pada intinya A grafik tidak memiliki garis singgung yang ditentukan, tetapi ada dua garis singgung satu sisi yang berbeda dengan lereng ke 1 dan ke 2. Jenis titik ini disebut titik sudut.

Pada intinya b di x→0 rasio adalah tanda konstan nilai yang sangat besar . Fungsi tersebut memiliki turunan tak hingga. Pada titik ini, grafik memiliki garis singgung vertikal. Jenis titik - "titik belok" dengan garis singgung vertikal.

Pada intinya c turunan satu sisi adalah jumlah tak terhingga dari tanda-tanda berbeda. Pada titik ini, grafik memiliki dua garis singgung vertikal yang bergabung. Ketik - "puncak" dengan garis singgung vertikal - kasing khusus dari titik sudut.