Prinsip tindakan terkecil, pertama kali secara eksplisit dinyatakan oleh Jacobi, mirip dengan prinsip Hamilton, tetapi kurang umum dan lebih sulit untuk dibuktikan. Prinsip ini hanya berlaku untuk kasus ketika koneksi dan fungsi gaya tidak bergantung pada waktu dan ketika, oleh karena itu, ada integral dari gaya hidup.
Integral ini terlihat seperti:
Prinsip Hamilton yang dinyatakan di atas menyatakan bahwa variasi integral

sama dengan nol ketika gerakan sebenarnya berpindah ke gerakan lain yang sangat dekat yang membawa sistem dari posisi awal yang sama ke posisi akhir yang sama dalam interval waktu yang sama.
Prinsip Jacobi, sebaliknya, mengungkapkan properti, gerak, yang tidak bergantung pada waktu. Jacobi menganggap integral
mendefinisikan tindakan. Prinsip yang dia tetapkan menyatakan bahwa variasi integral ini adalah nol ketika kita membandingkan gerakan sebenarnya dari sistem dengan gerakan lain yang sangat dekat yang membawa sistem dari posisi awal yang sama ke posisi akhir yang sama. Dalam hal ini, kita tidak memperhatikan interval waktu yang dihabiskan, tetapi kita mengamati persamaan (1), yaitu persamaan tenaga kerja dengan nilai konstanta h yang sama seperti pada gerakan sebenarnya.
Kondisi ekstrem yang diperlukan ini, secara umum, mengarah ke integral minimum (2), dari mana muncul nama prinsip tindakan terkecil. Kondisi minimum tampaknya paling alami, karena nilai T pada dasarnya positif, dan oleh karena itu integral (2) harus memiliki minimum. Keberadaan minimum dapat dibuktikan secara ketat hanya jika interval waktunya cukup kecil. Bukti proposisi ini dapat ditemukan dalam kursus terkenal Darboux tentang teori permukaan. Namun, kami tidak akan menyajikannya di sini dan membatasi diri pada penurunan kondisi
432. Bukti prinsip tindakan terkecil.
Dalam perhitungan yang sebenarnya kita menghadapi satu kesulitan yang tidak ada dalam pembuktian teorema Hamilton. Variabel t tidak lagi tetap independen dari variasi; jadi variasi q i dan q. terkait dengan variasi t oleh hubungan kompleks yang mengikuti dari Persamaan (1). Cara termudah untuk mengatasi kesulitan ini adalah dengan mengubah variabel bebas menjadi variabel yang nilainya terletak di antara batas konstan waktu tidak tergantung. Misalkan k adalah variabel bebas baru yang limitnya diasumsikan bebas dari t. Saat memindahkan sistem, parameter dan t akan menjadi fungsi dari variabel ini
Biarkan huruf prima q menunjukkan turunan dari parameter q terhadap waktu.
Karena tautan dianggap tidak bergantung pada waktu, koordinat Cartesian x, y, z adalah fungsi dari q yang tidak mengandung waktu. Oleh karena itu turunannya akan menjadi fungsi homogen linier dari q dan 7 akan menjadi bentuk kuadrat homogen dari q yang koefisiennya adalah fungsi dari q. Kita punya
![]()
Untuk membedakan turunan waktu dari q, kami menyatakan dengan tanda kurung, (q), turunan dari q, diambil sehubungan dengan dan diletakkan sesuai dengan ini
![]()
maka kita akan memiliki
![]()
dan integral (2), yang dinyatakan melalui variabel bebas baru A, akan berbentuk;

Turunan dapat dihilangkan dengan menggunakan teorema gaya hidup. Memang, integral dari kekuatan hidup adalah
![]()
![]()
Substitusikan ekspresi ini ke dalam rumus untuk , kita bawa integral (2) ke bentuk

Integral yang mendefinisikan tindakan dengan demikian mengambil bentuk akhir (3). Integran adalah akar kuadrat dari bentuk kuadrat dari besaran
Mari kita tunjukkan bahwa persamaan diferensial dari ekstrem dari integral (3) adalah persis persamaan Lagrange. Persamaan ekstrem, berdasarkan rumus umum kalkulus variasi, adalah:

Kami mengalikan persamaan dengan 2 dan melakukan diferensiasi parsial, dengan mempertimbangkan bahwa tidak mengandung maka kami dapatkan, jika kami tidak menulis indeks ,
Ini adalah persamaan ekstrem yang dinyatakan dalam variabel bebas Tugas sekarang adalah kembali ke variabel bebas
Karena adalah fungsi homogen derajat kedua dari dan merupakan fungsi homogen derajat pertama, kita memperoleh
Di sisi lain, kita dapat menerapkan teorema gaya hidup ke faktor turunan dalam persamaan ekstrem, yang mengarah, seperti yang kita lihat di atas, ke substitusi
![]()
Sebagai hasil dari semua substitusi, persamaan ekstrem direduksi menjadi bentuk
![]()
![]()
Dengan demikian kita telah sampai pada persamaan Lagrange.
433. Kasus ketika tidak ada kekuatan pendorong.
Dalam kasus ketika tidak ada kekuatan pendorong, ada persamaan untuk tenaga kerja dan kami memiliki

Syarat integral adalah minimum, dalam hal ini, nilai yang bersesuaian dari -10 harus terkecil. Jadi, ketika tidak ada kekuatan pendorong, maka di antara semua gerakan di mana gaya hidup mempertahankan nilai tertentu yang sama, gerakan yang sebenarnya adalah yang membawa sistem dari posisi awal ke posisi akhir dalam waktu singkat.
Jika sistem direduksi menjadi satu titik yang bergerak sepanjang permukaan tetap, maka gerakan sebenarnya, di antara semua gerakan di sepanjang permukaan, yang dilakukan dengan kecepatan yang sama, adalah gerakan di mana titik berpindah dari posisi awalnya ke posisi akhir. ke yang terpendek
jarak waktu. Dengan kata lain, suatu titik menggambarkan di permukaan garis terpendek antara dua posisinya, yaitu garis geodesik.
434. Catatan.
Prinsip aksi terkecil mengasumsikan bahwa sistem memiliki beberapa derajat kebebasan, karena jika hanya ada satu derajat kebebasan, maka satu persamaan akan cukup untuk menentukan gerakan. Karena gerak dalam hal ini dapat sepenuhnya ditentukan oleh persamaan gaya hidup, gerak aktual akan menjadi satu-satunya yang memenuhi persamaan ini, dan oleh karena itu tidak dapat dibandingkan dengan gerak lainnya.

Dalam kami secara singkat meninjau salah satu prinsip fisik yang paling luar biasa - prinsip tindakan paling sedikit, dan menetapkan contoh yang tampaknya bertentangan dengannya. Dalam artikel ini, kita akan melihat lebih dekat prinsip ini dan melihat apa yang terjadi dalam contoh ini.
Kali ini kita membutuhkan sedikit lebih banyak matematika. Namun, saya akan kembali mencoba menyajikan bagian utama artikel di tingkat dasar. Poin yang sedikit lebih ketat dan kompleks akan saya soroti dalam warna, mereka dapat dilewati tanpa mengurangi pemahaman utama artikel.
Kondisi perbatasan
Mari kita mulai dengan objek paling sederhana - sebuah bola yang bergerak bebas di ruang angkasa, yang tidak terpengaruh oleh gaya apa pun. Bola seperti itu, seperti diketahui, bergerak secara seragam dan lurus. Untuk kesederhanaan, mari kita asumsikan bahwa itu bergerak di sepanjang sumbu:
Untuk menggambarkan gerakannya secara akurat, sebagai suatu peraturan, kondisi awal diberikan. Misalnya, ditentukan bahwa pada saat awal waktu bola berada di titik dengan koordinat dan memiliki kecepatan . Dengan mengatur kondisi awal dalam bentuk ini, kami secara unik menentukan pergerakan bola selanjutnya - bola akan bergerak dengan kecepatan konstan, dan posisinya pada saat ini akan sama dengan posisi awal ditambah kecepatan dikalikan dengan waktu yang telah berlalu. : . Cara pengaturan kondisi awal ini sangat alami dan akrab secara intuitif. Kami telah memberikan semua informasi yang diperlukan tentang gerakan bola pada saat awal waktu, dan kemudian gerakannya ditentukan oleh hukum Newton.
Namun, ini bukan satu-satunya cara untuk menentukan pergerakan bola. Cara alternatif lain adalah dengan menentukan posisi bola pada dua waktu yang berbeda dan . Itu. atur bahwa:
1) pada saat bola berada di suatu titik (dengan koordinat );
2) pada saat bola berada di suatu titik (dengan koordinat ).
Ungkapan "berada pada titik" tidak berarti bahwa bola berada dalam keadaan diam pada titik tersebut. Pada saat itu bisa terbang melalui titik. Artinya posisinya pada saat itu bertepatan dengan titik. Hal yang sama berlaku untuk titik.
Kedua kondisi ini juga secara unik menentukan gerak bola. Pergerakannya mudah dihitung. Untuk memenuhi kedua kondisi tersebut, kecepatan bola jelas harus . Posisi bola pada saat waktu akan kembali sama dengan posisi awal ditambah kecepatan dikalikan dengan waktu yang telah berlalu:
Perhatikan bahwa dalam kondisi masalah, kita tidak perlu mengatur kecepatan awal. Itu ditentukan secara unik dari kondisi 1) dan 2).
Pengaturan kondisi dengan cara kedua terlihat tidak biasa. Mungkin tidak jelas mengapa mungkin perlu untuk mengaturnya dalam bentuk ini sama sekali. Namun, dalam prinsip tindakan terkecil, kondisi dalam bentuk 1) dan 2) yang digunakan, dan bukan dalam bentuk penentuan posisi awal dan kecepatan awal.
Lintasan dengan tindakan paling sedikit
Sekarang mari kita menyimpang sedikit dari gerak bebas sebenarnya dari bola dan pertimbangkan masalah matematika murni berikut ini. Katakanlah kita memiliki bola yang dapat kita gerakkan secara manual dengan cara apa pun yang kita suka. Dalam hal ini, kita perlu memenuhi kondisi 1) dan 2). Itu. dalam interval waktu antara dan kita harus memindahkannya dari titik ke titik . Ini dapat dilakukan dengan cara yang sangat berbeda. Masing-masing cara tersebut akan kita sebut lintasan bola dan dapat digambarkan sebagai fungsi dari posisi bola dari waktu ke waktu. Mari kita plot beberapa lintasan seperti itu pada grafik posisi bola terhadap waktu:
Misalnya, kita dapat memindahkan bola dengan kecepatan yang sama dengan (lintasan hijau). Atau kita bisa menjaganya di titik separuh waktu dan kemudian memindahkannya ke titik dengan kecepatan ganda (jalur biru). Anda dapat terlebih dahulu memindahkannya ke arah yang berlawanan, dan kemudian memindahkannya ke (jalur coklat). Anda dapat memindahkannya maju mundur (jalur merah). Secara umum, Anda dapat memindahkannya sesuka Anda, selama kondisi 1) dan 2) terpenuhi.
Untuk setiap lintasan seperti itu, kita dapat mencocokkan angka. Dalam contoh kami, yaitu. jika tidak ada gaya yang bekerja pada bola, jumlah ini sama dengan total akumulasi energi kinetik untuk seluruh waktu gerakannya dalam interval waktu antara dan dan disebut aksi.
Dalam hal ini, kata "akumulasi" energi kinetik tidak secara akurat menyampaikan artinya. Pada kenyataannya, energi kinetik tidak terakumulasi di mana pun, akumulasi hanya digunakan untuk menghitung aksi lintasan. Dalam matematika, ada konsep yang sangat bagus untuk akumulasi seperti itu - integralnya:Sebagai contoh, mari kita ambil bola 1 kg, atur beberapa kondisi batas dan hitung aksi untuk dua lintasan yang berbeda. Biarkan titik berada pada jarak 1 meter dari titik , dan waktu berjarak 1 detik dari waktu. Itu. kita harus memindahkan bola, yang pada saat awal waktu berada di titik, dalam satu detik pada jarak 1 m sepanjang sumbu.Tindakan biasanya dilambangkan dengan huruf. Simbol berarti energi kinetik. Integral ini berarti bahwa aksinya sama dengan akumulasi energi kinetik bola selama selang waktu dari .
Pada contoh pertama (lintasan hijau), kami memindahkan bola secara merata, mis. dengan kecepatan yang sama, yang, jelas, harus sama dengan: m / s. Energi kinetik bola pada setiap momen waktu adalah: = 1/2 J. Dalam satu detik, energi kinetik 1/2 J akan terakumulasi. Itu. aksi untuk lintasan tersebut adalah: J s.
Sekarang mari kita tidak segera memindahkan bola dari titik ke titik , tetapi menahannya di titik selama setengah detik, dan kemudian, untuk waktu yang tersisa, transfer secara merata ke titik . Pada setengah detik pertama, bola diam dan energi kinetiknya nol. Oleh karena itu, kontribusi terhadap aksi bagian lintasan ini juga sama dengan nol. Selama setengah detik kedua, kami menggerakkan bola dengan kecepatan ganda: m/s. Energi kinetik dalam hal ini akan sama dengan = 2 J. Kontribusi interval waktu ini terhadap aksi akan sama dengan 2 J dikalikan dengan setengah detik, mis. 1 J s. Oleh karena itu, aksi total untuk lintasan seperti itu sama dengan J s.
Demikian pula, setiap lintasan lain dengan kondisi batas 1) dan 2) yang diberikan oleh kami sesuai dengan angka tertentu yang sama dengan aksi untuk lintasan ini. Di antara semua lintasan seperti itu, ada lintasan dengan tindakan paling sedikit. Dapat dibuktikan bahwa lintasan ini adalah lintasan hijau, yaitu gerakan bola yang seragam. Untuk lintasan lainnya, tidak peduli seberapa rumitnya, aksinya akan lebih besar dari 1/2.
Dalam matematika, perbandingan seperti itu untuk setiap fungsi dari bilangan tertentu disebut fungsional. Cukup sering dalam fisika dan matematika ada masalah yang mirip dengan kita, yaitu. untuk menemukan fungsi yang nilai fungsi tertentunya minimal. Misalnya, salah satu masalah yang memiliki signifikansi historis yang besar bagi perkembangan matematika adalah masalah bachistochrone. Itu. Menemukan kurva di mana bola menggelinding paling cepat. Sekali lagi, setiap kurva dapat diwakili oleh fungsi h(x), dan setiap fungsi dapat diberi nomor, dalam hal ini, waktu bola menggelinding. Sekali lagi, masalahnya direduksi menjadi menemukan fungsi yang nilai fungsionalnya minimal. Cabang matematika yang menangani masalah seperti itu disebut kalkulus variasi.
Prinsip tindakan paling sedikit
Dalam contoh yang dibahas di atas, kami memiliki dua lintasan khusus yang diperoleh dengan dua cara berbeda.Lintasan pertama diperoleh dari hukum fisika dan sesuai dengan lintasan nyata dari bola bebas, yang tidak terpengaruh oleh gaya apa pun dan yang kondisi batasnya ditetapkan dalam bentuk 1) dan 2).
Lintasan kedua diperoleh dari masalah matematika untuk menemukan lintasan dengan kondisi batas yang diberikan 1) dan 2), yang aksinya minimal.
Prinsip tindakan terkecil menyatakan bahwa kedua jalur ini harus bertepatan. Dengan kata lain, jika diketahui bahwa bola bergerak sedemikian rupa sehingga kondisi batas 1) dan 2) terpenuhi, maka bola tersebut harus bergerak sepanjang lintasan yang aksinya minimal dibandingkan dengan lintasan lain dengan kondisi batas yang sama. .
Ini bisa dianggap sebagai kebetulan belaka. Anda tidak pernah tahu masalah di mana lintasan seragam dan garis lurus muncul. Namun, prinsip aksi terkecil ternyata menjadi prinsip yang sangat umum, yang juga berlaku dalam situasi lain, misalnya, untuk gerakan bola dalam medan gravitasi seragam. Untuk melakukan ini, Anda hanya perlu mengganti energi kinetik dengan perbedaan antara energi kinetik dan potensial. Selisih ini disebut Lagrangian atau fungsi Lagrange dan aksinya sekarang menjadi sama dengan total akumulasi Lagrangian. Faktanya, fungsi Lagrange berisi semua informasi yang diperlukan tentang sifat dinamis sistem.
Jika kita meluncurkan sebuah bola dalam medan gravitasi seragam sedemikian rupa sehingga ia terbang melewati suatu titik pada suatu waktu dan tiba di suatu titik pada suatu waktu , maka, menurut hukum Newton, akan terbang sepanjang parabola. Parabola inilah yang akan bertepatan dengan lintasan yang aksinya akan minimal.
Jadi, untuk benda yang bergerak dalam medan potensial, misalnya, dalam medan gravitasi bumi, fungsi Lagrange adalah: . Energi kinetik tergantung pada kecepatan tubuh, dan energi potensial tergantung pada posisinya, yaitu. koordinat. Dalam mekanika analitik, seluruh himpunan koordinat yang menentukan posisi sistem biasanya dilambangkan dengan satu huruf. Untuk bola yang bergerak bebas dalam medan gravitasi, berarti koordinat , dan .Untuk menunjukkan laju perubahan suatu besaran, dalam fisika sangat umum untuk meletakkan titik di atas besaran ini. Misalnya, ini menunjukkan laju perubahan koordinat , atau, dengan kata lain, kecepatan benda dalam arah . Menggunakan konvensi ini, kecepatan bola kami dalam mekanika analitik dilambangkan sebagai . Itu. berarti komponen kecepatan.
Karena fungsi Lagrange bergantung pada kecepatan dan koordinat, dan dapat juga secara eksplisit bergantung pada waktu (secara eksplisit bergantung pada waktu, yang berarti bahwa nilainya berbeda pada waktu yang berbeda, untuk kecepatan dan posisi bola yang sama), maka aksi di umum ditulis sebagai
Tidak selalu minimal
Namun, pada akhir bagian sebelumnya, kami mempertimbangkan contoh di mana prinsip tindakan paling sedikit jelas tidak berfungsi. Untuk melakukan ini, kami kembali mengambil bola bebas, di mana tidak ada gaya yang bekerja, dan menempatkan dinding kenyal di sebelahnya.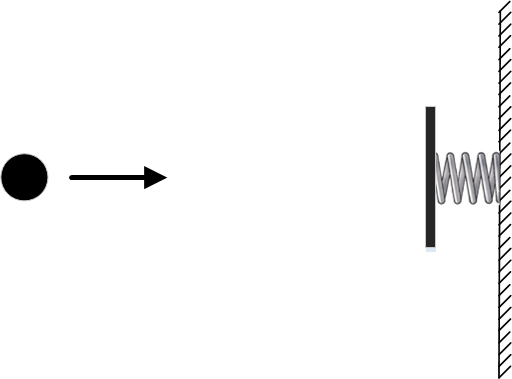
Kami menetapkan kondisi batas sedemikian rupa sehingga titik dan bertepatan. Itu. dan pada saat waktu dan pada saat waktu bola harus berada pada titik yang sama . Salah satu lintasan yang mungkin adalah bola berdiri diam. Itu. seluruh interval waktu antara dan itu akan berdiri di titik . Energi kinetik dan potensial dalam hal ini akan sama dengan nol, sehingga aksi untuk lintasan seperti itu juga akan sama dengan nol.
Sebenarnya, energi potensial dapat dianggap tidak sama dengan nol, tetapi dengan angka berapa pun, karena perbedaan energi potensial pada titik yang berbeda dalam ruang adalah penting. Namun, perubahan nilai energi potensial tidak mempengaruhi pencarian lintasan dengan aksi minimal. Hanya saja untuk semua lintasan nilai aksi akan berubah dengan angka yang sama, dan lintasan dengan aksi minimum akan tetap menjadi lintasan dengan aksi minimum. Untuk kenyamanan, untuk bola kami, kami akan memilih energi potensial sama dengan nol.Lintasan fisik lain yang mungkin dengan kondisi batas yang sama adalah lintasan di mana bola pertama kali terbang ke kanan, melewati titik pada waktu . Kemudian dia bertabrakan dengan pegas, menekannya, pegas, meluruskan, mendorong bola ke belakang, dan lagi-lagi terbang melewati titik. Anda dapat memilih kecepatan bola sehingga, setelah memantul dari dinding, bola itu terbang di atas titik tepat pada saat itu . Tindakan pada lintasan seperti itu pada dasarnya akan sama dengan energi kinetik yang terakumulasi selama penerbangan antara titik dan dinding dan kembali. Akan ada beberapa periode waktu ketika bola menekan pegas dan energi potensialnya meningkat, dan selama periode waktu ini energi potensial akan memberikan kontribusi negatif pada aksi. Tetapi jangka waktu seperti itu tidak akan terlalu besar dan tidak akan banyak mengurangi efeknya.

Angka tersebut menunjukkan kemungkinan lintasan bola secara fisik. Lintasan hijau sesuai dengan bola yang diam, sedangkan lintasan biru sesuai dengan bola yang memantul dari dinding yang kenyal.
Namun, hanya satu yang memiliki efek minimal, yaitu yang pertama! Lintasan kedua memiliki lebih banyak aksi. Ternyata dalam masalah ini ada dua lintasan yang mungkin secara fisik dan hanya satu dengan tindakan minimal. Itu. Dalam hal ini, prinsip tindakan terkecil tidak berfungsi.
Titik stasioner
Untuk memahami apa yang terjadi di sini, mari kita menyimpang dari prinsip tindakan terkecil dan berurusan dengan fungsi biasa. Mari kita ambil beberapa fungsi dan gambarkan grafiknya:
Pada grafik, saya menandai empat titik khusus dengan warna hijau. Apa yang umum untuk titik-titik ini? Bayangkan bahwa grafik fungsi adalah slide nyata di mana bola dapat menggelinding. Empat titik yang ditentukan adalah khusus karena jika Anda menempatkan bola tepat di titik ini, maka bola itu tidak akan menggelinding ke mana pun. Di semua titik lain, misalnya, titik E, dia tidak akan bisa berdiri diam dan akan mulai meluncur ke bawah. Titik-titik seperti itu disebut stasioner. Menemukan titik seperti itu adalah tugas yang berguna, karena setiap fungsi maksimum atau minimum, jika tidak memiliki jeda yang tajam, harus merupakan titik stasioner.
Jika kita mengklasifikasikan titik-titik ini lebih tepat, maka titik A adalah fungsi minimum absolut, yaitu. nilainya lebih kecil dari nilai fungsi lainnya. Titik B bukan maksimum atau minimum dan disebut titik pelana. Titik C disebut maksimum lokal, yaitu nilai di dalamnya lebih besar daripada di titik-titik tetangga fungsi. Dan titik D adalah minimum lokal, yaitu nilai di dalamnya lebih kecil daripada di titik-titik tetangga dari fungsi tersebut.
Cabang matematika yang disebut kalkulus terlibat dalam pencarian titik-titik tersebut. Dengan cara lain, kadang-kadang juga disebut analisis sangat kecil, karena dapat bekerja dengan jumlah yang sangat kecil. Dari sudut pandang analisis matematis, titik-titik stasioner memiliki satu sifat khusus, yang dengannya mereka ditemukan. Untuk memahami apa sifat ini, kita perlu memahami seperti apa fungsinya pada jarak yang sangat kecil dari titik-titik ini. Untuk melakukan ini, kami mengambil mikroskop dan melihatnya di titik-titik kami. Gambar tersebut menunjukkan bagaimana fungsi terlihat di sekitar berbagai titik pada berbagai perbesaran.

Dapat dilihat bahwa pada perbesaran yang sangat tinggi (yaitu, untuk deviasi x yang sangat kecil), titik-titik stasioner terlihat persis sama dan sangat berbeda dengan titik non-stasioner. Sangat mudah untuk memahami apa perbedaan ini - grafik fungsi pada titik stasioner menjadi garis horizontal ketat dengan peningkatan, dan pada titik non-stasioner menjadi miring. Itulah sebabnya bola, yang dipasang pada titik stasioner, tidak akan menggelinding.
Horizontalitas suatu fungsi pada titik stasioner dapat dinyatakan dengan cara lain: fungsi pada titik stasioner praktis tidak berubah dengan perubahan yang sangat kecil dalam argumennya, bahkan dibandingkan dengan perubahan argumen itu sendiri. Fungsi pada titik tidak stasioner dengan perubahan kecil berubah secara proporsional dengan perubahan. Dan semakin besar kemiringan fungsi, semakin banyak fungsi berubah ketika . Faktanya, ketika fungsi meningkat, itu menjadi lebih dan lebih seperti garis singgung grafik pada titik yang bersangkutan.
Dalam bahasa matematika yang ketat, ungkapan "fungsi praktis tidak berubah pada titik dengan perubahan yang sangat kecil" berarti bahwa rasio perubahan fungsi dan perubahan argumennya cenderung 0 karena cenderung 0:$$display$$\lim_(∆x \to 0) \frac (∆y(x_0))(∆x) = \lim_(x \to 0) \frac (y(x_0+∆x)-y(x_0) )(∆x) = 0$$tampilan$$
Untuk titik yang tidak stasioner, rasio ini cenderung ke angka bukan nol, yang sama dengan tangen kemiringan fungsi pada titik ini. Bilangan yang sama disebut turunan dari fungsi di titik tertentu. Turunan suatu fungsi menunjukkan seberapa cepat suatu fungsi berubah di sekitar titik tertentu dengan sedikit perubahan pada argumennya. Jadi, titik-titik stasioner adalah titik-titik di mana turunan suatu fungsi adalah 0.
lintasan stasioner
Dengan analogi dengan titik stasioner, kita dapat memperkenalkan konsep lintasan stasioner. Ingatlah bahwa untuk setiap lintasan kita memiliki nilai aksi tertentu, mis. beberapa nomor. Kemudian bisa ada lintasan sedemikian rupa sehingga untuk lintasan yang dekat dengannya dengan kondisi batas yang sama, nilai aksi yang sesuai praktis tidak akan berbeda dari aksi untuk lintasan paling stasioner. Lintasan seperti itu disebut stasioner. Dengan kata lain, setiap lintasan yang dekat dengan stasioner akan memiliki nilai aksi yang sangat sedikit berbeda dari aksi untuk lintasan stasioner tersebut.Sekali lagi, dalam bahasa matematika, "sedikit berbeda" memiliki arti yang tepat sebagai berikut. Mari kita asumsikan bahwa kita memiliki fungsi untuk fungsi dengan kondisi batas yang diperlukan 1) dan 2), yaitu. dan . Mari kita asumsikan bahwa lintasannya stasioner.Kita dapat mengambil fungsi lain sehingga dibutuhkan nilai nol di ujungnya, mis. = = 0. Juga ambil variabel , yang akan kita buat semakin kecil. Dari dua fungsi dan variabel ini, kita dapat membuat fungsi ketiga yang juga memenuhi syarat batas dan . Saat menurun, lintasan yang sesuai dengan fungsi akan semakin mendekati lintasan .
Dalam hal ini, untuk lintasan stasioner untuk kecil, nilai fungsional untuk lintasan akan berbeda sangat kecil dari nilai fungsional genap dibandingkan dengan . Itu.
$$display$$\lim_(ε \ke 0) \frac (S(x"(t))-S(x(t)))ε=\lim_(ε \to 0) \frac (S(x( t)+εg(t))-S(x(t)))ε = 0$$tampilan$$
Selain itu, ini harus benar untuk setiap lintasan yang memenuhi syarat batas = = 0.Perubahan fungsi dengan perubahan fungsi yang kecil (lebih tepatnya, bagian linier dari perubahan fungsi, sebanding dengan perubahan fungsi) disebut variasi fungsi dan dilambangkan dengan . Dari istilah "variasi" muncul nama "kalkulus variasi".
Untuk lintasan stasioner, variasi fungsi .
Metode menemukan fungsi stasioner (tidak hanya untuk prinsip aksi terkecil, tetapi juga untuk banyak masalah lainnya) ditemukan oleh dua ahli matematika - Euler dan Lagrange. Ternyata fungsi stasioner yang fungsinya dinyatakan oleh integral seperti integral aksi harus memenuhi persamaan tertentu, yang sekarang disebut persamaan Euler-Lagrange.
Prinsip aksi stasioner
Situasi dengan aksi minimum untuk lintasan mirip dengan situasi dengan fungsi minimum. Agar lintasan memiliki aksi paling sedikit, lintasan itu harus lintasan stasioner. Namun, tidak semua lintasan stasioner adalah lintasan dengan aksi minimal. Misalnya, lintasan stasioner mungkin memiliki aksi minimum secara lokal. Itu. itu akan memiliki tindakan yang lebih sedikit daripada lintasan tetangga lainnya. Namun, di suatu tempat yang jauh mungkin ada lintasan lain yang tindakannya akan lebih sedikit.Ternyata benda nyata belum tentu bergerak sepanjang lintasan dengan tindakan paling sedikit. Mereka dapat bergerak di sepanjang lintasan khusus yang lebih luas, yaitu lintasan stasioner. Itu. lintasan tubuh yang sebenarnya akan selalu diam. Oleh karena itu, prinsip aksi terkecil lebih tepat disebut prinsip aksi stasioner. Namun, menurut tradisi yang mapan, ini sering disebut prinsip tindakan terkecil, yang menyiratkan tidak hanya minimalitas, tetapi juga stasioneritas lintasan.
Sekarang kita dapat menulis prinsip aksi stasioner dalam bahasa matematika, seperti yang biasanya ditulis dalam buku teks:.Jika kita kembali ke contoh dengan bola dan dinding elastis, maka penjelasan situasi ini menjadi sangat sederhana sekarang. Di bawah kondisi batas yang diberikan bahwa bola harus berada di titik baik pada saat maupun pada saat itu, ada dua lintasan stasioner. Dan bola benar-benar dapat bergerak di sepanjang lintasan ini. Untuk secara eksplisit memilih salah satu lintasan, Anda dapat menerapkan kondisi tambahan pada gerakan bola. Misalnya, katakan bahwa bola harus memantul dari dinding. Kemudian lintasan akan ditentukan dengan jelas.Di sini, adalah koordinat umum, mis. satu set variabel yang secara unik menentukan posisi sistem.
- laju perubahan koordinat umum.
- Fungsi Lagrange, yang bergantung pada koordinat umum, kecepatannya dan, mungkin, waktu.
- tindakan yang bergantung pada lintasan spesifik sistem (yaitu dari).Lintasan sebenarnya dari sistem adalah stasioner, yaitu bagi mereka, variasi tindakan.
Dari prinsip tindakan paling sedikit (lebih tepatnya, tidak bergerak), beberapa konsekuensi luar biasa mengikuti, yang akan kita bahas di bagian selanjutnya.
Ketika saya pertama kali belajar tentang prinsip ini, saya memiliki perasaan mistisisme. Tampaknya alam secara misterius memilah-milah semua kemungkinan cara pergerakan sistem dan memilih yang terbaik dari mereka.
Hari ini saya ingin berbicara sedikit tentang salah satu prinsip fisik yang paling luar biasa - prinsip tindakan paling sedikit.
Latar Belakang
Sejak zaman Galileo, telah diketahui bahwa benda-benda yang tidak dikenai gaya apapun bergerak dalam garis lurus, yaitu sepanjang lintasan terpendek. Sinar cahaya juga merambat dalam garis lurus.Ketika dipantulkan, cahaya juga bergerak sedemikian rupa untuk berpindah dari satu titik ke titik lain dengan cara terpendek. Pada gambar, jalur terpendek adalah jalur hijau, di mana sudut datang sama dengan sudut pantul. Jalur lain, seperti yang merah, akan lebih panjang.

Ini mudah dibuktikan dengan hanya memantulkan jalur sinar ke sisi berlawanan dari cermin. Mereka ditampilkan dalam garis putus-putus dalam gambar.

Terlihat bahwa jalur hijau ACB berubah menjadi garis lurus ACB'. Dan jalur merah berubah menjadi garis putus-putus ADB ', yang tentu saja lebih panjang dari yang hijau.
Pada 1662, Pierre Fermat menyarankan bahwa kecepatan cahaya dalam zat padat, seperti kaca, lebih kecil daripada di udara. Sebelum ini, versi yang diterima secara umum adalah Descartes, yang menyatakan bahwa kecepatan cahaya dalam materi harus lebih besar daripada di udara untuk mendapatkan hukum pembiasan yang benar. Bagi Fermat, asumsi bahwa cahaya dapat bergerak lebih cepat dalam medium yang lebih padat daripada medium yang dijernihkan tampaknya tidak wajar. Oleh karena itu, ia berasumsi bahwa segala sesuatunya justru sebaliknya dan membuktikan hal yang menakjubkan - dengan asumsi ini, cahaya dibiaskan untuk mencapai tujuannya dalam waktu minimum.

Pada gambar lagi, warna hijau menunjukkan jalur yang sebenarnya dilalui berkas cahaya. Jalur yang ditandai dengan warna merah adalah yang terpendek, tetapi bukan yang tercepat, karena cahaya memiliki jalur yang lebih panjang untuk bergerak di kaca, dan kecepatannya lebih lambat di dalamnya. Yang tercepat adalah jalur sebenarnya dari berkas cahaya.
Semua fakta ini menunjukkan bahwa alam bertindak dengan cara yang rasional, cahaya dan benda bergerak dengan cara yang paling optimal, mengeluarkan usaha sesedikit mungkin. Tapi apa upaya ini, dan bagaimana menghitungnya, tetap menjadi misteri.
Pada tahun 1744, Maupertuis memperkenalkan konsep "aksi" dan merumuskan prinsip yang menurutnya lintasan sebenarnya dari suatu partikel berbeda dari yang lain dalam hal tindakan untuk itu minimal. Namun, Maupertuis sendiri belum bisa memberikan definisi yang jelas tentang apa yang dimaksud dengan tindakan ini. Formulasi matematika yang ketat dari prinsip tindakan terkecil dikembangkan oleh matematikawan lain - Euler, Lagrange, dan akhirnya diberikan oleh William Hamilton:

Dalam bahasa matematika, prinsip tindakan terkecil dirumuskan dengan cukup singkat, tetapi tidak semua pembaca dapat memahami arti dari notasi yang digunakan. Saya ingin mencoba menjelaskan prinsip ini dengan lebih jelas dan lebih sederhana.
tubuh longgar
Jadi, bayangkan Anda sedang duduk di dalam mobil pada suatu titik dan pada suatu titik waktu Anda diberi tugas sederhana: pada titik waktu tersebut Anda perlu mengemudikan mobil ke titik .
Bahan bakar untuk mobil mahal dan, tentu saja, Anda ingin menghabiskannya sesedikit mungkin. Mobil Anda dibuat menggunakan teknologi super terbaru dan dapat dipercepat atau diperlambat secepat yang Anda inginkan. Namun, itu dirancang sedemikian rupa sehingga semakin cepat, semakin banyak bahan bakar yang dikonsumsi. Selain itu, konsumsi bahan bakar sebanding dengan kuadrat kecepatan. Jika Anda mengemudi dua kali lebih cepat, Anda mengkonsumsi bahan bakar 4 kali lebih banyak dalam jumlah waktu yang sama. Selain kecepatan, konsumsi bahan bakar tentu saja dipengaruhi oleh massa mobil. Semakin berat mobil kita, semakin banyak bahan bakar yang dikonsumsi. Konsumsi bahan bakar mobil kami pada setiap saat adalah , mis. persis sama dengan energi kinetik mobil.
Jadi bagaimana Anda perlu mengemudi untuk sampai ke tujuan tepat waktu dan menggunakan bahan bakar sesedikit mungkin? Jelas bahwa Anda harus berjalan lurus. Dengan bertambahnya jarak yang ditempuh, bahan bakar yang akan dikonsumsi justru tidak berkurang. Dan kemudian Anda dapat memilih taktik yang berbeda. Misalnya, Anda dapat dengan cepat tiba di titik terlebih dahulu dan hanya duduk, menunggu waktu yang akan datang. Kecepatan mengemudi, dan karenanya konsumsi bahan bakar pada setiap saat, akan tinggi, tetapi waktu mengemudi juga akan berkurang. Mungkin konsumsi bahan bakar keseluruhan dalam hal ini tidak akan terlalu besar. Atau Anda dapat pergi secara merata, dengan kecepatan yang sama, sehingga, tanpa terburu-buru, tepat tiba pada saat waktu itu. Atau bagian dari jalan untuk pergi cepat, dan bagian lebih lambat. Apa cara terbaik untuk pergi?
Ternyata cara mengemudi yang paling optimal dan paling ekonomis adalah mengemudi dengan kecepatan konstan, seperti berada di titik tepat pada waktu yang ditentukan. Pilihan lain akan menggunakan lebih banyak bahan bakar. Anda dapat memeriksa sendiri dengan beberapa contoh. Alasannya adalah bahwa konsumsi bahan bakar meningkat dengan kuadrat kecepatan. Oleh karena itu, saat kecepatan meningkat, konsumsi bahan bakar meningkat lebih cepat daripada penurunan waktu mengemudi, dan konsumsi bahan bakar secara keseluruhan juga meningkat.
Jadi, kami menemukan bahwa jika sebuah mobil mengkonsumsi bahan bakar pada waktu tertentu sebanding dengan energi kinetiknya, maka cara paling ekonomis untuk pergi dari titik ke titik pada waktu yang ditentukan adalah dengan mengemudi secara merata dan dalam garis lurus, seperti sebuah benda bergerak tanpa adanya gaya yang bekerja padanya. Cara mengemudi lainnya akan menghasilkan konsumsi bahan bakar keseluruhan yang lebih tinggi.
Di medan gravitasi
Sekarang mari kita perbaiki mobil kita sedikit. Mari kita pasang mesin jet agar bisa terbang bebas ke segala arah. Secara umum, desainnya tetap sama, sehingga konsumsi bahan bakar tetap proporsional dengan energi kinetik mobil. Jika tugas sekarang diberikan untuk berangkat dari suatu titik waktu dan tiba di suatu titik pada waktu t, maka cara yang paling ekonomis, seperti sebelumnya, tentu saja, akan terbang secara seragam dan dalam garis lurus untuk tiba di titik tepat di waktu yang ditentukan t. Ini sekali lagi sesuai dengan gerakan bebas tubuh dalam ruang tiga dimensi.
Namun, perangkat yang tidak biasa dipasang di model mobil terbaru. Unit ini mampu menghasilkan bahan bakar secara harfiah dari nol. Tetapi desainnya sedemikian rupa sehingga semakin tinggi mobil, semakin banyak bahan bakar yang dihasilkan perangkat pada waktu tertentu. Output bahan bakar berbanding lurus dengan ketinggian di mana kendaraan saat ini berada. Selain itu, semakin berat mobil, semakin kuat perangkat yang dipasang di atasnya dan semakin banyak bahan bakar yang dihasilkan, dan output berbanding lurus dengan massa mobil. Peralatan ternyata sedemikian rupa sehingga keluaran bahan bakar persis sama dengan (di mana percepatan jatuh bebas), mis. energi potensial mobil.
Konsumsi bahan bakar pada setiap momen waktu sama dengan energi kinetik dikurangi energi potensial mobil (dikurangi energi potensial, karena kendaraan yang dipasang menghasilkan bahan bakar, dan tidak menghabiskan). Sekarang tugas kita adalah pergerakan mobil yang paling ekonomis antar titik dan itu menjadi lebih sulit. Gerak seragam bujursangkar dalam hal ini bukan yang paling efektif. Ternyata lebih optimal untuk mendaki sedikit, berlama-lama di sana, mengembangkan lebih banyak bahan bakar, dan kemudian turun ke titik. Dengan jalur penerbangan yang benar, konsumsi bahan bakar total karena pendakian akan menutupi biaya bahan bakar tambahan untuk menambah panjang jalur dan meningkatkan kecepatan. Jika dihitung dengan cermat, cara paling ekonomis untuk sebuah mobil adalah terbang dalam parabola, dalam lintasan yang sama persis dan dengan kecepatan yang persis sama dengan batu yang terbang di medan gravitasi bumi.

Di sini ada baiknya membuat penjelasan. Tentu saja, adalah mungkin untuk melempar batu dari suatu titik dengan banyak cara yang berbeda sehingga mengenai titik tersebut . Tetapi Anda harus melemparnya sedemikian rupa sehingga, setelah terbang keluar dari suatu titik pada waktu tertentu, ia mengenai suatu titik tepat pada waktunya. Gerakan inilah yang akan menjadi yang paling ekonomis untuk mobil kita.
Fungsi Lagrange dan prinsip tindakan terkecil
Sekarang kita dapat mentransfer analogi ini ke tubuh fisik yang nyata. Analog dari intensitas konsumsi bahan bakar untuk tubuh disebut fungsi Lagrange atau Lagrangian (untuk menghormati Lagrange) dan dilambangkan dengan huruf . Lagrangian menunjukkan berapa banyak "bahan bakar" yang dikonsumsi tubuh pada waktu tertentu. Untuk benda yang bergerak dalam medan potensial, Lagrangian sama dengan energi kinetiknya dikurangi energi potensialnya.Analog dari jumlah total bahan bakar yang dikonsumsi untuk seluruh waktu pergerakan, mis. nilai akumulasi Lagrangian selama seluruh waktu gerak disebut "aksi".
Prinsip tindakan terkecil adalah bahwa tubuh bergerak sedemikian rupa sehingga tindakan (yang tergantung pada lintasan gerak) adalah minimal. Dalam hal ini, orang tidak boleh lupa bahwa kondisi awal dan akhir diberikan, mis. di mana tubuh berada pada waktu dan waktu.
Dalam hal ini, tubuh tidak harus bergerak dalam medan gravitasi yang seragam, yang kami pertimbangkan untuk mobil kami. Anda dapat mempertimbangkan situasi yang sama sekali berbeda. Sebuah benda dapat berosilasi pada karet gelang, berayun pada bandul atau terbang mengelilingi Matahari, dalam semua kasus ini ia bergerak sedemikian rupa untuk meminimalkan "konsumsi bahan bakar total" yaitu. tindakan.
Jika sistem terdiri dari beberapa benda, maka Lagrangian sistem tersebut akan sama dengan energi kinetik total semua benda dikurangi energi potensial total semua benda. Dan sekali lagi, semua tubuh akan bergerak bersama sehingga efek dari seluruh sistem selama gerakan tersebut minimal.
Tidak begitu sederhana
Bahkan, saya sedikit curang dengan mengatakan bahwa tubuh selalu bergerak sedemikian rupa untuk meminimalkan tindakan. Meskipun dalam banyak kasus hal ini benar, adalah mungkin untuk memikirkan situasi di mana tindakannya jelas tidak minimal.Sebagai contoh, mari kita ambil sebuah bola dan letakkan di tempat yang kosong. Agak jauh dari itu, kami memasang dinding elastis. Katakanlah kita ingin bola berakhir di tempat yang sama setelah beberapa waktu. Di bawah kondisi yang diberikan ini, bola dapat bergerak dengan dua cara berbeda. Pertama, dia hanya bisa diam. Kedua, Anda bisa mendorongnya ke arah dinding. Bola akan mencapai dinding, memantul dan kembali. Jelas bahwa Anda dapat mendorongnya dengan kecepatan sedemikian rupa sehingga ia akan kembali pada waktu yang tepat.

Kedua varian gerakan bola itu mungkin, tetapi aksi dalam kasus kedua akan lebih besar, karena selama ini bola akan bergerak dengan energi kinetik yang tidak nol.
Bagaimana prinsip tindakan terkecil dapat diselamatkan sehingga berlaku dalam situasi seperti itu? Kami akan membicarakan ini di.
Mereka mematuhinya, sehubungan dengan itu prinsip ini merupakan salah satu ketentuan utama fisika modern. Persamaan gerak yang diperoleh dengan bantuannya disebut persamaan Euler-Lagrange.
Rumusan pertama dari prinsip tersebut diberikan oleh P. Maupertuis pada tahun 1999, dengan segera menunjukkan sifat universalnya, mengingat dapat diterapkan pada optik dan mekanika. Dari prinsip ini, ia menurunkan hukum pemantulan dan pembiasan cahaya.
Cerita
Maupertuis sampai pada prinsip ini dari perasaan bahwa kesempurnaan alam semesta membutuhkan ekonomi tertentu di alam dan bertentangan dengan pengeluaran energi yang tidak berguna. Gerakan alami harus sedemikian rupa untuk membuat beberapa kuantitas minimum. Itu hanya perlu untuk menemukan nilai ini, yang terus dia lakukan. Itu adalah produk dari durasi (waktu) gerakan di dalam sistem dengan dua kali jumlah, yang sekarang kita sebut energi kinetik sistem.
Euler (dalam "Refleksi sur quelques loix generales de la nature", 1748) mengadopsi prinsip tindakan terkecil, menyebut tindakan "usaha". Ekspresinya dalam statika sesuai dengan apa yang sekarang kita sebut energi potensial, sehingga pernyataannya tentang aksi terkecil dalam statika setara dengan kondisi energi potensial minimum untuk konfigurasi kesetimbangan.
Dalam mekanika klasik
Prinsip aksi terkecil berfungsi sebagai dasar fundamental dan standar untuk formulasi mekanika Lagrangian dan Hamilton.
Mari kita pertimbangkan konstruksinya sedemikian rupa Mekanika Lagrangian. Dengan menggunakan contoh sistem fisik dengan satu derajat kebebasan, kita ingat bahwa suatu tindakan adalah fungsional sehubungan dengan koordinat (digeneralisasikan) (dalam kasus satu derajat kebebasan - satu koordinat), yaitu, dinyatakan melalui bahwa setiap versi fungsi yang dapat dibayangkan dikaitkan dengan angka tertentu - suatu tindakan (dalam pengertian ini, kita dapat mengatakan bahwa suatu tindakan sebagai suatu fungsi adalah aturan yang memungkinkan, untuk setiap fungsi yang diberikan, untuk menghitung angka yang terdefinisi dengan baik - disebut juga tindakan). Tindakannya terlihat seperti:
di mana Lagrangian sistem tergantung pada koordinat umum , turunan pertamanya terhadap waktu , dan juga, mungkin, secara eksplisit pada waktu . Jika sistem memiliki lebih banyak derajat kebebasan, maka Lagrangian bergantung pada sejumlah besar koordinat umum dan turunan pertama kali. Dengan demikian, aksi adalah fungsional skalar tergantung pada lintasan tubuh.
Fakta bahwa aksinya adalah skalar membuatnya mudah untuk menulisnya dalam koordinat umum apa pun, yang utama adalah bahwa posisi (konfigurasi) sistem dicirikan secara unik oleh mereka (misalnya, alih-alih koordinat Cartesian, ini bisa menjadi kutub koordinat, jarak antara titik-titik sistem, sudut atau fungsinya, dll. d.).
Tindakan dapat dihitung untuk lintasan yang sepenuhnya sewenang-wenang, tidak peduli seberapa "liar" dan "tidak wajar" itu. Namun, dalam mekanika klasik, di antara seluruh rangkaian lintasan yang mungkin, hanya ada satu lintasan yang benar-benar akan dilalui benda. Prinsip aksi stasioner hanya memberikan jawaban atas pertanyaan tentang bagaimana tubuh akan benar-benar bergerak:
Ini berarti bahwa jika Lagrangian sistem diberikan, maka dengan menggunakan kalkulus variasi kita dapat menentukan dengan tepat bagaimana benda akan bergerak, pertama-tama memperoleh persamaan gerak - persamaan Euler-Lagrange, dan kemudian menyelesaikannya. Ini memungkinkan tidak hanya untuk secara serius menggeneralisasi perumusan mekanika, tetapi juga untuk memilih koordinat yang paling nyaman untuk setiap masalah spesifik, tidak terbatas pada masalah Cartesian, yang bisa sangat berguna untuk mendapatkan persamaan yang paling sederhana dan paling mudah diselesaikan.
di mana adalah fungsi Hamilton dari sistem yang diberikan; - koordinat (digeneralisasi), - impuls konjugasi (digeneralisasi), mencirikan bersama pada setiap saat waktu tertentu keadaan dinamis sistem dan, masing-masing merupakan fungsi waktu, dengan demikian mencirikan evolusi (pergerakan) sistem. Dalam hal ini, untuk mendapatkan persamaan gerak sistem dalam bentuk persamaan Hamilton kanonik, perlu untuk memvariasikan aksi yang ditulis dengan cara ini secara independen untuk semua dan .
Perlu dicatat bahwa jika pada prinsipnya mungkin untuk menemukan hukum gerak dari kondisi masalah, maka ini secara otomatis bukan berarti bahwa adalah mungkin untuk membangun suatu fungsi yang mengambil nilai stasioner selama gerak sebenarnya. Contohnya adalah gerakan bersama antara muatan listrik dan monopol - muatan magnet - dalam medan elektromagnetik. Persamaan gerak mereka tidak dapat diturunkan dari prinsip stasioneritas aksi. Demikian pula, beberapa sistem Hamilton memiliki persamaan gerak yang tidak mengikuti prinsip ini.
Contoh
Contoh-contoh sepele membantu mengevaluasi penggunaan prinsip operasi melalui persamaan Euler-Lagrange. Partikel bebas (massa m dan kecepatan v) dalam ruang Euclidean bergerak dalam garis lurus. Menggunakan persamaan Euler-Lagrange, ini dapat ditunjukkan dalam koordinat kutub sebagai berikut. Dengan tidak adanya potensi, fungsi Lagrange sama dengan energi kinetik
dalam sistem koordinat ortogonal.
Dalam koordinat kutub, energi kinetik, dan karenanya fungsi Lagrange, menjadi
Komponen radial dan sudut dari persamaan menjadi, masing-masing:
Memecahkan dua persamaan ini
Di sini, adalah catatan bersyarat integrasi fungsional lipatan tak terhingga atas semua lintasan x(t), dan merupakan konstanta Planck. Kami menekankan bahwa, pada prinsipnya, aksi dalam eksponensial muncul (atau dapat muncul) dengan sendirinya, ketika mempelajari operator evolusi dalam mekanika kuantum, namun, untuk sistem yang memiliki analog klasik (non-kuantum) eksak, itu persis sama dengan tindakan klasik biasa.
Analisis matematis dari ekspresi ini dalam batas klasik - untuk cukup besar , yaitu, untuk osilasi eksponen imajiner yang sangat cepat - menunjukkan bahwa sebagian besar dari semua lintasan yang mungkin dalam integral ini saling meniadakan dalam batas (secara formal, pada ) . Untuk hampir semua jalur, ada jalur di mana serangan fase akan persis berlawanan, dan mereka akan menambahkan hingga kontribusi nol. Hanya lintasan yang aksinya mendekati nilai ekstrem (untuk sebagian besar sistem - minimum) yang tidak dikurangi. Ini adalah fakta matematis murni dari teori fungsi variabel kompleks; misalnya, metode fase diam didasarkan padanya.
Akibatnya, partikel, sesuai sepenuhnya dengan hukum mekanika kuantum, bergerak sepanjang semua lintasan secara bersamaan, tetapi dalam kondisi normal, hanya lintasan yang dekat dengan stasioner (yaitu, klasik) yang berkontribusi pada nilai yang diamati. Karena mekanika kuantum menjadi klasik dalam batas energi tinggi, kita dapat berasumsi bahwa ini adalah - derivasi mekanika kuantum dari prinsip klasik stasioneritas aksi.
Dalam teori medan kuantum
Dalam teori medan kuantum, prinsip stasioneritas aksi juga berhasil diterapkan. Kepadatan Lagrangian di sini mencakup operator dari medan kuantum yang sesuai. Meskipun lebih tepat di sini pada intinya (dengan pengecualian batas klasik dan sebagian semiklasik) untuk berbicara bukan tentang prinsip stasioneritas aksi, tetapi tentang integrasi Feynman atas lintasan dalam konfigurasi atau ruang fase bidang ini - menggunakan Kepadatan Lagrangian baru saja disebutkan.
Generalisasi lebih lanjut
Secara lebih luas, aksi dipahami sebagai fungsi yang mendefinisikan pemetaan dari ruang konfigurasi ke himpunan bilangan real dan, secara umum, tidak harus integral, karena aksi non-lokal pada prinsipnya mungkin, setidaknya secara teoretis. Selain itu, ruang konfigurasi belum tentu merupakan ruang fungsi karena dapat memiliki geometri non-komutatif.
2.2. Prinsip tindakan paling sedikit
Pada abad ke-18, akumulasi dan sistematisasi lebih lanjut dari hasil ilmiah terjadi, ditandai dengan kecenderungan untuk menggabungkan pencapaian ilmiah individu ke dalam gambaran dunia yang teratur dan koheren melalui penerapan sistematis metode analisis matematis untuk mempelajari fenomena fisik. Karya banyak pemikir brilian ke arah ini telah mengarah pada penciptaan teori dasar dari program penelitian mekanistik - mekanika analitik, atas dasar berbagai teori fundamental yang telah dibuat yang menggambarkan kelas konsep tertentu.
fenomena: hidrodinamika, teori elastisitas, aerodinamika, dll. Salah satu hasil terpenting dari mekanika analitik adalah prinsip aksi terkecil (prinsip variasi), yang penting untuk memahami proses yang terjadi dalam fisika pada akhir abad ke-20.
Akar munculnya prinsip variasi dalam sains kembali ke Yunani Kuno dan dikaitkan dengan nama Bangau dari Alexandria. Ide dari setiap prinsip variasi adalah untuk memvariasikan (mengubah) nilai tertentu yang menjadi ciri proses tertentu, dan memilih dari semua proses yang mungkin proses yang nilai ini mengambil nilai ekstrem (maksimum atau minimum). Bangau mencoba menjelaskan hukum pemantulan cahaya dengan memvariasikan nilai yang mencirikan panjang lintasan yang dilalui seberkas cahaya dari sumber ke pengamat ketika dipantulkan dari cermin. Dia sampai pada kesimpulan bahwa dari semua jalur yang mungkin, seberkas cahaya memilih yang terpendek (dari semua kemungkinan geometris).
Pada abad ke-17, dua ribu tahun kemudian, matematikawan Prancis Fermat menarik perhatian pada prinsip Heron, memperluasnya ke media dengan indeks bias yang berbeda, dan oleh karena itu memformulasikannya kembali dalam bentuk waktu. Prinsip Fermat menyatakan bahwa dalam medium bias yang sifat-sifatnya tidak bergantung pada waktu, seberkas cahaya yang melewati dua titik memilih jalur untuk dirinya sendiri sehingga waktu yang diperlukan untuk melakukan perjalanan dari titik pertama ke titik kedua adalah minimal. Prinsip Heron ternyata merupakan kasus khusus dari prinsip Fermat untuk media dengan indeks bias konstan.
Prinsip Fermat menarik perhatian orang-orang sezaman. Di satu sisi, dia adalah bukti terbaik dari "prinsip ekonomi" di alam, dari rencana ilahi rasional yang diwujudkan dalam struktur dunia, di sisi lain, dia bertentangan dengan teori cahaya korpuskular Newton. Menurut Newton, ternyata pada media yang lebih rapat kecepatan cahaya seharusnya lebih besar, sedangkan menurut prinsip Fermat, pada media yang lebih rapat kecepatan cahaya menjadi lebih kecil.
Pada tahun 1740, matematikawan Pierre Louis Moreau de Maupertuis, secara kritis menganalisis prinsip Fermat dan mengikuti prinsip teologis.
motif logis tentang kesempurnaan dan perangkat paling ekonomis Semesta, dinyatakan dalam karya "Pada berbagai hukum alam yang tampaknya tidak sesuai" prinsip tindakan paling sedikit. Maupertuis meninggalkan waktu tersingkat Fermat dan memperkenalkan konsep baru - aksi. Aksinya sama dengan produk momentum benda (momentum = mV) dan lintasan yang ditempuh benda. Waktu tidak memiliki keunggulan dibandingkan ruang, dan sebaliknya. Oleh karena itu, cahaya tidak memilih jalur terpendek dan bukan waktu terpendek untuk menempuhnya, tetapi, menurut Maupertuis, "memilih jalur yang memberikan ekonomi yang lebih nyata: jalur yang dilaluinya adalah jalur yang besarnya tindakannya minimal." Prinsip tindakan terkecil dikembangkan lebih lanjut dalam karya Euler dan Lagrange; dia adalah dasar di mana Lagrange mengembangkan area baru analisis matematis - kalkulus variasi. Prinsip ini selanjutnya digeneralisasikan dan diselesaikan dalam karya Hamilton. Dalam bentuk umum, prinsip aksi terkecil menggunakan konsep aksi yang dinyatakan bukan dalam momentum, tetapi dalam fungsi Lagrange. Untuk kasus satu partikel bergerak dalam beberapa medan potensial, fungsi Lagrange dapat direpresentasikan sebagai perbedaan kinetika ![]() dan energi potensial:
dan energi potensial:
(Konsep "energi" dibahas secara rinci dalam Bab 3 bagian ini.)
Produknya disebut aksi elementer. Tindakan total adalah jumlah dari semua nilai selama seluruh interval waktu yang dipertimbangkan, dengan kata lain, tindakan total A:

Persamaan gerak partikel dapat diperoleh dengan menggunakan prinsip aksi terkecil, yang menurutnya gerakan nyata terjadi sedemikian rupa sehingga aksinya menjadi ekstrem, yaitu variasinya berubah menjadi 0:
![]()
Prinsip variasi Lagrange-Hamilton dengan mudah memungkinkan perluasan ke sistem yang terdiri dari non-
berapa banyak (banyak) partikel. Gerak sistem seperti itu biasanya dianggap dalam ruang abstrak (teknik matematika yang nyaman) dari sejumlah besar dimensi. Katakanlah, untuk N titik, beberapa ruang abstrak dari koordinat 3N partikel N diperkenalkan, membentuk sistem yang disebut ruang konfigurasi. Urutan keadaan sistem yang berbeda diwakili oleh kurva di ruang konfigurasi ini - lintasan. Mempertimbangkan semua kemungkinan jalur yang menghubungkan dua titik tertentu dari ruang dimensi 3N ini, dapat dipastikan bahwa gerakan nyata dari sistem terjadi sesuai dengan prinsip aksi terkecil: di antara semua lintasan yang mungkin, lintasan yang aksinya ekstrem seluruh interval waktu gerakan direalisasikan.
Saat meminimalkan aksi dalam mekanika klasik, persamaan Euler-Lagrange diperoleh, yang hubungannya dengan hukum Newton sudah diketahui. Persamaan Euler-Lagrange untuk Lagrangian medan elektromagnetik klasik berubah menjadi persamaan Maxwell. Jadi, kita melihat bahwa penggunaan Lagrangian dan prinsip aksi terkecil memungkinkan seseorang untuk mengatur dinamika partikel. Namun, Lagrangian memiliki satu fitur penting lagi, yang menjadikan formalisme Lagrangian sebagai yang utama dalam menyelesaikan hampir semua masalah fisika modern. Faktanya adalah bahwa bersama dengan mekanika Newton dalam fisika, sudah pada abad ke-19, hukum kekekalan dirumuskan untuk beberapa besaran fisika: hukum kekekalan energi, hukum kekekalan momentum, hukum kekekalan momentum sudut, hukum tentang kekekalan muatan listrik. Jumlah hukum kekekalan sehubungan dengan perkembangan fisika kuantum dan fisika partikel elementer di abad kita ini semakin banyak. Timbul pertanyaan bagaimana menemukan dasar umum untuk menulis persamaan gerak (misalnya, hukum Newton atau persamaan Maxwell) dan besaran yang dilestarikan dalam waktu. Ternyata dasar seperti itu adalah penggunaan formalisme Lagrangian, karena Lagrangian teori tertentu ternyata invarian (tidak berubah) sehubungan dengan transformasi yang sesuai dengan ruang abstrak spesifik yang dipertimbangkan dalam teori ini, yang menghasilkan konservasi hukum. Fitur-fitur Lagrangian ini
tidak mengarah pada kelayakan merumuskan teori fisika dalam bahasa Lagrangian. Realisasi keadaan ini datang ke fisika karena munculnya teori relativitas Einstein.
| " |
