Ini adalah bagian matematika yang agak menarik yang benar-benar dihadapi oleh semua mahasiswa pascasarjana dan mahasiswa. Namun, tidak semua orang menyukai matan. Beberapa gagal untuk memahami bahkan hal-hal dasar seperti studi fungsi yang tampaknya standar. Artikel ini bertujuan untuk mengoreksi kekeliruan tersebut. Ingin mempelajari lebih lanjut tentang analisis fungsi? Apakah Anda ingin tahu apa itu titik ekstrem dan bagaimana menemukannya? Maka artikel ini untuk Anda.
Penyelidikan grafik fungsi
Untuk memulainya, ada baiknya memahami mengapa perlu menganalisis grafik sama sekali. Ada fungsi sederhana yang mudah digambar. Contoh mencolok dari fungsi tersebut adalah parabola. Tidak sulit untuk menggambar grafiknya. Yang diperlukan hanyalah, menggunakan transformasi sederhana, untuk menemukan bilangan di mana fungsi tersebut bernilai 0. Dan pada prinsipnya, ini saja yang perlu Anda ketahui untuk menggambar grafik parabola.
Tetapi bagaimana jika fungsi yang kita butuhkan untuk membuat grafik jauh lebih rumit? Karena sifat-sifat fungsi kompleks agak tidak jelas, maka perlu dilakukan analisis menyeluruh. Hanya dengan demikian fungsi tersebut dapat direpresentasikan secara grafis. Bagaimana cara melakukannya? Anda dapat menemukan jawaban untuk pertanyaan ini di artikel ini.
Rencana analisis fungsi
Hal pertama yang harus dilakukan adalah melakukan studi dangkal fungsi, di mana kita akan menemukan domain definisi. Jadi, mari kita mulai secara berurutan. Domain definisi adalah himpunan nilai-nilai yang dengannya fungsi didefinisikan. Sederhananya, ini adalah angka yang dapat digunakan dalam fungsi alih-alih x. Untuk menentukan ruang lingkup, Anda hanya perlu melihat catatan. Misalnya, jelas bahwa fungsi y (x) \u003d x 3 + x 2 - x + 43 memiliki domain definisi - himpunan bilangan real. Nah, dengan fungsi seperti (x 2 - 2x) / x, semuanya sedikit berbeda. Karena angka dalam penyebut tidak boleh sama dengan 0, maka domain dari fungsi ini adalah semua bilangan real, kecuali nol.
Selanjutnya, Anda perlu menemukan apa yang disebut nol dari fungsi tersebut. Ini adalah nilai argumen yang seluruh fungsi mengambil nilai nol. Untuk melakukan ini, perlu menyamakan fungsi dengan nol, mempertimbangkannya secara rinci dan melakukan beberapa transformasi. Mari kita ambil fungsi yang sudah dikenal y(x) = (x 2 - 2x)/x. Dari pelajaran sekolah, kita tahu bahwa pecahan adalah 0 jika pembilangnya nol. Oleh karena itu, kami membuang penyebutnya dan mulai bekerja dengan pembilangnya, menyamakannya dengan nol. Kami mendapatkan x 2 - 2x \u003d 0 dan mengeluarkan x dari tanda kurung. Oleh karena itu x (x - 2) \u003d 0. Akibatnya, kami mendapatkan bahwa fungsi kami sama dengan nol ketika x sama dengan 0 atau 2.
Selama mempelajari grafik fungsi, banyak orang menemukan masalah berupa titik ekstrem. Dan itu aneh. Bagaimanapun, ekstrem adalah topik yang agak sederhana. Tidak percaya? Lihat sendiri dengan membaca bagian artikel ini, di mana kita akan berbicara tentang poin minimum dan maksimum.

Untuk memulainya, ada baiknya memahami apa itu ekstrem. Ekstrem adalah nilai batas yang dicapai suatu fungsi pada grafik. Dari sini ternyata ada dua nilai ekstrem - maksimum dan minimum. Agar lebih jelas, Anda bisa melihat gambar di atas. Pada area yang diselidiki, titik -1 adalah fungsi maksimum y (x) \u003d x 5 - 5x, dan titik 1, masing-masing, adalah minimum.
Juga, jangan bingung konsep satu sama lain. Titik ekstrem dari suatu fungsi adalah argumen di mana fungsi yang diberikan memperoleh nilai ekstrem. Pada gilirannya, ekstrem adalah nilai minimum dan maksimum fungsi. Sebagai contoh, perhatikan kembali gambar di atas. -1 dan 1 adalah titik ekstrem dari fungsi tersebut, dan 4 dan -4 adalah titik ekstrem itu sendiri.
Menemukan titik ekstrem

Tetapi bagaimana Anda menemukan titik ekstrem suatu fungsi? Semuanya cukup sederhana. Hal pertama yang harus dilakukan adalah mencari turunan dari persamaan tersebut. Katakanlah kita mendapat tugas: "Temukan titik ekstrem dari fungsi y (x), x adalah argumennya. Untuk lebih jelasnya, mari kita ambil fungsi y (x) \u003d x 3 + 2x 2 + x + 54. Mari kita bedakan dan dapatkan persamaan berikut: 3x 2 + 4x + 1. Hasilnya, kami mendapatkan persamaan kuadrat standar. Yang perlu dilakukan hanyalah menyamakannya dengan nol dan menemukan akarnya. Karena diskriminan lebih besar dari nol (D \u003d 16 - 12 \u003d 4), persamaan ini ditentukan oleh dua akar. Kami menemukannya dan mendapatkan dua nilai: 1/3 dan -1. Ini akan menjadi titik ekstrem dari fungsi tersebut. Namun, bagaimana Anda masih bisa menentukan siapa siapa? Titik mana yang maksimum dan mana yang minimum? Untuk melakukan ini, Anda perlu mengambil titik tetangga dan mencari nilainya. Misalnya, mari kita ambil angka -2, yang ada di sebelah kiri sepanjang koordinat garis dari -1. Kita substitusikan nilai ini ke persamaan kita y (-2) = 12 - 8 + 1 = 5. Hasilnya, kita mendapatkan bilangan positif. Artinya, pada interval dari 1/3 ke -1 fungsi meningkat, yang pada gilirannya berarti bahwa pada interval dari min dari tak terhingga ke 1/3 dan dari -1 hingga plus tak terhingga, fungsi menurun. Dengan demikian, kita dapat menyimpulkan bahwa angka 1/3 adalah titik minimum fungsi pada interval yang diselidiki, dan -1 adalah titik maksimum.

Perlu juga dicatat bahwa ujian tidak hanya membutuhkan untuk menemukan titik ekstrem, tetapi juga untuk melakukan beberapa jenis operasi dengannya (menambah, mengalikan, dll.). Karena alasan inilah perlu memberikan perhatian khusus pada kondisi masalah. Lagi pula, karena kurangnya perhatian, Anda bisa kehilangan poin.
Dari artikel ini, pembaca akan belajar tentang apa itu nilai fungsional ekstrem, serta tentang fitur penggunaannya dalam praktik. Studi tentang konsep semacam itu sangat penting untuk memahami dasar-dasar matematika yang lebih tinggi. Topik ini adalah dasar untuk studi yang lebih dalam dari kursus.
dalam kontak dengan
Apa itu ekstrem?
Dalam kursus sekolah, banyak definisi konsep "ekstrim" diberikan. Artikel ini dimaksudkan untuk memberikan pemahaman istilah yang paling dalam dan jelas bagi mereka yang tidak mengetahui masalah tersebut. Jadi, istilah dipahami sebagai sejauh mana interval fungsional memperoleh nilai minimum atau maksimum pada himpunan tertentu.
Ekstrem adalah nilai minimum dari fungsi dan maksimum pada saat yang bersamaan. Ada titik minimum dan titik maksimum, yaitu nilai ekstrem dari argumen pada grafik. Ilmu utama di mana konsep ini digunakan:
- statistik;
- kontrol mesin;
- ekonometrika.
Titik ekstrim memainkan peran penting dalam menentukan urutan fungsi yang diberikan. Sistem koordinat pada grafik yang terbaik menunjukkan perubahan posisi ekstrim tergantung pada perubahan fungsi.
Ekstrem dari fungsi turunan
Ada juga yang namanya "turunan". Penting untuk menentukan titik ekstrem. Penting untuk tidak mengacaukan poin minimum atau maksimum dengan nilai terbesar dan terkecil. Ini adalah konsep yang berbeda, meskipun mungkin tampak serupa.
Nilai fungsi merupakan faktor utama dalam menentukan cara mencari titik maksimum. Turunan tidak terbentuk dari nilai-nilai, tetapi secara eksklusif dari posisi ekstremnya dalam satu atau lain urutan.
Turunannya sendiri ditentukan berdasarkan data titik ekstrim, dan bukan nilai terbesar atau terkecil. Di sekolah-sekolah Rusia, garis antara kedua konsep ini tidak ditarik dengan jelas, yang mempengaruhi pemahaman topik ini secara umum.
Sekarang mari kita pertimbangkan hal seperti itu sebagai "ekstrim yang tajam". Sampai saat ini, ada nilai minimum akut dan nilai maksimum akut. Definisi tersebut diberikan sesuai dengan klasifikasi Rusia dari titik kritis suatu fungsi. Konsep titik ekstrem adalah dasar untuk menemukan titik kritis pada grafik.

Untuk mendefinisikan konsep seperti itu, digunakan teorema Fermat. Ini adalah yang paling penting dalam mempelajari titik-titik ekstrem dan memberikan gambaran yang jelas tentang keberadaan mereka dalam satu atau lain bentuk. Untuk memastikan ekstremitas, penting untuk membuat kondisi tertentu untuk penurunan atau peningkatan pada grafik.
Untuk menjawab pertanyaan "bagaimana menemukan poin maksimum" dengan tepat, Anda harus mengikuti ketentuan berikut:
- Menemukan area definisi yang tepat pada grafik.
- Mencari turunan dari suatu fungsi dan titik ekstrem.
- Memecahkan ketidaksetaraan standar untuk domain argumen.
- Mampu membuktikan di mana fungsi suatu titik pada graf terdefinisi dan kontinu.

Perhatian! Pencarian titik kritis dari suatu fungsi hanya mungkin jika ada turunan dari setidaknya orde kedua, yang dipastikan dengan proporsi yang tinggi dari keberadaan titik ekstrem.
Kondisi yang diperlukan untuk ekstrem dari fungsi
Agar ada ekstrem, penting bahwa ada titik minimum dan titik maksimum. Jika aturan ini dipatuhi hanya sebagian, maka kondisi keberadaan ekstrem dilanggar.

Setiap fungsi dalam posisi apapun harus dibedakan untuk mengidentifikasi makna barunya. Penting untuk dipahami bahwa kasus hilangnya suatu titik bukanlah prinsip utama untuk menemukan titik yang dapat diturunkan.
Sebuah ekstrim tajam, serta fungsi minimum, adalah aspek yang sangat penting dari memecahkan masalah matematika menggunakan nilai-nilai ekstrim. Untuk lebih memahami komponen ini, penting untuk merujuk pada nilai tabel untuk penugasan fungsional.
| Eksplorasi makna yang lengkap | Merencanakan Nilai |
| 1. Penentuan titik kenaikan dan penurunan nilai. 2. Mencari break point, ekstrim dan perpotongan dengan sumbu koordinat. 3. Proses penentuan perubahan posisi pada chart. 4. Penentuan indeks dan arah cembung dan cembung, dengan mempertimbangkan adanya asimtot. 5. Pembuatan tabel ringkasan penelitian dalam hal penentuan koordinatnya. 6. Menemukan interval kenaikan dan penurunan titik ekstrim dan akut. 7. Penentuan kecembungan dan kecekungan kurva. 8. Membangun grafik berdasarkan studi memungkinkan Anda menemukan minimum atau maksimum. |
Elemen utama, ketika perlu bekerja dengan ekstrem, adalah konstruksi grafiknya yang tepat. Guru sekolah sering tidak memberikan perhatian yang maksimal terhadap aspek penting seperti itu, yang merupakan pelanggaran berat terhadap proses pendidikan. Grafik dibangun hanya berdasarkan hasil studi data fungsional, definisi ekstrema tajam, serta titik-titik pada grafik. Ekstrem tajam turunan suatu fungsi ditampilkan pada plot nilai eksak menggunakan prosedur standar untuk menentukan asimtot. |
Perhatikan grafik fungsi kontinu y=f(x) ditunjukkan pada gambar.
Nilai fungsi pada titik x 1 akan lebih besar dari nilai fungsi di semua titik bertetangga baik ke kiri maupun ke kanan x satu . Dalam hal ini, fungsi dikatakan memiliki titik x 1 maks. Pada intinya x Fungsi 3 jelas juga sudah maksimal. Jika kita mempertimbangkan intinya x 2 , maka nilai fungsi di dalamnya lebih kecil dari semua nilai tetangganya. Dalam hal ini, fungsi dikatakan memiliki titik x 2 minimal. Demikian pula untuk intinya x 4 .
Fungsi y=f(x) pada intinya x 0 memiliki maksimum, jika nilai fungsi pada titik ini lebih besar dari nilainya di semua titik dari beberapa interval yang mengandung titik x 0 , yaitu jika ada lingkungan titik seperti itu x 0, yang untuk semua orang x≠x 0 , milik lingkungan ini, kami memiliki ketidaksetaraan f(x)<f(x 0 ) .
Fungsi y=f(x) Memiliki minimum pada intinya x 0 , jika ada lingkungan titik seperti itu x 0 , apa untuk semua orang? x≠x 0 milik lingkungan ini, kami memiliki ketidaksetaraan f(x)>f(x0.
Titik-titik di mana fungsi mencapai maksimum dan minimum disebut titik ekstrem, dan nilai fungsi pada titik-titik ini adalah titik ekstrem dari fungsi.
Mari kita perhatikan fakta bahwa suatu fungsi yang didefinisikan pada suatu segmen dapat mencapai maksimum dan minimumnya hanya pada titik-titik yang tercakup dalam segmen yang ditinjau.
Perhatikan bahwa jika suatu fungsi memiliki maksimum pada suatu titik, ini tidak berarti bahwa pada titik ini fungsi tersebut memiliki nilai maksimum di seluruh domain. Pada gambar yang dibahas di atas, fungsi pada titik x 1 memiliki maksimum, meskipun ada titik di mana nilai fungsi lebih besar dari pada titik x 1 . Secara khusus, f(x 1) < f(x 4) yaitu fungsi minimum lebih besar dari maksimum. Dari definisi maksimum, hanya berikut bahwa ini adalah nilai terbesar dari fungsi pada titik-titik yang cukup dekat dengan titik maksimum.
Teorema 1. (Kondisi yang diperlukan untuk keberadaan ekstrem.) Jika fungsi terdiferensiasi y=f(x) memiliki pada intinya x=x 0 ekstrim, maka turunannya pada titik ini menghilang.
Bukti. Biarkan, untuk kepastian, pada intinya x 0 fungsi memiliki maksimum. Kemudian untuk peningkatan yang cukup kecil x kita punya f(x 0 + Δ x)
Melewati ketidaksetaraan ini ke batas sebagai x→ 0 dan dengan mempertimbangkan bahwa turunan f "(x 0) ada, dan karenanya limit di sebelah kiri tidak bergantung pada bagaimana x→ 0, kita dapatkan: untuk x → 0 – 0 f"(x 0) 0 dan pada x → 0 + 0 f"(x 0) 0. Sejak f"(x 0) mendefinisikan suatu bilangan, maka kedua pertidaksamaan ini kompatibel hanya jika f"(x 0) = 0.
Teorema terbukti menyatakan bahwa poin maksimum dan minimum hanya dapat berada di antara nilai-nilai argumen yang turunannya hilang.
Kami telah mempertimbangkan kasus ketika suatu fungsi memiliki turunan di semua titik segmen tertentu. Apa yang terjadi jika turunannya tidak ada? Pertimbangkan contoh.
Contoh.
- kamu=|x|.
Fungsi tidak memiliki turunan di suatu titik x=0 (pada titik ini, grafik fungsi tidak memiliki garis singgung yang pasti), tetapi pada titik ini fungsi tersebut memiliki minimum, karena kamu(0)=0, dan untuk semua x≠ 0kamu > 0.
- Biarlah x< x
0 . Kemudian c< x
0 dan f "(c)> 0.
Jadi f "(c)(x-x 0)<
0 dan, oleh karena itu,
f(x) - f(x 0 )< 0, yaitu f(x)< f(x 0 ).
- Biarlah x > x 0 . Kemudian c> x 0 dan f"(c)< 0. Cara f "(c)(x-x 0)< 0. Jadi f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Temukan ruang lingkup suatu fungsi f(x).
- Tentukan turunan pertama dari suatu fungsi f"(x).
- Tentukan titik kritis, untuk ini:
- cari akar-akar nyata dari persamaan f"(x)=0;
- temukan semua nilai x di mana turunannya f"(x) tidak ada.
- Tentukan tanda turunan ke kiri dan kanan titik kritis. Karena tanda turunan tetap konstan di antara dua titik kritis, cukuplah untuk menentukan tanda turunan pada satu titik ke kiri dan pada satu titik di sebelah kanan titik kritis.
- Hitung nilai fungsi pada titik ekstrem.
- Temukan semua titik kritis suatu fungsi dalam interval ( a, b) dan hitung nilai fungsi pada titik-titik ini.
- Hitung nilai fungsi di ujung segmen untuk x=a, x=b.
- Dari semua nilai yang diperoleh, pilih yang terbesar dan terkecil.
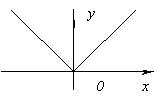
Fungsi tidak memiliki turunan di x=0, karena ia menuju tak terhingga ketika x=0. Namun pada titik ini, fungsinya sudah maksimal.

Fungsi tidak memiliki turunan di x=0 karena ![]() pada x→0. Pada titik ini, fungsi tidak memiliki maksimum atau minimum. Betulkah, f(x)=0 dan di x<0f(x)<0, а при x>0f(x)>0.
pada x→0. Pada titik ini, fungsi tidak memiliki maksimum atau minimum. Betulkah, f(x)=0 dan di x<0f(x)<0, а при x>0f(x)>0.

Jadi, dari contoh-contoh yang diberikan dan teorema yang dirumuskan, jelas bahwa fungsi dapat memiliki ekstrem hanya dalam dua kasus: 1) pada titik-titik di mana turunan ada dan sama dengan nol; 2) pada titik di mana turunan tidak ada.
Namun, jika pada suatu saat x 0 kita tahu itu f"(x 0 ) =0, maka tidak dapat disimpulkan bahwa pada titik x 0 fungsi memiliki ekstrem.
Misalnya. ![]() .
.

Tapi titik x=0 bukan titik ekstrem, karena di sebelah kiri titik ini nilai fungsi terletak di bawah sumbu Sapi, dan di atas di sebelah kanan.
Nilai argumen dari domain suatu fungsi, yang turunan fungsinya hilang atau tidak ada, disebut titik kritis.
Dari uraian di atas dapat disimpulkan bahwa titik-titik ekstrem suatu fungsi termasuk di antara titik-titik kritis, dan, bagaimanapun, tidak setiap titik kritis merupakan titik ekstrem. Oleh karena itu, untuk menemukan ekstrem dari fungsi tersebut, Anda perlu menemukan semua titik kritis dari fungsi tersebut, dan kemudian memeriksa masing-masing titik ini secara terpisah untuk maksimum dan minimum. Untuk ini, teorema berikut berfungsi.
Teorema 2. (Kondisi yang cukup untuk keberadaan ekstrem.) Biarkan fungsi kontinu pada beberapa interval yang mengandung titik kritis x 0 , dan terdiferensialkan di semua titik pada interval ini (kecuali, mungkin, titik itu sendiri x 0). Jika, ketika melewati dari kiri ke kanan melalui titik ini, turunannya berubah tanda dari plus ke minus, maka di titik x = x 0 fungsi memiliki maksimum. Jika, saat melewati x 0 dari kiri ke kanan, turunan berubah tanda dari minus ke plus, maka fungsi tersebut memiliki minimum pada titik ini.
Jadi, jika
Bukti. Mari kita asumsikan dulu bahwa ketika melewati x 0, turunannya berubah tanda dari plus ke minus, mis. untuk semua x dekat dengan intinya x 0 f "(x)> 0 untuk x< x 0 , f"(x)< 0 untuk x > x 0 . Mari kita terapkan teorema Lagrange pada perbedaan f(x) - f(x 0 ) = f "(c)(x- x 0), dimana c berada diantara x dan x 0 .
Jadi, untuk semua nilai x cukup dekat untuk x 0 f(x)< f(x 0 ) . Dan ini berarti pada intinya x 0 fungsi memiliki maksimum.
Bagian kedua dari teorema minimum dibuktikan dengan cara yang sama.

Mari kita ilustrasikan arti teorema ini pada gambar. Biarlah f"(x 1 ) =0 dan untuk sembarang x, cukup dekat untuk x 1, ketidaksetaraan
f"(x)< 0 at x< x 1 , f "(x)> 0 at x > x 1 .
Kemudian ke kiri titik x 1 fungsi meningkat, dan menurun di sebelah kanan, oleh karena itu, ketika x = x 1 fungsi berubah dari naik ke turun, yaitu memiliki maksimum.
Demikian pula, seseorang dapat mempertimbangkan poin x 2 dan x 3 .

Secara skematis, semua hal di atas dapat digambarkan dalam gambar:
Aturan untuk mempelajari fungsi y=f(x) untuk sebuah ekstrem
Contoh. Jelajahi fungsi untuk minimum dan maksimum.
NILAI FUNGSI TERBESAR DAN MINIMUM PADA INTERCEPT
terbesar nilai suatu fungsi pada suatu segmen adalah yang terbesar dari semua nilainya pada segmen ini, dan paling sedikit adalah yang terkecil dari semua nilainya.
Pertimbangkan fungsinya y=f(x) kontinu pada interval [ a, b]. Seperti diketahui, fungsi seperti itu mencapai nilai maksimum dan minimumnya, baik pada batas segmen, atau di dalamnya. Jika nilai maksimum atau minimum dari fungsi tercapai pada titik internal segmen, maka nilai ini adalah maksimum atau minimum fungsi, yaitu dicapai pada titik kritis.
Dengan demikian, kita mendapatkan yang berikut aturan untuk menemukan nilai terbesar dan terkecil dari suatu fungsi pada segmen [ a, b] :
>> Ekstrem
Fungsi ekstrem
definisi ekstrem
Fungsi y = f(x) disebut meningkat (memudar) dalam beberapa interval jika untuk x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).
Jika fungsi terdiferensiasi y \u003d f (x) pada segmen meningkat (menurun), maka turunannya pada segmen ini f " (x )> 0
(f"(x)< 0).
Dot x tentang ditelepon titik maksimum lokal (minimum) dari fungsi f (x ) jika ada lingkungan dari titik x o, untuk semua titik yang pertidaksamaannya f (x)≤ f (x o) (f (x)≥ f (x o )).
Titik maksimum dan minimum disebut titik ekstrim, dan nilai fungsi pada titik-titik ini adalah ekstrim.
titik ekstrim
Kondisi yang diperlukan untuk ekstrem . Jika titik x tentang adalah titik ekstrem dari fungsi f (x), maka salah satu f " (x o ) = 0, atau f(x o ) tidak ada. Titik-titik seperti itu disebut kritis, di mana fungsi itu sendiri didefinisikan pada titik kritis. Ekstrem suatu fungsi harus dicari di antara titik-titik kritisnya.
Syarat pertama yang cukup. Biarlah x tentang - titik kritis. jika f" (x ) saat melewati titik x tentang ubah tanda plus menjadi minus, lalu di titik x o fungsi memiliki maksimum, jika tidak, ia memiliki minimum. Jika turunan tidak berubah tanda saat melewati titik kritis, maka pada titik x tentang tidak ada ekstrem.
Syarat cukup kedua.
Misalkan fungsi f(x) memiliki
f" (x ) di sekitar titik x
tentang
dan turunan kedua di titik yang tepat x o. jika f"(x o) = 0, >0 ( <0), то точка x o adalah titik minimum (maksimum) lokal dari fungsi f(x). Jika = 0, maka seseorang harus menggunakan kondisi cukup pertama, atau melibatkan yang lebih tinggi.
Pada suatu segmen, fungsi y \u003d f (x) dapat mencapai nilai terkecil atau terbesar baik di titik kritis maupun di ujung segmen.
Contoh 3.22.
Keputusan. Sebagai f " (
Tugas untuk menemukan ekstrem dari suatu fungsi
Contoh 3.23. sebuah
Keputusan. x dan kamu kamu
0
≤ x≤
> 0, sedangkan x >a/4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
fungsi persegi.
unit).
Contoh 3.24. p
Keputusan. hal
S"
R = 2, H = 16/4 = 4.
Contoh 3.22.Tentukan ekstrem dari fungsi f (x) = 2x 3 - 15x 2 + 36x - 14.
Keputusan. Sebagai f " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), maka titik kritis fungsi x 1 \u003d 2 dan x 2 \u003d 3. Titik ekstrem hanya dapat berada di titik ini poin. Karena ketika melewati titik x 1 \u003d 2, turunannya berubah tanda dari plus ke minus, maka pada titik ini fungsinya maksimal. Ketika melewati titik x 2 \u003d 3, turunannya berubah tanda dari minus menjadi plus, oleh karena itu, pada titik x 2 \u003d 3, fungsinya memiliki minimum. Menghitung nilai fungsi dalam poin
x 1 = 2 dan x 2 = 3, kita menemukan ekstrem dari fungsi: maksimum f (2) = 14 dan minimum f (3) = 13.
Contoh 3.23.Perlu untuk membangun area persegi panjang di dekat dinding batu sehingga dipagari dengan wire mesh di tiga sisi, dan berdampingan dengan dinding di sisi keempat. Untuk ini ada sebuah meter linier dari grid. Pada rasio aspek apa situs akan memiliki area terbesar?
Keputusan.Tunjukkan sisi situs melalui x dan kamu. Luas situs sama dengan S = xy. Biarlah kamu adalah panjang sisi yang berdekatan dengan dinding. Maka, dengan syarat, persamaan 2x + y = a harus berlaku. Oleh karena itu y = a - 2x dan S = x (a - 2x), dimana
0
≤ x≤ a /2 (panjang dan lebar pad tidak boleh negatif). S "= a - 4x, a - 4x = 0 untuk x = a/4, dari mana
y \u003d a - 2 × a / 4 \u003d a / 2. Sejauh x = a /4 adalah satu-satunya titik kritis, mari kita periksa apakah tanda turunannya berubah ketika melewati titik ini. Untuk x a/4 S"> 0, sedangkan x >a/4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
fungsi S(a/4) = a/4(a - a/2) = a 2 /8 (persegi.
unit).
Karena S kontinu dan nilainya di ujung S(0) dan S(a/2) sama dengan nol, maka nilai yang ditemukan akan menjadi nilai terbesar dari fungsi tersebut. Jadi, aspek rasio yang paling menguntungkan dari situs di bawah kondisi masalah yang diberikan adalah y = 2x.
Contoh 3.24.Diperlukan untuk membuat tangki silinder tertutup dengan kapasitas V=16 p 50 m 3. Berapa dimensi tangki (jari-jari R dan tinggi H) agar dapat menggunakan bahan paling sedikit untuk pembuatannya?
Keputusan.Luas permukaan total silinder adalah S = 2 p R(R+H). Diketahui volume tabung V = p R 2 N N \u003d V / p R 2 \u003d 16 p / p R 2 \u003d 16 / R 2. Jadi S(R) = 2 p (R2+16/R). Kami menemukan turunan dari fungsi ini:
S"(R) \u003d 2 p (2R- 16 / R 2) \u003d 4 p (R- 8 / R 2). S" (R) = 0 untuk R 3 = 8, oleh karena itu,
R = 2, H = 16/4 = 4.
Fungsi, sama sekali tidak perlu mengetahui keberadaan turunan pertama dan kedua serta memahami makna fisisnya. Pertama, Anda perlu memahami hal berikut:
- ekstrem dari fungsi memaksimalkan atau, sebaliknya, meminimalkan nilai fungsi dalam lingkungan kecil yang sewenang-wenang;
- pada titik ekstrem seharusnya tidak ada diskontinuitas fungsi.
Dan sekarang hal yang sama, hanya dalam istilah sederhana. Lihatlah ujung bolpoin. Jika pena diletakkan secara vertikal, dengan tulisan berakhir, maka bagian paling tengah bola akan menjadi titik ekstrim – titik tertinggi. Dalam hal ini, kita berbicara tentang maksimum. Nah, jika Anda memutar pulpen dengan ujung tulisan ke bawah, maka di tengah bola sudah akan ada fungsi minimum. Dengan bantuan gambar yang diberikan di sini, Anda dapat membayangkan manipulasi yang terdaftar untuk pensil alat tulis. Jadi, ekstrem suatu fungsi selalu merupakan titik kritis: maksima atau minimanya. Bagian grafik yang berdekatan bisa tajam atau halus, tetapi harus ada di kedua sisi, hanya dalam hal ini titiknya adalah ekstrem. Jika grafik hanya ada di satu sisi, titik ini tidak akan menjadi ekstrem bahkan jika kondisi ekstrem terpenuhi di salah satu sisinya. Sekarang mari kita pelajari ekstrem fungsi dari sudut pandang ilmiah. Agar suatu titik dianggap ekstrem, perlu dan cukup bahwa:
- turunan pertama sama dengan nol atau tidak ada pada titik tersebut;
- turunan pertama berubah tanda pada titik ini.

Kondisi ini ditafsirkan agak berbeda dari sudut pandang turunan orde tinggi: untuk suatu fungsi yang terdiferensiasi pada suatu titik, cukup ada turunan orde ganjil yang tidak sama dengan nol, sedangkan semua turunan orde rendah harus ada dan sama dengan nol. Ini adalah interpretasi teorema paling sederhana dari buku teks, tetapi bagi kebanyakan orang biasa, perlu menjelaskan hal ini dengan sebuah contoh. Dasarnya adalah parabola biasa. Segera lakukan reservasi, pada titik nol memiliki minimum. Hanya sedikit matematika:
- turunan pertama (X 2) | = 2X, untuk titik nol 2X = 0;
- turunan kedua (2X) | = 2, untuk titik nol 2 = 2.

Sedemikian sederhana, kondisi yang menentukan ekstrem dari fungsi baik untuk turunan orde pertama dan turunan orde tinggi diilustrasikan. Dapat ditambahkan bahwa turunan kedua hanyalah turunan yang sama dari suatu orde ganjil, tidak sama dengan nol, yang disebutkan sedikit lebih tinggi. Ketika datang ke ekstrem dari fungsi dua variabel, kondisi harus dipenuhi untuk kedua argumen. Ketika generalisasi terjadi, maka turunan parsial ikut bermain. Artinya, perlu untuk keberadaan ekstrem pada titik di mana kedua turunan orde pertama sama dengan nol, atau setidaknya salah satunya tidak ada. Untuk kecukupan keberadaan ekstrem, ekspresi diselidiki, yang merupakan perbedaan antara produk turunan orde kedua dan kuadrat dari turunan orde kedua campuran fungsi. Jika ekspresi ini lebih besar dari nol, maka ada ekstrem, dan jika ada kesetaraan dengan nol, maka pertanyaannya tetap terbuka, dan penelitian tambahan diperlukan.
