Dengan matriks A, jika ada bilangan l sehingga AX = lX.

Dalam hal ini, nomor l disebut nilai eigen operator (matriks A) yang bersesuaian dengan vektor X.

Dengan kata lain, vektor eigen adalah vektor yang, di bawah aksi operator linier, berubah menjadi vektor collinear, yaitu. kalikan saja dengan beberapa angka. Sebaliknya, vektor yang tidak tepat lebih sulit untuk diubah.

Kami menulis definisi vektor eigen sebagai sistem persamaan:

Mari kita pindahkan semua suku ke ruas kiri:

Sistem terakhir dapat dituliskan dalam bentuk matriks sebagai berikut:

(A - lE)X \u003d O

Sistem yang dihasilkan selalu memiliki solusi nol X = O. Sistem yang semua suku bebasnya sama dengan nol disebut homogen. Jika matriks sistem seperti itu persegi, dan determinannya tidak sama dengan nol, maka menurut rumus Cramer, kita akan selalu mendapatkan solusi unik - nol. Dapat dibuktikan bahwa sistem memiliki solusi bukan-nol jika dan hanya jika determinan matriks ini sama dengan nol, yaitu

|A - lE| = = 0

Persamaan dengan l yang tidak diketahui ini disebut persamaan karakteristik (polinomial karakteristik) matriks A (operator linier).

Dapat dibuktikan bahwa polinomial karakteristik dari suatu operator linier tidak bergantung pada pilihan basis.

Sebagai contoh, mari kita cari nilai eigen dan vektor eigen dari operator linier yang diberikan oleh matriks A = .

Untuk melakukan ini, kami membuat persamaan karakteristik |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; nilai eigen l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

Untuk menemukan vektor eigen, kami memecahkan dua sistem persamaan

(A + 5E) X = O

(A - 7E) X = O

Untuk yang pertama, matriks yang diperluas akan berbentuk

,

dari mana x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, mis. X (1) \u003d (- (2/3) s; s).

Untuk yang kedua, matriks yang diperluas akan berbentuk

,

dari mana x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, mis. X (2) \u003d ((2/3) s 1; s 1).

Jadi, vektor eigen dari operator linier ini adalah semua vektor berbentuk (-(2/3)c; c) dengan nilai eigen (-5) dan semua vektor berbentuk ((2/3)c 1 ; c 1) dengan nilai eigen 7 .

Dapat dibuktikan bahwa matriks operator A pada basis yang terdiri dari vektor-vektor eigennya adalah diagonal dan berbentuk:

,

di mana l adalah nilai eigen dari matriks ini.

Kebalikannya juga benar: jika matriks A pada beberapa basis diagonal, maka semua vektor dari basis ini akan menjadi vektor eigen dari matriks ini.

Dapat juga dibuktikan bahwa jika suatu operator linier memiliki n nilai eigen yang berbeda secara berpasangan, maka vektor eigen yang bersesuaian adalah bebas linier, dan matriks dari operator ini pada basis yang bersesuaian memiliki bentuk diagonal.

Mari kita jelaskan ini dengan contoh sebelumnya. Mari kita ambil nilai tak-nol sembarang c dan c 1 , tetapi sedemikian rupa sehingga vektor X (1) dan X (2) bebas linier, mis. akan membentuk dasar. Misalnya, biarkan c \u003d c 1 \u003d 3, lalu X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Mari kita verifikasi independensi linier dari vektor-vektor ini:

12 0. Dalam basis baru ini, matriks A akan berbentuk A * = .

Untuk memverifikasi ini, kami menggunakan rumus A * = C -1 AC. Mari kita cari C -1 dulu.

C -1 = ;

Bentuk kuadrat

bentuk kuadrat f (x 1, x 2, x n) dari n variabel disebut jumlah, yang setiap sukunya merupakan kuadrat dari salah satu variabel, atau hasil kali dua variabel yang berbeda, diambil dengan koefisien tertentu: f (x 1 , x 2, x n) = (a ij = a ji).

Matriks A, terdiri dari koefisien-koefisien ini, disebut matriks bentuk kuadrat. Selalu simetris matriks (yaitu, matriks simetris tentang diagonal utama, a ij = a ji).

Dalam notasi matriks, bentuk kuadrat memiliki bentuk f(X) = X T AX, di mana

Memang

Sebagai contoh, mari kita tulis bentuk kuadrat dalam bentuk matriks.

Untuk melakukan ini, kami menemukan matriks berbentuk kuadrat. Elemen diagonalnya sama dengan koefisien pada kuadrat variabel, dan elemen lainnya sama dengan setengah dari koefisien yang sesuai dari bentuk kuadrat. Jadi

Biarkan kolom-matriks variabel X diperoleh dengan transformasi linier tak-degenerasi dari kolom-matriks Y, yaitu. X = CY, di mana C adalah matriks tak-degenerasi orde n. Maka bentuk kuadrat f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Jadi, di bawah transformasi linier non-degenerasi C, matriks bentuk kuadrat mengambil bentuk: A * = C T AC.

Sebagai contoh, mari kita cari bentuk kuadrat f(y 1, y 2) yang diperoleh dari bentuk kuadrat f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 dengan transformasi linier.

Bentuk kuadrat disebut resmi(Memiliki tampilan kanonik) jika semua koefisiennya a ij = 0 untuk i j, mis.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Matriksnya adalah diagonal.

Dalil(buktinya tidak diberikan di sini). Setiap bentuk kuadrat dapat direduksi menjadi bentuk kanonik menggunakan transformasi linier non-degenerasi.

Sebagai contoh, mari kita reduksi ke bentuk kanonik menjadi bentuk kuadrat
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Untuk melakukan ini, pertama-tama pilih kotak penuh untuk variabel x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

Sekarang kita pilih kotak penuh untuk variabel x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Kemudian transformasi linier non-degenerasi y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 dan y 3 \u003d x 3 membawa bentuk kuadrat ini ke bentuk kanonik f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Perhatikan bahwa bentuk kanonik dari bentuk kuadrat didefinisikan secara ambigu (bentuk kuadrat yang sama dapat direduksi menjadi bentuk kanonik dengan cara yang berbeda). Namun, bentuk kanonik yang diperoleh dengan berbagai metode memiliki sejumlah sifat umum. Secara khusus, jumlah suku dengan koefisien positif (negatif) dari bentuk kuadrat tidak bergantung pada bagaimana bentuk direduksi menjadi bentuk ini (misalnya, dalam contoh yang dipertimbangkan akan selalu ada dua koefisien negatif dan satu positif). Sifat ini disebut hukum inersia bentuk kuadrat.

Mari kita verifikasi ini dengan mengurangi bentuk kuadrat yang sama ke bentuk kanonik dengan cara yang berbeda. Mari kita mulai transformasi dengan variabel x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, di mana y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 dan y 3 = x 1 . Di sini, koefisien negatif -3 pada y 1 dan dua koefisien positif 3 dan 2 pada y 2 dan y 3 (dan menggunakan metode lain, kami mendapatkan koefisien negatif (-5) pada y 2 dan dua koefisien positif: 2 pada y 1 dan 1/20 untuk y 3).

Perlu juga diperhatikan bahwa pangkat suatu matriks berbentuk kuadrat, disebut pangkat dari bentuk kuadrat, sama dengan jumlah koefisien bukan-nol dari bentuk kanonik dan tidak berubah dalam transformasi linier.

Bentuk kuadrat f(X) disebut positif (negatif) yakin, jika untuk semua nilai variabel yang tidak serentak sama dengan nol, maka bernilai positif, yaitu f(X) > 0 (negatif, mis.
f(X)< 0).

Misalnya, bentuk kuadrat f 1 (X) \u003d x 1 2 + x 2 2 pasti positif, karena adalah jumlah kuadrat, dan bentuk kuadrat f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 pasti negatif, karena mewakili itu dapat direpresentasikan sebagai f 2 (X) \u003d - (x 1 - x 2) 2.

Dalam kebanyakan situasi praktis, agak lebih sulit untuk menetapkan ketegasan tanda dari bentuk kuadrat, jadi salah satu teorema berikut digunakan untuk ini (kami merumuskannya tanpa bukti).

Dalil. Suatu bentuk kuadrat adalah definit positif (negatif) jika dan hanya jika semua nilai eigen matriksnya positif (negatif).

Dalil(Kriteria Sylvester). Suatu bentuk kuadrat adalah definit positif jika dan hanya jika semua minor utama dari matriks bentuk ini adalah positif.

Mayor (sudut) minor Orde ke-k dari matriks A orde ke-n disebut determinan matriks, yang terdiri dari k baris dan kolom pertama dari matriks A ().

Perhatikan bahwa untuk bentuk kuadrat pasti negatif, tanda-tanda dari minor utama bergantian, dan minor orde pertama harus negatif.

Sebagai contoh, kita periksa bentuk kuadrat f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 untuk definiteness tanda.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Oleh karena itu, bentuk kuadrat adalah definit positif.

Metode 2. Minor utama dari matriks orde pertama A D 1 = a 11 = 2 > 0. Minor utama orde kedua D 2 = = 6 - 4 = 2 > 0. Oleh karena itu, menurut kriteria Sylvester, bentuk kuadrat adalah definit positif.

Kami memeriksa bentuk kuadratik lain untuk kepastian tanda, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metode 1. Mari kita buat matriks berbentuk kuadrat = . Persamaan karakteristik akan memiliki bentuk = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Oleh karena itu, bentuk kuadrat adalah definit negatif.

Metode 2. Minor utama dari matriks orde pertama A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Oleh karena itu, menurut kriteria Sylvester, bentuk kuadratnya pasti negatif (tanda-tanda dari minor utama bergantian, mulai dari minus).

Dan sebagai contoh lain, kami memeriksa bentuk kuadrat f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 untuk kepastian tanda.

Metode 1. Mari kita buat matriks berbentuk kuadrat = . Persamaan karakteristik akan memiliki bentuk = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Salah satu angka ini negatif dan yang lainnya positif. Tanda-tanda nilai eigen berbeda. Oleh karena itu, bentuk kuadrat tidak dapat berupa pasti negatif atau positif, mis. bentuk kuadrat ini tidak tanda-pasti (dapat mengambil nilai dari tanda apa pun).

Metode 2. Minor utama dari matriks orde pertama A D 1 = a 11 = 2 > 0. Minor utama orde kedua D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

Bagian pertama berisi ketentuan yang minimal diperlukan untuk memahami kemometrika, dan bagian kedua berisi fakta-fakta yang perlu Anda ketahui untuk pemahaman yang lebih dalam tentang metode analisis multivariat. Penyajiannya diilustrasikan dengan contoh yang dibuat di buku kerja Excel Matrix.xls yang menyertai dokumen ini.

Tautan ke contoh ditempatkan dalam teks sebagai objek Excel. Contoh-contoh ini bersifat abstrak; sama sekali tidak terkait dengan masalah kimia analitik. Contoh nyata penggunaan aljabar matriks dalam kemometrika dibahas dalam teks lain yang ditujukan untuk berbagai aplikasi kemometrik.

Sebagian besar pengukuran yang dilakukan dalam kimia analitik tidak langsung tetapi tidak langsung. Ini berarti bahwa dalam percobaan, alih-alih nilai analit C (konsentrasi) yang diinginkan, diperoleh nilai lain x(sinyal) terkait dengan tetapi tidak sama dengan C, yaitu. x(C) C. Sebagai aturan, jenis ketergantungan x(C) tidak diketahui, tetapi untungnya dalam kimia analitik sebagian besar pengukuran proporsional. Ini berarti bahwa sebagai konsentrasi C dalam sebuah kali, sinyal X akan meningkat dengan jumlah yang sama., yaitu. x(sebuah C) = sebuah x(C). Selain itu, sinyal juga bersifat aditif, sehingga sinyal dari sampel yang mengandung dua zat dengan konsentrasi C 1 dan C 2 akan sama dengan jumlah sinyal dari masing-masing komponen, yaitu. x(C1 + C2) = x(C1)+ x(C2). Proporsionalitas dan aditif bersama-sama memberi linearitas. Banyak contoh dapat diberikan untuk mengilustrasikan prinsip linieritas, tetapi cukup untuk menyebutkan dua contoh yang paling mencolok - kromatografi dan spektroskopi. Fitur kedua yang melekat dalam percobaan dalam kimia analitik adalah banyak saluran. Peralatan analitik modern secara bersamaan mengukur sinyal untuk banyak saluran. Misalnya, intensitas transmisi cahaya diukur untuk beberapa panjang gelombang sekaligus, mis. jangkauan. Oleh karena itu, dalam percobaan kita berhadapan dengan berbagai sinyal x 1 , x 2 ,...., x n mengkarakterisasi himpunan konsentrasi C 1 ,C 2 , ..., C m zat yang ada dalam sistem yang diteliti.

Beras. 1 Spektrum

Jadi, eksperimen analitik dicirikan oleh linearitas dan multidimensi. Oleh karena itu, lebih mudah untuk mempertimbangkan data eksperimen sebagai vektor dan matriks dan memanipulasinya menggunakan peralatan aljabar matriks. Keberhasilan pendekatan ini diilustrasikan oleh contoh yang ditunjukkan pada , yang menunjukkan tiga spektrum yang diambil untuk 200 panjang gelombang dari 4000 hingga 4796 cm-1. Pertama ( x 1) dan kedua ( x 2) spektrum diperoleh untuk sampel standar yang konsentrasi dua zat A dan B diketahui: pada sampel pertama [A] = 0,5, [B] = 0,1, dan pada sampel kedua [A] = 0,2, [ B] = 0,6. Apa yang dapat dikatakan tentang sampel baru yang tidak diketahui, spektrum yang ditunjukkan x 3 ?

Pertimbangkan tiga spektrum eksperimental x 1 , x 2 dan x 3 sebagai tiga vektor berdimensi 200. Dengan menggunakan aljabar linier, seseorang dapat dengan mudah menunjukkan bahwa x 3 = 0.1 x 1 +0.3 x 2 , jadi sampel ketiga jelas hanya mengandung zat A dan B dengan konsentrasi [A] = 0,5×0,1 + 0,2×0,3 = 0,11 dan [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Informasi dasar

1.1 Matriks

Matriks disebut tabel bilangan persegi panjang, misalnya

Beras. 2 Matriks

Matriks dilambangkan dengan huruf kapital tebal ( A), dan elemennya - dengan huruf kecil yang sesuai dengan indeks, mis. sebuah aku j . Indeks pertama nomor baris dan nomor kedua kolom. Dalam kemometrika, merupakan kebiasaan untuk menetapkan nilai maksimum indeks dengan huruf yang sama dengan indeks itu sendiri, tetapi dalam huruf kapital. Oleh karena itu, matriks A dapat juga ditulis sebagai ( sebuah aku j , saya = 1,..., Saya; j = 1,..., J). Untuk contoh matriks Saya = 4, J= 3 dan sebuah 23 = −7.5.

Pasangan angka Saya dan J disebut dimensi matriks dan dilambangkan sebagai Saya× J. Contoh matriks dalam kemometrika adalah seperangkat spektrum yang diperoleh untuk Saya sampel pada J panjang gelombang.

1.2. Operasi paling sederhana dengan matriks

Matriks bisa kalikan dengan angka. Dalam hal ini, setiap elemen dikalikan dengan angka ini. Sebagai contoh -

Beras. 3 Mengalikan matriks dengan angka

Dua matriks dengan dimensi yang sama dapat menjadi elemen-bijaksana melipat dan mengurangi. Sebagai contoh,

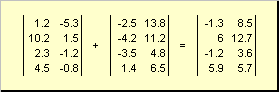
Beras. 4 Penambahan matriks

Sebagai hasil perkalian dengan bilangan dan penjumlahan, diperoleh matriks dengan dimensi yang sama.

Matriks nol adalah matriks yang terdiri dari nol. Ini ditunjuk HAI. Jelas bahwa A+HAI = A, A−A = HAI dan 0 A = HAI.

Matriks dapat mengubah urutan. Selama operasi ini, matriks dibalik, mis. baris dan kolom ditukar. Transposisi ditandai dengan tanda hubung, A" atau indeks A t . Jadi, jika A = {sebuah aku j , saya = 1,..., Saya; j = 1,...,J), kemudian A t = ( sebuah Ji , j = 1,...,J; saya = 1,..., Saya). Misalnya

Beras. 5 Transposisi matriks

Jelas bahwa ( A t) t = A, (A+B) t = A t + B t .

1.3. perkalian matriks

Matriks bisa berkembang biak, tetapi hanya jika mereka memiliki dimensi yang sesuai. Mengapa demikian akan menjadi jelas dari definisi. produk matriks A, dimensi Saya× K, dan matriks B, dimensi K× J, disebut matriks C, dimensi Saya× J, yang unsur-unsurnya adalah bilangan

Jadi untuk produk AB perlu bahwa jumlah kolom dalam matriks kiri A sama dengan jumlah baris pada matriks kanan B. Contoh produk matriks -

Gbr.6 Produk matriks

Aturan perkalian matriks dapat dirumuskan sebagai berikut. Untuk mencari elemen matriks C berdiri di persimpangan saya-baris dan j kolom -th ( c aku j) harus dikalikan elemen demi elemen saya-baris ke-ke dari matriks pertama A pada j-kolom ke-2 dari matriks kedua B dan jumlahkan semua hasilnya. Jadi dalam contoh yang ditunjukkan, elemen dari baris ketiga dan kolom kedua diperoleh sebagai jumlah dari produk-bijaksana elemen dari baris ketiga A dan kolom kedua B

Gbr.7 Elemen hasil kali matriks

Hasil kali matriks tergantung pada ordonya, mis. AB ≠ BA, setidaknya untuk alasan dimensional. Dikatakan tak komutatif. Namun, hasil kali matriks adalah asosiatif. Ini berarti bahwa ABC = (AB)C = A(SM). Selain itu, juga distributif, yaitu. A(B+C) = AB+AC. Jelas bahwa AO = HAI.

1.4. Matriks persegi

Jika jumlah kolom suatu matriks sama dengan jumlah barisnya ( Saya = J=N), maka matriks seperti itu disebut persegi. Pada bagian ini, kami hanya akan mempertimbangkan matriks seperti itu. Di antara matriks-matriks ini, seseorang dapat memilih matriks-matriks dengan sifat-sifat khusus.

Tersendiri matriks (dilambangkan Saya dan terkadang E) adalah matriks yang semua elemennya sama dengan nol, kecuali elemen diagonalnya sama dengan 1, yaitu

Jelas sekali AI = saya = A.

Matriks disebut diagonal, jika semua elemennya, kecuali elemen diagonalnya ( sebuah ii) sama dengan nol. Misalnya

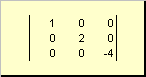
Beras. 8 Matriks diagonal

Matriks A disebut atas segitiga, jika semua elemennya yang terletak di bawah diagonal sama dengan nol, mis. sebuah aku j= 0, at saya>j. Misalnya

Beras. 9 Matriks segitiga atas

Matriks segitiga bawah didefinisikan dengan cara yang sama.

Matriks A ditelepon simetris, jika A t = A. Dengan kata lain sebuah aku j = sebuah Ji. Misalnya

Beras. 10 Matriks simetris

Matriks A ditelepon ortogonal, jika

A t A = A A t = Saya.

Matriks disebut normal jika

1.5. Jejak dan penentu

Mengikuti matriks persegi A(dilambangkan Tr( A) atau Sp( A)) adalah jumlah elemen diagonalnya,

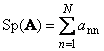
Sebagai contoh,

Beras. 11 Jejak matriks

Jelas bahwa

Sp(α A) = Sp( A) dan

Sp( A+B) = Sp( A)+ Sp( B).

Dapat ditunjukkan bahwa

Sp( A) = Sp( A t), Sp( Saya) = N,

dan juga itu

Sp( AB) = Sp( BA).

Karakteristik penting lainnya dari matriks persegi adalah penentu(dilambangkan dengan det( A)). Definisi determinan dalam kasus umum agak rumit, jadi kita akan mulai dengan opsi paling sederhana - matriks A dimensi (2×2). Kemudian

Untuk matriks (3×3), determinannya sama dengan

Dalam kasus matriks ( N× N) determinannya dihitung sebagai jumlah 1 2 3 ... N= N! suku, yang masing-masing sama dengan

indeks k 1 , k 2 ,..., k N didefinisikan sebagai semua kemungkinan permutasi berurutan r angka dalam himpunan (1, 2, ... , N). Perhitungan determinan matriks adalah prosedur yang kompleks, yang dalam praktiknya dilakukan dengan menggunakan program khusus. Sebagai contoh,

Beras. 12 Penentu Matriks

Kami hanya mencatat properti yang jelas:

det( Saya) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vektor

Jika matriks hanya memiliki satu kolom ( J= 1), maka benda tersebut disebut vektor. Lebih tepatnya, vektor kolom. Misalnya

Matriks yang terdiri dari satu baris juga dapat dipertimbangkan, misalnya

Objek ini juga merupakan vektor, tetapi vektor baris. Saat menganalisis data, penting untuk memahami vektor mana yang kita hadapi - kolom atau baris. Jadi spektrum yang diambil untuk satu sampel dapat dianggap sebagai vektor baris. Kemudian himpunan intensitas spektral pada beberapa panjang gelombang untuk semua sampel harus diperlakukan sebagai vektor kolom.

Dimensi vektor adalah jumlah elemennya.

Jelas bahwa vektor kolom apa pun dapat diubah menjadi vektor baris dengan transposisi, mis.

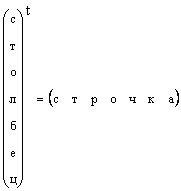
Dalam kasus di mana bentuk vektor tidak ditentukan secara spesifik, tetapi hanya dikatakan vektor, maka itu berarti vektor kolom. Kami juga akan mematuhi aturan ini. Sebuah vektor dilambangkan dengan huruf kecil huruf tebal langsung. Vektor nol adalah vektor yang semua elemennya sama dengan nol. Ini dilambangkan 0 .

1.7. Operasi paling sederhana dengan vektor

Vektor dapat ditambahkan dan dikalikan dengan angka dengan cara yang sama seperti matriks. Sebagai contoh,

Beras. 13 Operasi dengan vektor

Dua vektor x dan kamu ditelepon kolinear, jika ada bilangan sehingga

1.8. Produk dari vektor

Dua vektor dengan dimensi yang sama N bisa berlipat ganda. Misalkan ada dua vektor x = (x 1 , x 2 ,...,x N) t dan kamu = (kamu 1 , kamu 2 ,...,kamu N) t . Dipandu oleh aturan perkalian "baris demi kolom", kita dapat membuat dua produk darinya: x t kamu dan xy t . Pekerjaan pertama

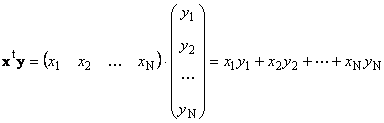
ditelepon skalar atau intern. Hasilnya adalah angka. Ini juga menggunakan notasi ( x,kamu)= x t kamu. Sebagai contoh,

Beras. 14 Produk dalam (skalar)

Pekerjaan kedua

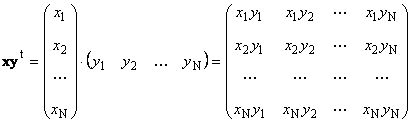
ditelepon luar. Hasilnya adalah matriks dimensi ( N× N). Sebagai contoh,

Beras. 15 Produk luar

Vektor yang hasil kali skalarnya sama dengan nol disebut ortogonal.

1.9. Norma vektor

Produk skalar dari vektor dengan dirinya sendiri disebut persegi skalar. Nilai ini

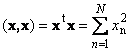
mendefinisikan persegi panjang vektor x. Untuk menunjukkan panjang (juga disebut norma vektor) notasi yang digunakan

Sebagai contoh,

Beras. 16 Vektor norma

Vektor satuan panjang (|| x|| = 1) disebut dinormalisasi. Vektor bukan nol ( x ≠ 0 ) dapat dinormalisasi dengan membaginya dengan panjang, yaitu x = ||x|| (x/||x||) = ||x|| e. Di Sini e = x/||x|| adalah vektor yang dinormalisasi.

Vektor disebut ortonormal jika semuanya ternormalisasi dan ortogonal berpasangan.

1.10. Sudut antar vektor

Produk skalar mendefinisikan dan injeksi antara dua vektor x dan kamu

Jika vektor-vektornya ortogonal, maka cosφ = 0 dan = /2, dan jika kolinear, maka cosφ = 1 dan = 0.

1.11. Representasi vektor dari sebuah matriks

Setiap matriks A ukuran Saya× J dapat direpresentasikan sebagai himpunan vektor

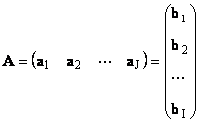
Di sini setiap vektor sebuah j adalah j-vektor kolom dan baris ke- b saya adalah saya-baris matriks A

1.12. Vektor bergantung linier

Vektor dengan dimensi yang sama ( N) dapat dijumlahkan dan dikalikan dengan suatu bilangan, seperti halnya matriks. Hasilnya adalah vektor dengan dimensi yang sama. Misalkan ada beberapa vektor dengan dimensi yang sama x 1 , x 2 ,...,x K dan bilangan yang sama α 1 , 2 ,...,α K. vektor

kamu= 1 x 1 + 2 x 2 +...+ K x K

ditelepon kombinasi linear vektor x k .

Jika ada angka bukan nol seperti itu k ≠ 0, k = 1,..., K, Apa kamu = 0 , maka himpunan vektor tersebut x k ditelepon bergantung linier. Jika tidak, vektor-vektor tersebut disebut bebas linier. Misalnya, vektor x 1 = (2, 2) t dan x 2 = (−1, 1) t bergantung linier, karena x 1 +2x 2 = 0

1.13. Peringkat matriks

Pertimbangkan satu set K vektor x 1 , x 2 ,...,x K ukuran N. Pangkat sistem vektor ini adalah jumlah maksimum vektor bebas linier. Misalnya di himpunan

hanya ada dua vektor bebas linier, misalnya x 1 dan x 2 , jadi rangkingnya adalah 2.

Jelas, jika ada lebih banyak vektor dalam himpunan daripada dimensinya ( K>N), maka mereka harus bergantung secara linier.

Peringkat matriks(dilambangkan dengan pangkat ( A)) adalah pangkat dari sistem vektor yang terdiri darinya. Meskipun setiap matriks dapat direpresentasikan dalam dua cara (vektor kolom atau vektor baris), ini tidak mempengaruhi nilai peringkat, karena

1.14. matriks terbalik

matriks persegi A Disebut non-degenerate jika memiliki keunikan membalik matriks A-1 , ditentukan oleh kondisi

A A −1 = A −1 A = Saya.

Matriks invers tidak ada untuk semua matriks. Kondisi yang diperlukan dan cukup untuk nondegenerasi adalah

det( A) 0 atau peringkat( A) = N.

Pembalikan matriks adalah prosedur kompleks yang memiliki program khusus. Sebagai contoh,

Beras. 17 Pembalikan matriks

Kami memberikan rumus untuk kasus paling sederhana - matriks 2 × 2

Jika matriks A dan B tidak berdegenerasi, maka

(AB) −1 = B −1 A −1 .

1.15. Matriks invers semu

Jika matriks A merosot dan matriks terbalik tidak ada, maka dalam beberapa kasus seseorang dapat menggunakan pseudo-invers matriks, yang didefinisikan sebagai matriks A+ itu

A A + A = A.

Matriks pseudo-invers bukan satu-satunya dan bentuknya tergantung pada metode konstruksi. Misalnya, untuk matriks persegi panjang, Anda dapat menggunakan metode Moore-Penrose.

Jika jumlah kolom lebih kecil dari jumlah baris, maka

A + =(A t A) −1 A t

Sebagai contoh,

Beras. 17a Pembalikan matriks semu

Jika jumlah kolom lebih besar dari jumlah baris, maka

A + =A t ( A A t) −1

1.16. Perkalian vektor dengan matriks

vektor x dapat dikalikan dengan matriks A dimensi yang sesuai. Dalam hal ini, vektor kolom dikalikan di sebelah kanan Kapak, dan string vektor ada di sebelah kiri x t A. Jika dimensi vektor J, dan dimensi matriks Saya× J maka hasilnya adalah vektor dimensi Saya. Sebagai contoh,

Beras. 18 Perkalian Vektor-Matriks

Jika matriks A- kotak ( Saya× Saya), maka vektor kamu = Kapak memiliki dimensi yang sama dengan x. Jelas bahwa

A(α 1 x 1 + 2 x 2) = 1 Kapak 1 + 2 Kapak 2 .

Oleh karena itu matriks dapat dianggap sebagai transformasi linier dari vektor. Secara khusus x = x, Sapi = 0 .

2. Informasi tambahan

2.1. Sistem persamaan linear

Biarlah A- ukuran matriks Saya× J, sebuah b- vektor dimensi J. Perhatikan persamaan

Kapak = b

terhadap vektor x, dimensi Saya. Pada dasarnya, ini adalah sistem Saya persamaan linier dengan J tidak dikenal x 1 ,...,x J. Sebuah solusi ada jika dan hanya jika

pangkat( A) = pangkat( B) = R,

di mana B adalah matriks dimensi yang diperbesar Saya×( J+1) terdiri dari matriks A, diisi dengan kolom b, B = (A b). Jika tidak, persamaan tidak konsisten.

Jika sebuah R = Saya = J, maka penyelesaiannya unik

x = A −1 b.

Jika sebuah R < Saya, maka ada banyak solusi berbeda yang dapat dinyatakan dalam kombinasi linier J−R vektor. Sistem persamaan homogen Kapak = 0 dengan matriks persegi A (N× N) memiliki solusi non-sepele ( x ≠ 0 ) jika dan hanya jika det( A) = 0. Jika R= pangkat( A)<N, maka ada N−R solusi bebas linier.

2.2. Bentuk bilinear dan kuadrat

Jika sebuah A adalah matriks persegi, dan x dan kamu- vektor dari dimensi yang sesuai, maka produk skalar dari bentuk x t Ay ditelepon bilinear bentuk yang ditentukan oleh matriks A. Pada x = kamu ekspresi x t Kapak ditelepon kuadrat membentuk.

2.3. Matriks pasti positif

matriks persegi A ditelepon pasti positif, jika untuk sembarang vektor bukan nol x ≠ 0 ,

x t Kapak > 0.

Itu negatif (x t Kapak < 0), non-negatif (x t Kapak 0) dan tidak positif (x t Kapak 0) matriks tertentu.

2.4. Dekomposisi Cholesky

Jika matriks simetris A pasti positif, maka ada matriks segitiga unik kamu dengan elemen positif, yang

A = kamu t kamu.

Sebagai contoh,

Beras. 19 Dekomposisi Cholesky

2.5. dekomposisi kutub

Biarlah A adalah matriks bujur sangkar berdimensi N× N. Lalu ada yang unik kutub pertunjukan

A = RS,

di mana S adalah matriks simetris non-negatif, dan R adalah matriks ortogonal. matriks S dan R dapat didefinisikan secara eksplisit:

S 2 = A A t atau S = (A A t) dan R = S −1 A = (A A t) A.

Sebagai contoh,

Beras. 20 Dekomposisi kutub

Jika matriks A merosot, maka penguraiannya tidak unik - yaitu: S masih sendiri, tapi R mungkin ada banyak. Dekomposisi polar mewakili matriks A sebagai kombinasi kompresi/peregangan S dan berbalik R.

2.6. Vektor eigen dan nilai eigen

Biarlah A adalah matriks persegi. vektor v ditelepon vektor sendiri matriks A, jika

Av = λ v,

di mana nomor disebut nilai eigen matriks A. Jadi, transformasi yang dilakukan matriks A atas vektor v, direduksi menjadi regangan atau kompresi sederhana dengan faktor . Vektor eigen ditentukan hingga perkalian dengan konstanta 0, yaitu. jika v adalah vektor eigen, maka v juga merupakan vektor eigen.

2.7. nilai eigen

Pada matriks A, dimensi ( N× N) tidak boleh lebih besar dari N nilai eigen. Mereka memuaskan persamaan karakteristik

det( A − λ Saya) = 0,

yang merupakan persamaan aljabar N-urutan. Secara khusus, untuk matriks 2 × 2, persamaan karakteristik memiliki bentuk

Sebagai contoh,

Beras. 21 Nilai Eigen

Himpunan nilai eigen 1 ,..., N matriks A ditelepon spektrum A.

Spektrum memiliki berbagai sifat. Secara khusus

det( A) = 1×...×λ N, Sp( A) = 1 +...+ N.

Nilai eigen dari matriks arbitrer dapat berupa bilangan kompleks, tetapi jika matriksnya simetris ( A t = A), maka nilai eigennya adalah nyata.

2.8. vektor eigen

Pada matriks A, dimensi ( N× N) tidak boleh lebih besar dari N eigenvectors, yang masing-masing sesuai dengan nilainya sendiri. Untuk menentukan vektor eigen v n Anda perlu menyelesaikan sistem persamaan homogen

(A − λ n Saya)v n = 0 .

Ini memiliki solusi non-sepele karena det( A-λ n Saya) = 0.

Sebagai contoh,

Beras. 22 vektor eigen

Vektor eigen matriks simetris adalah ortogonal.

Vektor eigen dari matriks persegi adalah vektor yang jika dikalikan dengan matriks tertentu menghasilkan vektor collinear. Dengan kata sederhana, ketika sebuah matriks dikalikan dengan vektor eigen, yang terakhir tetap sama, tetapi dikalikan dengan beberapa angka.

Definisi

Vektor eigen adalah vektor bukan-nol V, yang jika dikalikan dengan matriks persegi M, menjadi dirinya sendiri, ditambah sejumlah . Dalam notasi aljabar, ini terlihat seperti:

M × V = × V,

dimana adalah nilai eigen dari matriks M.

Mari kita pertimbangkan contoh numerik. Untuk memudahkan penulisan, angka-angka dalam matriks akan dipisahkan dengan titik koma. Katakanlah kita memiliki matriks:

• M = 0; 4;
• 6; 10.

Mari kita kalikan dengan vektor kolom:

• V = -2;

Saat mengalikan matriks dengan vektor kolom, kita juga mendapatkan vektor kolom. Dalam bahasa matematika yang ketat, rumus untuk mengalikan matriks 2 × 2 dengan vektor kolom akan terlihat seperti ini:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 berarti elemen matriks M, berdiri pada baris pertama dan kolom pertama, dan M22 adalah elemen yang terletak pada baris kedua dan kolom kedua. Untuk matriks kita, elemen-elemen ini adalah M11 = 0, M12 = 4, M21 = 6, M22 10. Untuk vektor kolom, nilainya adalah V11 = –2, V21 = 1. Menurut rumus ini, kita mendapatkan yang berikut hasil perkalian matriks bujur sangkar dengan vektor:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Untuk kenyamanan, kami menulis vektor kolom menjadi satu baris. Jadi, kita telah mengalikan matriks persegi dengan vektor (-2; 1), menghasilkan vektor (4; -2). Jelas, ini adalah vektor yang sama dikalikan dengan = -2. Lambda dalam hal ini menunjukkan nilai eigen dari matriks.

Vektor eigen suatu matriks adalah vektor collinear, yaitu suatu benda yang tidak berubah posisinya dalam ruang ketika dikalikan dengan matriks. Konsep kolinearitas dalam aljabar vektor mirip dengan istilah paralelisme dalam geometri. Dalam interpretasi geometris, vektor collinear adalah segmen berarah paralel dengan panjang yang berbeda. Sejak zaman Euclid, kita tahu bahwa satu garis memiliki jumlah garis tak terbatas yang sejajar dengannya, jadi logis untuk mengasumsikan bahwa setiap matriks memiliki jumlah vektor eigen yang tak terbatas.

Dari contoh sebelumnya, dapat dilihat bahwa (-8; 4), dan (16; -8), dan (32, -16) dapat menjadi vektor eigen. Semua ini adalah vektor collinear yang sesuai dengan nilai eigen λ = -2. Saat mengalikan matriks asli dengan vektor-vektor ini, kita masih akan mendapatkan vektor sebagai hasilnya, yang berbeda dari aslinya sebanyak 2 kali. Oleh karena itu, ketika memecahkan masalah untuk menemukan vektor eigen, diperlukan hanya menemukan objek vektor yang bebas linier. Paling sering, untuk matriks n × n, ada jumlah n-vektor eigen. Kalkulator kami dirancang untuk analisis matriks kuadrat orde kedua, sehingga hampir selalu dua vektor eigen akan ditemukan sebagai hasilnya, kecuali jika keduanya bertepatan.

Pada contoh di atas, kita mengetahui sebelumnya vektor eigen dari matriks asli dan secara visual menentukan bilangan lambda. Namun, dalam praktiknya, semuanya terjadi sebaliknya: pada awalnya ada nilai eigen dan baru kemudian ada vektor eigen.

Algoritma solusi

Mari kita lihat kembali matriks asli M dan coba cari kedua vektor eigennya. Jadi matriksnya terlihat seperti:

• M = 0; 4;
• 6; 10.

Untuk memulainya, kita perlu menentukan nilai eigen , yang untuk itu kita perlu menghitung determinan dari matriks berikut:

• (0 ); 4;
• 6; (10 ).

Matriks ini diperoleh dengan mengurangkan yang tidak diketahui dari elemen-elemen pada diagonal utama. Determinan ditentukan oleh rumus standar:

• detA = M11 × M21 M12 × M22
• detA = (0 ) × (10 ) 24

Karena vektor kita tidak boleh nol, kita mengambil persamaan yang dihasilkan sebagai bergantung linier dan menyamakan detA determinan kita dengan nol.

(0 ) × (10 ) 24 = 0

Buka kurung dan dapatkan persamaan karakteristik matriks:

2 10λ 24 = 0

Ini adalah persamaan kuadrat standar yang perlu diselesaikan dalam bentuk diskriminan.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Akar diskriminan adalah kuadrat(D) = 14, jadi 1 = -2, 2 = 12. Sekarang untuk setiap nilai lambda, kita perlu mencari vektor eigen. Mari kita nyatakan koefisien sistem untuk = -2.

• M × E = 2; 4;
• 6; 12.

Dalam rumus ini, E adalah matriks identitas. Berdasarkan matriks yang diperoleh, kami menyusun sistem persamaan linier:

2x + 4y = 6x + 12y

di mana x dan y adalah elemen dari vektor eigen.

Ayo kumpulkan semua X di kiri dan semua Y di kanan. Jelas - 4x = 8y. Bagilah ekspresi dengan - 4 dan dapatkan x = -2y. Sekarang kita dapat menentukan vektor eigen pertama dari matriks dengan mengambil nilai apa pun dari yang tidak diketahui (ingat tentang tak terhingga vektor eigen yang bergantung secara linier). Misalkan y = 1, maka x = -2. Oleh karena itu, vektor eigen pertama terlihat seperti V1 = (–2; 1). Kembali ke awal artikel. Objek vektor inilah yang kita kalikan matriksnya untuk mendemonstrasikan konsep vektor eigen.

Sekarang mari kita cari vektor eigen untuk = 12.

• M - × E = -12; 4
• 6; -2.

Mari kita buat sistem persamaan linier yang sama;

• -12x + 4y = 6x 2y
• -18x = -6y
• 3x=y.

Sekarang ambil x = 1, maka y = 3. Jadi, vektor eigen kedua terlihat seperti V2 = (1; 3). Saat mengalikan matriks asli dengan vektor ini, hasilnya akan selalu menjadi vektor yang sama dikalikan 12. Ini melengkapi algoritma solusi. Sekarang Anda tahu cara mendefinisikan vektor eigen suatu matriks secara manual.

• penentu;
• jejak, yaitu jumlah elemen pada diagonal utama;
• rank, yaitu jumlah maksimum baris/kolom bebas linier.

Program beroperasi sesuai dengan algoritma di atas, meminimalkan proses solusi. Penting untuk menunjukkan bahwa dalam program lambda dilambangkan dengan huruf "c". Mari kita lihat contoh numerik.

Contoh program

Mari kita coba mendefinisikan vektor eigen untuk matriks berikut:

• M=5; tigabelas;
• 4; 14.

Mari kita masukkan nilai-nilai ini ke dalam sel kalkulator dan dapatkan jawabannya dalam bentuk berikut:

• Peringkat matriks: 2;
• Penentu matriks: 18;
• Jejak matriks: 19;
• Perhitungan vektor eigen: c 2 19.00c + 18.00 (persamaan karakteristik);
• Perhitungan vektor eigen: 18 (nilai lambda pertama);
• Perhitungan vektor eigen: 1 (nilai lambda kedua);
• Sistem persamaan vektor 1: -13x1 + 13y1 = 4x1 4y1;
• Sistem persamaan vektor 2: 4x1 + 13y1 = 4x1 + 13y1;
• Vektor Eigen 1: (1; 1);
• Vektor Eigen 2: (-3.25; 1).

Dengan demikian, kami telah memperoleh dua vektor eigen bebas linier.

Kesimpulan

Aljabar linier dan geometri analitik adalah mata pelajaran standar untuk setiap mahasiswa baru di bidang teknik. Sejumlah besar vektor dan matriks menakutkan, dan mudah untuk membuat kesalahan dalam perhitungan yang rumit seperti itu. Program kami akan memungkinkan siswa untuk memeriksa perhitungan mereka atau secara otomatis memecahkan masalah menemukan vektor eigen. Ada kalkulator aljabar linier lainnya di katalog kami, gunakan dalam studi atau pekerjaan Anda.

www.situs memungkinkan Anda untuk menemukan. Situs melakukan perhitungan. Dalam beberapa detik, server akan memberikan solusi yang tepat. Persamaan karakteristik untuk matriks akan menjadi ekspresi aljabar yang ditemukan oleh aturan untuk menghitung determinan matriks matriks, sedangkan pada diagonal utama akan terdapat perbedaan nilai elemen diagonal dan variabelnya. Saat menghitung persamaan karakteristik untuk matriks online, setiap elemen matriks akan dikalikan dengan elemen lain yang sesuai matriks. Temukan dalam mode on line hanya mungkin untuk persegi matriks. Temukan operasi persamaan karakteristik untuk matriks online mengurangi untuk menghitung jumlah aljabar dari produk elemen matriks sebagai hasil dari menemukan determinan matriks, hanya untuk tujuan menentukan persamaan karakteristik untuk matriks online. Operasi ini menempati tempat khusus dalam teori matriks, memungkinkan Anda menemukan nilai eigen dan vektor menggunakan akar . Menemukan tugas persamaan karakteristik untuk matriks online adalah mengalikan elemen matriks dengan penjumlahan berikutnya dari produk-produk ini menurut aturan tertentu. www.situs menemukan persamaan karakteristik untuk matriks dimensi yang diberikan dalam mode on line. perhitungan persamaan karakteristik untuk matriks online untuk dimensi tertentu, ini adalah menemukan polinomial dengan koefisien numerik atau simbolis yang ditemukan oleh aturan untuk menghitung determinan matriks- sebagai jumlah produk dari elemen yang sesuai matriks, hanya untuk tujuan menentukan persamaan karakteristik untuk matriks online. Menemukan polinomial sehubungan dengan variabel untuk persegi matriks, sebagai definisi persamaan karakteristik untuk matriks, umum dalam teori matriks. Nilai akar polinomial persamaan karakteristik untuk matriks online digunakan untuk mendefinisikan vektor eigen dan nilai eigen untuk matriks. Namun, jika determinannya matriks akan menjadi nol, maka persamaan karakteristik matriks akan tetap ada, tidak seperti sebaliknya matriks. Untuk menghitung persamaan karakteristik untuk matriks atau cari beberapa sekaligus persamaan karakteristik matriks, Anda perlu menghabiskan banyak waktu dan tenaga, sementara server kami akan menemukan persamaan karakteristik untuk matriks online. Dalam hal ini, jawabannya dengan menemukan persamaan karakteristik untuk matriks online akan benar dan dengan akurasi yang cukup, bahkan jika angka ketika menemukan persamaan karakteristik untuk matriks online akan menjadi tidak rasional. On line www.situs entri karakter diperbolehkan dalam elemen matriks, yaitu persamaan karakteristik untuk matriks online dapat direpresentasikan dalam bentuk simbolik umum saat menghitung matriks persamaan karakteristik online. Berguna untuk memeriksa jawaban yang diperoleh ketika memecahkan masalah menemukan persamaan karakteristik untuk matriks online menggunakan situs www.situs. Saat melakukan operasi menghitung polinomial - persamaan karakteristik matriks, perlu untuk menjadi perhatian dan sangat terkonsentrasi dalam memecahkan masalah ini. Pada gilirannya, situs kami akan membantu Anda memeriksa keputusan Anda tentang topik tersebut matriks persamaan karakteristik online. Jika Anda tidak punya waktu untuk memeriksa masalah yang terpecahkan, maka www.situs pasti akan menjadi alat yang nyaman untuk memeriksa saat menemukan dan menghitung persamaan karakteristik untuk matriks online.

Definisi 9.3. vektor X ditelepon vektor sendiri matriks TETAPI jika ada nomor seperti itu λ, bahwa persamaan itu berlaku: TETAPI X= λ X, yaitu, hasil penerapan ke X transformasi linier yang diberikan oleh matriks TETAPI, adalah perkalian vektor ini dengan bilangan λ . Nomornya sendiri λ ditelepon nomor sendiri matriks TETAPI.

Substitusi ke dalam rumus (9.3) x` j = x j , kami memperoleh sistem persamaan untuk menentukan koordinat vektor eigen:

. (9.5)

Sistem homogen linier ini akan memiliki solusi non-trivial hanya jika determinan utamanya adalah 0 (aturan Cramer). Dengan menuliskan kondisi ini dalam bentuk:

kita mendapatkan persamaan untuk menentukan nilai eigen λ ditelepon persamaan karakteristik. Secara singkat dapat digambarkan sebagai berikut:

| A-λE | = 0, (9.6)

karena ruas kirinya adalah determinan matriks A-λE. Polinomial terhadap | A-λE| ditelepon polinomial karakteristik matriks a.

Sifat-sifat polinomial karakteristik:

1) Polinomial karakteristik dari transformasi linier tidak bergantung pada pilihan basis. Bukti. (lihat (9.4)), tetapi karena itu, . Dengan demikian, tidak tergantung pada pilihan dasar. Oleh karena itu, dan | A-λE| tidak berubah saat transisi ke basis baru.

2) Jika matriks TETAPI transformasi linier adalah simetris(itu. a ij = a ji), maka semua akar persamaan karakteristik (9.6) adalah bilangan real.

Sifat-sifat nilai eigen dan vektor eigen:

1) Jika kita memilih basis dari vektor eigen x 1, x 2, x 3 sesuai dengan nilai eigen 1 , 2 , 3 matriks TETAPI, maka pada basis ini transformasi linier A memiliki matriks diagonal:

(9.7) Bukti properti ini mengikuti definisi vektor eigen.

2) Jika nilai eigen transformasi TETAPI berbeda, maka vektor eigen yang bersesuaian dengannya bebas linier.

3) Jika polinomial karakteristik dari matriks TETAPI memiliki tiga akar yang berbeda, maka dalam beberapa basis matriks TETAPI memiliki bentuk diagonal.

Mari kita cari nilai eigen dan vektor eigen dari matriks Mari kita buat persamaan karakteristik: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Temukan koordinat vektor eigen yang sesuai dengan setiap nilai yang ditemukan λ. Dari (9.5) berikut bahwa jika X (1) ={x 1 , x 2 , x 3) adalah vektor eigen yang bersesuaian dengan λ 1 = -2, maka

adalah sistem kolaboratif tetapi tidak pasti. Solusinya dapat ditulis sebagai X (1) ={sebuah,0,-sebuah), di mana a adalah sembarang bilangan. Khususnya, jika Anda memerlukan | x (1) |=1, X (1) =

Substitusi ke dalam sistem (9.5) λ 2 =3, kami mendapatkan sistem untuk menentukan koordinat vektor eigen kedua - x (2) ={y1,y2,y3}:

, di mana X (2) ={b,-b,b) atau, asalkan | x (2) |=1, x (2) =

Untuk λ 3 = 6 tentukan vektor eigennya x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) atau dalam versi yang dinormalisasi

x (3) = Dapat dilihat bahwa X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = SM- 2bc + bc= 0. Jadi, vektor eigen dari matriks ini adalah ortogonal berpasangan.

Kuliah 10

Bentuk kuadrat dan hubungannya dengan matriks simetris. Sifat-sifat vektor eigen dan nilai eigen dari matriks simetris. Pengurangan bentuk kuadrat menjadi bentuk kanonik.

Definisi 10.1.bentuk kuadrat variabel nyata x 1, x 2,…, x n polinomial derajat kedua sehubungan dengan variabel-variabel ini disebut, yang tidak mengandung istilah bebas dan istilah derajat pertama.

Contoh bentuk kuadrat:

(n = 2),

(n = 3). (10.1)

Ingat definisi matriks simetris yang diberikan dalam kuliah terakhir:

Definisi 10.2. Matriks persegi disebut simetris, jika , yaitu, jika elemen matriks simetris terhadap diagonal utama adalah sama.

Sifat-sifat nilai eigen dan vektor eigen dari matriks simetris:

1) Semua nilai eigen dari matriks simetris adalah nyata.

Bukti (untuk n = 2).

Biarkan matriks TETAPI seperti: . Mari kita buat persamaan karakteristiknya:

(10.2) Cari diskriminannya:

Oleh karena itu, persamaan hanya memiliki akar real.

2) Vektor eigen dari matriks simetris adalah ortogonal.

Bukti (untuk n= 2).

Koordinat vektor eigen dan harus memenuhi persamaan.