Solusi grafis dari persamaan kuadrat Untuk mengkonsolidasikan kemampuan untuk membangun grafik dari berbagai fungsi; Untuk membentuk kemampuan menyelesaikan persamaan kuadrat secara grafis. Proyek dengan topik "Transformasi grafik suatu fungsi"

Solusi grafis dari persamaan kuadrat Untuk mengkonsolidasikan kemampuan untuk membangun grafik dari berbagai fungsi; Untuk membentuk kemampuan menyelesaikan persamaan kuadrat secara grafis. Brdsk 2009 Institusi pendidikan kota - Lyceum Ekonomi Pelajaran generalisasi dengan topik "Fungsi kuadrat", guru kelas 8 aljabar Fedoseeva T.M.

Memplot fungsi kuadrat Tentukan arah cabang: a>0 cabang ke atas; sebuah 0 cabang ke atas; a"> 0 cabang ke atas; a"> 0 cabang ke atas; a" title="(!LANG:Merencanakan fungsi kuadrat Tentukan arah cabang: a>0 cabang ke atas; a"> title="Memplot fungsi kuadrat Tentukan arah cabang: a>0 cabang ke atas; sebuah"> !}

0 cabang diarahkan ke atas; 2) simpul y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - sumbu parabola Titik kontrol: (0: -3), (3 ; 0) dan simetris terhadap sumbu x = 1 Kami membuat parabola. Cari titik "title="(!LANG: Mari kita buat grafik fungsi y=x 2 -2x-3 menggunakan algoritma: 1) a=1>0 cabang-cabangnya diarahkan ke atas; 2) simpul y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - sumbu parabola Titik kontrol: (0: -3), (3 ; 0) dan simetris terhadap sumbu x = 1 Kami membuat parabola. Menemukan titik" class="link_thumb"> 3 !} Mari kita buat grafik fungsi y=x 2 -2x-3 menggunakan algoritma: 1) a=1>0 cabang diarahkan ke atas; 2) simpul y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - sumbu parabola Titik kontrol: (0: -3), (3 ; 0) dan simetris terhadap sumbu x = 1 Kami membuat parabola. Kami menemukan titik persimpangan dengan sumbu OX: x 1 \u003d -1; x 2 \u003d 3 1 cara menyelesaikan persamaan x 2 -2x-3 \u003d 0 y x Memecahkan persamaan x 2 +2x-3 \u003d 0 0 cabang diarahkan ke atas; 2) simpul y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - sumbu parabola Titik kontrol: (0: -3), (3 ; 0) dan simetris terhadap sumbu x = 1 Kami membuat parabola. Kami menemukan titik "\u003e 0 cabang diarahkan ke atas; 2) atas y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - sumbu dari parabola Titik kontrol: (0: -3), (3; 0) dan simetris terhadap sumbu x = 1 Kami membuat parabola.Temukan titik potong dengan sumbu OX: x 1 \u003d -1; x 2 \u003d 3 1 cara untuk menyelesaikan persamaan x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Memecahkan persamaan x 2 + 2x-3 \u003d 0 "\u003e 0 cabang diarahkan ke atas; 2) simpul y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - sumbu parabola Titik kontrol: (0: -3), (3 ; 0) dan simetris terhadap sumbu x = 1 Kami membuat parabola. Cari titik "title="(!LANG: Mari kita buat grafik fungsi y=x 2 -2x-3 menggunakan algoritma: 1) a=1>0 cabang-cabangnya diarahkan ke atas; 2) simpul y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - sumbu parabola Titik kontrol: (0: -3), (3 ; 0) dan simetris terhadap sumbu x = 1 Kami membuat parabola. Menemukan titik"> title="Mari kita buat grafik fungsi y=x 2 -2x-3 menggunakan algoritma: 1) a=1>0 cabang diarahkan ke atas; 2) simpul y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - sumbu parabola Titik kontrol: (0: -3), (3 ; 0) dan simetris terhadap sumbu x = 1 Kami membuat parabola. Menemukan titik"> !}

Cara kedua: a). Mari kita bagi persamaan x 2 -2x-3=0 menjadi bagian x 2 = 2x+3 Mari kita tulis dua fungsi y= x 2 ; y \u003d 2x + 3 Kami membuat grafik fungsi-fungsi ini dalam satu sistem koordinat. Absis titik potong adalah akar-akar persamaan. 0 1 x y Selesaikan persamaan x 2 +2x-3=0

Cara ketiga: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Kami membangun grafik fungsi-fungsi ini dalam satu sistem koordinat. Absis titik potong adalah akar-akar persamaan. 0 1 x y Selesaikan persamaan x 2 +2x-3=0

Solusi grafis dari persamaan

Hai, 2009

pengantar

Kebutuhan untuk menyelesaikan persamaan kuadrat pada zaman dahulu disebabkan oleh kebutuhan untuk memecahkan masalah yang berkaitan dengan pencarian luas tanah dan pekerjaan tanah yang bersifat militer, serta perkembangan astronomi dan matematika itu sendiri. Orang Babilonia tahu cara menyelesaikan persamaan kuadrat sekitar tahun 2000 SM. Aturan untuk menyelesaikan persamaan ini, yang dinyatakan dalam teks Babilonia, pada dasarnya bertepatan dengan yang modern, tetapi tidak diketahui bagaimana Babel sampai pada aturan ini.

Rumus untuk memecahkan persamaan kuadrat di Eropa pertama kali dikemukakan dalam Kitab Abacus, yang ditulis pada tahun 1202 oleh ahli matematika Italia Leonardo Fibonacci. Bukunya berkontribusi pada penyebaran pengetahuan aljabar tidak hanya di Italia, tetapi juga di Jerman, Prancis, dan negara-negara Eropa lainnya.

Tetapi aturan umum untuk memecahkan persamaan kuadrat, dengan semua kemungkinan kombinasi koefisien b dan c, dirumuskan di Eropa hanya pada tahun 1544 oleh M. Stiefel.

Pada tahun 1591 François Viet memperkenalkan rumus untuk menyelesaikan persamaan kuadrat.

Beberapa jenis persamaan kuadrat dapat diselesaikan di Babel kuno.

Diophantus dari Alexandria dan Euclid , Al-Khawarizmi dan Umar Khayyam menyelesaikan persamaan secara geometris dan grafis.

Di kelas 7 kami mempelajari fungsi y \u003d C, y= kx , y = kx + m , y = x 2 ,y = - x 2 , di kelas 8 - y = x , y = |x |, y= kapak 2 + bx + c , y = k / x. Di buku teks aljabar kelas 9, saya melihat fungsi yang belum saya ketahui: y= x 3 , y= x 4 ,y= x 2 n , y= x - 2 n , y= 3 √x , ( x – sebuah ) 2 + (y - b ) 2 = r 2 dan lainnya. Ada aturan untuk membangun grafik dari fungsi-fungsi ini. Saya bertanya-tanya apakah ada fungsi lain yang mematuhi aturan ini.

Tugas saya adalah mempelajari grafik fungsi dan menyelesaikan persamaan secara grafik.

1. Apa fungsinya?

Grafik suatu fungsi adalah himpunan semua titik bidang koordinat, yang absisnya sama dengan nilai argumen, dan ordinatnya sama dengan nilai fungsi yang sesuai.

Fungsi linier diberikan oleh persamaan y= kx + b, di mana k dan b- beberapa nomor. Grafik dari fungsi ini adalah garis lurus.

Fungsi Proporsional Terbalik y= k / x, di mana k¹ 0. Grafik fungsi ini disebut hiperbola.

Fungsi ( x – sebuah ) 2 + (y – b ) 2 = r 2 , di mana sebuah , b dan r- beberapa nomor. Grafik fungsi ini adalah lingkaran berjari-jari r berpusat di titik A ( sebuah , b).

fungsi kuadrat kamu = kapak 2 + bx + c di mana sebuah, b , dengan- beberapa angka dan sebuah 0. Grafik fungsi ini adalah parabola.

persamaan y 2 ( sebuah – x ) = x 2 ( sebuah + x ) . Grafik persamaan ini akan menjadi kurva yang disebut strophoid.

persamaan ( x 2 + kamu 2 ) 2 = sebuah ( x 2 – kamu 2 ) . Grafik persamaan ini disebut lemniscate Bernoulli.

persamaan. Grafik persamaan ini disebut asteroid.

Melengkung (x 2 y 2 - 2 a x) 2 \u003d 4 a 2 (x 2 + y 2). Kurva ini disebut cardioid.

Fungsi: y= x 3 - parabola kubik, y= x 4 , y = 1/ x 2 .

2. Konsep persamaan, solusi grafisnya

persamaan adalah ekspresi yang mengandung variabel.

selesaikan persamaannya- ini berarti menemukan semua akarnya, atau membuktikan bahwa akarnya tidak ada.

Akar persamaan adalah angka yang, ketika disubstitusikan ke dalam persamaan, menghasilkan persamaan numerik yang benar.

Menyelesaikan Persamaan Secara Grafis memungkinkan Anda untuk menemukan nilai yang tepat atau perkiraan dari akar, memungkinkan Anda untuk menemukan jumlah akar persamaan.

Ketika merencanakan grafik dan menyelesaikan persamaan, sifat-sifat suatu fungsi digunakan, sehingga metode ini sering disebut grafik fungsional.

Untuk menyelesaikan persamaan, kami "membagi" menjadi dua bagian, memperkenalkan dua fungsi, memplot grafiknya, dan menemukan koordinat titik potong grafik. Absis dari titik-titik ini adalah akar dari persamaan.

3. Algoritma untuk membuat grafik suatu fungsi

Mengetahui grafik fungsi y= f ( x ) , Anda dapat merencanakan fungsi y= f ( x + m ) ,y= f ( x )+ aku dan y= f ( x + m )+ aku. Semua grafik ini diperoleh dari grafik fungsi y= f ( x ) menggunakan transformasi terjemahan paralel: on │ m │ satuan skala ke kanan atau kiri sepanjang sumbu x dan pada │ aku │ unit skala ke atas atau ke bawah di sepanjang sumbu kamu .

4. Solusi grafis dari persamaan kuadrat

Menggunakan contoh fungsi kuadrat, kita akan mempertimbangkan solusi grafis dari persamaan kuadrat. Grafik fungsi kuadrat adalah parabola.

Apa yang orang Yunani kuno ketahui tentang parabola?

Simbolisme matematika modern berasal dari abad ke-16.

Matematikawan Yunani kuno tidak memiliki metode koordinat maupun konsep fungsi. Namun, sifat parabola dipelajari oleh mereka secara rinci. Penemuan matematikawan kuno sungguh menakjubkan, karena mereka hanya bisa menggunakan gambar dan deskripsi verbal dari ketergantungan.

Sepenuhnya menjelajahi parabola, hiperbola, dan elips Apollonius dari Perga, yang hidup pada abad ke-3 SM. Dia juga memberi nama pada kurva-kurva ini dan menunjukkan kondisi apa yang dipenuhi oleh titik-titik yang terletak pada kurva tertentu (setelah semua, tidak ada rumus!).

Ada algoritma untuk membangun parabola:

Kami menemukan koordinat titik puncak parabola A (x 0; y 0): x 0 =- b /2 sebuah ;

Y 0 \u003d kapak sekitar 2 + di 0 + c;

Kami menemukan sumbu simetri parabola (garis lurus x \u003d x 0);

Menyusun tabel nilai untuk membangun titik kontrol;

Kami membangun titik-titik yang diperoleh dan membangun titik-titik yang simetris terhadapnya sehubungan dengan sumbu simetri.

1. Mari kita membangun parabola sesuai dengan algoritma kamu = x 2 – 2 x – 3 . Absis titik potong dengan sumbu x dan merupakan akar-akar persamaan kuadrat x 2 – 2 x – 3 = 0.

Ada lima cara untuk menyelesaikan persamaan ini secara grafis.

2. Mari kita pecah persamaan menjadi dua fungsi: kamu = x 2 dan kamu = 2 x + 3

3. Mari kita pecah persamaan menjadi dua fungsi: kamu = x 2 –3 dan kamu =2 x. Akar persamaan adalah absis titik potong parabola dengan garis.

4. Transformasikan persamaan x 2 – 2 x – 3 = 0 dengan memilih kotak penuh pada fungsi: kamu = ( x –1) 2 dan kamu =4. Akar persamaan adalah absis titik potong parabola dengan garis.

5. Kami membagi suku dengan suku kedua bagian dari persamaan x 2 – 2 x – 3 = 0 pada x, kita mendapatkan x – 2 – 3/ x = 0 Mari kita bagi persamaan ini menjadi dua fungsi: kamu = x – 2, kamu = 3/ x . Akar persamaan adalah absis titik potong garis dan hiperbola.

5. Solusi grafis persamaan derajat n

Contoh 1 selesaikan persamaannya x 5 = 3 – 2 x .

kamu = x 5 , kamu = 3 – 2 x .

Menjawab: x = 1.

Contoh 2 selesaikan persamaannya 3 √ x = 10 – x .

Akar persamaan ini adalah absis titik potong grafik dua fungsi: kamu = 3 √ x , kamu = 10 – x .

Menjawab: x=8.

Kesimpulan

Dengan memperhatikan grafik fungsi: y= kapak 2 + bx + c , y = k / x , y = x , y = |x |, y= x 3 , y= x 4 ,y= 3 √x , Saya perhatikan bahwa semua grafik ini dibangun sesuai dengan aturan terjemahan paralel relatif terhadap sumbu x dan kamu .

Menggunakan contoh penyelesaian persamaan kuadrat, kita dapat menyimpulkan bahwa metode grafis juga berlaku untuk persamaan derajat n.

Metode grafis untuk memecahkan persamaan itu indah dan dapat dimengerti, tetapi mereka tidak memberikan jaminan 100% untuk menyelesaikan persamaan apa pun. Absis titik potong grafik dapat berupa perkiraan.

Di kelas 9 dan di kelas senior, saya masih akan berkenalan dengan fungsi lain. Saya tertarik untuk mengetahui apakah fungsi-fungsi tersebut mematuhi aturan terjemahan paralel saat memplot grafiknya.

Tahun depan saya juga ingin mempertimbangkan masalah solusi grafis sistem persamaan dan pertidaksamaan.

literatur

1. Aljabar. kelas 7. Bagian 1. Buku teks untuk lembaga pendidikan / A.G. Mordkovich. Moskow: Mnemosyne, 2007.

2. Aljabar. kelas 8. Bagian 1. Buku teks untuk lembaga pendidikan / A.G. Mordkovich. Moskow: Mnemosyne, 2007.

3. Aljabar. Kelas 9 Bagian 1. Buku teks untuk lembaga pendidikan / A.G. Mordkovich. Moskow: Mnemosyne, 2007.

4. Glazer G.I. Sejarah matematika di sekolah. Kelas VII-VIII. – M.: Pencerahan, 1982.

5. Jurnal Matematika 5 2009; Nomor 8 tahun 2007; Nomor 23 Tahun 2008.

6. Solusi grafis persamaan situs Internet: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

Solusi grafis dari persamaan

Hai, 2009

pengantar

Tetapi aturan umum untuk memecahkan persamaan kuadrat, dengan semua kemungkinan kombinasi koefisien b dan c, dirumuskan di Eropa hanya pada tahun 1544 oleh M. Stiefel.

Pada tahun 1591 François Viet memperkenalkan rumus untuk menyelesaikan persamaan kuadrat.

Beberapa jenis persamaan kuadrat dapat diselesaikan di Babel kuno.

Diophantus dari Alexandria dan Euclid, Al-Khawarizmi dan Umar Khayyam menyelesaikan persamaan secara geometris dan grafis.

Di kelas 7 kami mempelajari fungsi y \u003d C, y=kx, y =kx+ m, y =x 2,y = -x 2, di kelas 8 - y =x, y =|x|, y=kapak2 + bx+ c, y =k/ x. Di buku teks aljabar kelas 9, saya melihat fungsi yang belum saya ketahui: y=x 3, y=x 4,y=x 2n, y=x- 2n, y= 3√x, (x– sebuah) 2 + (y -b) 2 = r 2 dan lainnya. Ada aturan untuk membangun grafik dari fungsi-fungsi ini. Saya bertanya-tanya apakah ada fungsi lain yang mematuhi aturan ini.

Tugas saya adalah mempelajari grafik fungsi dan menyelesaikan persamaan secara grafik.

1. Apa saja fungsinya?

Grafik suatu fungsi adalah himpunan semua titik bidang koordinat, yang absisnya sama dengan nilai argumen, dan ordinatnya sama dengan nilai fungsi yang sesuai.

Fungsi linier diberikan oleh persamaan y=kx+ b, di mana k dan b- beberapa nomor. Grafik dari fungsi ini adalah garis lurus.

Fungsi Proporsional Terbalik y=k/ x, di mana k 0. Grafik fungsi ini disebut hiperbola.

Fungsi (x– sebuah) 2 + (y -b) 2 = r2 , di mana sebuah, b dan r- beberapa nomor. Grafik fungsi ini adalah lingkaran berjari-jari r berpusat di titik A ( sebuah, b).

fungsi kuadrat kamu= kapak2 + bx+ c di mana sebuah,b, dengan- beberapa angka dan sebuah 0. Grafik fungsi ini adalah parabola.

persamaan pada2 (sebuah– x) = x2 (sebuah+ x) . Grafik persamaan ini akan menjadi kurva yang disebut strophoid.

/>Persamaan (x2 + kamu2 ) 2 = sebuah(x2 – kamu2 ) . Grafik persamaan ini disebut lemniscate Bernoulli.

persamaan. Grafik persamaan ini disebut asteroid.

Melengkung (x2 kamu2 – 2x)2 = 4 a2 (x2 + y2 ) . Kurva ini disebut cardioid.

Fungsi: y=x 3 - parabola kubik, y=x 4, y = 1/x 2.

2. Konsep persamaan, solusi grafisnya

persamaan adalah ekspresi yang mengandung variabel.

selesaikan persamaannya- ini berarti menemukan semua akarnya, atau membuktikan bahwa akarnya tidak ada.

Akar persamaan adalah angka yang, ketika disubstitusikan ke dalam persamaan, menghasilkan persamaan numerik yang benar.

Menyelesaikan Persamaan Secara Grafis memungkinkan Anda untuk menemukan nilai yang tepat atau perkiraan dari akar, memungkinkan Anda untuk menemukan jumlah akar persamaan.

Ketika merencanakan grafik dan menyelesaikan persamaan, sifat-sifat suatu fungsi digunakan, sehingga metode ini sering disebut grafik fungsional.

3. Algoritma untuk membuat grafik suatu fungsi

Mengetahui grafik fungsi y=f(x) , Anda dapat merencanakan fungsi y=f(x+ m) ,y=f(x)+ aku dan y=f(x+ m)+ aku. Semua grafik ini diperoleh dari grafik fungsi y=f(x) menggunakan transformasi terjemahan paralel: on │ m│ satuan skala ke kanan atau kiri sepanjang sumbu x dan pada │ aku│ unit skala ke atas atau ke bawah di sepanjang sumbu kamu.

4. Solusi grafis dari persamaan kuadrat

Menggunakan contoh fungsi kuadrat, kita akan mempertimbangkan solusi grafis dari persamaan kuadrat. Grafik fungsi kuadrat adalah parabola.

Apa yang orang Yunani kuno ketahui tentang parabola?

Simbolisme matematika modern berasal dari abad ke-16.

Ada algoritma untuk membangun parabola:

Tentukan koordinat titik puncak parabola A (x0; y0): X=- b/2 sebuah;

y0=aho2+in0+s;

Temukan sumbu simetri parabola (garis lurus x=x0);

HALAMAN_BREAK--

Menyusun tabel nilai untuk membangun titik kontrol;

Kami membangun titik-titik yang diperoleh dan membangun titik-titik yang simetris terhadapnya sehubungan dengan sumbu simetri.

1. Mari kita membangun parabola sesuai dengan algoritma kamu= x2 – 2 x– 3 . Absis titik potong dengan sumbu x dan merupakan akar-akar persamaan kuadrat x2 – 2 x– 3 = 0.

Ada lima cara untuk menyelesaikan persamaan ini secara grafis.

2. Mari kita pecah persamaan menjadi dua fungsi: kamu= x2 dan kamu= 2 x+ 3

3. Mari kita pecah persamaan menjadi dua fungsi: kamu= x2 –3 dan kamu=2 x. Akar persamaan adalah absis titik potong parabola dengan garis.

4. Transformasikan persamaan x2 – 2 x– 3 = 0 dengan memilih kotak penuh pada fungsi: kamu= (x–1) 2 dan kamu=4. Akar persamaan adalah absis titik potong parabola dengan garis.

5. Kami membagi suku dengan suku kedua bagian dari persamaan x2 – 2 x– 3 = 0 pada x, kita mendapatkan x– 2 – 3/ x= 0 Mari kita bagi persamaan ini menjadi dua fungsi: kamu= x– 2, kamu= 3/ x. Akar persamaan adalah absis titik potong garis dan hiperbola.

5. Solusi grafis persamaan derajatn

Contoh 1 selesaikan persamaannya x5 = 3 – 2 x.

kamu= x5 , kamu= 3 – 2 x.

Menjawab: x = 1.

Contoh 2 selesaikan persamaannya 3 √ x= 10 – x.

Akar persamaan ini adalah absis titik potong grafik dua fungsi: kamu= 3 √ x, kamu= 10 – x.

Menjawab: x=8.

Kesimpulan

Dengan memperhatikan grafik fungsi: y=kapak2 + bx+ c, y =k/ x, y =x, y =|x|, y=x 3, y=x 4,y= 3√x, Saya perhatikan bahwa semua grafik ini dibangun sesuai dengan aturan terjemahan paralel relatif terhadap sumbu x dan kamu.

Menggunakan contoh penyelesaian persamaan kuadrat, kita dapat menyimpulkan bahwa metode grafis juga berlaku untuk persamaan derajat n.

Di kelas 9 dan di kelas senior, saya masih akan berkenalan dengan fungsi lain. Saya tertarik untuk mengetahui apakah fungsi-fungsi tersebut mematuhi aturan terjemahan paralel saat memplot grafiknya.

Tahun depan saya juga ingin mempertimbangkan masalah solusi grafis sistem persamaan dan pertidaksamaan.

literatur

1. Aljabar. kelas 7. Bagian 1. Buku teks untuk lembaga pendidikan / A.G. Mordkovich. Moskow: Mnemosyne, 2007.

2. Aljabar. kelas 8. Bagian 1. Buku teks untuk lembaga pendidikan / A.G. Mordkovich. Moskow: Mnemosyne, 2007.

3. Aljabar. Kelas 9 Bagian 1. Buku teks untuk lembaga pendidikan / A.G. Mordkovich. Moskow: Mnemosyne, 2007.

4. Glazer G.I. Sejarah matematika di sekolah. Kelas VII-VIII. – M.: Pencerahan, 1982.

5. Jurnal Matematika 5 2009; Nomor 8 tahun 2007; Nomor 23 Tahun 2008.

6. Solusi grafis persamaan situs Internet: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

Dalam pelajaran video ini, topiknya “Fungsi y \u003d x 2. Solusi grafis dari persamaan. Selama pelajaran ini, siswa akan dapat berkenalan dengan cara baru menyelesaikan persamaan - grafis, yang didasarkan pada pengetahuan tentang sifat-sifat grafik fungsi. Guru akan menunjukkan cara menyelesaikan secara grafis fungsi y=x 2 .

Subjek:Fungsi

Pelajaran:Fungsi. Solusi grafis dari persamaan

Solusi grafis persamaan didasarkan pada pengetahuan tentang grafik fungsi dan sifat-sifatnya. Kami membuat daftar fungsi yang grafiknya kami ketahui:

1), grafiknya adalah garis lurus yang sejajar dengan sumbu x, melalui sebuah titik pada sumbu y. Perhatikan sebuah contoh: y=1:

Untuk nilai yang berbeda, kami mendapatkan keluarga garis lurus yang sejajar dengan sumbu x.

2) Fungsi proporsionalitas langsung grafik fungsi ini adalah garis lurus yang melalui titik asal. Pertimbangkan sebuah contoh:

Kami telah membuat grafik ini dalam pelajaran sebelumnya, ingatlah bahwa untuk membangun setiap garis, Anda perlu memilih titik yang memenuhinya, dan mengambil titik asal sebagai titik kedua.

Ingat peran koefisien k: ketika fungsi meningkat, sudut antara garis lurus dan arah positif sumbu x adalah lancip; ketika fungsi menurun, sudut antara garis lurus dan arah positif sumbu x adalah tumpul. Selain itu, ada hubungan berikut antara dua parameter k dengan tanda yang sama: untuk k positif, semakin besar, semakin cepat fungsi meningkat, dan negatif, fungsi menurun lebih cepat untuk nilai k modulo yang besar.

3) Fungsi linier. Ketika - kita mendapatkan titik potong dengan sumbu y dan semua garis semacam ini melewati titik (0; m). Selain itu, dengan bertambahnya fungsi, sudut antara garis dan arah positif sumbu x adalah lancip; ketika fungsi menurun, sudut antara garis lurus dan arah positif sumbu x adalah tumpul. Dan tentunya nilai k mempengaruhi laju perubahan nilai fungsi tersebut.

4). Grafik fungsi ini berbentuk parabola.

Pertimbangkan contoh.

Contoh 1 - selesaikan persamaan secara grafis:

Kami tidak tahu fungsi jenis ini, jadi kami perlu mengubah persamaan yang diberikan untuk bekerja dengan fungsi yang diketahui:

Kami mendapat fungsi yang sudah dikenal di kedua bagian persamaan:

Mari kita membuat grafik fungsi:

Grafik memiliki dua titik potong: (-1; 1); (2; 4)

Mari kita periksa apakah solusinya ditemukan dengan benar, substitusikan koordinat ke dalam persamaan:

Poin pertama ditemukan dengan benar.

, , , , , ,

Poin kedua juga ditemukan dengan benar.

Jadi, solusi dari persamaan tersebut adalah dan

Kami bertindak mirip dengan contoh sebelumnya: kami mengubah persamaan yang diberikan ke fungsi yang kami ketahui, memplot grafiknya, menemukan arus persimpangan, dan dari sini kami menunjukkan solusinya.

Kami mendapatkan dua fungsi:

Mari kita membuat grafik:

Grafik ini tidak memiliki titik potong, yang berarti bahwa persamaan yang diberikan tidak memiliki solusi

Kesimpulan: dalam pelajaran ini, kami meninjau fungsi yang kami ketahui dan grafiknya, mengingat propertinya, dan mempertimbangkan cara grafis untuk menyelesaikan persamaan.

1. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. dkk Aljabar 7. Edisi ke-6. M.: Pencerahan. 2010

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Aljabar 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. dan lain-lain Aljabar 7 .M.: Pendidikan. 2006

Tugas 1: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. dkk.Aljabar 7, no.494, hal.110;

Tugas 2: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. dan lain-lain Aljabar 7, No 495, butir 110;

Tugas 3: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. dkk.Aljabar 7, no.496, hal.110;

INSTITUT PENGEMBANGAN PROFESIONAL DAGESTAN

STAF PEDAGOGIS

JURUSAN PENDIDIKAN FISIKA DAN MATEMATIKA DAN TIK

Proyek

pada topik:

« Konstruksi dan p reformasi

grafik fungsi

dalam matematika sekolah »

Rabadanova P.A.

guru matematika

MBOU "Sekolah Menengah Kochubey"

Distrik Tarumovsky

2015

1. Pendahuluan……………………………………………………………….….3

2. Bab Saya. Tinjauan literatur tentang topik proyek…………………………..5

3. Bab II. Bagian empiris:

3.1. Metode dasar untuk mengubah grafik fungsi……….….7

3.2. Merencanakan sebuah genapdanfungsi ganjil……………….. 10

3.3. Memplot fungsi invers ………………………………. 11

3.4. Deformasi (kompresi dan tegangan) dari grafik………………….12

3.5 Kombinasi transfer, refleksi dan deformasi ……………………… 13

4. Tugas untuk solusi mandiri………………………..……14

5.Kesimpulan………………………………………………………………………15

6. Kesimpulan…………………………………………………………..………17

PENGANTAR

Transformasi graf fungsi merupakan salah satu konsep dasar matematika yang berhubungan langsung dengan kegiatan praktikum. Grafik mencerminkan variabilitas dan dinamisme dunia nyata, hubungan timbal balik antara objek dan fenomena nyata.

Garis fungsional adalah topik dasar yang tercakup dalam Ujian Negara Dasar dan Terpadu.Juga, banyak konsep matematika dipertimbangkan dengan metode grafis. Misalnya, kekuadratfungsi diperkenalkan dan dipelajari dalam hubungan dekat dengan persamaan kuadrat dan pertidaksamaan.Oleh karena itu berikut inimengajar siswa bagaimana membangun dan mengubah grafik dari suatu fungsi adalah salah satu tugas utama mengajar matematika di sekolah.

Studi tentang fungsi memungkinkan untuk menemukan tentangdomain definisi dan ruang lingkup fungsi, ruang lingkupPenurunan atau peningkatan laju, asimtot, intervaltanda kekonstanan, dll. Namun, untuk membuat grafikkov banyak fungsi dapatmenggunakan beberapa metodemembuatnya lebih mudahbangunan. Oleh karena itu, siswa harus memiliki kompetensi membangun grafik menurut skema metodologis.

Di atas mendefinisikanrelevansi topik penelitian.

Objek studi adalah studi tentang transformasi grafik garis fungsional dalam matematika sekolah.

Subyek studi - proses pembuatan dan transformasi graf fungsi di sekolah menengah.

Tujuan studi: pendidikan - terdiri dalam mengidentifikasi skema metodologis untuk membangun dan mengubah grafik fungsi;mengembangkan - pengembangan abstrak, algoritmik, pemikiran logis, imajinasi spasial;pendidikan - pendidikan budaya grafis anak sekolah, pembentukan keterampilan mental.

Tujuan mengarah pada keputusan berikut:tugas:

1. Menganalisis pendidikan dan metodologis pada masalah yang diteliti.

2. Identifikasi skema metodologistransformasi graf fungsi pada mata kuliah matematika sekolah.

3. Pilih metode dan cara yang paling efektifkonstruksi dan transformasi grafik fungsi di sekolah menengahberkontribusi pada: asimilasi materi pendidikan yang bermakna; meningkatkan aktivitas kognitif siswa; pengembangan kemampuan kreatif mereka.

HIPOTESA riset: pembentukan keterampilan grafis dalam proses mempelajari fungsi dan pendidikan budaya grafis siswa akan efektif jika siswa memiliki skema metodis untuk membangun dan mengubah grafik fungsi dalam kursus matematika sekolah.

BAB Saya . TINJAUAN PUSTAKA TENTANG TOPIK PROYEK.

Dalam persiapan untuk proyek ini, kami mempelajari literatur berikut:

Sivashinsky, I. Kh. Teorema dan masalah dalam aljabar, fungsi dasar - M., 2002. - 115 hal.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Fungsi dan grafik (teknik dasar) - M., 1985. - 120 s

V.Z.Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Matematika Dasar - M., 2010 (terbit ulang). - 590 hal.

Kuzmin, M. K. Konstruksi grafik fungsi - J. Matematika di sekolah. - 2003. - No. 5. - S.61-62.

Shilov G.E. Bagaimana cara membuat grafik? -M., 1982.

Ishak Tanatar. Transformasi geometris grafik fungsi - MTsNMO, 2012

PADAPerlu dicatat bahwa kemampuan untuk "membaca" perilaku suatu fungsi pada himpunan tertentu menggunakan grafik digunakan tidak hanya dalam pelajaran matematika, tetapi juga dalam aktivitas manusia praktis di mana ia harus berurusan dengan representasi grafik tertentu dari dependensi. Oleh karena itu, siswa harus dapat menentukan beberapa sifat-sifatnya dari grafik suatu fungsi.

Materi teoretis untuk transformasi grafik secara ketat dinyatakan dalam. Teknik ini disertai dengan ilustrasi dengan gambar, contoh berbagai kompleksitas dan solusinya, yang memungkinkan untuk memperdalam pengetahuan dan merencanakan fungsi yang kompleks.

Merupakan kursus pelatihan elektronik, yang volume dan isinya memenuhi persyaratan untuk kursus matematika sekolah menengah. Materi teoritis didukung dengan ilustrasi animasi grafis yang memberikan representasi visual dari topik yang diteliti. Kursus ini mencakup tiga modul: modul studi materi teoritis, modul pemeriksaan diri dan modul kontrol pengetahuan.

Dari , , skema charting metodis, contoh untuk pekerjaan independen digunakan untuk bagian empiris dari proyek.

Kesimpulan untuk bab 1

Studi literatur pendidikan dan metodis memungkinkan:

1. Identifikasi skema metodologismempelajari, membangun dan mengubah grafik fungsi dalam kursus matematika sekolah.

2. Pilih metode dan cara yang paling efektifkonstruksi dan transformasi grafik fungsi dalam matematika sekolah,berkontribusi:

asimilasi materi pendidikan yang bermakna;

meningkatkan aktivitas kognitif siswa;

pengembangan kemampuan kreatif mereka.

3. tunjukkan bahwa garis fungsional memiliki pengaruh yang signifikan dalam mempelajari berbagai konsep dalam matematika.

Bab 2. BAGIAN EMPIRIS

Dalam bab ini, kita akan mempertimbangkan metode utama untuk mengubah grafik fungsi, dan memberikan skema metodologis untuk membangun berbagai kombinasi grafik untuk berbagai fungsi.

2.1. TEKNIK DASAR UNTUK KONVERSI GRAF FUNGSI

Terjemahan sepanjang sumbu y

f ( x ) f ( x )+ b .

Untukmerencanakan suatu fungsikamu = f( x) + bjejakem:

1. buat grafik fungsikamu= f( x)

2. gerakkan sumbuabsis pada| b| unit dib>0 atau di| b| makansujud dib < 0. Diperoleh dalam sistem barugrafik dinat adalah grafik fungsikamu = f( x) + b.

2. Transfer sepanjang kapak absis

f ( x ) f ( x + sebuah ) .

kamu = f( x+ sebuah) jejakem:

3. Memplot fungsi dari bentuk kamu = f (- x )

f (x ) f (- x ).

Untuk memplot fungsikamu = f( - x) berikut:

plot sebuah fungsikamu = f( x)

mencerminkannya kembalirelatif terhadap sumbu y

grafik yang dihasilkan adalahgrafik fungsikamu = f( - X).

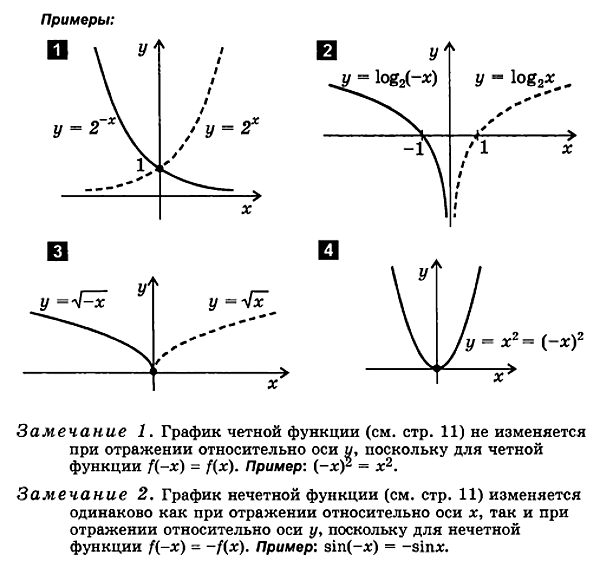
4. Merencanakan fungsi dari bentuk y= - f ( x )

f ( x ) - f ( x )

- f( x) berikut:

plot sebuah fungsikamu= f( x)

refleksikan terhadap sumbu x

2.2. Merencanakan sebuah genap dan fitur aneh

Saat merencanakanUntuk fungsi genap dan ganjil, akan lebih mudah untuk menggunakan properti berikut:

1. Grafik simmet fungsi genapberas relatif terhadap sumbu y.

2. Grafik fungsi ganjil simetris terhadap titik asal.

Untuk membuat grafik fungsi genap dan ganjil, cukup dengan memplot hanya cabang kanan grafik untuk nilai positif argumen. Cabang kiri diselesaikan secara simetris tentang asal untuk fungsi ganjil dan tentang sumbu y untuk fungsi genap.

Untuk memplot fungsi genap kamu = f ( x ) setelah duet:

buatlah cabang dari grafik fungsi ini hanya direntang nilai positif dari argumen x≥0.

HAIlacak cabang ini tentang sumbu y

Untuk memplot fungsi ganjil kamu = f ( x ) berikut:

bangun cabang grafik dari fungsi ini hanya diarea nilai positif dari argumen (х≥0).

HAIlacak cabang ini sehubungan dengan asalnyake daerah nilai x negatif.

2.3. Merencanakan fungsi invers

Seperti yang telah disebutkan, fungsi langsung dan fungsi terbalikmenunjukkan hubungan yang sama antar variabelx dan y, dengan satu-satunya perbedaan bahwa dalam fungsi invers inivariabel telah berubah peran, yang setara dengan perubahannotasi sumbu koordinat. Oleh karena itu, jadwalfungsi invers simetris dengan grafik fungsi langsungtentang bisektorSayadanAKU AKU AKUkoordinat sudut,yaitu relatif lurusy = x. Dengan demikian, kita mendapatkanaturan berikutnya.

Untuk memplot fungsi y = (x) kebalikan dari fungsikamu = f( x), harus dibangunjadwalkamu = f( x) dan mencerminkannya terhadap garis lurus y = x.

2.4. Deformasi (kompresi dan tegangan) dari grafik

1. Kompresi (perluasan) grafik sepanjang sumbu y

f ( x ) A ∙ f ( x ).

Untuk memplot fungsikamu= A∙ f( x) berikut:

8. Kompresi (perluasan) grafik sepanjang sumbu x

f( x)

Untuk memplot fungsi y= f( x) berikut:

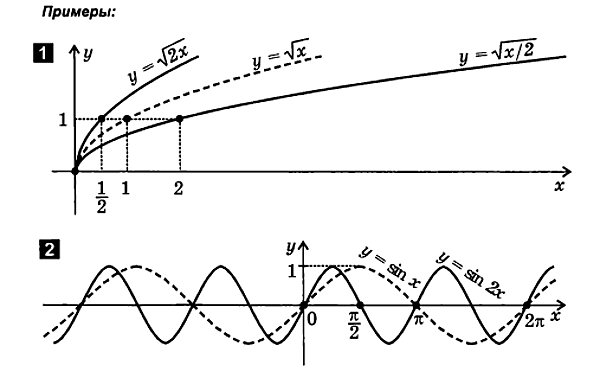
2.5. Kombinasi translasi, refleksi dan deformasi

Sangat sering ketika merencanakan grafik fungsi untukmengubah kombinasi.

Aplikasi yang konsisten dari sejumlah teknik postur seperti itumemungkinkan untuk menyederhanakan konstruksi grafik secara signifikan menggunakanmenjalankan fungsi dan sering menguranginya pada akhirnya menjadikonstruksi salah satu fungsi dasar yang paling sederhanation. Pertimbangkan bagaimana, mengingat hal di atas, berikut inimembuat grafik fungsi.

Mari kita perhatikan bahwa sudah waktunyadisarankan untuk melakukan penyederhanaan dok di penerus berikutnyaness.

Menggunakan paritas ataukeanehan fungsi.

Transfer sumbu.

Refleksi dan deformasi.

Konstruksi grafik dilakukan dalam urutan terbalik.

Contoh. Gambarkan sebuah fungsi

Konstruksi akan dilakukan dalam langkah-langkah berikut:

1. plot logaritma natural:

2. memeraske porosOY2 kali:;
3. ditampilkan secara simetristentang sumbuOY: ;
4. bergerak sepanjang sumbuSAPIpada(!!!) ke kanan::

5. tampilkan secara simetris tentang sumbuSAPI: ;
6. pindahsepanjang sumbuOY3 unit ke atas::

CONTOH GRAFIK KONSTRUKSI DAN KONVERSI FUNGSI

Contoh 1 Gambarkan sebuah fungsi.

Pertama, gambarkan grafik sinus, periodenya sama dengan:

grafik fungsidiperoleh dengan mengompresi grafikdua kali terhadap sumbu y. catatan .

Gambarkan sebuah fungsipada = 2 karenaX.

Gambarkan sebuah fungsikamu = dosax .

KESIMPULAN

Selama bekerja pada pekerjaan proyek, berbagai literatur pendidikan dan metodologis tentang masalah ini dianalisis. Hasil penelitian memungkinkan untuk mengidentifikasi aspek positif yang paling khas dari penelitian, konstruksi dan transformasi grafik fungsi dalam kursus matematika sekolah

Tujuan utama dari proyek ini adalah untuk mengembangkan keterampilan dan kemampuan siswa dalam membaca dan menggambar gambar, dalam pembentukan metode rasional kegiatan mandiri.

Kebutuhan untuk meningkatkan pendidikan grafis secara keseluruhan ditentukan tidak hanya oleh persyaratan produksi modern, tetapi juga oleh peran grafis dalam pengembangan pemikiran teknis dan kemampuan kognitif siswa. Kemampuan seseorang dalam mengolah informasi grafis merupakan salah satu indikator perkembangan mentalnya. Oleh karena itu, pelatihan grafis harus menjadi elemen integral dari pelatihan pendidikan umum.

temuan

Dengan demikian, proyek yang dikembangkan "Konstruksi dan transformasi grafik fungsi", yang didedikasikan untuk salah satu konsep sentral matematika - ketergantungan fungsional, difokuskan pada sistematisasi dan perluasan pengetahuan siswa. Studi tentang metode khusus untuk mengubah grafik fungsi dilakukan secara analitis dan grafis sesuai dengan skema metodologis yang ketat. Materi yang dikumpulkan dapat digunakan di kelas dan untuk pelatihan mandiri siswa. Berbagai bentuk dan metode organisasi dan pelatihan dapat digunakan untuk mengadakan kelas.

Portal untuk siswa. Latihan mandiri

ARTIKEL TERKAIT