დაღესტნის პროფესიული განვითარების ინსტიტუტი

პედაგოგიური პერსონალი

ფიზიკურ-მათემატიკური განათლებისა და ისტ-ის დეპარტამენტი

პროექტი

თემაზე:

« მშენებლობა და გვ რეფორმები

ფუნქციის გრაფიკები

სასკოლო მათემატიკაში »

რაბადანოვა პ.ა.

მათემატიკის მასწავლებელი

MBOU "ყოჩუბეის საშუალო სკოლა"

ტარუმოვსკის რაიონი

2015 წელი

1. შესავალი……………………………………………………………………..3

2. თავი მე. ლიტერატურის მიმოხილვა პროექტის თემაზე…………………………..5

3. თავი II. ემპირიული ნაწილი:

3.1. ფუნქციის გრაფიკების კონვერტაციის ძირითადი მეთოდები…………….7

3.2. ლუწის შედგენადაუცნაური ფუნქციები……………… 10

3.3. შებრუნებული ფუნქციის გამოსახვა…………………………… 11

3.4. გრაფიკების დეფორმაცია (შეკუმშვა და დაჭიმულობა).………………….12

3.5 გადატანის, არეკვლისა და დეფორმაციის ერთობლიობა………………………….13

4. ამოცანები დამოუკიდებელი გადაწყვეტისთვის………………………………14

5. დასკვნა………………………………………………………………………15

6. დასკვნები…………………………………………………………………………17

შესავალი

ფუნქციის გრაფიკების ტრანსფორმაცია არის ერთ-ერთი ფუნდამენტური მათემატიკური ცნება, რომელიც პირდაპირ კავშირშია პრაქტიკულ აქტივობებთან. გრაფიკებში ასახულია რეალური სამყაროს ცვალებადობა და დინამიკა, რეალური ობიექტებისა და ფენომენების ურთიერთმიმართება.

საბაზო და ერთიანი სახელმწიფო გამოცდების ძირითადი თემაა ფუნქციონალური ხაზი.ასევე, ბევრი მათემატიკური ცნება განიხილება გრაფიკული მეთოდებით. მაგალითად, რომკვადრატულიფუნქცია შემოტანილია და შესწავლილია კვადრატულ განტოლებებთან და უტოლობასთან მჭიდრო კავშირში.აქედან გამომდინარეობს, რომმოსწავლეებისთვის ფუნქციის გრაფიკების აგების და გარდაქმნის სწავლება სკოლაში მათემატიკის სწავლების ერთ-ერთი მთავარი ამოცანაა.

ფუნქციის შესწავლა იძლევა იმის გარკვევასფუნქციის განსაზღვრისა და ფარგლების სფერო, ფარგლებიკლებადი ან მზარდი მაჩვენებლები, ასიმპტომები, ინტერვალებინიშნის მუდმივობა და ა.შ. თუმცა, გრაფიკის ასაგებადkov ბევრი ფუნქცია შეიძლება იყოსგამოიყენეთ მრავალი მეთოდიგაუადვილეთშენობა. ამიტომ, მოსწავლეებს უნდა ჰქონდეთ კომპეტენცია მეთოდოლოგიური სქემების მიხედვით ააგონ გრაფიკები.

ზემოაღნიშნული განსაზღვრავსშესაბამისობა კვლევის თემები.

კვლევის ობიექტი არის სასკოლო მათემატიკაში ფუნქციური ხაზის გრაფიკების ტრანსფორმაციის შესწავლა.

სასწავლო საგანი - ფუნქციური გრაფიკების აგების და გარდაქმნის პროცესი საშუალო სკოლაში.

სწავლის მიზანი: საგანმანათლებლო - შედგება ფუნქციის გრაფიკების აგებისა და კონვერტაციის მეთოდოლოგიური სქემის განსაზღვრაში;განვითარებადი - აბსტრაქტული, ალგორითმული, ლოგიკური აზროვნების, სივრცითი წარმოსახვის განვითარება;საგანმანათლებლო - სკოლის მოსწავლეების გრაფიკული კულტურის განათლება, გონებრივი უნარების ჩამოყალიბება.

მიზნებმა განაპირობა შემდეგი გადაწყვეტილებადავალებები:

1. შესწავლილ პრობლემაზე საგანმანათლებლო და მეთოდოლოგიური ანალიზი.

2. მეთოდოლოგიური სქემების იდენტიფიცირებაფუნქციის გრაფიკების ტრანსფორმაცია მათემატიკის სასკოლო კურსში.

3. შეარჩიეთ ყველაზე ეფექტური მეთოდები და საშუალებებიფუნქციის გრაფიკების აგება და ტრანსფორმაცია საშუალო სკოლაშიწვლილი შეიტანოს: სასწავლო მასალის აზრობრივ ათვისებაში; მოსწავლეთა შემეცნებითი აქტივობის გაზრდა; მათი შემოქმედებითი შესაძლებლობების განვითარება.

ჰიპოთეზაკვლევა: გრაფიკული უნარების ჩამოყალიბება მოსწავლეთა ფუნქციების შესწავლისა და გრაფიკული კულტურის აღზრდის პროცესში ეფექტური, თუ მოსწავლეებს აქვთ სასკოლო მათემატიკის კურსში ფუნქციის გრაფიკების აგებისა და გარდაქმნის მეთოდური სქემა.

თავი მე . ლიტერატურის მიმოხილვა პროექტის თემაზე.

პროექტისთვის მომზადებისას შევისწავლეთ შემდეგი ლიტერატურა:

სივაშინსკი, ი.ხ.თეორემები და ამოცანები ალგებრაში, ელემენტარული ფუნქციები - მ., 2002. - 115გვ.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. ფუნქციები და გრაფიკები (ძირითადი ტექნიკა) - M., 1985. - 120 წ.

ვ.ზ.ზაიცევი, ვ.ვ. რიჟკოვი, მ.ი. სკანავი. დაწყებითი მათემატიკა - მ., 2010 (ხელახალი გამოცემა). - 590 გვ.

Kuzmin, M. K. ფუნქციის გრაფიკის აგება - J. მათემატიკა სკოლაში. - 2003. - No5. - S. 61-62.

შილოვი გ.ე. როგორ ავაშენოთ სქემები? - მ., 1982 წ.

ისააკ ტანატარი. ფუნქციების გრაფიკების გეომეტრიული გარდაქმნები - MTsNMO, 2012 წ

ATაღნიშნულია, რომ გრაფიკის გამოყენებით ფუნქციის გარკვეულ სიმრავლეზე ქცევის „წაკითხვის“ უნარი გამოიყენება არა მხოლოდ მათემატიკის მსვლელობისას, არამედ ადამიანის ნებისმიერ პრაქტიკულ საქმიანობაში, რომელშიც მას გარკვეული გრაფიკა აქვს. დამოკიდებულების წარმოდგენები. ამიტომ, სტუდენტებს უნდა შეეძლოთ მისი ზოგიერთი თვისების განსაზღვრა ფუნქციის გრაფიკიდან.

გრაფიკების ტრანსფორმაციის თეორიული მასალა მკაცრად არის მითითებული. ტექნიკას თან ახლავს ილუსტრაციები ნახატებით, სხვადასხვა სირთულის მაგალითებით და მათი გადაწყვეტილებებით, რაც შესაძლებელს ხდის ცოდნის გაღრმავებას და რთული ფუნქციების დასახვას.

წარმოადგენს ელექტრონულ სასწავლო კურსს, რომლის მოცულობა და შინაარსი აკმაყოფილებს საშუალო სკოლის მათემატიკის კურსის მოთხოვნებს. თეორიული მასალა დაფუძნებულია გრაფიკული ანიმაციური ილუსტრაციებით, რომლებიც იძლევა შესასწავლი თემის ვიზუალურ წარმოდგენას. კურსი მოიცავს სამ მოდულს: თეორიული მასალის შემსწავლელი მოდული, თვითგამოკვლევის მოდული და ცოდნის კონტროლის მოდული.

, , მეთოდური დიაგრამების სქემებიდან, პროექტის ემპირიული ნაწილისთვის გამოყენებული იქნა დამოუკიდებელი მუშაობის მაგალითები.

დასკვნა 1 თავის შესახებ

სასწავლო და მეთოდური ლიტერატურის შესწავლა საშუალებას აძლევდა:

1. მეთოდოლოგიური სქემის განსაზღვრასასკოლო მათემატიკის კურსში ფუნქციის გრაფიკების შესწავლა, აგება და ტრანსფორმაცია.

2. აირჩიეთ ყველაზე ეფექტური მეთოდები და საშუალებებიფუნქციის გრაფიკების აგება და ტრანსფორმაცია სასკოლო მათემატიკაში,წვლილი შეაქვს:

სასწავლო მასალის შინაარსიანი ათვისება;

მოსწავლეთა შემეცნებითი აქტივობის გაზრდა;

მათი შემოქმედებითი შესაძლებლობების განვითარება.

3. აჩვენე რომ ფუნქციურ ხაზს მნიშვნელოვანი გავლენა აქვს მათემატიკაში სხვადასხვა ცნების შესწავლაში.

თავი 2. ემპირიული ნაწილი

ამ თავში განვიხილავთ ფუნქციის გრაფიკების გარდაქმნის ძირითად მეთოდებს და მივცემთ მეთოდოლოგიურ სქემებს სხვადასხვა ფუნქციისთვის გრაფიკების სხვადასხვა კომბინაციების აგებისთვის.

2.1. ფუნქციების გრაფიკის კონვერტაციის ძირითადი ტექნიკა

თარგმანი y-ღერძის გასწვრივ

ვ ( x ) ვ ( x )+ ბ .

ამისთვისფუნქციის შედგენაწ = ვ( x) + ბკვალიem:

1. ფუნქციის გრაფიკის აგებაწ= ვ( x)

2. გადაადგილების ღერძიაბსციზაზე| ბ| ერთეულები ზებ>0 ან ზე| ბ| ჭამედამხობილი ზებ < 0. მიღებულია ახალ სისტემაშიdinat გრაფი არის ფუნქციის გრაფიკიწ = ვ( x) + ბ.

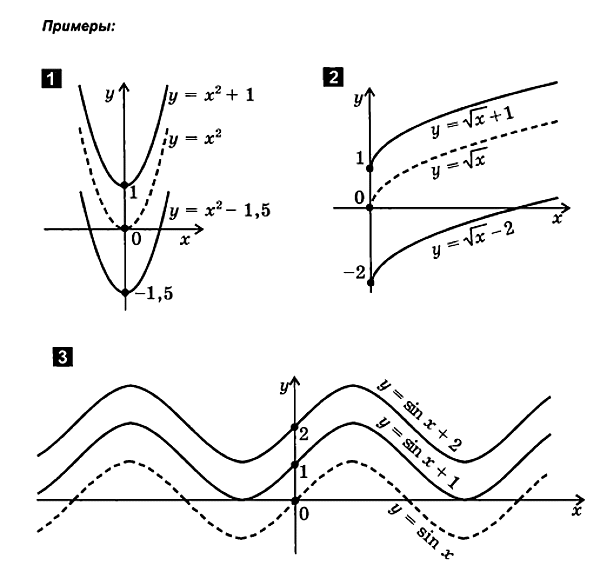
2. გადაცემა გასწვრივ ცულები აბსცისა

ვ ( x ) ვ ( x + ა ) .

წ = ვ( x+ ა) კვალიem:

3. ფორმის ფუნქციის გამოსახვა წ = ვ (- x )

ვ (x ) ვ (- x ).

ფუნქციის დასახატადწ = ვ( - x) შემდეგნაირად:

ფუნქციის დახატვაწ = ვ( x)

ასახავს მას უკანy-ღერძთან შედარებით

შედეგად მიღებული გრაფიკი არისფუნქციის გრაფიკიწ = ვ( - X).

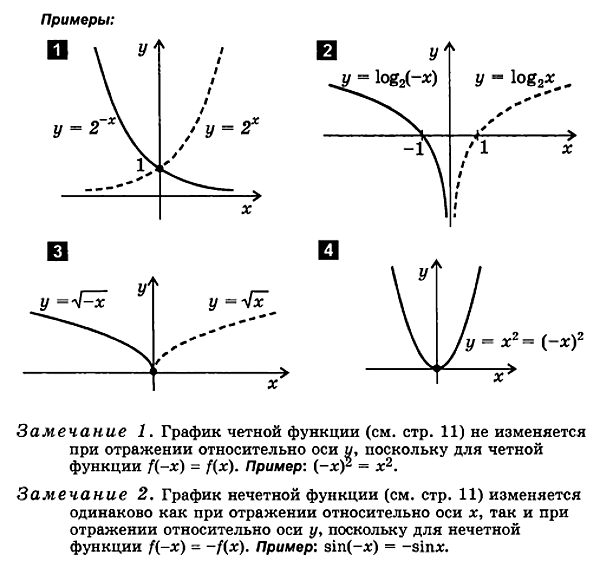
4. ფორმის ფუნქციის გამოსახვა y= - ვ ( x )

ვ ( x ) - ვ ( x )

- ვ( x) შემდეგნაირად:

ფუნქციის დახატვაწ= ვ( x)

ასახავს მას x ღერძზე

2.2. ლუწის შედგენა და უცნაური თვისებები

შეთქმულებისასლუწი და კენტი ფუნქციებისთვის მოსახერხებელია შემდეგი თვისებების გამოყენება:

1. ლუწი ფუნქციის სიმეტის გრაფიკიბრინჯი y-ღერძთან შედარებით.

2. კენტი ფუნქციის გრაფიკი სიმეტრიულია წარმოშობის მიმართ.

ლუწი და კენტი ფუნქციების გრაფიკების ასაგებად, საკმარისია არგუმენტის დადებითი მნიშვნელობებისთვის გრაფიკის მხოლოდ მარჯვენა ტოტის დახატვა. მარცხენა ტოტი სრულდება სიმეტრიულად კენტი ფუნქციის წარმოშობის შესახებ და ლუწი ფუნქციისთვის y-ღერძის შესახებ.

თანაბარი ფუნქციის დასახატად წ = ვ ( x ) შემდეგ დუეტი:

შექმენით ამ ფუნქციის გრაფიკის განშტოება მხოლოდარგუმენტის დადებითი მნიშვნელობების დიაპაზონი x≥0.

ოდახაზეთ ეს ტოტი y ღერძის გარშემო

კენტი ფუნქციის გამოსახატავად წ = ვ ( x ) შემდეგნაირად:

შექმენით ამ ფუნქციის გრაფიკის ფილიალი მხოლოდარგუმენტის დადებითი მნიშვნელობების ფართობი (х≥0).

ომიაკვლიეთ ამ შტოს წარმოშობის მიმართუარყოფითი x მნიშვნელობების რეგიონამდე.

2.3. შებრუნებული ფუნქციის გამოსახვა

როგორც უკვე აღვნიშნეთ, პირდაპირი და ინვერსიული ფუნქციებიაჩვენეთ იგივე ურთიერთობა ცვლადებს შორისx და y, იმ განსხვავებით, რომ შებრუნებულ ფუნქციაში ესენიაცვლადებმა შეცვალეს როლები, რაც ცვლილების ტოლფასიაკოორდინატთა ღერძების აღნიშვნა. ამიტომ, გრაფიკიშებრუნებული ფუნქცია სიმეტრიულია პირდაპირი ფუნქციის გრაფიკის მიმართბისექტრის შესახებმედაIIIკოორდინირებული კუთხეები,ანუ შედარებით სწორიy = x. ამრიგად, ჩვენ ვიღებთშემდეგი წესი.

y = ფუნქციის გამოსახატავად (x) ფუნქციის შებრუნებულიწ = ვ( x), უნდა აშენდესგანრიგიწ = ვ( x) და ასახავს მას სწორი ხაზის მიმართ y = x.

2.4. გრაფიკების დეფორმაცია (შეკუმშვა და დაჭიმულობა).

1. გრაფიკის შეკუმშვა (გაფართოება) y ღერძის გასწვრივ

ვ ( x ) ა ∙ ვ ( x ).

ფუნქციის დასახატადწ= ა∙ ვ( x) შემდეგნაირად:

8. გრაფიკის შეკუმშვა (გაფართოება) x ღერძის გასწვრივ

ვ( x)

y ფუნქციის გამოსახატავად= ვ( x) შემდეგნაირად:

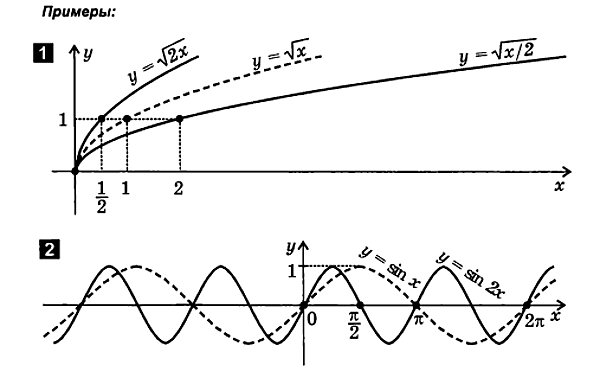
2.5. თარგმანის, ასახვისა და დეფორმაციის კომბინაცია

ძალიან ხშირად ფუნქციის გრაფიკების შედგენისასშეცვალეთ კომბინაცია.

რიგი ასეთი პოზის ტექნიკის თანმიმდევრული გამოყენებასაშუალებას გაძლევთ მნიშვნელოვნად გაამარტივოთ გრაფიკის აგება გამოყენებითგაშვებული ფუნქცია და ხშირად ამცირებს მას ბოლოსერთ-ერთი უმარტივესი ელემენტარული ფუნქციის აგებაtions. იფიქრეთ იმაზე, თუ როგორ მოჰყვება ის, ზემოაღნიშნულის გათვალისწინებითფუნქციის გრაფიკების აგება.

შეგახსენებთ, რომ დროამიზანშეწონილია განახორციელოს გამარტივებული დოკი მომდევნო მემკვიდრეშიness.

პარიტეტის გამოყენება ანფუნქციის უცნაურობა.

ცულების გადაცემა.

ანარეკლი და დეფორმაცია.

გრაფიკის აგება შესრულებულია საპირისპირო თანმიმდევრობით.

მაგალითი. დახაზეთ ფუნქცია

მშენებლობა განხორციელდება შემდეგი ეტაპებით:

1. გამოვსახოთ ბუნებრივი ლოგარითმი:

2. გაწურეთღერძამდეOY2 ჯერ:;
3. ჩვენება სიმეტრიულადღერძის შესახებOY: ;
4. გადაადგილება ღერძის გასწვრივოქსიზე(!!!) მარჯვნივ::

5. სიმეტრიულად ჩვენება ღერძის მიმართოქსი: ;
6. გადაადგილებაღერძის გასწვრივOY3 ერთეული ზემოთ::

ფუნქციების გრაფიკების აგების და კონვერტაციის მაგალითები

მაგალითი 1 დახაზეთ ფუნქცია.

ჯერ დახაზეთ სინუს გრაფიკი, მისი პერიოდი ტოლია:

ფუნქციის გრაფიკიმიღებული გრაფიკის შეკუმშვითორჯერ y-ღერძამდე.ჟურნალი .

დახაზეთ ფუნქციაზე = 2 cosX.

დახაზეთ ფუნქციაწ = ცოდვაx .

დასკვნა

საპროექტო სამუშაოებზე მუშაობისას გაანალიზდა ამ საკითხზე სხვადასხვა საგანმანათლებლო და მეთოდური ლიტერატურა. კვლევის შედეგებმა შესაძლებელი გახადა კვლევის ყველაზე დამახასიათებელი დადებითი ასპექტების გამოვლენა, ფუნქციის გრაფიკების აგება და ტრანსფორმაცია სასკოლო მათემატიკის კურსში

პროექტის მთავარი მიზანია მოსწავლეებს განუვითაროს ნახატების კითხვისა და ხატვის უნარ-ჩვევები და შესაძლებლობები, დამოუკიდებელი საქმიანობის რაციონალური მეთოდების ჩამოყალიბებაში.

მთლიანობაში გრაფიკული განათლების გაუმჯობესების აუცილებლობა ნაკარნახევია არა მხოლოდ თანამედროვე წარმოების მოთხოვნებით, არამედ გრაფიკის როლით სტუდენტების ტექნიკური აზროვნებისა და შემეცნებითი შესაძლებლობების განვითარებაში. ადამიანის გრაფიკული ინფორმაციის დამუშავების უნარი მისი გონებრივი განვითარების ერთ-ერთი მაჩვენებელია. ამიტომ, გრაფიკული სწავლება ზოგადსაგანმანათლებლო მომზადების განუყოფელი ელემენტი უნდა გახდეს.

დასკვნები

ამრიგად, შემუშავებული პროექტი „ფუნქციის გრაფიკების აგება და ტრანსფორმაცია“, რომელიც ეძღვნება მათემატიკის ერთ-ერთ ცენტრალურ ცნებას - ფუნქციონალურ დამოკიდებულებას, ორიენტირებულია მოსწავლეთა ცოდნის სისტემატიზაციასა და გაფართოებაზე. ფუნქციის გრაფიკების გარდაქმნის კონკრეტული მეთოდების შესწავლა ხორციელდება ანალიტიკური და გრაფიკული წესით მკაცრი მეთოდოლოგიური სქემების მიხედვით. შეგროვებული მასალა შეიძლება გამოყენებულ იქნას კლასში და მოსწავლეთა თვითტრენინგისთვის. გაკვეთილების ჩასატარებლად შეიძლება გამოყენებულ იქნას ორგანიზებისა და ტრენინგის სხვადასხვა ფორმა და მეთოდი.

კვადრატული განტოლების გრაფიკული ამოხსნა სხვადასხვა ფუნქციის გრაფიკების აგების უნარის კონსოლიდაცია; კვადრატული განტოლებების გრაფიკულად ამოხსნის უნარის ჩამოყალიბება. ბრდსკი 2009 მუნიციპალური საგანმანათლებლო დაწესებულება - ეკონომიკური ლიცეუმი განმაზოგადებელი გაკვეთილი თემაზე "კვადრატული ფუნქცია", ალგებრა მე-8 კლასის მასწავლებელი ფედოსეევა თ.მ.

კვადრატული ფუნქციის გამოსახვა ტოტების მიმართულების დადგენა: a>0 განშტოება ზემოთ; ა 0 ტოტი ზევით; a"> 0 ფილიალი ზევით; a"> 0 ფილიალი ზევით; a" title="(!LANG: კვადრატული ფუნქციის დახატვა ტოტის მიმართულების განსაზღვრა: a>0 განშტოება ზემოთ; a"> title="კვადრატული ფუნქციის გამოსახვა ტოტების მიმართულების დადგენა: a>0 განშტოება ზემოთ; ა"> !}

0 ტოტი მიმართულია ზემოთ; 2) წვერო y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - პარაბოლის ღერძი საკონტროლო წერტილები: (0: -3), (3 ; 0) და მათთვის სიმეტრიული x ღერძის მიმართ = 1 ჩვენ ვაშენებთ პარაბოლას. იპოვეთ წერტილი "title="(!LANG: ავაშენოთ y=x 2 -2x-3 ფუნქციის გრაფიკი ალგორითმის გამოყენებით: 1) a=1>0 ტოტები მიმართულია ზემოთ; 2) წვერო y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - პარაბოლის ღერძი საკონტროლო წერტილები: (0: -3), (3 ; 0) და მათთვის სიმეტრიული x ღერძის მიმართ = 1 ჩვენ ვაშენებთ პარაბოლას. წერტილის პოვნა" class="link_thumb"> 3 !}ავაშენოთ y=x 2 -2x-3 ფუნქციის გრაფიკი ალგორითმის გამოყენებით: 1) a=1>0 ტოტი მიმართულია ზემოთ; 2) წვერო y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - პარაბოლის ღერძი საკონტროლო წერტილები: (0: -3), (3 ; 0) და მათთვის სიმეტრიული x ღერძის მიმართ = 1 ჩვენ ვაშენებთ პარაბოლას. ჩვენ ვპოულობთ გადაკვეთის წერტილებს OX ღერძთან: x 1 \u003d -1; x 2 \u003d 3 1 განტოლების ამოხსნის გზა x 2 -2x-3 \u003d 0 y x განტოლების ამოხსნა x 2 +2x-3 \u003d 0 0 ტოტი მიმართულია ზემოთ; 2) წვერო y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - პარაბოლის ღერძი საკონტროლო წერტილები: (0: -3), (3 ; 0) და მათთვის სიმეტრიული x ღერძის მიმართ = 1 ჩვენ ვაშენებთ პარაბოლას. ჩვენ ვპოულობთ წერტილს "\u003e 0 ტოტები მიმართულია ზემოთ; 2) ზედა y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ღერძი პარაბოლის საკონტროლო წერტილები: (0: -3), (3; 0) და სიმეტრიული x = 1 ღერძის მიმართ ჩვენ ვაშენებთ პარაბოლას. იპოვეთ გადაკვეთის წერტილები OX ღერძთან: x 1 \u003d -1; x 2 \u003d 3 1 განტოლების ამოხსნის გზა x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 ამოხსენი განტოლება x 2 + 2x-3 \u003d 0 "\u003e 0 ტოტი მიმართულია ზემოთ; 2) წვერო y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - პარაბოლის ღერძი საკონტროლო წერტილები: (0: -3), (3 ; 0) და მათთვის სიმეტრიული x ღერძის მიმართ = 1 ჩვენ ვაშენებთ პარაბოლას. იპოვეთ წერტილი "title="(!LANG: ავაშენოთ y=x 2 -2x-3 ფუნქციის გრაფიკი ალგორითმის გამოყენებით: 1) a=1>0 ტოტები მიმართულია ზემოთ; 2) წვერო y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - პარაბოლის ღერძი საკონტროლო წერტილები: (0: -3), (3 ; 0) და მათთვის სიმეტრიული x ღერძის მიმართ = 1 ჩვენ ვაშენებთ პარაბოლას. წერტილის პოვნა"> title="ავაშენოთ y=x 2 -2x-3 ფუნქციის გრაფიკი ალგორითმის გამოყენებით: 1) a=1>0 ტოტი მიმართულია ზემოთ; 2) წვერო y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - პარაბოლის ღერძი საკონტროლო წერტილები: (0: -3), (3 ; 0) და მათთვის სიმეტრიული x ღერძის მიმართ = 1 ჩვენ ვაშენებთ პარაბოლას. წერტილის პოვნა"> !}

მეორე გზა: ა). x 2 -2x-3=0 განტოლება გავყოთ x 2 = 2x+3 ნაწილებად დავწეროთ ორი ფუნქცია y= x 2 ; y \u003d 2x + 3 ჩვენ ვაშენებთ ამ ფუნქციების გრაფიკებს ერთ კოორდინატულ სისტემაში. გადაკვეთის წერტილების აბსციები განტოლების ფესვებია. 0 1 x y ამოხსენით განტოლება x 2 +2x-3=0

მესამე გზა: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x ჩვენ ვაშენებთ ამ ფუნქციების გრაფიკებს ერთ კოორდინატულ სისტემაში. გადაკვეთის წერტილების აბსციები განტოლების ფესვებია. 0 1 x y ამოხსენით განტოლება x 2 +2x-3=0

განტოლებათა გრაფიკული ამოხსნა

ჰეიდეი, 2009 წელი

- შესავალი -

კვადრატული განტოლებების ამოხსნის აუცილებლობა ძველ დროში გამოწვეული იყო ამოცანების გადაჭრის აუცილებლობით, რომლებიც დაკავშირებულია სამხედრო ხასიათის მიწისა და მიწის სამუშაოების მოძიებასთან, აგრეთვე თავად ასტრონომიისა და მათემატიკის განვითარებასთან. ბაბილონელებმა იცოდნენ როგორ ამოეხსნათ კვადრატული განტოლებები ჩვენს წელთაღრიცხვამდე დაახლოებით 2000 წელს. ამ განტოლებების ამოხსნის წესი, რომელიც ნათქვამია ბაბილონურ ტექსტებში, არსებითად ემთხვევა თანამედროვეებს, მაგრამ უცნობია, როგორ მივიდნენ ბაბილონელები ამ წესამდე.

ევროში კვადრატული განტოლებების ამოხსნის ფორმულები პირველად ჩამოყალიბდა აბაკუსის წიგნში, რომელიც დაიწერა 1202 წელს იტალიელმა მათემატიკოსმა ლეონარდო ფიბონაჩის მიერ. მისმა წიგნმა ხელი შეუწყო ალგებრული ცოდნის გავრცელებას არა მარტო იტალიაში, არამედ გერმანიაში, საფრანგეთსა და ევროპის სხვა ქვეყნებში.

მაგრამ კვადრატული განტოლებების ამოხსნის ზოგადი წესი, b და c კოეფიციენტების ყველა შესაძლო კომბინაციით, ჩამოყალიბდა ევროᴨȇში მხოლოდ 1544 წელს მ.შტიფელის მიერ.

1591 წელს ფრანსუა ვიეტი შემოიღო კვადრატული განტოლებების ამოხსნის ფორმულები.

ზოგიერთი სახის კვადრატული განტოლება ამოხსნილი იყო ძველ ბაბილონში.

დიოფანტე ალექსანდრიელიდა ევკლიდე, ალ-ხვარიზმიდა ომარ ხაიამიამოხსნილი განტოლებები გეომეტრიული და გრაფიკული გზებით.

მე-7 კლასში ვისწავლეთ ფუნქციები y \u003d C, y=kx, y = კx+ მ, y =x 2 ,y=- x 2 , მე-8 კლასში - y = vx, y =|x|, ზე = ნაჯახი 2 + bx+ გ, y =კ / x. მე-9 კლასის ალგებრის სახელმძღვანელოში ვნახე ფუნქციები, რომლებიც ჯერ არ იყო ჩემთვის ცნობილი: y=x 3 , ზე = x 4 ,y=x 2 n, ზე = x - 2 n, ზე = 3ვ x, (x - ა) 2 + (y -ბ) 2 = რ 2 და სხვები. არსებობს ამ ფუნქციების გრაფიკების აგების წესები. მაინტერესებდა არის თუ არა სხვა ფუნქციები, რომლებიც ამ წესებს ემორჩილება.

ჩემი საქმეა ფუნქციების გრაფიკების შესწავლა და განტოლებების გრაფიკულად ამოხსნა.

1. რა ფუნქციებია

ფუნქციის გრაფიკი არის კოორდინატთა სიბრტყის ყველა წერტილის ერთობლიობა, რომელთა აბსციები უდრის არგუმენტების მნიშვნელობებს, ხოლო ორდინატები ტოლია ფუნქციის შესაბამისი მნიშვნელობების.

წრფივი ფუნქცია მოცემულია განტოლებით y=kx + ბ, სად კდა ბ- რამდენიმე რიცხვი. ამ ფუნქციის გრაფიკი არის სწორი ხაზი.

შებრუნებული პროპორციული ფუნქცია y=კ/ x, სადაც k 0. ამ ფუნქციის გრაფიკს ეწოდება giᴨȇrbola.

ფუნქცია (x - ა) 2 + (y -ბ) 2 = რ 2 , სად ა, ბდა რ- რამდენიმე რიცხვი. ამ ფუნქციის გრაფიკი არის r რადიუსის წრე, რომელიც ორიენტირებულია A წერტილზე ( ა, ბ).

კვადრატული ფუნქცია წ = ნაჯახი 2 + bx + გსადაც ა,ბ, თან- რამდენიმე რიცხვი და ა 0. ამ ფუნქციის გრაფიკი არის პარაბოლა.

განტოლება ზე 2 (ა - x) = x 2 (ა+ x) . ამ განტოლების გრაფიკი იქნება მრუდი, რომელსაც სტროფოიდი ეწოდება.

განტოლება (x 2 + წ 2 ) 2 = ა (x 2 - წ 2 ) . ამ განტოლების გრაფიკს ბერნულის ლემა ეწოდება.

განტოლება. ამ განტოლების გრაფიკს ასტროიდი ეწოდება.

მრუდი (x 2 წ 2 - 2 ცალი) 2 =4 ა 2 (x 2 + წ 2 ) . ამ მრუდს კარდიოიდი ეწოდება.

ფუნქციები: y=x 3 - კუბური პარაბოლა, y=x 4 , y = 1/x 2 .

2. განტოლების ცნება, მისი გრაფიკული ამოხსნა

განტოლება- გამოთქმა, რომელიც შეიცავს ᴨȇ.

განტოლების ამოხსნა- ეს ნიშნავს მისი ყველა ფესვის პოვნას, ან იმის დამტკიცებას, რომ ისინი არ არსებობს.

განტოლების ფესვი- ეს არის რიცხვი, მისი განტოლებაში ჩანაცვლებისას მიიღება სწორი რიცხვითი ტოლობა.

განტოლებების გრაფიკულად ამოხსნასაშუალებას გაძლევთ იპოვოთ ფესვების ზუსტი ან სავარაუდო მნიშვნელობა, საშუალებას გაძლევთ იპოვოთ განტოლების ფესვების რაოდენობა.

გრაფიკების აგებისა და განტოლებების ამოხსნისას გამოიყენება ფუნქციის თვისებები, ამ მხრივ მეთოდს ხშირად ფუნქციონალურ-გრაფიკულს უწოდებენ.

განტოლების ამოსახსნელად მას „ვყოფთ“ ორ ნაწილად, შემოგვაქვს ორი ფუნქცია, ვაშენებთ მათ გრაფიკებს, ვპოულობთ გრაფიკების გადაკვეთის წერტილების კოორდინატებს. ამ წერტილების აბსციები არის განტოლების ფესვები.

3. ფუნქციის გრაფიკის გამოსახვის ალგორითმი

ფუნქციის გრაფიკის ცოდნა y=ვ(x) , შეგიძლიათ დახაზოთ ფუნქციები y=ვ (x+ მ) ,y=ვ(x)+ ლდა y=ვ (x+ მ)+ ლ. ყველა ეს გრაფიკი მიღებულია ფუნქციის გრაფიკიდან y=ვ(x) პარალელური ᴨȇrenos-ის გარდაქმნის გამოყენებით: on ¦ მ¦ მასშტაბის ერთეულები მარჯვნივ ან მარცხნივ x-ღერძის გასწვრივ და შემდეგ ¦ ლ¦ მასშტაბის ერთეულები ზემოთ ან ქვემოთ ღერძის გასწვრივ წ.

4. კვადრატული განტოლების გრაფიკული ამოხსნა

კვადრატული ფუნქციის მაგალითის გამოყენებით განვიხილავთ კვადრატული განტოლების გრაფიკულ ამოხსნას. კვადრატული ფუნქციის გრაფიკი არის პარაბოლა.

რა იცოდნენ ძველმა ბერძნებმა პარაბოლის შესახებ?

თანამედროვე მათემატიკური სიმბოლიზმი წარმოიშვა მე-16 საუკუნეში.

ძველ ბერძენ მათემატიკოსებს არც კოორდინატთა მეთოდი ჰქონდათ და არც ფუნქციის კონცეფცია. თუმცა პარაბოლას თვისებები მათ დეტალურად შეისწავლეს. ძველი მათემატიკოსების გამომგონებლობა უბრალოდ გასაოცარია, რადგან მათ შეეძლოთ მხოლოდ ნახატებისა და დამოკიდებულებების სიტყვიერი აღწერების გამოყენება.

მან ყველაზე სრულად გამოიკვლია პარაბოლა, გიᴨȇბოლა და ელიფსი აპოლონიოს პერგაელი, რომელიც ცხოვრობდა ჩვენს წელთაღრიცხვამდე III საუკუნეში. მან ასევე დაასახელა ამ მრუდეები და მიუთითა, თუ რა პირობებს აკმაყოფილებს კონკრეტულ მრუდეზე მოთავსებული წერტილები (ბოლოს და ბოლოს, ფორმულები არ არსებობდა!).

პარაბოლის ასაგებად არსებობს ალგორითმი:

ჩვენ ვპოულობთ პარაბოლას A წვეროს კოორდინატებს (x 0; y 0): X 0 =- ბ/2 ა;

Y 0 \u003d ცული დაახლოებით 2 + 0 + c-ში;

ჩვენ ვპოულობთ პარაბოლის სიმეტრიის ღერძს (სწორი ხაზი x \u003d x 0);

შენობების საკონტროლო წერტილების მნიშვნელობების ცხრილის შედგენა;

მიღებულ წერტილებს ვაშენებთ და ვაშენებთ მათ სიმეტრიულ წერტილებს სიმეტრიის ღერძის მიმართ.

1. ავაშენოთ პარაბოლა ალგორითმის მიხედვით წ = x 2 - 2 x - 3 . ᴨȇ ღერძთან კვეთა წერტილების აბსციები x და არის კვადრატული განტოლების ფესვები x 2 - 2 x - 3 = 0.

ამ განტოლების გრაფიკულად ამოხსნის ხუთი გზა არსებობს.

2. დავყოთ განტოლება ორ ფუნქციად: წ= x 2 და წ= 2 x + 3

3. დავყოთ განტოლება ორ ფუნქციად: წ= x 2 -3 და წ =2 x. განტოლების ფესვები არის პარაბოლის წრფესთან კვეთის წერტილების აბსციები.

4. გადააქციეთ განტოლება x 2 - 2 x - 3 = 0 ფუნქციის სრული კვადრატის არჩევით: წ= (x -1) 2 და წ=4 . განტოლების ფესვებია პარაბოლას წრფესთან კვეთის წერტილების აბსციები.

5. განტოლების ორივე ნაწილს ვანაწილებთ ტერმინებს x 2 - 2 x - 3 = 0 ზე x, ვიღებთ x - 2 - 3/ x = 0 მოდით გავყოთ ეს განტოლება ორ ფუნქციად: წ = x - 2, წ = 3/ x. განტოლების ფესვები არის სწორი ხაზისა და გიᴨȇrbola-ს გადაკვეთის წერტილების აბსციები.

5. გრაფიკული გადაწყვეტახარისხის განტოლებებინ

მაგალითი 1განტოლების ამოხსნა x 5 = 3 - 2 x.

წ = x 5 , წ = 3 - 2 x.

პასუხი: x = 1.

მაგალითი 2განტოლების ამოხსნა 3 ვx = 10 - x.

ამ განტოლების ფესვები არის ორი ფუნქციის გრაფიკის გადაკვეთის წერტილის აბსციზა: წ = 3 ვx, წ = 10 - x.

პასუხი: x=8.

- დასკვნა -

ფუნქციის გრაფიკის გათვალისწინებით: ზე = ნაჯახი 2 + bx+ გ, y =კ / x, y = vx, y =|x|, y=x 3 , y=x 4 ,y= 3ვ x, შევამჩნიე, რომ ყველა ეს გრაფიკი აგებულია ᴨȇrenos პარალელური წესის მიხედვით ღერძებთან მიმართებაში. xდა წ.

კვადრატული განტოლების ამოხსნის მაგალითის გამოყენებით შეგვიძლია დავასკვნათ, რომ გრაფიკული მეთოდი ასევე გამოიყენება n ხარისხის განტოლებებზე.

განტოლებების ამოხსნის გრაფიკული მეთოდები ლამაზი და გასაგებია, მაგრამ ისინი არ იძლევა რაიმე განტოლების ამოხსნის 100%-იან გარანტიას. გრაფიკების ᴨȇ გადაკვეთის წერტილების აბსციები შეიძლება იყოს მიახლოებითი.

მე-9 კლასში და უფროს კლასებში კიდევ გავიცნობ სხვა ფუნქციებს. მაინტერესებს, ემორჩილება თუ არა ეს ფუნქციები პარალელური ᴨȇrenos-ის წესებს მათი გრაფიკების შედგენისას.

მომავალ წელს ასევე მინდა განვიხილო განტოლებათა და უტოლობათა სისტემების გრაფიკული ამოხსნის საკითხები.

ლიტერატურა

1. ალგებრა. მე-7 კლასი. ნაწილი 1. სახელმძღვანელო საგანმანათლებლო დაწესებულებებისათვის / ა.გ. მორდკოვიჩი. მოსკოვი: მნემოსინე, 2007 წ.

2. ალგებრა. მე-8 კლასი. ნაწილი 1. სახელმძღვანელო საგანმანათლებლო დაწესებულებებისათვის / ა.გ. მორდკოვიჩი. მოსკოვი: მნემოსინე, 2007 წ.

3. ალგებრა. მე-9 კლასი ნაწილი 1. სახელმძღვანელო საგანმანათლებლო დაწესებულებებისათვის / ა.გ. მორდკოვიჩი. მოსკოვი: მნემოსინე, 2007 წ.

4. გლეიზერ გ.ი. მათემატიკის ისტორია სკოლაში. VII-VIII კლასები. - მ.: განმანათლებლობა, 1982 წ.

5. ჟურნალი მათემატიკა №5 2009; No8 2007 წელი; No23 2008 წ.

6. განტოლებების გრაფიკული ამოხსნა ინტერნეტ საიტები: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3-6.htm.

განტოლებების ამოხსნის ერთ-ერთი გზა არის გრაფიკული მეთოდი. იგი ემყარება ფუნქციების შედგენას და მათი გადაკვეთის წერტილების განსაზღვრას. განვიხილოთ კვადრატული განტოლების ამოხსნის გრაფიკული გზა a*x^2+b*x+c=0.

გადაჭრის პირველი გზა

განტოლება a*x^2+b*x+c=0 გადავაქციოთ a*x^2 =-b*x-c სახით. ვაშენებთ ორი ფუნქციის გრაფიკებს y= a*x^2 (პარაბოლა) და y=-b*x-c (სწორი ხაზი). ვეძებთ გადაკვეთის წერტილებს. გადაკვეთის წერტილების აბსციები იქნება განტოლების ამოხსნა.

მაგალითით ვაჩვენოთ:ამოხსენით განტოლება x^2-2*x-3=0.

გადავიყვანოთ x^2 =2*x+3-ად. ვაშენებთ y= x^2 და y=2*x+3 ფუნქციების გრაფიკებს ერთ კოორდინატულ სისტემაში.

გრაფიკები იკვეთება ორ წერტილზე. მათი აბსციები იქნება ჩვენი განტოლების ფესვები.

ფორმულის ხსნარი

დამაჯერებლობისთვის, ჩვენ ვამოწმებთ ამ გადაწყვეტას ანალიტიკურად. ჩვენ ვხსნით კვადრატულ განტოლებას ფორმულით:

D = 4-4 * 1 * (-3) = 16.

X1= (2+4)/2*1 = 3.

X2 = (2-4)/2*1 = -1.

ნიშნავს, გადაწყვეტილებები ემთხვევა.

თავისი ნაკლი აქვს განტოლებების ამოხსნის გრაფიკულ მეთოდსაც, რომლის დახმარებითაც ყოველთვის არ არის შესაძლებელი განტოლების ზუსტი ამოხსნის მიღება. ვცადოთ x^2=3+x განტოლების ამოხსნა.

ავაშენოთ პარაბოლა y=x^2 და სწორი ხაზი y=3+x იმავე კოორდინატულ სისტემაში.

ისევ მიიღო მსგავსი ნიმუში. წრფე და პარაბოლა იკვეთება ორ წერტილზე. მაგრამ ჩვენ ვერ ვიტყვით ამ წერტილების აბსცისების ზუსტ მნიშვნელობებს, მხოლოდ მიახლოებით: x≈-1.3 x≈2.3.

თუ ჩვენ დავკმაყოფილდებით ასეთი სიზუსტის პასუხებით, მაშინ შეგვიძლია გამოვიყენოთ ეს მეთოდი, მაგრამ ეს იშვიათად ხდება. როგორც წესი, საჭიროა ზუსტი გადაწყვეტილებები. ამიტომ, გრაფიკული მეთოდი იშვიათად გამოიყენება და ძირითადად არსებული გადაწყვეტილებების შესამოწმებლად.

გჭირდებათ დახმარება სწავლაში?

წინა თემა:

სტუდენტების კვლევითი სამუშაო თემაზე:

"წრფივი ფუნქციის გამოყენება ამოცანების გადაჭრაში"

"ხაზოვანი ფუნქციის გრაფიკის გამოყენება პრობლემის გადაჭრაში"

MKOU "ბოგუჩარსკაიას No1 საშუალო სკოლა"

კვლევითი სამუშაო მათემატიკაში.

თემა: „წრფივი ფუნქციის გრაფიკის გამოყენება ამოცანების ამოსახსნელად“

7 "B" კლასი
ხელმძღვანელი: ფომენკო ოლგა მიხაილოვნა

ქალაქი ბოგუჩარი

1. შესავალი………………………………………………………………………… 2

2. ძირითადი ნაწილი…………………………………………………………………………………………………………………………………………………………………………………………………………………

2.1 ხაზოვანი ფუნქციის გრაფიკების გამოყენებით ტექსტური ამოცანების ამოხსნის ტექნიკა

2.2 გადაადგილების ტექსტური ამოცანების ამოხსნა გრაფიკების გამოყენებით

3. დასკვნა……………………………………………………………………… 11

4. ლიტერატურა…………………………………………………………………….12

შესავალი

„ალგებრა.7 კლასი“ განიხილავს დავალებებს, რომლებშიც მოცემული განრიგის მიხედვით საჭიროა რიგ კითხვაზე პასუხის გაცემა.

Მაგალითად:

№332 ზაფხულის მცხოვრები სახლიდან მანქანით სოფელში წავიდა. მან მანქანა ჯერ გზატკეცილზე და შემდეგ სოფლის გზაზე შეანელა. ზაფხულის მაცხოვრებლის გადაადგილების გრაფიკი ნაჩვენებია სურათზე. Უპასუხე შეკითხვებს:

ა) რამდენ ხანს იარა ზაფხულის მცხოვრებმა გზატკეცილზე და რამდენი კილომეტრი გაიარა; როგორი იყო მანქანის სიჩქარე გზის ამ მონაკვეთზე;

ბ) რამდენ ხანს იარა ზაფხულის მცხოვრებმა ქვეყნის გზაზე და რამდენი კილომეტრი გაიარა; როგორი იყო მანქანის სიჩქარე ამ მონაკვეთში;

გ) რამდენ ხანს გაიარა ზაფხულის მცხოვრებმა მთელი გზა სახლიდან სოფელამდე?

ლიტერატურასა და ინტერნეტში ამ თემაზე მასალების ძიების დროს, მე აღმოვაჩინე, რომ ბევრი ფიზიკური, და თუნდაც სოციალური და ეკონომიკური ფენომენი და პროცესი მსოფლიოში ხაზოვან ურთიერთობაშია, მაგრამ მე გადავწყვიტე მოძრაობა, როგორც. ყველაზე ნაცნობი და პოპულარული ყველა ჩვენგანს შორის. პროექტში აღვწერე სიტყვის ამოცანები და მათი ამოხსნა ხაზოვანი ფუნქციის გრაფიკების გამოყენებით.

ჰიპოთეზა:გრაფიკების დახმარებით თქვენ შეგიძლიათ არა მხოლოდ ფუნქციის თვისებების ვიზუალური წარმოდგენა, გაეცნოთ წრფივი ფუნქციის თვისებებს და მის კონკრეტულ ფორმას, პირდაპირპროპორციულობას, არამედ გადაჭრათ ტექსტური ამოცანები.

ჩემი კვლევის მიზანიიყო წრფივი ფუნქციის გრაფიკების გამოყენების შესწავლა ტექსტური ამოცანების გადასაჭრელად. ამ მიზნების მისაღწევად, შემდეგი დავალებები:

ხაზოვანი ფუნქციის გრაფიკების გამოყენებით გადაადგილებისთვის ტექსტური ამოცანების ამოხსნის მეთოდოლოგიის შესწავლა;

ისწავლეთ მოძრაობის ამოცანების ამოხსნა ამ მეთოდის გამოყენებით;

გააკეთეთ შედარებითი დასკვნები ამოცანების ამოხსნის უპირატესობებისა და უარყოფითი მხარეების შესახებ ხაზოვანი ფუნქციის გრაფიკების გამოყენებით.

კვლევის ობიექტი:ხაზოვანი ფუნქციის გრაფიკი.

კვლევის მეთოდი:

თეორიული (შესწავლა და ანალიზი), სისტემური ძიება, პრაქტიკული.

Მთავარი ნაწილი.

ჩემს კვლევაში გადავწყვიტე შევეცადე მიმეღო გრაფიკული ინტერპრეტაცია ჩვენს სახელმძღვანელოში წარმოდგენილი მოძრაობისთვის და შემდეგ განრიგის მიხედვით ვუპასუხე დავალების კითხვას. ასეთი ამოხსნისთვის მე ავიღე დავალებები მართკუთხა ერთიანი მოძრაობით ბილიკის ერთ მონაკვეთზე. აღმოჩნდა, რომ ბევრი პრობლემა ამ გზით უფრო მარტივად წყდება, ვიდრე ჩვეულებრივი გზით განტოლების გამოყენებით. ამ ტექნიკის ერთადერთი ნაკლი ის არის, რომ პრობლემის კითხვაზე პასუხის ზუსტად მისაღებად, თქვენ უნდა შეძლოთ საზომი ერთეულების მასშტაბის სწორად შერჩევა კოორდინატთა ღერძებზე. ამ მასშტაბის სწორ არჩევანში დიდ როლს თამაშობს ამოხსნის გამოცდილება. ამიტომ, გრაფიკების გამოყენებით ამოცანების გადაჭრის ხელოვნებას რომ დამეუფლო, დიდი რაოდენობით მომიწია მათი გათვალისწინება.

დააყენეთ კოორდინატთა სისტემა sOt აბსცისის ღერძით Ot და ორდინატთა ღერძით Os. ამისათვის, პრობლემის მდგომარეობიდან გამომდინარე, აუცილებელია აირჩიოთ საწყისი: ობიექტის მოძრაობის დასაწყისი ან რამდენიმე ობიექტიდან, შეირჩევა ის, ვინც ადრე დაიწყო მოძრაობა ან გაიარა უფრო დიდი მანძილი. აბსცისის ღერძზე მონიშნეთ დროის ინტერვალები მის საზომ ერთეულებში, ხოლო ორდინატულ ღერძზე მონიშნეთ მანძილი მისი საზომი ერთეულების შერჩეულ სკალაში.

წერტილები კოორდინატულ სიბრტყეზე უნდა იყოს მონიშნული ამოცანის მასშტაბის მიხედვით და ხაზები ზუსტად დახაზული უნდა იყოს. პრობლემის გადაჭრის სიზუსტე დამოკიდებულია ამაზე. აქედან გამომდინარე, ძალზე მნიშვნელოვანია კოორდინატთა ღერძებზე დაყოფის შკალის წარმატებით არჩევა: ის ისე უნდა შეირჩეს, რომ წერტილების კოორდინატები უფრო ზუსტად განისაზღვროს და, თუ შესაძლებელია, განთავსდეს კვანძოვან წერტილებზე, ე.ი. კოორდინატთა ღერძების განყოფილებების კვეთებზე. ზოგჯერ სასარგებლოა აბსცისის ღერძზე ერთეულ სეგმენტად ავიღოთ უჯრედების რაოდენობა, რომელიც არის პრობლემის პირობების ჯერადი დროის მიმართ, ხოლო ორდინატულ ღერძზე - უჯრედების რაოდენობა, რომელიც არის პირობების ნამრავლი. პრობლემის შესახებ მანძილის მიმართ. მაგალითად, დროში 12 წუთი მოითხოვს უჯრედების რაოდენობის არჩევას 5-ის ჯერადად, რადგან 12 წუთი არის საათის მეხუთედი.

გადაადგილებისთვის ტექსტური ამოცანების ამოხსნა გრაფიკების გამოყენებით

პასუხი: 9 კმ.

ამოხსნა განტოლების გამოყენებით:

x/12სთ. - დრო A-დან B-მდე

x/18 სთ. - უკან დრო

პასუხი: 9 კმ

დავალება 2. (No156 იუ.ნ. მაკარიჩევის სახელმძღვანელოში „ალგებრა 7“).

გზატკეცილზე ერთი და იგივე სიჩქარით მიდის ორი მანქანა. თუ პირველი გაზრდის სიჩქარეს 10 კმ/სთ-ით, ხოლო მეორე ამცირებს 10 კმ/სთ-ით, მაშინ პირველი დაფარავს იმდენს 2 ​​საათში, რამდენსაც მეორე 3 საათში. რამდენად სწრაფად მიდიან მანქანები?

ამოხსნა განტოლების გამოყენებით:

მოდით x კმ/სთ იყოს მანქანების სიჩქარე;

(x+10) და (x-10) შესაბამისად სიჩქარე გაზრდისა და შემცირების შემდეგ;

2(x+10)=3(x-10)

პასუხი: 50 კმ/სთ

ამოხსნა ხაზოვანი ფუნქციის გრაფიკით:

1. დავაყენოთ კოორდინატთა სიბრტყე sOt აბსცისის ღერძით Оt, რომელზედაც ვნიშნავთ მოძრაობის დროის ინტერვალებს და ორდინატთა ღერძს Os, რომელზეც ვნიშნავთ სატრანსპორტო საშუალებების გავლილ მანძილს.

2. აბსცისის ღერძის გასწვრივ დავდოთ განყოფილებები სასწორზე - ერთი საათი 5 უჯრედში (1 უჯრედში - 12 წუთი); ჩვენ ვიყენებთ განყოფილებებს y-ღერძის გასწვრივ, მაგრამ არ ვაკონკრეტებთ მასშტაბს.

3. ავაშენოთ I მანქანის მოძრაობის ხაზი: მოძრაობის დასაწყისი c წერტილში

4. ავაშენოთ მეორე II მანქანის მოძრაობის ხაზი: მოძრაობის დასაწყისი წერტილში კოორდინატით (0; 0). შემდეგი, ჩვენ აღვნიშნავთ თვითნებურ წერტილს (3;s 1) თვითმფრინავზე, რადგან ახალი სიჩქარით მანქანა გზაზე 3 საათის განმავლობაში იყო.

4. განვსაზღვროთ მანქანების v სიჩქარე მის შეცვლამდე. 1 აბსცისთან წრფეებზე მდებარე წერტილების ორდინატთა სხვაობა ავღნიშნოთ ∆s ნიშნით. პირობის მიხედვით ეს სეგმენტი შეესაბამება (10 + 10) კმ სიგრძეს, რადგან ერთში სიჩქარე შემცირდა, მეორეში კი 10 კმ/სთ-ით გაიზარდა. ეს ნიშნავს, რომ მანქანების მოძრაობის ხაზი სიჩქარის შეცვლამდე უნდა იყოს თანაბრად დაშორებული I და II ხაზებისგან და განლაგებული იყოს მათ შორის კოორდინატულ სიბრტყეზე.. განრიგის მიხედვით, Δs \u003d 2cl. შეესაბამება 20 კმ, v = 5 უჯრედი, ამიტომ ვხსნით პროპორციას v = 50 კმ/სთ.

პასუხი: 50 კმ/სთ.

დავალება 3

ამოხსნა ხაზოვანი ფუნქციის გრაფიკით:

საცნობარო წერტილი არის ჯოხი M

მონიშნეთ წერტილი N (0; 162).

პასუხი: 2 საათი 20 წუთი.

ამოხსნა განტოლების გამოყენებით:

162 -45(x+0.75)-36x=0

162-45x - 33.75 -36x = 0

81x=128.25

2)

პასუხი: 2 საათი 20 წუთი.

დავალება 4.

ველოსიპედისტმა დატოვა A წერტილი. ამასთან, მის შემდეგ მოტოციკლისტმა 16 კმ/სთ დატოვა B წერტილი, რომელიც ა-დან 20 კმ-ით არის დაშორებული. ველოსიპედისტი 12 კმ/სთ სიჩქარით მოძრაობდა. A წერტილიდან რა მანძილზე გაუსწრებს მოტოციკლისტი ველოსიპედისტს?

ამოხსნა ხაზოვანი ფუნქციის გრაფიკით:

1. დააყენეთ კოორდინატთა სიბრტყე sOt აბსცისის ღერძით Ot, რომელზედაც აღვნიშნავთ მოძრაობის დროის ინტერვალებს და y-ღერძი Os, რომელზეც მოვნიშნავთ მოტოციკლისტისა და ველოსიპედისტის მიერ გავლილ მანძილს.

2. სკალაზე დავხატოთ განყოფილებები: y ღერძის გასწვრივ - 2 უჯრედში 8 კმ; აბსცისის გასწვრივ - 2 უჯრედში - 1სთ.

3. ავაგოთ II მოტოციკლისტის მოძრაობის ხაზი: მისი მოძრაობის დასაწყისს ვნიშნავთ B (0; 0) კოორდინატების სათავეში. მოტოციკლისტი მოძრაობდა 16 კმ/სთ სიჩქარით, რაც ნიშნავს, რომ II სწორმა ხაზმა უნდა გაიაროს წერტილი კოორდინატებით (1; 16).

4. ავაგოთ I ველოსიპედისტის მოძრაობის ხაზი: მისი დასაწყისი იქნება A წერტილიდან (0; 20), რადგან წერტილი B მდებარეობს A წერტილიდან 20 კმ-ის დაშორებით და ის მოტოციკლისტთან ერთად დატოვა. ველოსიპედისტი მოძრაობდა 12 კმ/სთ სიჩქარით, რაც ნიშნავს, რომ ხაზი I უნდა გაიაროს წერტილი კოორდინატებით (1; 32).

5. იპოვეთ P (5; 80) - I და II ხაზების გადაკვეთის წერტილი, რომელიც ასახავს მოტოციკლისტისა და ველოსიპედის მოძრაობას: მისი ორდინატი აჩვენებს მანძილს B წერტილიდან, რომელზედაც მოტოციკლისტი დაეწევა ველოსიპედისტს. .

P(5; 80) |=s = 80, |=80 - 20 = 60(კმ) - მანძილი A წერტილიდან, რომელზეც მოტოციკლისტი დაეწევა ველოსიპედისტს..

პასუხი: 60 კმ.

ამოხსნა განტოლების გამოყენებით:

მოდით x km იყოს მანძილი A წერტილიდან შეხვედრის წერტილამდე

x /12 ველოსიპედისტის დრო

(x +20)/16 მოტოციკლისტის დრო

x /12=(x +20)/16

16x=12x+240

4x=240

x=60

პასუხი: 60 კმ

დავალება 5.

ქალაქებს შორის მანძილი მოტოციკლისტმა დაფარა 2 საათში, ხოლო ველოსიპედისტმა 5 საათში, ველოსიპედისტის სიჩქარე მოტოციკლისტის სიჩქარეზე 18 კმ/სთ ნაკლებია. იპოვეთ ველოსიპედისტისა და მოტოციკლისტის სიჩქარე და მანძილი ქალაქებს შორის.

ამოხსნა ხაზოვანი ფუნქციის გრაფიკით:

1. დააყენეთ კოორდინატთა სიბრტყე sOt აბსცისის ღერძით Ot, რომელზედაც ვნიშნავთ მოძრაობის დროის შუალედებს და y-ღერძს Os, რომელზეც ვნიშნავთ მანძილს.

2. აბსცისის ღერძის გასწვრივ 1 საათის განმავლობაში 2 უჯრედში ჩავდოთ განყოფილება.დავტოვოთ მანძილი ორდინატთა ღერძის გასწვრივ გაყოფის გარეშე.

3. დავხატოთ ველოსიპედისტის I მოძრაობის ხაზი 5 საათში და მოტოციკლისტის II მოძრაობის ხაზი 2 საათში. ორივე სტრიქონის ბოლოს უნდა ჰქონდეს იგივე ორდინატი.

4. დავხატოთ სეგმენტი აბსცისით 1 I და II წრფეებს შორის. ამ სეგმენტის სიგრძე ასახავს მანძილს 18 კმ-ის ტოლი. ნახატიდან ვიღებთ, რომ 3 უჯრა უდრის 18 კმ-ს, რაც ნიშნავს, რომ 1 უჯრედში არის 6 კმ.

5. შემდეგ განრიგის მიხედვით ვადგენთ ველოსიპედისტის სიჩქარეს 12 კმ/სთ, მოტოციკლისტის სიჩქარე 30 კმ/სთ, ქალაქებს შორის მანძილი 60 კმ.

ამოხსნა განტოლების გამოყენებით:

მოდით x კმ/სთ იყოს ველოსიპედისტის სიჩქარე, შემდეგ (x +18) კმ/სთ მოტოციკლისტის სიჩქარე

2(x+18)=5x

2x +36=5x

x=12

2) 12+18=30(კმ/სთ) მხედრის სიჩქარე

3) (კმ) მანძილი ქალაქებს შორის

პასუხი: 12 კმ/სთ; 30 კმ/სთ; 60 კმ

პასუხი: 60 კმ.

დავალება 6.

ნავი მდინარის გასწვრივ 30 კმ-ს გადის 3 საათსა და 20 წუთში, ხოლო დინების საწინააღმდეგოდ 28 კმ-ს 4 საათში. რამდენ მანძილზე დაფარავს ნავი ტბას 1,5 საათში?

ამოხსნა ხაზოვანი ფუნქციის გრაფიკით:

1. დააყენეთ კოორდინატთა სიბრტყე sOt აბსცისის ღერძით Ot, რომელზედაც აღვნიშნავთ მოძრაობის დროის ინტერვალებს და y-ღერძი Os, რომელზედაც ვნიშნავთ ნავის მიერ გავლილ მანძილს.

2. სკალაზე დავხატოთ განყოფილებები: y ღერძის გასწვრივ - ორ უჯრედში 4 კმ; აბსცისის ღერძის გასწვრივ - 6 უჯრედში - 1 საათი (1 უჯრედში - 10 წუთი), რადგან პრობლემის მდგომარეობის მიხედვით, დრო მოცემულია წუთებში.

3. ავაშენოთ ნავის მოძრაობის ხაზი მდინარე I-ზე: ხაზის დასაწყისი იქნება კოორდინატთან (0; 0) წერტილში. ნავი 30 კმ-ს გადის 3 საათსა და 20 წუთში, რაც ნიშნავს, რომ ხაზმა უნდა გაიაროს წერტილი კოორდინატით (; 30), რადგან 3სთ 20წთ. = სთ.

4. ავაგოთ ნავის მოძრაობის ხაზი მდინარის II დინების საწინააღმდეგოდ: ავიღოთ მოძრაობის დასაწყისს წერტილში კოორდინატით (0; 0). ნავი 4 საათში ცურავს 28 კმ-ს, რაც ნიშნავს, რომ მოძრაობის ხაზმა უნდა გაიაროს წერტილი კოორდინატთან (4; 28).

5. ავაგოთ ტბაზე ნავის მოძრაობის ხაზი: ავიღებთ მოძრაობის დასაწყისს წერტილში კოორდინატით (0; 0). ნავის საკუთარი მოძრაობის ხაზი უნდა განთავსდეს მდინარის გასწვრივ ნავის მოძრაობის ხაზებს შორის თანაბარ მანძილზე. ეს ნიშნავს, რომ ჩვენ უნდა გავყოთ სეგმენტი, რომელიც შედგება ყველა წერტილისგან აბსციზა 1-ით, მდინარის გასწვრივ მოძრაობის ხაზებს შორის და მოვნიშნოთ მისი შუა. (0; 0)-დან ამ მონიშნული წერტილიდან დავხატავთ სხივს, რომელიც იქნება მოძრაობის ხაზი ტბის გასწვრივ.

6. ამოცანის პირობის მიხედვით საჭიროა ვიპოვოთ ტბაზე ნავის მიერ გავლილი მანძილი 1,5 საათში, რაც ნიშნავს, რომ ამ ხაზზე უნდა განვსაზღვროთ წერტილის ორდინატი აბსცისით t = 1,5, | = s = 12, | = 12 კმ, ნავი ტბას 1,5 საათში გაივლის.

პასუხი: 12 კმ.

ამოხსნა განტოლებათა სისტემის გამოყენებით:

მოდით x კმ/სთ იყოს ტბის სიჩქარე და y კმ/სთ მდინარის სიჩქარე

პასუხი: 12 კმ.

დავალება 7.

ნავი მდინარის გასწვრივ მოძრაობს 34 კმ-ს, იმავდროულად, რაც 26 კმ დინების საწინააღმდეგოდ. ნავის საკუთარი სიჩქარეა 15 კმ/სთ. იპოვნეთ მდინარის სიჩქარე.

ამოხსნა ხაზოვანი ფუნქციის გრაფიკით:

1. დააყენეთ კოორდინატთა სიბრტყე sOt აბსცისის ღერძით Ot, რომელზედაც აღვნიშნავთ მოძრაობის დროის ინტერვალებს და y-ღერძი Os, რომელზეც ვნიშნავთ ნავის მიერ გავლილ მანძილს.

2. სკალაზე დავხატოთ განყოფილებები: y ღერძის გასწვრივ - 1 უჯრედში 1კმ; აბსცისის ღერძზე დროს ვტოვებთ დანაყოფების გარეშე.

3. ავაგოთ ნავის მოძრაობის I ხაზი მდინარის გასწვრივ 0 კმ-დან 34 კმ წერტილამდე: ხაზის დასაწყისი იქნება კოორდინატთან (0; 0) წერტილში. მეორე კოორდინატი იქნება (x. 34).

4. ავაგოთ ნავის მოძრაობის II ხაზი მდინარის დინების საწინააღმდეგოდ 0 კმ-დან 26 კმ წერტილამდე: ხაზის დასაწყისი იქნება კოორდინატთან (0; 0) წერტილში. მეორე კოორდინატი იქნება ( x; 26).

5. დახაზეთ III სხივი საწყისიდან (0; 0) თვითნებური სეგმენტის შუაში, რომელიც შედგება ერთი და იგივე აბსცისის მქონე ყველა წერტილისგან I და II მოძრაობის ორ ხაზს შორის. ეს სხივი ასახავს ნავის მოძრაობას, როგორც ნავის საკუთარი სიჩქარე არის საშუალო არითმეტიკული 2 სიჩქარის მდინარის ზემოთ და ქვემოთ. მიღებულ სხივზე ვპოულობთ წერტილს 15-ის ორდინატით, რადგან ნავის საკუთარი სიჩქარეა 15 კმ/სთ. ნაპოვნი წერტილის აბსციზა შეესაბამება 1 საათის გაყოფას.

6. მდინარის სიჩქარის საპოვნელად საკმარისია ვიპოვოთ სეგმენტის სიგრძე აბსცისით 1 III სტრიქონიდან II ხაზამდე. მდინარის სიჩქარე 2 კმ/სთ-ია.

პასუხი: 2კმ/სთ

ამოხსნა განტოლების გამოყენებით:

მდინარის სიჩქარე x კმ/სთ

34 / (15 + x) \u003d 26 / (15-x) პროპორციის ამოხსნით, მივიღებთ:

პასუხი: 2კმ/სთ

დასკვნა.

უპირატესობები:

ამოცანები შეიძლება მოკლედ ჩაიწეროს;

ნაკლოვანებები:

ლიტერატურა.

1. მაკარიჩევი იუ.

2.ბულინინ ვ., გრაფიკული მეთოდების გამოყენება ტექსტური ამოცანების ამოხსნისას, სასწავლო და მეთოდური გაზეთი „მათემატიკა“, No14, 2005 წ.

3. Zvavich L.I. დიდაქტიკური მასალები ალგებრაზე მე-7 კლასისთვის.

დოკუმენტის შინაარსის ნახვა
"სიტყვები"

მე-7 კლასში ალგებრის გაკვეთილებზე გავეცანი თემას „ხაზოვანი ფუნქცია. წრფივი ფუნქციების გრაფიკების ურთიერთგანლაგება. ვისწავლე წრფივი ფუნქციის გრაფიკების აგება, ვისწავლე მისი თვისებები, ვისწავლე გრაფიკების ფარდობითი პოზიციის დადგენა მოცემული ფორმულების გამოყენებით. მე შევნიშნე, რომ იუ.ნ. მაკარიჩევის სახელმძღვანელოში

„ალგებრა.7 კლასი“ განიხილავს დავალებებს, რომლებშიც მოცემული განრიგის მიხედვით საჭიროა რიგ კითხვაზე პასუხის გაცემა. ასეთი დავალების მაგალითი წარმოდგენილია სლაიდზე.

მოცემული განრიგის მიხედვით შეიძლება დადგინდეს, რომ

და მე გამიჩნდა კითხვა, შესაძლებელია თუ არა მოძრაობის ამოცანების ამოხსნა არა მოქმედებებით ან განტოლებების გამოყენებით, არამედ ამისთვის წრფივი ფუნქციის გრაფიკის გამოყენება?

სლაიდზე წარმოდგენილია ჰიპოთეზა, მიზნები და ამოცანები

ჩემს კვლევაში გადავწყვიტე შევეცადე მიმეღო გრაფიკული ინტერპრეტაცია ჩვენს სახელმძღვანელოში წარმოდგენილი მოძრაობისთვის და შემდეგ განრიგის მიხედვით ვუპასუხე დავალების კითხვას. ასეთი ამოხსნისთვის მე ავიღე დავალებები მართკუთხა ერთიანი მოძრაობით ბილიკის ერთ მონაკვეთზე.

აღმოჩნდა, რომ ამ გზით ბევრი პრობლემა წყდება. ამ ტექნიკის ერთადერთი ნაკლი ის არის, რომ პრობლემის კითხვაზე პასუხის ზუსტად მისაღებად, თქვენ უნდა შეძლოთ საზომი ერთეულების მასშტაბის სწორად შერჩევა კოორდინატთა ღერძებზე. ამ მასშტაბის სწორ არჩევანში დიდ როლს თამაშობს ამოხსნის გამოცდილება. ამიტომ, გრაფიკების გამოყენებით ამოცანების გადაჭრის ხელოვნებას რომ დამეუფლო, დიდი რაოდენობით მომიწია მათი გათვალისწინება.

ტექსტური ამოცანების გადაჭრის ტექნიკა ხაზოვანი ფუნქციის გრაფიკების გამოყენებით.

ტექსტური პრობლემის გადასაჭრელად ხაზოვანი ფუნქციის გრაფიკების გამოყენებით, თქვენ უნდა:

დააყენეთ კოორდინატთა სისტემა ამისათვის, პრობლემის მდგომარეობის მიხედვით, უნდა აირჩიოთ საწყისი: ობიექტის მოძრაობის დასაწყისი ან რამდენიმე ობიექტიდან, ის, ვინც ადრე დაიწყო მოძრაობა ან გაიარა უფრო დიდი მანძილი. შერჩეული. აბსცისის ღერძზე მონიშნეთ დროის ინტერვალები მის საზომ ერთეულებში, ხოლო ორდინატულ ღერძზე მონიშნეთ მანძილი მისი საზომი ერთეულების შერჩეულ სკალაში.

დახაზეთ პრობლემის დებულებაში მითითებული თითოეული ობიექტის მოძრაობის ხაზები სწორი ხაზების მინიმუმ ორი წერტილის კოორდინატებით. როგორც წესი, ობიექტის სიჩქარე იძლევა ინფორმაციას მისი მოძრაობის დაწყებიდან დროის ერთ ერთეულში მანძილის გავლის შესახებ. თუ ობიექტი უფრო გვიან იწყებს მოძრაობას, მაშინ მისი გადაადგილების საწყისი წერტილი გადაადგილდება მოცემული რაოდენობის ერთეულებით საწყისიდან მარჯვნივ x-ღერძის გასწვრივ. თუ ობიექტი იწყებს მოძრაობას საცნობარო წერტილიდან გარკვეული მანძილით დაშორებული ადგილიდან, მაშინ მისი მოძრაობის დაწყების წერტილი გადაადგილდება ზემოთ y-ღერძის გასწვრივ.

კოორდინატულ სიბრტყეზე რამდენიმე ობიექტის შეხვედრის წერტილი მითითებულია მათი მოძრაობის ამსახველი ხაზების გადაკვეთის წერტილით, რაც ნიშნავს, რომ ამ წერტილის კოორდინატები გვაწვდიან ინფორმაციას შეხვედრის დროისა და შეხვედრის ადგილის დაშორების შესახებ საწყისიდან.

ორი ობიექტის გადაადგილების სიჩქარეში განსხვავება განისაზღვრება სეგმენტის სიგრძით, რომელიც შედგება ყველა წერტილისგან აბსცისა 1-ით, რომელიც მდებარეობს ამ ობიექტების მოძრაობის ხაზებს შორის.

წერტილები კოორდინატულ სიბრტყეზე უნდა იყოს მონიშნული ამოცანის მასშტაბის მიხედვით და ხაზები ზუსტად დახაზული უნდა იყოს. პრობლემის გადაჭრის სიზუსტე დამოკიდებულია ამაზე.

ამოცანა 1. (No673 იუ.ნ. მაკარიჩევის სახელმძღვანელოში „ალგებრა 7“).

ველოსიპედისტმა AB გზა 12 კმ/სთ სიჩქარით გაიარა. დაბრუნებულმა მან განავითარა სიჩქარე 18 კმ/სთ და უკან დაბრუნების გზაზე 15 წუთით ნაკლები გაატარა ვიდრე A-დან B-მდე გზაზე რამდენი კილომეტრია A-დან B-მდე.

ამოხსნა განტოლების გამოყენებით:

მოდით x კმ იყოს მანძილი A-დან B-მდე.

x/12სთ. - დრო A-დან B-მდე

x/18 სთ. - უკან დრო

რადგან უკანა გზაზე მან 15 წუთით ნაკლები დახარჯა, განტოლებას შევადგენთ

პასუხი: 9 კმ

ამოხსნა ხაზოვანი ფუნქციის გრაფიკით:

1. კოორდინატთა სიბრტყე sOtc დავაყენოთ აბსცისის ღერძით Ot, რომელზედაც ვნიშნავთ მოძრაობის დროის ინტერვალებს და y-ღერძს Os, რომელზედაც ვნიშნავთ მანძილს.

2. სკალაზე დავხატოთ განყოფილებები: y ღერძის გასწვრივ - ერთ უჯრედში 3 კმ; აბსცისის ღერძის გასწვრივ - ერთი საათი 4 უჯრედში (1 უჯრედში - 15 წთ).

3. ავაშენოთ იქ მოძრაობის ხაზი: მონიშნეთ მოძრაობის დასაწყისი წერტილით (0; 0). ველოსიპედისტი მოძრაობდა 12 კმ/სთ სიჩქარით, რაც ნიშნავს, რომ სწორმა ხაზმა უნდა გაიაროს წერტილი (1; 12).

4. ავაშენოთ მოძრაობის ხაზი უკან: მონიშნეთ ხაზის ბოლო წერტილით (; 0), რადგან ველოსიპედისტმა დასაბრუნებლად 15 წუთით ნაკლები დახარჯა. ის მოძრაობდა 18კმ/სთ სიჩქარით, რაც ნიშნავს, რომ ხაზის შემდეგ წერტილს აქვს კოორდინატი (;18).

5. შენიშვნა (; 9) - წრფეების გადაკვეთის წერტილი: მისი ორდინატი აჩვენებს მანძილს: s = 9.

პასუხი: 9 კმ.

დავალება 2 (No 757 იუ.ნ. მაკარიჩევის სახელმძღვანელოში „ალგებრა 7“)

მანძილი M და N ბურჯებს შორის არის 162 კმ. საავტომობილო გემი პიერ M-დან 45 კმ/სთ სიჩქარით გაემგზავრა. 45 წუთის შემდეგ მისკენ N-დან პიერს კიდევ ერთი მოტორიანი გემი გაემგზავრა, რომლის სიჩქარე 36 კმ/სთ-ია. პირველი გემის გასვლიდან რამდენ საათში შეხვდებიან ისინი?

ამოხსნა განტოლების გამოყენებით:

დაე, x საათში იყოს შეხვედრა

162 -45(x+0.75)-36x=0

162-45x - 33.75 -36x = 0

81x=128.25

2)

პასუხი: 2 საათი 20 წუთი.

ამოხსნა ხაზოვანი ფუნქციის გრაფიკით:

1. დააყენეთ კოორდინატთა სიბრტყე sOt აბსცისის ღერძით Ot, რომელზედაც აღვნიშნავთ მოძრაობის დროის ინტერვალებს და y-ღერძი Os, რომელზეც.

გაითვალისწინეთ მანძილი M-დან პიერ N-მდე, ტოლია 162 კმ. დასაწყისი

საცნობარო წერტილი არის ჯოხი M

2. სკალაზე დავხატოთ განყოფილებები: y ღერძის გასწვრივ - ორ უჯრედში 18 კმ; აბსცისის ღერძის გასწვრივ - ერთი საათი 6 უჯრედში (1 უჯრედში - 10 წთ.), ვინაიდან დავალების პირობა განსაზღვრავს დროს წუთებში.

მონიშნეთ წერტილი N (0; 162).

3. ავაშენოთ პირველი გემის I მოძრაობის ხაზი: მისი მოძრაობის დასაწყისი იქნება კოორდინატების მქონე წერტილში (0; 0). პირველი გემი მიცურავდა 45 კმ/სთ სიჩქარით, რაც ნიშნავს, რომ სწორმა ხაზმა უნდა გაიაროს წერტილი კოორდინატებით (1; 45).

4. ავაგოთ მეორე გემის II მოძრაობის ხაზი: მოძრაობის დასაწყისი იქნება c წერტილში.

კოორდინატები (; 162), ვინაიდან მან დატოვა N წერტილი, M-დან 162 კმ დაშორებით, 45 წთ. პირველზე გვიან და 45 წთ. \u003d სთ. მეორე გემი მიცურავდა 36 კმ/სთ სიჩქარით, რაც ნიშნავს, რომ სწორმა ხაზმა უნდა გაიაროს წერტილი (; 126), რადგან მეორე გემი დატოვა M წერტილის მიმართულებით: 162 - 36 \ u003d 126 (კმ).

5. I და II წრფეების გადაკვეთის წერტილი არის A წერტილი (; 108). წერტილის აბსციზა აჩვენებს დროს, რომლის შემდეგაც პირველი გემის გასვლის შემდეგ ისინი ერთმანეთს შეხვდნენ: t =, |=h = 2h20min. - პირველი გემის გამგზავრების შემდეგ ორი გემის შეხვედრის დრო.

პასუხი: 2 საათი 20 წუთი.

დასკვნა.

კვლევის ბოლოს მოვახერხე ამომეცნო პრობლემების გრაფიკული გადაჭრის დადებითი და უარყოფითი მხარეები.

უპირატესობები:

ამოცანები შეიძლება მოკლედ ჩაიწეროს;

მცირე რაოდენობით მუშაობა საკმაოდ მარტივია.

ნაკლოვანებები:

ძნელია დიდ ციფრებთან მუშაობა.

პრეზენტაციის შინაარსის ნახვა
"პროექტი"