>Всем привет!!! Существует ли формула, по которой из матрицы можно убрать масштабирование, не зная коэффициентов масштабирования???
Сразу вспомнили полярное разложение. Что-де, матрица M представляется в виде O * P. Где O ортогональная, а P положительно определенная, симметричная – то есть матрица сжатия или растяжения. Вот матрицу O мы и возьмем.
Встает вопрос. А если раскладывать M с другой стороны, то получим P’ * O’. Разложение в другом порядке, с другими априори матричками. Почему бы не взять O’? Я мучался минут пять вопросом, пока не вспомнил, как ставил студентам незачет по этому поводу. Матрица O’ на самом деле совпадает с матрицей O. Если вы недавно закончили университет или еще учитесь – можете даже попытаться доказать сей факт.
Итак, полярное разложение:
Для нахождения положительного квадратного корня из матрицы в позитивной науке предлагается посчитать собственные числа. Для каждого собственного числа найти собственное подространство, потом аккуратно изготовить собственно квадратный корень из оператора.
Я как представил, что получится для матрицы, близкой к единичной, аж вздрогнул. Все умрет на неточностях флоата, ранги у матриц съедут – полный коллапс обещает быть.
А почему бы благородным донам не попробовать итерации, которые божествены, как известно?
Вот, корень из числа ищется методом Ньютона. Последовательность a_{i+1} = 0.5 * (a_i + x / a_i); гордо сходится к квадратному корню из x. Для пробы взял чью-то библиотечку про mat3x3 и наклепал матричный аналог.
Прямой аналог метода Ньютона шустро сходится за 3-4 итерации, тесты проходят как легкий ветерок. Получается полярное разложение для матриц, работоспособность алгоритма очевидна из элементарной спектральной теории операторов. Очевидна после получаса скрипа мозгом.
Итак, полярное разложение мы нашли. Вопрос – зачем? И тут я вынужден перейти к основному поинту своего доклада. Учение – зло. Время, которые вы потратили на вспоминание спектральной теории операторов, успешно потрачено впустую.
Разложение Scale Shear Rotate ищется на раз. Применяем процесс ортогонализации и ортонормализации к матрице. По столбцам. Получаем отличную матрицу. И чем результат будет хуже? Да ничем!
Увидел я пост с кодом на паскале, который и считает это самое Scale Shear Rotate разложение, и внезапно понял, что у меня нет аргументов за полярное разложение. Которое требует хрен знает какой вычислительной техники.
Конечно, есть мелкие возражения, почти придирки. К примеру, что tangent space проще считать ортонормальным. Вычислительно проще. Обычно считают dPosition/du, нормаль, а третий вектор берут перпендикулярным к этой паре. Ясно, что метод несимметричный относительно текстурных координат, какая из них первая, какая вторая – совершенно непонятно. Вроде бы правильно применить полярное разложение к матрице локального преобразования.
Может, заметите вы разницу между “правильным” полярным разложением и “неправильным” процессом ортогонализации по столбцам. Скорее не заметите. И уж точно картинка не станет лучше.
P.S. А вот еще анимации хранить в Scale Shear Rotate очень круто. Три вектора, один кватернион. Shear почти всегда 0, Scale почти всегда 1, константные треки можно выкинуть. А там где неконстантные треки – как-нить выжать за счет специализации шаблона. Или еще чего.
Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
где А, В, С - задаваемые матрицы, Х - искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X - B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат . Рекомендуется также ознакомиться с основными действиями над матрицами .Пример №1
. Задание
. Найти решение матричного уравнения
Решение
. Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Обратная матрица A -1: ![]()
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1: ![]()
Матрицу X ищем по формуле: X = A -1 ·C·B -1
![]()
Ответ:
Пример №2
. Задание.
Решить матричное уравнение ![]()
Решение
. Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3
. Задание. Найти решение матричного уравнения

Решение
. Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T: 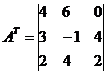
Обратная матрица A -1: 
Матрицу X ищем по формуле: X = B·A -1

Ответ: >
С помощью матричного онлайн калькулятора вы можете сложить , вычитать , умножить , транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень , умножить матрицу на число , сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы , проводить исключение Гаусса , решить матричное уравнение AX=B , сделать LU разложение матрицы , вычислить ядро (нуль пространство) матрицы , сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта .
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы и вводить числа в виде a или a /b , где a и b целые или десятичные числа (b положительное число). Например 12/67, -67.78/7.54, 327.6, -565.
Кнопка в верхем левом углу матрицы открывает меню (Рис.1) для преобразования исходной матрицы (создание единичной матрицы , нулевой матрицы или очищать содержимое ячеек ).

При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы и , а также преобразовать на месте элементы матрицы в обыкновенную дробь, смешанную дробь или в десятичное число.
Вычисление суммы, разности, произведения матриц онлайн
сумму , разность или произведение матриц . Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу . Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы . Теорию вычисления обратной матрицы смотрите .
Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы . Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы . Теорию вычисления определителя матрицы смотрите .
Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы .
Для вычисления ранга матрицы:
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы . Теорию вычисления ранга матрицы смотрите .
Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу . Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
Учтите, что матрицы и должны иметь равное количество строк.
Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU) , где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение, при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
Для LU(LUP)-разложения:
Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы.
1)
Рассмотрим сначала действительные матрицы. Предположим, что из матрицы $%A$% извлекается корень, т.е. существует матрица $%B$% такая, что $%B \cdot B=A$%. Предположим также, что матрица $%B$% может быть приведена к диагональному виду, т.е. существует матрица $%S$% такая что $%S^{-1}BS=B"$%, где $%B"$%- диагональная матрица. Из равенств $%B"B"=S^{-1}BSS^{-1}BS=S^{-1}BBS=S^{-1}AS$% следует, что $%A"=S^{-1}AS$% - тоже диагональная матрица, т.е. матрицы $%A$% и $%B$% приводятся к диагональному виду одним и тем же преобразованием. Т.к. элементы штрихованных матриц - это собственные значения нештрихованных, то из приведенных рассуждений вытекают следующие выводы.
1.1)Если матрица $%A$% является симметричной положительно определенной матрицей, то из нее извлекается корень в виде действительной матрицы.
1.2) Алгоритм вычисления корня из такой матрицы следующий: решить задачу на собственные значения, извлечь из собственных значений корни, составить из них диагональную матрицу, применить к ней преобразование, обратное к преобразованию, переводящему матрицу $%A$% к диагональному виду.
1.3) Количество различных матриц $%B$% равно $%2^n$%, т.к. для каждого собственного значения есть 2 значения корня - положительное и отрицательное.
2) Для комплексной матрицы рассуждения останутся в силе, если заменить симметричность на унитарность. Требование положительной определенности при этом, естественно, снимется.
3)
Решение для общего случая.
Предположим, что преобразование $%S$% приводит матрицу $%B$% не к диагональному, а к верхнему треугольному виду, т.е. матрица $%B"$% является верхней треугольной. Такое преобразование существует для любой квадратной матрицы. Легко убедиться, что матрица $%A"$% при этом тоже получится верхней треугольной, причем, диагональные элементы матрицы $%A"$% будут квадратами соответствующих диагональных элементов матрицы $%B"$%. Это позволяет найти все диагональные элементы матрицы $%B"$% извлечением корня из диагональных элементов матрицы $%A"$%, а затем по цепочке найти и все остальные элементы матрицы $%B"$%. Отсюда получаются следующие выводы.
3.1) Из любой комплексной матрицы извлекается корень, в общем случае таких корней $%2^n$%, но среди них могут быть совпадающие (кратные).
3.2) Алгоритм вычисления корней следующий: преобразовать матрицу $%A$% к верхнему треугольному виду, найти матрицу $%B"$% по сформулированному алгоритму и сделать обратное преобразование.
3.3) Необходимым и достаточным условием вещественности корней из вещественной матрицы является не отрицательность диагональных элементов после преобразования матрицы к треугольному виду. Не отрицательность детерминанта является условием необходимым, но недостаточным.
Дополнение 1 (ответ на комментарий) . Вы имели в виду "к треугольному виду". Вообще, в пп. 1, 2 все абсолютно четко, а над п.3 нужно, видимо, еще подумать. Дело в том, что метод Гаусса может не сводиться к преобразованию $%S^{-1}AS$%, а на этом основано доказательство. Т.е. доказательство применимо только к тем матрицам, которые приводятся к треугольному виду преобразованием $%S^{-1}AS$%.
Дополнение 2 . Похоже, в п.3 в целом все правильно, только нужно использовать преобразование матрицы $%A$% к Жордановой форме - для этого преобразования всегда есть матрица, получающаяся из решения задачи на собственные значения. Проблема в том, что квадрат Жордановой матрицы не является Жордановой матрицей (хотя является треугольной и даже двухдиагональной). Строгое обоснование алгоритма требует доказательства следующей теоремы: "Если $%A"=B"^2$% и $%A"$%- Жорданова матрица, то $%B"$%- треугольная матрица". Утверждение кажется верным, но как доказать - пока не знаю.
