Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений х i с вероятностями р i , называется сумма:

Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f (x ):

(6б )

Несобственный интеграл (6б ) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М (Х ) не существует). Математическое ожидание характеризует среднее значение случайной величины Х . Его размерность совпадает с размерностью случайной величины.

Свойства математического ожидания:

Дисперсия. Дисперсией случайной величины Х называется число:

Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М (Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:

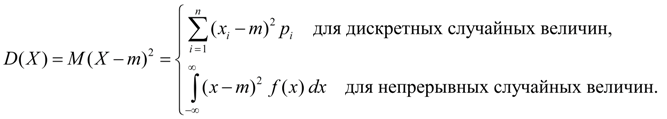(9)

Здесь m = М (Х ).

Свойства дисперсии:

Среднее квадратичное отклонение:

(11)

Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.

Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения . Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х 0 называется математическое ожидание М (Х – х 0 )k . Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:

(12)

Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:

(13)

Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:

(14)

Из (7) следует, что центральный момент первого порядка всегда равен нулю:

Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С , а отклонение от центра не меняется: Х – m = (Х – С ) – (m – С ).
Теперь очевидно, что дисперсия – это центральный момент второго порядка :

Асимметрия. Центральный момент третьего порядка:

(17)

служит для оценки асимметрии распределения . Если распределение симметрично относительно точки х = m , то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии :

(18)

Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).

Рис. 2. Виды асимметрии распределений.

Эксцесс. Центральный момент четвертого порядка:

(19)

служит для оценки так называемого эксцесса , определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения, то в качестве эксцесса принимается величина:

(20)

На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.

Рис. 3. Кривые распределения с различной степенью крутости (эксцессом).

Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.

Мода дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным . Если кривая распределения имеет более одного максимума, то распределение называется полимодальным . Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными . В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального , т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.

Медиана случайной величины Х – это ее значение Ме , для которого имеет место равенство: т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме . Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис. 2). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают.

Мода - наиболее вероятное значение случайной величины . При симметричном распределении относительно среднего мода совпадает с математическим ожиданием . Если значения случайной величины не повторяются, мода отсутствует.  

Точка на оси х, соответствующая максимуму кривой плотности распределения , называется модой, то есть мода - это наиболее вероятное значение случайной величины . Однако, мода существует не у всех распределений. В качестве примера можно привести равномерное распределение . В этом случае определение центра распределение как моды невозможно. Моду обычно обозначают как Мо.  

Существуют понятия моды и медианы случайной величины.  

Очевидно, что в случае симметричного медиана совпадает с модой и математическим ожиданием.  

Исходя из того, что мода основывается не на единичных замерах, а на большом объеме наблюдений, ее нельзя считать случайной величиной . На величину моды никакого влияния не оказывают различного рода задержки в работе и потери нормальных ее темпов.  

Иногда при анализе эмпирических распределений пользуются понятиями моды и медианы распределения, " . .. Модой называется наиболее вероятное значение случайной величины,  

Расширительным теоретико-вероятностным толкованием феномена лотереи является понятие вероятностного распределения случайной величины . С его помощью определяют вероятности того, что случайная величина примет те или иные свой возможные значения. Обозначим через у случайную величину , а через у - ее возможные значения. Тогда для дискретной случайной величины , которая может принимать возможные значения У, у2, УЗ,. .., уп удобной формой вероятностного распределения следует считать зависимость Р(у = у), которую обычно называют вероятностным рядом, шт рядом распределения. На практике для оперативной обобщенной оценки вероятностного распределения величин риска часто используют так называемые числовые и другие характеристики распределения случайных результатов математическое ожидание , дисперсия, среднее квадратическое (стандартное) отклонение, коэффициент вариации , мода, медиана и др. (см., например, и др.). Иными словами, для быстрого и целостного восприятия предприниматель стремится (или просто вы-  

На основе данных Госкомстата СССР о распределении населения по среднедушевому совокупному доходу попробуем сравнить показатели среднего , медианного и модального доходов (табл. 1). Из таблицы видно что средний доход по абсолютной величине превосходит медианный и модальный доходы , причем рост его происходит в основном за счет увеличения доли лиц, имеющих высокие доходы, то есть использование показателя среднего дохода приводит к существенному завышению уровня доходов основной массы населения и в значительной мере скрывает процесс их дифференциации. Значения модального дохода тяготеют к нижним группам распределения и отклоняются от медианного дохода в меньшую сторону. Однако попадание моды в тот или иной интервал зачастую носит случайный характер достаточно небольшого изменения в распределении - и мода окажется уже в соседнем интервале. Например, в 1989 году наиболее распространенным являлся уровень дохода от 100 до 125 рублей (такой доход получали 16.1% населения), однако ввиду незначительных сдвигов в доходах, происшедших за 1989-1990 годы, наиболее распространенным интервалом оказался следующий интервал (125-150 рублей), а само значение моды возросло на 15.6 руб. Кроме того, доля населения в модальном интервале дохода может превышать другие доли весьма незначительно.  

Для того чтобы охарактеризовать центр распределения логарифмически нормальной случайной величины a, можно использовать наряду с уже вычисленным математическим ожиданием Ma моду (локальный максимум плотности /(a a)) тос1а = ехр(ц-ст2) и  

Mode - мода. Наиболее вероятное значение случайной величины.  

МОДА - понятие

Кроме математического ожидания и дисперсии, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные черты распределения.

Определение. Модой Мо(Х) случайной величины X называется ее наиболее вероятное значение (для которого вероятность р г или плотность вероятности

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным (рис. 3.13).

Мода Мо(Х), при которой вероятность р { или плотность вероятности (р(х) достигает глобального максимума, называется наивероятнейшим значением случайной величины (на рис. 3.13 это Мо(Х) 2).

Определение. Медианой Ме(Х) непрерывной случайной величины X называется такое ее значение , для которого

т.е. вероятность того, что случайная величина X примет значение, меньшее медианы Ме(Х) или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая х = Ме(Х ), проходящая через точку с абсциссой, равной Ме(Х ), делит площадь фигуры иод кривой распределения на две равные части (рис. 3.14). Очевидно, что в точке х = Ме(Х) функция распределения равна 1/2, т.е. Р(Ме(Х)) = 1/2 (рис. 3.15).

Отметим важное свойство медианы случайной величины: математическое ожидание абсолютной величины отклонения случайной величины X от постоянной величины С минимально тогда , когда эта постоянная С равна медиане Ме(Х) = т , т.е.

(свойство аналогично свойству (3.10") минимальности среднего квадрата отклонения случайной величины от ее математического ожидания).

О Пример 3.15. Найти моду, медиану и математическое ожидание случайной величины X с плотностью вероятности ф(х) = 3х 2 при хе.

Решение. Кривая распределения представлена на рис. 3.16. Очевидно, что плотность вероятности ф(х) максимальна при х = Мо(Х) = 1.

Медиану Ме(Х) = Ь найдем из условия (3.28):

откуда

Математическое ожидание вычислим по формуле (3.25):

Взаимное расположение точек М(Х)> Ме(Х) и Мо(Х) в порядке возрастания абсцисс показано на рис. 3.16. ?

Наряду с отмеченными выше числовыми характеристиками для описания случайной величины используется понятие квантилей и процентных точек.

Определение. Квантилем уровня у-квантилем)

называется такое значение х ц случайной величины , при котором функция ее распределения принимает значение, равное д, т.е.

Некоторые квантили получили особое название. Очевидно, что введенная выше медиана случайной величины есть квантиль уровня 0,5, т.е. Ме(Х) = х 05 . Квантили дг 0 2 5 и х 075 получили название соответственно нижнего и верхнего квартилейК

С понятием квантиля тесно связано понятие процентной точки. Под ЮОуХо-ной точкой подразумевается квантиль х х ({ , т.е. такое значение случайной величины X, при котором

0 Пример 3.16. По данным примера 3.15 найти квантиль х 03 и 30%-ную точку случайной величины X.

Решение. По формуле (3.23) функция распределения

Квантиль.г 0 з найдем из уравнения (3.29), т.е. х$ 3 =0,3, откуда Л"оз -0,67. Найдем 30%-ную точку случайной величины X, или квантиль х 0 7 , из уравнения х$ 7 = 0,7, откуда х 0 7 «0,89. ?

Среди числовых характеристик случайной величины особое значение имеют м о м е н т ы - начальные и центральные.

Определение. Начальным моментом к-го порядка случайной величины X называется математическое ожидание к-й степени этой величины :

Определение. Центральным моментом к-го порядка случайной величины X называется математическое ожидание к-й степени отклонения случайной величины X от ее математического ожидания :

Формулы для вычисления моментов для дискретных случайных величин (принимающих значения х 1 с вероятностями р,) и непрерывных (с плотностью вероятности ср(х)) приведены в табл. 3.1.

Таблица 3.1

Нетрудно заметить, что при к = 1 первый начальный момент случайной величины X есть ее математическое ожидание, т.е. ч х = М[Х) = а, при к = 2 второй центральный момент - дисперсия, т.е. р 2 = Т)(Х).

Центральные моменты р А могут быть выражены через начальные моменты но формулам:

и т.д.

Например, ц 3 = М(Х-а)* = М(Х*-ЗаХ 2 +За 2 Х-а->) = М(Х*)~ -ЗаМ{Х 2)+За 2 М(Х)~ а 3 = у 3 -Зу^ + Зу(у, -у^ = у 3 - Зу^ + 2у^ (при выводе учли, что а = М(Х) = V, - неслучайная величина). ?

Выше отмечено, что математическое ожидание М(Х), или первый начальный момент, характеризует среднее значение или положение, центр распределения случайной величины X на числовой оси; дисперсия О(Х), или второй центральный момент р 2 , - с т с - пень рассеяния распределения X относительно М(Х). Для более подробного описания распределения служат моменты высших порядков.

Третий центральный момент р 3 служит для характеристики а с и м - м е т р и и (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на о 3 , где а - среднее квадратическое отклонение случайной величины X. Полученная величина А называется коэффициентом асимметрии случайной величины.

Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии Л = 0.

На рис. 3.17 показаны две кривые распределения: I и II. Кривая I имеет положительную (правостороннюю) асимметрию (Л > 0), а кривая II - отрицательную (левостороннюю) (Л

Четвертый центральный момент р 4 служит для характеристики к р у - тост и (о с т р о в е р ш и н н о с т и или п л о с к о в е р ш и н - пости) распределения.

Мода - значение во множестве наблюдений, которое встречается наиболее часто

Мо = X Mо + h Мо * (f Мо - f Мо-1) : ((f Мо - f Мо-1) + (f Мо - f Мо+1)),

здесь X Mо - левая граница модального интервала, h Мо - длина модального интервала, f Мо-1 - частота премодального интервала, f Мо - частота модального интервала, f Мо+1 - частота послемодального интервала.

Модой абсолютно непрерывного распределения называют любую точку локального максимума плотности распределения. Для дискретных распределений модой считают любое значение a i , вероятность которого p i больше, чем вероятности соседних значений

Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме , т.е.

М е =(n+1) /2 Р(Х < Ме) = Р(X > Ме )

Равномерно распределенная НСВ

Равномерное распределение. Непрерывная случайная величина называется равномерно распределенной на отрезке (), если ее функция плотности распределения (рис. 1.6,а ) имеет вид :

Обозначение: – СВ распределена равномерно на .

Соответственно функция распределения на отрезке (рис. 1.6, б ):

Рис. 1.6. Функции случайной величины, распределенной равномерно на [a ,b ]: а – плотности вероятностей f (x ); б – распределения F (x )

Математическое ожидание и дисперсия данной СВ определяются выражениями:

В силу симметрии функции плотности, совпадает с медианой. Моды равномерное распределение не имеет

Пример 4. Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 2 минут. Найти интегральную и дифференциальную функции распределения этой случайной величины.

27.Нормальный закон распределения вероятностей

Непрерывная случайная величина x имеет нормальльное распределение с параметрами: m,s > 0, если плотность распределения вероятностей имеет вид:

где: m – математическое ожидание, s– среднеквадратическое отклонение.

Нормальное распределение называют еще гауссовским по имени немецкого математика Гаусса . Тот факт, что случайная величина имеет нормальное распределение с параметрами: m, , обозначают так: N (m,s), где: m=a=M[X];

Достаточно часто в формулах математическое ожидание обозначают через а . Если случайная величина распределена по закону N(0,1), то она называется нормированной или стандартизированной нормальной величиной. Функция распределения для нее имеет вид:

График плотности нормального распределения, который называют нормальной кривой или кривой Гаусса, изображен на рис.5.4.

Рис. 5.4. Плотность нормального распределения

свойства случайной величины, имеющей нормальный закон распределения.

1. Если , то для нахождения вероятности попадания этой величины в заданный интервал (х 1 ;х 2 ) используется формула:

2. Вероятность того, что отклонение случайной величины от ее математического ожидания не превысит величину (по абсолютной величине), равна:

3. "Правило трех сигм" . Если случайная величина , то практически достоверно, что ее значения заключены в интервале (). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры ( и ), ориентировочно определить интервал практических значений случайной величины.

Показательное распределение

Случайная величина X имеет экспоненциальное распределение с параметром , если её плотность имеет вид

Интегрируя плотность, получаем функцию экспоненциального распределения:

сновные характеристики показательного распределения:

Графики плотности и функции полученного показательного распределения