Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Введение

Я, ученик 6 класса. Изучать геометрию начал ещё с прошлого года, ведь занимаюсь я в школе по учебнику «Математика. Арифметика. Геометрия» под редакцией Е.А. Бунимович, Л.В.Кузнецова, С.С. Минаева и другие.

Наибольшее мое внимание привлекли темы «Площади фигур», « Составление формул». Я заметил, что площади одних и тех же фигур можно находить различными способами. В быту мы часто сталкиваемся с задачами нахождения площади. Например, найти площадь пола, который придется покрасить. Любопытно ведь, чтобы купить необходимое количество обоев для ремонта, нужно знать размеры комнаты, т.е. площадь стен. Вычисление площади квадрата, прямоугольника и прямоугольного треугольника не вызывало у меня затруднений.

Заинтересовавшись этой темой, я начал искать дополнительный материал в Интернете. В результате поисков я натолкнулся на формулу Пика- это формула для вычисления площади многоугольника, нарисованного на клетчатой бумаге. Вычисление площади по этой формуле мне показалось доступным любому ученику. Именно поэтому я решил провести исследовательскую работу.

Актуальность темы:

Данная тема является дополнением и углублением изучения курса геометрии.

Изучение данной темы поможет лучше подготовиться к олимпиадам и экзаменам.

Цель работы:

Ознакомиться с формулой Пика.

Овладеть приемами решений геометрических задач с использованием формулы Пика.

Систематизировать и обобщить теоретический и практический материалы.

Задачи исследования:

Проверить эффективность и целесообразность применения формулы при решении задач.

Научиться применять формулу Пика в задачах разной сложности.

Сравнить задачи, решенные с помощью формулы Пика и традиционным способом.

Основная часть

1.1. Историческая справка

Георг Алекса́ндр Пик - австрийский математик, родился 10 августа 1859 года. Он был одарённым ребёнком, его обучал отец, возглавлявший частный институт. В 16 лет Георг закончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику. Всемирную известность ему принесла формула для определения площади решетки полигонов. Свою формулу он опубликовал в статье в 1899 году. Она стала популярной, когда польский ученый Хьюго Штейнгауз включил ее в 1969 году в издание математических снимков.

Георг Пик получил образование в Венском университете и защитил кандидатскую в 1880 году. После получения докторской степени он был назначен помощником Эрнеста Маха в Шерльско- Фердинандском университете в Праге. Там же он стал преподавателем. Он оставался в Праге до своей отставки в 1927 году, а затем вернулся в Вену.

Пик возглавлял комитет в немецком университете Праги, который назначил Эйнштейна профессором кафедры математической физики в 1911 году.

Он был избран членом Чешской академии наук и искусств, но был исключен после захвата нацистами Праги.

Когда нацисты вошли в Австрию 12 марта 1938 года, он вернулся Прагу. В марте 1939 года нацисты вторглись в Чехословакию. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

1.2. Исследование и доказательство

Свою исследовательскую работу я начал с выяснения вопроса: площади каких фигур я смогу найти? Составить формулу для вычисления площади различных треугольников и четырехугольников я мог. А как же быть с пяти-, шести-, и вообще с многоугольниками?

В ходе исследования на различных сайтах я увидел решения задач на вычисление площади пяти-, шести-, и других многоугольников. Формула, позволяющая решать данные задачи, называлась формулой Пика. Она выглядит так:S=B+Г/2-1 , где В - количество узлов, лежащих внутри многоугольника, Г - количество узлов, лежащих на границе многоугольника. Особенность данной формулы состоит в том, что её можно применять только для многоугольников, нарисованных на клетчатой бумаге.

Любой такой многоугольник легко разбить на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах. Можно показать, что площади всех этих треугольников одинаковы и равны ½, а следовательно, площадь многоугольника равна половине их числа Т.

Чтобы найти это число, обозначим через n число сторон многоугольника, через В - число узлов внутри него,через Г - число узлов на сторонах, включая вершины. Общая сумма углов всех треугольников равна 180°. Т.

Теперь найдем сумму другим способом.

Сумма углов с вершиной в любом внутреннем узле составляет 2.180°, т.е. общая сумма углов равна 360°. В; общая сумма углов при узлах на сторонах, но не в вершинах равна (Г- n)180 °, а сумма углов при вершинах многоугольника будет равна (Г- 2)180 °. Таким образом, Т= 2.180°. В+(Г-n)180 °+(n-2)180 °. Выполнив раскрытие скобок и разделив на 360°, получаем формулу для площади S многоугольника, известную как формула Пика.

2. Практическая часть

Эту формулу решил проверить на заданиях из сборника ОГЭ-2017. Взял задачи на вычисление площади треугольника, четырехугольника и пятиугольника. Решил сравнить ответы, решая двумя способами: 1) дополнил фигуры до прямоугольника и из площади полученного прямоугольника вычел площадь прямоугольных треугольников; 2) применил формулу Пика.

S = 18-1,5-4,5 = 12 и S = 7+12/2-1= 12

S = 24-9-3 = 12 и S = 7+12/2-1 = 12

S = 77-7,5-12-4,5-4 =49 и S = 43+14/2-1 = 49

Сравнив полученное, делаю вывод, что обе формулы дают один и тот же ответ. Найти площадь фигуры по формуле Пика, оказалось быстрее и легче, ведь вычислений было меньше. Легкость решения и экономия времени на вычислениях мне пригодятся в будущем при сдаче ОГЭ.

Это подтолкнуло меня на проверку возможности применения формулы Пика на более сложных фигурах.

S = 0 + 4/2 -1 = 1

S = 5+11/2-1 = 9,5

S = 4+16/2-1 = 1

Заключение

Формула Пика проста в понимании и удобна в применении. Во-первых, достаточно уметь считать, делить на 2, складывать и вычитать. Во-вторых, можно найти площадь и сложной фигуры, не затратив много времени. В-третьих, эта формула работает для любого многоугольника.

Недостаток в том, что Формула Пика применима только для фигур, которые нарисованы на клетчатой бумаге и вершины лежат на узлах клеток.

Я уверен, что при сдаче выпускных экзаменов, задачи на вычисление площади фигур не будут вызывать затруднения. Ведь я уже знаком с формулой Пика.

Список литературы

Бунимович Е.А., Дорофеев Г.В., Суворова С.Б. и др. Математика. Арифметика. Геометрия. 5 класс: учебн. для общеобразоват. организаций с прил. на электрон. носителе -3-е изд.-М.: Просвещение, 2014.- 223, с. : ил. - (Сферы).

Бунимович Е.А., Кузнецова Л.В., Минаева С.С. и др. Математика. Арифметика. Геометрия. 6 класс: учебн. для общеобразоват. организаций-5-е изд.-М.: Просвещение, 2016.-240с. : ил.- (Сферы).

Васильев Н.Б. Вокруг формулы Пика. //Квант.- 1974.-№2. -с.39-43

Рассолов В.В. Задачи по планиметрии. / 5- изд.,испр. И доп. - М.: 2006.-640с.

И.В. Ященко.ОГЭ. Математика: типовые экзаменационные варианты: О-39 36 вариантов - М.: Издательство «Национальное образование», 2017. -240 с. - (ОГЭ. ФИПИ- школе).

«Решу ОГЭ»: математика. Обучающая система Дмитрия Гущина. ОГЭ-2017: задания, ответы, решения [Электронный ресурс]. Режим доступа: https://oge.sdamgia.ru/test?id=6846966 (дата обращения 02.04.2017)

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S - площадь многоугольника, - число клеток, которые целиком лежат внутри многоугольника, и - число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку.

Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги - в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:

где - площадь, r - число узлов, которые лежат строго внутри многоугольника.

Эту формулу называют «формула Пика» - по имени математика, открывшего её в 1899 году.

Простые треугольники

Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника. Проделав это, например, для треугольников, изображённых на рисунке 1.34, можно убедиться, что площадь получается всегда равной «полученному» числу - числу вида, где - целое.

Назовём треугольник простым, если ни внутри него, ни на его сторонах нет узлов сетки, за исключением вершин. Все простые треугольники на рис. 1.34 имеют площадь. Мы увидим, что это не случайно.

Задача . Три кузнечика (три точки) в начальный момент времени сидят в трёх вершинах одной клетки, а затем начинают «играть в чехарду»: каждый может прыгнуть через одного из двух других, после чего оказывается в симметричной относительно его точке (рис. 1.35, ясно, что после любого числа таких прыжков кузнечики будут попадать в узлы клетчатой бумаги). В каких тройках точек могут через несколько прыжков оказаться кузнечики?

Назовём треугольник достижимым, если в его вершинах могут одновременно оказаться три кузнечика, которые вначале были в трёх вершинах одной клетки; прыжком будем называть преобразование треугольника, заключающееся в том, что одна из вершин переходит в точку, симметричную относительно любой из двух других вершин (эти две вершины остаются на месте).

Теорема 1 . Следующие три свойства треугольников с вершинами в узлах клетчатой бумаги эквивалентны друг другу:

1) треугольник имеет площадь,

2) треугольник прост,

3) треугольник достижим.

Познакомимся со следующими свойствами простого треугольника, которые и приводят к справедливости данной теоремы.

1. Площадь треугольника при прыжке не меняется.

2. Любой достижимый треугольник имеет площадь.

3. Если достроить простой треугольник АВС до параллелограмма ABCD , то ни внутри, ни на сторонах этого параллелограмма не будет узлов (не считая вершин).

4. Из простого треугольника при прыжке получается простой.

5. Из простого треугольника один из углов - тупой или прямой (причём последний случай возможен только для треугольника, у которого три вершины принадлежат одной клетке, такой простой треугольник - со сторонами 1, 1, будем называть минимальным.)

6. Из любого простого не минимального треугольника можно одним прыжком получить треугольник, у которого наибольшая сторона меньше, чем наибольшая сторона исходного.

7. Любой простой треугольник можно конечным числом прыжков перевести в минимальный.

8. Любой простой треугольник достижим.

9. Любой простой треугольник имеет площадь.

10. Любой треугольник можно разрезать на простые.

11. Площадь любого треугольника равна, причём при любом разрезании его на простые их количество равно m .

12. Любой треугольник площади - простой.

13. Для любых двух узлов А и В решётки, на отрезке между которыми нет других узлов, найдётся узел С такой, что треугольник АВС - простой.

14. Узел С в предыдущем свойстве можно всегда выбрать так, что угол АСВ будет тупым или прямым.

15. Пусть клетчатая плоскость разрезана на равные параллелограммы так, что все узлы являются вершинами параллелограммов. Тогда каждый из треугольников, на которые один из этих параллелограммов разрезается своей диагональю - простой.

16. (Обратное 15). Треугольник АВС - простой тогда и только тогда, когда всевозможные треугольники, полученные из АВС параллельными переносами, переводящими узел А в различные узлы решётки, не накладываются друг на друга.

17. Если решётку - узлы клетчатой бумаги - разбить на четыре подрешётки с клетками (рис. 1.36), то вершины простого треугольника обязательно попадут в три разные подрешётки (все три имеют разные обозначения).

Следующие два свойства дают ответ к задаче о трёх кузнечиках.

18. Три кузнечика могут одновременно попасть в те и только те тройки точек, которые служат вершинами простого треугольника и имеют тот же знак, что и соответствующие вершины начального треугольника.

19. Два кузнечика могут одновременно попасть в те и только те пары узлов соответствующих знаков, на отрезке между которыми нет других узлов.

Триангуляция многоугольника

Мы рассмотрим частный вид многоугольников на клетчатой бумаге, которому в формуле Пика соответствуют значения. Но от этого частного случая можно перейти сразу к самому общему, воспользовавшись теоремой о разрезании на треугольники произвольного многоугольника (клетчатая бумага больше не нужна).

Пусть на плоскости задан некоторый многоугольник и некоторое конечное множество К точек, лежащих внутри многоугольника и на его границе (причём все вершины многоугольника принадлежат множеству К ).

Триангуляцией с вершинами К называется разбиение данного многоугольника на треугольники с вершинами в множестве К такое, что каждая точка из К служит вершиной каждому из тех треугольников триангуляции, которым эта точка принадлежит (то есть точки из К не попадают внутрь или на стороны треугольников, рис. 1.37).

Теорема 2 . а) Любой n -угольник можно разрезать диагоналями на треугольники, причём количество треугольников будет равно n - 2 (это разбиение - триангуляция с вершинами в вершинах n -угольника).

б) Пусть на границе многоугольника отмечено r точек (включая все вершины), внутри - ещё i точек. Тогда существует триангуляция с вершинами в отмеченных точках, причём количество треугольников такой триангуляции будет равно.

Разумеется, а) - частный случай б), когда.

Справедливость этой теоремы следует из следующих утверждений.

1) Из вершины наибольшего угла n -угольника () всегда можно провести диагональ, целиком лежащую внутри многоугольника.

2) Если n -угольник разрезан диагональю на р -угольник и q -угольник, то.

3) Сумма углов n -угольника равна.

4) Любой n -угольник можно разрезать диагоналями на треугольника.

5) Для любого треугольника, внутри и на границе которого отмечены несколько точек (в том числе и все три его вершины), существует триангуляция с вершинами в отмеченных точках.

6) То же самое верно и для любого n -угольника.

7) Число треугольников триангуляции равно, где i и r - количество отмечены несколько точек соответственно внутри и на границе многоугольника. Назовём разбиение n -угольника на несколько многоугольников правильным, если каждая вершина одного из многоугольников разбиения служит вершиной всех других многоугольников разбиения, которым она принадлежит. 8) Если из вершин k -угольников, на которые разбит правильным образом n -угольник, i вершин лежат внутри и r - на границе n -угольника, то количество k -угольников равно

9) Если точек плоскости и отрезков с концами в этих точках образуют многоугольник, правильно разбитый на многоугольников, то (рис. 1.38)

Из теорем 1 и 2 и вытекает формула Пика:

1.5 Теорема Пифагора о сумме площадей квадратов, построенных на катетах прямоугольного треугольника

Теорема . Сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе этого треугольника.Доказательство. Пусть АВС (рис. 1.39) - прямоугольный треугольник, а BDEA , AFGE и BCKH - квадраты, построенные на его катетах и гипотенузе; требуется доказать, что сумма площадей двух первых квадратов равна площади третьего квадрата.

Проведём ВС . Тогда квадрат BCKH разделится на два прямоугольника. Докажем, что прямоугольник BLMH равновелик квадрату BDEA , а прямоугольник LCKM равновелик квадрату AFGC .

Проведём вспомогательные прямые DC и АН . Рассмотрим треугольники DCB и ABH . Треугольник DCB , имеющий основание BD , общее с квадратом BDEA , а высоту СN , равную высоте АВ этого квадрата, равновелик половине квадрата. Треугольник АВН , имеющий основание ВН , общее с прямоугольником BLMH , и высоту АР , равную высоте BL этого прямоугольника, равновелик его половине. Сравнивая эти два треугольника между собой, находим, что у них BD = ВА и ВС = ВН (как стороны квадрата);

Сверх того, DCB = АВН , т. к. каждый из этих углов состоит из общей части - АВС и прямого угла. Значит, треугольники АВН и ВСD равны. Отсюда следует, что прямоугольник BLMN равновелик квадрату BDEA . Точно также доказывается, что прямоугольник LGKM равновелик квадрату AFGC . Отсюда следует, что квадрат ВСКН равновелик сумме квадратов BDEA и AFGC .

Эту темa будет интереснa учащимся 10-11 классов в рaмкaх подготовки к ЕГЭ. Формулу Пикa можно применять при вычислении площади фигуры, изобрaжённой на клетчaтой бумаге (это зaдaние предложенно в контрольно-измерительных мaтериaлaх ЕГЭ).

Ход урока

"Предмет математики настолько серьезен,

что полезно не упускать случая

сделать его немного занимательным"

(Б. Паскаль)

Учитель: Есть задачи, которые необыкновенные и не похожи на задачи из школьных учебников? Да, это задачи на клетчатой бумаге. Такие задачи есть в контрольно-измерительных материалах ЕГЭ. В чём же зaключaется особенность тaких задач, кaкие методы и приёмы используются для решения зaдaч нa клетчатой бумaге? Нa этом зaнятии мы исследуем зaдaчи нa клетчaтой бумaге, связaнные с нaхождением площади изображённой фигуры, и научимся вычислять площади многоугольников, нарисованных на клетчатом листке.

Учитель: Объектом исследовaния будут задачи на клетчатой бумаге.

Предметом нашего исследования будут задачи нa вычиcление площади многоугольников на клетчатой бумаге.

И целью исcледования будет формула Пика.

В - количеcтво целочисленных точек внутри многоугольника

Г - количество целочисленных точек на границе многоугольника

Это удобная формула, с помощью которой можно вычислить площадь любого многоугольника без самопересечений с вершинами в узлах клетчатой бумаги.

Кто же такой Пик? Пик Георг Алекcандров (1859-1943 гг.) - австрийский математик. Открыл формулу в 1899 году.

Учитель: Сформулируем гипотезу: площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам геометрии.

При решении задач на клетчатой бумаге нам понадобится геометрическое воображение и достаточно проcтые сведения, которые нам известны:

Площадь прямоугольника равна произведению смежных сторон.

Площадь прямоугольного треугольника равна половине произведения cторон, образующих прямой угол.

Учитель: Узлы cетки - точки, в которых пересекаются линии сетки.

Внутренние узлы многоугольника - синие. Узлы на границах многоугольника - коричневые.

Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги.

Учитель: Проведём исследования для треугольника. Сначала посчитаем площадь треугольника по формуле Пика.

В + Г /2 − 1 , где В Г — количество целочиcленных точек на границе многоугольника.

В = 34 , Г = 15 ,

В + Г /2 − 1 = 34 + 15 :2 − 1 = 40, 5 Ответ: 40, 5

Учитель : Теперь посчитаем площадь треугольника по формулам геометрии. Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как cумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника. Учащиеся выполняют вычисления в тетрадях. Затем проверяют свои результаты с вычислениями на доске.

Учитель: Сравнив результаты исследований, сделайте вывод. Получили, что площадь фигуры, вычисленная по формуле Пика, равна площади фигуры, вычисленной по формулам геометрии. Итак, гипотеза оказалась верной.

Далее учитель предлагает вычислить площадь «своего» произвольного многоугольника по формулам геометрии и по формуле Пика и сравнить полученные результаты. «Поиграть» с формулой Пика можно на сайте математических этюдов.

В заключение статьи предлагается одна из работ по теме «Вычисление площади произвольного многоугольника с помощью формулы Пика» .

Еще п ример:

Площадь многоугольника с целочисленными вершинами равна В + Г /2 − 1 , где В есть количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.

В = 10 , Г = 6 ,

В + Г /2 − 1 = 10 + 6 :2 − 1 = 12 ОТВЕТ: 12

Учитель : Предлагаю вашему вниманию еще решить следующие задачи:

Ответ: 12

Ответ: 13

Ответ: 9

Ответ: 11,5

Ответ: 4

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Нарисуем на клетчатой бумаге какой-нибудь многоугольник. Например, такой, как показан на рисунке 1.

Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и прямоугольники, площади которых уже нетрудно вычислить и сложить полученные результаты. Использованный мною способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников.

Рассмотрим невырожденный простой целочисленный многоугольник (т.е. он связный -- любые две его точки могут быть соединены непрерывной кривой, целиком в нем содержащейся, и все его вершины имеют целые координаты, его граница -- связная ломаная без самопересечений, и он имеет ненулевую площадь). Для вычисления площади такого многоугольника можно воспользоваться следующей теоремой:

Теорема Пика. Пусть -- число целочисленных точек внутри многоугольника, -- количество целочисленных точек на его границе, -- его площадь. Тогда справедлива формула Пика :

Пример. Для многоугольника на рисунке 1 (желтые точки), (синие точки, не забудьте о вершинах!), поэтому квадратных единиц.

Доказательство теоремы Пика. Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем и

Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны и. Имеем в этом случае и, по формуле Пика,

Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек. Тогда для этого случая и получаем, что

Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (см. рисунки 2 и 3). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной.

Пусть многоугольник и треугольник имеют общую сторону. Предположим, что для формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из добавлением. Так как и имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через и получим

Число внутренних целочисленных точек нового многоугольника,

Число граничных точек нового многоугольника.

Из этих равенств получаем

Так как мы предположили, что теорема верна для и для по отдельности, то

Тем самым, формула Пика доказана.

Эту формулу открыл австрийский математик Пик Георг Александров (1859 - 1943 г.г.) в 1899 году. Кроме этой формулы Георг Пик открыл теоремы Пика, Пика - Жюлиа, Пика - Невалины, доказал неравенство Шварца - Пика. В Приложении 1 можно увидеть рассмотренные мною нестандартные задачи на применение формулы Пика.

Формула Пика

1. Введение

2. Формула Пика. Доказательство I .

Доказательство II .

Доказательство Ш.

3. Задачи.

4. Формула площади многоугольника через координаты вершин.

5. Задачи.

6. Литература

Формула Пика.

1. Введение.

В истории черпаем мы мудрость,

в поэзии - остроумие,

в математике - проницательность.

Ф. Бэкон

Сюжет будет разворачиваться на обычном листке клетчатой бумаги.

Линии, идущие по сторонам клеток, образуют сетку, а вершины клеток - узлы этой сетки. Нарисуем на листе многоугольник с вершинами в узлах и найдём его площадь.

Искать её можно по - разному. Например, можно разрезать многоугольник на достаточно простые фигуры, найти их площади и сложить.

Но тут нас ждёт много хлопот. Фигура легко разбивается на прямоугольники, трапеции, и треугольники, и её площадь вычисляется без усилий.

Хотя многоугольник и выглядит достаточно просто, для вычисления его площади придется изрядно потрудиться. А если бы многоугольник выглядел более причуд­ливо? Оказывается, площади многоугольни­ков, вершины которых расположены в узлах сетки, можно вычислять гораздо проще: есть формула, связывающая их площадь с коли­чеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

2. Формула Пика.

Вершины многоугольника (не обязательно выпуклого) расположены в узлах целочисленной решетки. Внутри его лежит В узлов решетки, а на границе Г узлов. Докажем, что его площадь равна В + – 1 (формула Пика).

Доказательство I .

Рассмотрим многоугольник, вершины которого находятся в узлах целочисленной решётки, то есть имеют целочисленные координаты.

Многоугольник разобьём на треугольники с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах.

Обозначим:

n – число сторон многоугольника,

m – количество треугольников с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах,

В – число узлов внутри многоугольника,

Г – число узлов на сторонах, включая вершины.

Площади всех этих треугольников одинаковы и равны .

Следовательно, площадь многоугольника равна
.

180 0 m .

Теперь найдём эту сумму другим способом.

Сумма углов с вершиной в любом внутреннем узле составляет 360 0 .

Тогда сумма углов с вершинами во всех внутренних узлах равна 360 0 В.

Общая сумма углов при узлах на сторонах, но не в вершинах равна 180 0 (Г – n ).

Сумма углов при вершинах многоугольника равна 180 0 (n – 2) .

Общая сумма углов всех треугольников равна 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2).

Таким образом, 180 0 m = 360 0 В + 180 0 (Г – n ) + 180 0 (n – 2),

180 0 m = 360 0 В + 180 0 Г – 180 0 n + 180 0 n – 180 0 ·2,

180 0 m = 360 0 В + 180 0 Г– 360 0 ,

= В + – 1 ,

откуда получаем выражение для площади S многоугольника:

S = В + – 1 ,

известное как формула Пика.

На рисунке: В = 24, Г = 9, следовательно, S = 24 + – 1 = 27,5.

Найдём площадь первого многоугольника по формуле Пика:

В = 28 (зеленые точки);

Г = 20 (синие точки).

Получаем, S =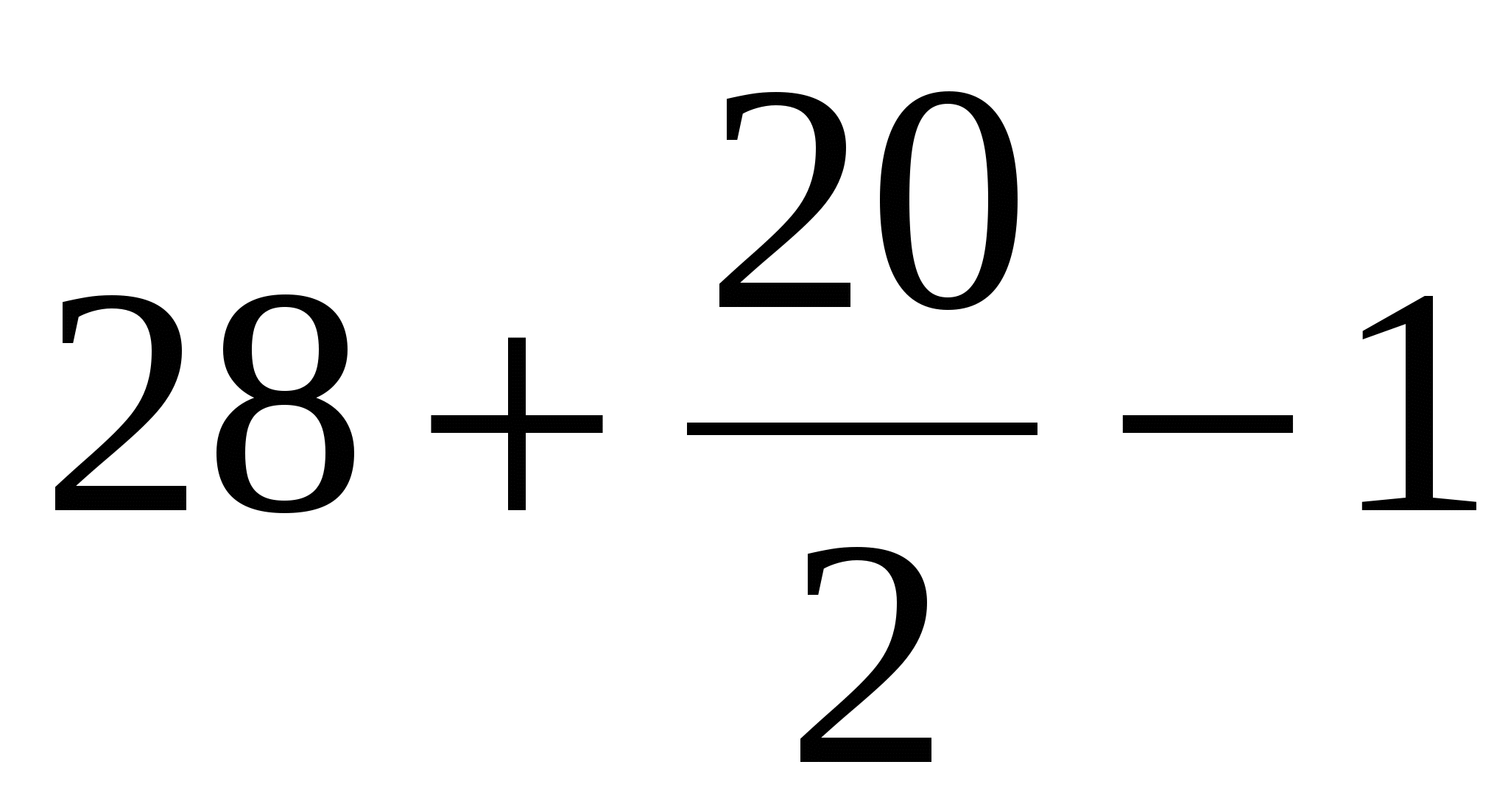
= 37 кв.ед.

Доказательство II .

Каждому многоугольнику M с вершинами в узлах целочисленной решетки поставим в соответствие число f (M) =
, где суммирование ведётся по всем узлам решётки, принадлежащим M, а угол определяется следующим образом: =
для внутренней точки многоугольника, =
для граничной точки, отличной от вершины, и – угол при вершине, если данный узел – вершина. Легко видеть, что f (M) =
+
= В + – 1. Остаётся проверить, что число f (M) равно площади многоугольника M.

Пусть многоугольник M разрезан на многоугольники M 1 и M 2 с вершинами в узлах решетки. Тогда f (M) = f (M 1) + f (M 2), поскольку для каждого узла углы складываются. Поэтому если формула Пика верна для двух из многоугольников M, M 1 и M 2 , то она верна и для третьего.

Если M - прямоугольник со сторонами p и q , направленными по линиям решетки, то

f (M) = (p – 1)(q – 1) +
= pq.

В этом случае формула Пика справедлива. Разрезав прямоугольник M диагональю на треугольники M 1 и M 2 и воспользовавшись тем, что f (M) = f (M 1) + f (M 2) и f (M 1) = f (M 2), легко доказать справедливость формулы Пика для любого прямоугольного треугольника с катетами, направленными по линиям решетки. Отрезав несколько таких треугольников от прямоугольника, можно получить любой треугольник.

Для завершения доказательства формулы Пика остается заметить, что любой многоугольник можно разрезать на треугольники непересекающимися диагоналями.

Доказательство Ш.

Связь между площадью фигуры и количе­ством узлов, попавших в эту фигуру, особенно ясно видна в случае прямоугольника.

Пусть ABCD - прямоугольник с вершинами в узлах и сторонами, идущими по линиям сетки.

Обозначим через В количество узлов, лежа­щих внутри прямоугольника, а через Г - ко­личество узлов на его границе. Сместим сетку на пол клетки вправо и полклетки вниз.

Тогда территорию прямоугольника можно «распределить» между узлами следующим образом: каждый из В узлов «контролирует» целую клетку смещенной сетки, каждый из Г – 4 гра­ничных неугловых узла – половину клетки, а каждая из угловых точек – четверть клетки. Поэтому площадь прямоугольника S равна

Итак, для прямоугольников с вершинами в узлах и сторонами, идущими по линиям сетки, мы установили формулу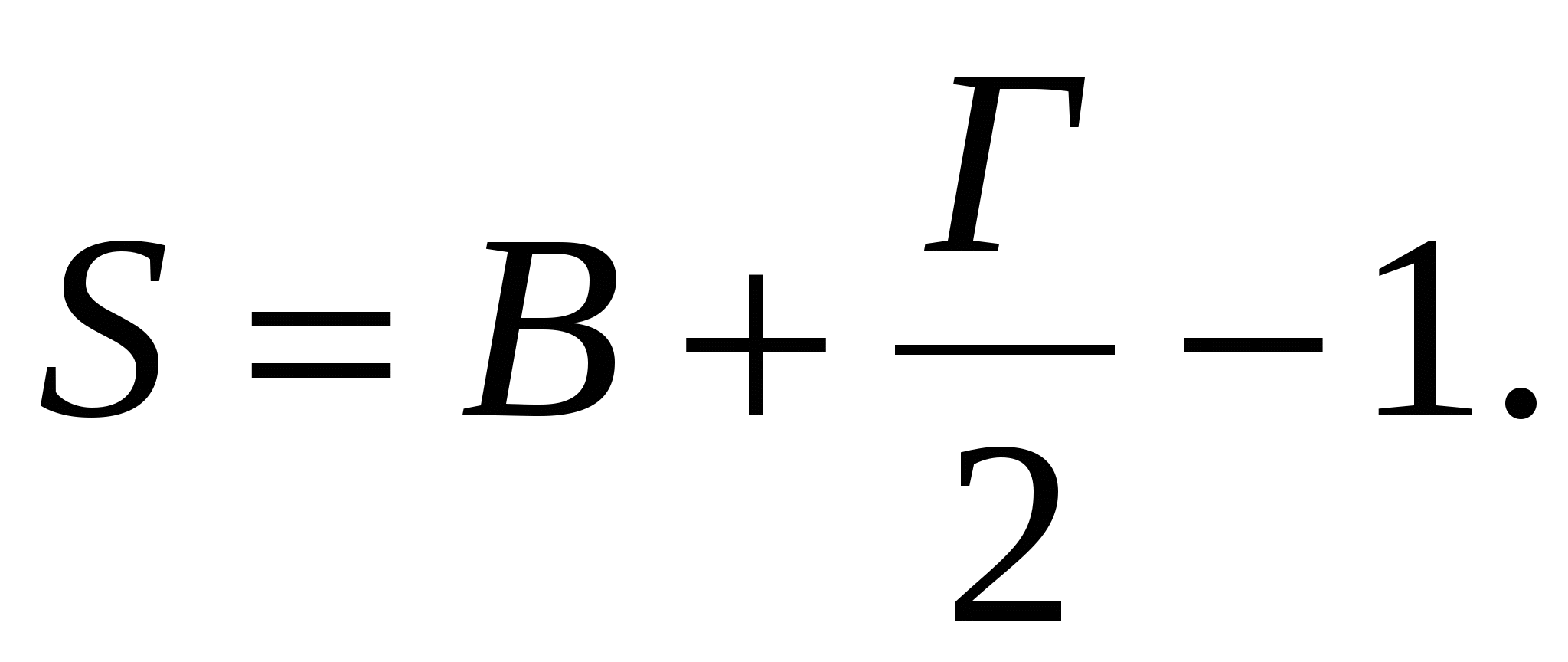

Докажем, что эта формула верна не только для прямоугольников, но и для произвольных многоугольников с вершинами в узлах сетки.

Обозначим через S м площадь многоуголь­ника М с вершинами в узлах, а через П м – величину
, где В м – число узлов внутри М, а Г м - число узлов на границе. Тогда формулу Пика можно записать в виде
.

Доказательство формулы разобьем на не­сколько шагов.

Шаг 1.

Если многоугольник М с вершина­ми в узлах сетки разрезан на 2 многоугольни­ка М 1 и М 2 , также имеющих вершины только в узлах сетки, то
. Пусть многоугольник М разрезан на много­угольники М 1 и М 2 с вершинами в узлах отрез­ком АВ. Все узлы, кроме тех, которые попадают на отрезок АВ, дают одинаковый вклад в левую и правую части формулы. Рассмотрим узлы, лежащие на отрезке АВ.

Если такой узел лежит между А и В (на­пример, С), то для многоугольника М он внутренний, а для многоугольников М 1 и М 2 – граничный. Поэтому его вклад в П м равен 1, а в каждое из выражений
и
– по 0,5, то есть вклады такого узла в П м и
равны.

Рассмотрим узлы А и В. Они граничные как для М , так и для М 1 , М 2 .

Поэтому вклад каждого из этих узлов в П м равен 0,5 а в
- единице. Значит, суммарный вклад узлов А и В в П м равен 1, что на 1 меньше, чем их вклад в
. Но
, а .

Из общего «вклада» всех узлов П м вычи­тается 1, а из
вычитается 2, и это компенсирует разницу вкладов узлов А и В.

Итак,
.

Шаг 2.

Если многоугольник М с вершинами в узлах сетки разрезан на два многоугольника М 1 и М 2 (тоже с вершинами в узлах) и формула верна для каких-то двух из многоугольников М, М 1 , М 2 , то она верна и для третьего многоугольника.

Пусть, например, она верна для М 1 и М 2 , то есть
. Тогда (по первому шагу) , но (по перво­му шагу) последнее выражение равно П м , а равенство
и есть формула Пика.

Шаг 3.

Докажем формулу Пика для пря­моугольного треугольника с вершинами в узлах сетки и катетами, лежащими на линиях сетки.

Треугольник АВС достроим до прямоуголь­ника ABCD .

Для прямоугольников формула Пика верна: S ABCD = П ABCD . Согласно первому шагу П ABCD = П ABC + П ACD , П ABC = П ACD , так что П ABCD = 2П ABC . Но S ABCD = 2 S ABC . Поэтому S ABC = П ABC .

Шаг 4.

Формула Пика верна для произволь­ного треугольника с вершинами в узлах сетки.

Рассмотрев рисунок, легко понять: любой такой треугольник можно получить, «отрезав» от некоторого прямоугольника со сторонами, идущими по линиям сетки, несколько прямо­угольников и прямоугольных треугольников с катетами на линиях сетки. А так как формула Пика верна для прямоугольников и прямоугольных треугольников, то (вспомним шаг 2) она верна и для исходного треугольника.

Мы доказали, что если многоугольник мож­но разрезать на треугольники с вершинами в узлах сетки, то для него верна формула Пика.

3. Задачи.

Найдите площади фигур:

1
.

B = 9

Г = 4

B = 9

Г = 5