Prova

Deixe ser ABC" é um triângulo arbitrário. Vamos por cima B reta paralela à reta CA (essa linha reta é chamada de linha reta euclidiana). Marque um ponto nele D para que os pontos UMA e D deitar em lados opostos de uma linha reta BC.Ângulos DBC e ACB igual a uma cruz interna deitada, formada por uma secante BC com linhas paralelas CA e BD. Portanto, a soma dos ângulos de um triângulo nos vértices B e Com igual ao ângulo ABD.A soma de todos os três ângulos de um triângulo é igual à soma dos ângulos ABD e BAC. Como esses ângulos são internos unilaterais para paralelos CA e BD na secante AB, então sua soma é 180°. O teorema foi provado.

Consequências

Do teorema segue que qualquer triângulo tem dois ângulos agudos. De fato, aplicando a prova por contradição, suponha que o triângulo tenha apenas um ângulo agudo ou nenhum ângulo agudo. Então este triângulo tem pelo menos dois ângulos, cada um dos quais é pelo menos 90°. A soma desses ângulos não é menor que 180°. Mas isso é impossível, pois a soma de todos os ângulos de um triângulo é 180°. Q.E.D.

Generalização para a teoria simplex

Onde é o ângulo entre as faces i e j do simplex.

Notas

• Em uma esfera, a soma dos ângulos de um triângulo sempre excede 180°, a diferença é chamada de excesso esférico e é proporcional à área do triângulo.
• No plano de Lobachevsky, a soma dos ângulos de um triângulo é sempre menor que 180°. A diferença também é proporcional à área do triângulo.

Veja também

Fundação Wikimedia. 2010.

• Taylor
• Ponte do Cisne Inferior

Veja o que é o "Teorema da soma dos ângulos de um triângulo" em outros dicionários:

Teorema da soma do ângulo do polígono- Propriedade dos polígonos na geometria euclidiana: A soma dos ângulos n de um polígono é 180°(n 2). Conteúdo 1 Prova 2 Observação ... Wikipedia

teorema de Pitágoras- O teorema de Pitágoras é um dos teoremas fundamentais da geometria euclidiana, estabelecendo a relação entre os lados de um triângulo retângulo. Conteúdo 1 ... Wikipédia

Área de um triângulo

teorema de Pitágoras- O teorema de Pitágoras é um dos teoremas fundamentais da geometria euclidiana, estabelecendo a relação entre os lados de um triângulo retângulo. Conteúdo 1 Declarações 2 Provas ... Wikipedia

Teorema do cosseno- O teorema do cosseno é uma generalização do teorema de Pitágoras. O quadrado de um lado de um triângulo é igual à soma dos quadrados de seus outros dois lados sem dobrar o produto desses lados pelo cosseno do ângulo entre eles. Para um triângulo plano com lados a, b, c e ângulo α ... ... Wikipedia

Triângulo- Este termo tem outros significados, veja Triângulo (significados). Um triângulo (no espaço euclidiano) é uma figura geométrica formada por três segmentos de linha que conectam três pontos não lineares. Três pontos, ... ... Wikipédia

Sinais de igualdade de triângulos- Notação padrão Triângulo é o polígono mais simples com 3 vértices (cantos) e 3 lados; uma parte de um plano limitada por três pontos que não estão na mesma linha reta e três segmentos de linha conectando esses pontos em pares. Os vértices de um triângulo ... Wikipedia

Euclides- Matemático grego antigo. Trabalhou em Alexandria no século III. BC e. A obra principal "Começos" (15 livros), contendo os fundamentos da matemática antiga, geometria elementar, teoria dos números, teoria geral das relações e um método para determinar áreas e volumes, ... ... dicionário enciclopédico

EUCLIDES- (morreu entre 275 e 270 aC) matemático grego antigo. Informações sobre a hora e local de seu nascimento não chegaram até nós, mas sabe-se que Euclides viveu em Alexandria e o auge de sua atividade cai no reinado de Ptolomeu I no Egito ... ... Grande Dicionário Enciclopédico

GEOMETRIA NÃO EUCLIDANA- geometria semelhante à geometria de Euclides na medida em que define o movimento das figuras, mas difere da geometria euclidiana em que um de seus cinco postulados (segundo ou quinto) é substituído por sua negação. Negação de um dos postulados euclidianos ... ... Enciclopédia Collier

Metas e objetivos:

Educacional:

• repetir e generalizar o conhecimento sobre o triângulo;
• provar o teorema da soma do triângulo;
• verificar de forma prática a correção da formulação do teorema;
• aprender a aplicar os conhecimentos adquiridos na resolução de problemas.

Em desenvolvimento:

• desenvolver o pensamento geométrico, o interesse pelo assunto, a atividade cognitiva e criativa dos alunos, o discurso matemático, a capacidade de adquirir conhecimento de forma independente.

Educacional:

• desenvolver as qualidades pessoais dos alunos, como determinação, perseverança, precisão, capacidade de trabalhar em equipe.

Equipamento: projetor multimídia, triângulos feitos de papel colorido, material didático "Matemática ao vivo", computador, tela.

Fase preparatória: o professor dá ao aluno a tarefa de preparar uma base histórica sobre o teorema "A soma dos ângulos de um triângulo".

Tipo de lição: aprendendo novo material.

Durante as aulas

I. Momento organizacional

Saudações. Atitude psicológica dos alunos para o trabalho.

II. Aquecimento

Conhecemos a figura geométrica “triângulo” nas lições anteriores. Vamos repetir o que sabemos sobre o triângulo?

Os alunos trabalham em grupos. Eles têm a oportunidade de se comunicar uns com os outros, cada um para construir independentemente o processo de cognição.

O que aconteceu? Cada grupo faz suas sugestões e o professor as escreve na lousa. Os resultados estão sendo discutidos:

Imagem 1

III. Formulamos a tarefa da lição

Então, já sabemos muito sobre o triângulo. Mas nem todos. Cada um de vocês tem triângulos e transferidores em sua mesa. O que você acha, que tarefa podemos formular?

Os alunos formulam a tarefa da lição - encontrar a soma dos ângulos de um triângulo.

4. Explicação do novo material

Parte prática(contribui para a atualização de conhecimentos e habilidades de autoconhecimento) Meça os ângulos com um transferidor e encontre sua soma. Anote os resultados em um caderno (ouça as respostas recebidas). Descobrimos que a soma dos ângulos acabou sendo diferente para todos (isso pode acontecer porque o transferidor foi aplicado incorretamente, o cálculo foi realizado descuidadamente etc.).

Dobre ao longo das linhas pontilhadas e descubra a que mais a soma dos ângulos do triângulo é igual:

a)
Figura 2

b)
Figura 3

dentro)
Figura 4

G)
Figura 5

e)
Figura 6

Após a conclusão do trabalho prático, os alunos formulam a resposta: A soma dos ângulos de um triângulo é igual à medida em graus do ângulo expandido, ou seja, 180°.

Professor: Em matemática, o trabalho prático só permite fazer algum tipo de afirmação, mas precisa ser comprovada. Uma afirmação cuja validade é estabelecida por prova é chamada de teorema. Que teorema podemos formular e provar?

Alunos: A soma dos ângulos de um triângulo é 180 graus.

Referência histórica: A propriedade da soma dos ângulos de um triângulo foi estabelecida no antigo Egito. A prova dada nos livros didáticos modernos encontra-se nos comentários de Proclo sobre os Elementos de Euclides. Proclo afirma que esta prova (Fig. 8) foi descoberta pelos pitagóricos (século V aC). No primeiro livro dos Elementos, Euclides apresenta outra demonstração do teorema da soma dos ângulos de um triângulo, que é fácil de entender com a ajuda de um desenho (Fig. 7):

Figura 7

Figura 8

Os desenhos são exibidos na tela através de um projetor.

O professor se oferece para provar o teorema com a ajuda de desenhos.

Em seguida, a prova é realizada usando o CMD "Live Mathematics". O professor no computador projeta a prova do teorema.

Teorema da soma dos ângulos dos triângulos: "A soma dos ângulos de um triângulo é 180°"

Figura 9

Prova:

a)

Figura 10

b)

Figura 11

dentro)

Figura 12

Os alunos no caderno fazem um breve registro da prova do teorema:

Teorema: A soma dos ângulos de um triângulo é 180°.

Figura 13

Dado:Δ ABC

Provar: A + B + C = 180°.

Prova:

O que precisava ser comprovado.

V. Física. minuto.

VI. Explicação do novo material (continuação)

A consequência do teorema na soma dos ângulos de um triângulo é derivada pelos próprios alunos, o que contribui para o desenvolvimento da capacidade de formular seu próprio ponto de vista, expressá-lo e discuti-lo:

Em qualquer triângulo, ou todos os ângulos são agudos, ou dois ângulos agudos, e o terceiro obtuso ou reto.

Se todos os ângulos de um triângulo são agudos, então ele é chamado ângulo agudo.

Se um dos ângulos de um triângulo é obtuso, então ele é chamado obtuso.

Se um dos ângulos de um triângulo é reto, então ele é chamado retangular.

O teorema da soma do triângulo nos permite classificar os triângulos não apenas pelos lados, mas também pelos ângulos. (Ao introduzir os tipos de triângulos, os alunos preenchem uma tabela)

tabela 1

Vista em triângulo	Isósceles	Equilátero	Versátil
Retangular
obtuso
ângulo agudo

VII. Consolidação do material estudado.

1. Resolver problemas oralmente:

(Os desenhos são exibidos na tela através do projetor)

(resumo básico)

Geometria visual 7º ano. Resumo de referência No. 4 A soma dos ângulos de um triângulo.

Grande cientista francês do século XVII Blaise Pascal quando criança, ele adorava mexer com formas geométricas. Ele estava familiarizado com o transferidor e sabia como medir ângulos. O jovem pesquisador notou que para todos os triângulos a soma dos três ângulos é a mesma - 180°. “Como você pode provar isso? pensou Pascal. “Afinal, você não pode verificar a soma dos ângulos de todos os triângulos - há um número infinito deles.” Então ele cortou dois cantos do triângulo com uma tesoura e os prendeu no terceiro canto. Descobriu-se um ângulo desenvolvido, que, como você sabe, é igual a 180 °. Foi sua primeira descoberta. O futuro destino do menino já estava predeterminado.

Neste tópico, você aprenderá cinco características da igualdade do triângulo retângulo e talvez a propriedade mais popular de um triângulo retângulo de 30°. Soa assim: a perna oposta a um ângulo de 30 ° é igual à metade da hipotenusa. Dividindo um triângulo equilátero com uma altura, obtemos imediatamente uma prova dessa propriedade.

TEOREMA. A soma dos ângulos de um triângulo é 180°. Para provar isso, traçamos uma linha através do vértice paralela à base. Os ângulos escuros são iguais e os ângulos cinza são iguais, pois se encontram em linhas paralelas. O canto escuro, o canto cinza e o canto no vértice formam um canto reto, sua soma é 180°. Segue do teorema que os ângulos de um triângulo equilátero são 60° cada e que a soma dos ângulos agudos de um triângulo retângulo é 90°.

canto externo triângulo é chamado de ângulo adjacente ao ângulo do triângulo. Portanto, às vezes os ângulos do próprio triângulo são chamados de ângulos internos.

TEOREMA sobre o ângulo externo de um triângulo. O ângulo externo de um triângulo é igual à soma de dois ângulos internos que não são adjacentes a ele. De fato, um canto externo e dois internos não adjacentes a ele completam o canto preenchido até 180°. Segue-se do teorema que um ângulo externo é maior do que qualquer ângulo interno não adjacente a ele.

TEOREMA sobre as relações entre lados e ângulos de um triângulo. Em um triângulo, o lado maior é oposto ao ângulo maior e o lado maior é oposto ao ângulo maior. Segue-se disso: 1) A perna é menor que a hipotenusa. 2) A perpendicular é menor que a inclinação.

Distância do ponto à linha . Como a perpendicular é menor que qualquer oblíqua traçada a partir do mesmo ponto, seu comprimento é tomado como a distância do ponto à linha.

desigualdade triangular . O comprimento de qualquer lado de um triângulo é menor que a soma de seus outros dois lados, ou seja, uma< b + с , b< а + с , com< а + b . Consequência. O comprimento da polilinha é maior que o segmento que conecta suas extremidades.

SINAIS DE IGUALDADE
TRIÂNGULOS RETANGULARES

Em duas pernas. Se dois catetos de um triângulo retângulo são respectivamente iguais a dois catetos de outro triângulo, então tais triângulos são congruentes.

Ao longo da perna e ângulo agudo adjacente. Se a perna e o ângulo agudo adjacente a ela de um triângulo retângulo são respectivamente iguais à perna e ao ângulo agudo adjacente a ela de outro triângulo, então tais triângulos são congruentes.

Ao longo da perna e ângulo agudo oposto. Se a perna e o ângulo agudo oposto de um triângulo retângulo são respectivamente iguais à perna e ao ângulo agudo oposto de outro triângulo, então tais triângulos são congruentes.

Por hipotenusa e ângulo agudo. Se a hipotenusa e o ângulo agudo de um triângulo retângulo são respectivamente iguais à hipotenusa e ao ângulo agudo de outro triângulo, então esses triângulos são congruentes.

A prova destes critérios reduz-se imediatamente a um dos critérios de igualdade de triângulos.

Por perna e hipotenusa. Se o cateto e a hipotenusa de um triângulo retângulo são respectivamente iguais ao cateto e à hipotenusa de outro triângulo retângulo, então tais triângulos são congruentes.

Prova. Aplicamos triângulos com pernas iguais. Obtemos um triângulo isósceles. Sua altura traçada a partir do topo também será a mediana. Então as segundas pernas dos triângulos são iguais, e os triângulos são iguais em três lados.

TEOREMA na propriedade de uma perna oposta a um ângulo de 30°. O cateto oposto ao ângulo de 30° é igual à metade da hipotenusa. Prova-se completando o triângulo para um equilátero.

TEOREMA sobre a propriedade dos pontos da bissetriz do ângulo. Qualquer ponto da bissetriz de um ângulo é equidistante de seus lados. Se um ponto é equidistante dos lados de um ângulo, então ele está na bissetriz do ângulo. Provado desenhando duas perpendiculares aos lados do ângulo e considerando triângulos retângulos.

Segundo grande ponto . As bissetrizes de um triângulo se cruzam em um ponto.

Distância entre linhas paralelas. TEOREMA. Todos os pontos de cada uma das duas retas paralelas estão à mesma distância da outra reta. A definição da distância entre linhas paralelas segue do teorema.

Definição. A distância entre duas retas paralelas é a distância de qualquer ponto de uma das retas paralelas à outra reta.

Demonstrações detalhadas de teoremas

Este é o resumo de referência nº 4 em geometria na 7ª série. Escolha os próximos passos:

Triângulo . Triângulos agudos, obtusos e retângulos.

As pernas e a hipotenusa. Triângulo isósceles e equilátero.

A soma dos ângulos de um triângulo.

O canto externo do triângulo. Sinais de igualdade de triângulos.

Linhas e pontos maravilhosos em um triângulo: alturas, medianas,

bissetrizes, mediana e perpendiculares, ortocentro,

centro de gravidade, centro do círculo circunscrito, centro do círculo inscrito.

Teorema de Pitágoras. A proporção de aspecto de um triângulo arbitrário.

Triângulo é um polígono com três lados (ou três cantos). Os lados de um triângulo são frequentemente indicados por letras minúsculas, que correspondem às letras maiúsculas que denotam vértices opostos.

Se todos os três ângulos são agudos ( fig. 20), então isso Triângulo agudo . Se um dos cantos estiver certo(C, fig.21), isso é triângulo retângulo; ladosa, bformando um ângulo reto são chamados pernas; lateralcoposto ao ângulo reto é chamado hipotenusa. Se um dosângulos obtusos (B, fig.22), isso é triângulo obtuso.


Triângulo ABC (Fig. 23) - isósceles, E se dois seus lados são iguaisuma= c); esses lados iguais são chamados lateral, o terceiro é chamado base triângulo. Triângulo ABC (Fig. 24) - equilátero, E se tudo seus lados são iguaisuma = b = c). Em geral ( uma ≠ b ≠ c) temos escaleno triângulo .

Propriedades básicas dos triângulos. Em qualquer triângulo:

1. Há um ângulo maior oposto ao lado maior e vice-versa.

2. Ângulos iguais são opostos a lados iguais e vice-versa.

Em particular, todos os ângulos equilátero triângulo são iguais.

3. A soma dos ângulos de um triângulo é 180 º .

Das duas últimas propriedades segue-se que cada ângulo em um ângulo equilátero

triângulo é 60 º.

4. Continuando um dos lados do triângulo (AC, fig. 25), Nós temos externo

ângulo BCD . O ângulo externo de um triângulo é igual à soma dos ângulos internos,

não relacionado a isso :BCD=A+B.

5. Algum lado de um triângulo é menor que a soma dos outros dois lados e mais

suas diferenças (uma < b + c, uma > b – c;b < uma + c, b > uma – c;c < uma + b,c > uma – b).

Sinais de igualdade de triângulos.

Os triângulos são congruentes se forem respectivamente iguais:

uma ) dois lados e o ângulo entre eles;

b ) dois cantos e o lado adjacente a eles;

c) três lados.

Sinais de igualdade de triângulos retângulos.

Dois retangular triângulos são congruentes se uma das seguintes condições for verdadeira:

1) suas pernas são iguais;

2) o cateto e a hipotenusa de um triângulo são iguais ao cateto e hipotenusa do outro;

3) a hipotenusa e o ângulo agudo de um triângulo são iguais à hipotenusa e o ângulo agudo do outro;

4) a perna e o ângulo agudo adjacente de um triângulo são iguais à perna e o ângulo agudo adjacente do outro;

5) a perna e o ângulo agudo oposto de um triângulo são iguais à perna e oposto ao ângulo agudo do outro.

Linhas e pontos maravilhosos em um triângulo.

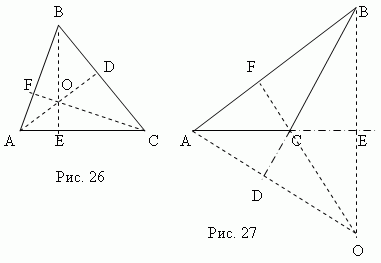
Altura triângulo éperpendicular,caiu de qualquer vértice para o lado oposto ( ou sua continuação). Este lado é chamadoa base do triângulo . As três alturas de um triângulo sempre se cruzamem um pontochamado ortocentro triângulo. O ortocentro de um triângulo agudo (ponto O , Fig. 26) está localizado dentro do triângulo, eortocentro de um triângulo obtuso (ponto O , Fig.27) – fora; O ortocentro de um triângulo retângulo coincide com o vértice do ângulo reto.

Mediana - Esse segmento de linha , conectando qualquer vértice de um triângulo com o ponto médio do lado oposto. Três medianas de um triângulo (AD , BE , CF , fig.28) se cruzam em um ponto O , que sempre está dentro do triângulo e sendo dele Centro de gravidade. Este ponto divide cada mediana 2:1 a partir do topo.

Bissetriz - Esse segmento de bissetriz canto de cima a ponto interseção com o lado oposto. Três bissetrizes de um triângulo (AD , BE , CF , fig.29) se cruzam em um ponto Oh, sempre deitado dentro de um triângulo e sendo centro do círculo inscrito(ver seção "Inscritoe polígonos circunscritos).

A bissetriz divide o lado oposto em partes proporcionais aos lados adjacentes ; por exemplo, na Fig.29 AE : CE = AB : BC .

perpendicular mediana é uma perpendicular traçada a partir da média pontos do segmento (lados). Três mediatrizes do triângulo ABC(KO , MO , NO , fig.30 ) se interceptam em um ponto O, que é Centro círculo circunscrito (pontos K, M, N os pontos médios dos lados de um triângulo ABC).

Em um triângulo agudo, este ponto está dentro do triângulo; em obtuso - fora; em um retângulo - no meio da hipotenusa. Ortocentro, centro de gravidade, centro do círculo circunscrito e centro do círculo inscrito coincidem apenas em um triângulo equilátero.

Teorema de Pitágoras. Em um triângulo retângulo, o quadrado do comprimentoA hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.

A prova do teorema de Pitágoras obviamente segue da Fig.31. Considere um triângulo retângulo ABC com pernas a, b e hipotenusa c.

Vamos construir um quadrado AKMB usando a hipotenusa AB como um lado. Entãoestender os lados de um triângulo retângulo abc para obter um quadrado CDEF , cujo lado é igual aa + b.Agora está claro que a área de um quadrado CDEF é ( a+b) 2 . Por outro lado, este a área é igual a somaáreas quatro triângulos retângulos e quadrado AKMB , ou seja

c 2 + 4 (ab / 2) = c 2 + 2 ab,

daqui,

c 2 + 2 ab= (a+b) 2 ,

e finalmente temos:

c 2 =uma 2 +b 2 .

A proporção de aspecto de um triângulo arbitrário.

No caso geral (para um triângulo arbitrário) temos:

c 2 =uma 2 +b 2 – 2ab· porque c,

onde C - ângulo entre os ladosuma e b .

>>Geometria: A soma dos ângulos de um triângulo. Lições completas

TEMA DA LIÇÃO: A soma dos ângulos de um triângulo.

Lições objetivas:

• Consolidação e teste dos conhecimentos dos alunos sobre o tema: "A soma dos ângulos de um triângulo";
• Prova das propriedades dos ângulos de um triângulo;
• A utilização desta propriedade na resolução dos problemas mais simples;
• A utilização de material histórico para o desenvolvimento da atividade cognitiva dos alunos;
• Incutir a habilidade de precisão na construção de desenhos.

Lições objetivas:

• Verifique a capacidade dos alunos para resolver problemas.

Plano de aula:

1. Triângulo;
2. Teorema da soma dos ângulos de um triângulo;
3. Exemplo de tarefa.

Triângulo.

Arquivo: Triângulo O.gif- o polígono mais simples com 3 vértices (cantos) e 3 lados; uma parte de um plano limitada por três pontos e três segmentos de linha conectando esses pontos em pares.
Três pontos no espaço que não estão em uma linha reta correspondem a um e apenas um plano.
Qualquer polígono pode ser dividido em triângulos - esse processo é chamado triangulação.
Há uma seção de matemática inteiramente dedicada ao estudo dos padrões de triângulos - Trigonometria.

Teorema da soma dos ângulos de um triângulo.

File:T.gif O teorema da soma dos ângulos do triângulo é um teorema clássico da geometria euclidiana que afirma que a soma dos ângulos de um triângulo é 180°.

Prova" :

Seja Δ ABC. Vamos traçar uma linha paralela a (AC) através do vértice B e marcar o ponto D nele de modo que os pontos A e D fiquem em lados opostos da linha BC. Então o ângulo (DBC) e o ângulo (ACB) são iguais como cruzes internas situadas nas linhas paralelas BD e AC e na secante (BC). Então a soma dos ângulos do triângulo nos vértices B e C é igual ao ângulo (ABD). Mas o ângulo (ABD) e o ângulo (BAC) no vértice A do triângulo ABC são internos de um lado com as linhas paralelas BD e AC e secante (AB), e sua soma é 180°. Portanto, a soma dos ângulos de um triângulo é 180°. O teorema foi provado.

Consequências.

O ângulo externo de um triângulo é igual à soma dos dois ângulos do triângulo que não são adjacentes a ele.

Prova:

Seja Δ ABC. O ponto D está na linha AC de modo que A está entre C e D. Então BAD é externo ao ângulo do triângulo no vértice A e A + BAD = 180°. Mas A + B + C = 180° e, portanto, B + C = 180° – A. Portanto, BAD = B + C. O corolário está provado.

Consequências.

Um ângulo externo de um triângulo é maior do que qualquer ângulo do triângulo que não seja adjacente a ele.

Tarefa.

O ângulo externo de um triângulo é o ângulo adjacente a qualquer ângulo desse triângulo. Prove que um ângulo externo de um triângulo é igual à soma de dois ângulos do triângulo que não são adjacentes a ele.
(Figura 1)

Decisão:

Seja Δ ABC ∠DAC externo (Fig.1). Então ∠DAC=180°-∠BAC (de acordo com a propriedade dos ângulos adjacentes), de acordo com o teorema da soma dos ângulos de um triângulo ∠B+∠C =180°-∠BAC. Destas igualdades obtemos ∠DAC=∠B+∠C

Fato interessante:

A soma dos ângulos de um triângulo :

Na geometria de Lobachevsky, a soma dos ângulos de um triângulo é sempre menor que 180. Na geometria de Euclides, é sempre igual a 180. Na geometria riemanniana, a soma dos ângulos de um triângulo é sempre maior que 180.

Da história da matemática:

Euclides (século III aC) na obra “Inícios” dá a seguinte definição: “Paralelas são linhas retas que estão no mesmo plano e, estendendo-se indefinidamente em ambas as direções, não se encontram em nenhum dos lados”.
Posidônio (século I aC) "Duas linhas retas no mesmo plano, equidistantes uma da outra"
O antigo cientista grego Pappus (século III aC) introduziu o símbolo de linhas paralelas - sinal =. Posteriormente, o economista inglês Ricardo (1720-1823) utilizou este símbolo como sinal de igual.
Somente no século 18 eles começaram a usar o símbolo de linhas paralelas - o sinal ||.
A ligação viva entre gerações não se interrompe um momento, todos os dias aprendemos a experiência acumulada pelos nossos antepassados. Os antigos gregos, com base em observações e experiência prática, tiraram conclusões, expressaram hipóteses e, em seguida, em reuniões de cientistas - simpósios (literalmente "festa") - tentaram fundamentar e provar essas hipóteses. Naquela época, formou-se a afirmação: "A verdade nasce na disputa".

Questões:

1. O que é um triângulo?
2. O que diz o teorema da soma do triângulo?
3. Qual é o ângulo externo do triângulo?