Desenhe um polígono em papel quadriculado. Por exemplo, como mostrado na Figura 1.

Vamos tentar calcular sua área agora. Como fazer isso? Provavelmente, a maneira mais fácil é dividi-lo em triângulos e retângulos de ângulo reto, cujas áreas já são fáceis de calcular e somar os resultados. O método que usei é simples, mas muito trabalhoso e, além disso, não é adequado para todos os polígonos.

Considere um polígono inteiro simples não degenerado (ou seja, ele é conectado - quaisquer dois de seus pontos podem ser conectados por uma curva contínua que está inteiramente contida nele, e todos os seus vértices têm coordenadas inteiras, seu limite é uma polilinha conectada sem auto-interseções, e tem um quadrado diferente de zero). Para calcular a área de tal polígono, você pode usar o seguinte teorema:

Teorema de Pick. Seja o número de pontos inteiros dentro do polígono, seja o número de pontos inteiros em seu limite e seja sua área. Então Fórmula de escolha:

Exemplo. Para o polígono da Figura 1 (pontos amarelos), (pontos azuis, não se esqueça dos vértices!), portanto, unidades quadradas.

Prova do teorema de Pick. Primeiro, observe que a fórmula de Pick é verdadeira para o quadrado unitário. De fato, neste caso temos

Considere um retângulo com lados sobre as linhas da treliça. Sejam os comprimentos de seus lados iguais a e. Temos neste caso e, de acordo com a fórmula Pick,

Considere agora um triângulo retângulo com pernas sobre os eixos coordenados. Tal triângulo é obtido a partir de um retângulo com lados e, considerado no caso anterior, cortando-o na diagonal. Deixe os pontos inteiros ficarem na diagonal. Então para este caso temos que

Agora considere um triângulo arbitrário. Ele pode ser obtido cortando vários triângulos retângulos e, possivelmente, um retângulo de um retângulo (veja as figuras 2 e 3). Como a fórmula de Pick é verdadeira tanto para um retângulo quanto para um triângulo retângulo, obtemos que também será verdadeira para um triângulo arbitrário.

Resta dar o último passo: passar de triângulos para polígonos. Qualquer polígono pode ser dividido em triângulos (por exemplo, por diagonais). Portanto, só precisamos provar que ao adicionar qualquer triângulo a um polígono arbitrário, a fórmula de Pick permanece verdadeira.

Deixe que o polígono e o triângulo tenham um lado comum. Suponha que a fórmula de Pick seja válida para, e provaremos que também será válida para o polígono obtido pela adição. Como e têm um lado comum, todos os pontos inteiros deste lado, exceto dois vértices, tornam-se pontos internos do novo polígono. Os vértices serão pontos de fronteira. Vamos denotar o número de pontos comuns por e obter

O número de pontos inteiros internos do novo polígono,

O número de pontos de limite para o novo polígono.

Destas igualdades obtemos

Como assumimos que o teorema é verdadeiro para e para separadamente, então

Assim, a fórmula de Pick está provada.

Esta fórmula foi descoberta pelo matemático austríaco Peak Georg Aleksandrov (1859 - 1943) em 1899. Além desta fórmula, Georg Pick descobriu os teoremas Pick, Pick - Julia, Pick - Nevalina, provou a desigualdade de Schwarz - Pick. NO Apêndice 1 você pode ver as tarefas não padronizadas que considerei para aplicar a fórmula Pick.

Fórmula de pico

1. Introdução

2. Fórmula de pico. Prova I.

Prova II.

A prova de Sh.

3. Tarefas.

4. A fórmula para a área de um polígono em termos das coordenadas dos vértices.

5. Tarefas.

6. Literatura

Fórmula de pico.

1. Introdução.

Extraímos sabedoria da história,

na poesia - sagacidade,

em matemática - insight.

F. Bacon

O enredo se desenrolará em um pedaço regular de papel quadriculado.

As linhas que percorrem os lados das células formam uma grade, e os vértices das células são os nós dessa grade. Vamos desenhar um polígono na folha com vértices nos nós e encontrar sua área.

Você pode procurá-lo de diferentes maneiras. Por exemplo, você pode cortar um polígono em formas bastante simples, encontrar suas áreas e somá-las.

Mas aqui estamos em um monte de problemas. A figura é facilmente dividida em retângulos, trapézios e triângulos, e sua área é calculada sem esforço.

Embora o polígono pareça bastante simples, será necessário muito trabalho para calcular sua área. E se o polígono parecesse mais sofisticado? Acontece que as áreas dos polígonos cujos vértices estão localizados nos nós da grade podem ser calculadas de maneira muito mais simples: existe uma fórmula que relaciona sua área com o número de nós situados dentro e na borda do polígono. Esta fórmula maravilhosa e simples é chamada de fórmula de Pick.

2. Fórmula de pico.

Os vértices de um polígono (não necessariamente convexos) estão localizados nos nós de uma rede inteira. Dentro dele estão os nós B da rede e na borda dos nós G. Vamos provar que sua área é B + – 1 (fórmula do pico).

Prova I.

Considere um polígono cujos vértices estão nos nós de uma rede inteira, ou seja, eles possuem coordenadas inteiras.

Dividimos o polígono em triângulos com vértices nos nós da rede, que não contêm nós dentro ou nos lados.

Indicar:

né o número de lados do polígono,

mé o número de triângulos com vértices nos nós da rede que não contêm nós dentro ou nos lados,

B é o número de nós dentro do polígono,

Г é o número de nós nos lados, incluindo os vértices.

As áreas de todos esses triângulos são iguais e iguais.

Portanto, a área do polígono é
.

180 0 m .

Agora vamos encontrar essa soma de uma maneira diferente.

A soma dos ângulos com um vértice em qualquer nó interno é 360 0 .

Então a soma dos ângulos com vértices em todos os nós internos é igual a 360 0 V.

A soma total dos ângulos nos nós dos lados, mas não nos vértices, é 180 0 (G - n).

A soma dos ângulos nos vértices do polígono é 180 0 ( n – 2) .

A soma total dos ângulos de todos os triângulos é 360 0 V + 180 0 (G - n) + 180 0 (n – 2).

Então 180 0 m\u003d 360 0 V + 180 0 (G - n) + 180 0 (n – 2),

180 0 m\u003d 360 0 V + 180 0 G - 180 0 n + 180 0 n– 180 0 2,

180 0 m\u003d 360 0 V + 180 0 G– 360 0,

= B + – 1 ,

de onde obtemos a expressão para a área S do polígono:

S= B + – 1 ,

conhecida como fórmula de Pick.

Na figura: V = 24, D = 9, portanto,S = 24 + – 1 = 27,5.

Encontre a área do primeiro polígono usando a fórmula Peak:

B = 28 (pontos verdes);

D = 20 (pontos azuis).

Obtemos, S =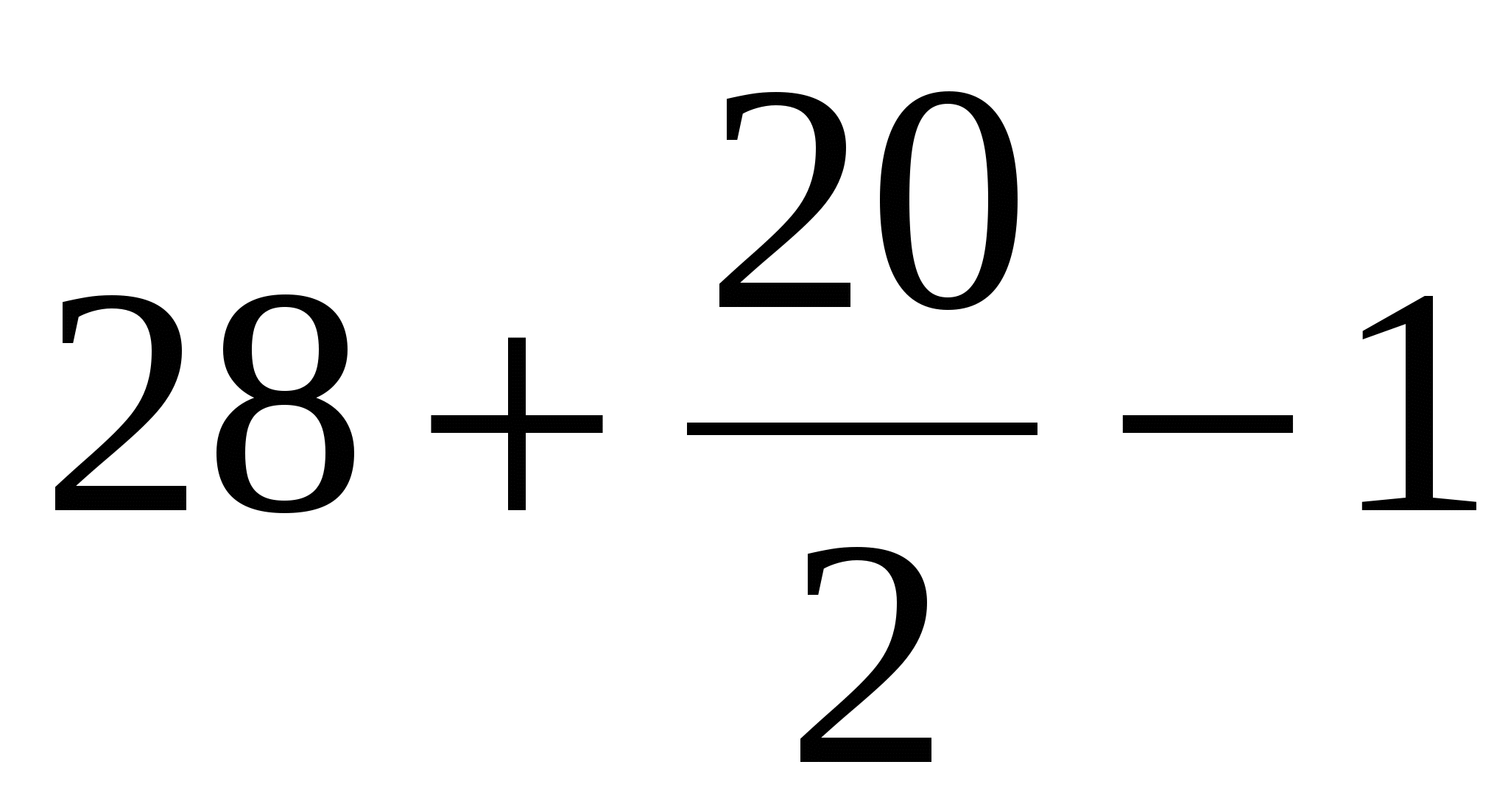
= 37 unidades quadradas

Prova II.

A cada polígono M com vértices nos nós de uma rede inteira, atribuímos o número f (M) =
, onde a soma é sobre todos os nós da rede pertencentes a M, e o ângulo é definido da seguinte forma: =
para um ponto interior de um polígono, =
para um ponto de fronteira que não seja um vértice, e – ângulo no vértice, se o nó dado for um vértice. É fácil ver que f(M) =
+
= B + – 1. Resta verificar se o número f (M) é igual à área do polígono M.

Seja o polígono M cortado nos polígonos M 1 e M 2 com vértices nos nós da rede. Então f(M) = f(M 1) + f(M 2), pois para cada nó os ângulos se somam. Portanto, se a fórmula de Pick é verdadeira para dois dos polígonos M, M 1 e M 2, então também é verdadeira para o terceiro.

Se M é um retângulo com lados p e q, direcionado ao longo das linhas da rede, então

f (M) = (p – 1)(q – 1) +
= pq.

Nesse caso, a fórmula de Pick é válida. Cortando o retângulo M diagonalmente em triângulos M 1 e M 2 e usando o fato de que f (M) = f (M 1) + f (M 2) ef (M 1) = f (M 2), é fácil para provar a validade da fórmula de Pick para qualquer triângulo retângulo com catetos direcionados ao longo das linhas da rede. Ao cortar vários desses triângulos de um retângulo, qualquer triângulo pode ser obtido.

Para completar a prova da fórmula de Pick, resta notar que qualquer polígono pode ser cortado em triângulos por diagonais que não se cruzam.

A prova de Sh.

A conexão entre a área de uma figura e o número de nós que se enquadram nessa figura é especialmente clara no caso de um retângulo.

Deixar ABCD- um retângulo com vértices nos nós e lados seguindo as linhas da grade.

Denotado por NO o número de nós que se encontram dentro do retângulo, e através Gé o número de nós em seu limite. Mova a grade meia célula para a direita e meia célula para baixo.

Então o território do retângulo pode ser "distribuído" entre os nós da seguinte forma: cada um dos NO nós "controlam" toda a célula da grade deslocada, cada um dos G- 4 nós de não canto de limite - metade da célula e cada um dos pontos de canto - um quarto da célula. Portanto, a área do retângulo S é

Então, para retângulos com vértices em nós e lados seguindo linhas de grade, estabelecemos a fórmula

Vamos provar que esta fórmula é verdadeira não apenas para retângulos, mas também para polígonos arbitrários com vértices nos nós da grade.

Denotado por S m área do polígonoM com vértices em nós, e atravésP m - valor
, OndeNO m é o número de nós dentroM, uma G m é o número de nós na fronteira. Então a fórmula de Pick pode ser escrita como
.

Dividimos a prova da fórmula em várias etapas.

Passo 1.

Se polígonoM com vértices em nós de grade cortados em 2 polígonosM 1 e M 2 , também tendo vértices apenas nos nós da grade, então
. Deixe o polígonoM corte em polígonosM 1 e M 2 com vértices em nós por um segmento AB. Todos os nós, exceto aqueles que caem no segmentoAB, dar a mesma contribuição para as partes esquerda e direita da fórmula. Considere os nós do segmento AB.

Se tal nó estiver entre A e B (por exemplo, C), então para um polígonoM é interno, e para polígonosM 1 e M 2 - fronteira. Assim, sua contribuição paraP m é igual a 1, e em cada uma das expressões
e
– 0,5 cada, ou seja, as contribuições de tal nó paraP m e
são iguais.

Considere os nós A e B. Eles são limites tanto para M, e para M 1 , M 2 .

Portanto, a contribuição de cada um desses nós paraP m é 0,5 a
- unidade. Isso significa que a contribuição total dos nós A e B paraP m é igual a 1, que é 1 a menos que sua contribuição para
. Mas
, uma .

Da "contribuição" total de todos os nós P m 1 é subtraído de
2 é subtraído, e isso compensa a diferença nas contribuições dos nós A e B.

Então,
.

Passo 2

Se polígono M com vértices nos nós da grade cortados em dois polígonos M 1 e M 2 (também com vértices em nós) e a fórmula é verdadeira para dois dos polígonos MILÍMETROS 1 , M 2 , então também é verdadeiro para o terceiro polígono.

Seja, por exemplo, verdadeiro paraM 1 e M 2 , isso é
. Então (no primeiro passo), mas em primeiro passo), a última expressão é igual aP m , e igualdade
e há a fórmula Pick.

etapa 3

Vamos provar a fórmula de Pick para um triângulo retângulo com vértices nos nós da grade e pernas nas linhas da grade.

Triângulo abc construir para um retângulo ABCD .

Para retângulos, a fórmula de Pick está correta: S ABCD = P ABCD . De acordo com o primeiro passo P ABCD = P abc + P ACD , P abc = P ACD , assim P ABCD = 2P abc . Mas S ABCD = 2 S abc . É por isso S abc = P abc .

Passo 4

A fórmula de Pick está correta para um triângulo arbitrário com vértices nos nós da grade.

Tendo examinado a figura, é fácil entender: qualquer triângulo pode ser obtido “cortando” de algum retângulo com lados correndo ao longo das linhas da grade, vários retângulos e triângulos retângulos com pernas nas linhas da grade. E como a fórmula de Pick é verdadeira para retângulos e triângulos retângulos, então (lembre-se do passo 2) também é verdadeira para o triângulo original.

Nós provamos que se um polígono pode ser cortado em triângulos com vértices nos nós da grade, então a fórmula de Pick é verdadeira para ele.

3. Tarefas.

Encontre a área das figuras:

1
.

B=9

G = 4

B=9

G = 5

Calculando a área de uma figura.

Escolha o método

O trabalho de um aluno da escola secundária 5B MBOU nº 23 em Irkutsk

Balsukova Alexandra

Responsável: Khodyreva T.G.

2014

Calculando a área de uma figura. Escolha o método

Objeto de estudo : tarefas em papel quadriculado

Objeto de estudo : problemas para calcular a área de um polígono em papel quadriculado, métodos e técnicas para resolvê-los.

Métodos de pesquisa Palavras-chave: comparação, generalização, analogia, estudo da literatura e recursos da Internet, análise da informação.

Propósito do estudo:

escolha as informações principais, interessantes e compreensíveis

Analisar e organizar as informações recebidas

Encontre diferentes métodos e técnicas para resolver problemas em papel quadriculado

verifique as fórmulas para calcular as áreas de formas geométricas usando a fórmula Peak

Criar uma apresentação eletrônica do trabalho para apresentar o material coletado

A geometria é a ferramenta mais poderosa para o refinamento de nossas faculdades mentais e nos permite pensar e raciocinar corretamente.

(G. Galileu)

Relevância do tema

A paixão pela matemática geralmente começa com o pensamento sobre um problema. Assim, ao estudar o tópico "Áreas de polígonos", surge a questão de saber se existem tarefas diferentes das tarefas consideradas no livro didático. Tais tarefas incluem tarefas em papel quadriculado. Qual é a peculiaridade de tais problemas, existem métodos e técnicas especiais para resolver problemas em papel quadriculado. Em uma aula de matemática, o professor nos apresentou um método interessante para calcular polígonos. Comecei a estudar a literatura, recursos da Internet sobre este tema. Parece que coisas fascinantes podem ser encontradas em um plano quadriculado, isto é, em um pedaço de papel sem fim, alinhado em quadrados idênticos. Acontece que as tarefas associadas ao papel quadriculado são bastante diversas. Aprendi a calcular as áreas dos polígonos desenhados em um papel quadriculado. Para muitas tarefas no papel em uma gaiola não existe uma regra geral de resolução, métodos e técnicas específicas. Esta é sua propriedade que determina seu valor para o desenvolvimento não de uma habilidade ou habilidade educacional específica, mas em geral a capacidade de pensar, refletir, analisar, procurar analogias, ou seja, essas tarefas desenvolvem habilidades de pensamento em seu sentido mais amplo.

E também aprendi que tais tarefas são consideradas nos materiais de controle e medição do GIA e do Exame Estadual Unificado. Portanto, considero o estudo deste material útil para sua aplicação não apenas no processo educacional adicional, mas também na resolução de problemas não padronizados das Olimpíadas.

2.O conceito de área

Quadrado- característica numérica de uma figura geométrica bidimensional, mostrando o tamanho dessa figura. Historicamente, o cálculo de área era chamado de . Uma figura que tem área é chamada quadratura .

A área de uma figura plana em termos de geometria

1. Quadrado- a medida de uma figura plana em relação à figura padrão, que é um quadrado com um lado igual a um comprimento.

2. Quadrado- uma característica numérica atribuída a figuras planas de uma determinada classe (por exemplo, polígonos). A área de um quadrado com um lado igual a uma unidade de comprimento, tomada igual a uma unidade de área

3. Quadrado- um valor positivo, cujo valor numérico tem as seguintes propriedades:

 Figuras iguais têm áreas iguais;

 Se uma figura for dividida em partes que são figuras simples (ou seja, aquelas que podem ser divididas em um número finito de triângulos planos), a área dessa figura é igual à soma das áreas de sua peças;

 A área de um quadrado com um lado igual à unidade de medida é igual a um.

Assim, podemos concluir que a área não é um valor específico, mas apenas dá alguma característica condicional de uma figura plana. Para encontrar a área de uma figura arbitrária, é necessário determinar quantos quadrados com um lado igual a um comprimento ela contém. Por exemplo, vamos pegar um retângulo no qual um centímetro quadrado cabe exatamente 6 vezes. Isso significa que a área do retângulo é de 6 cm2.

A escolha da área de um quadrado com lado igual à unidade de medida como unidade mínima de medida para todas as áreas não é acidental. Este é o resultado de um acordo entre as pessoas que surgiu no curso da seleção secular "natural". Além disso, houve outras propostas para uma unidade de medida. Assim, por exemplo, foi proposto tomar a área de um triângulo equilátero como tal unidade (ou seja, qualquer figura plana poderia ser representada como uma “soma” de um certo número de triângulos equiláteros), o que levaria a um alteração na representação numérica das áreas.

Assim, fórmulas para calcular áreas apareceram na matemática e não foram imediatamente percebidas por uma pessoa - isso muitos cientistas que vivem em diferentes épocas e diferentes países. (Fórmulas erradas não encontraram lugar na ciência e caíram no esquecimento). As verdadeiras fórmulas foram suplementadas, corrigidas e fundamentadas ao longo de milhares de anos, até chegarem até nós em sua forma moderna.

É claro medição de área consiste em comparar a área de uma determinada figura com a área de uma figura tomada como unidade de medida. Como resultado da comparação, um certo número é obtido - o valor numérico da área da figura fornecida. Esse número mostra quantas vezes a área de uma determinada figura é maior (ou menor) que a área da figura, tomada como unidade de área.

T Assim, podemos concluir que a área é uma grandeza artificial, historicamente introduzida pelo homem para medir alguma propriedade de uma figura plana. A necessidade de inserir tal valor deveu-se à necessidade crescente de saber qual é o tamanho deste ou daquele território, quanto grão é necessário para semear um campo ou calcular a superfície do piso para decoração de azulejos ornamentais.

Fórmula de pico

Para estimar a área de um polígono em papel quadriculado, basta calcular quantas células esse polígono cobre (tomamos a área da célula como uma unidade). Mais precisamente, seS é a área do polígono, B é o número de células que estão inteiramente dentro do polígono e G é o número de células que têm um interior. Consideraremos apenas esses polígonos, cujos vértices estão nos nós do papel quadriculado - naqueles em que as linhas de grade do polígono cruzam pelo menos um ponto comum.

A área de qualquer triângulo desenhado em papel quadriculado pode ser facilmente calculada representando-a como a soma ou diferença das áreas de triângulos retângulos e retângulos cujos lados seguem as linhas de grade que passam pelos vértices do triângulo desenhado.

Para calcular a área de tal polígono, você pode usar o seguinte teorema:

Teorema . Deixar - o número de pontos inteiros dentro do polígono, - o número de pontos inteiros em seu limite, - sua área. EntãoFórmula de escolha:

Exemplo. Para o polígono da figuraeu = 7 (pontos vermelhos), 9 (pontos verdes), entãoS = 7+ 9/2 -1 = 10,5 unidades quadradas.

Teorema de Pick- resultado clássico e .

A área de um triângulo com vértices nos nós e não contendo nós dentro ou nos lados (exceto os vértices) é igual a 1/2. Este fato.

3. História

A fórmula de Pick foi descoberta pelo matemático austríaco Georg Alexander (1859-1942) em . Aos 16 anos, Georg terminou a escola e entrou. Aos 20 anos recebeu o direito de ensinar física e matemática. Em 1884 Peak foi para para . Lá ele conheceu outro aluno de Klein,. Mais tarde, em 1885, voltou aonde passou o resto de sua carreira científica.

Georg Pick era amigo de Einstein. Pick e Einstein não apenas compartilhavam interesses científicos, mas também eram apaixonados por música. Pick, que tocava em um quarteto formado por professores universitários, apresentou Einstein às sociedades científicas e musicais de Praga.

O círculo de interesses matemáticos de Peak era extremamente amplo. Em particular, ele tem mais de 50 artigos científicos. O teorema de Pick, descoberto por ele em 1899, era amplamente conhecido por calcular a área de um polígono. Na Alemanha, este teorema está incluído nos livros escolares.

4.Aplicações da fórmula de Pick

A fórmula Pick é usada não apenas para calcular as áreas dos polígonos, mas também para resolver muitos problemas do nível das Olimpíadas.

Alguns exemplos de uso da fórmula de Pick ao resolver problemas:

1) O rei do xadrez deu a volta no tabuleiro de 8 × 8 células, tendo visitado cada

campo home exatamente uma vez e com o último movimento retornando ao original

campo. Uma linha quebrada ligando em série os centros dos campos que

o rei passou, não tem auto-interseções. Que área pode

limitar esta linha quebrada? (O lado da célula é 1.)

Segue-se imediatamente da fórmula Pick que a área limitada pelo lo-

mana é 64/2 − 1 = 31; aqui os nós da rede são os centros 64

campos e, por suposição, todos eles estão no limite do polígono. Então

Assim, embora existam muitas dessas "trajetórias" do rei, mas todas elas

polígonos limite de áreas iguais.

Tarefas dos materiais de controle e medição do GIA e do Exame Estadual Unificado

Tarefa B3

Encontre a área da figura representada em papel quadriculado com um tamanho de célula de 1 cm 1 cm (veja a Fig.). Dê sua resposta em centímetros quadrados.

4. Conclusão

No processo de pesquisa, estudei literatura de referência, de ciência popular. Aprendi que o problema de encontrar a área de um polígono com vértices nos nós da grade inspirou o matemático austríaco Pick em 1899 a provar a maravilhosa fórmula de Pick.

Como resultado do meu trabalho, ampliei meus conhecimentos de resolução de problemas em papel quadriculado, determinei por mim mesmo a classificação dos problemas em estudo e me convenci de sua diversidade.

Aprendi a calcular as áreas dos polígonos desenhados em uma folha quadriculada.As tarefas consideradas têm um nível de dificuldade diferente - do simples ao olímpico. Todos podem encontrar entre elas tarefas de um nível de complexidade viável, a partir das quais será possível passar a resolver as mais difíceis.

Cheguei à conclusão de que o tema que me interessava é bastante multifacetado, as tarefas em papel quadriculado são diversas, os métodos e técnicas para resolvê-los também são diversos. Por isso, decidi continuar trabalhando nessa direção.

5. Literatura utilizada:

1. N. B. Vasil'ev, "Around the Pick formula", Kvant. - 1974. - Nº 12

2. Kokse Prasolov VV Tarefas em planimetria. - M.: MTsNMO, 2006.t e r G.S.M. Introdução à geometria. - M.: Nauka, 1966

3. Roslova L.O., Sharygin I.F. Medidas. - M.: Ed. "Mundo Aberto", 2005.

Recursos da Internet:

:

Feedback sobre o trabalho

“Cálculo das áreas de figuras planas. Método de escolha"

A consideração deste tópico aumentará a atividade cognitiva do aluno, que mais tarde nas aulas de geometria começará a ver a harmonia do desenho e deixará de perceber a geometria (e a matemática em geral) como uma ciência chata.

Revisado pelo professor de matemática

Khodyreva Tatyana Georgievna

Existe uma fórmula maravilhosa que permite contar área do polígono na grade de coordenadas quase sem erros. Não é nem uma fórmula, é real teorema. À primeira vista, pode parecer complicado. Mas é o suficiente para resolver algumas tarefas - e você entenderá como esse recurso é legal. Então vá em frente!

Vamos começar com uma nova definição:

Um nó de pilha de coordenadas é qualquer ponto que se encontra na interseção das linhas verticais e horizontais desta grade.

Designação:

Na primeira foto, os nós não estão marcados. O segundo tem 4 nós. Por fim, na terceira foto, todos os 16 nós estão marcados.

O que isso tem a ver com o problema B5? O fato é que os vértices do polígono em tais problemas sempre situam-se nos nós da rede. Como consequência, o seguinte teorema funciona para eles:

Teorema. Considere um polígono em uma grade de coordenadas cujos vértices estão nos nós dessa grade. Então a área do polígono é:

onde n é o número de nós dentro do polígono dado, k é o número de nós que se encontram em seu limite (nós de fronteira).

Como exemplo, considere um triângulo comum em uma grade de coordenadas e tente marcar os nós internos e limites.

A primeira foto mostra um triângulo comum. Na segunda figura, seus nós internos são marcados, cujo número é n = 10. Na terceira figura, os nós situados na borda são marcados, há k = 6 deles no total.

Talvez muitos leitores não entendam como contar os números n e k. Comece com nós internos. Tudo é óbvio aqui: pintamos o triângulo com um lápis e vemos quantos nós estão sombreados.

Com nós de limite, é um pouco mais complicado. borda poligonal - linha quebrada fechada, que intercepta a grade de coordenadas em muitos pontos. A maneira mais fácil é marcar algum ponto "inicial" e depois contornar o resto.

Os nós de fronteira serão apenas os pontos na polilinha em que eles se cruzam simultaneamente três linhas:

1. Na verdade, uma linha quebrada;
2. Linha de grade horizontal;
3. Linha vertical.

Vamos ver como tudo funciona em problemas reais.

Uma tarefa. Encontre a área de um triângulo se o tamanho da célula for 1 x 1 cm:

Primeiro, vamos marcar os nós que ficam dentro do triângulo, bem como em sua borda:

Acontece que existe apenas um nó interno: n = 1. Existem seis nós de fronteira: três coincidem com vértices triangulares, e mais três estão nas laterais. Total k = 6.

Agora calculamos a área usando a fórmula:

Isso é tudo! Problema resolvido.

Uma tarefa. Encontre a área de um quadrilátero representado em papel quadriculado com um tamanho de célula de 1 cm por 1 cm. Dê sua resposta em centímetros quadrados.

Novamente, marcamos os nós interno e limite. Existem n = 2 nós internos. Nós de fronteira: k = 7, dos quais 4 são vértices do quadrilátero, e mais 3 estão nas laterais.

Resta substituir os números n e k na fórmula da área:

Preste atenção no último exemplo. Este problema foi realmente proposto no trabalho de diagnóstico em 2012. Se você trabalhar de acordo com o esquema padrão, terá que fazer muitas construções adicionais. E pelo método dos nós, tudo é resolvido quase oralmente.

Nota importante sobre as áreas

Mas a fórmula não é tudo. Vamos reescrever um pouco a fórmula, trazendo os termos do lado direito a um denominador comum. Nós temos:

Os números n e k são o número de nós, são sempre inteiros. Portanto, o numerador inteiro também é um inteiro. Dividimos por 2, o que implica um fato importante:

A área é sempre expressa número inteiro ou fração. Além disso, no final da fração há sempre “cinco décimos”: 10,5; 17,5 etc

Assim, a área do problema B5 é sempre expressa como um inteiro ou uma fração da forma ***.5. Se a resposta for diferente, significa que um erro foi cometido em algum lugar. Tenha isso em mente quando você fizer o exame real de matemática!

Para usar a visualização de apresentações, crie uma conta do Google (conta) e faça login: https://accounts.google.com

Legendas dos slides:

Concluído por um aluno da escola secundária No. 7 8 "A" classe Yunosheva Ksenia Instrutor: Babina Natalya Alekseevna Salsk 2011 "Peak Formula"

Objetivos do trabalho: Descobrir a existência de outra, diferente do currículo escolar, fórmula para encontrar a área de um polígono reticulado. Áreas de aplicação da fórmula desejada.

Introdução. A educação matemática recebida nas escolas de educação geral é um componente essencial da educação geral e da cultura geral do homem moderno. Nesta fase, o sistema escolar é projetado para onze anos de educação. Todos os alunos ao final da décima primeira série terão que fazer o Exame Estadual Unificado, que mostrará o nível de conhecimento adquirido enquanto estudava na escola. Mas o currículo escolar nem sempre fornece as formas mais racionais de resolver quaisquer problemas. Por exemplo, olhando os resultados do Exame Estadual Unificado em 2010, fica claro que muitos alunos perdem pontos devido à tarefa B6. Comecei a descobrir como economizar tempo e resolver esse problema corretamente.

Tarefa B6. As figuras são representadas em papel quadriculado com células medindo 1 cm por 1 cm (ver figura). Encontre sua área em centímetros quadrados.

Então, para ainda resolver essa tarefa, preciso aplicar as fórmulas para encontrar a área, que estudamos no 8º ano. Mas vai levar muito tempo, e preciso responder a pergunta o mais rápido possível, porque o tempo para o exame é estritamente limitado. Portanto, depois de fazer pesquisas, descobri que existe o teorema de Pick, que não é estudado no currículo escolar, mas que me ajudará a lidar com a tarefa mais rapidamente.

Referência histórica. Georg Alexander Pick (10 de agosto de 1859 - 26 de julho de 1942) foi um matemático austríaco. Ele morreu no campo de concentração de Terezin. É conhecido hoje por causa da fórmula de Pick para determinar a área de uma rede de polígonos. Ele publicou sua fórmula em um jornal em 1899, tornou-se popular quando Hugo Steinhaus a incluiu em uma edição de 1969 da Mathematical Pictures. Pick estudou na Universidade de Viena e completou seu doutorado em 1880. Após receber seu doutorado, foi nomeado assistente de Ernest Mach na Universidade Scherl-Ferdinand, em Praga. Ele se tornou um professor lá em 1881. Tirando uma licença da universidade em 1884, ele começou a trabalhar com Felix Klein na Universidade de Leipzig. Ele permaneceu em Praga até sua aposentadoria em 1927, quando retornou a Viena. Pick presidiu o comitê da (então) Universidade Alemã de Praga que nomeou Albert Einstein professor de física matemática em 1911. Pick foi eleito membro da Academia Tcheca de Ciências e Artes, mas foi expulso após a tomada de Praga pelos nazistas. Depois de se aposentar em 1927, Pick retornou a Viena, cidade onde nasceu. Após o Anschluss, quando os nazistas entraram na Áustria em 12 de março de 1938, Pieck retornou a Praga. Em março de 1939, os nazistas invadiram a Tchecoslováquia. Georg foi enviado ao campo de concentração de Terezin em 13 de julho de 1942. Ele morreu duas semanas depois.

Teorema de Pick. O teorema de Pick é um resultado clássico da geometria combinatória e da geometria dos números. A área de um polígono com vértices inteiros é igual à soma B + D/2 - 1, onde B é o número de pontos inteiros dentro do polígono e D é o número de pontos inteiros na fronteira do polígono.

Uma prova lisonjeira do teorema de Pick. Qualquer tal polígono pode ser facilmente dividido em triângulos com vértices nos nós da rede, não contendo nós dentro ou nos lados. Pode-se mostrar que as áreas de todos esses triângulos são iguais e iguais a 1/2 e, portanto, a área do polígono é igual à metade de seu número T. Para encontrar esse número, denotamos por n o número de lados do polígono, por i - o número de nós dentro dele e por b - o número de nós nos lados, incluindo os vértices. A soma total dos ângulos de todos os triângulos é πТ. Agora vamos encontrar essa soma de uma maneira diferente. A soma dos ângulos com um vértice em qualquer nó interno é 2 π , ou seja, a soma total desses ângulos é 2 π i ; a soma total dos ângulos nos nós dos lados, mas não nos vértices, é (b - n) π, e a soma dos ângulos nos vértices do polígono é (n - 2) π. Assim, π T \u003d 2i π + (b - n) π + (n - 2) π, a partir do qual obtemos uma expressão para a área S de um polígono, conhecida como fórmula de Pick. Por exemplo, na figura b = 9, i = 24 e, portanto, a área do polígono é 27,5.

Inscrição. Então, de volta à tarefa B6. Agora, conhecendo a nova fórmula, podemos encontrar facilmente a área desse quadrilátero. Como B é 5; D - 14, depois 5 + 14: 2-1 \u003d 11 (cm ao quadrado) A área desse quadrilátero é de 11 cm ao quadrado.

Usando a mesma fórmula, podemos encontrar a área de um triângulo. Desde B-14, G-10, então 14+10:2-1=18 (cm²) A área deste triângulo é 18 cm².

Se B-9, D-12, então: 9+12:2-1=14 (cm ao quadrado) A área deste quadrilátero é 14 cm ao quadrado.

Escopo da fórmula. Além do fato de que a fórmula é usada em vários tipos de exames, trabalhos e assim por diante, ela acompanha todo o mundo ao nosso redor.

De acordo com a fórmula de Peak S = B + ½ G-1 1) corpo B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) cauda B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24

De acordo com a fórmula de Peak S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10,5-1 \u003d 45,5

Conclusão. Como resultado, cheguei à conclusão de que existem muitas maneiras diferentes de resolver problemas da área que não são estudados no currículo escolar e mostrei-os usando a fórmula Pick como exemplo.

Diretório. Um polígono sem auto-interseções é chamado de polígono de rede se todos os seus vértices estiverem em pontos com coordenadas inteiras (no sistema de coordenadas cartesianas). Um ponto no plano de coordenadas é chamado de inteiro se ambas as suas coordenadas são inteiras.