Функция МЕДИАНА в Excel используется для анализа диапазона числовых значений и возвращает число, которое является серединой исследуемого множества (медианой). То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.

Примеры использования функции МЕДИАНА в Excel

При исследовании возрастных групп студентов использовались данные случайно выбранной группы учащихся в ВУЗе. Задача – определить срединный возраст студентов.

Исходные данные:

Формула для расчета:

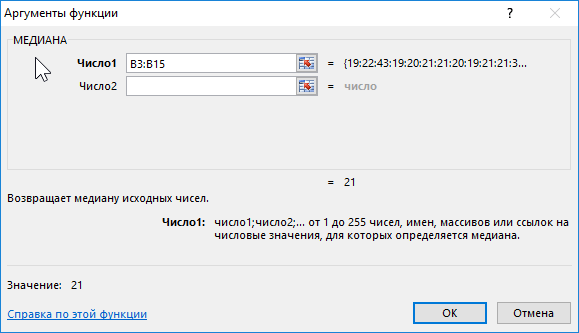
Описание аргумента:

• B3:B15 – диапазон исследуемых возрастов.

Полученный результат:

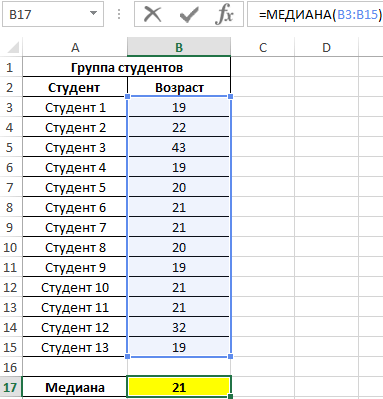
То есть в группе есть студенты, возраст которых меньше 21 года и больше этого значения.



Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения

Во время вечернего обхода в больнице каждому больному была замерена температура тела. Продемонстрировать целесообразность использования параметра медиана вместо среднего значения для исследования ряда полученных значений.

Исходные данные:

Формула для нахождения среднего значения:

Формула для нахождения медианы:

Как видно из показателя среднего значения, в среднем температура у пациентов выше нормы, однако это не соответствует действительности. Медиана показывает, что как минимум у половины пациентов наблюдается нормальная температура тела, не превышающая показатель 36,6.

Внимание! Еще одним методом определения центральной тенденции является мода (наиболее часто встречающееся значение в исследуемом диапазоне). Чтобы определить центральную тенденцию в Excel следует использовать функцию МОДА. Обратите внимание: в данном примере значения медианы и моды совпадают:

То есть срединная величина, делящая одно множество на подмножества меньших и больших значений также является и наиболее часто встречающимся значением в множестве. Как видно, у большинства пациентов температура составляет 36,6.

Пример расчета медианы при статистическом анализе в Excel

Пример 3. В магазине работают 3 продавца. По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.

Исходная таблица данных:

Для характеристики эффективности будем использовать сразу три показателя: среднее значение, медиана и мода. Определим их для каждого работника с использованием формул СРЗНАЧ, МЕДИАНА и МОДА соответственно:

Для определения степени разброса данных используем величину, которая является суммарным значением модуля разницы среднего значения и моды, среднего значения и медианы соответственно. То есть коэффициент x=|av-med|+|av-mod|, где:

• av – среднее значение;
• med – медиана;
• mod – мода.

Рассчитаем значение коэффициента x для первого продавца:

Аналогично проведем расчеты для остальных продавцов. Полученные результаты:

Определим продавца, которому будет выдана премия:

Примечание: функция НАИМЕНЬШИЙ возвращает первое минимальное значение из рассматриваемого диапазона значений коэффициента x.

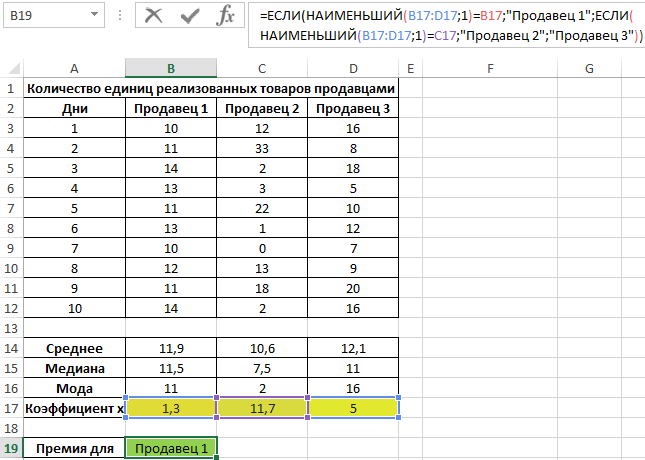
Коэффициент x является некоторой количественной характеристикой стабильности работы продавцов, которую ввел экономист магазина. С его помощью удалось определить диапазон с наименьшими отклонениями значений. Этот способ демонстрирует, как можно использовать сразу три метода определения центральной тенденции для получения наиболее достоверных результатов.

Особенности использования функции МЕДИАНА в Excel

Функция имеет следующий синтаксис:

МЕДИАНА(число1; [число2];...)

Описание аргументов:

• число1 – обязательный аргумент, характеризующий первое числовое значение, содержащееся в исследуемом диапазоне;
• [число2] – необязательный второй (и последующие аргументы, всего до 255 аргументов), характеризующий второе и последующие значения исследуемого диапазона.

Примечания 1:

1. При расчетах удобнее передавать сразу весь диапазон исследуемых значений вместо последовательного ввода аргументов.
2. В качестве аргументов принимаются данные числового типа, имена, содержащие числа, данные ссылочного типа и массивы (например, =МЕДИАНА({1;2;3;5;7;10})).
3. При расчете медианы учитываются ячейки, содержащие пустые значения или логические ИСТИНА, ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно. Например, результат выполнения функции с логическими значениями в аргументах (ИСТИНА;ЛОЖЬ) эквивалентен результату выполнения с аргументами (1;0) и равен 0,5.
4. Если один или несколько аргументов функции принимают текстовые значения, которые не могут быть преобразованы в числовые, или содержат коды ошибок, результатом выполнения функции будет код ошибки #ЗНАЧ!.
5. Для определения медианы выборки могут быть использованы другие функции Excel: ПРОЦЕНТИЛЬ.ВКЛ, КВАРТИЛЬ.ВКЛ, НАИБОЛЬШИЙ Примеры использования:

• =ПРОЦЕНТИЛЬ.ВКЛ(A1:A10;0,5), поскольку по определению медиана – 50-я процентиль.
• =КВАРТИЛЬ.ВКЛ(A1:A10;2), так как медиана – 2-я квартиль.
• =НАИБОЛЬШИЙ(A1:A9;СЧЁТ(A1:A9)/2), но только если количество чисел в диапазоне является нечетным числом.

Примечания 2:

1. Если в исследуемом диапазоне все числа распределены симметрично относительно среднего значения, среднее арифметическое и медиана для данного диапазона будут эквивалентны.
2. При больших отклонениях данных в диапазоне («разбросе» значений) медиана лучше отражает тенденцию распределения значений, чем среднее арифметическое. Отличным примером является использование медианы для определения реального уровня зарплат у населения государства, в котором чиновники получают на порядок больше обычных граждан.
3. Диапазон исследуемых значений может содержать:

• Нечетное количество чисел. В этом случае медианой будет являться единственное число, разделяющее диапазон на два подмножества больших и меньших значений соответственно;
• Четное количество чисел. Тогда медиана вычисляется как среднее арифметическое для двух числовых значений, разделяющих множество на два указанных выше подмножества.

КОНТРОЛЬНАЯ РАБОТА

На тему: "Мода. Медиана. Способы их расчета"

Введение

Средние величины и связанные с ними показатели вариации играют в статистике очень большую роль, что обусловлено предметом ее изучения. Поэтому данная тема является одной из центральных в курсе.

Средняя является очень распространенным обобщающим показателям в статистике. Это объясняется тем, что только с помощью средней можно охарактеризовать совокупность по количественно варьирующему признаку. Средней величиной в статистике называется обобщающая характеристика совокупности однотипных явлений по какому-либо количественно варьирующему признаку. Средняя показывает уровень этого признака, отнесенный к единице совокупности.

Изучая общественные явления и стремясь выявить их характерные, типичные черты в конкретных условиях места и времени, статистики широко используют средние величины. С помощью средних можно сравнивать между собой различные совокупности по варьирующим признакам.

Средние, которые применяются в статистике, относятся к классу степенных средних. Из степенных средних наиболее часто применяется средняя арифметическая, реже – средняя гармоническая; средняя гармоническая применяется только при исчислении средних темпов динамики, а средняя квадратическая – только при исчислении показателей вариации.

Средняя арифметическая есть частное от деления суммы вариант на их число. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака у отдельных ее единиц. Средняя арифметическая – наиболее распространенный вид средних, так как она соответствует природе общественных явлений, где объем варьирующих признаков в совокупности чаще всего образуется именно как сумма значений признака у отдельных единиц совокупности.

По своему определяющему свойству средняя гармоническая должна применяться тогда, когда общий объем признака образуется как сумма обратных значений вариант. Ее применяют тогда, когда в зависимости от имеющего материала веса приходиться не умножать, а делить на варианты или, что то же самое, умножать на обратное их значение. Средняя гармоническая в этих случаях – это величина обратная средней арифметической из обратных значений признака.

К средней гармонической следует прибегать в тех случаях, когда в качестве весов применяются не единицы совокупности – носители признака, а произведения этих единиц на значение признака.

1. Определение моды и медианы в статистике

Средние арифметическая и гармоническая являются обобщающими характеристиками совокупности по тому или иному варьирующему признаку. Вспомогательными описательными характеристиками распределения варьирующего признака являются мода и медиана.

Модой в статистике называется величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.

Медианной в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.

Мода и медиана в отличии от степенных средних являются конкретными характеристиками, их значение имеет какая-либо конкретная варианта в вариационном ряду.

Мода применяется в тех случаях, когда нужно охарактеризовать наиболее часто встречающуюся величину признака. Если надо, например, узнать наиболее распространенный размер заработной платы на предприятии, цену на рынке, по которой было продано наибольшее количество товаров, размер ботинок, пользующийся наибольшим спросом у потребителей, и т.д., в этих случаях прибегают к моде.

Медиана интересна тем, что показывает количественную границу значение варьирующего признака, которую достигла половина членов совокупности. Пусть средняя заработная плата работников банка составила 650000 руб. в месяц. Эта характеристика может быть дополнена, если мы скажем, что половина работников получила заработную плату 700000 руб. и выше, т.е. приведем медиану. Мода и медиана являются типичными характеристиками в тех случаях, когда взяты совокупности однородные и большой численности.

2. Нахождение моды и медианы в дискретном вариационном ряду

Найти моду и медиану в вариационном ряду, где значения признака заданы определенными числами, не представляет большой трудности. Рассмотрим таблицу 1. с распределение семей по числу детей.

Таблица 1. Распределение семей по числу детей

Очевидно, в этом примере модой будет семья, имеющая двоих детей, так как этому значению варианты соответствует наибольшее число семей. Могут быть распределения, где все варианты встречаются одинаково часто, в этом случае моды нет или, иначе, можно сказать, что все варианты одинаково модальны. В других случаях не одна, а две варианты могут быть наибольшей частоты. Тогда будет две моды, распределение будет бимодальным. Бимодальные распределения могут указывать на качественную неоднородность совокупности по исследуемому признаку.

Чтобы найти медиану в дискретном вариационном ряд, нужно сумму частот разделить пополам и к полученному результату добавить ½. Так, в распределении 185 семьи по числу детей медианой будет: 185/2 + ½ = 93, т.е. 93-я варианта, которая делит упорядоченный ряд пополам. Каково же значение 93-ей варианты? Для того чтобы это выяснить, нужно накапливать частоты, начиная, от наименьшей варианты. Сумма частот 1-й и 2-й вариант равна 40. Ясно, что здесь 93 варианты нет. Если прибавить к 40 частоту 3-й варианты, то получим сумму, равную 40 + 75 = 115. Следовательно, 93-я варианта соответствует третьему значению варьирующего признака, и медианой будет семья, имеющая двоих детей.

Мода и медиана в данном примере совпали. Если бы у нас была четная сумма частот (например, 184), то, применяя указанную выше формулу, получим номер медианной варианты, 184/2 + ½ =92,5. Поскольку варианты с дробным номером не существует, полученный результат указывает, что медиана находится посередине между 92 и 93 вариантами.

3. Расчет моды и медианы в интервальном вариационном ряду

Описательный характер моды и медианы связан с тем, что в них не погашаются индивидуальные отклонения. Они всегда соответствуют определенной варианте. Поэтому мода и медиана не требуют для своего нахождения расчетов, если известны все значения признака. Однако в интервальном вариационном ряду для нахождения приближенного значения моды и медианы в пределах определенного интервала прибегают к расчетам.

Для расчета определенного значения модальной величины признака, заключенного в интервале, применяют формулу:

М о = Х Мо + i Мо *(f Мо – f Мо-1)/((f Мо – f Мо-1) + (f Мо – f Мо+1)),

Где Х Мо – минимальная граница модального интервала;

i Мо – величина модального интервала;

f Мо – частота модального интервала;

f Мо-1 – частота интервала, предшествующего модальному;

f Мо+1 – частота интервала, следующего за модальным.

Покажем расчет моды на примере, приведенном в таблице 2.

Таблица 2. Распределение рабочих предприятия по выполнению норм выработки

Чтобы найти моду, первоначально определим модальный интервал данного ряда. Из примера видно, что наибольшая частота соответствует интервалу, где варианта лежит в пределах от 100 до 105. Это и есть модальный интервал. Величина модального интервала равна 5.

Подставляя числовые значения из таблицы 2. в указанную выше формулу, получим:

М о = 100 + 5 * (104 -12)/((104 – 12) + (104 – 98)) = 108,8

Смысл этой формулы заключается в следующем: величину той части модального интервала, которую нужно добавить к его минимальной границе, определяют в зависимости от величины частот предшествующего и последующего интервалов. В данном случае к 100 прибавляем 8,8, т.е. больше половины интервала, потому что частота предшествующего интервала меньше частоты последующего интервала.

Исчислим теперь медиану. Для нахождения медианы в интервальном вариационном ряду определяем сначала интервал, в котором она находится (медианный интервал). Таким интервалом будет такой, комулятивная частота которого равна или превышает половину суммы частот. Комулятивные частоты образуются путем постепенного суммирования частот, начиная от интервала с наименьшим значением признака. Половина суммы частот у нас равна 250 (500:2). Следовательно, согласно таблицы 3. медианным интервалом будет интервал со значением заработной платы от 350000 руб. до 400000 руб.

Таблица 3. Расчет медианы в интервальном вариационном ряду

До этого интервала сумма накопленных частот составила 160. Следовательно, чтобы получить значение медианы, необходимо прибавить еще 90 единиц (250 – 160).

Медианой Ме называют такое значение признака, которое приходится на середину ранжированного ряда и делит его на две равные по числу единиц части. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака, превышающие медиану, другая – меньше медианы.

Медиану используют вместо средней арифметической, когда крайние варианты ранжированного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.

В дискретном вариационном ряду, содержащем нечетное число единиц, медиана равна варианте признака, имеющей номер :
,
где N – число единиц совокупности.
В дискретном ряду, состоящем из четного числа единиц совокупности, медиана определяется как средняя из вариант, имеющих номера и :
.
В распределении рабочих по стажу работы медиана равна средней из вариант, имеющих в ранжированном ряду номера 10: 2 = 5 и 10: 2 + 1 = 6. Варианты пятого и шестого признака равны 4 годам, таким образом
года
При вычислении медианы в интервальном ряду сначала находят медианный интервал , (т. е. содержащий медиану), для чего используют накопленные частоты или частости. Медианным является интервал, накопленная частота которого равна или превышает половину всего объема совокупности. Затем значение медианы рассчитывается по формуле:
,
где – нижняя граница медианного интервала;
– ширина медианного интервала;
– накопленная частота интервала, предшествующего медианному;
– частота медианного интервала.
Рассчитаем медиану ряда распределения рабочих по размеру зарплаты (см. лекцию «Сводка и группировка статистических данных»).
Медианным является интервал заработной платы 800-900 грн., поскольку его кумулятивная частота равна 17, что превышает половину суммы всех частот (). Тогда
Ме=800+100грн.
Полученное значение говорит о том, половина рабочих имеют заработную плату ниже 875 грн., но это выше среднего ее размера.
Для определения медианы можно вместо кумулятивных частот использовать кумулятивные частости .
Медиана, как и мода, не зависит от крайних значений вариант, поэтому также применяется для характеристики центра в рядах распределения с неопределенными границами.
Свойство медианы :сумма абсолютных величин отклонений вариант от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической):

Это свойство медианы используется на транспорте при проектировании расположения трамвайных и троллейбусных остановок, бензоколонок, сборочных пунктов и т..д.
Пример. На шоссе длиной 100 км расположено 10 гаражей. Для проектирования строительства бензоколонки были собраны данные о числе предполагаемых ездок на заправку по каждому гаражу.
Таблица 2 – Данные о количестве ездок на заправку по каждому гаражу.

Нужно поставить бензоколонку так, чтобы общий пробег автомашин на заправку был наименьшим.
Вариант 1. Если бензоколонку поставить в середине шоссе, т. е. на 50-ом километре (центр диапазона изменения признака), то пробеги с учетом числа ездок составят:
а) в одном направлении:
;
б) в противоположном:
;
в) общий пробег в оба направления: .

Вариант 2. Если бензоколонку поставить на среднем участке шоссе, определенном по формуле средней арифметической с учетом числа ездок:

Медиану можно определить графически, по кумуляте (см. лекцию «Сводка и группировка статистических данных»). Для этого последнюю ординату, равную сумме всех частот или частостей, делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения и дает значение медианы.

4. Мода. Медиана. Генеральная и выборочная средняя

Мода на экране, медиана в треугольнике, а средние – это температура по больнице и в палате. Продолжаем наш практический курс занимательной статистики (Занятие 1) изучением центральных характеристик статистической совокупности , названия которых вы видите в заголовке. И начнём мы с его конца, поскольку о средних величинах речь зашла практически с первых же абзацев темы. Для подготовленных читателей оглавление :

• Генеральная и выборочная средняя – вычисление по первичным данным и для сформированного дискретного вариационного ряда;
• Мода – определение и нахождение для дискретного случая;
• Медиана – общее определение, как найти медиану;
• Средняя, мода и медиана интервального вариационного ряда – вычисление по первичным данным и по готовому ряду. Формулы моды и медианы,
• Квартили, децили, перцентили – коротко о главном.

ну а «чайникам» лучше ознакомиться с материалом по порядку:

Итак, пусть исследуется некоторая генеральная совокупность объёма , а именно её числовая характеристика , не важно, дискретная или непрерывная (Занятия 2, 3 ).

Генеральной средней называется среднее арифметическое всех значений этой совокупности:

Если среди чисел есть одинаковые (что характерно для дискретного ряда ) , то формулу можно записать в более компактном виде:
, где
варианта повторяется раз;
варианта – раз;
варианта – раз;
…
варианта – раз.

Живой пример вычисления генеральной средней встретился в Примере 2 , но чтобы не занудничать, я даже не буду напоминать его содержание.

Далее. Как мы помним, обработка всей генеральной совокупности часто затруднена либо невозможна, и поэтому из неё организуют представительную выборку объема , и на основании исследования этой выборки делают вывод обо всей совокупности.

Выборочной средней называется среднее арифметическое всех значений выборки:

и при наличии одинаковых вариант формула запишется компактнее:
– как сумма произведений вариант на соответствующие частоты .

Выборочная средняя позволяет достаточно точно оценить истинное значение , чего вполне достаточно для многих исследований. При этом, чем больше выборка, тем точнее будет эта оценка.

Практику начнём, а точнее продолжим, с дискретного вариационного ряда и знакомого условия:

Пример 8

По результатам выборочного исследования рабочих цеха были установлены их квалификационные разряды: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5, 5, 2, 3, 6, 5, 4, 6, 4, 3.

Как решать задачу? Если нам даны первичные данные (исходные необработанные значения), то их можно тупо просуммировать и разделить результат на объём выборки:
– среднестатистический квалификационный разряд рабочих цеха.

Но во многих задачах требуется составить вариационный ряд (см. Пример 4 ) :

– или же этот ряд предложен изначально (что бывает чаще). И тогда, мы, конечно, используем «цивилизованную» формулу:

Мода . Мода дискретного вариационного ряда – это варианта с максимальной частотой. В данном случае . Моду легко отыскать по таблице, и ещё легче на полигоне частот – это абсцисса самой высокой точки:


Иногда таковых значений несколько (с одинаковой максимальной частотой), и тогда модой считают каждое из них.

Если все или почти все варианты различны (что характерно для интервального ряда ), то модальное значение определяется несколько другим способом, о котором во 2-й части урока.

Медиана . Медиана вариационного ряда* – это значение, которая делит его на две равные части (по количеству вариант).

Но теперь нам нужно найти среднюю, моду и медиану.

Решение : чтобы найти среднюю по первичным данным, лучше всего просуммировать все варианты и разделить полученный результат на объём совокупности:
ден. ед.

Эти подсчёты, кстати, займут не так много времени и при использовании оффлайн калькулятора. Но если есть Эксель, то, конечно, забиваем в любую свободную ячейку =СУММ(, выделяем мышкой все числа, закрываем скобку ) , ставим знак деления / , вводим число 30 и жмём Enter . Готово.

Что касается моды, то её оценка по исходным данным, становится непригодна. Хоть мы и видим среди чисел одинаковые, но среди них запросто может найтись пять так шесть-семь вариант с одинаковой максимальной частотой, например, частотой 2. Кроме того, цены могут быть округлёнными. Поэтому модальное значение рассчитывается по сформированному интервальному ряду (о чём чуть позже) .

Чего не скажешь о медиане: забиваем в Эксель =МЕДИАНА(, выделяем мышью все числа, закрываем скобку ) и жмём Enter : . Причём, здесь даже ничего не нужно сортировать.

Но в Примере 6 была проведена сортировка по возрастанию (вспоминаем и сортируем – ссылка выше) , и это хорошая возможность повторить формальный алгоритм отыскания медианы. Делим объём выборки пополам:

И поскольку она состоит из чётного количества вариант, то медиана равна среднему арифметическому 15-й и 16-й варианты упорядоченного (!) вариационного ряда:

ден. ед.

Ситуация вторая . Когда дан готовый интервальный ряд (типичная учебная задача).

Продолжаем анализировать тот же пример с ботинками, где по исходным данным был составлен ИВР . Для вычисления средней потребуются середины интервалов:

– чтобы воспользоваться знакомой формулой дискретного случая:

– отличный результат! Расхождение с более точным значением (), вычисленным по первичным данным, составляет всего 0,04.

По сути дела, здесь мы приблизили интервальный ряд дискретным, и это приближение оказалось весьма эффективным. Впрочем, особой выгоды тут нет, т.к. при современном программном обеспечении не составляет труда вычислить точное значение даже по очень большому массиву первичных данных. Но это при условии, что они нам известны:)

С другими центральными показателями всё занятнее.

Чтобы найти моду, нужно найти модальный интервал (с максимальной частотой) – в данной задаче это интервал с частотой 11, и воспользоваться следующей страшненькой формулой:
, где:

– нижняя граница модального интервала;
– длина модального интервала;
– частота модального интервала;
– частота предыдущего интервала;
– частота следующего интервала.

Таким образом:
ден. ед. – как видите, «модная» цена на ботинки заметно отличается от средней арифметической .

Не вдаваясь в геометрию формулы, просто приведу гистограмму относительных частот и отмечу :


откуда хорошо видно, что мода смещена относительно центра модального интервала в сторону левого интервала с бОльшей частотой. Логично.

Справочно разберу редкие случаи:

– если модальный интервал крайний, то либо ;

– если обнаружатся 2 модальных интервала, которые находятся рядом, например, и , то рассматриваем модальный интервал , при этом близлежащие интервалы (слева и справа) по возможности тоже укрупняем в 2 раза.

– если между модальными интервалами есть расстояние, то применяем формулу к каждому интервалу, получая тем самым 2 или бОльшее количество мод.

Вот такой вот депеш мод:)

И медиана. Если дан готовый интервальный ряд, то медиана рассчитывается чуть по менее страшной формуле, но сначала нудно (описка по Фрейду:)) найти медианный интервал – это интервал, содержащий варианту (либо 2 варианты), которая делит вариационный ряд на две равные части.

Выше я рассказал, как определить медиану, ориентируясь на относительные накопленные частоты , здесь же сподручнее рассчитать «обычные» накопленные частоты . Вычислительный алгоритм точно такой же – первое значение сносим слева (красная стрелка) , и каждое следующее получается как сумма предыдущего с текущей частотой из левого столбца (зелёные обозначения в качестве примера) :

Всем понятен смысл чисел в правом столбце? – это количество вариант, которые успели «накопиться» на всех «пройденных» интервалах, включая текущий.

Поскольку у нас чётное количество вариант (30 штук), то медианным будет тот интервал, который содержит 30/2 = 15-ю и 16-ю варианту. И ориентируясь по накопленным частотам, легко прийти к выводу, что эти варианты содержатся в интервале .

Формула медианы:
, где:
– объём статистической совокупности;
– нижняя граница медианного интервала;
– длина медианного интервала;
– частота медианного интервала;
– накопленная частота предыдущего интервала.

Таким образом:
ден. ед. – заметим, что медианное значение, наоборот, оказалось смещено правее, т.к. по правую руку находится значительное количество вариант:


И справочно особые случаи.

В силу того, что исследователь не располагает данными об объеме продаж в каждом обменном пункте, расчет средней арифметической с целью определения средней цены за доллар нецелесообразен.

Медиана ряда чисел

Однако можно определить то значение признака, которое носит название медиана (Ме). Медиана

Номер медианы: №Ме = ;

Мода

Таблица 3.6.

f — сумма частот ряда;

S накопительные частоты

S — накопленные частоты.

На рис. 3.2. Изображена гистограмма ряда распределения банков по размеру прибыли (по данным табл. 3.6.).

х — размер прибыли, млн. руб.,

f — число банков.

"МЕДИАНА УПОРЯДОЧЕННОГО РЯДА"

Текстовая HTML-версия публикации

Конспект урока алгебры в 7 классе

Тема урока: «МЕДИАНА УПОРЯДОЧЕННОГО РЯДА».

учитель Озёрной школы филиал МКОУ Бурковская СОШ Ерёменко Татьяна Алексеевна
Цели:
понятие медианы как статистической характеристики упорядоченного ряда; формировать умение находить медиану для упорядоченных рядов с четным и нечетным числом членов; формировать умение интерпретировать значения медианы в зависимости от практической ситуации, закрепление понятия среднего арифметического набора чисел. Развивать навыки самостоятельной работы. Формировать интерес к математике.
Ход урока

Устная работа.
Даны ряды: 1) 4; 1; 8; 5; 1; 2) ; 9; 3; 0,5; ; 3) 6; 0,2; ; 4; 6; 7,3; 6. Найдите: а) наибольшее и наименьшее значения каждого ряда; б) размах каждого ряда; в) моду каждого ряда.
II. Объяснение нового материала.
Работа по учебнику. 1. Рассматрим задачу с п. 10 учебника. Что означает упорядоченный ряд? Подчеркну, что перед нахождением медианы нужно всегда упорядочить ряд данных. 2.На доске знакомимся с правилами нахождения медианы для рядов с четным и нечетным числом членов:
Медианой

упорядоченного

ряда
чисел
с

нечетным

числом

членов
называется число, записанное посередине, а
медианой

упорядоченного ряда
чисел
с четным числом членов
называется среднее арифметическое двух чисел, записанных посредине.
Медианой

произвольного

ряда
называется медиана 1 3 1 7 5 4 соответствующего упорядоченного ряда.
Отмечу, что показатели- среднее арифметическое, мода и медиана по

разному

характеризуют

данные,

полученные

результате

наблюдений.

III. Формирование умений и навыков.
1-я группа. Упражнения на применение формул нахождения медианы упорядоченного и неупорядоченного ряда. 1.
№ 186.
Решение: а) Число членов ряда п = 9; медиана Ме = 41; б) п = 7, ряд упорядочен, Ме = 207; в) п = 6, ряд упорядочен, Ме = = 21; г) п = 8, ряд упорядочен, Ме = = 2,9. Ответ: а) 41; б) 207; в) 21; г) 2,9. Учащиеся комментируют способ нахождения медианы. 2. Найдите среднее арифметическое и медиану ряда чисел: а) 27, 29, 23, 31, 21, 34; в) ; 1. б) 56, 58, 64, 66, 62, 74. Решение: Для нахождения медианы необходимо каждый ряд упорядочить: а) 21, 23, 27, 29, 31, 34. п = 6; X = = 27,5; Ме = = 28; 20 22 2 + 2, 6 3, 2 2 + 1125 ; ; ; 3636 21 23 27 29 31 34 165 66 +++++ = 27 29 2 + б) 56, 58, 62, 64, 66, 74.

Как найти медиану в статистике

п = 6; X = 63,3; Ме = = 63; в) ; 1. п = 5; X = : 5 = 3: 5 = 0,6; Ме = . 3.
№ 188
(устно). Ответ: да; б) нет; в) нет; г) да. 4. Зная, что в упорядоченном ряду содержится т чисел, где т – нечетное число, укажите номер члена, являющегося медианой, если т равно: а) 5; б) 17; в) 47; г) 201. Ответ: а) 3; б) 9; в) 24; г) 101. 2-я группа. Практические задачи на нахождение медианы соответствующего ряда и интерпретацию полученного результата. 1.
№ 189.
Решение: Число членов ряда п = 12. Для нахождения медианы ряд нужно упорядочить: 136, 149, 156, 158, 168, 174, 178, 179, 185, 185, 185, 194. Медиана ряда Ме = = 176. Выработка за месяц была больше медианы у следующих членов артели: 56 58 62 64 66 74 380 66 +++++ =≈ 62 64 2 + 1125 ; ; ; 3636 1125 12456 18 1:5:5 6336 6 6 ++++ ⎛⎞ ++++ = = ⎜⎟ ⎝⎠ 2 3 67 174 178 22 xx + + = 1) Квитко; 4) Бобков; 2) Баранов; 5) Рылов; 3) Антонов; 6) Астафьев. Ответ: 176. 2.
№ 192.
Решение: Упорядочим ряд данных: 30, 31, 32, 32, 32, 32, 32, 32, 33, 35, 35, 36, 36, 36, 38, 38, 38, 40, 40, 42; число членов ряда п = 20. Размах A = x max – x min = 42 – 30 = 12. Мода Мо = 32 (это значение встречается 6 раз – чаще других). Медиана Ме = = 35. В данном случае размах показывает наибольший разброс времени на обработку детали; мода показывает наиболее типическое значение времени обработки; медиана – время обработки, которое не превысили половина токарей. Ответ: 12; 32; 35.
IV. Итог урока.
– Что называется медианой ряда чисел? – Может ли медиана ряда чисел не совпадать ни с одним из чисел ряда? – Какое число является медианой упорядоченного ряда, содержащего 2п чисел? 2п – 1 чисел? – Как найти медиану неупорядоченного ряда?
Домашнее задание:
№ 187, № 190, № 191, № 254. 10 11 35 35 22 xx + + =

В раздел основное общее образование

Мода и медиана

К средним величинам относят также моду и медиану.

Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней (арифметической, гармонической и др.) невозможен или нецелесообразен.

Например, выборочное обследование в г. Омске 12 коммерческих пунктов обмена валюты позволило зафиксировать различные цены за доллар при его продаже (данные на 10 октября 1995г. при биржевом курсе доллара -4493руб).

В силу того, что исследователь не располагает данными об объеме продаж в каждом обменном пункте, расчет средней арифметической с целью определения средней цены за доллар нецелесообразен. Однако можно определить то значение признака, которое носит название медиана (Ме). Медиана лежит в середине ранжированного ряда и делит его пополам.

Расчет медианы по несгруппированным данным производится следующим образом:

а) расположим индивидуальные значения признака в возрастающем порядке:

4500 4500 4535 4540 4550 4560 4560 4560 4560 4570 4570 4570

б) определим порядковый номер медианы по формуле:

в нашем примере это означает, что медиана в данном случае расположена между шестым и седьмым значениями признака в ранжированном ряду, так как ряд имеет четное число индивидуальных значений. Таким образом, Ме равна средней арифметической из соседних значений: 4550, 4560.

в) рассмотрим порядок вычисления медианы в случае нечетного числа индивидуальных значений.

Допустим, мы наблюдаем не 12, а 11 пунктов обмена валюты, тогда ранжированный ряд будет выглядеть следующим образом (отбрасываем 12-й пункт):

4500 4500 4535 4540 4550 4560 4560 4560 4560 4570 4570

Номер медианы: №Ме = ;

на шестом месте стоит = 4560, который и является медианой: Ме=4560. По обе стороны от нее находится одинаковое число пунктов.

Мода — это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака.

В нашем случае модальной ценой за доллар можно назвать 4560 руб.: это значение повторяется 4 раза, чаще, чем все другие.

На практике моду и медиану находят, как правило, по сгруппированным данным. В результате группировки был получен ряд распределения банков по величине полученной прибыли за год (табл. 3.6.).

Таблица 3.6.

Группировка банков по величине полученной прибыли за год

Для определения медианы надо подсчитать сумму накопительных частот. Наращивание итого продолжается до получения накопительной суммы частот, превышающей половину суммы частот. В нашем примере сумма накопленных частот (12), превышающая половину всех значений (20:2). Этому значению соответствует медианный интервал, который содержит медиану (5,5 — 6,4). Определим ее значение по формуле:

где начальное значение интервала, содержащего медиану;

— величина медианного интервала;

f — сумма частот ряда;

— сумма накопительных частот, предшествующих медианному интервалу;

— частота медианного интервала.

Таким образом, 50% банков имеют прибыль 6,1 млн. руб., а 50% банков — более 6,1 млн. руб.

Наибольшая частота соответствует также интервалу 5,5 — 6,4, т.е. мода должна находиться в этом интервале. Ее величину определим по формуле:

где — начальное значение интервала, содержащего моду;

— величина модального интервала;

— частота модального интервала;

— частота интервала, предшествующего модальному;

— частота интервала, следующего за модальным.

Приведенная формула моды может быть использована в вариационных рядах с равными интервалами.

Таким образом, в данной совокупности наиболее часто встречается размер прибыли 6,10 млн. руб.

Медиану и моду можно определить графически. Медиана определяется по кумуляте (рис. 3.1.). Для ее построения надо рассчитать накопительные частоты и частости. Накопительные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение, и определяется последовательным суммированием частот интервалов. При построении кумулятыы интервального ряда распределения нижней границе первого интервала соответствует частота, равная нулю, а верхней границе — вся частота данного интервала. Верхней границе второго интервала соответствует накопительная частота, равная сумме частот первых двух интервалов, и т.д.

Построим кумулятивную кривую по данным табл. 6 о распределении банков по размеру прибыли.

S накопительные частоты

3,7-4,6 4,6-5,5 5,5-6,4 6,4-7,3 7,3-8,2 Х прибыль

Рис. 3.1. Кумулята ряда распределения банков по размеру прибыли:

х — размер прибыли, млн. руб.,

S — накопленные частоты.

Для определения медианы высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.

Мода определяется по гистограмме распределения. Гистограмма строится так:

на оси абсцисс откладываются равные отрезки, которые в принятом масштабе соответствуют величине интервалов вариационного ряда. На отрезках строятся прямоугольники, площади которых пропорциональны частотам (или частостям) интервала.

Медиана в статистике

3.2. Изображена гистограмма ряда распределения банков по размеру прибыли (по данным табл. 3.6.).

3,7-4,6 4,6-5,5 5,5-6,4 6,4-7,3 7,3-8,2 Х

Рис. 3.2. Распределение коммерческих банков по размеру прибыли:

х — размер прибыли, млн. руб.,

f — число банков.

Для определения моды правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника — с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Медиана (статистика)

Медиана (статистика) , в математической статистике — число, характеризующее выборку (например, набор чисел). Если все элементы выборки различны, то медиана — это такое число выборки, что ровно половина из элементов выборки больше него, а другая половина меньше него. В более общем случае медиану можно найти, упорядочив элементы выборки по возрастанию или убыванию и взяв средний элемент. Например, выборка {11, 9, 3, 5, 5} после упорядочивания превращается в {3, 5, 5, 9, 11} и её медианой является число 5. Если в выборке чётное число элементов, медиана может быть не определена однозначно: для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора {1, 3, 5, 7} принимают равной 4).

Другими словами, медианой в статистике называется значение, которое делит ряд пополам таким образом, что по обе стороны от нее (вниз или вверх) расположено одинаковое число единиц данной совокупности.

Задача №1. Расчёт средней арифметической, модального и медианного значения

Из-за этого свойства данный показатель имеет еще несколько названий: 50-й перцентиль или квантиль 0,5.

• Среднее значение
  
• Медиана
  
• Мода
  

Медиана (статистика)

Медиана (статистика) , в математической статистике — число, характеризующее выборку (например, набор чисел). Если все элементы выборки различны, то медиана — это такое число выборки, что ровно половина из элементов выборки больше него, а другая половина меньше него. В более общем случае медиану можно найти, упорядочив элементы выборки по возрастанию или убыванию и взяв средний элемент. Например, выборка {11, 9, 3, 5, 5} после упорядочивания превращается в {3, 5, 5, 9, 11} и её медианой является число 5.

5.5 Мода и медиана. Их вычисление в дискретных и интервальных вариационных рядах

Если в выборке чётное число элементов, медиана может быть не определена однозначно: для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора {1, 3, 5, 7} принимают равной 4).

Другими словами, медианой в статистике называется значение, которое делит ряд пополам таким образом, что по обе стороны от нее (вниз или вверх) расположено одинаковое число единиц данной совокупности. Из-за этого свойства данный показатель имеет еще несколько названий: 50-й перцентиль или квантиль 0,5.

Медиану используют вместо средней арифметической, когда крайние варианты ранжированного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.

Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:

• Среднее значение — среднее арифметическое, которое вычисляется сложением множества чисел с последующим делением полученной суммы на их количество.
  Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
• Медиана — число, которое является серединой множества чисел: половина чисел имеют значения большие, чем медиана, а половина чисел — меньшие.
  Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
• Мода — число, наиболее часто встречающееся в данном множестве чисел.
  Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.

Урок алгебры в 7 классе.

Тема «Медиана как статистическая характеристика».

Учитель Егорова Н.И.

Цель урока: сформировать у учащихся представление о медиане набора чисел и умение вычислять ее для несложных числовых наборов, закрепление понятия среднего арифметического набора чисел.

Тип урока: объяснение нового материала.

Ход урока

1. Организационный момент.

Сообщить тему урока и сформулировать его цели.

2. Актуализация прежних знаний.

Вопросы учащимся:

Что называется средним арифметическим набора чисел?

Где располагается среднее арифметическое внутри набора чисел?

Что характеризует среднее арифметическое набора чисел?

Где часто применяется среднее арифметическое набора чисел?

Устные задачи:

Найти среднее арифметическое набора чисел:

Проверка домашнего задания.

Учебник: №169, №172.

3. Изучение нового материала.

На предыдущем уроке мы познакомились с такой статистической характеристикой как среднее арифметическое набора чисел. Сегодня мы посвятим урок еще одной статистической характеристике – медиане.

Не только среднее арифметическое показывает, где на числовой прямой располагаются числа какого-либо набора и где их центр. Другим показателем является медиана.

Медианой набора чисел называется такое число, которое разделяет набор на две равные по численности части. Вместо “медиана” можно было бы сказать “середина”.

Сначала на примерах разберем, как найти медиану, а затем дадим строгое определение.

Рассмотрим следующий устный пример с применением проектора

В конце учебного года 11 учеников 7-го класса сдали норматив по бегу на 100 метров. Были зафиксированы следующие результаты:

После того как ребята пробежали дистанцию, к преподавателю подошел Петя и спросил, какой у него результат.

“Самый средний результат: 16,9 секунды”, – ответил учитель

“Почему?” – удивился Петя. – Ведь среднее арифметическое всех результатов – примерно 18,3 секунды, а я пробежал на секунду с лишним лучше. И вообще, результат Кати (18,4) гораздо ближе к среднему, чем мой”.

“Твой результат средний, так как пять человек пробежали лучше, чем ты, и пять – хуже. То есть ты как раз посередине”, – сказал учитель.

Записать алгоритм нахождения медианы набора чисел:

Упорядочить числовой набор (составить ранжированный ряд).

Одновременно зачеркиваем “самое большое” и “самое маленькое” числа данного набора чисел до тех пор, пока не останется одно число или два числа.

Если осталось одно число, то оно и есть медиана.

Если осталось два числа, то медианой будет среднее арифметическое двух оставшихся чисел.

Предложить учащимся самостоятельно сформулировать определение медианы набора чисел, затем прочитать в учебнике определение медианы (стр. 40), далее решить № 186(а,б), № 187(а) учебника (стр.41).

Замечание:

Обратить внимание учащихся на важное обстоятельство: медиана практически не чувствительна к значительным отклонениям отдельных крайних значений наборов чисел. В статистике это свойство называется устойчивостью. Устойчивость статистического показателя – очень важное свойство, оно страхует нас от случайных ошибок и отдельных недостоверных данных.

4. Закрепление изученного материала.

Решение задач.

Обозначим х-среднее арифметическое, Ме-медиана.

Набор чисел: 1,3,5,7,9.

х=(1+3+5+7+9):5=25:5=5,

Набор чисел: 1,3,5,7,14.

х=(1+3+5+7+14):5=30:5=6.

а) Набор чисел: 3,4,11,17,21

б) Набор чисел: 17,18,19,25,28

в) Набор чисел:25, 25, 27, 28, 29, 40, 50

Вывод: медиана набора чисел, состоящего из нечетного числа членов равна числу, стоящему посередине.

а) Набор чисел:2, 4, 8, 9.

Ме = (4+8):2=12:2=6

б) Набор чисел:1,3,5,7,8,9.

Ме = (5+7):2=12:2=6

Медиана набора чисел, содержащего четное число членов равна полусумме двух чисел, стоящих посередине.

Ученик получил в течении четверти следующие оценки по алгебре:

5, 4, 2, 5, 5, 4, 4, 5, 5, 5.

Найдите средний балл и медиану этого набора.

Найдем средний балл, то есть среднее арифметическое:

х= (5+4+2+5+5+4+4+5+5+5): 10=44:10 = 4,4

Найдем медиану этого набора чисел:

Упорядочим набор чисел: 2,4,4,4,5,5,5,5,5,5

Всего 10 чисел, чтобы найти медиану надо взять два средних числа и найти их полусумму.

Ме = (5+5):2 = 5

Вопрос к учащимся: Если бы вы были учителем, какую бы вы поставили оценку за четверть этому ученику? Ответ обоснуйте.

Президент компании получает зарплату 300000 руб. три его заместителя получают по 150000 руб., сорок служащих – по 50000 руб. и зарплата уборщицы составляет 10000 руб. Найдите среднее арифметическое и медиану зарплат в компании. Какую из этих характеристик выгоднее использовать президенту в рекламных целях?

х = (300000+3·150000+40·50000+10000):(1+3+40+1) = 2760000:45=61333,33 (руб.)

№ 6. Устно.

А) Сколько чисел в наборе, если его медианой служит ее девятый член?

Б) Сколько чисел в наборе, если его медианой служит среднее арифметическое 7-го и 8-го членов?

В) В наборе из семи чисел наибольшее число увеличили на 14. Изменится ли при этом и как среднее арифметическое и медиана?

Г) Каждое из чисел набора увеличили на 3. Что произойдет со средним арифметическим и медианой?

Конфеты в магазине продают на вес. Чтобы узнать, сколько конфет содержится в одном килограмме, Маша решила найти вес одной конфеты. Она взвесила несколько конфет и получила следующие результаты:

12, 13, 14, 12, 15, 16, 14, 13, 11.

Для оценки веса одной конфеты пригодны обе характеристики, т.к. они не сильно отличаются друг от друга.

Итак, для характеристики статистической информации используют среднее арифметическое и медиану. Во многих случаях какая-то из характеристик может не иметь никакого содержательного смысла (например, имея сведения о времени дорожно-транспортных происшествий, вряд ли имеет смысл говорить о среднем арифметическом этих данных).

Домашнее задание:пункт 10, № 186(в,г), № 190.

5. Итоги урока. Рефлексия.

1. «Статистические исследования: сбор и группировка статистических данных»

   Урок

   … темы , предлагаемые для седьмого класса . ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ. § 1. Статистические характеристики . П 1. Среднее арифметическое, размах и мода 1ч. П 2. Медиана как статистическая характеристика …

2. Рабочая программа учебного курса «алгебра» в 7 классе (базовый уровень) пояснительная записка

   Рабочая программа

   … п.10 Медиана как статистическая характеристика 23 п.9 Среднее арифметическое, размах и мода 24 Контрольная работа № 2 по теме …

3. Рабочая программа. Математика. 5 класс с. Канаши. 2011г

   Рабочая программа

   … уравнений. Среднее арифметическое, размах и мода. Медиана как статистическая характеристика . Цель – систематизировать и обобщить сведения о … и навыков, полученных на уроках по данным темам (курс алгебры 10 класса ). 11 класс (4 часа в неделю …

4. Приказ №51 от «30» август 2012 г. Рабочая программа по алгебре 7 класс

   Рабочая программа

   … учебным материалом Медиана как статистическая характеристика Знать определение среднего арифметического, размаха, моды и медианы как статистической характеристики Фронтальная и индивидуальная …

5. Рабочая программа по математике 7 класс ii ступень базовый уровень (1)

   Рабочая программа

   Как найти медиану ряда

   же, как в 6 классе . Изучение темы завершается ознакомлением учащихся с про­стейшими статистическими характеристиками : средним … М. : Издательский дом «Генжер», 2009. 3. Жохов, В. И. Уроки алгебры в 7 классе : кн. для учителя / В. И. Жохов …

Другие похожие документы..