На этом уроке мы поговорим о показательной и логарифмической функциях. Их обычно изучают вместе, так как они взаимно обратные. Мы поговорим о применении этих функций, о том, почему именно эти функции выделены для изучения.

Показательная функция используется при описании всех явлений, которые мы называем лавинообразными процессами. Если сказать четче, то это процессы, где изменение величины пропорционально уже имеющемуся количеству величины (чем больше, тем больше меняется; чем меньше, тем меньше меняется).

Примером такого процесса является размножение бактерий. Рассмотрим такую задачу. В стакане есть одна бактерия. Каждую секунду она делится на две бактерии, новые бактерии так же каждую секунду делятся на две и т.д. За минуту весь стакан был заполнен бактериями. Сколько бактерий было в стакане за секунду до этого?

Хочется сказать, что было заполнено чуть меньше целого стакана, где-то , но правильный ответ: половина стакана. Если заполнена половина стакана, то через секунду каждая бактерия разделится на части, и они заполнят весь стакан. Как видим, первая половина стакана заполнялась секунд, а вторая половина заполнилась лишь за секунду.

Таяние ледников

Наверняка все слышали о проблеме таяния льдов на планете. Почему возникают такие процессы оледенения и, наоборот, потепления? Они были и раньше, хотя сейчас говорят, что ключевое влияние на их скорость оказывает деятельность человека. Есть разные гипотезы, но это не так важно.

Важнее то, что уменьшение количества льда увеличивает количество поглощаемой солнечной энергии. То есть, чем меньше становится льда, тем быстрее он будет таять. Процесс экспоненциальный, или, по-другому, самовызывающийся, самоподпитывающийся.

Такой процесс описывается показательной функцией (или экспонентой) : (Рис. 1). - основание, , , а - показатель степени, изменяющаяся величина.

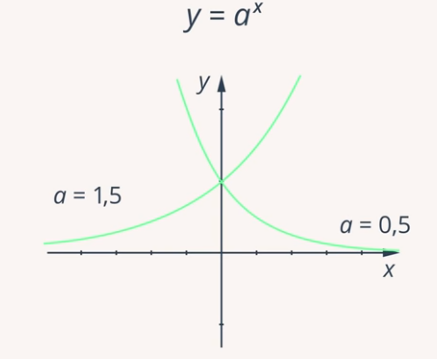
Рис. 1. График функции

Еще один пример показательной функции, который многим знаком, - сложные проценты . Если мы кладем деньги в банк под фиксированный процент, при этом деньги не снимаем, а процент начисляется на всю имеющуюся сумму, то сумма, которую мы получим через периодов: , где - начальный вклад, - процентная ставка, - количество пройденных периодов (лет, месяцев и т.п.). Сначала сумма будет расти медленно, но затем рост ускорится.

Еще один хороший пример. Если возвести в степень, то мы получим приблизительно , а вот в степени , это практически . Если представить этот пример в виде процентов, то в первом случае начисляется в день, тогда за год сумма увеличится в раз. А во втором случае снимается один процент в день, тогда через год почти ничего не останется.

При этом одной из характерных особенностей показательной функции является то, что до при такой схеме сумма уменьшиться не может. Похожий пример из ядерной физики - период полураспада. У радиоактивных элементов есть период полураспада, например, за лет масса вещества уменьшится в раза (Рис. 2).

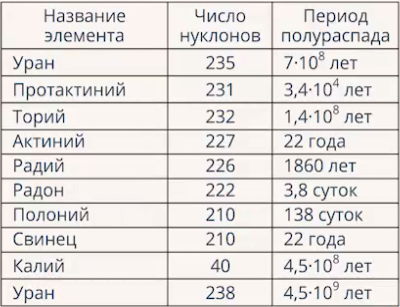
Рис. 2. Таблица периодов полураспада некоторых элементов

То есть если мы имели килограмм вещества, то за первые лет уйдет грамм вещества (достаточно много), а за следующие лет - уже грамм и т.д. А потом будет период, где за лет уйдет около грамма вещества. Это пример убывающей экспоненты.

Если рассмотреть множество всех функций и выделить среди них те, которые обладают следующим свойством: , то оно будет выполнено для показательных функций: .