По мере развития общества, усложнения производства развивалась и математика. Движение от простого к сложному. От обычного учёта методом сложения и вычитания, при их многократном повторении, пришли к понятию умножения и деления. Сокращение многократно повторяемой операции умножения стало понятием возведения в степень. Первые таблицы зависимости чисел от основания и числа возведения в степень были составлены ещё в VIII веке индийским математиком Варасена. С них и можно отсчитывать время возникновения логарифмов.

Исторический очерк

Возрождение Европы в XVI веке стимулировало и развитие механики. Требовался большой объем вычисления , связанных с умножением и делением многозначных чисел. Древние таблицы оказали большую услугу. Они позволяли заменять сложные операции на более простые – сложение и вычитание. Большим шагом вперёд стала работа математика Михаэля Штифеля, опубликованная в 1544 году, в которой он реализовал идею многих математиков. Что позволило использовать таблицы не только для степеней в виде простых чисел, но и для произвольных рациональных.

В 1614 году шотландец Джон Непер, развивая эти идеи, впервые ввёл новый термин «логарифм числа». Были составлены новые сложные таблицы для расчёта логарифмов синусов и косинусов, а также тангенсов. Это сильно сократило труд астрономов.

Стали появляться новые таблицы, которые успешно использовались учёными на протяжении трёх веков. Прошло немало времени, прежде чем новая операция в алгебре приобрела свой законченный вид. Было дано определение логарифма, и его свойства были изучены.

Только в XX веке с появлением калькулятора и компьютера человечество отказалось от древних таблиц, успешно работавших на протяжении XIII веков.

Сегодня мы называем логарифмом b по основанию a число x, которое является степенью числа а, чтобы получилось число b. В виде формулы это записывается: x = log a(b).

Например, log 3(9) будет равен 2. Это очевидно, если следовать определению. Если 3 возвести в степень 2, то получим 9.

Так, сформулированное определение ставит только одно ограничение, числа a и b должны быть вещественными.

Разновидности логарифмов

Классическое определение носит название вещественный логарифм и фактически является решением уравнения a x = b. Вариант a = 1 является пограничным и не представляет интереса. Внимание: 1 в любой степени равно 1.

Вещественное значение логарифма определено только при основании и аргументе больше 0, при этом основание не должно равняться 1.

Особое место в области математики играют логарифмы, которые будут называться в зависимости от величины их основания:

Правила и ограничения

Основополагающим свойством логарифмов является правило: логарифм произведения равен логарифмической сумме. log abp = lоg a(b) + log a(p).

Как вариант этого утверждения будет: log с(b/p) = lоg с(b) — log с(p), функция частного равна разности функций.

Из предыдущих двух правил легко видно, что: lоg a(b p) = p * log a(b).

Среди других свойств можно выделить:

Замечание. Не надо делать распространённую ошибку - логарифм суммы не равен сумме логарифмов.

Многие века операция поиска логарифма была довольно трудоёмкой задачей. Математики пользовались известной формулой логарифмической теории разложения на многочлен:

ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*((x^n)/n), где n - натуральное число больше 1, определяющее точность вычисления.

Логарифмы с другими основаниями вычислялись, используя теорему о переходе от одного основания к другому и свойстве логарифма произведения.

Так как этот способ очень трудоёмкий и при решении практических задач трудноосуществим, то использовали заранее составленные таблицы логарифмов, что значительно ускоряло всю работу.

В некоторых случаях использовали специально составленные графики логарифмов, что давало меньшую точность, но значительно ускоряло поиск нужного значения. Кривая функции y = log a(x), построенная по нескольким точкам, позволяет с помощью обычной линейки находить значения функции в любой другой точке. Инженеры длительное время для этих целей использовали так называемую миллиметровую бумагу.

В XVII веке появились первые вспомогательные аналоговые вычислительные условия, которые к XIX веку приобрели законченный вид. Наиболее удачное устройство получило название логарифмическая линейка. При всей простоте устройства, её появление значительно ускорило процесс всех инженерных расчётов, и это переоценить трудно. В настоящее время уже мало кто знаком с этим устройством.

Появление калькуляторов и компьютеров сделало бессмысленным использование любых других устройств.

Уравнения и неравенства

Для решения различных уравнений и неравенств с использованием логарифмов применяются следующие формулы:

• Переход от одного основания к другому: lоg a(b) = log c(b) / log c(a);
• Как следствие предыдущего варианта: lоg a(b) = 1 / log b(a).

Для решения неравенств полезно знать:

• Значение логарифма будет положительным только в том случае, когда основание и аргумент одновременно больше или меньше единицы; если хотя бы одно условие нарушено, значение логарифма будет отрицательным.
• Если функция логарифма применяется к правой и левой части неравенства, и основание логарифма больше единицы, то знак неравенства сохраняется; в противном случае он меняется.

Примеры задач

Рассмотрим несколько вариантов применения логарифмов и их свойства. Примеры с решением уравнений:

Рассмотрим вариант размещения логарифма в степени:

• Задача 3. Вычислить 25^log 5(3). Решение: в условиях задачи запись аналогична следующей (5^2)^log5(3) или 5^(2 * log 5(3)). Запишем по-другому: 5^log 5(3*2), или квадрат числа в качестве аргумента функции можно записать как квадрат самой функции (5^log 5(3))^2. Используя свойства логарифмов, это выражение равно 3^2. Ответ: в результате вычисления получаем 9.

Практическое применение

Являясь исключительно математическим инструментом, кажется далёким от реальной жизни, что логарифм неожиданно приобрёл большое значение для описания объектов реального мира. Трудно найти науку, где его не применяют. Это в полной мере относится не только к естественным, но и гуманитарным областям знаний.

Логарифмические зависимости

Приведём несколько примеров числовых зависимостей:

Механика и физика

Исторически механика и физика всегда развивались с использованием математических методов исследования и одновременно служили стимулом для развития математики, в том числе логарифмов. Теория большинства законов физики написана языком математики. Приведём только два примера описания физических законов с использованием логарифма.

Решать задачу расчёта такой сложной величины как скорость ракеты можно, применяя формулу Циолковского, которая положила начало теории освоения космоса:

V = I * ln (M1/M2), где

• V – конечная скорость летательного аппарата.
• I – удельный импульс двигателя.
• M 1 – начальная масса ракеты.
• M 2 – конечная масса.

Другой важный пример - это использование в формуле другого великого учёного Макса Планка, которая служит для оценки равновесного состояния в термодинамике.

S = k * ln (Ω), где

• S – термодинамическое свойство.
• k – постоянная Больцмана.
• Ω – статистический вес разных состояний.

Химия

Менее очевидным будет использования формул в химии, содержащих отношение логарифмов. Приведём тоже только два примера:

• Уравнение Нернста, условие окислительно-восстановительного потенциала среды по отношению к активности веществ и константой равновесия.
• Расчёт таких констант, как показатель автопролиза и кислотность раствора тоже не обходятся без нашей функции.

Психология и биология

И уж совсем непонятно при чём здесь психология. Оказывается, сила ощущения хорошо описывается этой функцией как обратное отношение значения интенсивности раздражителя к нижнему значению интенсивности.

После вышеприведённых примеров уже не удивляет, что и в биологии широко используется тема логарифмов. Про биологические формы, соответствующие логарифмическим спиралям, можно писать целые тома.

Другие области

Кажется, невозможно существование мира без связи с этой функцией, и она правит всеми законами. Особенно, когда законы природы связаны с геометрической прогрессией. Стоит обратиться к сайту МатПрофи, и таких примеров найдётся множество в следующих сферах деятельности:

Список может быть бесконечным. Освоив основные закономерности этой функции, можно окунуться в мир бесконечной мудрости.

Определение логарифма

Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить b .

Числом е в математике принято обозначать предел, к которому стремиться выражение

Число е является иррациональным числом - числом, несоизмеримым с единицей, оно не может быть точно выраженным ни целым ни дробным рациональным числом.

Буква е - первая буква латинского слова exponere - выставлять напоказ, отсюда в математике название экспоненциальная - показательная функция.

Число е широко применяется в математике, и во всех науках, так или иначе применяющих для своих нужд математические расчеты.

Логарифмы. Свойства логарифмов

Определение: Логарифмом положительного числа b по основанию называется показатель степени с, в которую надо возвести число а, чтобы получить число b.

Основное логарифмическое тождество:

7) Формула перехода к новому основанию:

lna = log e a, e ≈ 2,718…

Задачи и тесты по теме «Логарифмы. Свойства логарифмов»

• Логарифмы — Важные темы для повторения ЕГЭ по математике

Для успешного выполнения заданий по данной теме Вы должны знать определение логарифма, свойства логарифмов, основное логарифмическое тождество, определения десятичного и натурального логарифмов. Основные типы задач по данной теме — это задачи на вычисление и преобразование логарифмических выражений. Рассмотрим их решение на следующих примерах.

Решение: Используя свойства логарифмов, получим

Решение: используя свойства степени, получим

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Свойства логарифмов, формулировки и доказательства.

Логарифмы обладают рядом характерных свойств. В этой статье мы разберем основные свойства логарифмов . Здесь мы дадим их формулировки, запишем свойства логарифмов в виде формул, покажем примеры их применения, а также приведем доказательства свойств логарифмов.

Навигация по странице.

Основные свойства логарифмов, формулы

Для удобства запоминания и использования представим основные свойства логарифмов в виде списка формул. В следующем пункте дадим их формулировки, доказательства, примеры использования и необходимые пояснения.

Свойство логарифма единицы: log a 1=0 для любого a>0 , a≠1 .

Логарифм числа, равного основанию: log a a=1 при a>0 , a≠1 .

Свойство логарифма степени основания: log a a p =p , где a>0 , a≠1 и p – любое действительное число.

Логарифм произведения двух положительных чисел: log a (x·y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
и свойство логарифма произведения n положительных чисел: log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Свойство логарифма частного: , где a>0 , a≠1 , x>0 , y>0 .

Логарифм степени числа: log a b p =p·log a |b| , где a>0 , a≠1 , b и p такие числа, что степень b p имеет смысл и b p >0 .

Следствие: , где a>0 , a≠1 , n – натуральное число, большее единицы, b>0 .

Следствие 1: , a>0 , a≠1 , b>0 , b≠1 .

Следствие 2: , a>0 , a≠1 , b>0 , p и q – действительные числа, q≠0 , в частности при b=a имеем .

Формулировки и доказательства свойств

Переходим к формулированию и доказательству записанных свойств логарифмов. Все свойства логарифмов доказываются на основе определения логарифма и вытекающего из него основного логарифмического тождества, а также свойств степени.

Начнем со свойства логарифма единицы . Его формулировка такова: логарифм единицы равен нулю, то есть, log a 1=0 для любого a>0 , a≠1 . Доказательство не вызывает сложностей: так как a 0 =1 для любого a , удовлетворяющего указанным выше условиям a>0 и a≠1 , то доказываемое равенство log a 1=0 сразу следует из определения логарифма.

Приведем примеры применения рассмотренного свойства: log 3 1=0 , lg1=0 и .

Переходим к следующему свойству: логарифм числа, равного основанию, равен единице , то есть, log a a=1 при a>0 , a≠1 . Действительно, так как a 1 =a для любого a , то по определению логарифма log a a=1 .

Примерами использования этого свойства логарифмов являются равенства log 5 5=1 , log 5,6 5,6 и lne=1 .

Логарифм степени числа, равного основанию логарифма, равен показателю степени . Этому свойству логарифма отвечает формула вида log a a p =p , где a>0 , a≠1 и p – любое действительное число. Это свойство напрямую следует из определения логарифма. Заметим, что оно позволяет сразу указать значение логарифма, если есть возможность представить число под знаком логарифма в виде степени основания, подробнее об этом мы поговорим в статье вычисление логарифмов.

К примеру, log 2 2 7 =7 , lg10 -4 =-4 и .

Логарифм произведения двух положительных чисел x и y равен произведению логарифмов этих чисел: log a (x·y)=log a x+log a y , a>0 , a≠1 . Докажем свойство логарифма произведения. В силу свойств степени a log a x+log a y =a log a x ·a log a y , а так как по основному логарифмическому тождеству a log a x =x и a log a y =y , то a log a x ·a log a y =x·y . Таким образом, a log a x+log a y =x·y , откуда по определению логарифма вытекает доказываемое равенство.

Покажем примеры использования свойства логарифма произведения: log 5 (2·3)=log 5 2+log 5 3 и .

Свойство логарифма произведения можно обобщить на произведение конечного числа n положительных чисел x 1 , x 2 , …, x n как log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n . Данное равенство без проблем доказывается методом математической индукции.

Например, натуральных логарифм произведения можно заменить суммой трех натуральных логарифмов чисел 4 , e , и .

Логарифм частного двух положительных чисел x и y равен разности логарифмов этих чисел. Свойству логарифма частного соответствует формула вида , где a>0 , a≠1 , x и y – некоторые положительные числа. Справедливость этой формулы доказывается как и формула логарифма произведения: так как , то по определению логарифма .

Приведем пример использования этого свойства логарифма: .

Переходим к свойству логарифма степени . Логарифм степени равен произведению показателя степени на логарифм модуля основания этой степени. Запишем это свойство логарифма степени в виде формулы: log a b p =p·log a |b| , где a>0 , a≠1 , b и p такие числа, что степень b p имеет смысл и b p >0 .

Сначала докажем это свойство для положительных b . Основное логарифмическое тождество позволяет нам представить число b как a log a b , тогда b p =(a log a b) p , а полученное выражение в силу свойство степени равно a p·log a b . Так мы приходим к равенству b p =a p·log a b , из которого по определению логарифма заключаем, что log a b p =p·log a b .

Осталось доказать это свойство для отрицательных b . Здесь замечаем, что выражение log a b p при отрицательных b имеет смысл лишь при четных показателях степени p (так как значение степени b p должно быть больше нуля, в противном случае логарифм не будет иметь смысла), а в этом случае b p =|b| p . Тогда b p =|b| p =(a log a |b|) p =a p·log a |b| , откуда log a b p =p·log a |b| .

Например, и ln(-3) 4 =4·ln|-3|=4·ln3 .

Из предыдущего свойства вытекает свойство логарифма из корня : логарифм корня n -ой степени равен произведению дроби 1/n на логарифм подкоренного выражения, то есть, , где a>0 , a≠1 , n – натуральное число, большее единицы, b>0 .

Доказательство базируется на равенстве (смотрите определение степени с дробным показателем), которое справедливо для любых положительных b , и свойстве логарифма степени: .

Вот пример использования этого свойства: .

Теперь докажем формулу перехода к новому основанию логарифма вида . Для этого достаточно доказать справедливость равенства log c b=log a b·log c a . Основное логарифмическое тождество позволяет нам число b представить как a log a b , тогда log c b=log c a log a b . Осталось воспользоваться свойством логарифма степени: log c a log a b =log a b·log c a . Так доказано равенство log c b=log a b·log c a , а значит, доказана и формула перехода к новому основанию логарифма .

Покажем пару примеров применения этого свойства логарифмов: и .

Формула перехода к новому основанию позволяет переходить к работе с логарифмами, имеющими «удобное» основание. Например, с ее помощью можно перейти к натуральным или десятичным логарифмам, чтобы можно было вычислить значение логарифма по таблице логарифмов. Формула перехода к новому основанию логарифма также позволяет в некоторых случаях находить значение данного логарифма, когда известны значения некоторых логарифмов с другими основаниями.

Часто используется частный случай формулы перехода к новому основанию логарифма при c=b вида . Отсюда видно, что log a b и log b a – взаимно обратные числа. К примеру, .

Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a: .

Осталось доказать свойства сравнения логарифмов.

Воспользуемся методом от противного. Предположим, что при a 1 >1 , a 2 >1 и a 1 2 и при 0 1 справедливо log a 1 b≤log a 2 b . По свойствам логарифмов эти неравенства можно переписать как и соответственно, а из них следует, что log b a 1 ≤log b a 2 и log b a 1 ≥log b a 2 соответственно. Тогда по свойствам степеней с одинаковыми основаниями должны выполняться равенства b log b a 1 ≥b log b a 2 и b log b a 1 ≥b log b a 2 , то есть, a 1 ≥a 2 . Так мы пришли к противоречию условию a 1 2 . На этом доказательство завершено.

Основные свойства логарифмов

• Материалы к уроку
• Скачать все формулы

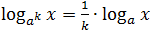
Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы - это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами .

Эти правила обязательно надо знать - без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного - все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Рассмотрим два логарифма с одинаковыми основаниями: log a x и log a y . Тогда их можно складывать и вычитать, причем:

Итак, сумма логарифмов равна логарифму произведения, а разность - логарифму частного. Обратите внимание: ключевой момент здесь - одинаковые основания . Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры - и убедитесь:

Задача. Найдите значение выражения: log 6 4 + log 6 9.

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log 6 4 + log 6 9 = log 6 (4 · 9) = log 6 36 = 2.

Задача. Найдите значение выражения: log 2 48 − log 2 3.

Основания одинаковые, используем формулу разности:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Задача. Найдите значение выражения: log 3 135 − log 3 5.

Снова основания одинаковые, поэтому имеем:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные - подобные выражения на полном серьезе (иногда - практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

• log a x n = n · log a x ;
• 
• 

Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить - в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Задача. Найдите значение выражения: log 7 49 6 .

Избавимся от степени в аргументе по первой формуле:
log 7 49 6 = 6 · log 7 49 = 6 · 2 = 12

Задача. Найдите значение выражения:

[Подпись к рисунку]

Заметим, что в знаменателе стоит логарифм, основание и аргумент которого являются точными степенями: 16 = 2 4 ; 49 = 7 2 . Имеем:

[Подпись к рисунку]

Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели - получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log 2 7. Поскольку log 2 7 ≠ 0, можем сократить дробь - в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

Пусть дан логарифм log a x . Тогда для любого числа c такого, что c > 0 и c ≠ 1, верно равенство:

[Подпись к рисунку]

В частности, если положить c = x , получим:

[Подпись к рисунку]

Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача. Найдите значение выражения: log 5 16 · log 2 25.

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

А теперь «перевернем» второй логарифм:

[Подпись к рисунку]

Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Задача. Найдите значение выражения: log 9 100 · lg 3.

Основание и аргумент первого логарифма - точные степени. Запишем это и избавимся от показателей:

[Подпись к рисунку]

Теперь избавимся от десятичного логарифма, перейдя к новому основанию:

[Подпись к рисунку]

Основное логарифмическое тождество

Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

1. n = log a a n

2. В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.

   Вторая формула - это фактически перефразированное определение. Она так и называется: основное логарифмическое тождество.

   В самом деле, что будет, если число b возвести в такую степень, что число b в этой степени дает число a ? Правильно: получится это самое число a . Внимательно прочитайте этот абзац еще раз - многие на нем «зависают».

   Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.

   [Подпись к рисунку]

   Заметим, что log 25 64 = log 5 8 - просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:

   [Подпись к рисунку]

   Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂

   Логарифмическая единица и логарифмический ноль

   В заключение приведу два тождества, которые сложно назвать свойствами - скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

   1. log a a = 1 - это логарифмическая единица. Запомните раз и навсегда: логарифм по любому основанию a от самого этого основания равен единице.
   2. log a 1 = 0 - это логарифмический ноль. Основание a может быть каким угодно, но если в аргументе стоит единица - логарифм равен нулю! Потому что a 0 = 1 - это прямое следствие из определения.

   Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее - и решайте задачи.

   Логарифм. Свойства логарифма (сложение и вычитание).

   Свойства логарифма вытекают из его определения. И так логарифм числа b по основанию а определяется как показатель степени, в которую надо возвести число a , чтобы получить число b (логарифм существует только у положительных чисел).

   Из данной формулировки следует, что вычисление x=log a b , равнозначно решению уравнения a x =b. Например, log 2 8 = 3 потому, что 8 = 2 3 . Формулировка логарифма дает возможность обосновать, что если b=a с , то логарифм числа b по основанию a равен с . Также ясно, что тема логарифмирования тесно взаимосвязана с темой степени числа.

   С логарифмами, как и с любыми числами, можно выполнять операции сложения, вычитания и всячески трансформировать. Но ввиду того, что логарифмы — это не совсем ординарные числа, здесь применимы свои особенные правила, которые называются основными свойствами .

   Сложение и вычитание логарифмов.

   Возьмем два логарифма с одинаковыми основаниями: log a x и log a y . Тогда сними возможно выполнять операции сложения и вычитания:

   Как видим, сумма логарифмов равняется логарифму произведения, а разность логарифмов — логарифму частного. Причем это верно если числа а , х и у положительны и а ≠ 1.

   Важно обращать внимание, что основным аспектом в данных формулах выступают одни и те же основания. Если основания отличаются друг от друга, эти правила не применимы!

   Правила сложения и вычитания логарифмов с одинаковыми основаниями читаются не только с лева на право, но и на оборот. В результате мы имеем теоремы логарифма произведения и логарифма частного.

   Логарифм произведения двух положительных чисел равен сумме их логарифмов; перефразируя данную теорему получим следующее, если числа а , x и у положительны и а ≠ 1 , то:

   Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя. Говоря по другому, если числа а , х и у положительны и а ≠ 1 , то:

   Применим вышеизложенные теоремы для решения примеров :

   Если числа x и у отрицательны, то формула логарифма произведения становится бессмысленной. Так, запрещено писать:

   так как выражения log 2 (-8) и log 2 (-4) вообще не определены (логарифмическая функция у = log 2 х определена лишь для положительных значений аргументах ).

   Теорема произведения применима не только для двух, но и для неограниченного числа сомножителей. Это означает, что для всякого натурального k и любых положительных чисел x 1 , x 2 , . . . ,x n существует тождество:

   Из теоремы логарифма частного можно получить еще одно свойство логарифма. Общеизвестно, что log a 1= 0, следовательно,

   А значит имеет место равенство:

   Логарифмы двух взаимно обратных чисел по одному и тому же основанию будут различны друг от друга исключительно знаком. Так:

   Логарифм. Свойства логарифмов

   Логарифм. Свойства логарифмов

   Рассмотрим равенство . Пусть нам известны значения и и мы хотим найти значение .

   То есть мы ищем показатель степени, в которую нужно взвести чтобы получить .

   Пусть переменная может принимать любое действительное значение, тогда на переменные и накладываются такие ограничения: o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   Если нам известны значения и , и перед нами стоит задача найти неизвестное , то для этой цели вводится математическое действие, которое называется логарифмирование .

   Чтобы найти значение , мы берем логарифм числа по основанию :

   Логарифмом числа по основанию называется показатель степени, в которую надо возвести , чтобы получить .

   То есть основное логарифмическое тождество :

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   является по сути математической записью определения логарифма .

   Математическая операция логарифмирование является обратной по отношению к операции возведения в степень, поэтому свойства логарифмов тесно связаны со свойствами степени.

   Перечислим основные свойства логарифмов :

   (o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ title=»d1″/>

   4.

   5.

   Следующая группа свойств позволяет представить показатель степени выражения, стоящего под знаком логарифма, или стоящего в основании логарифма в виде коэффициента перед знаком логарифма:

   6.

   7.

   8.

   9.

   Следующая группа формул позволяет перейти от логарифма с данным основанием к логарифму с произвольным основанием, и называется формулами перехода к новому основанию :

   10.

   12. (следствие из свойства 11)

   

   Следующие три свойства не очень известны, однако они часто используются при решении логарифмических уравнений, или при упрощении выражений, содержащих логарифмы:

   13.

   14.

   15.

   Частные случаи:

   — десятичный логарифм

   — натуральный логарифм

   При упрощении выражений, содержащих логарифмы применяется общий подход:

   1. Представляем десятичные дроби в виде обыкновенных.

   2. Смешанные числа представляем в виде неправильных дробей.

   3. Числа, стоящие в основании логарифма и под знаком логарифма раскладываем на простые множители.

   4. Стараемся привести все логарифмы к одному основанию.

   5. Применяем свойства логарифмов.

   Давайте рассмотрим примеры упрощения выражений, содержащих логарифмы.

   Пример 1.

   Вычислить:

   Упростим все показатели степеней: наша задача привести их к логарифмам, в основании которых стоит то же число, что и в основании степtни.

   ==(по свойству 7)=(по свойству 6) =

   Подставим показатели, которые у нас получились в исходное выражение. Получим:

   Ответ: 5,25

   Пример 2. Вычислить:

   

   Приведем все логарифмы к основанию 6 (при этом логарифмы из знаменателя дроби «перекочуют» в числитель):

   Разложим числа, стоящие под знаком логарифма на простые множители:

   Применим свойства 4 и 6:

   Введем замену

   Получим:

   Ответ: 1

   Логарифм . Основное логарифмическое тождество.

   Свойства логарифмов. Десятичный логарифм. Натуральный логарифм.

   Логарифмом положительного числа N по основанию (b > 0, b 1) называется показатель степени x , в которую нужно возвести b , чтобы получить N .

   Эта запись равнозначна следующей: b x = N .

   П р и м е р ы: log 3 81 = 4 , так как 3 4 = 81 ;

   log 1/3 27 = – 3 , так как (1/3) — 3 = 3 3 = 27 .

   Вышеприведенное определение логарифма можно записать в виде тождества:

   

   Основные свойства логарифмов.

   2) log 1 = 0 , так как b 0 = 1 .

   3) Логарифм произведения равен сумме логарифмов сомножителей:

   4) Логарифм частного равен разности логарифмов делимого и делителя:

   5) Логарифм степени равен произведению показателя степени на логарифм её основания:

   Следствием этого свойства является следующее: логарифм корня равен логарифму подкоренного числа, делённому на степень корня:

   

   6) Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак лога рифма:

   

   Два последних свойства можно объединить в одно:

   

   7) Формула модуля перехода (т. e . перехода от одного основания логарифма к другому основанию):

   

   В частном случае при N = a имеем:

   

   Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg , т.е. log 10 N = lg N . Логарифмы чисел 10, 100, 1000, . p авны соответственно 1, 2, 3, …, т.е. имеют столько положительных

   единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1, 0.01, 0.001, . p авны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц, сколько нулей стоит в логарифмируемом числе перед единицей (считая и нуль целых). Логарифмы остальных чисел имеют дробную часть, называемую мантиссой . Целая часть логарифма называется характеристикой . Для практического при менения десятичные логарифмы наиболее удобны.

   Натуральным логарифмом называется логарифм по основанию е . Он обозначается ln , т.е. log e N = ln N . Число е является иррациональным, его приближённое значение 2.718281828. Оно является пределом, к которому стремится число (1 + 1 / n ) n при неограниченном возрастании n (см. первый замечательный предел на странице «Пределы числовых последовательностей»).
   Как это ни покажется странным, натуральные логарифмы оказались очень удобными при проведении различного рода операций, связанных с анализом функций. Вычисление логарифмов по основанию е осуществляется гораздо быстрее, чем по любому другому основанию.

• Что нужно сегодня для усыновления ребенка в России? Усыновление в России, кроме ответственного личного решения, предполагает ряд процедур государственной проверки кандидатов. Жесткий отбор на подготовительном этапе способствует более […]
• Сведения бесплатно по ИНН или ОГРН из реестра налоговой по всей России - онлайн На Едином портале Налоговых услуг могут быть получены сведения о государственной регистрации юридических лиц, индивидуальных предпринимателей, […]
• Наказание за езду без документов (водительские права, страховка, СТС) Иногда по забывчивости водители садятся за руль без ВУ и получают штраф за езду без документов. Напомним, что автолюбитель за рулём при себе в обязательном порядке […]
• Цветы мужчин. Какие цветы можно подарить мужчине? Какие цветы мужчине можно подарить? «Мужских» цветов не так много, но есть такие, которые дарят мужчинам. Маленький цветочный список перед вами: Хризантемы. Розы. Гвоздики. […]
• Служебная записка – это специальная форма документа, которая используется во внутренней среде предприятия и служит для быстрого решения текущих производственных проблем. Обычно этот документ составляется с целью внесения какого-либо […]
• Когда и как получить накопительную часть пенсии в Сбербанке? Сбербанк является банком-партнером государственного пенсионного фонда. На основании этого граждане, оформившие накопительную пенсию, могли переводить в него накопительную часть […]
• Детские пособия в Ульяновске и Ульяновской области в 2018 году Кроме того, во всех субъектах работают программы, утвержденные федеральным законодательством. Разберем, кто и на какие льготы может рассчитывать. Как региональные власти […]
• Подробное руководство, как составить доверенность на представление интересов физического лица в суде В гражданском или арбитражном иске, в административном или уголовном деле интересы и истца, и ответчика могут представляться поверенным: […]

В соотношении

может быть поставлена задача отыскания любого из трех чисел по двум другим, заданным. Если даны а и то N находят действием возведения в степень. Если даны N и то а находят извлечением корня степени х (или возведением в степень ). Теперь рассмотрим случай, когда по заданным а и N требуется найти х.

Пусть число N положительно: число а положительно и не равно единице: .

Определение. Логарифмом числа N по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить число N; логарифм обозначается через

Таким образом, в равенстве (26.1) показатель степени находят как логарифм N по основанию а. Записи

имеют одинаковый смысл. Равенство (26.1) иногда называют основным тождеством теории логарифмов; в действительности оно выражает определение понятия логарифма. По данному определению основание логарифма а всегда положительно и отлично от единицы; логарифмируемое число N положительно. Отрицательные числа и нуль логарифмов не имеют. Можно доказать, что всякое число при данном основании имеет вполне определенный логарифм. Поэтому равенство влечет за собой . Заметим, что здесь существенно условие в противном случае вывод был бы не обоснован, так как равенство верно при любых значениях х и у.

Пример 1. Найти

Решение. Для получения числа следует возвести основание 2 в степень Поэтому.

Можно проводить записи при решении таких примеров в следующей форме:

Пример 2. Найти .

Решение. Имеем

В примерах 1 и 2 мы легко находили искомый логарифм, представляя логарифмируемое число как степень основания с рациональным показателем. В общем случае, например для и т. д., этого сделать не удастся, так как логарифм имеет иррациональное значение. Обратим внимание на один связанный с этим утверждением вопрос. В п. 12 мы дали понятие о возможности определения любой действительной степени данного положительного числа. Это было необходимо для введения логарифмов, которые, вообще говоря, могут быть иррациональными числами.

Рассмотрим некоторые свойства логарифмов.

Свойство 1. Если число и основание равны, то логарифм равен единице, и, обратно, если логарифм равен единице, то число и основание равны.

Доказательство. Пусть По определению логарифма имеем а откуда

Обратно, пусть Тогда по определению

Свойство 2. Логарифм единицы по любому основанию равен нулю.

Доказательство. По определению логарифма (нулевая степень любого положительного основания равна единице, см. (10.1)). Отсюда

что и требовалось доказать.

Верно и обратное утверждение: если , то N = 1. Действительно, имеем .

Прежде чем сформулировать следующее свойство логарифмов, условимся говорить, что два числа а и b лежат по одну сторону от третьего числа с, если они оба либо больше с, либо меньше с. Если одно из этих чисел больше с, а другое меньше с, то будем говорить, что они лежат по разные стороны от с.

Свойство 3. Если число и основание лежат по одну сторону от единицы, то логарифм положителен; если число и основание лежат по разные стороны от единицы, то логарифм отрицателен.

Доказательство свойства 3 основано на том, что степень а больше единицы, если основание больше единицы и показатель положителен или основание меньше единицы и показатель отрицателен. Степень меньше единицы, если основание больше единицы и показатель отрицателен или основание меньше единицы и показатель положителен.

Требуется рассмотреть четыре случая:

Ограничимся разбором первого из них, остальные читатель рассмотрит самостоятельно.

Пусть тогда в равенстве показатель степени не может быть ни отрицательным, ни равным нулю, следовательно, он положителен, т. е. что и требовалось доказать.

Пример 3. Выяснить, какие из указанных ниже логарифмов положительны, какие отрицательны:

Решение, а) так как число 15 и основание 12 расположены по одну сторону от единицы;

б) , так как 1000 и 2 расположены по одну сторону от единицы; при этом несущественно, что основание больше логарифмируемого числа;

в) , так как 3,1 и 0,8 лежат по разные стороны от единицы;

г) ; почему?

д) ; почему?

Следующие свойства 4-6 часто называют правилами логарифмирования: они позволяют, зная логарифмы некоторых чисел, найти логарифмы их произведения, частного, степени каждого из них.

Свойство 4 (правило логарифмирования произведения). Логарифм произведения нескольких положительных чисел по данному основанию равен сумме логарифмов этих чисел по тому же основанию.

Доказательство. Пусть даны положительные числа .

Для логарифма их произведения напишем определяющее логарифм равенство (26.1):

Отсюда найдем

Сравнив показатели степени первого и последнего выражений, получим требуемое равенство:

Заметим, что условие существенно; логарифм произведения двух отрицательных чисел имеет смысл, но в этом случае получим

В общем случае, если произведение нескольких сомножителей положительно, то его логарифм равен сумме логарифмов модулей этих сомножителей.

Свойство 5 (правило логарифмирования частного). Логарифм частного положительных чисел равен разности логарифмов делимого и делителя, взятых по тому же основанию. Доказательство. Последовательно находим

что и требовалось доказать.

Свойство 6 (правило логарифмирования степени). Логарифм степени какого-либо положительного числа равен логарифму этого числа, умноженному на показатель степени.

Доказательство. Запишем снова основное тождество (26.1) для числа :

что и требовалось доказать.

Следствие. Логарифм корня из положительного числа равен логарифму подкоренного числа, деленному на показатель корня:

Доказать справедливость этого следствия можно, представив как и воспользовавшись свойством 6.

Пример 4. Прологарифмировать по основанию а:

а) (предполагается, что все величины b, с, d, е положительны);

б) (преполагается, что ).

Решение, а) Удобно перейти в данном выражении к дробным степеням:

На основании равенств (26.5)-(26.7) теперь можно записать:

Мы замечаем, что над логарифмами чисел производятся действия более простые, чем над самими числами: при умножении чисел их логарифмы складываются, при делении - вычитаются и т.д.

Именно поэтому логарифмы получили применение в вычислительной практике (см. п. 29).

Действие, обратное логарифмированию, называется потенцированием, а именно: потенцированием называется действие, с помощью которого по данному логарифму числа находится само это число. По существу потенцирование не является каким-либо особым действием: оно сводится к возведению основания в степень (равную логарифму числа). Термин «потенцирование» можно считать синонимом термина «возведенение в степень».

При потенцировании надо пользоваться правилами, обратными по отношению к правилам логарифмирования: сумму логарифмов заменить логарифмом произведения, разность логарифмов - логарифмом частного и т. д. В частности, если перед знаком логарифма находится какой-либо множитель, то его при потенцировании нужно переносить в показатель степени под знак логарифма.

Пример 5. Найти N, если известно, что

Решение. В связи с только что высказанным правилом потенцирования множители 2/3 и 1/3, стоящие перед знаками логарифмов в правой части данного равенства, перенесем в показатели степени под знаками этих логарифмов; получим

Теперь разность логарифмов заменим логарифмом частного:

для получения последней дроби в этой цепочке равенств мы предыдущую дробь освободили от иррациональности в знаменателе (п. 25).

Свойство 7. Если основание больше единицы, то большее число имеет больший логарифм (а меньшее - меньший), если основание меньше единицы, то большее число имеет меньший логарифм {а меньшее - больший).

Это свойство формулируют также и как правило логарифмирования неравенств, обе части которых положительны:

При логарифмировании неравенств по основанию, большему единицы, знак неравенства сохраняется, а при логарифмировании по основанию, меньшему единицы, знак неравенства меняется на противоположный (см. также п. 80).

Доказательство основано на свойствах 5 и 3. Рассмотрим случай, когда Если , то и, логарифмируя, получим

(а и N/М лежат по одну сторону от единицы). Отсюда

Случай а следует , читатель разберет самостоятельно.

274. Замечания.

а) Если в выражении, которое требуется вычислить, встречается сумма или разность чисел, то их надо находить без помощи таблиц обыкновенным сложением или вычитанием. Напр.:

log (35 +7,24) 5 = 5 log (35 + 7,24) = 5 log 42,24.

б) Умея логарифмировать выражения, мы можем, обратно, по данному результату логарифмирования найти то выражение, от которого получился этот результат; так, если

log х = log a + log b - 3 log с ,

то легко сообразить, что

в) Прежде чем перейти к рассмотрению устройства логарифмических таблиц, мы укажем некоторые свойства десятичных логарифмов, т.е. таких, в которых за основание принято число 10 (только такие логарифмы употребляются для вычислений).

Глава вторая.

Свойства десятичных логарифмов.

275 . а ) Так как 10 1 = 10, 10 2 = 100, 10 3 =1000, 10 4 = 10000 и т. д., то log 10 = 1, log 100 = 2, log 1000 = 3, log 10000 = 4, и т. д.

Значит, логарифм целого числа, изображаемого единицею с нулями, есть целое положительное число, содержащее столько единиц, сколько нулей в изображении числа.

Таким образом: log 100 000 = 5 , log 1000 000 = 6 , и т. д.

б ) Так как

log 0,1 = -l; log 0,01 = - 2; log 0,001 == -3; log 0,0001 = - 4, и т. д.

Значит, логарифм десятичной дроби, изображаемой единицею с предшествующими нулями, есть целое отрицательное число содержащее столько отрицательных единиц, сколько нулей в изображении дроби, считая в том числе и 0 целых.

Таким образом: log 0,00001= - 5, log 0,000001 = -6, и т. д.

в) Возьмем целое число, не изображаемое единицею с нулями, напр. 35, или целое число с дробью, напр. 10,7. Логарифм такого числа не может быть целым числом, так как, возвысив 10 в степень с целым показателем (положительным или отрицательным), мы получим 1 с нулями (следующими за 1, или ей предшествующими). Предположим теперь, что логарифм такого числа есть какая-нибудь дробь a / b . Тогда мы имели бы равенства

Но эти равенства невозможны, как как 10 а есть 1 с нулями, тогда как степени 35 b и 10,7 b ни при каком показателе b не могут дать 1 c нулями. Значит, нельзя допустить, чтобы log 35 и log 10,7 были равны дробям. Но из свойств логарифмической функции мы знаем (), что всякое положительное число имеет логарифм; следовательно, каждое из чисел 35 и 10,7 имеет свой логарифм, и так как он не может быть ни числом целым, ни числом дробным, то он есть число иррациональное и, следовательно, не может быть выражен точно посредством цифр. Обыкновенно иррациональные логарифмы выражают приближенно в виде десятичной дроби с несколькими десятичными знаками. Целое число этой дроби (хотя бы это было „0 целых") называется характеристикой , а дробная часть - мантиссой логарифма. Если, напр., логарифм есть 1,5441 , то характеристика его равна 1 , а мантисса есть 0,5441 .

г) Возьмем какое-нибудь целое или смешанное число, напр. 623 или 623,57 . Логарифм такого числа состоит из характеристики и мантиссы. Оказывается, что десятичные логарифмы обладают тем удобством, что характеристику их мы всегда можем найти по одному виду числа . Для этого сосчитаем, сколько цифр в данном целом числе, или в целой части смешанного числа, В наших примерах этих цифр 3 . Поэтому каждое из чисел 623 и 623,57 больше 100, но меньше 1000; значит, и логарифм каждого из них больше log 100 , т. е. больше 2 , но меньше log 1000 , т. е. меньше 3 (вспомним, что большее число имеет и больший логарифм). Следовательно, log 623 = 2 ,..., и log 623,57 = 2 ,... (точки заменяют собою неизвестные мантиссы).

Подобно этому найдем:

10 < 56,7 < 100 1 < log56,7 < 2 log 56,7 = 1,...

1000 < 8634 < 10 000 3 < log8634 < 4 log 8634 = 3,...

Пусть вообще в данной целом числе, или в целой части данного смешанного числа, содержится m цифр. Так как самое малое целое число, содержащее m цифр, есть 1 с m - 1 нулями на конце, то (обозначая данное число N ) можем написать неравенства:

и следовательно,

m - 1 < log N < m ,

log N = (m - 1) + положительная дробь .

Значит, характеристика logN = m - 1 .

Мы видим таким образом, что характеристика логарифма целого или смешанного числа содержит столько положительных единиц, сколько цифр в целой части числа без одной.

Заметив это, мы можем прямо писать:

log 7,205 = 0,...; log 83 = 1,...; log 720,4 = 2,... и т. п.

д) Возьмем несколько десятичных дробей, меньших 1 (т. е. имеющих 0 целых): 0,35; 0,07; 0,0056; 0,0008, и т. п.

Таким образом, каждый из этих логарифмов заключен между двумя целыми отрицательными числами, различающимися на одну единицу; поэтому каждый из них равен меньшему из этих отрицательных чисел, увеличенному на некоторую положительную дробь. Напр., log0,0056= -3 + положительная дробь . Предположим, что эта дробь будет 0,7482. Тогда, значит:

log 0,0056 = - 3 + 0,7482 (= - 2,2518).

Такие суммы, как - 3 + 0,7482 , состоящие из целого oтрицательного числа.и положительной десятичной дроби, условились при логарифмических вычислениях писать сокращенно так: 3 ,7482 (Такое число читается: 3 с минусом, 7482 десятитысячных .), т. е. ставят знак минус над характеристикой с целью показать, что он относится только к этой характеристике, а не к мантиссе, которая остается положительной. Таким образом, из приведенной выше таблички видно, что

log 0,35 == 1 ,....; log 0,07 = 2 ,....; log 0,0008 = 4 ,....

Пусть вообще . есть десятичная дробь, у которой перед первой значащей цифрой α стоит m нулей, считая в том числе и 0 целых. Тогда, очевидно, что

- m < log A < - (m - 1).

Так как из двух целых чисел:- m и - (m - 1) меньшее есть - m , то

log А = - m + положительная дробь ,

и потому характеристика log А = - m (при положительной мантиссе).

Таким образом, характеристика логарифма десятичной дроби, меньшей 1, содержит в себе столько отрицательных единиц, сколько нулей в изображении десятичной дроби перед первой значащей цифрой, считая в том числе и нуль целых; мантисса же такого логарифма положительна.

е) Умножим какое-нибудь число N (целое или дробное - всe равно) на 10, на 100 на 1000..., вообще на 1 c нулями. Посмотрим, как от этого изменится log N . Так как логарифм произведения равен сумме логарифмов сомножителей, то

log (N 10) = log N + log 10 = log N + 1;

log (N 100) = log N + log 100 = log N + 2;

log (N 1000) = log N + log 1000 = log N + 3; и т. д.

Когда к log N мы прибавляем какое-нибудь целое число, то это число мы может всегда прибавлять к характеристике, а не к мантиссе.

Так, если log N = 2,7804, то 2,7804 + 1 =3,7804; 2,7804 + 2 = 4,7801 и т. п.;

или если log N = 3 ,5649, то 3 ,5649 + 1 = 2 ,5649; 3 ,5649 + 2 = 1 ,5649, и т. п.

От умножения числа на 10, 100, 1000,.., вообще на 1 с нулями, мантисса логарифма не изменяется, а характеристика увеличивается на столько единиц, сколько нулей во множителе .

Подобно этому, приняв во внимание, что логарифм частного равен логарифму делимого без логарифма делителя, мы получим:

log N / 10 = log N- log 10 = log N -1;

log N / 100 = log N- log 100 = log N -2;

log N / 1000 = log N- log 1000 = log N -3; и т. п.

Если условимся при вычитании целого числа из логарифма вычитать это целое число всегда из характеристики, а мантиссу оставлять без изменения, то можно сказать:

От деления числа на 1 с нулями мантисса логарифма не изменяется, а характеристика уменьшается на столько единиц, сколько нулей в делителе.

276. Следствия. Из свойства (е ) можно вывести следующие два следствия:

а) Мантисса логарифма десятичного числа не изменяется от перенесения в числе запятой , потому что перенесение запятой равносильно умножению или делению на 10, 100, 1000 и т. д. Таким образом, логарифмы чисел:

0,00423, 0,0423, 4,23, 423

отличаются только характеристиками, но не мантиссами (при условии, что все мантиссы положительны).

б) Мантиссы чисел, имеющих одну и ту же значащую часть, но отличающихся только нулями на конце, одинаковы: так, логарифмы чисел: 23, 230, 2300, 23 000 отличаются только характеристиками.

Замечание. Из указанных свойств десятичных логарифмов видно, что характеристику логарифма целого числа и десятичной дроби мы можем находить без помощи таблиц (в этом заключается большое удобство десятичных логарифмов); вследствие этого в логарифмических таблицах помещаются только одни мантиссы; кроме того, так как нахождение логарифмов дробей сводится к нахождению логарифмов целых чисел (логарифм дроби = логарифму числителя без логарифма знаменателя), то в таблицах помещаются мантиссы логарифмов только целых чисел.

Глава третья.

Устройство и употребление четырехзначных таблиц.

277. Системы логарифмов. Системою логарифмов называется совокупность логарифмов, вычисленных для ряда последовательных целых чисел по одному и тому же основанию. Употребительны две системы: система обыкновенных или десятичных логарифмов, в которых за основание взято число 10 , и система так называемых натуральных логарифмов, в которых за основание (по некоторым причинам, которые уясняются в других отделах математики) взято иррациональное число 2,7182818 ... Для вычислений употребляются десятичные логарифмы, вследствие тех удобств, которые были нами указаны, когда мы перечисляли свойства таких логарифмов.

Натуральные логарифмы называются также Неперовыми по имени изобретателя логарифмов, шотландского математика Непера (1550-1617 гг.), а десятичные логарифмы - Бригговыми по имени профессора Бригга (современника и друга Непера), впервые составившего таблицы этих логарифмов .

278. Преобразование отрицательного логарифма в такой, у которого мантисса положительна, и обратное преобразование. Мы видели, что логарифмы чисел, меньших 1, отрицательны. Значит, они состоят из отрицательной характеристики и отрицательной мантиссы. Такие логарифмы всегда можно преобразовать так, что у них мантисса будет положительная, а характеристика останется отрицательной. Для этого достаточно прибавить к мантиссе положительную единицу, а к характеристике - отрицательную (от чего, конечно, величина логарифма не изменится).

Если, напр., мы имеем логарифм - 2,0873 , то можно написать:

- 2,0873 = - 2 - 1 + 1 - 0,0873 = - (2 + 1) + (1 - 0,0873) = - 3 + 0,9127,

или сокращенно:

Обратно, всякий логарифм с отрицательной характеристикой и положительной мантиссой можно превратить в отрицательный. Для этого достаточно к положительной мантиссе приложить отрицательную единицу, а к отрицательной характеристике - положительную : так, можно написать:

279. Описание четырехзначных таблиц. Для решения большинства практических задач вполне достаточны четырехзначные таблицы, обращение с которыми весьма просто . Таблицы эти (с надписью на верху их „логарифмы") помещены в конце этой книги, а небольшая часть их (для объяснения расположения) напечатана на этой странице. В них содержатся мантиссы

Логарифмы.

логарифмов всех целых чисел от 1 до 9999 включительно, вычисленные с четырьмя десятичными знаками, причем последний из этих знаков увеличен на 1 во всех тех случаях, когда 5-й десятичный знак должен был бы оказаться 5 или более 5; следовательно, 4-значные таблицы дают приближенные мантиссы с точностью до 1 / 2 десятитысячной доли (с недостатком или с избытком).

Так как характеристику логарифма целого числа или десятичной дроби мы можем, на основании свойств десятичных логарифмов, проставить непосредственно, то из таблиц мы должны взять только мантиссы; при этом надо вспомнить, что положение запятой в десятичном числе, а также число нулей, стоящих в конце числа, не имеют влияния на величину мантиссы. Поэтому при нахождении мантиссы по данному числу мы отбрасываем в этом числе запятую, а также и нули на конце его, если таковые есть, и находим мантиссу образовавшегося после этого целого числа. При этом могут представиться следующие случаи.

1) Целое число состоит из 3-х цифр. Напр., пусть надо найти мантиссу логарифма числа 536. Первые две цифры этого числа, т. е. 53, находим в таблицах в первом слева вертикальном столбце (см. таблицу). Найдя число 53, продвигаемся от него по горизонтальной строке вправо до пересечения этой строчки с вертикальным столбцом, проходящим через ту из цифр 0, 1, 2, 3,... 9, поставленных наверху (и внизу) таблицы, которая представляет собою 3-ю цифру данного числа, т. е. в нашем примере цифру 6. В пересечении получим мантиссу 7292 (т. е. 0,7292), принадлежащую логарифму числа 536. Подобно этому для числа 508 найдем мантиссу 0,7059, для числа 500 найдем 0,6990 и т. п.

2) Целое число состоит из 2-х или из 1-й цифры. Тогда мысленно приписываем к этому числу один или два нуля и находим мантиссу для образовавшегося таким образом трехзначного числа. Напр., к числу 51 приписываем один нуль, от чего получаем 510 и находим мантиссу 7070; к числу 5 приписываем 2 нуля и находим мантиссу 6990 и т. д.

3) Целое число выражается 4 цифрами. Напр., надо найти мантиссу log 5436. Тогда сначала находим в таблицах, как было сейчас указано, мантиссу для числа, изображенного первыми 3-мя цифрами данного числа, т. е. для 543 (эта мантисса будет 7348); затем продвигаемся от найденной мантиссы по горизонтальной строке направо (в правую часть таблицы, расположенную за жирной вертикальной чертой) до пересечения с вертикальным столбцом, проходящим через ту из цифр: 1, 2 3,... 9, стоящих на верху (и в низу) этой части таблицы, которая представляет собою 4-ю цифру данного числа, т. е. в нашем примере цифру 6. В пересечении находим поправку (число 5), которую надо приложить в уме к мантиссе 7348, чтобы получить мантиссу числа 5436; мы получим таким образом мантиссу 0,7353.

4) Целое число выражается 5-ю или более цифрами. Тогда отбрасываем все цифры, кроме первых 4-х, и берем приближенное четырехзначное число, причем последнюю цифру этого числа увеличиваем на 1 в том. случае, когда отбрасываемая 5-я цифра числа есть 5 или больше 5. Так, вместо 57842 мы берем 5784, вместо 30257 берем 3026, вместо 583263 берем 5833 и т. и. Для этого округленного четырехзначного числа находим мантиссу так, как было сейчас объяснено.

Руководствуясь этими указаниями, найдем для примера логарифмы следующих чисел:

36,5; 804,7; 0,26; 0,00345; 7,2634; 3456,06.

Прежде всего, не обращаясь пока к таблицам, проставим одни характеристики, оставляя место для мантисс, которые выпишем после:

log 36,5 = 1,.... log 0,00345 = 3 ,....

log 804,7 = 2,.... log 7,2634 = 0,....

log 0,26 = 1 ,.... log 3456,86 = 3,....

log 36,5 = 1,5623; log 0,00345 = 3 ,5378;

log 804,7 = 2,9057; log 7,2634 = 0,8611;

log 0,26 = 1 ,4150; log 3456,86 = 3,5387.

280. Замечание . В некоторых четырехзначных таблицах (напр, в таблицах В. Лорченко и Н. Оглоблина, С. Глазенапа, Н. Каменьщикова ) поправки на 4-ю цифру данного числа не помещены. Имея дело с такими таблицами, приходится поправки эти находить при помощи простого вычисления, которое можно выполнять на основании следующей истины: если числа превосходят 100, а разности между ними меньше 1, то без чувствительной погрешности можно принять, что разности между логарифмами пропорциональны разностям между соответствующими числами . Пусть, напр., надо найти мантиссу, соответствующую числу 5367. Мантисса эта, конечно, та же самая, что и для числа 536,7. Находим в таблицах для числа 536 мантиссу 7292. Сравнивая эту мантиссу с соседней вправо мантиссой 7300, соответствующей числу 537, мы замечаем, что если число 536 увеличится на 1, то мантисса его увеличится на 8 десятитысячных (8 есть так называемая табличная разность между двумя соседними мантиссами); если же число 536 увеличится на 0,7, то мантисса его увеличится не на 8 десятитысячных, а на некоторое меньшее число х десятитысячных, которое, согласно допущенной пропорциональности, должно удовлетворять пропорции:

х : 8 = 0,7: 1; откуда х = 8 07 = 5,6,

что по округлении составляет 6 десятитысячных. Значит, мантисса для числа 536,7 (и следовательно, для числа 5367) будет: 7292 + 6 = 7298.

Заметим, что нахождение по двум рядом стоящим в таблицах числам промежуточного числа называется интерполированием. Интерполирование, описанное здесь, называется пропорциональным , так как оно основано на допущении, что изменение логарифма пропорционально изменению числа. Оно называется также линейным , так как предполагает, что графически изменение логарифмической функции выражается прямою линией.

281. Предел погрешности приближенного логарифма. Если число, которого логарифм отыскивается, есть число т о ч н о е, то за предел погрешности его логарифма, найденного но 4-значным таблицам, можно, как мы говорили в , принять 1 / 2 десятитысячной доли. Если же данное число не точное , то к этому пределу погрешности надо еще добавить предел другой погрешности, происходящей от неточности самого числа. Доказано (мы опускаем это доказательство), что за такой предел можно принять произведение

a (d +1) десятитысячных.,

в котором а есть предел погрешности самого неточного числа в предположении, что в его целой части взяты 3 цифры , a d табличная разность мантисс, соответствующих двум последовательным трехзначным числам, между которыми заключается данное неточное число. Таким образом предел окончательной погрешности логарифма выразится тогда формулой:

1 / 2 + a (d +1) десятитысячных

Пример . Найти log π , принимая за π приближенное число 3,14, точное до 1 / 2 сотой.

Перенеся в числе 3,14 запятую после 3-й цифры, считая слева, мы получим трехзначное число 314, точное до 1 / 2 единицы; значит, предел погрешности неточного числа, т. е. то, что мы обозначили буквой а , есгь 1 / 2 Из таблиц находим:

log 3,14 = 0,4969.

Табличная разность d между мантиссами чисел 314 и 315 равна 14, поэтому погрешность найденного логарифма будет менее

1 / 2 + 1 / 2 (14 +1) = 8 десятитысячных .

Так как о логарифме 0,4969 мы не знаем, с недостатком ли он или с избытком, то можем только ручаться, что точный логарифм π заключается между 0,4969 - 0,0008 и 0,4969 + 0,0008, т. е. 0,4961 < log π < 0,4977.

282. Найти число по данному логарифму . Для нахождения числа по данному логарифму могут служить те же таблицы, по которым отыскиваются мантиссы данных чисел; но удобнее пользоваться другими таблицами, в которых помещены так называемые антилогарифмы, т. е. числа, соответствующие данным мантиссам. Таблицы эти, обозначенные надписью сверху „антилогарифмы", помещены в конце этой книги вслед за таблицами логарифмов; небольшая часть их помещена на этой странице (для объяснения).

Пусть дана 4-значная мантисса 2863 (на характеристику не обращаем внимания) и требуется найти соответствующее целое число. Тогда, имея таблицы антилогарифмов, надо пользоваться ими совершенно так же, как было раньше объяснено для нахождения мантисс по данному числу, а именно: первые 2 цифры мантиссы мы находим в первом слева столбце. Затем продвигаемся от этих цифр по горизонтальной строке вправо до пересечения с вертикальным столбцом, идущим от 3-й цифры мантиссы, которую надо искать в верхней строке (или в нижней). В пересечении находим четырехзначное число 1932, соответствующее мантиссе 286. Затем от этого числа продвигаемся дальше по горизонтальной строке направо до пересечения с вертикальным столбцом, идущим от 4-й цифры мантиссы, которую надо найти наверху (или внизу) среди поставленных там цифр 1, 2, 3,... 9. В пересечении мы находим поправку 1, которую надо приложить (в уме) к найденному раньше числу 1032, чтобы получить число, соответствующее мантиссе 2863.

Таким образом, число это будет 1933. После этого, обращая внимание на характеристику, надо в числе 1933 поставить занятую на надлежащем месте. Например:

если log x = 3,2863, то х = 1933,

„ log x = 1,2863, „ х = 19,33,

, log x = 0,2&63, „ х = 1,933,

„ log x = 2 ,2863, „ х = 0,01933

Вот еще примеры:

log x = 0,2287, х = 1,693,

log x = 1 ,7635, х = 0,5801,

log x = 3,5029, х = 3184,

log x = 2 ,0436, х = 0,01106.

Если в мантиссе указано 5 или более цифр, то берем только первые 4 цифры, отбрасывая остальные (и увеличивая 4-ю цифру на 1, если 5-я цифра есть пять или более). Напр., вместо мантиссы 35478 берем 3548, вместо 47562 берем 4756.

283. Замечание. Поправку на 4-ю и следующие цифры мантиссы можно находить и посредством интерполирования. Так, если мантисса будет 84357, то, найдя число 6966, соответствущее мантиссе 843 мы можем рассуждать далее так:: если мантисса увеличивается на 1 (тысячную), т. е. сделаетоя 844, то число, как видно из таблиц, увеличится на 16 единиц; если же мантисса увеличится не на 1 (тысячную), а на 0,57 (тысячной), то число увеличится на х единиц, причем х должно удовлетворять пропорции:

х : 16 = 0,57: 1, откуда х = 16 0,57 = 9,12.

Значит, искомое число будет 6966+ 9,12 = 6975,12 или (ограничиваясь только четырьмя цифрами) 6975.

284. Предел погрешности найденного числа. Доказано, что в том случае, когда в найденном числе запятая стоит после 3-й слева цифры, т. е. когда характеристика логарифма есть 2, за предел погрешности можно принять сумму

где а есть предел погрешности логарифма (выраженный в десятитысячных долях), по которому отыскивалось число, и d - разность между мантиссами двух трехзначных последовательных чисел, между которыми заключается найденное число (с запятой после 3-й цифры слева). Когда характеристика будет не 2, а какая-нибудь иная, то в найденном числе запятую придется перенести влево или вправо, т. е. разделить или умножить число на некоторую степень 10. При этом погрешность результата также разделится или умножится на ту же степень 10.

Пусть, например, мы отыскиваем число по логарифму 1,5950 , о котором известно, чго он точен до 3 десятитысячных; значит, тогда а = 3 . Число, соответствующее этому логарифму, найденное по таблице антилогарифмов, есть 39,36 . Перенеся запятую после 3-й цифры слева, будем иметь число 393,6 , заключающееся между 393 и 394 . Из таблиц логарифмов видим, что разность между мантиссами, соответствующими этим двум числам, составляет 11 десятитысячных; значит d = 11 . Погрешность числа 393,6 будет меньше

Значит, погрешность числа 39,36 будет меньше 0,05 .

285. Действия над логарифмами с отрицательными характеристиками. Сложение и вычитание логарифмов не представляют никаких затруднений, как это видно из следующих примеров:

Не представляет никаких затруднений также и умножение логарифма на положительное число, напр.:

В последнем примере отдельно умножена положительная мантисса на 34, затем отрицательная характеристика на 34.

Если логарифм о отрицательной характеристикой и положительной мантиссой умножается на отрицательное число, то поступают двояко: или предварительно данный логарифм обращают в отрицательный, или же умножают отдельно мантиссу и характеристику и результаты соединяют вместе, например:

3 ,5632 (- 4) = - 2,4368 (- 4) = 9,7472;

3 ,5632 (- 4) = + 12 - 2,2528 = 9,7472.

При делении могут представиться два случая: 1) отрицательная характеристика делится и 2) не делится на делитель. В первом случае отдельно делят характеристику и мантиссу:

10 ,3784: 5 = 2 ,0757.

Во втором случае прибавляют к характеристике столько отрицательных единиц, чтобы образовавшееся число делилось на делитель; к мантиссе прибавляют столько же положительных единиц:

3 ,7608: 8 = (- 8 + 5,7608) : 8 = 1 ,7201.

Это преобразование надо совершать в уме, так что действие располагается так:

286. Замена вычитаемых логарифмов слагаемыми. При вычислении какого-нибудь сложного выражения помощью логарифмов приходится некоторые логарифмы складывать, другие вычитать; в таком случае, при обыкновенном способе совершения действий, находят отдельно сумму слагаемых логарифмов, потом сумму вычитаемых и из первой суммы вычитают вторую. Напр., если имеем:

log х = 2,7305 - 2 ,0740 + 3 ,5464 - 8,3589 ,

то обыкновенное выполнение действий расположится так:

Есть однако возможность заменить вычитание сложением. Так:

Теперь можно расположить вычисление так:

287. Примеры вычислений.

Пример 1 . Вычислить выражение:

если А = 0,8216, В = 0,04826, С= 0,005127 и D = 7,246.

Логарифмируем данное выражение:

log х = 1 / 3 log A + 4 log В - 3 log С - 1 / 3 log D

Теперь, для избежания излишней потери времени и для уменьшения возможности ошибок, прежде всего расположим все вычисления, не исполняя пока их и не обращаясь, следовательно, к таблицам:

После этого берем таблицы и проставляем логарифмы на оставленных свободных местах:

Прeдел погрешности. Сначала найдем предел погрешности числа x 1 = 194,5 , равный:

Значит, прежде всего надо найти а , т. е. предел погрешности приближенного логарифма, выраженный в десятитысячных долях. Допустим, что данные числа А, В, С и D все точные. Тогда погрешности в отдельных логарифмах будут следующие (в десятитысячных долях):

в logА .......... 1 / 2

в 1 / 3 log A ......... 1 / 6 + 1 / 2 = 2 / 3

( 1 / 2 прибавлена потому, что при делении на 3 логарифма 1,9146 мы округлили частное, отбросив 5-ю цифру его, и, следовательно, сделали еще ошибку,меньшую 1 / 2 десятитысячной).

Теперь находим предел погрешности логарифма:

а = 2 / 3 + 2 + 3 / 2 + 1 / 6 = 4 1 / 3 (десятитысячных).

Определим далее d . Так как x 1 = 194,5 , то 2 целых последовательных числа, между которыми заключается x 1 будут 194 и 195 . Табличная разность d между мантиссами, соответствующими этим числам, равна 22 . Значит, предел погрешности числа x 1 есть:

Так как x = x 1 : 10, то предел погрешности в числе x равен 0,3:10 = 0,03 . Таким образом, найденное нами число 19,45 разнится от точного числа менее, чем на 0,03 . Так как мы не знаем, с недостатком или с избытком найдено наше приближение, то можем только ручаться, что

19,45 + 0,03 > х > 19,45 - 0,03 , т. е.

19,48 > х > 19,42 ,

и потому, если примем х =19,4 , то будем иметь приближение с недостатком с точностью до 0,1.

Пример 2. Вычислить:

х = (- 2,31) 3 5 √72 = - (2,31) 3 5 √72 .

Так как отрицательные числа не имеют логарифмов, то предварительно находим:

х" = (2,31) 3 5 √72

по разложению:

log х" = 3 log 2,31 + 1 / 5 log72 .

После вычисления окажется:

х" = 28,99 ;

следовательно,

x = - 28,99 .

Пример 3 . Вычислить:

Сплошного логарифмирования здесь применить нельзя, так как под знаком корня стоит с у м м а. В подобных случаях вычисляют формулу по частям .

Сначала находим N = 5 √8 , потом N 1 = 4 √3 ; далее простым сложением определяем N + N 1 , и, наконец, вычисляем 3 √N + N 1 ; окажется:

N = 1,514 , N 1 = 1,316 ; N + N 1 = 2,830 .

log x = log 3 √2,830 = 1 / 3 log 2,830 = 0,1506 ;

x = 1,415 .

Глава четвертая.

Показательные и логарифмические уравнения.

288. Показательными уравнениями называются такие, в которых неизвестное входит в показатель степени, а логарифмическими - такие, в которых неизвестное входит под знаком log . Такие уравнения могут быть разрешаемы только в частных случаях, причем приходится основываться на свойствах логарифмов и на том начале, что если числа равны, то равны и их логарифмы, и, обратно, если логарифмы равны, то равны и соответствующие им числа.

Пример 1. Решить уравнение: 2 x = 1024 .

Логарифмируем обе части уравнения:

Пример 2. Решить уравнение: a 2x - a x = 1 . Положив a x = у , получим квадратное уравнение:

y 2 - у - 1 = 0 ,

Так как 1-√5 < 0 , то последнее уравнение невозможно (функция a x всегда есть число положительное), а первое дает:

Пример 3. Решить уравнение:

log (а + x ) + log (b + х ) = log (с + x ) .

Уравнение можно написать так:

log [(а + x ) (b + х )] = log (с + x ) .

Из равенства логарифмов заключаем о равенстве чисел:

(а + x ) (b + х ) = с + x .

Это есть квадратное уравнение, решение которого не представляет затруднений.

Глава пятая.

Сложные проценты, срочные уплаты и срочные взносы.

289. Основная задача на сложные проценты. В какую сумму обратится капитал а рублей, отданный в рост по р сложных процентов, по прошествии t лет (t - целое число)?

Говорят, что капитал отдан по сложным процентам, если принимаются во внимание так называемые „проценты на проценты", т. е. если причитающиеся на капитал процентные деньги присоединяются в конце каждого года к капиталу для наращения их процентами в следующие годы.

Каждый рубль капитала, отданного по р %, в течение одного года принесет прибыли p / 100 рубля, и, следовательно, каждый рубль капитала через 1 год обратится в 1 + p / 100 рубля (напр., если капитал отдан по 5 % , то каждый рубль его через год обратится в 1 + 5 / 100 , т. е. в 1,05 рубля).

Обозначив для краткости дробь p / 100 одною буквою, напр, r , можем сказать, что каждый рубль капитала через год обратится в 1 + r рублей; следовательно, а рублей обратятся через 1 год в а (1 + r ) руб. Еще через год, т. е. через 2 года от начала роста, каждый рубль из этих а (1 + r ) руб. обратится снова в 1 + r руб.; значит, весь капитал обратится в а (1 + r ) 2 руб. Таким же образом найдем, что через три года капитал будет а (1 + r ) 3 , через четыре года будет а (1 + r ) 4 ,... вообще через t лет, если t есть целое число, он обратится в а (1 + r ) t руб. Таким образом, обозначив через А окончательный капитал, будем иметь следующую формулу сложных процентов:

А = а (1 + r ) t где r = p / 100 .

Пример. Пусть a =2 300 руб., p = 4, t =20 лет; тогда формула дает:

r = 4 / 100 = 0,04 ; А = 2 300 (1,04) 20 .

Чтобы вычислить А , применяем логарифмы:

log a = log 2 300 + 20 log 1,04 = 3,3617 + 20 0,0170 = 3,3617+0,3400 = 3,7017.

A = 5031 рубль.

Замечание. В этом примере нам пришлось log 1,04 умножить на 20 . Так как число 0,0170 есть приближенное значение log 1,04 с точностью до 1 / 2 десятитысячной доли, то произведение этого числа на 20 будет точно только до 1 / 2 20, т. е. до 10 десятитысячных =1 тысячной. Поэтому в сумме 3,7017 мы не можем ручаться не только за цифру десятитысячных, но и за цифру тысячных. Чтобы в подобных случаях можно было получить большую точность, лучше для числа 1 + r брать логарифмы не 4-значные, а с большим числом цифр, напр. 7-значные. Для этой цели мы приводим здесь небольшую табличку, в которой выписаны 7-значные логарифмы для наиболее употребительных значений р .

290. Основная задача на срочные уплаты. Некто занял а рублей по р % с условием погасить долг, вместе с причитающимися на него процентами, в t лет, внося в конце каждого года одну и ту же сумму. Какова должна быть эта сумма?

Сумма x , вносимая ежегодно при таких условиях, называется срочною уплатою. Обозначим опять буквою r ежегодные процентные деньги с 1 руб., т. е. число p / 100 . Тогда к концу первого года долг а возрастает до а (1 + r ), аза уплатою х рублей он сделается а (1 + r )-х .

К концу второго года каждый рубль этой суммы снова обратится в 1 + r рублей, и потому долг будет [а (1 + r )-х ](1 + r ) = а (1 + r ) 2 - x (1 + r ), а за уплатою x рублей окажется: а (1 + r ) 2 - x (1 + r ) - х . Таким же образом убедимся, что к концу 3-го года долг будет

а (1 + r ) 3 - x (1 + r ) 2 - x (1 + r ) - x ,

и вообще и концу t -го года он окажется:

а (1 + r ) t - x (1 + r ) t -1 - x (1 + r ) t -2 ... - x (1 + r ) - x , или

а (1 + r ) t - x [ 1 + (1 + r ) + (1 + r ) 2 + ...+ (1 + r ) t -2 + (1 + r ) t -1 ]

Многочлен, стоящий внутри скобок , представляет сумму членов геометрической прогрессии; у которой первый член есть 1 , последний (1 + r ) t -1 , а знаменатель (1 + r ). По формуле для суммы членов геометрической прогрессии (отдел 10 глава 3 § 249) находим:

и величина долга после t -ой уплаты будет:

По условию задачи, долг в конце t -го года должен равняться 0 ; поэтому:

откуда

При вычислении этой формулы срочных уплат помощью логарифмов мы должны сначала найти вспомогательное число N = (1 + r ) t по логарифму: log N= t log (1 + r ) ; найдя N , вычтем из него 1, тогда получим знаменатель формулы для х, после чего вторичным логарифмированием найдем:

log х = log a + log N + log r - log (N - 1) .

291. Основная задача на срочные взносы. Некто вносит в банк в начале каждого года одну и ту же сумму а руб. Определить, какой капитал образуется из этих взносов по прошествии t лет, если банк платит по р сложных процентов.

Обозначив через r ежегодные процентные деньги с 1 рубля, т. е. p / 100 , рассуждаем так: к концу первого года капитал будет а (1 + r );

в начале 2-го года к этой сумме прибавится а рублей; значит, в это время капитал окажется а (1 + r ) + a . К концу 2-го года он будет а (1 + r ) 2 + а (1 + r );

в начале 3-го года снова вносится а рублей; значит, в это время капитал будет а (1 + r ) 2 + а (1 + r ) + а ; к концу 3-го он окажется а (1 + r ) 3 + а (1 + r ) 2 + а (1 + r ) Продолжая эти рассуждения далее, найдем, чтo к концу t -го года искомый капитал A будет:

Такова формула срочных взносов, делаемых в начале каждого года.

Ту же формулу можно получить и таким рассуждением:. первый взнос в а рублей, находясь в банке t лет, обратится, согласно формуле сложных процентов, в а (1 + r ) t руб. Второй взнос, находясь в банке одним годом меньше, т. е. t - 1 лет, обратится в а (1 + r ) t- 1 руб. Подобно этому третий взнос даст а (1 + r ) t- 2 и т. д., и, наконец, последний взнос, находясь в банке только 1 год, обратится в а (1 + r ) руб. Значит, окончательный капитал A руб. будет:

A = а (1 + r ) t + а (1 + r ) t- 1 + а (1 + r ) t- 2 + . . . + а (1 + r ),

что, после упрощения, дает найденную выше формулу.

При вычислении помощью логарифмов этой формулы надо поступить так же, как и при вычислении формулы срочных уплат, т. е. сначала найти число N = (1 + r ) t по его логарифму: log N= t log (1 + r ), затем число N- 1 и уже тогда логарифмировить формулу:

log A = log a + log (1 + r ) + log (N - 1) - 1оg r

Замечание. Если бы срочный взнос в а руб. производился не в начале, а в конце каждого года (как, напр., вносится срочная уплата х для погашения долга), то, рассуждая подобно предыдущему, найдем, что к концу t -го года искомый капитал А" руб. будет (считая в том числе и последний взнос а руб., не приносящий процентов):

A" = а (1 + r ) t- 1 + а (1 + r ) t- 2 + . . . + а (1 + r ) + а

что равно:

т. е. А" оказывается в (1 + r ) pаз менее А , что и надо было ожидать, так как каждый рубль капитала А" лежит в банке годом меньше, чем соответствующий рубль капитала А .

\(a^{b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)

Объясним проще. Например, \(\log_{2}{8}\) равен степени, в которую надо возвести \(2\), чтоб получить \(8\). Отсюда понятно, что \(\log_{2}{8}=3\).

Примеры:		\(\log_{5}{25}=2\)		т.к. \(5^{2}=25\)
		\(\log_{3}{81}=4\)		т.к. \(3^{4}=81\)
		\(\log_{2}\)\(\frac{1}{32}\) \(=-5\)		т.к. \(2^{-5}=\)\(\frac{1}{32}\)

Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:

Аргумент логарифма обычно пишется на его уровне, а основание - подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».

Как вычислить логарифм?

Чтобы вычислить логарифм - нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Например , вычислите логарифм: а) \(\log_{4}{16}\) б) \(\log_{3}\)\(\frac{1}{3}\) в) \(\log_{\sqrt{5}}{1}\) г) \(\log_{\sqrt{7}}{\sqrt{7}}\) д) \(\log_{3}{\sqrt{3}}\)

а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:

\(\log_{4}{16}=2\)

\(\log_{3}\)\(\frac{1}{3}\) \(=-1\)

в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!

\(\log_{\sqrt{5}}{1}=0\)

г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе.

\(\log_{\sqrt{7}}{\sqrt{7}}=1\)

д) В какую степень надо возвести \(3\), чтобы получить \(\sqrt{3}\)? Из мы знаем, что – это дробная степень, и значит квадратный корень - это степень \(\frac{1}{2}\) .

\(\log_{3}{\sqrt{3}}=\)\(\frac{1}{2}\)

Пример : Вычислить логарифм \(\log_{4\sqrt{2}}{8}\)

Решение :

\(\log_{4\sqrt{2}}{8}=x\)		Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма: \(\log_{a}{c}=b\) \(\Leftrightarrow\) \(a^{b}=c\)
\((4\sqrt{2})^{x}=8\)		Что связывает \(4\sqrt{2}\) и \(8\)? Двойка, потому что и то, и другое число можно представить двойки: \(4=2^{2}\) \(\sqrt{2}=2^{\frac{1}{2}}\) \(8=2^{3}\)
\({(2^{2}\cdot2^{\frac{1}{2}})}^{x}=2^{3}\)		Слева воспользуемся свойствами степени: \(a^{m}\cdot a^{n}=a^{m+n}\) и \((a^{m})^{n}=a^{m\cdot n}\)
\(2^{\frac{5}{2}x}=2^{3}\)		Основания равны, переходим к равенству показателей
\(\frac{5x}{2}\) \(=3\)		Умножим обе части уравнения на \(\frac{2}{5}\)
		Получившийся корень и есть значение логарифма

Ответ : \(\log_{4\sqrt{2}}{8}=1,2\)

Зачем придумали логарифм?

Чтобы это понять, давайте решим уравнение: \(3^{x}=9\). Просто подберите \(x\), чтобы равенство сработало. Конечно, \(x=2\).

А теперь решите уравнение: \(3^{x}=8\).Чему равен икс? Вот в том-то и дело.

Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как \(x=\log_{3}{8}\).

Хочу подчеркнуть, что \(\log_{3}{8}\), как и любой логарифм - это просто число . Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: \(1,892789260714.....\)

Пример : Решите уравнение \(4^{5x-4}=10\)

Решение :

\(4^{5x-4}=10\)		\(4^{5x-4}\) и \(10\) никак к одному основанию не привести. Значит тут не обойтись без логарифма. Воспользуемся определением логарифма: \(a^{b}=c\) \(\Leftrightarrow\) \(\log_{a}{c}=b\)
\(\log_{4}{10}=5x-4\)		Зеркально перевернем уравнение, чтобы икс был слева
\(5x-4=\log_{4}{10}\)		Перед нами . Перенесем \(4\) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу.
\(5x=\log_{4}{10}+4\)		Поделим уравнение на 5
\(x=\)\(\frac{\log_{4}{10}+4}{5}\)		Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Ответ : \(\frac{\log_{4}{10}+4}{5}\)

Десятичный и натуральный логарифмы

Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:

Натуральный логарифм: логарифм, у которого основание - число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).

То есть, \(\ln{a}\) это то же самое, что и \(\log_{e}{a}\)

Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg{a}\).

То есть, \(\lg{a}\) это то же самое, что и \(\log_{10}{a}\) , где \(a\) - некоторое число.

Основное логарифмическое тождество

У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:

\(a^{\log_{a}{c}}=c\)

Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.

Вспомним краткую запись определения логарифма:

если \(a^{b}=c\), то \(\log_{a}{c}=b\)

То есть, \(b\) – это тоже самое, что \(\log_{a}{c}\). Тогда мы можем в формуле \(a^{b}=c\) написать \(\log_{a}{c}\) вместо \(b\). Получилось \(a^{\log_{a}{c}}=c\) – основное логарифмическое тождество.

Остальные свойства логарифмов вы можете найти . С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.

Пример : Найдите значение выражения \(36^{\log_{6}{5}}\)

Решение :

Ответ : \(25\)

Как число записать в виде логарифма?

Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\).

Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\) . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается

\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}...\)

Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.

Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:

\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}...\)

И с четверкой:

\(4=\log_{2}{16}=\log_{3}{81}=\log_{4}{256}=\log_{5}{625}=\log_{6}{1296}=\log_{7}{2401}...\)

И с минус единицей:

\(-1=\) \(\log_{2}\)\(\frac{1}{2}\) \(=\) \(\log_{3}\)\(\frac{1}{3}\) \(=\) \(\log_{4}\)\(\frac{1}{4}\) \(=\) \(\log_{5}\)\(\frac{1}{5}\) \(=\) \(\log_{6}\)\(\frac{1}{6}\) \(=\) \(\log_{7}\)\(\frac{1}{7}\) \(...\)

И с одной третьей:

\(\frac{1}{3}\) \(=\log_{2}{\sqrt{2}}=\log_{3}{\sqrt{3}}=\log_{4}{\sqrt{4}}=\log_{5}{\sqrt{5}}=\log_{6}{\sqrt{6}}=\log_{7}{\sqrt{7}}...\)

Любое число \(a\) может быть представлено как логарифм с основанием \(b\): \(a=\log_{b}{b^{a}}\)

Пример : Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)

Решение :

Ответ : \(1\)