Цели урока:

Сформировать знания, умения и навыки эффективного применения обобщенного метода интервалов, основанного на свойстве непрерывных функций;

Сформулировать алгоритм действий, приводящий к равносильным преобразованиям;

Научить самостоятельно применять его при решении неравенств;

Осуществлять перенос знаний, умений и навыков в новые условия.

Образовательная: систематизация, закрепление, обобщение знаний, умений и навыков.

Воспитательная: воспитание потребности полноценной последовательной аргументации, аккуратности, самостоятельности.

Развивающая: развитие математической логики, формирование математического стиля мышления (четкой расчлененности хода рассуждений), познавательного интереса.

1) Введение, постановка цели и задач урока - 2 мин.

2) Проверка домашнего задания - 2 мин. (фронтальная работа, самоконтроль).

3) Математическое обоснование этапов решения неравенств методом интервалов - 4 мин (подготовленные ответы учащихся).

4) Повторение свойств неравенств – 2 мин.

5) Подготовка к усвоению (изучению) нового учебного материала через повторение и актуализацию опорных знаний – 5 мин. (фронтальная работа, ответы на вопросы, проблемные ситуации).

6) Обобщенный метод интервалов для решения неравенств, первичное осмысление – 13 мин. (коллективное решение неравенств методом интервалов: на доске и в тетрадях).

7) Информация о домашнем задании, инструкция о выполнении – 1 мин.

8) Закрепление новых знаний – 15 мин. (самостоятельная работа – вариант 1).

9) Подведение итогов урока, рефлексия – 1 мин.

1) Введение, постановка цели и задач урока. (Рассказ учителя)

1) Необходимость более широкого применения метода интервалов в школе диктуется идеологией всего процесса обучения математике. Речь идет о том, что функциональная линия (одна из главных при изучении основ математики) получает мощную технологическую поддержку. Метод интервалов базируется на таких важнейших характеристиках функциональной зависимости, как нули функции, промежутки ее знакопостоянства и монотонности. Тогда становится более наглядным функциональное происхождение уравнений и неравенств, а также методов их решения. Более наглядными становятся категории непрерывности функции, поведение ее графика в окрестностях точек бесконечного разрыва, теоремы о корне, знакопостоянстве, экстремальных точках и их видах. И все это органично увязывается в одно функциональное целое.

С другой стороны, неоценимое значение имеет и геометризация используемых объектов исследования, т.е. наглядно, образно представить весь используемый математический инструментарий функциональной зависимости.

Базовые принципы, заложенные в основу метода интервалов:

• функциональный (обобщенный) подход;
• опора на геометризацию функциональных свойств;
• визуализация исследования.

Это приводит к следующим преимуществам метода по сравнению с другими, использующимися в такого же рода задачах: простота и скорость достижения цели; наглядность (и возможность контроля или перепроверки); экономность в вычислительных средствах и времени; широта охвата всей ситуации, формирование и развитие навыков обобщенного мышления и анализа, а также связанные с этим умения делать логические выводы.

2) Проверка домашнего задания. (Слайд №4)

3) Рассказ о методе интервалов для решения неравенств. (Ответы учащихся).

Математическое обоснование решения неравенств методом интервалов.

1) Рассмотрим неравенства: (x-2)(x-3)>0. (слайд № 5)

Можно решать так: Произведение (частное) двух множителей положительно тогда и только тогда, когда оба множителя одного знака, т.е. неравенство равносильно совокупности двух систем: (слайд № 6)

Из первой системы получаем x >3, из второй x < 2.

Решением является объединение решений двух систем.

Ответ:

Графический метод (слайд № 7)

Другой метод – метод интервалов (слайд № 8).

Его идея состоит в следующем.

Отметим на числовой прямой нули (корни) многочлена (x-2)(x-3), стоящего

в левой части неравенства, т.е. числа 2 и 3.

Когда x >3 (правее большего корня), то (x-2)(x-3)>0, так как каждый множитель положителен.

Если двигаться по оси в отрицательном направлении, то при переходе через точку х=3 множитель (х-3) поменяет знак. В произведении (х-2)(х-3) появится один отрицательный множитель, в результате (х-2)(х-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

Теперь легко записать решение неравенства:

Вывод: произведение может изменить знак лишь при переходе через точки х=2 и х=3

и, следовательно, сохраняет знак на каждом из полученных промежутков.

На этом простом примере легко понять идею метода интервалов, но нельзя увидеть его заметных преимуществ.

Рациональность метода интервалов, его могущество рассмотрим на следующем примере (слайд № 9, 10,11, 12))

2) Решить неравенство (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9)(x-10)>0.

Чтобы решить это неравенство с помощью совокупности систем, пришлось бы рассматривать совокупность, состоящую из 512 систем по 10 неравенств в каждой системе.

Применим метод интервалов. Отметим на числовой прямой нули многочлена. На промежутке x>10 многочлен будет положительным, так как каждый множитель положителен. При переходе через каждый следующий корень многочлен будет менять знак, так как в произведении будет появляться дополнительный отрицательный множитель. Теперь легко записать решение неравенства, используя чередование знаков.

Преимущества метода интервалов.

• простота и скорость достижения цели;
• наглядность (и возможность контроля или перепроверки);
• значительное сокращение объема вычислительной работы и времени;
• широта охвата всей ситуации;
• формирование и развитие навыков обобщенного мышления и анализа, а также связанные с этим умения делать логические выводы.

Замечание. Очень удобно решать неравенства, левая часть которых разложена на множители, так как не представляет труда найти нули (корни).

Задание: Решить неравенство методом интервалов (x+3) 3 (x-4) 2 (x-5)>0 (Слайд 13)

4) Повторение свойств неравенств.

а) Вопрос: Какие неравенства называют равносильными?

(Два неравенства называются равносильными, если любое решение первого неравенства является решением второго и, обратно, любое решение второго является решением первого).

Или: два неравенства называются равносильными, если множества их решений совпадают.

Слайд 14. Повторение свойств неравенств.

Слайд 15. Дать ответ на вопрос и объяснить.

Равносильны ли неравенства?

1) 4х-5<0 и 4х<5

2) -2х+5>0 и 2х-5<0

3) -3х 2 +5х-7>0 и 3х 2 -5х+7<0

4) (х+1)>0 и (х 2 +5х+10)(х+1)>0

5) Устная фронтальная работа по подготовке к усвоению (изучению) нового учебного материала через повторение и актуализацию опорных знаний.

Слайд 16. Определение функции непрерывной в точке.

Слайд 17. Свойство непрерывных функций.

Слайд 18. Найти промежутки непрерывности.

Слайд 19. Найди ошибку.

Слайд 20. Решить неравенство устно,
используя график.

Слайд 21, 22. Замена неравенства на равносильное условие.

Решить неравенство

Данное неравенство равносильно условию f(x)< 0, считая

Следовательно, надо найти все значения x, для которых выполнено условие f(x)< 0.

6) Обобщенный метод интервалов для решения неравенств, первичное осмысление – 10 мин. (коллективное решение неравенств методом интервалов: на доске и в тетрадях).

Слайд 23 . Алгоритм. Обобщенный метод решения неравенств.

Решение неравенств f(x)>0, f(x)> 0, f(x)<0, f(x)< 0 методом интервалов. (Схема)

Слайд 24 и 25. Решение неравенства по алгоритму. (Комментарии ко всем пунктам алгоритма).

Слайд 26 . Графическая иллюстрация решения этого неравенства.

Слайд 27. Решить неравенство на доске и в тетрадях .

Слайд 28. Графическая иллюстрация решения этого неравенства.

Слайд 29. Решить неравенство на доске и в тетрадях

Слайд 30. Графическая иллюстрация решения этого неравенства.

Слайд 31, 32. Решить неравенство устно, по рисунку

7) Информация о домашнем задании. (Решить методом интервалов вариант №2 )

8) Закрепление новых знаний (самостоятельная работа, вариант №1).

9) Подведение итогов урока, самоконтроль по готовым решениям (слайды 33, 34, 35), повторение алгоритма обобщенного метода интервалов и его применения.

10) Анализ усвоения материала и интереса учащихся к теме. Этот метод является универсальным при решении любых неравенств, в том числе, рациональных, с модулем, иррациональных, показательных, логарифмических, так как метод интервалов сводит решение неравенств к решению уравнений, нахождение области определения и значения функции в точке не вызывает затруднений. Но пришлось приводить примеры неравенств, где применение этого метода не оправдано, где рациональнее применить другие методы решения неравенств.

Презентация “Применение непрерывности при решении неравенств”. (35 слайдов)

Определение 4. Функция называется непрерывной на отрезке, если она непрерывна в каждой точке этого отрезка (в точке a непрерывна справа, т.е. , а в точке b непрерывна слева, т. е.).

Все основные элементарные функции непрерывны в области их определения.

Свойства функций, непрерывных на отрезке:

• 1) Если функция непрерывна на отрезке, то она ограничена на этом отрезке (первая теорема Вейерштрасса).
• 2) Если функция непрерывна на отрезке, то на этом отрезке она достигает своего наименьшего значения и наибольшего значения (вторая теорема Вейерштрасса) (см. рис. 2).
• 3) Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то внутри отрезка существует хотя бы одна точка такая, что (теорема Больцано-Коши).

Точки разрыва функции и их классификация

функция непрерывность точка отрезок

Точки, в которых условие непрерывности не выполняется, называются точками разрыва этой функции. Если - точка разрыва функции, то в ней не выполняется хотя бы одно из трех условий непрерывности функции, указанных в определениях 1, 2, а именно:

1) Функция определена в окрестности точки, но не определена в самой точке. Так функция, рассмотренная в примере 2 а) имеет разрыв в точке, так как не определена в этой точке.

2) Функция определена в точке и ее окрестности, существуют односторонние пределы и, но они не равны между собой: . Например, функция из примера 2 б) определена в точке и ее окрестности, но, так как, а.

3) Функция определена в точке и ее окрестности, существуют односторонние пределы и, они равны между собой, но не равны значению функции в точке: . Например, функция. Здесь - точка разрыва: в этой точке функция определена, существуют односторонние пределы и, равные между собой, но, т. е. .

Точки разрыва функции классифицируются следующим образом.

Определение 5. Точка называется точкой разрыва первого рода функции, если в этой точке существуют конечные пределы и, но они не равны между собой: . Величина называется при этом скачком функции в точке.

Определение 6 . Точка называется точкой устранимого разрыва функции, если в этой точке существуют конечные пределы и, они равны между собой: , но сама функция не определена в точке, или определена, но.

Определение 7. Точка называется точкой разрыва второго рода функции, если в этой точке хотя бы один из односторонних пределов (или) не существует или равен бесконечности.

Пример 3. Найти точки разрыва следующих функций и определить их тип: а) б)

Решение. а) Функция определена и непрерывна на интервалах, и, так как на каждом из этих интервалов она задана непрерывными элементарными функциями. Следовательно, точками разрыва данной функции могут быть только те точки, в которых функция меняет свое аналитическое задание, т.е. точки и. Найдем односторонние пределы функции в точке:

Так как односторонние пределы существуют и конечны, но не равны между собой, то точка является точкой разрыва первого рода. Скачок функции:

Для точки находим.

Непрерывность функции на промежутке

Наименование параметра	Значение
Тема статьи:	Непрерывность функции на промежутке
Рубрика (тематическая категория)	Математика

Определœение. Функция принято называть непрерывной на интервале, в случае если она непрерывна в каждой точке этого интервала.

В случае если функция определœена при х = а и при этом f (х ) = f (а ),

то говорят, что f (х ) в точке а непрерывна справа . Аналогично, в случае если f (х ) = f (b ), то говорят, что в точке b эта функция непрерывна слева .

Определœение. Функция принято называть непрерывной на отрезке [a , b ], в случае если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева).

Наибольшим значением функции у = f (x ) на отрезке [a , b f (x 1), что f (x ) £ f (x 1) для всœех х Î [a , b ].

Наименьшим значением функции у = f (x ) на отрезке [a , b ] принято называть такое её значение f (x 2), что f (x ) ³ f (x 2) для всœех х Î [a , b ].

Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.

Теорема 3.3.1. Функция, непрерывная на отрезке [a , b ], достигает на нём своего наименьшего значения m и наибольшего значения M , то есть существуют такие точки x 1 и x 2 этого отрезка, что f (x 1) = m , f (x 2) = M .

Теорема имеет простой геометрический смысл (см. рис.2).

Теорема 3.3.2. В случае если функция у = f (x ) непрерывна на отрезке [a , b ] и на его концах принимает неравные значения f (а ) = А, f (b ) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [a , b ] такая, что f (с ) = С.

Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f (x ).

Следствие. В случае если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль.

Геометрический смысл следствия иллюстрируется на рис.4.

Вопросы для самоконтроля

1. Какая функция принято называть непрерывной в точке?

2. Приведите еще одно эквивалентное определœение через приращение функции и аргументов.

3. Что можно сказать о сумме, разности, произведении и частном двух непрерывных функций?

4. При каких значениях аргумента целая рациональная и дробно-рациональная функции непрерывны?

5. Когда сложная функция непрерывна в точке?

6. Что принято называть точкой разрыва функций?

7. Какие точки называются точками разрыва первого рода?

8. Какая величина принято называть скачком функции?

9. Разъясните понятия ""точка устранимого разрыва"". Приведите примеры.

10. Какие точки называются точками разрыва второго рода? Приведите примеры.

11. Разъясните понятия: ""непрерывность на интервале"", ""непрерывность справа"", ""непрерывность слева"", ""непрерывность на отрезке"".

12. Дайте определœение наибольшего и наименьшего значения функций.

13. Сформулируйте теорему о связи непрерывности на отрезке с наибольшим и наименьшим значениями функции. Разъясните ее на рисунке.

14. Сформулируйте теорему о связи непрерывности функций на отрезке с отрезком значений функций. Проиллюстрируйте ее геометрический смысл на рисунке.

15. Приведите следствие из вышеуказанной теоремы и его геометрическую интерпретацию.

ЛЕКЦИЯ №4

Тема лекции: Производная функции

План лекции: Понятие производной, её геометрический и физический смысл. Основные правила дифференцирования. Производная сложной функции. Некоторые приложения производной.

4.1. Понятие производной, её геометрический и физический смысл

Рассмотрим функцию у = f (x ), заданную в интервале ]a , b [. Пусть х Î ]a , b [ и х Î ]a , b [, тогда приращение функции в точке х 0 выражается формулой Dу = f (x 0 + Dх ) – f (x 0).

Определœение. Производной функции у = f (x ) в точке х 0 принято называть предел отношения приращения этой функции к приращению аргумента͵ когда последнее стремится к нулю:

f’ (x 0) = или y" (x 0) =.

Геометрический смысл производной : производная от данной функции в точке равна тангенсу угла между осью Ох и касательной к графику этой функции в соответствующей точке (см. рис.1):

f" (x 0) = tg a.

Определение . Если функция f (x ) определена на отрезке [a, b ], непрерывна в каждой точке интервала (a, b ), в точке a непрерывна справа, в точке b непрерывна слева, то говорят, что функция f (x ) непрерывна на отрезке [a, b ].

Другими словами, функция f (x ) непрерывна на отрезке [a, b ], если выполнены три условия:

1) "x 0 Î(a, b ): f (x ) = f (x 0);

2) f (x ) = f (a );

3) f (x ) = f (b ).

Для функций, непрерывных на отрезке, рассмотрим некоторые свойства, которые сформулируем в виде следующих теорем, не проводя доказательств.

Теорема 1 . Если функция f (x ) непрерывна на отрезке [a, b ], то она достигает на этом отрезке своего наименьшего и своего наибольшего значения.

Эта теорема утверждает (рис. 1.15), что на отрезке [a, b ] найдется такая точка x 1 , что f (x 1) £ f (x ) для любых x из [a, b ] и что найдется точка x 2 (x 2 Î[a, b ]) такая, что "x Î[a, b ] (f (x 2) ³ f (x )).

Значение f (x 1) является наибольшим для данной функции на [a, b ], а f (x 2) – наименьшим. Обозначим: f (x 1) = M , f (x 2) = m . Так как для f (x ) выполняется неравенство: "x Î[a, b ] m £ f (x ) £ M , то получаем следующее следствие из теоремы 1.

Следствие . Если функция f (x ) непрерывна на отрезке, то она ограничена на этом отрезке.

Теорема 2 . Если функция f (x ) непрерывна на отрезке [a,b ] и на концах отрезка принимает значения разных знаков, то найдется такая внутренняя точка x 0 отрезка [a, b ], в которой функция обращается в 0, т.е. $x 0 Î (a, b ) (f (x 0) = 0).

Эта теорема утверждает, что график функции y = f (x ), непрерывной на отрезке [a, b ], пересекает ось Ox хотя бы один раз, если значения f (a ) и f (b ) имеют противоположные знаки. Так, (рис. 1.16) f (a ) > 0, f (b ) < 0 и функция f (x ) обращается в 0 в точках x 1 , x 2 , x 3 .

Теорема 3 . Пусть функция f (x ) непрерывна на отрезке [a, b ], f (a ) = A , f (b ) = B и A ¹ B . (рис. 1.17). Тогда для любого числа C , заключенного между числами A и B , найдется такая внутренняя точка x 0 отрезка [a, b ], что f (x 0) = C .

Следствие . Если функция f (x ) непрерывна на отрезке [a, b ], m – наименьшее значение f (x ), M – наибольшее значение функции f (x ) на отрезке [a, b ], то функция принимает (хотя бы один раз) любое значение m , заключенное между m и M , а потому отрезок [m, M ] является множеством всех значений функции f (x ) на отрезке [a, b ].

Заметим, что если функция непрерывна на интервале (a, b ) или имеет на отрезке [a, b ] точки разрыва, то теоремы 1, 2, 3 для такой функции перестают быть верными.

В заключение рассмотрим теорему о существовании обратной функции.

Напомним, что под промежутком понимается отрезок либо интервал, либо полуинтервал конечный или бесконечный.

Теорема 4 . Пусть f (x ) непрерывна на промежутке X , возрастает (или убывает) на X и имеет множеством значений промежуток Y . Тогда для функции y = f (x ) существует обратная функция x = j (y ), определенная на промежутке Y , непрерывная и возрастающая (или убывающая) на Y с множеством значений X .

Замечание . Пусть функция x = j (y ) является обратной для функции f (x ). Так как обычно аргумент обозначают через x , а функцию через y , то запишем обратную функцию в виде y = j (x ).

Пример 1 . Функция y = x 2 (рис. 1.8, а) на множестве X = , если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b , непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a , b ], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a , b ], то найдётся хотя бы одна точка x 1 Î [a , b ] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x 1) ≥ f(x) . Аналогично найдётся такая точка x 2 , в которой значение функции будет самым маленьким из всех значений на отрезке: f(x 1) ≤ f(x) .

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x 2 и x 2 ".

Замечание . Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a , b ). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a , b ], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a , b ] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка найдется, по крайней мере, одна точка x = C , в которой функция обращается в ноль: f(C) = 0, где a < C< b

Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x) , соответствующие концам отрезка [a , b ] лежат по разные стороны от оси Ox , то этот график хотя бы в одной точке отрезка пересекает ось Ox . Разрывные функции этим свойством могут не обладать.

Эта теорема допускает следующее обобщение.

Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a , b ] и f(a) = A , f(b) = B . Тогда для любого числа C , заключённого между A и B , найдётся внутри этого отрезка такая точка C Î [a , b ], что f(c) = C .

Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x) . Пусть f(a) = A , f(b) = B . Тогда любая прямая y = C , где C – любое число, заключённое между A и B , пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C , при котором f(c) = C .

Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности:

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента x из этого промежутка функция y=f(x) имеет определенное значение.

Рассмотрим два значения аргумента: исходное x 0 и новое x .

Разность x– x 0 называется приращением аргумента x в точке x 0 и обозначается Δx . Таким образом, Δx = x – x 0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x 0 +Δx , т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x 0 значение функции было f(x 0 ), то в новой точке x функция будет принимать значение f(x) = f(x 0 +Δx) .

Разность y – y 0 = f(x) – f(x 0 ) называется приращением функции y = f(x) в точке x 0 и обозначается символом Δy . Таким образом,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Обычно исходное значение аргумента x 0 считается фиксированным, а новое значение x – переменным. Тогда y 0 = f(x 0 ) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δx также будут переменными и формула (1) показывает, что Dy является функцией переменной Δx .

Составим отношение приращения функции к приращению аргумента

Найдем предел этого отношения при Δx →0. Если этот предел существует, то его называют производной данной функции f(x) в точке x 0 и обозначают f "(x 0). Итак,

Производной данной функции y = f(x) в точке x 0 называется предел отношения приращения функции Δy к приращению аргумента Δx , когда последнее произвольным образом стремится к нулю.

Заметим, что для одной и той же функции производная в различных точках x может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x . Эта функция обозначается f "(x )

Производная обозначается символами f "(x),y ", . Конкретное значение производной при x = a обозначается f "(a ) или y "| x=a .

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Для непосредственного нахождения производной по определению можно применить следующее практическое правило :

Примеры.

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t , где s – путь, пройденный к моменту времени t , v – скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние s будет зависеть от времени t , т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t 0 . К этому моменту точка прошла путь s=s(t 0 ). Определим скорость v материальной точки в момент времени t 0 .

Для этого рассмотрим какой-нибудь другой момент времени t 0 + Δt . Ему соответствует пройденный путь s=s(t 0 + Δt ). Тогда за промежуток времени Δt точка прошла путь Δs=s(t 0 + Δt) –s(t).

Рассмотрим отношение . Оно называется средней скоростью в промежутке времени Δt . Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t 0 (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt .

Итак, скоростью движения в данный момент времени t 0 (мгновенной скоростью) называется предел средней скорости в промежутке от t 0 до t 0 +Δt , когда Δt →0:

,

т.е. скорость неравномерного движения это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М 0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M 0 M . Если точка М начинает перемещаться по кривой, а точка М 0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М 0 с любой стороны секущая стремится занять положение определенной прямой М 0 Т , то прямая М 0 Т называется касательной к кривой в данной точке М 0 .

Т.о., касательной к кривой в данной точке М 0 называется предельное положение секущей М 0 М , когда точка М стремится вдоль кривой к точке М 0 .

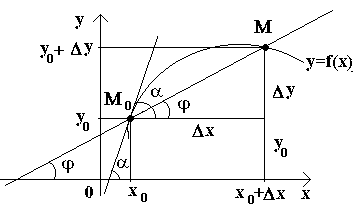
Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х 0 функция принимает значение y 0 =f(x 0). Этим значениям x 0 и y 0 на кривой соответствует точка М 0 (x 0 ; y 0). Дадим аргументу x 0 приращение Δх . Новому значению аргумента соответствует наращенное значение функции y 0 +Δ y=f(x 0 –Δx) . Получаем точку М(x 0 +Δx ; y 0 +Δy). Проведем секущую М 0 М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox . Составим отношение и заметим, что .

Если теперь Δx →0, то в силу непрерывности функции Δу →0, и поэтому точка М , перемещаясь по кривой, неограниченно приближается к точке М 0 . Тогда секущая М 0 М будет стремиться занять положение касательной к кривой в точке М 0 , а угол φ→α при Δx →0, где через α обозначили угол между касательной и положительным направлением оси Ox . Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

т.е. f "(x) = tg α .

Т.о., геометрически у "(x 0) представляет угловой коэффициент касательной к графику этой функции в точке x 0 , т.е. при данном значении аргумента x , производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М 0 (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х 2 в точке М (-1; 1).

Ранее мы уже видели, что (x 2)" = 2х . Но угловой коэффициент касательной к кривой есть tg α = y "| x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а ; b ] или интервала (а ; b ), то говорят, что она дифференцируема на отрезке [а ; b ] или соответственно в интервале (а ; b ).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство . Если , то

,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx →0. Но тогда

Δy =f "(x 0 ) Δx +αΔx => Δy →0 при Δx →0, т.е f(x) – f(x 0) →0 при x →x 0 , а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

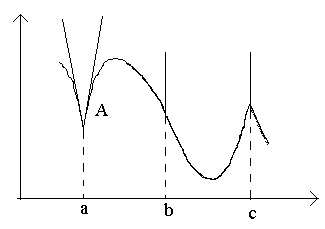
Рассмотрим на рисунке точки а, b, c.

В точке a при Δx →0 отношение не имеет предела (т.к. односторонние пределы различны при Δx →0–0 и Δx →0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Δx →0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.