Definition 9.3. Vector X called own vector matrices BUT if there is such a number λ, that the equality holds: BUT X= λ X, that is, the result of applying to X linear transformation given by the matrix BUT, is the multiplication of this vector by the number λ . The number itself λ called own number matrices BUT.

Substituting into formulas (9.3) x` j = λx j , we obtain a system of equations for determining the coordinates of the eigenvector:

. (9.5)

This linear homogeneous system will have a non-trivial solution only if its main determinant is 0 (Cramer's rule). By writing this condition in the form:

we get an equation for determining the eigenvalues λ called characteristic equation. Briefly, it can be represented as follows:

| A-λE | = 0, (9.6)

since its left side is the determinant of the matrix A-λE. Polynomial with respect to λ | A-λE| called characteristic polynomial matrices A.

Properties of the characteristic polynomial:

1) The characteristic polynomial of a linear transformation does not depend on the choice of the basis. Proof. (see (9.4)), but Consequently, . Thus, does not depend on the choice of basis. Hence, and | A-λE| does not change upon transition to a new basis.

2) If the matrix BUT linear transformation is symmetrical(those. a ij = a ji), then all the roots of the characteristic equation (9.6) are real numbers.

Properties of eigenvalues ​​and eigenvectors:

1) If we choose a basis from eigenvectors x 1, x 2, x 3 corresponding to the eigenvalues λ 1 , λ 2 , λ 3 matrices BUT, then in this basis the linear transformation A has a diagonal matrix:

(9.7) The proof of this property follows from the definition of eigenvectors.

2) If the transformation eigenvalues BUT are different, then the eigenvectors corresponding to them are linearly independent.

3) If the characteristic polynomial of the matrix BUT has three different roots, then in some basis the matrix BUT has a diagonal shape.

Let's find the eigenvalues ​​and eigenvectors of the matrix Let's make the characteristic equation: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Find the coordinates of the eigenvectors corresponding to each found value λ. From (9.5) it follows that if X (1) ={x 1 , x 2 , x 3) is the eigenvector corresponding to λ 1 = -2, then

is a collaborative but indeterminate system. Its solution can be written as X (1) ={a,0,-a), where a is any number. In particular, if you require that | x (1) |=1, X (1) =

Substituting into the system (9.5) λ 2 =3, we get a system for determining the coordinates of the second eigenvector - x (2) ={y1,y2,y3}:

, where X (2) ={b,-b,b) or, provided | x (2) |=1, x (2) =

For λ 3 = 6 find the eigenvector x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) or in the normalized version

x (3) = It can be seen that X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = bc- 2bc + bc= 0. Thus, the eigenvectors of this matrix are pairwise orthogonal.

Lecture 10

Quadratic forms and their connection with symmetric matrices. Properties of eigenvectors and eigenvalues ​​of a symmetric matrix. Reduction of a quadratic form to a canonical form.

Definition 10.1.quadratic form real variables x 1, x 2,…, x n a polynomial of the second degree with respect to these variables is called, which does not contain a free term and terms of the first degree.

Examples of quadratic forms:

(n = 2),

(n = 3). (10.1)

Recall the definition of a symmetric matrix given in the last lecture:

Definition 10.2. The square matrix is ​​called symmetrical, if , that is, if the matrix elements symmetric with respect to the main diagonal are equal.

Properties of eigenvalues ​​and eigenvectors of a symmetric matrix:

1) All eigenvalues ​​of a symmetric matrix are real.

Proof (for n = 2).

Let the matrix BUT looks like: . Let's make the characteristic equation:

(10.2) Find the discriminant:

Therefore, the equation has only real roots.

2) The eigenvectors of a symmetric matrix are orthogonal.

Proof (for n= 2).

The coordinates of the eigenvectors and must satisfy the equations.

Diagonal-type matrices are most simply arranged. The question arises whether it is possible to find a basis in which the matrix of a linear operator would have a diagonal form. Such a basis exists.
Let a linear space R n and a linear operator A acting in it be given; in this case, the operator A takes R n into itself, that is, A:R n → R n .

Definition. A non-zero vector is called an eigenvector of the operator A if the operator A translates into a vector collinear to it, that is, . The number λ is called the eigenvalue or eigenvalue of the operator A corresponding to the eigenvector .
We note some properties of eigenvalues ​​and eigenvectors.
1. Any linear combination of eigenvectors of the operator A corresponding to the same eigenvalue λ is an eigenvector with the same eigenvalue.
2. Eigenvectors operator A with pairwise distinct eigenvalues ​​λ 1 , λ 2 , …, λ m are linearly independent.
3. If the eigenvalues ​​λ 1 =λ 2 = λ m = λ, then the eigenvalue λ corresponds to no more than m linearly independent eigenvectors.

So, if there are n linearly independent eigenvectors corresponding to different eigenvalues ​​λ 1 , λ 2 , …, λ n , then they are linearly independent, therefore, they can be taken as the basis of the space R n . Let us find the form of the matrix of the linear operator A in the basis of its eigenvectors, for which we act with the operator A on the basis vectors: then .
Thus, the matrix of the linear operator A in the basis of its eigenvectors has a diagonal form, and the eigenvalues ​​of the operator A are on the diagonal.
Is there another basis in which the matrix has a diagonal form? The answer to this question is given by the following theorem.

Theorem. The matrix of a linear operator A in the basis (i = 1..n) has a diagonal form if and only if all vectors of the basis are eigenvectors of the operator A.

Rule for finding eigenvalues ​​and eigenvectors

Let the vector , where x 1 , x 2 , …, x n - coordinates of the vector relative to the basis and is the eigenvector of the linear operator A corresponding to the eigenvalue λ , i.e. . This relation can be written in matrix form

. (*)

Equation (*) can be considered as an equation for finding , and , that is, we are interested in non-trivial solutions, since the eigenvector cannot be zero. It is known that nontrivial solutions of a homogeneous system of linear equations exist if and only if det(A - λE) = 0. Thus, for λ to be an eigenvalue of the operator A it is necessary and sufficient that det(A - λE) = 0.
If the equation (*) is written in detail in coordinate form, then we get a system of linear homogeneous equations:

(1)
where is the matrix of the linear operator.

System (1) has a nonzero solution if its determinant D is equal to zero

We got an equation for finding eigenvalues.
This equation is called the characteristic equation, and its left side is called the characteristic polynomial of the matrix (operator) A. If the characteristic polynomial has no real roots, then the matrix A has no eigenvectors and cannot be reduced to a diagonal form.
Let λ 1 , λ 2 , …, λ n be the real roots of the characteristic equation, and there may be multiples among them. Substituting these values ​​in turn into system (1), we find the eigenvectors.

Example 12. The linear operator A acts in R 3 according to the law , where x 1 , x 2 , .., x n are the coordinates of the vector in the basis , , . Find the eigenvalues ​​and eigenvectors of this operator.
Solution. We build the matrix of this operator:
.
We compose a system for determining the coordinates of eigenvectors:

We compose the characteristic equation and solve it:

.
λ 1,2 = -1, λ 3 = 3.
Substituting λ = -1 into the system, we have:
or
Because , then there are two dependent variables and one free variable.
Let x 1 be a free unknown, then We solve this system in any way and find the general solution of this system: The fundamental system of solutions consists of one solution, since n - r = 3 - 2 = 1.
The set of eigenvectors corresponding to the eigenvalue λ = -1 has the form: , where x 1 is any number other than zero. Let's choose one vector from this set, for example, by setting x 1 = 1: .
Arguing similarly, we find the eigenvector corresponding to the eigenvalue λ = 3: .
In the space R 3 the basis consists of three linearly independent vectors, but we have obtained only two linearly independent eigenvectors, from which the basis in R 3 cannot be formed. Consequently, the matrix A of a linear operator cannot be reduced to a diagonal form.

Example 13 Given a matrix .
1. Prove that the vector is an eigenvector of the matrix A. Find the eigenvalue corresponding to this eigenvector.
2. Find a basis in which the matrix A has a diagonal form.
Solution.
1. If , then is an eigenvector

.
Vector (1, 8, -1) is an eigenvector. Eigenvalue λ = -1.
The matrix has a diagonal form in the basis consisting of eigenvectors. One of them is famous. Let's find the rest.
We are looking for eigenvectors from the system:

Characteristic equation: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Find the eigenvector corresponding to the eigenvalue λ = -3:

The rank of the matrix of this system is equal to two and is equal to the number of unknowns, therefore this system has only a zero solution x 1 = x 3 = 0. x 2 here can be anything other than zero, for example, x 2 = 1. Thus, the vector (0 ,1,0) is an eigenvector corresponding to λ = -3. Let's check:
.
If λ = 1, then we get the system
The rank of the matrix is ​​two. Cross out the last equation.
Let x 3 be the free unknown. Then x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Assuming x 3 = 1, we have (-3,-9,1) - an eigenvector corresponding to the eigenvalue λ = 1. Check:

.
Since the eigenvalues ​​are real and different, the vectors corresponding to them are linearly independent, so they can be taken as a basis in R 3 . Thus, in the basis , , matrix A has the form:
.
Not every matrix of a linear operator A:R n → R n can be reduced to a diagonal form, since for some linear operators there may be less than n linearly independent eigenvectors. However, if the matrix is ​​symmetric, then exactly m linearly independent vectors correspond to the root of the characteristic equation of multiplicity m.

Definition. A symmetric matrix is ​​a square matrix in which the elements that are symmetric with respect to the main diagonal are equal, that is, in which .
Remarks. 1. All eigenvalues ​​of a symmetric matrix are real.
2. Eigenvectors of a symmetric matrix corresponding to pairwise different eigenvalues ​​are orthogonal.
As one of the numerous applications of the studied apparatus, we consider the problem of determining the form of a second-order curve.

With matrix A, if there is a number l such that AX = lX.

In this case, the number l is called eigenvalue operator (matrix A) corresponding to the vector X.

In other words, an eigenvector is a vector that, under the action of a linear operator, transforms into a collinear vector, i.e. just multiply by some number. In contrast, improper vectors are more difficult to transform.

We write the definition of the eigenvector as a system of equations:

Let's move all the terms to the left side:

The last system can be written in matrix form as follows:

(A - lE)X \u003d O

The resulting system always has a zero solution X = O. Such systems in which all free terms are equal to zero are called homogeneous. If the matrix of such a system is square, and its determinant is not equal to zero, then according to Cramer's formulas, we will always get a unique solution - zero. It can be proved that the system has non-zero solutions if and only if the determinant of this matrix is ​​equal to zero, i.e.

|A - lE| = = 0

This equation with unknown l is called characteristic equation (characteristic polynomial) matrix A (linear operator).

It can be proved that the characteristic polynomial of a linear operator does not depend on the choice of basis.

For example, let's find the eigenvalues ​​and eigenvectors of the linear operator given by the matrix A = .

To do this, we compose the characteristic equation |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; eigenvalues ​​l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

To find the eigenvectors, we solve two systems of equations

(A + 5E) X = O

(A - 7E) X = O

For the first of them, the expanded matrix will take the form

,

whence x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, i.e. X (1) \u003d (- (2/3) s; s).

For the second of them, the expanded matrix will take the form

,

whence x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, i.e. X (2) \u003d ((2/3) s 1; s 1).

Thus, the eigenvectors of this linear operator are all vectors of the form (-(2/3)c; c) with eigenvalue (-5) and all vectors of the form ((2/3)c 1 ; c 1) with eigenvalue 7 .

It can be proved that the matrix of the operator A in the basis consisting of its eigenvectors is diagonal and has the form:

,

where l i are the eigenvalues ​​of this matrix.

The converse is also true: if the matrix A in some basis is diagonal, then all vectors of this basis will be eigenvectors of this matrix.

It can also be proved that if a linear operator has n pairwise distinct eigenvalues, then the corresponding eigenvectors are linearly independent, and the matrix of this operator in the corresponding basis has a diagonal form.

Let's explain this with the previous example. Let us take arbitrary non-zero values ​​c and c 1 , but such that the vectors X (1) and X (2) are linearly independent, i.e. would form a basis. For example, let c \u003d c 1 \u003d 3, then X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Let us verify the linear independence of these vectors:

12 ≠ 0. In this new basis, the matrix A will take the form A * = .

To verify this, we use the formula A * = C -1 AC. Let's find C -1 first.

C -1 = ;

Quadratic forms

quadratic form f (x 1, x 2, x n) from n variables is called the sum, each term of which is either the square of one of the variables, or the product of two different variables, taken with a certain coefficient: f (x 1, x 2, x n) = (a ij = a ji).

The matrix A, composed of these coefficients, is called matrix quadratic form. It's always symmetrical matrix (i.e., a matrix symmetric about the main diagonal, a ij = a ji).

In matrix notation, the quadratic form has the form f(X) = X T AX, where

Indeed

For example, let's write the quadratic form in matrix form.

To do this, we find a matrix of a quadratic form. Its diagonal elements are equal to the coefficients at the squares of the variables, and the remaining elements are equal to half of the corresponding coefficients of the quadratic form. That's why

Let the matrix-column of variables X be obtained by a nondegenerate linear transformation of the matrix-column Y, i.e. X = CY, where C is a non-degenerate matrix of order n. Then the quadratic form f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Thus, under a non-degenerate linear transformation C, the matrix of the quadratic form takes the form: A * = C T AC.

For example, let's find the quadratic form f(y 1, y 2) obtained from the quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 by a linear transformation.

The quadratic form is called canonical(It has canonical view) if all its coefficients a ij = 0 for i ≠ j, i.e.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Its matrix is ​​diagonal.

Theorem(the proof is not given here). Any quadratic form can be reduced to a canonical form using a non-degenerate linear transformation.

For example, let us reduce to the canonical form the quadratic form
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

To do this, first select the full square for the variable x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Now we select the full square for the variable x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Then the non-degenerate linear transformation y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 and y 3 \u003d x 3 brings this quadratic form to the canonical form f (y 1, y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Note that the canonical form of a quadratic form is defined ambiguously (the same quadratic form can be reduced to the canonical form in different ways). However, canonical forms obtained by various methods have a number of common properties. In particular, the number of terms with positive (negative) coefficients of a quadratic form does not depend on how the form is reduced to this form (for example, in the considered example there will always be two negative and one positive coefficient). This property is called the law of inertia of quadratic forms.

Let us verify this by reducing the same quadratic form to the canonical form in a different way. Let's start the transformation with the variable x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, where y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) x 3 and y 3 = x 1 . Here, a negative coefficient -3 at y 1 and two positive coefficients 3 and 2 at y 2 and y 3 (and using another method, we got a negative coefficient (-5) at y 2 and two positive coefficients: 2 at y 1 and 1/20 for y 3).

It should also be noted that the rank of a matrix of a quadratic form, called the rank of the quadratic form, is equal to the number of non-zero coefficients of the canonical form and does not change under linear transformations.

The quadratic form f(X) is called positively (negative) certain, if for all values ​​of the variables that are not simultaneously equal to zero, it is positive, i.e. f(X) > 0 (negative, i.e.
f(X)< 0).

For example, the quadratic form f 1 (X) \u003d x 1 2 + x 2 2 is positive definite, because is the sum of squares, and the quadratic form f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 is negative definite, because represents it can be represented as f 2 (X) \u003d - (x 1 - x 2) 2.

In most practical situations, it is somewhat more difficult to establish the sign-definiteness of a quadratic form, so one of the following theorems is used for this (we formulate them without proofs).

Theorem. A quadratic form is positive (negative) definite if and only if all eigenvalues ​​of its matrix are positive (negative).

Theorem(Sylvester's criterion). A quadratic form is positive definite if and only if all principal minors of the matrix of this form are positive.

Major (corner) minor The k-th order of the matrix A of the n-th order is called the determinant of the matrix, composed of the first k rows and columns of the matrix A ().

Note that for negative-definite quadratic forms, the signs of the principal minors alternate, and the first-order minor must be negative.

For example, we examine the quadratic form f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 for sign-definiteness.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Therefore, the quadratic form is positive definite.

Method 2. The main minor of the first order of the matrix A D 1 = a 11 = 2 > 0. The main minor of the second order D 2 = = 6 - 4 = 2 > 0. Therefore, according to the Sylvester criterion, the quadratic form is positive definite.

We examine another quadratic form for sign-definiteness, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Method 1. Let's construct a matrix of quadratic form А = . The characteristic equation will have the form = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Therefore, the quadratic form is negative definite.

Method 2. The main minor of the first order of the matrix A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Therefore, according to the Sylvester criterion, the quadratic form is negative definite (the signs of the principal minors alternate, starting from minus).

And as another example, we examine the quadratic form f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 for sign-definiteness.

Method 1. Let's construct a matrix of quadratic form А = . The characteristic equation will have the form = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

One of these numbers is negative and the other is positive. The signs of the eigenvalues ​​are different. Therefore, a quadratic form cannot be either negative or positive definite, i.e. this quadratic form is not sign-definite (it can take values ​​of any sign).

Method 2. The main minor of the first order of the matrix A D 1 = a 11 = 2 > 0. The main minor of the second order D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

SYSTEM OF HOMOGENEOUS LINEAR EQUATIONS

A system of homogeneous linear equations is a system of the form

It is clear that in this case , because all elements of one of the columns in these determinants are equal to zero.

Since the unknowns are found by the formulas , then in the case when Δ ≠ 0, the system has a unique zero solution x = y = z= 0. However, in many problems the question of whether a homogeneous system has solutions other than zero is of interest.

Theorem. For a system of linear homogeneous equations to have a nonzero solution, it is necessary and sufficient that Δ ≠ 0.

So, if the determinant is Δ ≠ 0, then the system has a unique solution. If Δ ≠ 0, then the system of linear homogeneous equations has an infinite number of solutions.

Examples.

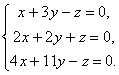
Eigenvectors and Matrix Eigenvalues

Let a square matrix be given , X is some matrix-column whose height coincides with the order of the matrix A. .

In many problems, one has to consider the equation for X

where λ is some number. It is clear that for any λ this equation has a zero solution .

The number λ for which this equation has nonzero solutions is called eigenvalue matrices A, a X for such λ is called own vector matrices A.

Let's find the eigenvector of the matrix A. Because the E∙X=X, then the matrix equation can be rewritten as or . In expanded form, this equation can be rewritten as a system of linear equations. Really .

And therefore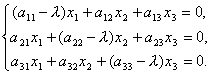

So, we got a system of homogeneous linear equations for determining the coordinates x 1, x2, x 3 vector X. For the system to have non-zero solutions, it is necessary and sufficient that the determinant of the system be equal to zero, i.e.

This is a 3rd degree equation with respect to λ. It's called characteristic equation matrices A and serves to determine the eigenvalues ​​λ.

Each eigenvalue λ corresponds to an eigenvector X, whose coordinates are determined from the system at the corresponding value of λ.

Examples.

VECTOR ALGEBRA. VECTOR CONCEPT

When studying various branches of physics, there are quantities that are completely determined by setting their numerical values, for example, length, area, mass, temperature, etc. Such values ​​are called scalar. However, in addition to them, there are also quantities, for the determination of which, in addition to the numerical value, it is also necessary to know their direction in space, for example, the force acting on the body, the speed and acceleration of the body when it moves in space, the magnetic field strength at a given point in space and etc. Such quantities are called vector quantities.

Let us introduce a rigorous definition.

Directional segment Let's call a segment, relative to the ends of which it is known which of them is the first and which is the second.

Vector a directed segment is called, having a certain length, i.e. This is a segment of a certain length, in which one of the points limiting it is taken as the beginning, and the second - as the end. If a A is the beginning of the vector, B is its end, then the vector is denoted by the symbol, in addition, the vector is often denoted by a single letter . In the figure, the vector is indicated by a segment, and its direction by an arrow.

module or long vector is called the length of the directed segment that defines it. Denoted by || or ||.

The so-called zero vector, whose beginning and end coincide, will also be referred to as vectors. It is marked. The zero vector has no definite direction and its modulus is equal to zero ||=0.

Vectors and are called collinear if they are located on the same line or on parallel lines. In this case, if the vectors and are equally directed, we will write , oppositely.

Vectors located on straight lines parallel to the same plane are called coplanar.

Two vectors and are called equal if they are collinear, have the same direction, and are equal in length. In this case, write .

It follows from the definition of equality of vectors that a vector can be moved parallel to itself by placing its origin at any point in space.

For example.

LINEAR OPERATIONS ON VECTORS

1. Multiplying a vector by a number.

   The product of a vector by a number λ is a new vector such that:

   The product of a vector and a number λ is denoted by .

   

   For example, is a vector pointing in the same direction as the vector and having a length half that of the vector .

   The entered operation has the following properties:

2. Addition of vectors.

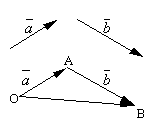
   Let and be two arbitrary vectors. Take an arbitrary point O and construct a vector . After that, from the point A set aside the vector . The vector connecting the beginning of the first vector with the end of the second is called sum of these vectors and is denoted .

   

   The formulated definition of vector addition is called parallelogram rule, since the same sum of vectors can be obtained as follows. Set aside from the point O vectors and . Construct a parallelogram on these vectors OABC. Since the vectors , then the vector , which is the diagonal of the parallelogram drawn from the vertex O, will obviously be the sum of vectors .

   

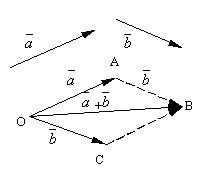
   It is easy to check the following vector addition properties.

3. Difference of vectors.

   A vector collinear to a given vector , equal in length and oppositely directed, is called opposite vector for a vector and is denoted by . The opposite vector can be considered as the result of vector multiplication by the number λ = –1: .