Введение.

Бурное развитие жидкостной хроматографии в последние 10 лет обусловлено, главным образом, интенсивной разработкой теоретических основ и практическим использованием ее высокоэффективного варианта, а также созданием и промышленным выпуском необходимых сорбентов и аппаратуры.

Отличительной особенностью высокоэффективной жидкостной хроматографии (ВЭЖХ) является использование сорбентов с размером зерен 3-10 мкм, что обеспечивает быстрый массоперенос при очень высокой эффективности разделения.

В настоящее время ВЭЖХ по темпам развития вышла на первое место среди инструментальных методов, обогнав даже газовую хроматографию. Важнейшее преимущество ВЭЖХ по сравнению с газовой хроматографией - возможность исследования практически любых объектов без каких-либо ограничений по их физико-химическим свойствам, например, по температурам кипения или молекулярной массе.

Сегодня ВЭЖХ представляет собой хорошо оформленный инструментальный метод, который широко применяют в самых различных областях науки и техники. Особенно велико его значение в таких важнейших областях, как биохимия, молекулярная биология, контроль загрязнений окружающей среды,а также в химической, нефтехимической, пищевой и фармацевтической промышленности.

поскольку необходимо учитывать целый ряд весьма специфических тре­бований, обусловленных следующими особенностями мето­дики.

а. Колонки для ВЭЖХ наполняют носителем с очень ма­лым диаметром частиц. В результате при таких объемных ско­ростях растворителя, которые необходимы для быстрого разде­ления пробы, на колонке создается высокое давление.

б. Детекторы, применяемые в ВЭЖХ, чувствительны к флуктуации потока и давления элюента (шумы). Более того, при применении концентрационных детекторов необходима еще более высокая стабильность объемной скорости элюента.

в. Процесс хроматографического разделения сопровождает­ся рядом антагонистических эффектов, так, например, диспер­гирование образца в подвижной фазе ведет к смешению раз­деляемых компонентов и снижает максимальную концентрацию вещества в элюируемом пике (в детекторе). Диспергирование наблюдается на всех участках системы от точки ввода пробы до детектора.

г. Растворители, выполняющие роль подвижной фазы, ча­сто способны вызывать коррозию аппаратуры. Это в первую очередь относится к растворителям, используемым в обращен-но-фазовой хроматографии, которая предпочтительна в биохи­мических приложениях ВЭЖХ.

Специфику ВЭЖХ как инструментальной методики необхо­димо учитывать в процессе разработки, создания и эксплуата­ции этих систем. Для создания коммерческих образцов хрома-тографических систем и их компонентов, достаточно надеж­ных, простых и безопасных в работе с приемлемым соотноше­нием между ценой и техническими характеристиками, потре­бовалось более десяти лет поисков и исследований. Наметив­шиеся в последнее время тенденции к уменьшению колонок (как длины, так и диаметра) заставляют предъявлять новые требования к инструментам.

1.1. ЭФФЕКТИВНОСТЬ И СЕЛЕКТИВНОСТЬ

Хроматография - это метод разделения компонентов смеси, основанный на различии в равновесном распределении их меж­ду двумя" несмешивающимися фазами, одна из которых непо­движна, а другая подвижна. Компоненты образца движутся по колонке, когда они находятся в подвижной фазе, и остаются на месте, когда находятся в неподвижной фазе. Чем больше срод­ство компонента к неподвижной фазе и чем меньше - к подвиж­ной, тем медленнее он движется по колонке и тем дольше в ней удерживается. За счет различия в сродстве компонентов смеси к неподвижной и подвижной фазам достигается основная цель хроматографии - разделение за приемлемый промежуток вре­мени смеси на отдельные полосы (пики) компонентов по мере их продвижения по колонке с подвижной фазой.

Из этих общих представлений ясно, что хроматографическое разделение возможно, только в том случае, если компоненты образца, попадая в колонку при вводе пробы, во-первых, будут растворены в подвижной фазе и, во-вторых, будут взаимодейст­вовать (удерживаться) с неподвижной фазой. Если при вводе пробы какие-то компоненты находятся не в виде раствора, они будут отфильтрованы и не будут участвовать в хроматографи-ческом процессе. Точно так же компоненты, не взаимодействую­щие с неподвижной фазой, пройдут через колонку с подвижной фазой, не разделяясь на компоненты.

Примем условие, что какие-то два компонента растворимы в подвижной фазе и взаимодействуют с неподвижной фазой, т. е. хроиатографический процесс может протекать без наруше­ний. В этом случае после прохождения смеси через колонку можно получить хроматограммы вида а, б или в (рис. 1.1). Эти хроматограммы иллюстрируют хроматографические разделения, отличающиеся эффективностью (а и б) при равной селективно­сти и селективностью (б и в) при равной эффективности.

Эффективность колонки тем выше, чем уже пик получается при том же времени удерживания. Эффективность колонки изме­ряется числом теоретических тарелок (ЧТТ) N : чем выше эф-

Рис. 1.2. Параметры хрома-тографического пика и рас­чет числа теоретических та­релок:

t R - время удерживания пика; h - высота пика; Wj/j - шири­на пика на половине его высоты

Рис. 1.1. Вид хроматограммы в зависимости от эффективности и селектив­ности колонки:

а - обычная селективность, пониженная эффективность (меньше теоретических тарелок); б - обычные селективность и эффективность; в - обычная эффективность, повышенная селективность (больше отношение времен удерживания компонентов)

фективность, тем больше ЧТТ, тем меньше расширение пика первоначально узкой полосы по мере прохождения ее через ко­лонку, тем уже пик на выходе из колонки. ЧТТ характеризует число ступеней установления равновесия между подвижной и не­подвижной фазами.

Зная число теоретических тарелок, приходящееся на колонку, и длину колонки L (мкм), а также средний диаметр зерна сор­бента d c (мкм), легко получить значения высоты, эквивалент­ной теоретической тарелке (ВЭТТ), а также приведенной вы­соты, эквивалентной теоретической тарелке (ПВЭТТ):

ВЭТТ = L / N

ПВЭТТ =B3TT/d c .

Имея значения ЧТТ, ВЭТТ и ПВЭТТ, можно легко сравни­вать эффективность колонок разных типов, разной длины, за­полненных разными по природе и зернению сорбентами. Срав­нивая ЧТТ двух колонок одной длины, сравнивают их эффек­тивность. При сравнении ВЭТТ сравнивают колонки с сорбен­тами одинакового зернения, имеющими разную длину. Нако­нец, величина ПВЭТТ позволяет для двух любых колонок оце­нить качество сорбента, во-первых, и качество заполнения коло­нок, во-вторых, независимо от длины колонок, зернения сорбен­тами его природы.

Селективность колонки играет большую роль в достижении хроматографического разделения.

Селективность колонки зависит от очень многих факторов, и искусство экспериментатора в большой мере определяется умением воздействовать на селективность разделения. Для это­го в руках хроматографиста находятся три очень важных фак­тора: выбор химической природы сорбента, выбор состава рас­творителя и его модификаторов и учет химической структуры и свойств разделяемых компонентов. Иногда заметное влияние на селективность оказывает изменение температуры колонки, меняющее коэффициенты распределения веществ между по­движной и неподвижной фазами.

При рассмотрении разделения двух компонентов на хрома­тограмме и его оценке важным параметром является разреше­ние R s , которое связывает времена выхода и ширину пиков обо­их разделяемых компонентов

Разрешение как параметр, характеризующий разделение пи­ков, увеличивается по мере возрастания селективности, отра­жаемой ростом числителя, и роста эффективности, отражаемой снижением значения знаменателя из-за уменьшения ширины пи­ков. Поэтому быстрый прогресс жидкостной хроматографии привел к изменению понятия «жидкостная хроматография вы­сокого давления» - оно было заменено на «жидкостную хрома­тографию высокого разрешения» (при этом сокращенная запись термина на английском языке сохранилась HPLC как наибо­лее правильно характеризующее направление развития совре­менной жидкостной хроматографии).

Таким образом, размывание в колонке уменьшается и эф­фективность повышается, когда используют более мелкий сор­бент, более равномерный по составу (узкая фракция), более плотно и равномерно упакованный в колонке, при использова­нии более тонких слоев привитой фазы, менее вязких раствори­телей и оптимальных скоростей потока.

Однако наряду с размыванием полосы хроматографической зоны в процессе разделения в колонке может происходить так­же и размывание ее в устройстве для ввода пробы, в соедини­тельных капиллярах инжектор - колонка и колонка - детек­тор, в ячейке детектора и в некоторых вспомогательных устрой­ствах (микрофильтры для улавливания механических частиц из пробы, устанавливаемые после инжектора, предколонки, ре­акторы-змеевики и др.)- Размывание при этом тем больше, чем больше внеколоночный объем по сравнению с удерживаемым объемом пика. Имеет также значение и то, в каком месте на­ходится мертвый объем: чем уже хроматографическая зова, тем большее размывание даст мертвый объем. Поэтому особое вни­мание следует уделять конструированию той части хроматогра­фа, где хроматографическая зона наиболее узкая (инжектор и устройства от инжектора до колонки) - здесь внеколоночное размывание наиболее опасно и сказывается наиболее сильно. Хотя считается, что в хорошо сконструированных хроматогра­фах источники дополнительного внеколоночного размывания должны быть сведены до минимума, тем не менее каждый новый прибор, каждая переделка хроматографа должны обяза­тельно заканчиваться тестированием на колонке и сравнением полученной хроматограммы с паспортной. Если наблюдается ис­кажение пика, резкое снижение эффективности, следует тща­тельно проинспектировать вновь введенные в систему капилля­ры и другие устройства.

Размывание вне колонки и его неправильная оценка могут привести к значительной (более 50%) потере эффективности, особенно в тех случаях, когда относительно давно сконструиро­ванные хроматографы пытаются использовать для высокоско­ростной ВЭЖХ, микроколоночной ВЭЖХ и других вариантов современной ВЭЖХ, требующих микроинжекторов, соединитель­ных капилляров с внутренним диаметром 0,05-0,15 мм мини­мальной длины, колонок вместимостью 10-1000 мкл, детекто­ров с микрокюветами емкостью 0,03-1 мкл и с высоким быстро­действием, высокоскоростных самописцев и интеграторов.

1.2. УДЕРЖИВАНИЕ И СИЛА РАСТВОРИТЕЛЯ

Для того чтобы анализируемые вещества разделялись на ко­лонке, как уже упоминалось выше, коэффициент емкости k " должен быть больше 0, т. е. вещества должны удерживаться неподвижной фазой, сорбентом. Однако коэффициент емкости не должен быть и слишком большим, чтобы получить приемле­мое время элюирования. Если для данной смеси веществ выбра­на неподвижная фаза, которая их удерживает, то дальнейшая работа по разработке методики анализа заключается в выборе такого растворителя, который обеспечил бы в идеальном случае различные для всех компонентов, но приемлемо не очень боль­шие k ". Этого добиваются, меняя элюирующую силу раствори­теля.

В случае адсорбционной хроматографии на силикагеле или оксиде алюминия, как правило, силу двухкомпонентного рас­творителя (например, гексана с добавкой изопропанола) увели­чивают, увеличивая в нем содержание полярного компонента (изопропанола), или же уменьшают, уменьшая содержание изо­пропанола. Если содержащие полярного компонента становится слишком малым (менее 0,1%), следует заменить его более сла­бым по элюирующей силе. Так же поступают, заменяя на дру­гие либо полярную, либо неполярную составляющую и в том^ случае, если данная система не обеспечивает желаемой селек­тивности по отношению к интересующим компонентам смеси. При подборе систем растворителей принимают во внимание как растворимости компонентов смеси, так и элюотропнЬе ряды растворителей, составленные разными авторами.

Примерно так же подбирают силу растворителя в случае ис­пользования привитых полярных фаз (нитрил, амино, диол, нитро и др.), учитывая возможные химические реакции и ис­ключая опасные для фазы растворители (например и кетоны для аминофазы).

В случае обращенно-фазной хроматографии силу раствори­теля увеличивают, повышая содержание в элюенте органичес­кой составляющей (метанола, ацетонитрила или ТГФ) и умень­шают, добавляя больше воды. Если не удается добиться же­лаемой селективности, используют другую органическую состав­ляющую либо пытаются изменить ее с помощью разных доба­вок (кислот, ион-парных реагентов и др.).

При разделениях методом ионообменной хроматографии си­лу растворителя меняют, увеличивая или уменьшая концентра­цию буферного раствора или меняя рН, в некоторых случаях используют модификацию органическими веществами.

Однако, особенно в случае сложных природных и биологи­ческих смесей, зачастую не удается подобрать силу раствори­теля таким образом, чтобы все компоненты пробы элюирова-лись за приемлемый срок. Тогда приходится прибегать к гра­диентному элюированию, т. е. использовать растворитель, элюи-рующая сила которого в процессе анализа изменяется так, что она постоянно увеличивается по заранее заданной программе. Таким приемом удается добиться элюирования всех компонен­тов сложных смесей за относительно короткий промежуток вре­мени и их разделения на компоненты в виде узких пиков.

1.3. РАЗМЕР ЧАСТИЦ СОРБЕНТА, ПРОНИЦАЕМОСТЬ И ЭФФЕКТИВНОСТЬ

Рассматривая размывание в колонке, мы указывали, что эффективность колонки (ВЭТТ) зависит от размера частиц сорбента. В большой степени бурное развитие ВЭЖХ за послед­ние 10-12 лет было обусловлено, во-первых, разработкой спо­собов получения сорбентов с размером частиц от 3 до 10 мкм и с узким фракционным составом, обеспечивающих высокую эффективность при хорошей проницаемости, во-вторых, ^разра­боткой способов заполнения этими сорбентами колонок и, в-третьих, разработкой и серийным выпуском жидкостных хро­матографов, имеющих рассчитанные на высокие давления насо­сы, инжекторы и детекторы с кюветами малого объема, способ­ные регистрировать пики малого объема.

Для хорошо упакованных суспензионным способом колонок приведенная высота, эквивалентная теоретической тарелке (ПВЭТТ), может составлять 2 независимо от того, использо­вали ли для упаковки частицы с размером 3, 5, 10 или 20 мкм. В этом случае мы получим соответственно колонки (при стан­дартной длине их 250 мм) эффективностью 41670, 25000, 12500 и 6250 т.т. Кажется естественным выбрать наиболее эффектив­ную колонку, заполненную частицами размером 3 мкм. Однако за эту эффективность придется заплатить использованием при работе очень высокого давления и относительно невысокой скоростью разделения, так как имеющийся насос, скорее всего, будет и^пособен* прокачивать через такую колонку растворитель с высокой объемной скоростью. Здесь мы как раз и сталкива­емся с вопросом о связи размера частиц сорбента, эффективно­сти и проницаемости колонок.

Если выразить отсюда фактор сопротивления колонки--безраз­мерную величину, получим следующее уравнение:

Фактор сопротивления для колонок, упакованных микрочасти­цами одного вида по одному и тому же способу, меняется не­значительно и составляет следующие значения:

Вид частиц ».... Неправильная Сферическая

форма форма

Сухая упаковка. . . . . 1000-2000 800-1200

Суспензионная упаковка. . . 700-1500 500-700

Давление на входе в колонку пропорционально линейной скорости потока, фактору сопротивления колонки, вязкости рас­творителя и длине колонки и обратно пропорционально квадра­ту диаметра частиц.

Применив эту зависимость для вышеописанных колонок с частицами диаметром 3, 5, 10 и 20 мкм и предположив посто­янными линейную скорость потока, фактор сопротивления ко­лонки и вязкость растворителя, получим для колонок равной длины соотношение давлений на входе 44:16:4:1. Таким об­разом, если для обращенно-фазного сорбента с размером час­тиц 10 мкм при использовании систем растворителей метанол - . вода (70:30) обычно на стандартной колонке при расходе рас­творителя 1 мл/мин давление на входе в колонку составляет 5 МПа, то для частиц 5 мкм - 20 МПа и для 3 мкм - 55 МПа. При использовании силикагеля и менее вязкой системы рас­творителей гексан - изопропанол (100:2) значения будут су­щественно ниже: соответственно 1, 4 и 11 МПа. Если в случае обращенно-фазного сорбента применение частиц размером Змкм очень проблематично, а 5 мкм возможно, но не на всех при­борах, то для нормально-фазного проблем с давлением не воз­никает. Следует отметить, что для современной скоростной ВЭЖХ характерно использование более высокого расхода рас­творителей, чем в вышерассмотренном примере, поэтому тре­бования к давлению возрастают еще больше.

Однако в тех случаях, когда для разделения требуется оп­ределенное число теоретических тарелок и желательно осуще­ствить скоростной анализ, картина несколько меняется. Так как длины колонок с сорбентами зернением 3, 5, 10 мкм при равной эффективности будут соответственно 7,5; 12,5 и 25 см, то и соотношение давлений на входе в колонки изменится доЗ,3:2:1. Соответственно продолжительность анализа на таких колонках равной эффективности будет соотноситься как 0,3:0,5:1, т. е. при переходе от 10 к 5 и 3 мкм продолжительность анализа со­кратится в 2 и 3,3 раза. За это ускорение анализа приходится расплачиваться пропорционально более высоким давлением на входе в колонку.

Приведенные данные справедливы для тех случаев, когда сорбенты разного зернения имеют одинаковые кривые распреде­ления частиц по размеру, колонки набиты одинаковым спосо­бом и имеют одинаковый фактор сопротивления колонки. Сле­дует иметь в виду, что трудность получения узких фракций сор­бента возрастает по мере уменьшения размера частиц и что. фракции от разных производителей имеют разный фракционный состав. Поэтому фактор сопротивления колонок будет меняться в зависимости от зернения, типа сорбента, способа упаковки колонок и др.

КЛАССИФИКАЦИЯ МЕТОДОВ ВЭЖХ ПО МЕХАНИЗМУ РАЗДЕЛЕНИЯ

Большинство проводимых методом ВЭЖХ разделений основа­но на смешанном механизме взаимодействия веществ с сорбен­том, обеспечивающим большее или меньшее удерживание ком­понентов в колонке. Механизмы разделения в более или менее чистом виде на практике встречаются достаточно редко, напри­мер, адсорбционный при использовании абсолютно безводного силикагеля и безводного гексана для разделения ароматических углеводородов.

При смешанном механизме удерживания для веществ раз­ного строения и молекулярной массы можно оценить вклад в удерживание адсорбционного, распределительного, эксклюзион-ного и других механизмов. Однако для лучшего понимания и представления о механизмах разделения в ВЭЖХ целесообраз­но рассматривать разделения с преобладанием того или иного механизма как относящиеся к определенному виду хроматогра­фии, например, к ионообменной хроматографии.

2.1.1 АДСОРБЦИОННАЯ ХРОМАТОГРАФИЯ

Разделение методом адсорбционной хроматографии осущест­вляется в результате взаимодействия вещества с адсорбентами, такими, как силикагель или оксид алюминия, имеющими на по­верхности активные центры. Различие в способности к взаимо­действию с адсорбционными центрами разных молекул пробы приводит к их разделению на зоны в процессе движения с подвижной фазой по колонке. Достигаемое при этом разделение зон компонентов зависит от взаимодействия как с растворите­лем, так и с адсорбентом.

В основе сорбции на поверхности адсорбента, имеющего гид-роксильные группы, лежит специфическое взаимодействие меж­ду полярной поверхностью адсорбента и полярными (или спо­собным поляризоваться) группами или участками молекул. К таким взаимодействиям относят диполь-дипольное взаимодей­ствие между постоянными или индуцированными диполями, об­разование водородной связи вплоть до образования я-комплек-сов или комплексов с переносом заряда. Возможным и доста­точно частым в практической работе является проявление хемо-сорбции, которая может привести к значительному повышению времени удерживания, резкому снижению эффективности, появ­лению продуктов разложения или необратимой сорбции веще­ства.

Изотермы адсорбции веществ имеют линейную, выпуклую или вогнутую форму. При линейной изотерме адсорбции пик ве­щества симметричен и время удерживания не зависит от разме­ра пробы. Чаще всего изотермы адсорбции веществ нелинейны и имеют выпуклую"форму, что приводит к некоторой асиммет­рии пика с образованием хвоста.

Наибольшее применение в ВЭЖХ находят адсорбенты из силикагеля с разным объемом пор, поверхностью, диаметром пор. Значительно реже используют оксид алюминия и крайне редко--другие адсорбенты, широко применяющиеся в класси­ческой колоночной и тонкослойной хроматографии. Основная причина этого - недостаточная механическая прочность боль­шинства прочих адсорбентов, не позволяющая упаковывать их я использовать при повышенных давлениях, характерных для вэжх.

Полярные группы, обусловливающие адсорбцию и находя­щиеся на поверхности силикагеля и оксида алюминия, по свой­ствам близки. Поэтому обычно порядок элюирования смесей ве­ществ и элюотропный ряд растворителей для них одинаковы. Однако различие химического строения силикагеля и оксида алюминия иногда приводит к появлению различий в селектив­ности-- тогда предпочтение отдают тому или другому адсор­бенту, более подходящему для данной конкретной задачи. На­пример, оксид алюминия обеспечивает большую избиратель­ность при разделении некоторых многоядерных ароматических углеводородов.

Предпочтение, отдаваемое обычно силикагелю по сравнению с оксидом алюминия, объясняется более широким выбором си-ликагелей по пористости, поверхности и диаметру пор, а также значительно более высокой каталитической активностью оксида алюминия, нередко приводящей к искажению результатов ана­лиза вследствие разложения компонентов пробы либо их необ­ратимой хемосорбции.

2.1.2 Недостатки адсорбционной хроматографии, ограничивающие ее использование

Популярность адсорбционной хроматографии по мере разви­тия метода ВЭЖХ постепенно падала, она все больше заменя­лась и продолжает заменяться на другие варианты, такие, как обращенно-фазная и нормально-фазная ВЭЖХ на сорбентах с-привитой фазой. Какие же недостатки адсорбционной хромато­графии привели к этому?

Прежде всего, это большая длительность процессов уравно­вешивания адсорбентов с растворителями, содержащими воду в микроколичествах, трудность приготовления таких раствори­телей с определенной и воспроизводимой влажностью. Из это­го следуют плохая воспроизводимость параметров удерживания, разрешения, селективности. По этой же причине невозможно использовать градиентное элюирование - возврат к исходному состоянию настолько длителен, что значительно превосходит выигрыш времени за счет использования градиента.

Существенные недостатки адсорбентов, особенно оксида алюминия, связанные с частыми случаями перегруппировок чувствительных к катализу соединений, их разложения, необра­тимой сорбции, также общеизвестны и неоднократно отмеча-лить в литературе. Необратимо сорбирующиеся вещества, на­капливаясь на начальном участке колонки, меняют природу сорбента, могут привести к повышению сопротивления колонки или даже к полной ее забивке. Последний недостаток может быть устранен путем использования предколонки, которая по- мере повышения сопротивления и забивки заменяется на новую* или перезаполняется новым сорбентом. Однако необратимая сорбция, имеющая место и в этом случае, приводит к получе­нию хроматограммы, на которой полностью или частично от­сутствуют чувствительные к сорбции или каталитическому раз­ложению компоненты пробы.

2.2. РАСПРЕДЕЛИТЕЛЬНАЯ ХРОМАТОГРАФИЯ

Распределительная хроматография - это вариант ВЭЖХ, в котором разделение смеси на компоненты осуществляется за счет различия их коэффициентов распределения между двумя несмешивающимися фазами: растворителем (подвижная фа­за) и фазой на сорбенте (неподвижная фаза). Исторически пер­выми были сорбенты такого типа, которые получали нанесением жидких фаз (оксидипропионитрила, парафинового масла и др.) на пористые носители, аналогично тому, как готовили и готовят сорбенты для газожидкостной хроматографии (ГЖХ). Однако сразу же обнаружились и недостатки таких сорбентов, основ­ным из которых было относительно быстрое смывание фазы с носителя. За счет этого количество фазы в колонке постепенно уменьшалось, времена удерживания также уменьшались, на на­чальном участке колонки появлялись не покрытые фазой центры адсорбции, вызывавшие образование хвостов пиков. С этим недостатком боролись, насыщая растворитель нанесен­ной фазой еще до его попадания в колонку. Унос также умень­шался, когда использовали более вязкие и менее растворимые полимерные фазы, однако в этом случае из-за затруднения диффузии из толстых полимерных пленок эффективность колонок заметно снижалась.

Логическим оказалось привить химическими связями жид­кую фазу к носителю таким образом, чтобы унос ее стал физи­чески невозможен, т. е. превратить носитель и фазу в одно це­лое- в так называемый привито-фазный сорбент.

В дальнейшем усилия исследователей были направлены на поиск реагентов, прививка которых протекала бы достаточно быстро и полно, а образовавшиеся связи были максимально устойчивыми. Такими реагентами стали алкилхлорсиланы и их производные, позволившие по сходной технологии получать привито-фазные сорбенты разного типа и с разными как по­лярными, так и неполярными группами на поверхности.

Успешное применение сорбентов последнего типа для ВЭЖХ способствовало росту их производства самыми разными произ­водителями. Каждая фирма производила такие сорбенты, как правило, на основе своего вида силикагеля и по своей техноло­гии, которая обычно составляет «ноу-хау» производства. В ре­зультате большое количество сорбентов, называющихся хими­чески совершенно одинаково (например, силикагель с привитым октадецилсиланом), имеют очень сильно различающиеся хро-матографические характеристики. Это связано с тем, что сили­кагель может иметь поры шире или уже, разную поверхность, пористость, его поверхность до прививки может гидроксилиро-ваться или нет, прививаться могут моно-, ди- или трихлорсила-ны, условия прививки могут давать мономерный, полимерный или смешанный слой фазы, используются разные методы удале­ния остатков реагентов, может использоваться или не исполь­зоваться дополнительная дезактивация силанольных и других активных групп.

Сложность технологии прививки реагентов и подготовки сырья и материалов, ее многостадийность приводят к тому, что даже полученные по одной технологии ка одной фирме-произво­дителе партии сорбентов могут иметь несколько разные хрома-тографические характеристики. Особенно это касается тех слу­чаев, когда такие сорбенты используют для анализа многоком­понентных смесей, содержащих вещества, заметно различаю щиеся по количеству и положению функциональных групп, по* роду функциональности .

Учитывая вышеуказанное, всегда следует стремиться к то­му* чтобы при использовании описанной в литературе методи­ки анализа применять именно тот самый сорбент и те же усло­вия работы. В этом случае вероятность того, что работу не удастся воспроизвести, является минимальной. Если же такой возможности нет, а берется сорбент другой фирмы с аналогич­ной привитой фазой, нужно быть готовым к тому, что потребу­ется длительная работа по переделке методики. При этом су­ществует вероятность (и ее следует учитывать), что на этом сорбенте даже и после длительной разработки можно не до­биться требуемого разделения. Наличие в литературе многих описанных методик разделения на давно производимых старых сорбентах стимулирует их дальнейшее производство и примене­ние по этой причине. Однако в тех случаях, когда приходится переходить к разработке оригинальных методик, особенно при­менительно к веществам, склонным к разложению, хемосорб-ции, перегруппировкам, целесообразно начинать работу на сор­бентах, разработанных в последнее время и выпускаемых по> новым, улучшенным вариантам технологии. Новые сорбенты имеют более однородный фракционный состав, более однород­ное и полное покрытие поверхности привитой фазой, более со­вершенные окончательные стадии обработки сорбентов.

2.3. ИОНООБМЕННАЯ ХРОМАТОГРАФИЯ

В ионообменной хроматографии разделение компонентов смеси достигается за счет обратимого взаимодействия ионизи­рующихся веществ с ионными группами сорбента. Сохранение электронейтральности сорбента обеспечивается наличием спо­собных к ионному обмену противоионов, расположенных в не­посредственной близости к поверхности. Ион введенного образ­ца, взаимодействуя с фиксированным зарядом сорбента, обме­нивается с противоионом. Вещества, имеющие разное сродство " к фиксированным зарядам, разделяются на анионитах или на катеонитах. Аниониты имеют на поверхности положительно за­ряженные группы и сорбируют из подвижной фазы анионы. Ка-тиониты соответственно содержат группы с -отрицательным за­рядом, взаимодействующие с катионами.

В качестве подвижной фазы используют водные растворы " солей кислот, оснований и растворители типа жидкого аммиа­ка, т. е. системы растворителей, имеющих высокое значение ди­электрической проницаемости е и большую тенденцию ионизи­ровать соединения. Обычно работают с буферными растворами, позволяющими регулировать значение рН.

При хроматографичеоком разделении ионы анализируемого вещества конкурируют с ионами, содержащимися в элюенте, стремясь вступить во взаимодействие с противоположно заря­женными группами сорбента. Отсюда следует, что ионообмен­ную хроматографию можно применять для разделения любых соединений, которые могут быть каким-либо образом ионизированы. Можно провести анализ даже нейтральных молекул Сахаров в виде их комплексов с борат-ионом:

Сахар + ВО 3 2 - = Сахар -ВО 3 2 -.

Ионообменная хроматография незаменима при разделении вы­сокополярных веществ, которые без перевода в производные не могут быть проанализированы методом ГЖХ. К таким со­единениям относятся аминокислоты, пептиды, сахара.

Ионообменную хроматографию широко применяют в медици­не, биологии, биохимии , для контроля окружающей среды, при анализе содержания лекарств и их метаболитов в крови и моче, ядохимикатов в пищевом сырье, а также для раз­деления неорганических соединений, в том числе радиоизотопов, лантаноидов, актиноидов и др. Анализ биополимеров (белков, нуклеиновых кислот и др.), на который обычно затрачивали часы или дни, с помощью ионообменной хроматографии прово­дят за 20-40 мин с лучшим разделением. Применение ионооб­менной хроматографии в биологии позволило наблюдать за об­разцами непосредственно в биосредах, уменьшая возможность перегруппировки или изомеризации, что может привести к не­правильной интерпретации конечного результата. Интересно ис­пользование данного метода для контроля изменений, происхо­дящих с биологическими жидкостями . Применение пори­стых слабых анионообменников на силикагелевой основе позво­лило разделить пептиды . V

Механизм ионного обмена можно представить в виде сле­дующих уравнений:

для анионного обмена

X- + R+Y- ч ->■ Y-+R+X-.

для катионного обмена |

X+ + R-Y+ ч=* Y++R-X+.

В первом случае ион образца Х~ конкурирует с ионом по­движной фазы Y~ за ионные центры R+ ионообменника, а во втором в конкуренцию с ионами подвижной фазы Y+ за ион­ные центры R~ вступают катионы образца Х+.

Естественно, что ионы образца, слабо взаимодействующие с ионообменником, при этой конкуренции будут слабо удержи­ваться на колонке и первыми вымываются с нее и, наоборот, более сильно удерживаемые ионы будут элюировать из колонки последними. Обычно возникают BTqpH4Hbie взаимодействия не­ионной природы за счет адсорбции или водородных связей об­разца с неионной частью матрицы или за счет ограниченной растворимости образца в подвижной фазе. Трудно выделить «классическую» ионообменную хроматографию в «чистом» ви­де, и поэтому некоторые хроматографисты исходят из эмпири­ческих, а не теоретических закономерностей при ионообменной хроматографии.

Разделение конкретных веществ зависит в первую очередь от выбора наиболее подходящего сорбента и подвижной фазы. В качестве неподвижных фаз в ионообменной хроматографии применяют ионообменные смолы и силикагели с привитыми ионогенными группами.

2.4. ЭКСКЛЮЗИОННАЯ ХРОМАТОГРАФИЯ

Зксклюзионная хроматография представляет собой вариант! жидкостной хроматографии, в котором разделение происходит за счет распределения молекул между растворителем, находя­щимся внутри пор сорбента, и растворителем, протекающим " между его частицами.

В отличие от остальных вариантов ВЭЖХ, где разделение идет за счет различного взаимодействия компонентов с поверхностью сорбента, роль твердого наполнителя в эксклюзионной хроматографии заключается только в формировании пор определенного размера, а неподвижной фазой является растворитель, заполняющий эти поры. Поэтому применение термина «сорбент» к данным наполнителям в определенной степени ус­ловно.

Принципиальной особенностью метода является возможность разделения молекул по их размеру в растворе в диапазоне прак­тически любых молекулярных масс - от 10 2 до 10 8 , что дела­ет ч его незаменимым для исследования синтетических и биопо­лимеров.

По традиции процесс, проводимый в органических раствори­телях, все еще часто называют гель-проникающей, а в водных системах - гель-фильтрационной хроматографией. В данной книге для обоих вариантов принят единый термин, который происходит от английского «Size Exclusion» - исключение по размеру - и в наиболее полной степени отражает механизм процесса.

Детальный разбор существующих представлений о весьма сложной теории процесса эксклюзионной хроматографии прове­ден в монографиях.

Полный объем растворителя в колонке Vt (его часто назы­вают полным объемом колонки, так как Vd не принимает учас­тия в хроматографическом процессе) представляет собой сум­му объемов подвижной и неподвижной фаз.

Удерживание молекул в зксклюзионной колонке определяет­ся вероятностью их диффузии в поры и зависит от соотношения размеров молекул и пор, что схематически показано на рис. 2.15. Коэффициент распределения Ка, как и в других вариантах хро­матографии, представляет собой отношение концентраций ве­щества в неподвижной и подвижной фазах.

Так как подвижная и неподвижная фазы имеют одинаковый состав, то Kd вещества, для которого обе фазы одинаково до­ступны, равен единице. Эта ситуация реализуется для молекул С самыми малыми размерами (в том числе и молекул раствори­теля), которые проникают во все поры (см. рис. 2.15) и поэто­му движутся через колонку наиболее медленно. Их удерживае­мый объем равен полному объему растворителя Vt-

Рис. 2.15. Модель разделения молекул по меру в эксклюзионной хроматографии

Все молекулы, размер которых больше размера пор сорбен­та, не могут попасть в них (полная эксклюзия) и проходят по-каналам между частицами. Они элюируются из колонки с од­ним и тем же удерживаемым объемом, равным объему подвиж­ной фазы V 0 - Коэффициент распределения для этих молекул ра­вен нулю.

Молекулы промежуточного размера, способные проникать только в какую-то часть пор, удерживаются в колонке в соот­ветствии с их размером. Коэффициент распределения этих мо­лекул изменяется в "пределах от нуля до единицы и характери­зует долю объема пор, доступных для молекул данного размера. Их удерживаемый объем определяется суммой У о и доступной части объема пор.

КАЧЕСТВЕННЫЙ АНАЛИЗ

Хроматографист, начинающий работать в области высоко­эффективной жидкостной хроматографии, должен ознакомиться с основами качественного анализа. Качественный анализ при­меняют для идентификации известного продукта, полученного новым путем или находящегося в смеси с другими продукта­ми." Он необходим при выделении из сложных биологических, химических смесей различных компонентов, что особенно важ­но в медицине, криминалистике, экологии, для контроля за на-| хождением некоторых лекарствен химических продуктов и их метаболитов в биомл.тер.иалах..„. "Знакомство с основами каче­ственного" анализа поможет избежать типичных ошибок, на­пример/отличить примеси в образце от примесей в раствори-теле или проверять чистоту вещества не на одной длине волны спектрофотометра, а на разных и т. д.

Прежде чем приступить к анализу, необходимо установить, весь ли образец элюируется из колонки данной системой ра­створителей или нет. Чтобы быть уверенным в полном элюи-ровании, необходимо собрать всю вытекающую из колонки жидкость, упарить растворитель, взвесить остаток и найти степень извлечения образца.

Идентификацию компонентов в ВЭЖХ можно проводить тремя способами: 1) использовать информацию об удержива­нии; 2) исследовать зоны, полученные при разделении в колон­ке жидкостного хроматографа, методами спектрального или химического анализа; 3) непосредственно подключить спект-ральный анализатор к колонке.

Для регистрации пиков в хроматографии используют удер­живаемый объем V R или время удерживания t R . Обе величины являются характеристикой вещества в данной хроматографиче­ской системе. Так как время удерживания разделяемого веще­ства состоит из времени взаимодействия в колонке и времени прохождения пустых участков трубки, оно меняется от прибора к прибору. Удобно иметь вещество, не удерживаемое данной колонкой, приняв его за стандарт, время и объем удер­живания которого t 0 , V o . Хроматографирование вещества и стандарта необходимо проводить при одних и тех же условиях (давлении и скорости потока). При идентификации по данным об удерживании, известные индивидуальные вещества, которые могут присутствовать в об­разцах, разделяют в той же самой хроматографической систе­ме, и для них получают значения t R . Сравнивая эти значения t R с временем удерживания неизвестного пика, можно обнару­жить, что они либо совпадают, и тогда вероятно, что пики со­ответствуют одному и тому же веществу, либо t R известного вещества не соответствует t R неизвестной зоны. Тогда все же возможна ориентировочная оценка значений t R веществ, не до­ступных для непосредственного измерения степени их удержи­вания. Рассмотрим оба варианта.

В первом случае, очевидно, необходимо предварительное изучение образца для постулирования присутствия в нем кон­кретных веществ. При работе с простыми смесями нетрудно определить, совпадает ли степень удерживания зон образца и известных веществ, или нет, т. е. значения t B одинаковы или различаются. В случае сложных смесей сразу несколько ве­ществ могут элюироваться со схожими значениями t R , и реально получаемые при хроматографическом разделении зоны пере­крываются. В результате получение точных значений t R для различных зон становится невозможным. Надежность иденти­фикации возрастает при повышении разрешающей способности, более тщательном контроле условий разделения, многократном измерении значений t R и усреднении найденных величин. При этом хроматографическое разделение известного и неизве­стного веществ должно чередоваться. При разделении сложных смесей значение t R вещества может изменяться под влиянием матрицы самого образца. Такое воздействие возможно в нача­ле хроматограммы и при перекрывании пиков; возможно также затягивание зон, о чем уже упоминалось.

В подобных случаях следует добавить стандарт к образцу в соотношении 1: 1. Если вещества идентичны, значение t R исходного вещества не изменится, и на хроматограмме полу­чают только один пик. Если имеется прибор с циклической системой хроматографирования, то для надежности идентифи­кации желательно смесь пропускать через колонку несколько раз.

Сведения о степени удерживания можно найти и в литера­туре, однако ценность этой информации ограничена. Так как колонки даже одной партии дают плохую воспроизводимость, литературные значения не всегда соответствуют истинному значению t R на данной колонке. Для адсорбционной хромато­графии возможно, однако, предсказание t R на основании лите­ратурных данных. Другая трудность, связанная с использова­нием литературных значений t R , - сложность их поиска в специальной литературе, хотя библиографические обзоры, пуб­ликуемые в Jornal of chromatography, имеют обновляемый указатель по типам веществ.

Во втором случае, когда времена удерживания известных соединений и зон образца не совпадают, имеется возможность предсказать время удерживания неизвестного компонента. Вполне надежны предсказания относительного удерживания на основании данных о структуре в пространственно-эксклюзионной хроматографии. Менее точны они в адсорбционной, распределительной хроматографии и особенно при работе на химически привязанной фазе. Для ионной и ион-парной хрома­тографии веществ с известной р Ка возможны лишь приблизи­тельные определения значений tR . Всегда легче предсказать от­носительное удерживание или значение *х, чем абсолютные зна­чения k ". Относительные значения t R легче оценить для родствен­ных соединений или производных, например замещенных алкилкарбоновых кислот или производных бензола.

При изократическом разделении гомологов или олигомеров иногда наблюдается следующая закономерность:

\ gk " = A + Bn ,

где А и В - константы для ряда выбранных образцов и для данной хрома-тографической системы (на одной и той же колонке, с такой же подвижной и неподвижной фазами); п - число одинаковых структурных единиц в мо­лекуле образца.

Введение в молекулу образца функциональной группы / бу­дет приводить к изменению k " в первом уравнении на некото­рый постоянный коэффициент а/ в данной хроматографической системе. Можно получить групповые константы а/ для различ­ных замещающих групп /, значения которых будут возрастать при увеличении полярности функциональных групп во всех видах хроматографии, кроме обращенно-фазной, где значения констант будут уменьшаться с увеличением полярности.

Некоторые групповые константы а/ для различных заме­щающих групп / приведены в табл. 9.1.

В адсорбционной хроматографии первое уравнение не всег­да применимо, так как оно справедливо при условии, что все изомеры имеют одно и то же значение k ", что не всегда соблю­дается. Можно, однако, построить график зависимости lgfe" одних и тех же соединений на одной колонке относительно lgfe" тех же соединений, но на другой колонке или относитель­но соответствующих характеристик в тонкослойной хромато­графии, например, lg[(l-Rf ) IRf ].

При сопоставлении данных об удерживании веществ можно использовать значения коэффициента емкости k ", так как на него в отличие от t R не влияют скорость подвижной фазы и геометрические особенности колонки.

Разделение на химически привязанной фазе аналогично разделению по методу распределительной хроматографии с аналогичными фазами, и поэтому данные по экстракции при равновесном состоянии могут быть использованы для пред­сказания времени удерживания.

В ионообменной хроматографии на степень удерживания влияют три фактора: степень ионизации кислот и оснований, заряд ионизированной молекулы и способность вещества из водной подвижной фазы, используемой в ионообменной хрома­тографии, мигрировать в органическую фазу. Последнее зави­сит от молекулярной массы соединения и его гидрофобности. Следовательно, более сильные кислоты или основания сильнее удерживаются при анионообменном или катионообменном раз­делении. При снижении рК а отдельной кислоты, входящей в образец, удерживание возрастает при разделении ряда кислот за счет анионного обмена, а при увеличении р/С о увеличивает­ся удерживание оснований при их разделении за счет катион-ного обмена.

Таким образом, совпадение значений времени удерживания известного вещества с наблюдаемым дает возможность пред­положить их идентичность. Достоверность идентификации воз­растает, если проводить сравнение хроматограмм известного вещества и неизвестного компонента в различных условиях. Если вещества в адсорбционной и обращенно-фазной или ион-нообменной и эксклюзионной хроматографии ведут себя одина­ково, надежность идентификации возрастает. Если достовер­ность идентификации при равенстве относительного удерживания составляет 90%, то при изучении поведения этих же веществ в условиях существенно отличающихся достоверность иденти­фикации составляет уже 99%.

Ценной характеристикой вещества, применяемой при иден­тификации, является отношение сигналов, полученных для данного вещества на двух разных детекторах. Анализируемое вещество после выхода из колонки проходит сначала через первый детектор, затем через второй, а сигналы, поступающие с детекторов, регистрируются одновременно при помощи мно­гоперьевого самописца или на двух самописцах. Обычно при­меняют последовательное соединение ультрафиолетового детек­тора (более чувствительного, но селективного) с рефрактомет­ром, или ультрафиолетового с детектором по флуоресценции, или двух ультрафиолетовых детекторов, работающих на раз­ных длинах волн. Относительный отклик, т. е. отношение сиг­нала рефрактометра к сигналу фотометра, является характе­ристикой вещества при условии, что оба детектора работают в своем линейном диапазоне; это проверяется введением раз­личных количеств одного и того же вещества. Качественную информацию можно получить, работая на фотометрических детекторах, снабженных устройством для остановки потока (Stop flow) и позволяющих регистрировать спектр выходящего" из колонки пика, пока он находится в проточной кювете, сравнивая его со спектром известного соединения.

Значительный интерес при идентификации представляют со­временные, пока еще дорогие, спектрофотометры с диодной решеткой.

Совершенно неизвестное вещество невозможно идентифици­ровать только с помощью высокоэффективной жидкостной хро­матографии, необходимы и другие методы.

КОЛИЧЕСТВЕННЫЙ АНАЛИЗ

Количественная жидкостная хроматография является хоро-(шо разработанным аналитическим методом, не уступающим по точности количественной газовой хроматографии и значительно превышающим точность ТСХ или электрофореза. К со­жалению, в ВЭЖХ не существует детектора, который имел бы близкую чувствительность для соединений различного химиче­ского строения (как катарометр в ГЖХ). Поэтому для полу­чения количественных результатов калибровка прибора обяза­тельна.

Количественный анализ состоит из следующих стадий: 1) хроматографическое разделение; 2) измерение площадей или высот пика; 3) расчет количественного состава смеси на основании хроматографических данных; 4) интерпретация по­лученных результатов, т. е. статистическая обработка. Рас­смотрим все эти стадии.

4.1. ХРМАТОГРАФИЧЕСКОЕ РАЗДЕЛЕНИЕ

При отборе пробы могут быть допущены ошибки. Особенно важно избежать ошибки и отобрать адекватную представи­тельную пробу неоднородных твердых образцов, легколетучих или неустойчивых веществ, а также сельскохозяйственных про­дуктов и биоматериалов. Неоднородные образцы, например, пищевых продуктов, тщательно перемешивают и квартуют. Проводя эту операцию многократно, добиваются однородности пробы.

Погрешности и потери веществ могут быть допущены на стадии экстракции, выделения, очистки и т. д.

Образцы должны быть полностью растворены, а их раст­воры приготовлены с точностью ±0,1%. Растворять образец желательно в подвижной фазе, что исключит возможность осаждения его после введения в хроматограф. Если растворе­ние в подвижной фазе невозможно, то следует применять ра­створитель, смешивающийся с ней, и вводить в хроматограф объемы образца (менее 25 мкл).

Значительные погрешности могут быть при вводе пробы за счет ее фракционирования, утечек и размывания пиков. Размывание пиков вызывает образование хвостов, приводящих к частичному перекрыванию пиков, и как следствие этого к погрешностям при детектировании. Для ввода пробы при ко­личественном анализе предпочтительнее использовать петле­вые клапанные устройства, а не шприцы из-за более высокой точности.и меньшей зависимости от индивидуальных особен­ностей операторов.

При хроматографическом разделении веществ также могут возникнуть осложнения, приводящие к искажению данных: количественного анализа. Возможно разложение или превра­щение пробы во время хроматографического процесса или не­обратимая адсорбция вещества на данной колонке. Важно убедиться в отсутствии этих нежелательных явлений и при не­обходимости провести регенерацию колонки или заменить ее. Перекрывание пиков и образование хвостов также можно уменьшить, изменяя условия хроматографирования.

Нельзя использовать в количественном анализе пики лож­ные или нечеткой формы, а также пики, время выхода которых близко к to , поскольку возможно недостаточное их разделение. Обычно используют пики со значением й"^0,5. Наивысшая эффективность колонки достигается при введении 10~ 5 -10~ 6 г растворенного вещества на 1 г сорбента. При введении боль­ших количеств образца зависимость высоты пика от нагрузки может оказаться нелинейной и потребоваться количественная оценка по площадям пиков.

К существенному искажению результатов хроматографиче­ского разделения приводят погрешности, связанные с детекти­рованием, или усилением. Каждый детектор характеризуется специфичностью, линейностью и чувствительностью. Особенно важна проверка на селективность при анализе микропримесей. Отклик УФ-детекторов может изменяться на вещества со схожими функциональными группами в 10 4 раз. Необходимо от­клик детектора прокалибровать для каждого определяемого вещества. Естественно, что вещества, не поглощающие в УФ-области, не дадут сигнала на самописец при использовании в качестве детектора фотометра. При использовании рефракто­метра возможно появление отрицательных пиков. Кроме того, этот детектор необходимо термостатировать, чего не требуется для УФ-детектора.

Линейностью детектора определяется размер вводимой пробы. Необходимо помнить, что скорость потока через колон­ку, температура колонки и детектора, а также его конструкция влияют на точность количественного анализа. Погрешности при передаче электрического сигнала на выходное устройство (са­мописец), интегратор или на ЭВМ могут возникать за счет наводки шумов, отсутствия заземления, колебания напряжения в сети и т. д.

4.2. ИЗМЕРЕНИЕ ПЛОЩАДЕЙ ИЛИ ВЫСОТ ПИКОВ

Высотой пик h (рис. 10.1) называют расстояние от верши­ны пика до базовой линии, его измеряют линейной либо под­считывают число делений на самописце. Некоторые электрон­ные интеграторы и вычислительные машины дают информацию о высоте пиков. Положение базовой линии смещенных пиков находят путем интерполирования значений ординат, соответ­ствующих началу и концу пика (пик 1 и 3 см. рис. 10.1). Для повышения точности необходимо иметь пологую стабиль­ную базовую линию. В случае неразделенных пиков базовую линию строят между началом и концом пика, а не заменяют нулевой линией. Так как высота пиков менее зависит от влия­ния соседних перекрывающихся пиков, оценка по высоте пика точнее, и ее почти всегда используют при анализе микропри­месей.

Площадь пика можно определять различными способами. Рассмотрим некоторые из них.

1. Планиметрический метод заключается в том, что пик обводят ручным планиметром, представляющим собой прибор механически определяющий площадь пика. Метод точен, но трудоемок и плохо воспроизводим. Применение этого метода нежелательно.

2. Метод бумажных силуэтов - пик вырезают и взвешивают. Метод хорошо воспроизводим, но трудоемок, при этом уничто­жается хроматограмма. Применимость его зависит от одно­родности диаграммной ленты. Метод также не может быть широко рекомендован.

4. Метод триангуляции состоит в построении треугольника путем проведения касательных к сторонам пика. Вершина тре­угольника находится выше, чем вершина пика. Увеличение площади, образованной этой продленной вершиной, будет по­следовательным для всей хроматограммы и не слишком по­влияет на точность. Кроме того, некоторая площадь, теряемая при проведении касательных, будет компенсирована. Основание треугольника определяют пересечением касательных с базовой линией, а площадь - произведением 7г основания на высоту. Для определения площадей асимметричных пиков этот метод наилучший. Однако воспроизводимость при построении каса­тельных различными операторами различна и, следовательно; низкая.

5. Метод с применением дискового интегратора основан на электромеханическом приспособлении, присоединенном к само­писцу. Перо, прикрепленное к интегратору, перемещается по полосе внизу ленты со скоростью, пропорциональной переме­щению пера самописца.

Как и при ручном измерении, пик должен оставаться на шкале самописца, однако регулировки, компенсирующие сме­щение базовой линии и неполное разделение смежных пиков, снижает надежность и увеличивает продолжительность ана­лиза.

Метод более точен, чем ручные методы измерения, особен­но при асимметричных пиках, и дает преимущество в скорости. Кроме того, он обеспечивает постоянную количественную за­пись анализа.

6. Методы с применением электронных интеграторов, опре­деляющих площадь пиков и печатающих информацию об этой площади и о временах удерживания, могут включать коррек­цию смещения базовой линии и определять площадь лишь ча­стично разделенных пиков. Основные преимущества - точность, скорость, независимость действия от работы самописца. Инте­граторы имеют память, и их можно программировать для кон­кретного анализа, используя предварительно заложенную про­грамму. К достоинствам интегратора относят его способность использовать поправочные коэффициенты на отклик детектора при пересчете исходных данных о площадях пиков, компенси­руя различие чувствительности детектора к разным веществам. Подобные системы экономят время, улучшают аналитическую точность и полезны для рутинного аналитического анализа.

7. В жидкостной хроматографии широко применяют ЭВМ, измеряющие площади пиков. Они выводят на печать полное сообщение, включая название веществ, площади пиков, време­на удерживания, поправочные коэффициенты на отклик детек­тора и содержание (в масс.%) для различных компонентов образца.

Для функции двух переменных, заданной как z = f (x , y ) .

Записывается двойной интеграл так:

Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x , а сверху и снизу – равенствами, в которых слева переменная y . Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.

Вычислить двойной интеграл - значит найти число, равное площади упомянутой фигуры D .

Пока мы не касаемся определения двойного интеграла , а будем учиться его вычислять. Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь отметить, что определение двойного интеграла также связано с упоминавшейся фигурой D .

В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D - криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.

Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D , которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.

Случай прямоугольной области:

Случай криволинейной области:

А это уже решение знакомых нам определённых интегралов , в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D , будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.

Сведение двойного интеграла к повторному

Случай прямоугольной области

Пусть для такой функции существует двойной интеграл

Чтобы вычислить этот двойной интеграл , нужно свести его к повторному интегралу, который имеет вид

.

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем - внешний (левый) определённый интеграл.

Можно и поменять ролями x и y

.

Пример 1. Вычислить двойной интеграл

Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.

.

Пример 2. Вычислить двойной интеграл

,

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

Вычислить двойной интеграл самостоятельно, а затем посмотреть решение

Случай криволинейной или треугольной области

Пусть снова дана функция двух переменных f (x , y ) , а ограничения для D : уже несколько другого вида:

Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области - прямые x = a и x = b , но снизу и сверху - кривые, которые заданы уравнениями и . Иными словами, и - функции.

Пусть для такой функции также существует двойной интеграл

Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

.

Здесь пределы интегрирования a и b - числа, а и - функции. В случае треугольной области одна из функций или - это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем - левый определённый интеграл.

Точно так же можно поменять ролями x и y . Тогда повторный интеграл будет иметь вид

.

Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).

Пример 5. Вычислить двойной интеграл

,

Решение. Сводим данный двойной интеграл к повторному интегралу

.

На чертеже строим область интегрирования и видим, что она треугольная:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:

.

Вычисляем первое слагаемое:

Вычисляем второе слагаемое:

Вычисляем третье слагаемое:

Получаем сумму, которая и будет решением данного двойного интеграла:

.

Пример 6. Вычислить двойной интеграл

Решение. Сводим данный двойной интеграл к повторному интегралу

На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.

.

Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):

Результат и будет решением данного двойного интеграла.

x -правильная и неправильная, y -правильная и неправильная области интегрирования

Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:

1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;

2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.

Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x , то область интегрирования называется x -неправильной. Если же прямая y = y 0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x -правильной

Аналогично, если границу, заданную линиями, выраженными через y , прямая x = x 0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y -неправильной. Вывести теперь признаки y -правильной области, надо полагать, совсем просто.

До сих пор мы рассматривали примеры с x -неправильными и y -правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.

Пример 7. Вычислить двойной интеграл , область интегрирования которого ограничена линиями y = x , xy = 1 , y = 2 .

Решение. Область интегрирования является y -неправильной, так как её нижнюю границу нельзя задать одной линией y = y (x ) . Как видно на рисунке выше, нижняя граница складывается из y = x (тёмно-бордовая) и xy = 1 (зелёная). Поэтому прямой x = 1 (чёрная) можем разбить область интегрирования на две части - и .

Вычисляется этот двойной интеграл так:

Смена порядка интегрирования

Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.

Смена порядка интегрирования образно может быть описана следующими словами О"Генри: "Так ведёт себя обитатель джунглей - зверь, попав в клетку, и так ведёт себя обитатель клетки - человек, заблудившись в джунглях сомнений". Результат, так же по О"Генри один и тот же: "Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая по нему взад и вперёд". (О"Генри . Шехерезада с Мэдисон-сквера .)

Тогда, если левый интеграл у нас по переменной x , а правый - по y , то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для "нового" игрека нужно "позаимствовать" у "старого" икса, а пределы интегрирования для "нового" икса получить в виде обратной функции , разрешив относительно икса уравнение, задававшее предел для игрека.

Пример 8.

.

Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу - правым. Пределы интегрирования для "нового" игрека позаимствуем у "старого" икса, то есть нижний предел равен нулю, а верхний - единице. Пределы интегрирования для "старого" игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:

(нижний) и (верхний).

Таким образом, после смены порядка интегрирования повторный интеграл запишется так:

.

После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y -неправильную или x -неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.

Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.

Пример 9. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1 , y = 3 , x = 0 , x = 2y .

При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC , которые заданы уравнениями y = 1 и y = x /2 , что видно на рисунке ниже.

Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ . Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:

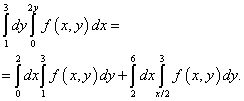
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.

Пример 10. Сменить порядок интегрирования для повторного интеграла

.

Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0 , x = 2 и кривыми и .

Как видно на рисунке ниже, прямая, параллельная оси 0x , будет пересекать нижнюю границу области интегрирования более чем в двух точках.

Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.

Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:

Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.

И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге - расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла - таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и - почти на автомате - на разбиении области и опустим само решение.

Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:

y - 2x ≤ 0;
2y - x ≥ 0;
xy ≤ 2.

Решение. В явном виде (через x и y "без примесей") линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:

y ≤ 2x ;
y ≥ x /2;
y ≤ 2/x .

Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2 . Но область интегрирования оказалась y -неправильной, так как её верхнюю границу нельзя задать одной линией y = y (x ) .

Транскрипт

1 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика СП КОРОЛЕВА» КРАТНЫЕ ИНТЕГРАЛЫ задачи и упражнения Утверждено Редакционно-издательским советом университета в качестве методических указаний С А М А Р А Издательство СГАУ

2 УДК 7 7 Составитель ОМ Карпилова Рецензент канд техн наук доц Г Н Г у т м а н Кратные интегралы задачи и упражнения: метод указания / сост ОМ Карпилова Самара: Изд-во Самар гос аэрокосм ун-та с Сборник содержит образцы решения типовых задач по темам: двойные интегралы тройные интегралы приложения кратных интегралов В каждой теме рассматриваются типовые задачи подробно разбираются методы их решения и предлагаются задачи для самостоятельной работы В приложении даны варианты индивидуального домашнего задания Все задания составлены в соответствии с программой по курсу математики для студентов технических вузов Методические указания подготовлены на кафедре общей инженерной подготовки и предназначены для студентов института энергетики и транспорта Самарского государственного аэрокосмического университета УДК 7 7 Самарский государственный аэрокосмический университет

3 ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ В ДЕКАРТОВЫХ КООРДИНАТАХ Для вычисления двойного интеграла его представляют в виде повторного двукратного интеграла f f Решение примеров Пример Перейти от b a f к повторному интегралу и расставить пределы интегрирования если область ограничена линиями: а 6; б; в; г контуром треугольника ABC где A; B;6 C;; д Решение: а Построим область: прямая параллельная оси О; прямая параллельная оси О; 6 прямая проходящая через точки;6 и 6; Область это треугольник АВС рис Чтобы найти координаты точки С надо решить систему уравнений Рис 6 Отсюда С; Поэтому внутри области Чтобы выяснить как изменяется проведем прямую параллельную оси O и пересекающую область Эта прямая входит в область по линии а выходит по линии 6 или 6 Поэтому 6 Таким образом область можно задать системой неравенств: 6 Теперь легко расставить пределы в двукратном интеграле: f 6 f

4 б Построим: парабола прямая параллельная оси O рис Найдем координаты точек А и В Для этого решим систему ± Проведем прямую параллельную оси O и пересекающую область Эта линия входит в область по параболе и выходит по прямой Рис Таким образом область задается неравенствами f f: Поэтому в Построим область рис: парабола симметричная относительно оси O с вершиной в начале координат; положительная ветвь параболы у симметричной относительно оси O с вершиной в начале координат Рис Найдем точки пересечения этих линий: Возводя обе части уравнения в квадрат получим Отсюда Таким образом линии и пересекаются в точках О; и А; Проведя прямую параллельную O и пересекающую область видим что линия входа а линия выхода

5 Таким образом: поэтому f f г Построим треугольник рис Из чертежа ясно что внутри области Прямая параллельная O и пересекающая область входит в треугольник по стороне АС и выходит по стороне АВ Уравнение прямой проходящей через две точки M и M имеет вид Воспользовавшись этой формулой напишем уравнения сторон АВ и АС: АВ: откуда те; 6 АС: откуда те Таким образом: Поэтому f f д Построим область Для этого преобразуем уравнение границы: Выделим полный квадрат относительно переменной: Получившееся уравнение задает окружность радиусом с центром в точке; рис Рис Рис Чтобы расставить пределы интегрирования надо записать уравнения верхней и нижней половины окружности линии входа в область и выхода из области Разрешим исходное уравнение относительно: ±

6 Очевидно что верхней половине окружности соответствует уравнение нижней Таким образом: поэтому f f Пример Переменить порядок интегрирования: б 6 ; f f ; а в f f Решение: а Область интегрирования задается системой неравенств: Построим область рис6: верхняя половина параболы нижняя половина параболы При перемене порядка интегрирования интеграл примет вид c f Рис 6 Найдем координаты точек пересечения параболы и прямой: ± Таким образом А; В; Проведем прямую параллельно оси O пересекающую область Линия входа этой в область парабола линия выхода прямая Таким образом область можно задать и системой неравенств: Тогда f f 6

7 б В данном случае область интегрирования задается системой неравенств: 6 Построим эту область рис7: 6 гипербола прямая Найдем координаты точек А и В В точке А следовательно В точке В следовательно Таким образом А; В; При перемене порядка интегрирования интеграл примет вид f Рис 7 c Так как то c ; Проведем прямую параллельную оси O и пересекающую область Линия 6 входа гипербола откуда Линия выхода прямая откуда 6 Область задается неравенствами: 6 Окончательно получим 6 6 f f в Построим области: и: Граница области определяется уравнением ± Возводя обе части уравнения в квадрат получим уравнение параболы вершина кото- рой находится в точке; а осью симметрии является ось O Рис Граница области задается следующими уравнениями: прямая проходящая через начало координат и верхняя ветвь параболы Таким образом область интегрирования рис 7

8 Чтобы расставить пределы интегрирования найдем координаты точек пересечения линий границы Для этого решим систему уравнений; Отсюда Таким образом А; В; При перемене порядка интегрирования внешний интеграл будем брать по переменной внутренний по Поэтому проведем прямую пересекающую область и параллельную оси Ох Она входит в область по линии и выходит по линии Итак меняя порядок интегрирования получаем f f f Здесь перемена порядка интегрирования упрощает выкладки так как вместо вычисления двух интегралов понадобится вычислить всего один Пример Вычислить; ; где область ограничена линиями Решение Построим область рис 9: прямая параллельная оси O и прямые проходящие через начало координат Для вычисления интеграла перейдем от двойного интеграла к повторному Так как область можно задать системой неравенств: то Рис 9 Вычисляем сначала внутренний интеграл считая постоянной величиной так как интегрирование ведется по переменной: Теперь осталось вычислить получившийся внешний интеграл:

9 Таким образом Пример Вычислить Решение Построим область: ось O прямая параллельная оси O прямая проходящая через начало координат рис Прямые и пересекаются в точке A ; Переходя к двукратному интегралу и вычисляя его получим если ограничена линиями по формулам приведения Рис 9

10 Задачи для самостоятельного решения Расставить пределы интегрирования в повторных интегралах к которым сводится f если область ограничена линиями: а; б; в; г; д треугольник АВС где А; В; С; Переменить порядок интегрирования: а f ; б f ; в f ; г f Вычислить двойные интегралы считая что область ограничена указанными линиями: а; 7 ; б; ; в; ; г е; 6 Ответы а f ; б f ; в г f ; д а f ; б f f ; в f ; г f а; 7 б; в; f 6 г е е f ;

11 ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ Если на плоскости заданы и декартова и полярная системы координат причем полюс совпадает с началом координат а полярная ось совмещена с осью Ох то для перехода к полярным координатам используют формулы Рис При этом если область ограничена лучами α β и кривыми рис то f β α f Решение примеров Пример Вычислить > Решение Построим область рис: окружность радиуса прямые проходящие через начало координат Так как область представляет собой часть круга удобно перейди к полярным координатам При этом полюс совместим с точкой О; а полярную ось пустим по оси O Тогда где область ограничена линиями Рис Теперь надо описать область в полярной системе координат Угол внутри области меняется от до см рис Прямая k наклонена к оси O

12 под углом тангенс которого равен k Поэтому tg ; tg Отсюда; Итак внутри области Луч исходящий из полюса О и пересекающий выходит из области по окружности уравнение которой в полярных координатах имеет вид Таким образом область описывается системой неравенств: Теперь легко расставить пределы в повторном интеграле и вычислить его Пример Вычислить е где кольцо Решение Так как область ограничена окружностями 9 и 9 рис удобно перейти к полярным координатам: Тогда уравнения границ примут вид; 9 Рис Чтобы расставить пределы интегрирования в повторном интеграле заметим что внутри области угол принимает все значения от до Проведем из начала координат луч пересекающий область Он входит в область по линии и выходит по линии Таким образом: Тогда

13 9 9 9 е е е е е е е е е е е е Пример Вычислить если определяется неравенствами: Решение Построим область Для этого преобразуем уравнение границы: Итак граница это окружность радиуса с центром в точке; Так как то верхняя половина круга рис Перейдем к полярным координатам: Рис Уравнение границы в полярных координатах примет вид Полагая получим Область целиком расположена в первой четверти поэтому Таким образом в полярных координатах область задается неравенствами Теперь можно вычислить двойной интеграл

14 Задачи для самостоятельного решения Вычислить переходя к полярным координатам: где верхняя половина круга 6 где область удовлетворяет неравенствам где область ограничена линиями 9 6 где ограничена линиями 6 где область ограничена кривыми Ответы; ; ; ; ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ Двойной интеграл применяется при вычислении: а площади плоской фигуры ограниченной областью: S ; б объема цилиндрического тела ограниченного сверху непрерывной поверхностью f снизу плоскостью и сбоку прямой цилиндрической поверхностью вырезающей на плоскости O область:

15 f ; в площади поверхности заданной уравнением f проекцией которой на плоскость O является область: σ Кроме того двойные интегралы используются в механике для вычисления: а массы плоской пластинки занимающей область плоскости O и имеющей переменную поверхностную плотность γ γ: M γ ; б статистических моментов пластинки относительно осей O и O: ; M γ ; M γ в координат центра тяжести пластинки: γ M ц; M γ Решение примеров ц M M γ γ 6 Пример Найти площадь области ограниченной линиями Решение Построим область Уравнение задает параболу уравнение прямую проходящую через начало координат рис Чтобы найти точки пересечения этих линий решим систему уравнений: Отсюда Тогда Таким образом прямая пересекает параболу в точках; и А; По формуле S Рис Пример Найти площадь фигуры ограниченной линиями вне первой окружности;

16 Решение Уравнение задает окружность радиуса с центром в начале координат Уравнение задает окружность радиуса с центром в точке;: Требуется найти площадь фигуры AmBnА рис 6 Здесь удобно перейти к полярным координатам Тогда первое уравнение примет вид Второе уравнение: Рис 6 Чтобы определить координаты точек А и В решим совместно систему уравнений ± Итак; А; В Область AmBn можно задать неравенствами По формуле 6 S Пример Найти объем тела ограниченного координатными плоскостями и плоскостью Решение Построим тело рис 7 и его проекцию на плоскость O рис 6

17 По формуле Рис 7 Рис В примере область это треугольник ОАВ изображенный на рис а поверхность определяется уравнением плоскости откуда Таким образом Пример Найти объем тела ограниченного координатными плоскостями плоскостью и поверхностью Решение Тело изображено на рис 9 Плоскость проходит параллельно оси O; параболоид вершина которого находится в точке;; Проекцией тела на плоскость O является треугольник АВО рис АВ линия пересечения плоскости с плоскостью поэтому уравнение прямой AB: откуда 7

18 По формуле Рис 9 Рис цилиндром 6 Пример Найти объем тела ограниченного параболоидом и плоскостями и Решение Тело изображено на рис Для удобства расстановки пределов интегрирования построим проекцию тела на плоскость O рис По формуле Рис Рис

19 7 6 Пример 6 Найти объем тела ограниченного поверхностями 7 Решение Данное тело ограничено двумя параболоидами рис Линия пересечения параболоидов определяется системой уравнений Из первого уравнения Итак линией пересечения является окружность радиуса лежащая в плоскости: Проекция этой линии на плоскость O тоже окружность поэтому удобно перейти к полярным координатам Рис Объем тела можно подсчитать как разность объемов двух цилиндрических тел: Пример 7 Найти площадь поверхности сферы внутри цилиндра 9 Решение Цилиндр вырезает на поверхности сферы две части симметричные относительно плоскости O рис В силу симметрии достаточно вычислить площадь поверхности только верхней «шапочки» и результат удвоить 9

20 Для вычисления воспользуемся формулой Так как в нее входят частные производные вычислим и У нас поэтому из уравнения сферы Тогда Рис Таким образом по формуле σ Проекция поверхности на плоскость O круг удобно перейти к полярным координатам В полярной системе координат уравнение окружности вид Итак в полярных координатах σ 9 следовательно 9 примет Так как мы считали площадь только верхней «шапочки» то вся площадь поверхности равна σ σ n Пример Найти центр тяжести однородной пластинки ABC если A;- B; C; ;- Решение Для вычисления координат центра тяжести воспользуемся формулами 6 Так как пластинка однородна то поверхностная плотность γ постоянна поэтому формулы примут вид ц; ц

21 Из рисунка рис видно что пластинка имеет форму трапеции и симметрична относительно оси O поэтому Запишем уравнения прямых BC и A воспользовавшись формулой определяющей уравнение прямой проходящей через две заданные точки: ц BC: ; A: Рис Вычислим теперь отдельно числитель и знаменатель дроби определяющей координату: ц 9 В знаменателе стоит интеграл равный площади области те площади трапеции ABC Поэтому h ; можно вычислить этот AB C интеграл и непосредственно Таким образом ц; ц Пример 9 Найти массу верхней половины эллипса если плотность в каждой точке равна ординате точки b a Решение Плотность в каждой точке равна ординате те γ По формуле M γ Для верхней половины эллипса рис 6 b поэтому a Рис 6

22 M a a a a b a b a a a b a a a b a a a a b Задачи для самостоятельного решения a ab Найти площадь фигуры ограниченной линиями: а; б; в a ; г a a ; д Найти объем тела ограниченного поверхностями: а; б; в a ; г Найти площадь указанной поверхности: а части плоскости 6 заключенной в первом октанте; б части плоскости a вырезаемой цилиндром a ; в параболоида внутри цилиндра; г параболоида отсекаемого параболическим цилиндром и плоскостью Найти центр тяжести трапеции ABC где A; B; C; ; если плотность в каждой точке равна абсциссе этой точки Найти центр тяжести однородной фигуры ограниченной параболой и прямой 6 Найти массу круглой пластинки радиуса если поверхностная плотность в каждой точке пропорциональна расстоянию от центра круга Ответы а; б; в; г a a ; д 6 а 6; б; в a ; г a a

23 а; б a ; в; г ц ц ц ц 6 6 k ВЫЧИСЛЕНИЕ ТРОЙНЫХ ИНТЕГРАЛОВ В ДЕКАРТОВЫХ КООРДИНАТАХ Для вычисления тройного интеграла его представляют в виде трехкратного интеграла: Решение примеров Пример Перейти от f b a f f к трехкратному и расставить пределы интегрирования если область ограничена: а плоскостью и координатными плоскостями; б конусом и плоскостью h; в шаром Решение а Построим область и проекцию этой области на плоскость O рис 7 Прямая АВ это линия пересечения плоскости с плоскостью поэтому ее уравнение Таким образом это ОАВ Рис 7 Рис Из рис легко увидеть что Проведя прямую параллельную оси O и пересекающую треугольник ОАВ рис замечаем что она входит в по линии а выходит по линии те

24 Чтобы выяснить пределы изменения проведем прямую параллельную оси O и пересекающую область рис 7 Она входит в область по поверхности и выходит по поверхности те Таким образом область можно описать системой неравенств 6 поэтому f f 6 б Для расстановки пределов в трехкратном интеграле построим область и ее проекцию на плоскость O область рис 9 Уравнение линии ограничивающей область получают решая систему уравнений h h Рис 9 То есть круг радиусом h с центром в начале координат Проводя прямые параллельные O и O пересекающие и получаем что описывается системой неравенств h h h h h Поэтому h h h h h f f

25 Можно выбрать в трехкратном интеграле другой порядок интегрирования тогда естественно изменятся и пределы интегрирования Например представим исходный интеграл в виде c f Чтобы расставить пределы интегрирования спроектируем на плоскость O и проведем прямые параллельные O и O и пересекающие соответственно и рис В этом случае задается неравенствами: h поэтому h f f Рис в Построим область и ее проекцию на плоскость O рис Рис Из чертежа видно что

26 f f f f Пример Вычислить если тело ограничено координатными плоскостями плоскостью и конусом Решение Построим тело и его проекцию на плоскость O рис Из чертежа видно что описывается неравенствами: Рис Таким образом 6 6

27 Задачи для самостоятельного решения Перейти от f к трехкратному интегралу и расставить пределы интегрирования если тело ограничено: а эллипсоидом; 9 б параболоидом и плоскостью; в координатными плоскостями и плоскостью 6 Вычислить если тело ограничено плоскостями и сферой Вычислить если тело ограничено плоскостями Вычислить и конусом Ответы 9 если тело ограничено плоскостями а f ; б f ; в f 6 ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНОМ ИНТЕГРАЛЕ ЦИЛИНДРИЧЕСКИЕ И СФЕРИЧЕСКИЕ КООРДИНАТЫ Формулы перехода к цилиндрическим координатам рис: ; ; ; Формулы перехода к сферическим координатам θ r рис: r θ ; r θ ; r θ ; r θrθ Здесь; θ ; r 7

28 Решение примеров Пример Вычислить Рис Рис если ограничено конусом и плоскостью Решение Тело изображено на рис Линия пересечения конуса и плоскости имеет уравнение те Таким образом проекция тела на плоскость O круг рис6 Рис Рис 6 Перейдем к цилиндрическим координатам: ; ; ; В этих координатах уравнение окружности изображенной на рис 6 уравнение конуса а тело задается неравенствами; ; Итак

29 v Пример Вычислить если тело ограничено поверх- ностями Решение Построим область; плоскости Чтобы построить поверхность преобразуем уравнение: Это уравнение определяет круговой цилиндр в основании которого лежит круг радиуса с центром в точке;; Таким образом область интегрирования это цилиндр рис 7 Поэтому удобно воспользоваться цилиндрическими координатами В этих координатах уравнение цилиндрической поверхности ограничивающей область интегрирования примет вид То есть откуда Исходя из этого область можно описать системой неравенств; ; Рис 7 9

30 Итак Пример Вычислить где тело верхняя половина шара Решение Так как здесь область интегрирования является частью шара удобно перейти к сферическим координатам: r r r r r r r r r r r r r θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ Задачи для самостоятельного решения Вычислить если ограничено поверхностями Вычислить где ограничено поверхностями

31 Вычислить Вычислить если ограничено поверхностями если шар Ответы ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ Тройной интеграл применяется при вычислении: а объема тела Ω: ; 7 Ω б массы тела занимающего область Ω с переменной объемной плотностью γ: M γ ; Ω в координат центра тяжести тела Ω: ц γ M Ω ц γ 9 M Ω ц γ M Ω где М масса тела Если тело однородно то в формулах 9 можно положить γ ; M Решение примеров Пример Найти объем тела ограниченного цилиндром и плоскостями Решение Тело и его проекция на плоскость O изображены на рис Рис Чтобы найти координаты точек А и В решим систему уравнений:

32 ± A ; B; Таким образом область Ω описывается системой неравенств; ; По формуле 7 Ω Пример Найти массу тела ограниченного плоскостями если плотность в каждой точке γ Решение Построим тело Ω и его проекцию на плоскость O рис 9 Рис 9 Плоскость пересекается с плоскостью по прямой Решив систему получим координаты точки А; Таким образом тело Ω описывается системой неравенств; ; По формуле масса тела M Ω Пример Вычислить массу тела ограниченного плоскостями 9 и параболическим цилиндром если плотность в каждой точке пропорциональна абсциссе и на единице расстояния от плоскости O равна

33 Решение Плотность пропорциональна абсциссе; следовательно k γ На единице расстояния от плоскости O плотность равна; следовательно при γ Тогда k k Таким образом γ Построим тело Ω и его проекцию на плоскость O рис Рис Чтобы найти координаты точки А решим систему уравнений; 9 A Таким образом область можно задать системой неравенств Ω Ω 9: По формуле масса тела равна Ω M Пример Найти координаты центра тяжести тела ограниченного нижней половиной сферы и параболоидом если плотность в каждой точке пропорциональна квадрату расстояния от оси O

34 Решение Построим тело Вершина параболоида точке; ; Уравнение находится в можно преобразовать к виду те оно задает сферу радиуса с центром в точке; ; Итак тело имеет вид представленный на рис Проекцией этого тела на плоскость O является окружность Ее уравнение можно получить решив систему уравнений В плоскости уравнение линии пересечения имеет вид Уравнение проекции тела Ω на плоскость имеет тот же вид Ω Рис Поскольку окружность удобно при вычислении перейти к цилиндрическим координатам; ; В этих координатах уравнение границы Ω имеет вид; а угол удовлетворяет условию Уравнение параболоида в цилиндрических координатах откуда Уравнение сферы: ± Для нижней половины Переменная плотность по условию задачи пропорциональна квадрату расстояния от оси O те γ k В цилиндрических координатах γ k Так как тело симметрично относительно оси O то очевидно что центр тяжести лежит на этой оси те ц; ц Для вычисления ц воспользуемся формулой 9: ц γ M Ω Вычислим сначала массу тела M [формула ]:

35 6 k k k k k k k k M γ Ω Ω Ω Теперь вычислим Ω Ω Ω γ k k k k k k k k k k По формуле k k ц Итак центр тяжести рассматриваемого тела имеет координаты; ; 7

36 Задачи для самостоятельного решения 6 Найти объем тела ограниченного: а плоскостями; б параболоидом и плоскостью; в поверхностями и 6 Найти массу тела ограниченного: а сферами если плотность γ k ; б поверхностями если плотность γ k ; в конусом и плоскостью b если плотность пропорциональна ординате точки и на единице расстояния от плоскости O равна γ 6 Найти координаты центра тяжести однородного тела ограниченного плоскостями a Ответы 6 а; б; в 6 9 k γb 6 а k ; б; в 6 6 C ;; 6

37 Вариант ПРИЛОЖЕНИЕ ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ДОМАШНИХ ЗАДАНИЙ Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности цилиндра заключенную внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного сферой и параболоидом если плотность в любой точке равна аппликате этой точки Вариант Найти центр тяжести плоской фигуры ограниченной линией и одной полуволной синусоиды Найти площадь поверхности конуса отсеченную плоскостями Найти объем тела ограниченного поверхностями Найти массу тела ограниченного частью шара радиуса находящейся в первом октанте если плотность в любой точке равна расстоянию от точки до плоскости O Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности конуса внутри цилиндра 9 Найти объем тела ограниченного поверхностями 9 9 Найти массу тела ограниченного сферическим слоем между поверхностями 9 и 6 если плотность в каждой точке обратно пропорциональна расстоянию от точки до начала координат Вариант Найти центр тяжести плоской фигуры ограниченной линиями 6 > Найти площадь поверхности расположенную внутри цилиндра 6 Найти объем тела ограниченного поверхностями 7

38 Найти массу тела ограниченного прямым круговым цилиндром радиуса высотой если плотность в каждой точке равна квадрату расстояния от точки до оси симметрии цилиндра Вариант Найти центр тяжести плоской фигуры ограниченной окружностью с центром в начале координат радиусом и двумя лучами расположенными симметрично относительно оси O и образующими между собой угол Найти площадь поверхности конуса расположенную внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного координатными плоскостями и плоскостью 6 если плотность в каждой точке равна абсциссе этой точки Вариант 6 Найти центр тяжести плоской фигуры ограниченной осью O и верхней частью эллипса b a Найти площадь поверхности цилиндра отсеченную плоскостями Найти объем тела ограниченного поверхностями 6 Найти массу тела ограниченного поверхностями 6 если плотность в каждой точке равна аппликате этой точки Вариант 7 Найти центр тяжести плоской фигуры ограниченной кардиоидой 7 Найти площадь поверхности конуса вырезанную цилиндром Указание Перейти к полярным координатам Найти объем тела ограниченного поверхностями Найти массу тела ограниченного поверхностями > если плотность равна ординате точки Вариант Найти центр тяжести плоской фигуры ограниченной линиями p

39 Найти площадь поверхности параболоида внутри цилиндра Найти объем тела ограниченного поверхностями 6 Найти массу тела ограниченного поверхностями если плотность в каждой точке равна Вариант 9 Найти центр тяжести плоской фигуры ограниченной линиями 9 9 > Найти площадь поверхности тела ограниченного сферой и параболоидом Найти объем тела ограниченного поверхностями 6 9 вне цилиндра Найти массу тела ограниченного сферическим слоем между поверхностями 6 если плотность обратно пропорциональна расстоянию точки от начала координат Вариант Найти центр тяжести плоской фигуры ограниченной линией и прямой ОА проходящей через начало координат и точку A ; Найти площадь поверхности сферы вырезанную цилиндром Найти объем тела ограниченного поверхностями; внутри цилиндров Найти массу тела ограниченного шаром радиусом если плотность пропорциональна кубу расстояния от центра шара и на единице расстояния равна γ ; Вариант Найти центр тяжести плоской фигуры ограниченной линиями 6 Найти площадь поверхности цилиндра между плоскостями Найти объем тела ограниченного поверхностями Найти массу тела ограниченного цилиндрической поверхностью и плоскостями если плотность равна ординате точки 9

40 Вариант Найти центр тяжести плоской фигуры ограниченной кардиоидой Найти площадь поверхности шара заключенную внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного октантом шара координатными плоскостями и плоскостью если плотность в каждой точке равна аппликате этой точки Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности параболоида заключенную между цилиндром и плоскостью c a b Найти массу тела ограниченного параболоидом и плоскостью если плотность равна сумме квадратов координат точки Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности цилиндра заключенную между плоскостью O и поверхностью Найти объем тела ограниченного поверхностями Найти массу тела ограниченного цилиндром 6 если плотность пропорциональна квадрату расстояния от точки до оси цилиндра Вариант Найти центр тяжести плоской фигуры ограниченной линиями α α tg tg Найти площадь поверхности конуса расположенную внутри цилиндра Найти объем тела ограниченного поверхностями

41 Найти массу тела ограниченного поверхностями > если плотность равна ординате точки Вариант 6 Найти центр тяжести плоской фигуры ограниченной линиями 6 Найти площадь поверхности шара 6 внутри цилиндров Найти объем тела ограниченного поверхностями b a a b Найти массу тела ограниченного поверхностями если плотность равна аппликате точки Вариант 7 Найти центр тяжести равнобедренного прямоугольного треугольника с катетом если плотность в каждой точке пропорциональна квадрату расстояния от вершины прямого угла Найти площадь поверхности конуса вырезанную цилиндром Указание Перейти к полярным координатам Найти объем тела ограниченного поверхностями 9 Найти массу шара радиуса если плотность пропорциональна кубу расстояния от центра шара и на единице расстояния равна γ Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности параболоида заключенную в первом октанте Параболоид ограничен плоскостью 6 Найти объем тела ограниченного поверхностями 6 Найти массу части шара радиуса находящейся в первом октанте если плотность в каждой точке равна расстоянию от плоскости O Вариант 9 Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности тела ограниченного сферой и параболоидом

42 Найти объем тела ограниченного поверхностями Найти массу тела ограниченного прямым круговым цилиндром радиусом высотой если плотность равна квадрату расстояния точки от центра основания цилиндра Вариант Найти центр тяжести плоской фигуры ограниченной линиями > Найти площадь поверхности сферы 9 вырезанную цилиндром Найти объем тела ограниченного поверхностями Найти массу шара радиуса если плотность пропорциональна кубу расстояния от центра и на единице расстояния равна γ Вариант Найти центр тяжести плоской фигуры ограниченной линиями ± tg 6 Найти площадь поверхности цилиндра внутри цилиндра Найти объем тела ограниченного поверхностями внутри цилиндра Найти массу тела ограниченного общей частью двух шаров если плотность пропорциональна расстоянию от точки до плоскости O Вариант Найти центр тяжести плоской фигуры ограниченной кардиоидой Найти площадь поверхности конуса отсеченную плоскостями Найти объем тела ограниченного поверхностями вне цилиндра 6 Найти массу части шара радиуса находящейся в первом октанте если плотность в каждой точке равна расстоянию до плоскости O

43 Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности параболоида 6 заключенную между цилиндром и плоскостью Найти объем тела ограниченного поверхностями Найти массу тела ограниченного сферическим слоем между поверхностями 6 если плотность обратно пропорциональна расстоянию от начала координат Вариант Найти центр тяжести плоской фигуры ограниченной линиями 9 Найти площадь поверхности расположенную внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного параболоидом и плоскостью если плотность равна сумме квадратов координат точки Вариант Найти центр тяжести плоской фигуры ограниченной линиями Найти площадь поверхности конуса внутри цилиндра Найти объем тела ограниченного поверхностями Найти массу тела ограниченного общей частью двух шаров если плотность пропорциональна расстоянию от точки до плоскости O

44 СОДЕРЖАНИЕ ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ В ДЕКАРТОВЫХ КООРДИНАТАХ ДВОЙНОЙ ИНТЕГРАЛ В ПОЛЯРНЫХ КООРДИНАТАХ ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ ВЫЧИСЛЕНИЕ ТРОЙНЫХ ИНТЕГРАЛОВ В ДЕКАРТОВЫХ КООРДИНАТАХ ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНОМ ИНТЕГРАЛЕ ЦИЛИНДРИЧЕСКИЕ И СФЕРИЧЕСКИЕ КООРДИНАТЫ 7 6 ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ ПРИЛОЖЕНИЕ ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ДОМАШНИХ ЗАДАНИЙ 7 Учебное издание КРАТНЫЕ ИНТЕГРАЛЫ задачи и упражнения Методические указания Составитель Карпилова Ольга Михайловна Редактор Ю Н Л и т в и н о в а Доверстка Ю Н Л и т в и н о в а Подписано в печать Формат 6х /6 Бумага офсетная Печать офсетная Усл печ л 7 Тираж экз Заказ Арт С-9/ Самарский государственный аэрокосмический университет 6 Самара Московское шоссе Изд-во Самарского государственного аэрокосмического университета 6 Самара Московское шоссе

Cos, sin, J dd dd d d 5 Вычислить zdd zddz ddz, где внешняя сторона поверхности z, отсекаемая плоскостью z Р е ш е н и е Поверхность представляет собой параболоид, заданный явно уравнением z Поэтому

ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ» Кафедра «Высшая математика» ВЫСШАЯ МАТЕМАТИКА. МАТЕМАТИКА. МАТЕМАТИКА (СПЕЦГЛАВЫ). МАТЕМАТИЧЕСКИЙ АНАЛИЗ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РАСЧЕТНЫМ ЗАДАНИЯМ ПО КУРСУ ВЫСШЕЙ МАТЕМАТИКИ «ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РЯДЫ КРАТНЫЕ ИНТЕГРАЛЫ» ЧАСТЬ III ТЕМА КРАТНЫЕ ИНТЕГРАЛЫ ОГЛАВЛЕНИЕ Вычисление двойных и тройных

Министерство транспорта Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Российский университет транспорта (МИИТ)» ИТТСУ Кафедра «Высшая и вычислительная

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 9 Вычисление двойного интеграла в полярных координатах Приложения двойных интегралов Рассмотрим частный случай замены переменных часто используемый при вычислении двойного интеграла

Двойные интегралы Примеры решения задач 1. Свести двойной интеграл f(x, y) dx dy к повторному двумя способами (по формуле (1) и по формуле (2)), если G область, ограниченная кривыми x = 1, y = x 2, y =

Выражение массы тела через тройной интеграл в цилиндрических координатах Определения и формулы для решения задач Определение Цилиндрическим брусом ориентированным по оси O рис Называется тело G ограниченное

Министерство образования Республики Беларусь БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра инженерной математики Н.А. Кондратьева О.Г. Вишневская Н.К. Прихач МАТЕМАТИКА Методическое пособие

Пособие предназначено для студентов заочников КГТУ второго года обучения. В пособии в краткой и доступной форме рассмотрены темы: Кратные интегралы, Криволинейные интегралы, Ряды, Теория вероятностей.

Министерство науки и образования Российской Федерации Московский Государственный Университет Геодезии и Картографии АВ Аристархова, НГ Бабаева Индивидуальные задания по высшей математике КРАТНЫЕ ИНТЕГРАЛЫ

БАНК ЗАДАЧ ПО ТЕМЕ «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ» * Изменить порядок интегрирования + d d * Найти площадь плоской области, ограниченной линиями =, =, = * Вычислить (D) + acctg d, где) +, + 9, = (D область,

МИНИСТЕРСТВО КУЛЬТУРЫ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КИНО И

Часть. Примерные экзаменационные задачи по математике А. Простейшие задания на три балла.. Вычислить интегралы arcsin д) II семестр ИСиА, и 9 гр. и) 6 n к) 5 6 5 ж) 6 г) cos з) z arcsin z. Вычислить производную

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)» Институт транспортной техники

3 область (D) В нашем случае n - вектор нормали к плоскости XOY те n k { } = ϕ, ϕ, Тогда = =, а n { } cos γ =, + + (ϕ) (ϕ) (ϕ) (ϕ) dq = + + dd Замечание Если поверхность (Q) правильная в направлении

ЗАДАЧНИК ПО МАТЕМАТИКЕ (тенические факультеты, семестр) 7 Интегралы Найдите интегралы d d sin + d + + d + d + d 7 (+) d + + 8 d 9 cos d cos + d cos d + 8 d 9 d d + d 9 + d + 7 tg d 8 cosd cos sin 9 d

ЛЕКЦИЯ N 45 Кратные интегралы в полярных, цилиндрических и сферических координатах Приложения кратных интегралов Двойной интеграл в полярных координатах Тройной интеграл в цилиндрических и сферических

Глава. Кратные интегралы.. Занятие... Сведение двойного интеграла к повторному При вычислении двойных интегралов следует различать два случая. () Первый случай. Область интегрирования ограничена слева

ВЫСШИЙ КОЛЛЕДЖ СВЯЗИ СБОРНИК ТИПОВЫХ РАСЧЕТОВ по дисциплине «ВЫСШАЯ МАТЕМАТИКА» часть II для студентов специальности Т 000 Почтовая связь Минск 00 Составитель Рябенкова ЛА Издание утверждено на заседании

ЛЕКЦИЯ Линии второго порядка гиперболу В качестве примера найдем уравнения задающие окружность, параболу, эллипс и Окружность Окружностью называется множество точек плоскости, равноудалённых от заданной

Тройной интеграл Волченко Ю.М. Содержание лекции Понятие тройного интеграла. Условия его существования. Теорема о среднем. Вычисление тройного интеграла в декартовых и криволинейных координатах. Тройной

ЛЕКЦИЯ N. Вычисление кратных интегралов..вычисление двойного интеграла в прямоугольных декартовых координатах.....вычисление двойного интеграла (произвольная область).....тройной интеграл.....вычисление

Введение Методические указания содержат 26 вариантов индивидуальных домашних заданий по темам «Прямая на плоскости и в пространстве», «Плоскость», «Кривые и поверхности второго порядка». Под индивидуальными

Содержание Введение Кратные, криволинейные и поверхностные интегралы Элементы теории поля Задачи для аудиторных занятий Краткие сведения из теории Образцы решения задач Задачи для самоподготовки Тестовая

Практическое занятие 6 Поверхностные интегралы 6 Определение свойства вычисление и приложения поверхностного интеграла -го рода 6 Определение свойства и вычисление поверхностного интеграла -го рода 6 Определение

Б. М. Маврин, Е. И. Балаев ИЗОБРАЖЕНИЕ ТЕЛ ВРАЩЕНИЯ Практикум Самара 2005 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ

Двойные интегралы Задачи и упражнения для самостоятельной работы 1. Сведите двойной интеграл f(x, y) dx dy к повторному двумя способами, если: G а) G треугольник с вершинами (1, 1), (4, 1), (4, 4); б)

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая математика» И Н Пирогова Аналитическая геометрия в примерах и задачах Екатеринбург

Занятия 1-2. Определенный интеграл и его приложения I. Используя формулу Ньютона-Лейбница, вычислить определенный интеграл: 1. (2 + 2) 2. / 3. (4.) 5. 6. 7. 8. Ефимов-Поспелов 7.324-7.352, 7.380-7.385,

Лекция 7 Несобственные интегралы Несобственными интегралами называются определенные интегралы, для которых не выполнено хотя бы одно из условий существования определенного (собственного) интеграла:)либо

14-е занятие. Тройные интегралы Матем. анализ, прикл. матем., 3-й семестр Повторение A1 В следующем интеграле перейти к полярным координатам и расставить пределы интегрирования в том и другом порядке:

Министерство образования Российской Федерации Ярославский государственный университет им. П.Г. Демидова Кафедра дискретного анализа ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ Задачи Ярославль Составитель канд.

МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ) ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Варианты контрольных заданий Задачник МОСКОВСКИЙ АВТОМОМОБИЛЬНО-ДОРОЖНЫЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая и прикладная математика» П И Гниломедов ПРИЛОЖЕНИЯ КРАТНЫХ И КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени

Приложение 5 Министерство сельского хозяйства Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Саратовский государственный аграрный университет

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ. Прямая линия 1. Вычислите периметр треугольника, вершинами которого служат точки A(6; 7), B(3; 3), C(1; 5). 2. Найдите точку, равноудаленную от точек A(7;

Министерство образования и науки Российской Федерации Ярославский государственный университет им. П. Г. Демидова Кафедра алгебры и математической логики Кривые второго порядка Часть I Методические указания

Содержание Кратные интегралы Понятие кратного интеграла Двойные интегралы. Области на плоскости................. Повторный интеграл................ 3.3 Вычисление двойного интеграла в декартовых координатах.......................

Практическое занятие 14 Тема: Парабола План 1. Определение и каноническое уравнение параболы.. Геометрические свойства параболы. Взаимное расположение параболы и прямой, проходящей через ее центр. Основные

1 Простейшие задачи аналитической геометрии на плоскости 11 Расстояние между двумя точками Рассмотрим прямоугольную систему координат (декартовую, рис Рис 1 Любой точки M соответствуют координаты OA x

МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УЛЬЯНОВСКОЕ ВЫСШЕЕ АВИАЦИОННОЕ УЧИЛИЩЕ ГРАЖДАНСКОЙ АВИАЦИИ (ИНСТИТУТ)

Глава 5. Тройной интеграл. 5.1. Определение тройного интеграла. После введения в предыдущей главе понятия двойного интеграла естественно было бы провести его дальнейшее обобщение на трехмерное пространство

АЛГЕБРАИЧЕСКИЕ ЛИНИИ НА ПЛОСКОСТИ.. ЛИНИИ ПЕРВОГО ПОРЯДКА (ПРЯМЫЕ НА ПЛОСКОСТИ... ОСНОВНЫЕ ТИПЫ УРАВНЕНИЙ ПРЯМЫХ НА ПЛОСКОСТИ Ненулевой вектор n перпендикулярный заданной прямой называется нормальным

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА ИМЕНИ ИМГУБКИНА ТС Филиппова АНФилиппов МЕТОДИЧЕСКИЕ УКАЗАНИЯ к изучению темы «Кратные и криволинейные

Пензенский государственный педагогический университет имени ВГБелинского ОГНикитина ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ Учебное пособие Пенза Печатается по решению редакционно-издательского

Тема ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ Лекция.. Прямые на плоскости П л а н. Метод координат на плоскости.. Прямая в декартовых координатах.. Условие параллельности и перпендикулярности

ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ ÌÃÒÓ Московский государственный технический университет имени Н.Э. Баумана Факультет «Фундаментальные науки» Кафедра «Математическое моделирование» À.Í. Êàíàòíèêîâ, À.Ï. Êðèùåíêî

Глава 5 Поверхностные интегралы -го типа (продолжение) 5 Задачи в классе Задача 5 (4349) Вычислить интеграл где часть поверхности конуса z d, x = ρ cos ϕ sin α, y = ρ sin ϕ sin α, z = ρ cos α ((ρ h,

Федеральное агентство по образованию Уральский государственный лесотехнический университет Кафедра Сопротивления материалов и теоретической механики В. А. Калентьев В. М. Калинин Л. Т. Раевская Н. И. Чащин

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ ЗАНЯТИЕ ПЛОСКОСТЬ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ Написать векторное уравнение плоскости и объяснить смысл величин, входящих в это уравнение Написать общее уравнение плоскости

3 Пример Записать выражения для статических моментов плоской материальной области (D) На основании формул (3) с учетом фигуры (Φ) имеем: ρ, dd, ρ, dd Исходя из механического смысла статического момента,

Задача 1 Найти координаты центра тяжести полуокружности y = r 2 x 2. Задача 5 площадь части поверхности z = 1 4 xy, расположенной внутри поверхности x 2 + y 2 = 16. Задача 2 Изменить порядок интегрирования

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ НАЦИОНАЛЬНАЯ МЕТАЛЛУРГИЧЕСКАЯ АКАДЕМИЯ УКРАИНЫ МЕТОДИЧЕСКИЕ УКАЗАНИЯ к решению задач по дисциплине Высшая математика и варианты контрольных заданий практические

Практические занятия по курсу высшей математики (III семестр) на основе учебного пособия «Сборник индивидуальных заданий по высшей математике», том 3, под ред. Рябушко А.П. для студентов дневной формы

Московский государственный технический университет имени Н.Э. Баумана Факультет «Фундаментальные науки» Кафедра «Вычислительная математика и математическая физика» А.И. Левина КРАТНЫЕ ИНТЕГРАЛЫ Электронное

Интегральное исчисление функции нескольких переменных интегралов двойного тройного криволинейного по длине дуги (первого рода) поверхностного по площади поверхности (первого рода) Пусть функция f() определена

1.3. Занятие 3 1.3.1. Вычисление тройных интегралов в декартовых координатах Пусть пространственная область, D ее проекция на плоскость Oxy. Область называется -правильной, если любая вертикальная прямая

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Белорусский национальный технический университет Кафедра инженерной математики ВЫСШАЯ МАТЕМАТИКА Руководство к решению задач для студентов механико-технологического

Практическое занятие 1 Тема: Гипербола План 1 Определение и каноническое уравнение гиперболы Геометрические свойства гиперболы Взаимное расположение гиперболы и прямой, проходящей через ее центр Асимптоты

Раньше мы доказывали свойства определенного интеграла, пользуясь его определением, как предела сумм . Совершенно так же можно доказать и основные свойства кратных интегралов. Для простоты мы все функции будем считать непрерывными, так что интегралы от них безусловно имеют смысл.

I. Постоянный множитель можно выносить за знак интеграла, и интеграл от конечной суммы функций равен сумме интегралов от слагаемых:

II. Если область разложена на конечное число частей [например на две части , то интеграл по всей области равен сумме интегралов по всем частям:

III. Если в области , то

В частности :

IV. Если сохраняет знак в области (а), то имеет место теорема о среднем, выражающаяся формулой

где - некоторая точка, лежащая внутри области (а).

В частности, при получаем

где - площадь области .

Аналогичные свойства имеют место и для трехкратного интеграла. Заметим, что при определении двукратного и трехкратного интеграла как предела суммы считается всегда, что область интегрирования конечна и подынтегральная функция во всяком случае ограничена, т. е. существует такое положительное число А, что во всех точках N области интегрирования. Если эти условия не выполнены, то интеграл может существовать как несобственный интеграл аналогично тому, как это имело место для простого определенного интеграла . Мы займемся несобственными кратными интегралами в § 8.

Кратный интеграл

интеграл от функции, заданной в какой-либо области на плоскости, в трёхмерном или n -мерном пространстве. Среди К. и. различают двойные интегралы, тройные интегралы и т. д. n -кратные интегралы.

Пусть функция f (x, y ) задана в некоторой области D плоскости хОу. Разобьем область D на n частичных областей d i , площади которых равны s i , выберем в каждой области d i точку (ξ i , η i ) (см. рис. ) и составим интегральную сумму

Если при неограниченном уменьшении максимального диаметра частичных областей d i суммы S имеют предел независимо от выбора точек (ξ i , η i ), то этот предел называют двойным интегралом от функции f (x, у ) по области D и обозначают

Аналогично определяется тройной интеграл и вообще n -кратный интеграл.

Для существования двойного интеграла достаточно, например, чтобы область D была замкнутой квадрируемой областью (См. Квадрируемая область), а функция f (x, y ) была непрерывна в D. К. и. обладают рядом свойств, аналогичных свойствам простых Интеграл ов. Для вычисления К. и. обычно приводят его к повторному интегралу (См. Повторный интеграл). В специальных случаях для сведения К. и. к интегралам меньшей размерности могут служить Грина формулы и Остроградского формула . К. и. имеют обширные применения: с их помощью выражаются объёмы тел, их массы, статические моменты, моменты инерции и т. п.

Большая советская энциклопедия. - М.: Советская энциклопедия . 1969-1978 .

Смотреть что такое "Кратный интеграл" в других словарях:

Интеграл от функции нескольких переменных. Определяется при помощи интегральных сумм, аналогично определенному интегралу от функции одного переменного (см. Интегральное исчисление). В зависимости от числа переменных различают двойные, тройные, n… … Большой Энциклопедический словарь

Определенный интеграл от функции нескольких переменных. Имеются различные понятия К. и. (интеграл Римана, интеграл Лебега, интеграл Лебега Стилтьеса и др.). Кратный интеграл Римана вводится на основе Жордана меры Пусть Е измеримое по Жордану… … Математическая энциклопедия

В математическом анализе кратным или многократным интегралом называют множество интегралов, взятых от переменных. Например: Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число. Содержание 1… … Википедия

Интеграл от функции нескольких переменных. Определяется при помощи интегральных сумм, аналогично определённому интегралу от функции одного переменного (см. Интегральное исчисление). В зависимости от числа переменных различают двойные, тройные, n… … Энциклопедический словарь

Интеграл от функции нескольких переменных. Определяется при помощи интегральных сумм, аналогично определ. интегралу от функции одного переменного (см. Интегральное исчисление). В зависимости от числа переменных различают двойные, тройные, я… … Естествознание. Энциклопедический словарь

Примечание: всюду в данной статье, где используется знак имеется в виду (кратный) интеграл Римана, если не оговорено обратное; всюду в данной статье, где говорится об измеримости множества, имеется в виду измеримость по Жордану, если не… … Википедия

Кратный интеграл вида где являющийся средним значением степени 2k модуля тригонометрической суммы. Теорема Виноградова о величине этого интеграла теорема о среднем лежит в основе оценок сумм Вейля. Литература Виноградова инте … Википедия

Определённый интеграл как площадь фигуры У этого термина существуют и другие значения, см. Интеграл (значения). Интеграл функции … Википедия

Интеграл, в к ром последовательно выполняется интегрирование по разным переменным, т. е. интеграл вида (1) Функция f(x, y).определена на множестве А, лежащем в прямом произведении XX Y пространств Xи У, в к рых заданы s конечные меры mx и my,… … Математическая энциклопедия

Интеграл, взятый вдоль какой либо кривой на плоскости или в пространстве. Различают К. и. 1 го и 2 го типов. К. и. 1 го типа возникает, например, при рассмотрении задачи о вычислении массы кривой переменной плотности; он обозначается… … Большая советская энциклопедия