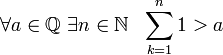Исторически первыми возникли натуральные числа $N$, как результат пересчета пердметов. Множество этих чисел бесконечно и образует натуральный ряд $N=\{1, 2, 3, ..., n, ...\}$. В этом множестве выполнимы операции сложения и умножения. Для выполнения операции вычитания потребовались новые числа, что привело к появлению множества целых чисел: $Z$. $Z=N_+\cup N_- \cup \{0\}$. Таким образом в множестве целых чисел всегда выполняются операции сложения, умножения, вычитания.
Рациональные числа
Необходимость выполнения деления привела к множеству рациональных чисел $Q$. $Q=\{\frac{m}{n}, m\in Z, n\in N\}$.
Определение. Два рациональных числа равны: $\frac{m_1}{n_1}=\frac{m_2}{n_2}$ - если $m_1\cdot n_2=n_1\cdot m_2$. Это означает, что всякое рациональное число можно представить единственным образом в виде несократмой дроби $\frac{m}{n}$. $НОД(m, n)=1$.
Свойства множества рациональных чисел
1. В результате арифметических операций над рациональными числами (сложение, умножение, вычитание, деление, кроме деления на ноль) получается рациональное число.
2. Множество рациональных чисел упорядочено, то есть для любой пары рациональных чисел $a$ и $b$ либо $a
3. Множество рациональных чисел плотно, то есть для любой пары рациональных чисел $a$ и $b$ существует такое рациональное число $c$, что $a Всякое положительное рациональное число всегда можно представить в виде десятичной дроби: либо конечной, либо бесконечной периодической. Например: $\frac{3}{5}=0,6$, $\frac{1}{3}=0,333...=0,(3)$. $\frac{m}{n}=a_0,a_1a_1...a_kb_1b_2b_3...b_nb_1b_2b_3...b_n...$. $b_1b_2b_3...b_n...$ - называется периодом десятичной дроби, где не все $b_i=0$. Заметим, что конечная дробь может быть записана в виде бесконечной периодической с нулем в периоде. $\frac{m}{n}=a_0,a_1a_1...a_k000000...$, $a_k\ne0$. Однако, чаще встречается другое представление рациональных чисел в виде десятичной дроби: $\frac{m}{n}=a_0,a_1a_1...(a_k-1)999...$. Отрицательные рациональные числа $-\frac{m}{n}$ записываютсяв виде десятичного разложения рационального числа вида $\frac{m}{n}$, взятого с противоположным знаком. Число $0$ представляется в виде $0,000...$. Таким образом, всякое рациональное число всегда представимо в виде бесконечной десятичной периодической дроби не содержащей $0$ в периоде, кроме самого числа $0$. Такое представление единственное. Множество рациональных чисел замкнуто относительно четырёх арифметических операций. Однако в множестве рациональных чисел не всегда имеет место решение простейшего уравнения вида $x^2-n=0$. Поэтому возникает необходимость введения новых чисел. Покажем, что среди рациональных чисел нет числа, квадрат которого равен трём. Доказательство проведём методом от противного. Предположим, что существует рациональное число $\frac{m}{n}$ такое, что его квадрат равен трём: $\left(\frac{m}{n}\right)^2=3\;\;\;(1)$. $\frac{m^2}{n^2}=3$, $m^2=3n^2.\;\;\;(2)$ Правая часть равенства (2) делится на 3. Значит и $m^2$ делится на 3, следовательно $m$ делится на 3, а это значит, что $m=3k$. Подставим в равенство (2), получим: $3k^2=n^2.\;\;\;(3)$ Левая часть равенства $(3)$ делится на $3$, значит и правая часть делится на $3$. Следовательно $n^2$ делится на $3$, значит и $n$ делится на $3$, откуда $n=3p$. В результате получаем: $\frac{m}{n}=\frac{3k}{3p}$, то есть дробь $\frac{m}{n}$ оказалась сократимой, что противоречит предположению. Значит, среди рациональных чисел нет такого числа, квадрат которого равен трём. Но число, квадрат которого равен трём, существует. Оно представимо в виде бесконечной непериодической дроби. И мы получили новый вид чисел. Назовём их иррациональными. Определение.
Иррациональным числом называется любая бесконечная непериодическая дробь. Множество всех бесконечных непериодических дробей называется множеством иррациональных чисел и обозначается $I$. Объединение множества рациональных чисел $Q$ и иррациональных чисел $I$ даёт множество действительных чисел $R$: $Q\cup I=R$. Таким образом всякое действительное число представимо в виде бесконечной десятичной дроби: периодической в случае рационального числа и непериодической в случае иррационального числа. Для действительных чисел $a=a_0,a_1a_2a_3\ldots a_n\ldots$, $b=b_0,b_1b_2b_3\ldots b_n\ldots$ сравнение осуществляется следующим образом: 1) Пусть $a$ и $b$ оба положительны: $a>0$, $b>0$, тогда: $a=b$, если для любого $k$ $a_k=b_k$; $a>b$, если $\exists s$ $\forall k 2) Пусть $a>0$, $b<0$, или иначе: $b<0 3) Пусть $a$ и $b$ оба отрицательны: $a<0$, $b<0$, тогда: $a=b$, если для $-a=-b$; Существуют числа другой природы - к ним часто приводит операция извлечения квадратного корня (и не только она, просто мы с вами этого пока не знаем). Значит, нам нужно более обстоятельно познакомиться с новыми числами. Но сначала попробуем систематизировать наши знания о «старых», т. е. о рациональных, числах. 1. Некоторые символы математического языка
Это были целые числа, обыкновенные дроби, десятичные дроби. Для всех этих чисел можно использовать один и тот же способ записи, который мы сейчас и обсудим. 5 = 5,00000... = 5,(0). Так же обстоит дело и с числом 8,377: 8,377 = 8,377000... = 8,377(0). Чтобы все было аккуратно, говорят так: 8,377 - конечная десятичная дробь, а 8,377000... - бесконечная десятичная дробь. Вообще, любое рациональное число можно записать в виде бесконечной десятичной периодической дроби. Замечание.
Этот вывод удобен для теории, но не очень удобен для практики. Ведь если дана конечная десятичная дробь 8,377, то зачем нужна ее запись в виде 8,377(0)? Поэтому обычно говорят так: любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби. Множество рациональных чисел обозначается и может быть записано таком в виде: При этом оказывается, что разные записи могут представлять одну и ту же дробь, например, и , (все дроби, которые можно получить друг из друга умножением или делением на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых
дробей со взаимно простыми целым числителем и натуральным знаменателем: Здесь - наибольший общий делитель чисел и . Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа знаменатель , то является целым числом. Множество рациональных чисел располагается на числовой оси всюду плотно: между любыми двумя различными рациональными числами расположено хотя бы одно рациональное число (а значит, и бесконечное множество рациональных чисел). Тем не менее, оказывается, что множество рациональных чисел имеет счётную мощность (то есть все его элементы можно перенумеровать). Заметим, кстати, что ещё древние греки убедились в существовании чисел, не представимых в виде дроби (например, они доказали, что не существует рационального числа, квадрат которого равен 2) Свойства
Основные свойства
Множество рациональных чисел удовлетворяют шестнадцати основным свойствам, которые легко могут быть получены из свойств целых чисел. Дополнительные свойства
Все остальные свойства, присущие рациональным числам, не выделяют в основные, потому что они, вообще говоря, уже не опираются непосредственно на свойства целых чисел, а могут быть доказаны исходя из приведённых основных свойств или непосредственно по определению некоторого математического объекта. Таких дополнительных свойств очень много. Здесь имеет смысл привести лишь некоторые из них. 25..Множество J иррациональных чисел Примеры иррациональных чисел
: Обозначается множество иррациональных чисел большой английской буквой [ай] - " I ". Среди множества чисел иррациональные числа занимают особое место. Они не входят в рациональные числа. Иррациональные числа
(в отличие от рациональных) невозможно представить в виде дроби a / b , где a ∈ Z (a принадлежит целым числам), b∈N (b принадлежит натуральным числам). 26.Множество R действительных чисел Вещественное число
Материал из Википедии - свободной энциклопедии Перейти к: навигация, поиск Веще́ственное
, или действи́тельное число
- математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений . Числовая прямая Если натуральные числа возникли в процессе счета, рациональные - из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Таким образом, расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами
. Наглядно понятие вещественного числа можно представить себе при помощи числовой прямой
. Если на прямой выбрать направление, начальную точку и единицу длины для измерения отрезков, то каждому вещественному числу можно поставить в соответствие определённую точку на этой прямой, и обратно, каждая точка будет представлять некоторое, и притом только одно, вещественное число. Вследствие этого соответствия термин числовая прямая обычно употребляется в качестве синонима множества вещественных чисел. Понятие вещественного числа прошло долгий путь становления. Ещё в Древней Греции в школе Пифагора, которая в основу всего ставила целые числа и их отношения, было открыто существование несоизмеримых величин
(несоизмеримость стороны и диагонали квадрата), то есть в современной терминологии - чисел, не являющихся рациональными. Вслед за этим Евдоксом Книдским была предпринята попытка построить общую теорию числа, включавшую несоизмеримые величины. После этого, на протяжении более двух тысяч лет, никто не ощущал необходимости в точном определении понятия вещественного числа, несмотря на постепенное расширение этого понятия . Лишь во второй половине XIX века, когда развитие математического анализа потребовало перестройки его основ на новом, более высоком уровне строгости, в работах К. Вейерштрасса, Р. Дедекинда, Г. Кантора, Э. Гейне, Ш. Мере была создана строгая теория вещественных чисел. С точки зрения современной математики, множество вещественных чисел - непрерывное упорядоченное поле. Это определение, или эквивалентная система аксиом, в точности определяет понятие вещественного числа в том смысле, что существует только одно, с точностью до изоморфизма, непрерывное упорядоченное поле. Множество вещественных чисел имеет стандартное обозначение - R
(«полужирное R»), или (англ. blackboard bold
«R») от лат. realis
- действительный. 27.Системы счисления Система счисле́ния
- символический метод записи чисел, представление чисел с помощью письменных знаков. Система счисления: Системы счисления подразделяются на позиционные
, непозиционные
и смешанные
.Иррациональные числа
Действительные числа
Сравнение действительных чисел
Рассмотрим, например, целое число 5, обыкновенную дробь и десятичную дробь 8,377. Целое число 5 можно записать в виде бесконечной десятичной дроби: 5,0000... Десятичную дробь 8,377 также можно записать в виде бесконечной десятичной дроби
: 8,377000... Для числа воспользуемся методом «деления углом»:
Как видите, начиная со второй цифры после запятой происходит повторение одной и той же группы цифр: 18, 18, 18, ... . Таким образом, = 0,3181818... . Короче это записывают так: 0,3(18). Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь - бесконечной десятичной периодической дробью.
бесконечной десятичной периодической дроби. Для этого надо в периоде записать число 0:
Таким образом, и число 5, и число , и число 8,377 удалось записать в виде бесконечной десятичной периодической дроби.![]()