पिछले पाठ में, हमने सीखा कि दशमलव भिन्नों को कैसे जोड़ना और घटाना है (पाठ "दशमलव भिन्नों को जोड़ना और घटाना")। उसी समय, उन्होंने अनुमान लगाया कि सामान्य "दो-कहानी" अंशों की तुलना में गणना कितनी सरल है।

दुर्भाग्य से, दशमलव अंशों के गुणा और भाग के साथ, यह प्रभाव नहीं होता है। कुछ मामलों में, दशमलव अंकन भी इन कार्यों को जटिल बनाता है।

सबसे पहले, आइए एक नई परिभाषा पेश करें। हम उससे बहुत बार मिलेंगे, और न केवल इस पाठ में।

किसी संख्या का महत्वपूर्ण हिस्सा ट्रेलरों सहित पहले और अंतिम गैर-शून्य अंकों के बीच सब कुछ है। हम केवल संख्याओं के बारे में बात कर रहे हैं, दशमलव बिंदु को ध्यान में नहीं रखा जाता है।

किसी संख्या के सार्थक भाग में सम्मिलित अंक सार्थक अंक कहलाते हैं। उन्हें दोहराया जा सकता है और शून्य के बराबर भी हो सकता है।

उदाहरण के लिए, कई दशमलव भिन्नों पर विचार करें और उनके संगत महत्वपूर्ण भागों को लिखें:

1. 91.25 → 9125 (महत्वपूर्ण आंकड़े: 9; 1; 2; 5);
2. 0.008241 → 8241 (महत्वपूर्ण आंकड़े: 8; 2; 4; 1);
3. 15.0075 → 150075 (महत्वपूर्ण आंकड़े: 1; 5; 0; 0; 7; 5);
4. 0.0304 → 304 (महत्वपूर्ण आंकड़े: 3; 0; 4);
5. 3000 → 3 (केवल एक महत्वपूर्ण आंकड़ा है: 3)।

कृपया ध्यान दें: संख्या के महत्वपूर्ण भाग के अंदर शून्य कहीं नहीं जाता है। हमने पहले ही कुछ इसी तरह का सामना किया है जब हमने सीखा कि दशमलव अंशों को साधारण अंशों में कैसे परिवर्तित किया जाए (पाठ "दशमलव भिन्न" देखें)।

यह बिंदु बहुत महत्वपूर्ण है, और यहां इतनी बार त्रुटियां की जाती हैं कि मैं निकट भविष्य में इस विषय पर एक परीक्षण प्रकाशित करूंगा। अभ्यास करना सुनिश्चित करें! और हम, एक महत्वपूर्ण भाग की अवधारणा से लैस होकर, वास्तव में, पाठ के विषय पर आगे बढ़ेंगे।

दशमलव गुणन

गुणन संक्रिया में लगातार तीन चरण होते हैं:

1. प्रत्येक भिन्न के लिए महत्वपूर्ण भाग लिखिए। आपको दो साधारण पूर्णांक मिलेंगे - बिना किसी हर और दशमलव अंक के;
2. इन नंबरों को किसी भी सुविधाजनक तरीके से गुणा करें। सीधे, यदि संख्याएँ छोटी हैं, या किसी स्तंभ में हैं। हमें वांछित अंश का महत्वपूर्ण भाग मिलता है;
3. पता लगाएं कि संबंधित महत्वपूर्ण भाग प्राप्त करने के लिए दशमलव बिंदु को मूल भिन्नों में कहां और कितने अंकों से स्थानांतरित किया गया है। पिछले चरण में प्राप्त महत्वपूर्ण भाग पर रिवर्स शिफ्ट करें।

मैं आपको एक बार फिर याद दिला दूं कि महत्वपूर्ण भाग के किनारों पर शून्य को कभी भी ध्यान में नहीं रखा जाता है। इस नियम की उपेक्षा करने से त्रुटियाँ होती हैं।

1. 0.28 12.5;
2. 6.3 1.08;
3. 132.5 0.0034;
4. 0.0108 1600.5;
5. 5.25 10,000।

हम पहली अभिव्यक्ति के साथ काम करते हैं: 0.28 12.5।

1. आइए इस व्यंजक से संख्याओं के महत्वपूर्ण भागों को लिखें: 28 और 125;
2. उनका उत्पाद: 28 125 = 3500;
3. पहले गुणक में, दशमलव बिंदु को 2 अंक दाईं ओर (0.28 → 28) स्थानांतरित किया जाता है, और दूसरे में - एक और 1 अंक। कुल मिलाकर, तीन अंकों के बाईं ओर एक बदलाव की आवश्यकता है: 3500 → 3.500 = 3.5।

अब आइए व्यंजक 6.3 1.08 से निपटें।

1. आइए महत्वपूर्ण भागों को लिखें: 63 और 108;
2. उनका उत्पाद: 63 108 = 6804;
3. फिर से, दो शिफ्ट दाईं ओर: क्रमशः 2 और 1 अंकों से। कुल मिलाकर - फिर से 3 अंक दाईं ओर, इसलिए रिवर्स शिफ्ट बाईं ओर 3 अंक होगी: 6804 → 6.804। इस बार अंत में कोई शून्य नहीं है।

हमें तीसरी अभिव्यक्ति मिली: 132.5 0.0034।

1. महत्वपूर्ण भाग: 1325 और 34;
2. उनका उत्पाद: 1325 34 = 45,050;
3. पहले अंश में, दशमलव बिंदु 1 अंक से दाईं ओर जाता है, और दूसरे में - 4 तक। कुल: 5 दाईं ओर। हम 5 से बाईं ओर शिफ्ट करते हैं: 45050 → .45050 = 0.4505। शून्य को अंत में हटा दिया गया था, और सामने जोड़ा गया ताकि "नंगे" दशमलव बिंदु न छोड़ें।

निम्नलिखित अभिव्यक्ति: 0.0108 1600.5।

1. हम महत्वपूर्ण भाग लिखते हैं: 108 और 16 005;
2. हम उन्हें गुणा करते हैं: 108 16 005 = 1 728 540;
3. हम दशमलव बिंदु के बाद संख्याएँ गिनते हैं: पहली संख्या में 4 हैं, दूसरे में - 1. कुल - फिर से 5. हमारे पास है: 1,728,540 → 17.28540 = 17.2854। अंत में, "अतिरिक्त" शून्य हटा दिया गया था।

अंत में, अंतिम अभिव्यक्ति: 5.25 10,000।

1. महत्वपूर्ण भाग: 525 और 1;
2. हम उन्हें गुणा करते हैं: 525 1 = 525;
3. पहली भिन्न को 2 अंकों को दाईं ओर स्थानांतरित किया जाता है, और दूसरे भिन्न को 4 अंकों को बाईं ओर स्थानांतरित किया जाता है (10,000 → 1.0000 = 1)। कुल 4 - 2 = 2 अंक बाईं ओर। हम 2 अंकों से दाईं ओर एक रिवर्स शिफ्ट करते हैं: 525, → 52 500 (हमें शून्य जोड़ना था)।

अंतिम उदाहरण पर ध्यान दें: चूंकि दशमलव बिंदु अलग-अलग दिशाओं में चलता है, कुल बदलाव अंतर के माध्यम से होता है। यह एक बहुत महत्वपूर्ण मुद्दा है! यहाँ एक और उदाहरण है:

1.5 और 12,500 की संख्या पर विचार करें। हमारे पास: 1.5 → 15 (1 से दाईं ओर शिफ्ट); 12 500 → 125 (2 को बाईं ओर शिफ्ट करें)। हम दाईं ओर 1 अंक और फिर बाईं ओर 2 अंक "कदम" करते हैं। परिणामस्वरूप, हमने बाईं ओर 2 - 1 = 1 अंक बढ़ा दिया।

दशमलव विभाजन

डिवीजन शायद सबसे कठिन ऑपरेशन है। बेशक, यहां आप गुणन के साथ सादृश्य द्वारा कार्य कर सकते हैं: महत्वपूर्ण भागों को विभाजित करें, और फिर दशमलव बिंदु को "स्थानांतरित करें"। लेकिन इस मामले में, कई सूक्ष्मताएं हैं जो संभावित बचत को नकारती हैं।

तो आइए एक सामान्य एल्गोरिथ्म को देखें जो थोड़ा लंबा है, लेकिन बहुत अधिक विश्वसनीय है:

1. सभी दशमलवों को उभयनिष्ठ भिन्नों में बदलें। थोड़े से अभ्यास के साथ, यह कदम आपको कुछ ही सेकंड में ले जाएगा;
2. परिणामी भिन्नों को शास्त्रीय तरीके से विभाजित करें। दूसरे शब्दों में, पहले अंश को "उल्टे" दूसरे से गुणा करें (पाठ "संख्यात्मक अंशों का गुणा और भाग" देखें);
3. यदि संभव हो, तो परिणाम को दशमलव के रूप में लौटाएं। यह कदम भी तेज है, क्योंकि अक्सर हर में पहले से ही दस की शक्ति होती है।

काम। व्यंजक का मान ज्ञात कीजिए:

1. 3,51: 3,9;
2. 1,47: 2,1;
3. 6,4: 25,6:
4. 0,0425: 2,5;
5. 0,25: 0,002.

हम पहली अभिव्यक्ति पर विचार करते हैं। सबसे पहले, आइए ओबी अंशों को दशमलव में बदलें:

हम दूसरी अभिव्यक्ति के साथ भी ऐसा ही करते हैं। पहले अंश का अंश फिर से कारकों में विघटित हो जाता है:

तीसरे और चौथे उदाहरण में एक महत्वपूर्ण बिंदु है: दशमलव अंकन से छुटकारा पाने के बाद, रद्द करने योग्य अंश दिखाई देते हैं। हालांकि, हम यह कटौती नहीं करेंगे।

अंतिम उदाहरण दिलचस्प है क्योंकि दूसरे अंश का अंश एक अभाज्य संख्या है। यहां कारक बनाने के लिए कुछ भी नहीं है, इसलिए हम इसे "रिक्त के माध्यम से" मानते हैं:

कभी-कभी विभाजन का परिणाम पूर्णांक में होता है (मैं अंतिम उदाहरण के बारे में बात कर रहा हूं)। इस मामले में, तीसरा चरण बिल्कुल नहीं किया जाता है।

इसके अलावा, विभाजित करते समय, "बदसूरत" अंश अक्सर दिखाई देते हैं जिन्हें दशमलव में परिवर्तित नहीं किया जा सकता है। यह वह जगह है जहां विभाजन गुणा से भिन्न होता है, जहां परिणाम हमेशा दशमलव रूप में व्यक्त किए जाते हैं। बेशक, इस मामले में, अंतिम चरण फिर से नहीं किया जाता है।

तीसरे और चौथे उदाहरण पर भी ध्यान दें। उनमें हम दशमलव से प्राप्त साधारण भिन्नों को जानबूझकर कम नहीं करते हैं। अन्यथा, यह व्युत्क्रम समस्या को जटिल बना देगा - अंतिम उत्तर को फिर से दशमलव रूप में प्रदर्शित करना।

याद रखें: एक भिन्न की मूल संपत्ति (गणित में किसी भी अन्य नियम की तरह) का अर्थ यह नहीं है कि इसे हर जगह और हमेशा, हर अवसर पर लागू किया जाना चाहिए।

इस ट्यूटोरियल में, हम इनमें से प्रत्येक ऑपरेशन को एक-एक करके देखेंगे।

पाठ सामग्री

दशमलव जोड़ना

जैसा कि हम जानते हैं, दशमलव में एक पूर्णांक भाग और एक भिन्नात्मक भाग होता है। दशमलव जोड़ते समय, पूर्णांक और भिन्नात्मक भागों को अलग-अलग जोड़ा जाता है।

उदाहरण के लिए, आइए दशमलव 3.2 और 5.3 जोड़ें। किसी कॉलम में दशमलव भिन्नों को जोड़ना अधिक सुविधाजनक होता है।

सबसे पहले, हम इन दो अंशों को एक कॉलम में लिखते हैं, जबकि पूर्णांक भागों को पूर्णांक भागों के नीचे होना चाहिए, और भिन्नात्मक अंशों के नीचे होना चाहिए। स्कूल में, इस आवश्यकता को कहा जाता है "अल्पविराम के तहत अल्पविराम".

आइए भिन्नों को एक कॉलम में लिखें ताकि अल्पविराम अल्पविराम के नीचे हो:

हम भिन्नात्मक भागों को जोड़ना शुरू करते हैं: 2 + 3 \u003d 5. हम अपने उत्तर के भिन्नात्मक भाग में पाँच लिखते हैं:

अब हम पूर्णांक भागों को जोड़ते हैं: 3 + 5 = 8. हम अपने उत्तर के पूर्णांक भाग में आठ लिखते हैं:

अब हम पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करते हैं। ऐसा करने के लिए, हम फिर से नियम का पालन करते हैं "अल्पविराम के तहत अल्पविराम":

उत्तर मिला 8.5. तो व्यंजक 3.2 + 5.3 8.5 . के बराबर है

वास्तव में, सब कुछ उतना सरल नहीं है जितना पहली नज़र में लगता है। यहां भी, नुकसान हैं, जिनके बारे में हम अब बात करेंगे।

दशमलव में स्थान

सामान्य संख्याओं की तरह दशमलव के भी अपने अंक होते हैं। ये दसवें स्थान, सौवें स्थान, हजारवें स्थान हैं। इस मामले में, अंक दशमलव बिंदु के बाद शुरू होते हैं।

दशमलव बिंदु के बाद पहला अंक दसवें स्थान के लिए जिम्मेदार है, दूसरा अंक दशमलव बिंदु के बाद सौवें स्थान के लिए, तीसरा अंक दशमलव बिंदु के बाद हजारवें स्थान के लिए है।

दशमलव अंक कुछ उपयोगी जानकारी संग्रहीत करते हैं। विशेष रूप से, वे रिपोर्ट करते हैं कि दशमलव में कितने दसवें, सौवें और हज़ारवें हिस्से हैं।

उदाहरण के लिए, दशमलव 0.345 . पर विचार करें

वह स्थान जहाँ त्रिगुण स्थित होता है, कहलाता है दसवां स्थान

वह स्थान जहाँ चार स्थित होते हैं, कहलाते हैं सौवां स्थान

वह स्थान जहाँ पाँच स्थित होते हैं, कहलाते हैं हजारवें

आइए इस आंकड़े को देखें। हम देखते हैं कि दसवीं की श्रेणी में एक तीन है। इससे पता चलता है कि दशमलव भिन्न 0.345 में तीन दहाई होते हैं।

यदि हम भिन्नों को जोड़ते हैं, और फिर हमें मूल दशमलव भिन्न 0.345 . प्राप्त होता है

यह देखा जा सकता है कि पहले तो हमें इसका उत्तर मिला, लेकिन इसे दशमलव भिन्न में बदलकर 0.345 प्राप्त किया।

दशमलव भिन्नों को जोड़ते समय सामान्य संख्याओं को जोड़ने के समान सिद्धांतों और नियमों का पालन किया जाता है। दशमलव अंशों का जोड़ अंकों से होता है: दसवें को दसवें, सौवें से सौवें, हज़ारवें से हज़ारवें भाग में जोड़ा जाता है।

अतः दशमलव भिन्नों को जोड़ते समय नियम का पालन करना आवश्यक है "अल्पविराम के तहत अल्पविराम". अल्पविराम के तहत अल्पविराम वही क्रम प्रदान करता है जिसमें दसवें को दसवें, सौवें से सौवें, हज़ारवें से हज़ारवें भाग में जोड़ा जाता है।

उदाहरण 1व्यंजक 1.5 + 3.4 . का मान ज्ञात कीजिए

सबसे पहले, हम भिन्नात्मक भाग 5 + 4 = 9 जोड़ते हैं। हम अपने उत्तर के भिन्नात्मक भाग में नौ लिखते हैं:

अब हम पूर्णांक भागों 1 + 3 = 4 को जोड़ते हैं। हम अपने उत्तर के पूर्णांक भाग में चारों को लिखते हैं:

अब हम पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करते हैं। ऐसा करने के लिए, हम फिर से "अल्पविराम के तहत अल्पविराम" नियम का पालन करते हैं:

उत्तर मिला 4.9. अतः व्यंजक 1.5 + 3.4 का मान 4.9 . है

उदाहरण 2व्यंजक का मान ज्ञात कीजिए: 3.51 + 1.22

हम इस अभिव्यक्ति को "अल्पविराम के तहत अल्पविराम" नियम का पालन करते हुए एक कॉलम में लिखते हैं।

सबसे पहले, भिन्नात्मक भाग, अर्थात् सौवां 1+2=3 जोड़ें। हम अपने उत्तर के सौवें भाग में त्रिक लिखते हैं:

अब 5+2=7 का दसवां हिस्सा जोड़ें। हम अपने उत्तर के दसवें भाग में सात लिखते हैं:

अब सारे भाग 3+1=4 जोड़ें। हम अपने उत्तर के पूरे भाग में चार लिखते हैं:

हम "अल्पविराम के तहत अल्पविराम" नियम का पालन करते हुए पूर्णांक भाग को अल्पविराम से अलग करते हैं:

उत्तर मिला 4.73। अतः व्यंजक 3.51 + 1.22 का मान 4.73 . है

3,51 + 1,22 = 4,73

सामान्य संख्याओं की तरह, दशमलव भिन्नों को जोड़ते समय, . इस मामले में, एक अंक उत्तर में लिखा जाता है, और बाकी को अगले अंक में स्थानांतरित कर दिया जाता है।

उदाहरण 3व्यंजक का मान ज्ञात कीजिए 2.65 + 3.27

हम इस अभिव्यक्ति को एक कॉलम में लिखते हैं:

5+7=12 का सौवां भाग जोड़ें। हमारे उत्तर के सौवें भाग में संख्या 12 फिट नहीं होगी। इसलिए, सौवें भाग में, हम संख्या 2 लिखते हैं, और इकाई को अगले बिट में स्थानांतरित करते हैं:

अब हम 6+2=8 के दहाई को जोड़ते हैं और पिछले ऑपरेशन से हमें जो इकाई मिली है, हमें 9 मिलता है। हम अपने उत्तर के दसवें हिस्से में संख्या 9 लिखते हैं:

अब सारे भाग 2+3=5 डाल दें। हम अपने उत्तर के पूर्णांक भाग में संख्या 5 लिखते हैं:

उत्तर मिला 5.92। अतः व्यंजक 2.65 + 3.27 का मान 5.92 . है

2,65 + 3,27 = 5,92

उदाहरण 4व्यंजक 9.5 + 2.8 . का मान ज्ञात कीजिए

इस व्यंजक को एक कॉलम में लिखें

हम भिन्नात्मक भाग 5 + 8 = 13 जोड़ते हैं। संख्या 13 हमारे उत्तर के भिन्नात्मक भाग में फिट नहीं होगी, इसलिए हम पहले संख्या 3 लिखते हैं, और इकाई को अगले अंक में स्थानांतरित करते हैं, या इसे पूर्णांक में स्थानांतरित करते हैं। अंश:

अब हम पूर्णांक भागों को जोड़ते हैं 9+2=11 प्लस इकाई जो हमें पिछले ऑपरेशन से मिली थी, हमें 12 मिलता है। हम अपने उत्तर के पूर्णांक भाग में संख्या 12 लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

उत्तर मिला 12.3. अतः व्यंजक 9.5 + 2.8 का मान 12.3 . है

9,5 + 2,8 = 12,3

दशमलव भिन्नों को जोड़ते समय, दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या समान होनी चाहिए। यदि पर्याप्त अंक नहीं हैं, तो भिन्नात्मक भाग में ये स्थान शून्य से भरे हुए हैं।

उदाहरण 5. व्यंजक का मान ज्ञात कीजिए: 12.725 + 1.7

इस व्यंजक को एक कॉलम में लिखने से पहले, आइए दोनों भिन्नों में दशमलव बिंदु के बाद अंकों की संख्या समान करें। दशमलव भिन्न 12.725 में दशमलव बिंदु के बाद तीन अंक होते हैं, जबकि भिन्न 1.7 में केवल एक होता है। तो 1.7 के अंत में आपको दो शून्य जोड़ने होंगे। तब हमें भिन्न 1,700 प्राप्त होता है। अब आप इस व्यंजक को एक कॉलम में लिख सकते हैं और गणना करना शुरू कर सकते हैं:

5+0=5 का हज़ारवाँ भाग जोड़ें। हम अपने उत्तर के हजारवें भाग में 5 अंक लिखते हैं:

2+0=2 का सौवां भाग जोड़ें। हम अपने उत्तर के सौवें भाग में संख्या 2 लिखते हैं:

7+7=14 का दसवां हिस्सा जोड़ें। संख्या 14 हमारे उत्तर के दसवें हिस्से में फिट नहीं होगी। इसलिए, हम पहले संख्या 4 लिखते हैं, और इकाई को अगले बिट में स्थानांतरित करते हैं:

अब हम पूर्णांक भागों को जोड़ते हैं 12+1=13 प्लस इकाई जो हमें पिछले ऑपरेशन से मिली थी, हमें 14 मिलता है। हम अपने उत्तर के पूर्णांक भाग में संख्या 14 लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

उत्तर मिला 14,425। अतः व्यंजक का मान 12.725+1.700 है 14.425

12,725+ 1,700 = 14,425

दशमलव का घटाव

दशमलव अंशों को घटाते समय, आपको उन्हीं नियमों का पालन करना चाहिए जो जोड़ते समय: "अल्पविराम के तहत अल्पविराम" और "दशमलव बिंदु के बाद अंकों की समान संख्या"।

उदाहरण 1व्यंजक का मान ज्ञात कीजिए 2.5 - 2.2

हम इस अभिव्यक्ति को "अल्पविराम के तहत अल्पविराम" नियम का पालन करते हुए एक कॉलम में लिखते हैं:

हम भिन्नात्मक भाग 5−2=3 की गणना करते हैं। हम अपने उत्तर के दसवें भाग में संख्या 3 लिखते हैं:

पूर्णांक भाग 2−2=0 की गणना करें। हम अपने उत्तर के पूर्णांक भाग में शून्य लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

हमें उत्तर 0.3 मिला। तो व्यंजक 2.5 - 2.2 का मान 0.3 . के बराबर है

2,5 − 2,2 = 0,3

उदाहरण 2व्यंजक 7.353 - 3.1 . का मान ज्ञात कीजिए

इस व्यंजक में दशमलव बिंदु के बाद अंकों की एक भिन्न संख्या होती है। भिन्न 7.353 में दशमलव बिंदु के बाद तीन अंक होते हैं, और भिन्न 3.1 में केवल एक होता है। इसका अर्थ है कि भिन्न 3.1 में, दोनों भिन्नों में अंकों की संख्या समान बनाने के लिए अंत में दो शून्य जोड़े जाने चाहिए। तब हमें 3,100 मिलते हैं।

अब आप इस व्यंजक को एक कॉलम में लिख सकते हैं और इसकी गणना कर सकते हैं:

उत्तर मिला 4,253। अतः व्यंजक 7.353 - 3.1 का मान 4.253 . है

7,353 — 3,1 = 4,253

सामान्य संख्याओं की तरह, यदि घटाना असंभव हो जाता है, तो कभी-कभी आपको आसन्न बिट से एक उधार लेना होगा।

उदाहरण 3व्यंजक 3.46 - 2.39 . का मान ज्ञात कीजिए

6−9 का सौवां भाग घटाएं। संख्या 6 से संख्या 9 घटाएं नहीं। इसलिए, आपको आसन्न अंक से एक इकाई लेने की आवश्यकता है। पड़ोसी अंक से एक को उधार लेने के बाद, संख्या 6 संख्या 16 में बदल जाती है। अब हम 16−9=7 के सौवें हिस्से की गणना कर सकते हैं। हम अपने उत्तर के सौवें भाग में सात को लिखते हैं:

अब दसवां घटाएं। चूँकि हमने दहाई की श्रेणी में एक इकाई ली थी, वहाँ जो आंकड़ा था वह एक इकाई कम हो गया। दूसरे शब्दों में, दसवां स्थान अब संख्या 4 नहीं है, बल्कि संख्या 3 है। आइए 3−3=0 के दसवें हिस्से की गणना करें। हम अपने उत्तर के दसवें भाग में शून्य लिखते हैं:

अब पूर्णांक भागों 3−2=1 को घटाएं। हम इकाई को अपने उत्तर के पूर्णांक भाग में लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

उत्तर मिला 1.07. तो व्यंजक का मान 3.46−2.39 1.07 . के बराबर है

3,46−2,39=1,07

उदाहरण 4. व्यंजक का मान ज्ञात कीजिए 3−1.2

यह उदाहरण एक पूर्णांक से दशमलव घटाता है। आइए इस व्यंजक को एक कॉलम में लिखें ताकि दशमलव भिन्न 1.23 का पूर्णांक भाग संख्या 3 . के अंतर्गत हो

अब दशमलव बिंदु के बाद अंकों की संख्या को समान बनाते हैं। ऐसा करने के लिए, संख्या 3 के बाद, अल्पविराम लगाएं और एक शून्य जोड़ें:

अब दहाई घटाएँ: 0−2। संख्या 2 को शून्य से न घटाएं। इसलिए, आपको आसन्न अंक से एक इकाई लेने की आवश्यकता है। आसन्न अंक से एक को उधार लेकर, 0 संख्या 10 में बदल जाता है। अब आप 10−2=8 के दसवें हिस्से की गणना कर सकते हैं। हम अपने उत्तर के दसवें भाग में आठ लिखते हैं:

अब पूरे भागों को घटा दें। पहले, संख्या 3 पूर्णांक में स्थित थी, लेकिन हमने इससे एक इकाई उधार ली थी। नतीजतन, यह संख्या 2 में बदल गया। इसलिए, हम 2 से 1 घटाते हैं। 2−1=1. हम इकाई को अपने उत्तर के पूर्णांक भाग में लिखते हैं:

पूर्णांक भाग को अल्पविराम से भिन्नात्मक भाग से अलग करें:

उत्तर 1.8 मिला। तो व्यंजक 3−1.2 का मान 1.8 . है

दशमलव गुणन

दशमलव को गुणा करना आसान और मजेदार भी है। दशमलवों को गुणा करने के लिए, आपको अल्पविरामों को अनदेखा करते हुए उन्हें नियमित संख्याओं की तरह गुणा करना होगा।

उत्तर प्राप्त करने के बाद, पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना आवश्यक है। ऐसा करने के लिए, आपको दोनों अंशों में दशमलव बिंदु के बाद अंकों की संख्या गिनने की जरूरत है, फिर उत्तर में दाईं ओर समान अंकों की संख्या गिनें और अल्पविराम लगाएं।

उदाहरण 1व्यंजक का मान ज्ञात कीजिए 2.5 × 1.5

हम इन दशमलव अंशों को अल्पविरामों को अनदेखा करते हुए साधारण संख्याओं के रूप में गुणा करते हैं। अल्पविराम को अनदेखा करने के लिए, आप अस्थायी रूप से कल्पना कर सकते हैं कि वे पूरी तरह से अनुपस्थित हैं:

हमें 375 मिले। इस संख्या में, पूरे भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना आवश्यक है। ऐसा करने के लिए, आपको दशमलव बिंदु के बाद 2.5 और 1.5 के अंशों में अंकों की संख्या गिनने की आवश्यकता है। पहले भिन्न में दशमलव बिंदु के बाद एक अंक होता है, दूसरे भिन्न में भी एक होता है। कुल दो अंक।

हम 375 नंबर पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर से दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

उत्तर मिला 3.75। अतः व्यंजक 2.5 × 1.5 का मान 3.75 . है

2.5 x 1.5 = 3.75

उदाहरण 2व्यंजक का मान ज्ञात कीजिए 12.85 × 2.7

आइए अल्पविरामों को अनदेखा करते हुए इन दशमलवों को गुणा करें:

हमें 34695 मिले। इस संख्या में, आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको 12.85 और 2.7 के अंशों में दशमलव बिंदु के बाद अंकों की संख्या की गणना करने की आवश्यकता है। अंश 12.85 में दशमलव बिंदु के बाद दो अंक होते हैं, अंश 2.7 में एक अंक होता है - कुल तीन अंक।

हम 34695 नंबर पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर से तीन अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

उत्तर मिला 34,695। अतः व्यंजक 12.85 × 2.7 का मान 34.695 . है

12.85 × 2.7 = 34.695

एक दशमलव को एक नियमित संख्या से गुणा करना

कभी-कभी ऐसी स्थितियां होती हैं जब आपको एक दशमलव अंश को एक नियमित संख्या से गुणा करने की आवश्यकता होती है।

एक दशमलव और एक साधारण संख्या को गुणा करने के लिए, आपको दशमलव में अल्पविराम की परवाह किए बिना उन्हें गुणा करना होगा। उत्तर प्राप्त करने के बाद, पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना आवश्यक है। ऐसा करने के लिए, आपको दशमलव अंश में दशमलव बिंदु के बाद अंकों की संख्या गिनने की आवश्यकता है, फिर उत्तर में, अंकों की समान संख्या को दाईं ओर गिनें और अल्पविराम लगाएं।

उदाहरण के लिए, 2.54 को 2 . से गुणा करें

हम अल्पविराम को अनदेखा करते हुए दशमलव अंश 2.54 को सामान्य संख्या 2 से गुणा करते हैं:

हमें संख्या 508 मिली है। इस संख्या में, आपको पूर्णांक भाग को भिन्नात्मक भाग से अल्पविराम से अलग करना होगा। ऐसा करने के लिए, आपको दशमलव बिंदु के बाद अंश 2.54 में अंकों की संख्या गिनने की आवश्यकता है। भिन्न 2.54 में दशमलव बिंदु के बाद दो अंक होते हैं।

हम 508 नंबर पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर से दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

उत्तर मिला 5.08. अतः व्यंजक 2.54 × 2 का मान 5.08 . है

2.54 x 2 = 5.08

दशमलव को 10, 100, 1000 . से गुणा करना

दशमलव को 10, 100, या 1000 से गुणा करना उसी तरह किया जाता है जैसे दशमलव को नियमित संख्याओं से गुणा करना। दशमलव अंश में अल्पविराम को अनदेखा करते हुए गुणा करना आवश्यक है, फिर उत्तर में, पूर्णांक भाग को भिन्नात्मक भाग से अलग करें, दाईं ओर अंकों की समान संख्या गिनें क्योंकि दशमलव में दशमलव बिंदु के बाद अंक थे अंश।

उदाहरण के लिए, 2.88 को 10 . से गुणा करें

आइए दशमलव भिन्न में अल्पविराम को अनदेखा करते हुए दशमलव भिन्न 2.88 को 10 से गुणा करें:

हमें 2880 मिले। इस संख्या में, आपको अल्पविराम से पूरे भाग को भिन्नात्मक भाग से अलग करना होगा। ऐसा करने के लिए, आपको दशमलव बिंदु के बाद अंश 2.88 में अंकों की संख्या गिनने की आवश्यकता है। हम देखते हैं कि भिन्न 2.88 में दशमलव बिंदु के बाद दो अंक होते हैं।

हम संख्या 2880 पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर से दो अंक गिनने और अल्पविराम लगाने की आवश्यकता है:

उत्तर मिला 28.80। हम अंतिम शून्य को छोड़ देते हैं - हमें 28.8.8.8 मिलता है। अतः व्यंजक 2.88 × 10 का मान 28.8 . है

2.88 x 10 = 28.8

दशमलव भिन्नों को 10, 100, 1000 से गुणा करने का दूसरा तरीका है। यह विधि बहुत सरल और अधिक सुविधाजनक है। यह इस तथ्य में समाहित है कि दशमलव अंश में अल्पविराम दाईं ओर उतने ही अंकों से आगे बढ़ता है जितने गुणक में शून्य होते हैं।

उदाहरण के लिए, पिछले उदाहरण 2.88×10 को इस प्रकार हल करते हैं। कोई गणना दिए बिना, हम तुरंत कारक 10 को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसका एक शून्य है। अब भिन्न 2.88 में हम दशमलव बिंदु को एक अंक से दाईं ओर ले जाते हैं, हमें 28.8 मिलता है।

2.88 x 10 = 28.8

आइए 2.88 को 100 से गुणा करने का प्रयास करें। हम तुरंत कारक 100 को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसके दो शून्य हैं। अब भिन्न 2.88 में हम दशमलव बिंदु को दो अंकों से दाहिनी ओर ले जाते हैं, हमें 288 . प्राप्त होता है

2.88 x 100 = 288

आइए 2.88 को 1000 से गुणा करने का प्रयास करें। हम तुरंत कारक 1000 को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें तीन शून्य हैं। अब भिन्न 2.88 में हम दशमलव बिंदु को तीन अंकों से दाईं ओर ले जाते हैं। तीसरा अंक नहीं है, इसलिए हम एक और शून्य जोड़ते हैं। नतीजतन, हमें 2880 मिलते हैं।

2.88 x 1000 = 2880

दशमलव को 0.1 0.01 और 0.001 से गुणा करना

दशमलव को 0.1, 0.01 और 0.001 से गुणा करना उसी तरह काम करता है जैसे दशमलव को दशमलव से गुणा करना। सामान्य संख्याओं की तरह भिन्नों को गुणा करना और उत्तर में अल्पविराम लगाना आवश्यक है, दाईं ओर जितने अंक हैं, उतने ही अंकों की गणना दशमलव बिंदु के बाद दोनों भिन्नों में होती है।

उदाहरण के लिए, 3.25 को 0.1 . से गुणा करें

हम इन भिन्नों को सामान्य संख्याओं की तरह गुणा करते हैं, अल्पविरामों को अनदेखा करते हुए:

हमें 325 मिले। इस संख्या में, आपको अल्पविराम से पूरे भाग को भिन्नात्मक भाग से अलग करना होगा। ऐसा करने के लिए, आपको दशमलव बिंदु के बाद 3.25 और 0.1 के अंशों में अंकों की संख्या की गणना करने की आवश्यकता है। भिन्न 3.25 में दशमलव बिंदु के बाद दो अंक होते हैं, भिन्न 0.1 में एक अंक होता है। कुल तीन अंक।

हम 325 नंबर पर लौटते हैं और दाएं से बाएं जाना शुरू करते हैं। हमें दाईं ओर तीन अंक गिनने और अल्पविराम लगाने की आवश्यकता है। तीन अंक गिनने के बाद, हम पाते हैं कि संख्याएँ समाप्त हो गई हैं। इस मामले में, आपको एक शून्य जोड़ने और अल्पविराम लगाने की आवश्यकता है:

हमें उत्तर 0.325 मिला। अतः व्यंजक 3.25 × 0.1 का मान 0.325 . है

3.25 x 0.1 = 0.325

दशमलव को 0.1, 0.01 और 0.001 से गुणा करने का दूसरा तरीका है। यह विधि बहुत आसान और अधिक सुविधाजनक है। यह इस तथ्य में समाहित है कि दशमलव अंश में अल्पविराम बाईं ओर उतने ही अंकों से आगे बढ़ता है जितने गुणक में शून्य होते हैं।

उदाहरण के लिए, पिछले उदाहरण 3.25 × 0.1 को इस प्रकार हल करते हैं। कोई गणना दिए बिना, हम तुरंत कारक 0.1 को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसका एक शून्य है। अब भिन्न 3.25 में हम दशमलव बिंदु को एक अंक से बाईं ओर ले जाते हैं। अल्पविराम को एक अंक बाईं ओर ले जाने पर, हम देखते हैं कि तीनों से पहले कोई और अंक नहीं हैं। इस मामले में, एक शून्य जोड़ें और अल्पविराम लगाएं। नतीजतन, हमें 0.325 . मिलता है

3.25 x 0.1 = 0.325

आइए 3.25 को 0.01 से गुणा करने का प्रयास करें। 0.01 के गुणक को तुरंत देखें। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसके दो शून्य हैं। अब भिन्न 3.25 में हम अल्पविराम को बाईं ओर दो अंकों से घुमाते हैं, हमें 0.0325 . मिलता है

3.25 x 0.01 = 0.0325

आइए 3.25 को 0.001 से गुणा करने का प्रयास करें। 0.001 के गुणक को तुरंत देखें। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि इसमें तीन शून्य हैं। अब भिन्न 3.25 में हम दशमलव बिंदु को तीन अंकों से बाईं ओर ले जाते हैं, हमें 0.00325 . मिलता है

3.25 × 0.001 = 0.00325

दशमलव को 0.1, 0.001 और 0.001 से गुणा करके 10, 100, 1000 से गुणा करने में भ्रमित न हों। अधिकांश लोग एक सामान्य गलती करते हैं।

जब 10, 100, 1000 से गुणा किया जाता है, तो अल्पविराम को उतने अंकों से दाईं ओर ले जाया जाता है, जितने गुणक में शून्य होते हैं।

और जब 0.1, 0.01 और 0.001 से गुणा किया जाता है, तो अल्पविराम बाईं ओर उतने अंकों से चला जाता है जितने गुणक में शून्य होते हैं।

यदि पहली बार में याद रखना मुश्किल है, तो आप पहली विधि का उपयोग कर सकते हैं, जिसमें सामान्य संख्याओं के साथ गुणा किया जाता है। उत्तर में, आपको दाहिनी ओर जितने अंक हैं उतने अंकों की गणना करके पूर्णांक भाग को भिन्नात्मक भाग से अलग करना होगा क्योंकि दोनों अंशों में दशमलव बिंदु के बाद अंक होते हैं।

छोटी संख्या को बड़ी संख्या से विभाजित करना। उन्नत स्तर, उच्च स्तर।

पिछले पाठों में से एक में, हमने कहा था कि छोटी संख्या को बड़ी संख्या से विभाजित करने पर एक भिन्न प्राप्त होता है, जिसके अंश में भाज्य होता है और हर में भाजक होता है।

उदाहरण के लिए, एक सेब को दो में विभाजित करने के लिए, आपको अंश में 1 (एक सेब) लिखना होगा, और हर में 2 (दो मित्र) लिखना होगा। परिणाम एक अंश है। तो प्रत्येक मित्र को एक सेब मिलेगा। दूसरे शब्दों में, आधा सेब। एक अंश एक समस्या का उत्तर है एक सेब को दो के बीच कैसे विभाजित करें

यह पता चला है कि यदि आप 1 को 2 से विभाजित करते हैं तो आप इस समस्या को और हल कर सकते हैं। आखिरकार, किसी भी भिन्न में एक भिन्नात्मक बार का अर्थ है विभाजन, जिसका अर्थ है कि इस विभाजन को एक अंश में भी अनुमति है। पर कैसे? हम इस तथ्य के अभ्यस्त हैं कि लाभांश हमेशा भाजक से अधिक होता है। और यहाँ, इसके विपरीत, लाभांश भाजक से कम है।

सब कुछ स्पष्ट हो जाएगा यदि हम याद रखें कि अंश का अर्थ है कुचलना, विभाजित करना, विभाजित करना। इसका अर्थ है कि इकाई को आप जितने चाहें उतने भागों में विभाजित किया जा सकता है, न कि केवल दो भागों में।

छोटी संख्या को बड़ी संख्या से भाग देने पर एक दशमलव भिन्न प्राप्त होता है, जिसमें पूर्णांक भाग 0 (शून्य) होगा। भिन्नात्मक भाग कुछ भी हो सकता है।

तो, आइए 1 को 2 से भाग दें। आइए इस उदाहरण को एक कोने से हल करते हैं:

एक को ऐसे ही दो भागों में विभाजित नहीं किया जा सकता है। यदि आप एक प्रश्न पूछते हैं "एक में कितने दो होते हैं" , तो उत्तर 0 होगा। इसलिए, निजी तौर पर हम 0 लिखते हैं और अल्पविराम लगाते हैं:

अब, हमेशा की तरह, हम भागफल को भाजक से गुणा करके शेषफल निकालते हैं:

वह क्षण आ गया है जब इकाई को दो भागों में विभाजित किया जा सकता है। ऐसा करने के लिए, प्राप्त एक के दाईं ओर एक और शून्य जोड़ें:

हमें 10 मिला। हम 10 को 2 से भाग देते हैं, हमें 5 मिलता है। हम अपने उत्तर के भिन्नात्मक भाग में पाँच लिखते हैं:

अब हम गणना को पूरा करने के लिए अंतिम शेषफल निकालते हैं। 5 को 2 से गुणा करने पर हमें 10 . प्राप्त होता है

हमें उत्तर 0.5 मिला। तो भिन्न 0.5 . है

दशमलव भिन्न 0.5 का उपयोग करके आधा सेब भी लिखा जा सकता है। यदि हम इन दो हिस्सों (0.5 और 0.5) को जोड़ते हैं, तो हमें फिर से मूल एक पूरा सेब मिलता है:

इस बिंदु को भी समझा जा सकता है यदि हम कल्पना करें कि 1 सेमी को दो भागों में कैसे विभाजित किया जाता है। यदि आप 1 सेंटीमीटर को 2 भागों में विभाजित करते हैं, तो आपको 0.5 सेमी . मिलता है

उदाहरण 2व्यंजक 4:5 . का मान ज्ञात कीजिए

चार में कितने फाइव होते हैं? बिल्कुल भी नहीं। हम निजी 0 में लिखते हैं और अल्पविराम लगाते हैं:

हम 0 को 5 से गुणा करते हैं, हमें 0 मिलता है। हम चार के नीचे शून्य लिखते हैं। इस शून्य को लाभांश से तुरंत घटाएं:

आइए अब चारों को 5 भागों में विभाजित (विभाजित) करना शुरू करते हैं। ऐसा करने के लिए, 4 के दाईं ओर, हम शून्य जोड़ते हैं और 40 को 5 से विभाजित करते हैं, हमें 8 मिलता है। हम आठ को निजी में लिखते हैं।

हम 8 को 5 से गुणा करके उदाहरण को पूरा करते हैं, और 40 प्राप्त करते हैं:

हमें उत्तर 0.8 मिला। अतः व्यंजक 4:5 का मान 0.8 . है

उदाहरण 3व्यंजक 5: 125 . का मान ज्ञात कीजिए

पांच में 125 कितनी संख्याएं हैं? बिल्कुल भी नहीं। हम निजी में 0 लिखते हैं और अल्पविराम लगाते हैं:

हम 0 को 5 से गुणा करते हैं, हमें 0 मिलता है। हम पांच के नीचे 0 लिखते हैं। पांच 0 . में से तुरंत घटाएं

अब पांचों को 125 भागों में विभाजित (विभाजित) करते हैं। ऐसा करने के लिए, इस पाँच के दाईं ओर, हम शून्य लिखते हैं:

50 को 125 से विभाजित करें। 50 में 125 कितनी संख्याएँ हैं? बिल्कुल भी नहीं। अतः भागफल में हम पुनः 0 . लिखते हैं

हम 0 को 125 से गुणा करते हैं, हमें 0 मिलता है। हम इस शून्य को 50 के नीचे लिखते हैं। 50 . में से तुरंत 0 घटाएं

अब हम संख्या 50 को 125 भागों में विभाजित करते हैं। ऐसा करने के लिए, 50 के दाईं ओर, हम एक और शून्य लिखते हैं:

500 को 125 से विभाजित करें। 500 की संख्या में 125 कितनी संख्याएँ हैं। 500 की संख्या में चार संख्याएँ 125 हैं। हम चार को निजी में लिखते हैं:

हम 4 को 125 से गुणा करके उदाहरण को पूरा करते हैं, और 500 . प्राप्त करते हैं

हमें उत्तर 0.04 मिला। अतः व्यंजक 5: 125 का मान 0.04 . है

शेषफल के बिना संख्याओं का विभाजन

तो, आइए इकाई के बाद भागफल में अल्पविराम लगाते हैं, जिससे यह संकेत मिलता है कि पूर्णांक भागों का विभाजन समाप्त हो गया है और हम भिन्नात्मक भाग पर आगे बढ़ते हैं:

शेष 4 . में शून्य जोड़ें

अब हम 40 को 5 से भाग देते हैं, हमें 8 मिलता है। हम आठ को अकेले में लिखते हैं:

40−40=0. शेष में 0 प्राप्त किया। तो विभाजन पूरी तरह से पूरा हो गया है। 9 को 5 से भाग देने पर 1.8 का दशमलव प्राप्त होता है:

9: 5 = 1,8

उदाहरण 2. शेषफल के बिना 84 को 5 से भाग दें

पहले हम शेषफल के साथ हमेशा की तरह 84 को 5 से विभाजित करते हैं:

शेष में निजी 16 और 4 और प्राप्त हुए। अब हम इस शेषफल को 5 से विभाजित करते हैं। हम निजी क्षेत्र में अल्पविराम लगाते हैं, और शेष 4 . में 0 जोड़ते हैं

अब हम 40 को 5 से विभाजित करते हैं, हमें 8 मिलता है। हम दशमलव बिंदु के बाद भागफल में आठ लिखते हैं:

और यह जाँच कर उदाहरण पूरा करें कि क्या अभी भी शेष है:

एक दशमलव को एक नियमित संख्या से विभाजित करना

एक दशमलव भिन्न, जैसा कि हम जानते हैं, एक पूर्णांक और एक भिन्नात्मक भाग होता है। दशमलव अंश को एक नियमित संख्या से विभाजित करते समय, सबसे पहले आपको चाहिए:

• दशमलव अंश के पूर्णांक भाग को इस संख्या से विभाजित करें;
• पूर्णांक भाग विभाजित होने के बाद, आपको तुरंत निजी भाग में अल्पविराम लगाने और सामान्य विभाजन की तरह गणना जारी रखने की आवश्यकता है।

उदाहरण के लिए, आइए 4.8 को 2 . से भाग दें

आइए इस उदाहरण को एक कोने के रूप में लिखें:

अब हम पूरे भाग को 2 से भाग करते हैं। चार को दो से विभाजित करते हैं। हम ड्यूस को निजी तौर पर लिखते हैं और तुरंत अल्पविराम लगाते हैं:

अब हम भागफल को भाजक से गुणा करते हैं और देखते हैं कि क्या भाग से कोई शेष बचता है:

4−4=0. शेष शून्य है। हम अभी तक शून्य नहीं लिखते हैं, क्योंकि हल पूरा नहीं हुआ है। फिर हम गणना करना जारी रखते हैं, जैसा कि साधारण विभाजन में होता है। 8 नीचे लें और इसे 2 . से विभाजित करें

8: 2 = 4. हम चार को भागफल में लिखते हैं और भाजक से तुरंत गुणा करते हैं:

उत्तर 2.4 मिला। व्यंजक मान 4.8: 2 बराबर 2.4

उदाहरण 2व्यंजक का मान ज्ञात कीजिए 8.43:3

हम 8 को 3 से विभाजित करते हैं, हमें 2 मिलता है। दोनों के तुरंत बाद अल्पविराम लगाएं:

अब हम भागफल को भाजक 2 × 3 = 6 से गुणा करते हैं। हम छह को आठ के नीचे लिखते हैं और शेषफल पाते हैं:

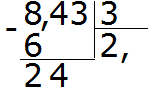
हम 24 को 3 से भाग देते हैं, हमें 8 मिलता है। हम आठ को अकेले में लिखते हैं। हम भाग के शेष को खोजने के लिए इसे तुरंत भाजक से गुणा करते हैं:

24−24=0. शेष शून्य है। शून्य अभी तक दर्ज नहीं किया गया है। लाभांश के अंतिम तीन लें और 3 से विभाजित करें, हमें 1 मिलता है। इस उदाहरण को पूरा करने के लिए तुरंत 1 को 3 से गुणा करें:

उत्तर 2.81 मिला। अतः व्यंजक 8.43: 3 का मान 2.81 . के बराबर है

दशमलव को दशमलव से विभाजित करना

दशमलव भिन्न को दशमलव भिन्न में विभाजित करने के लिए, लाभांश में और भाजक में, अल्पविराम को अंकों की उतनी ही संख्या से दाईं ओर ले जाएँ जितने कि भाजक में दशमलव बिंदु के बाद होते हैं, और फिर एक नियमित संख्या से विभाजित करते हैं।

उदाहरण के लिए, 5.95 को 1.7 . से भाग दें

आइए इस व्यंजक को एक कोने के रूप में लिखें

अब, भाजक में और भाजक में, हम अल्पविराम को दाईं ओर उतने ही अंकों से ले जाते हैं जितने कि भाजक में दशमलव बिंदु के बाद होते हैं। भाजक का दशमलव बिंदु के बाद एक अंक होता है। इसलिए हमें लाभांश और भाजक में अल्पविराम को एक अंक से दाईं ओर ले जाना चाहिए। स्थानांतरण:

दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, दशमलव अंश 5.95 भिन्न 59.5 में बदल गया। और दशमलव अंश 1.7, दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, सामान्य संख्या 17 में बदल गया। और हम पहले से ही जानते हैं कि दशमलव अंश को सामान्य संख्या से कैसे विभाजित किया जाए। आगे की गणना मुश्किल नहीं है:

विभाजन को सुविधाजनक बनाने के लिए अल्पविराम को दाईं ओर ले जाया जाता है। इसकी अनुमति इस तथ्य के कारण दी जाती है कि जब लाभांश और भाजक को एक ही संख्या से गुणा या विभाजित किया जाता है, तो भागफल नहीं बदलता है। इसका क्या मतलब है?

यह विभाजन की दिलचस्प विशेषताओं में से एक है। इसे निजी संपत्ति कहा जाता है। व्यंजक 9: 3 = 3 पर विचार करें। यदि इस व्यंजक में भाज्य और भाजक को एक ही संख्या से गुणा या भाग किया जाता है, तो भागफल 3 नहीं बदलेगा।

आइए भाज्य और भाजक को 2 से गुणा करें और देखें कि क्या होता है:

(9 × 2) : (3 × 2) = 18: 6 = 3

जैसा कि उदाहरण से देखा जा सकता है, भागफल नहीं बदला है।

यही बात तब होती है जब हम भाजक और भाजक में अल्पविराम लगाते हैं। पिछले उदाहरण में, जहां हमने 5.91 को 1.7 से विभाजित किया था, हमने लाभांश और भाजक में अल्पविराम को एक अंक दाईं ओर ले जाया था। अल्पविराम को स्थानांतरित करने के बाद, भिन्न 5.91 को भिन्न 59.1 में और भिन्न 1.7 को सामान्य संख्या 17 में परिवर्तित किया गया था।

वास्तव में, इस प्रक्रिया के अंदर, 10 से गुणा हुआ। यहाँ यह कैसा दिखता है:

5.91 × 10 = 59.1

इसलिए, भाजक में दशमलव बिंदु के बाद अंकों की संख्या इस बात पर निर्भर करती है कि भाज्य और भाजक को किससे गुणा किया जाएगा। दूसरे शब्दों में, भाजक में दशमलव बिंदु के बाद अंकों की संख्या निर्धारित करेगी कि लाभांश में कितने अंक हैं और भाजक में अल्पविराम को दाईं ओर ले जाया जाएगा।

दशमलव भाग 10, 100, 1000

दशमलव को 10, 100, या 1000 से विभाजित करना उसी तरह किया जाता है जैसे . उदाहरण के लिए, आइए 2.1 को 10 से भाग दें। आइए इस उदाहरण को एक कोने से हल करें:

लेकिन एक दूसरा तरीका भी है। यह हल्का है। इस पद्धति का सार यह है कि भाजक में अल्पविराम को बाईं ओर उतने अंकों से स्थानांतरित किया जाता है जितने कि भाजक में शून्य होते हैं।

आइए पिछले उदाहरण को इस तरह हल करें। 2.1: 10. हम डिवाइडर को देखते हैं। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि एक शून्य है। तो विभाज्य 2.1 में, आपको अल्पविराम को बाईं ओर एक अंक से स्थानांतरित करने की आवश्यकता है। हम अल्पविराम को एक अंक से बाईं ओर ले जाते हैं और देखते हैं कि कोई और अंक नहीं बचा है। इस मामले में, हम संख्या से पहले एक और शून्य जोड़ते हैं। नतीजतन, हमें 0.21 . मिलता है

आइए 2.1 को 100 से विभाजित करने का प्रयास करें। 100 की संख्या में दो शून्य होते हैं। तो विभाज्य 2.1 में, आपको अल्पविराम को बाईं ओर दो अंकों से स्थानांतरित करने की आवश्यकता है:

2,1: 100 = 0,021

आइए 2.1 को 1000 से विभाजित करने का प्रयास करें। 1000 की संख्या में तीन शून्य होते हैं। तो विभाज्य 2.1 में, आपको अल्पविराम को बाईं ओर तीन अंकों से स्थानांतरित करने की आवश्यकता है:

2,1: 1000 = 0,0021

दशमलव विभाजन 0.1, 0.01 और 0.001

दशमलव को 0.1, 0.01 और 0.001 से विभाजित करना उसी तरह किया जाता है जैसे . लाभांश और भाजक में, आपको अल्पविराम को दाईं ओर उतने अंकों से स्थानांतरित करने की आवश्यकता होती है जितने कि भाजक में दशमलव बिंदु के बाद होते हैं।

उदाहरण के लिए, आइए 6.3 को 0.1 से भाग दें। सबसे पहले, हम भाज्य में और भाजक में दायीं ओर उतने ही अंकों से अल्पविराम लगाते हैं जितने कि भाजक में दशमलव बिंदु के बाद होते हैं। भाजक का दशमलव बिंदु के बाद एक अंक होता है। इसलिए हम लाभांश में अल्पविराम और भाजक को एक अंक से दाईं ओर ले जाते हैं।

दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, दशमलव अंश 6.3 सामान्य संख्या 63 में बदल जाता है, और दशमलव अंश 0.1, दशमलव बिंदु को एक अंक से दाईं ओर ले जाने के बाद, एक में बदल जाता है। और 63 को 1 से विभाजित करना बहुत आसान है:

तो व्यंजक 6.3:0.1 का मान 63 . के बराबर है

लेकिन एक दूसरा तरीका भी है। यह हल्का है। इस पद्धति का सार यह है कि भाजक में अल्पविराम को दाईं ओर उतने अंकों से स्थानांतरित किया जाता है जितने कि भाजक में शून्य होते हैं।

आइए पिछले उदाहरण को इस तरह हल करें। 6.3:0.1। आइए डिवाइडर को देखें। हम इसमें रुचि रखते हैं कि इसमें कितने शून्य हैं। हम देखते हैं कि एक शून्य है। तो विभाज्य 6.3 में, आपको अल्पविराम को एक अंक से दाईं ओर ले जाने की आवश्यकता है। हम अल्पविराम को एक अंक से दाईं ओर ले जाते हैं और 63 . प्राप्त करते हैं

आइए 6.3 को 0.01 से भाग देने का प्रयास करें। भाजक 0.01 में दो शून्य होते हैं। तो विभाज्य 6.3 में, आपको अल्पविराम को दो अंकों से दाईं ओर ले जाने की आवश्यकता है। लेकिन लाभांश में दशमलव बिंदु के बाद केवल एक अंक होता है। इस मामले में, अंत में एक और शून्य जोड़ा जाना चाहिए। परिणामस्वरूप, हमें 630 . प्राप्त होता है

आइए 6.3 को 0.001 से विभाजित करने का प्रयास करें। 0.001 के भाजक में तीन शून्य होते हैं। तो विभाज्य 6.3 में, आपको अल्पविराम को तीन अंकों से दाईं ओर ले जाने की आवश्यकता है:

6,3: 0,001 = 6300

स्वतंत्र समाधान के लिए कार्य

क्या आपको सबक पसंद आया?
हमारे नए Vkontakte समूह में शामिल हों और नए पाठों की सूचनाएं प्राप्त करना शुरू करें

नियमित संख्या की तरह।

2. हम पहले दशमलव भिन्न के लिए और दूसरे के लिए दशमलव स्थानों की संख्या गिनते हैं। हम उनकी संख्या जोड़ते हैं।

3. अंतिम परिणाम में, हम दाएं से बाएं इतनी संख्या में अंक गिनते हैं जैसे वे ऊपर के पैराग्राफ में निकले, और एक अल्पविराम लगाएं।

दशमलव गुणा करने के नियम।

1. अल्पविराम पर ध्यान दिए बिना गुणा करें।

2. गुणनफल में, हम दशमलव बिंदु के बाद उतने ही अंकों को अलग करते हैं जितने दोनों कारकों में अल्पविराम के बाद होते हैं।

एक दशमलव अंश को एक प्राकृत संख्या से गुणा करने पर, आपको यह करना होगा:

1. अल्पविराम को अनदेखा करते हुए संख्याओं को गुणा करें;

2. परिणामस्वरूप, हम एक अल्पविराम लगाते हैं ताकि उसके दाईं ओर उतने ही अंक हों जितने दशमलव भिन्न में हैं।

एक कॉलम द्वारा दशमलव अंशों का गुणन।

आइए एक उदाहरण देखें:

हम दशमलव भिन्नों को एक कॉलम में लिखते हैं और अल्पविरामों को अनदेखा करते हुए उन्हें प्राकृत संख्याओं के रूप में गुणा करते हैं। वे। हम 3.11 को 311 और 0.01 को 1 मानते हैं।

परिणाम 311 है। इसके बाद, हम दोनों भिन्नों के लिए दशमलव स्थानों (अंकों) की संख्या की गणना करते हैं। पहले दशमलव में 2 अंक हैं और दूसरे में 2 अंक हैं। दशमलव अंकों के बाद अंकों की कुल संख्या:

2 + 2 = 4

हम परिणाम के दाएं से बाएं चार वर्णों की गणना करते हैं। अंतिम परिणाम में, आपको अल्पविराम से अलग करने की आवश्यकता से कम अंक हैं। इस मामले में, बाईं ओर शून्य की लापता संख्या को जोड़ना आवश्यक है।

हमारे मामले में, पहला अंक गायब है, इसलिए हम बाईं ओर 1 शून्य जोड़ते हैं।

टिप्पणी:

किसी भी दशमलव भिन्न को 10, 100, 1000, इत्यादि से गुणा करने पर, दशमलव भिन्न में अल्पविराम दायीं ओर उतने स्थानों तक चला जाता है, जितने एक के बाद शून्य होते हैं।

उदाहरण के लिए:

70,1 . 10 = 701

0,023 . 100 = 2,3

5,6 . 1 000 = 5 600

टिप्पणी:

दशमलव को 0.1 से गुणा करना; 0.01; 0.001; और इसी तरह, आपको इस भिन्न में अल्पविराम को बाईं ओर उतने वर्णों तक ले जाने की आवश्यकता है जितनी इकाई के सामने शून्य हैं।

हम शून्य पूर्णांक गिनते हैं!

उदाहरण के लिए:

12 . 0,1 = 1,2

0,05 . 0,1 = 0,005

1,256 . 0,01 = 0,012 56

दशमलव अंश का उपयोग तब किया जाता है जब आपको गैर-पूर्णांक संख्याओं पर संचालन करने की आवश्यकता होती है। यह तर्कहीन लग सकता है। लेकिन इस प्रकार की संख्याएँ गणितीय संक्रियाओं को बहुत सुविधाजनक बनाती हैं जिन्हें उनके साथ किया जाना चाहिए। यह समझ समय के साथ आती है, जब उनका लेखन परिचित हो जाता है, और पढ़ने में कठिनाई नहीं होती है, और दशमलव अंशों के नियमों में महारत हासिल होती है। इसके अलावा, सभी क्रियाएं पहले से ज्ञात लोगों को दोहराती हैं, जो इससे सीखी जाती हैं प्राकृतिक संख्याएं।आपको बस कुछ विशेषताओं को याद रखने की जरूरत है।

दशमलव परिभाषा

एक दशमलव एक गैर-पूर्णांक संख्या का एक विशेष प्रतिनिधित्व है जिसमें एक भाजक है जो 10 से विभाज्य है और उत्तर एक और संभवतः शून्य है। दूसरे शब्दों में, यदि हर 10, 100, 1000, इत्यादि है, तो अल्पविराम का उपयोग करके संख्या को फिर से लिखना अधिक सुविधाजनक है। फिर पूर्णांक भाग उसके सामने स्थित होगा, और फिर भिन्नात्मक भाग। इसके अलावा, संख्या के दूसरे भाग का रिकॉर्ड हर पर निर्भर करेगा। भिन्नात्मक भाग में अंकों की संख्या हर के बराबर होनी चाहिए।

उपरोक्त को इन संख्याओं के साथ चित्रित किया जा सकता है:

9/10=0,9; 178/10000=0,0178; 3,05; 56 003,7006.

दशमलव का उपयोग करने के कारण

गणितज्ञों को कई कारणों से दशमलव की आवश्यकता होती है:

रिकॉर्डिंग को सरल बनाएं। ऐसा अंश हर और अंश के बीच डैश के बिना एक रेखा के साथ स्थित होता है, जबकि दृश्यता प्रभावित नहीं होती है।

तुलना में सरलता। यह केवल उन संख्याओं को सहसंबंधित करने के लिए पर्याप्त है जो समान स्थिति में हैं, जबकि साधारण भिन्नों के साथ उन्हें एक सामान्य भाजक तक लाना होगा।

गणना का सरलीकरण।

कैलकुलेटर सामान्य भिन्नों को पेश करने के लिए डिज़ाइन नहीं किए गए हैं; वे सभी कार्यों के लिए दशमलव संकेतन का उपयोग करते हैं।

ऐसे नंबरों को सही तरीके से कैसे पढ़ें?

उत्तर सरल है: एक साधारण मिश्रित संख्या की तरह एक भाजक के साथ जो कि 10 का एक गुणक है। एकमात्र अपवाद पूर्णांक मान के बिना भिन्न हैं, फिर पढ़ते समय आपको "शून्य पूर्णांक" कहने की आवश्यकता होती है।

उदाहरण के लिए, 45/1000 का उच्चारण इस प्रकार किया जाना चाहिए पैंतालीस हजारवां, जबकि 0.045 की तरह ध्वनि होगी शून्य बिंदु पैंतालीस हज़ारवां.

एक मिश्रित संख्या जिसमें एक पूर्णांक भाग 7 के बराबर और एक अंश 17/100 है, जिसे 7.17 के रूप में लिखा जाएगा, दोनों स्थितियों में पढ़ा जाएगा सात दशमलव सत्रह सौवां.

भिन्नों के अंकन में अंकों की भूमिका

डिस्चार्ज को नोट करना सही है - यही गणित की आवश्यकता है। यदि आप गलत जगह पर अंक लिखते हैं तो दशमलव और उनके अर्थ महत्वपूर्ण रूप से बदल सकते हैं। हालाँकि, यह पहले भी सच रहा है।

दशमलव भिन्न के पूर्णांक भाग के अंकों को पढ़ने के लिए, आपको केवल प्राकृतिक संख्याओं के लिए ज्ञात नियमों का उपयोग करने की आवश्यकता है। और दाहिनी ओर उन्हें प्रतिबिंबित किया जाता है और अलग तरह से पढ़ा जाता है। यदि पूरे भाग में "दसियों" की आवाज़ आती है, तो दशमलव बिंदु के बाद यह पहले से ही "दसवां" होगा।

यह इस तालिका में स्पष्ट रूप से देखा जा सकता है।

दशमलव स्थान तालिका

कक्षा	हजारों			इकाइयों			,	अंश
स्राव होना	सौ	दिसम्बर	इकाइयों	सौ	दिसम्बर	इकाइयों		दसवां	सौवां	हज़ारवां	दस हज़ारवां

मिश्रित संख्या को दशमलव के रूप में कैसे लिखें?

यदि हर में 10 या 100 और अन्य के बराबर संख्या होती है, तो एक भिन्न को दशमलव में कैसे परिवर्तित किया जाए, यह प्रश्न सरल है। ऐसा करने के लिए, इसके सभी घटक भागों को एक अलग तरीके से फिर से लिखना पर्याप्त है। निम्नलिखित बिंदु इसमें मदद करेंगे:

भिन्न के अंश को थोड़ा अलग लिखें, इस समय दशमलव बिंदु अंतिम अंक के बाद दाईं ओर स्थित है;

अल्पविराम को बाईं ओर ले जाएं, यहां सबसे महत्वपूर्ण बात यह है कि संख्याओं को सही ढंग से गिनना है - आपको इसे कई पदों पर स्थानांतरित करने की आवश्यकता है क्योंकि हर में शून्य हैं;

यदि उनमें से पर्याप्त नहीं हैं, तो शून्य खाली पदों पर दिखाई देना चाहिए;

अंश के अंत में जो शून्य थे, उनकी अब आवश्यकता नहीं है, और उन्हें पार किया जा सकता है;

अल्पविराम से पहले एक पूर्णांक भाग जोड़ें, यदि वह नहीं था, तो यहां शून्य भी दिखाई देगा।

ध्यान। आप उन शून्यों को पार नहीं कर सकते जो अन्य संख्याओं से घिरे हैं।

आप इस बारे में पढ़ सकते हैं कि ऐसी स्थिति में कैसे रहें जहां हर में न केवल एक और शून्य की संख्या हो, एक अंश को दशमलव में कैसे परिवर्तित किया जाए, आप थोड़ा नीचे पढ़ सकते हैं। यह महत्वपूर्ण जानकारी है जिसे आपको अवश्य पढ़ना चाहिए।

यदि हर एक मनमाना संख्या है तो भिन्न को दशमलव में कैसे बदलें?

यहां दो विकल्प हैं:

जब हर को एक संख्या के रूप में दर्शाया जा सकता है जो किसी भी घात के लिए दस है।

अगर ऐसा ऑपरेशन नहीं किया जा सकता है।

इसे कैसे जांचें? आपको हर का गुणनखंड करना होगा। यदि गुणनफल में केवल 2 और 5 मौजूद हैं, तो सब कुछ ठीक है, और अंश आसानी से अंतिम दशमलव में बदल जाता है। अन्यथा, यदि 3, 7 और अन्य दिखाई देते हैं अभाज्य सँख्या,तो परिणाम अनंत होगा। गणितीय कार्यों में उपयोग में आसानी के लिए ऐसे दशमलव अंश को गोल करने की प्रथा है। इस पर थोड़ा नीचे चर्चा की जाएगी।

इस तरह के दशमलव अंश कैसे प्राप्त किए जाते हैं, इसका अध्ययन, ग्रेड 5। उदाहरण यहां बहुत मददगार होंगे।

मान लीजिए कि हर में संख्याएँ हैं: 40, 24 और 75। उनके लिए अभाज्य गुणनखंडों में अपघटन इस प्रकार होगा:

• 40=2 2 2 5;
• 24=2 2 2 3;
• 75=5 5 3.

इन उदाहरणों में, केवल पहली भिन्न को अंतिम भिन्न के रूप में दर्शाया जा सकता है।

एक साधारण भिन्न को अंतिम दशमलव में बदलने के लिए एल्गोरिथम

भाजक के अभाज्य गुणनखंडों में गुणनखंडन की जाँच करें और सुनिश्चित करें कि इसमें 2 और 5 शामिल होंगे।

इन संख्याओं में इतने 2 और 5 जोड़ें कि वे एक समान संख्या बन जाएं। वे अतिरिक्त गुणक का मूल्य देंगे।

इस संख्या से हर और अंश को गुणा करें। परिणाम एक साधारण अंश है, जिसकी रेखा के नीचे कुछ हद तक 10 है।

यदि कार्य में इन क्रियाओं को मिश्रित संख्या के साथ किया जाता है, तो इसे पहले इस रूप में दर्शाया जाना चाहिए गलत अंश।और उसके बाद ही वर्णित परिदृश्य के अनुसार कार्य करें।

एक गोल दशमलव के रूप में एक सामान्य अंश का प्रतिनिधित्व

किसी भिन्न को दशमलव में बदलने का यह तरीका किसी को और भी आसान लगेगा। क्योंकि इसमें ज्यादा एक्शन नहीं है। आपको बस अंश को हर से विभाजित करने की आवश्यकता है।

दशमलव बिंदु के दाईं ओर दशमलव भाग वाली कोई भी संख्या अनंत संख्या में शून्य निर्दिष्ट की जा सकती है। इस संपत्ति का उपयोग किया जाना चाहिए।

सबसे पहले पूरे हिस्से को लिख लें और उसके बाद कॉमा लगाएं। यदि भिन्न सही है, तो शून्य लिखें।

फिर हर द्वारा अंश का विभाजन करना आवश्यक है। ताकि उनके पास अंकों की संख्या समान हो। अर्थात्, अंश के दाईं ओर आवश्यक संख्या में शून्य निर्दिष्ट करें।

पूरा एक कॉलम में विभाजनजब तक आवश्यक अंकों की संख्या डायल नहीं की जाती। उदाहरण के लिए, यदि आपको सौवें तक पूर्णांक बनाने की आवश्यकता है, तो उत्तर में उनमें से 3 होने चाहिए। सामान्य तौर पर, अंत में प्राप्त करने की आवश्यकता से एक अंक अधिक होना चाहिए।

इंटरमीडिएट के उत्तर को दशमलव बिंदु के बाद रिकॉर्ड करें और नियमों के अनुसार गोल करें। यदि अंतिम अंक 0 से 4 तक है, तो आपको इसे त्यागने की आवश्यकता है। और जब यह 5-9 के बराबर हो जाए, तो उसके सामने वाले को पिछले वाले को हटाकर एक से बढ़ाना चाहिए।

दशमलव से साधारण पर लौटें

गणित में, ऐसी समस्याएं होती हैं जब दशमलव अंशों को साधारण अंशों के रूप में प्रस्तुत करना अधिक सुविधाजनक होता है, जिसमें हर के साथ एक अंश होता है। आप राहत की सांस ले सकते हैं: यह ऑपरेशन हमेशा संभव है।

इस प्रक्रिया के लिए, आपको निम्न कार्य करने होंगे:

पूर्णांक भाग लिखिए, यदि यह शून्य के बराबर है, तो कुछ भी लिखने की आवश्यकता नहीं है;

एक भिन्नात्मक रेखा खींचना;

इसके ऊपर, दाईं ओर से संख्याएँ लिखें, यदि पहले शून्य हैं, तो उन्हें काट दिया जाना चाहिए;

रेखा के नीचे मूल भिन्न में दशमलव बिंदु के बाद जितने भी अंक हों उतने शून्यों वाली इकाई लिखिए।

दशमलव को सामान्य भिन्न में बदलने के लिए आपको बस इतना ही करना है।

आप दशमलव के साथ क्या कर सकते हैं?

गणित में, यह दशमलव अंशों के साथ कुछ निश्चित क्रियाएं होंगी जो पहले अन्य संख्याओं के लिए की गई थीं।

वो हैं:

तुलना;

जोड़ना और घटाना;

गुणन और भाग।

पहली क्रिया, तुलना, प्राकृतिक संख्याओं के लिए कैसे की गई थी, इसके समान है। यह निर्धारित करने के लिए कि कौन सा बड़ा है, आपको पूर्णांक भाग के अंकों की तुलना करने की आवश्यकता है। यदि वे समान हो जाते हैं, तो वे भिन्नात्मक पर स्विच करते हैं और उसी तरह अंकों से उनकी तुलना करते हैं। उच्चतम क्रम में सबसे बड़े अंक वाली संख्या उत्तर होगी।

दशमलव को जोड़ना और घटाना

ये शायद सबसे सरल कदम हैं। क्योंकि इन्हें प्राकृत संख्याओं के नियमों के अनुसार निष्पादित किया जाता है।



इसलिए, दशमलव अंशों को जोड़ने के लिए, उन्हें एक कॉलम में अल्पविराम लगाकर एक दूसरे के नीचे लिखा जाना चाहिए। इस तरह के रिकॉर्ड के साथ, पूर्णांक भाग अल्पविराम के बाईं ओर और आंशिक भाग दाईं ओर दिखाई देते हैं। और अब आपको संख्याओं को थोड़ा-थोड़ा करके जोड़ना होगा, जैसा कि प्राकृतिक संख्याओं के साथ किया जाता है, अल्पविराम को नीचे ले जाना। आपको संख्या के भिन्नात्मक भाग के सबसे छोटे अंक से जोड़ना शुरू करना होगा। यदि दाहिने आधे भाग में पर्याप्त संख्याएँ नहीं हैं, तो शून्य जोड़ें।

घटाव उसी तरह काम करता है। और यहां नियम लागू होता है, जो उच्चतम अंक से एक इकाई लेने की संभावना का वर्णन करता है। यदि घटाए गए अंश में सबट्रेंड की तुलना में दशमलव बिंदु के बाद कम अंक होते हैं, तो शून्य को बस इसे असाइन किया जाता है।

स्थिति उन कार्यों के साथ थोड़ी अधिक जटिल है जहाँ आपको दशमलव अंशों का गुणा और भाग करने की आवश्यकता होती है।

विभिन्न उदाहरणों में दशमलव को गुणा कैसे करें?

दशमलव भिन्नों को एक प्राकृत संख्या से गुणा करने का नियम इस प्रकार है:

अल्पविराम को अनदेखा करते हुए उन्हें एक कॉलम में लिख दें;

गुणा करें जैसे कि वे प्राकृतिक थे;

एक अल्पविराम से अलग करें जितने अंक मूल संख्या के भिन्नात्मक भाग में थे।

एक विशेष मामला एक उदाहरण है जिसमें एक प्राकृतिक संख्या किसी भी शक्ति के 10 के बराबर होती है। फिर, एक उत्तर प्राप्त करने के लिए, आपको अल्पविराम को दाईं ओर ले जाने की आवश्यकता है, क्योंकि किसी अन्य कारक में शून्य हैं। दूसरे शब्दों में, जब 10 से गुणा किया जाता है, तो अल्पविराम एक अंक से बदल जाता है, 100 से - उनमें से दो होंगे, और इसी तरह। यदि भिन्नात्मक भाग में पर्याप्त अंक नहीं हैं, तो आपको रिक्त पदों पर शून्य लिखने की आवश्यकता है।

वह नियम जिसका उपयोग तब किया जाता है जब कार्य में आपको दशमलव अंशों को उसी संख्या के दूसरे से गुणा करने की आवश्यकता होती है:

अल्पविरामों को अनदेखा करते हुए उन्हें एक के नीचे एक लिख दें;

गुणा करें जैसे कि वे प्राकृतिक संख्याएं हों;

एक अल्पविराम से अलग करें जितने अंक दोनों मूल अंशों के भिन्नात्मक भागों में एक साथ थे।

एक विशेष मामले के रूप में, उदाहरणों को प्रतिष्ठित किया जाता है जिसमें कारकों में से एक 0.1 या 0.01 के बराबर होता है और इसी तरह। उनमें, आपको प्रस्तुत कारकों में अंकों की संख्या से अल्पविराम को बाईं ओर ले जाने की आवश्यकता है। अर्थात्, यदि 0.1 से गुणा किया जाता है, तो अल्पविराम एक स्थान से स्थानांतरित हो जाता है।

दशमलव भिन्न को विभिन्न कार्यों में कैसे विभाजित करें?

दशमलव भिन्नों को एक प्राकृत संख्या से विभाजित करने पर निम्नलिखित नियम के अनुसार कार्य किया जाता है:

उन्हें एक कॉलम में विभाजित करने के लिए लिखें, जैसे कि वे स्वाभाविक थे;

सामान्य नियम के अनुसार विभाजित करें जब तक कि पूरा भाग समाप्त न हो जाए;

उत्तर में अल्पविराम लगाएं;

भिन्नात्मक घटक को तब तक विभाजित करना जारी रखें जब तक कि शेष शून्य न हो जाए;

यदि आवश्यक हो, तो आप आवश्यक संख्या में शून्य निर्दिष्ट कर सकते हैं।

यदि पूर्णांक भाग शून्य के बराबर है, तो वह उत्तर में भी नहीं होगा।

अलग-अलग, दस, एक सौ, आदि के बराबर संख्याओं में विभाजन होता है। ऐसी समस्याओं में, आपको भाजक में शून्य की संख्या से अल्पविराम को बाईं ओर ले जाने की आवश्यकता होती है। ऐसा होता है कि पूर्णांक भाग में पर्याप्त अंक नहीं होते हैं, तो इसके बजाय शून्य का उपयोग किया जाता है। यह देखा जा सकता है कि यह ऑपरेशन 0.1 और समान संख्याओं से गुणा करने के समान है।

दशमलव का विभाजन करने के लिए, आपको इस नियम का उपयोग करना होगा:

भाजक को एक प्राकृतिक संख्या में बदल दें, और ऐसा करने के लिए, इसमें अल्पविराम को दाईं ओर अंत तक ले जाएँ;

अंकों की समान संख्या से अल्पविराम और विभाज्य में स्थानांतरित करें;

पिछले परिदृश्य का पालन करें।

अलग दिखना 0.1 से विभाजन; 0.01और अन्य समान संख्याएँ। ऐसे उदाहरणों में, भिन्नात्मक भाग में अंकों की संख्या से अल्पविराम को दाईं ओर स्थानांतरित कर दिया जाता है। यदि वे खत्म हो गए हैं, तो आपको लापता शून्य की संख्या निर्दिष्ट करने की आवश्यकता है। यह ध्यान देने योग्य है कि यह क्रिया 10 और समान संख्याओं से विभाजन को दोहराती है।



निष्कर्ष: यह सब अभ्यास के बारे में है

सीखने में कुछ भी आसान या सहज नहीं होता है। नई सामग्री में मज़बूती से महारत हासिल करने में समय और अभ्यास लगता है। गणित कोई अपवाद नहीं है।

ताकि दशमलव अंशों के विषय में कठिनाई न हो, आपको उनके साथ यथासंभव अधिक से अधिक उदाहरण हल करने की आवश्यकता है। आखिरकार, एक समय था जब प्राकृतिक संख्याओं का जोड़ भ्रमित करने वाला था। और अब सब ठीक है।

इसलिए, एक प्रसिद्ध वाक्यांश को स्पष्ट करने के लिए: निर्णय लें, निर्णय लें और फिर से निर्णय लें। फिर इस तरह की संख्या वाले कार्यों को एक और पहेली की तरह आसानी से और स्वाभाविक रूप से किया जाएगा।

वैसे, पहेलियों को पहले हल करना मुश्किल होता है, और फिर आपको सामान्य आंदोलनों को करने की आवश्यकता होती है। गणितीय उदाहरणों में भी यही सच है: एक ही रास्ते पर कई बार जाने के बाद, आप अब यह नहीं सोचेंगे कि कहाँ मुड़ना है।