चेकर्ड पेपर पर बहुभुज बनाएं। उदाहरण के लिए, जैसा कि चित्र 1 में दिखाया गया है।
आइए अब इसके क्षेत्रफल की गणना करने का प्रयास करें। यह कैसे करना है? संभवत: सबसे आसान तरीका यह है कि इसे समकोण त्रिभुजों और आयतों में तोड़ दिया जाए, जिनके क्षेत्रों की गणना करना और परिणामों को जोड़ना पहले से ही आसान है। मैंने जिस विधि का उपयोग किया है वह सरल है, लेकिन बहुत बोझिल है, और इसके अलावा, यह सभी बहुभुजों के लिए उपयुक्त नहीं है।
एक गैर-पतित सरल पूर्णांक बहुभुज पर विचार करें (अर्थात, यह जुड़ा हुआ है - इसके किन्हीं दो बिंदुओं को एक निरंतर वक्र द्वारा जोड़ा जा सकता है जो पूरी तरह से इसमें समाहित है, और इसके सभी कोने में पूर्णांक निर्देशांक हैं, इसकी सीमा बिना एक कनेक्टेड पॉलीलाइन है आत्म-चौराहे, और इसमें एक गैर-शून्य वर्ग है)। ऐसे बहुभुज के क्षेत्रफल की गणना करने के लिए, आप निम्नलिखित प्रमेय का उपयोग कर सकते हैं:
पिक का प्रमेय।मान लीजिए बहुभुज के अंदर पूर्णांक बिंदुओं की संख्या हो, इसकी सीमा पर पूर्णांक बिंदुओं की संख्या हो, और इसका क्षेत्रफल हो। फिर चयन सूत्र:
उदाहरण।चित्र 1 में बहुभुज के लिए (पीले बिंदु), (नीले बिंदु, शीर्षों को न भूलें!), इसलिए वर्ग इकाइयाँ।

पिक के प्रमेय का प्रमाण।सबसे पहले, ध्यान दें कि पिक का सूत्र इकाई वर्ग के लिए सही है। दरअसल, इस मामले में हमारे पास है
एक आयत पर विचार करें जिसकी भुजाएँ जालीदार रेखाओं पर पड़ी हों। माना इसकी भुजाओं की लंबाई और के बराबर है। हमारे पास इस मामले में है और, पिक फॉर्मूला के अनुसार,

अब एक समकोण त्रिभुज पर विचार करें जिसके पैर निर्देशांक अक्षों पर पड़े हों। ऐसा त्रिभुज पक्षों के साथ एक आयत से प्राप्त किया जाता है और, पिछले मामले में इसे तिरछे काटकर माना जाता है। मान लीजिए कि पूर्णांक बिंदु विकर्ण पर स्थित हैं। फिर इस मामले के लिए हमें वह मिलता है
अब एक मनमाना त्रिभुज पर विचार करें। यह कई समकोण त्रिभुजों को काटकर प्राप्त किया जा सकता है और, संभवतः, एक आयत से एक आयत (आंकड़े 2 और 3 देखें)। चूँकि पिक का सूत्र एक आयत और एक समकोण त्रिभुज दोनों के लिए सत्य है, हम पाते हैं कि यह एक स्वेच्छ त्रिभुज के लिए भी सत्य होगा।


यह अंतिम चरण लेना बाकी है: त्रिकोण से बहुभुज की ओर बढ़ना। किसी भी बहुभुज को त्रिभुजों में विभाजित किया जा सकता है (उदाहरण के लिए, विकर्णों द्वारा)। इसलिए, हमें केवल यह साबित करने की आवश्यकता है कि किसी भी त्रिभुज को एक मनमाना बहुभुज में जोड़ने पर, पिक का सूत्र सत्य रहता है।
माना बहुभुज और त्रिभुज की एक उभयनिष्ठ भुजा है। मान लें कि पिक सूत्र के लिए मान्य है, और साबित करें कि यह जोड़ से प्राप्त बहुभुज के लिए भी मान्य है। चूँकि और इनका एक उभयनिष्ठ पक्ष है, इस तरफ स्थित दो शीर्षों को छोड़कर सभी पूर्णांक बिंदु नए बहुभुज के आंतरिक बिंदु बन जाते हैं। शीर्ष सीमा बिंदु होंगे। आइए हम उभयनिष्ठ बिंदुओं की संख्या को द्वारा निरूपित करें और प्राप्त करें
नए बहुभुज के आंतरिक पूर्णांक बिंदुओं की संख्या,
नए बहुभुज के लिए सीमा बिंदुओं की संख्या।
इन समानताओं से हमें प्राप्त होता है
चूँकि हमने यह मान लिया था कि प्रमेय अलग-अलग के लिए और के लिए सत्य है, तो
इस प्रकार, पिक सूत्र सिद्ध होता है।
इस सूत्र की खोज ऑस्ट्रियाई गणितज्ञ पीक जॉर्ज अलेक्जेंड्रोव (1859 - 1943) ने 1899 में की थी। इस फॉर्मूले के अलावा, जॉर्ज पिक ने पिक, पिक - जूलिया, पिक - नेवलिना प्रमेय की खोज की, श्वार्ज - पिक असमानता को साबित किया। पर परिशिष्ट 1आप उन गैर-मानक कार्यों को देख सकते हैं जिन पर मैंने पिक फॉर्मूला लागू करने के लिए विचार किया है।
पीक फॉर्मूला
1। परिचय
2. शिखर सूत्र। सबूत मैं।
प्रमाण द्वितीय।
श्री का प्रमाण।
3. कार्य।
4. कोने के निर्देशांक के संदर्भ में बहुभुज के क्षेत्रफल का सूत्र।
5. कार्य।
6. साहित्य
शिखर सूत्र।
1। परिचय।
हम इतिहास से ज्ञान लेते हैं,
कविता में - बुद्धि,
गणित में - अंतर्दृष्टि।
एफ बेकन
प्लॉट चेकर पेपर के एक नियमित टुकड़े पर प्रकट होगा।
कोशिकाओं के किनारों के साथ जाने वाली रेखाएं एक ग्रिड बनाती हैं, और कोशिकाओं के कोने इस ग्रिड के नोड होते हैं। आइए शीट पर नोड्स पर कोने के साथ एक बहुभुज बनाएं और इसका क्षेत्रफल ज्ञात करें।
आप इसे अलग-अलग तरीकों से खोज सकते हैं। उदाहरण के लिए, आप एक बहुभुज को काफी सरल आकृतियों में काट सकते हैं, उनका क्षेत्रफल ज्ञात कर सकते हैं और उन्हें जोड़ सकते हैं।
लेकिन यहां हम बहुत परेशानी में हैं। आकृति आसानी से आयतों, समलम्बाकार और त्रिभुजों में विभाजित हो जाती है, और इसके क्षेत्रफल की गणना सहजता से की जाती है।
हालांकि बहुभुज काफी सरल दिखता है, इसके क्षेत्रफल की गणना करने में बहुत काम लगेगा। क्या होगा अगर बहुभुज कट्टर लग रहा था? यह पता चला है कि बहुभुज के क्षेत्र जिनके कोने ग्रिड के नोड्स पर स्थित हैं, उनकी गणना अधिक सरलता से की जा सकती है: एक सूत्र है जो उनके क्षेत्र को अंदर और बहुभुज की सीमा पर स्थित नोड्स की संख्या से संबंधित करता है। इस अद्भुत और सरल सूत्र को पिक का सूत्र कहते हैं।
2. शिखर सूत्र।
एक बहुभुज के कोने (जरूरी नहीं कि उत्तल हो) एक पूर्णांक जाली के नोड्स पर स्थित होते हैं। इसके अंदर जाली के बी नोड्स और जी नोड्स की सीमा पर स्थित है। आइए हम सिद्ध करें कि इसका क्षेत्रफल B + . है  - 1 (पीक का सूत्र)।
- 1 (पीक का सूत्र)।
सबूत मैं।
एक बहुभुज पर विचार करें जिसके शीर्ष एक पूर्णांक जालक के नोड्स पर हैं, अर्थात् उनके पास पूर्णांक निर्देशांक हैं।

हम बहुभुज को जाली के नोड्स पर कोने के साथ त्रिभुजों में विभाजित करते हैं, जिसमें अंदर या किनारों पर नोड्स नहीं होते हैं।

निरूपित करें:
एनबहुभुज के पक्षों की संख्या है,
एमजाली के नोड्स पर शीर्षों के साथ त्रिभुजों की संख्या है जिसमें नोड्स या तो अंदर या किनारों पर नहीं होते हैं,
बी बहुभुज के अंदर नोड्स की संख्या है,
कोने सहित पक्षों पर नोड्स की संख्या है।
इन सभी त्रिभुजों के क्षेत्रफल समान और समान हैं।
इसलिए, बहुभुज का क्षेत्रफल है  .
.
180 0 एम .
आइए अब इस राशि को दूसरे तरीके से खोजें।
किसी भी आंतरिक नोड पर एक शीर्ष के साथ कोणों का योग 360 0 है।
फिर सभी आंतरिक नोड्स पर कोने वाले कोणों का योग 360 0 V है।
पक्षों पर नोड्स पर कोणों का कुल योग, लेकिन शीर्षों पर नहीं, 180 0 (G - एन).
बहुभुज के शीर्षों पर कोणों का योग 180 0 है ( एन – 2) .
सभी त्रिभुजों के कोणों का कुल योग होता है 360 0 वी + 180 0 (जी - एन) + 180 0 (एन – 2).
तो 180 0 एम\u003d 360 0 वी + 180 0 (जी - एन) + 180 0 (एन – 2),
180 0 एम\u003d 360 0 वी + 180 0 जी - 180 0 एन + 180 0 एन- 180 0 2,
180 0 एम\u003d 360 0 वी + 180 0 जी- 360 0,
 = बी +
= बी +  – 1 ,
– 1 ,
जहाँ से हमें बहुभुज के क्षेत्रफल S का व्यंजक प्राप्त होता है:
एस= बी +  – 1 ,
– 1 ,
पिक सूत्र के रूप में जाना जाता है।
चित्र में: V = 24, D = 9, इसलिए,एस = 24 + – 1 = 27,5.

शिखर सूत्र का उपयोग करके पहले बहुभुज का क्षेत्रफल ज्ञात कीजिए:

बी = 28 (हरा बिंदु);
डी = 20 (नीला बिंदु)।
हम पाते हैं, एस = 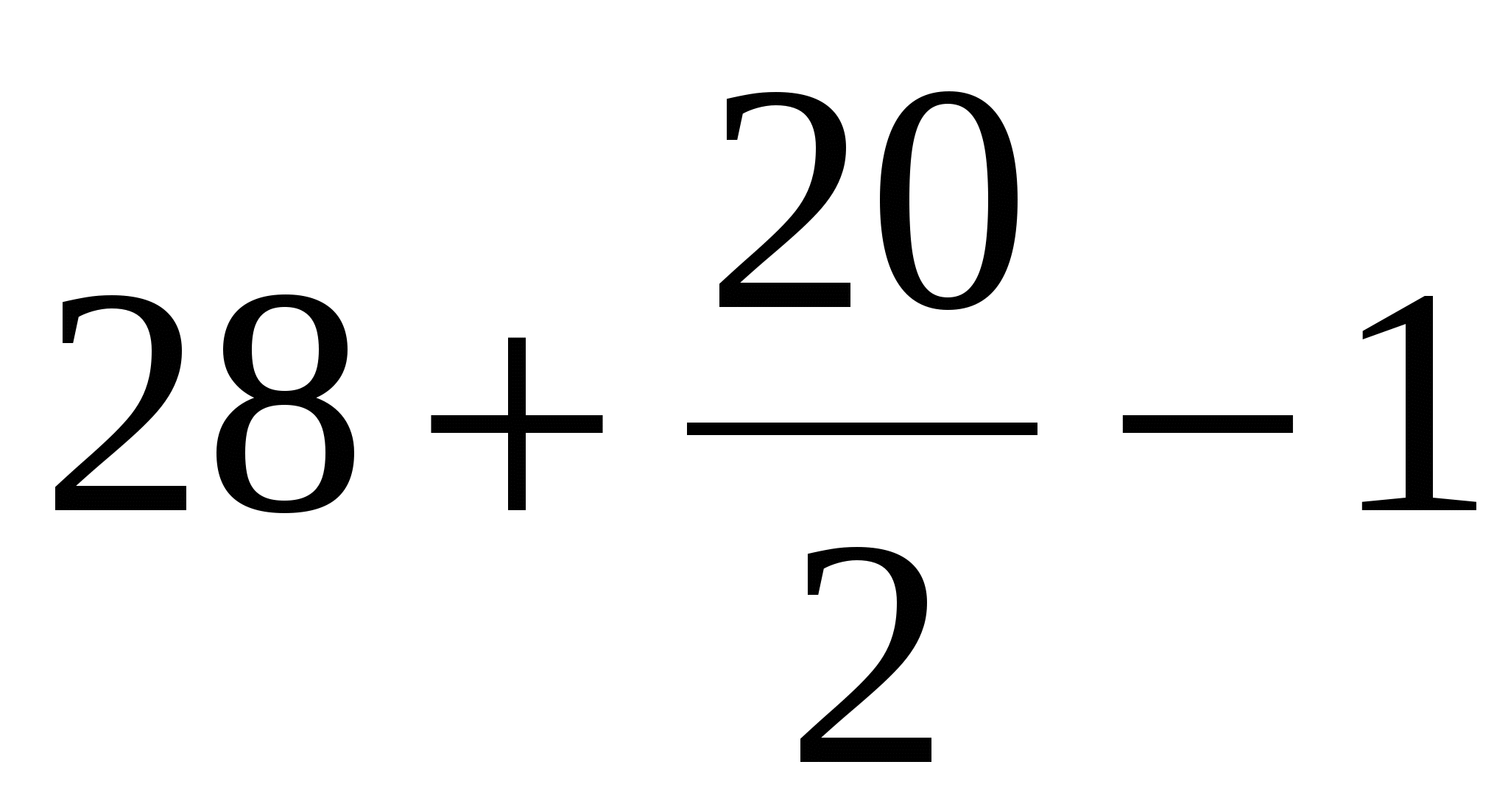 = 37 वर्ग इकाई
= 37 वर्ग इकाई
प्रमाण द्वितीय।
प्रत्येक बहुभुज एम के लिए एक पूर्णांक जाली के नोड्स पर शिखर के साथ हम संख्या एफ (एम) = असाइन करते हैं  , जहां एम से संबंधित सभी जाली नोड्स पर योग है, और कोण
, जहां एम से संबंधित सभी जाली नोड्स पर योग है, और कोण  निम्नानुसार परिभाषित किया गया है:
निम्नानुसार परिभाषित किया गया है:  =
=  एक बहुभुज के आंतरिक बिंदु के लिए,
एक बहुभुज के आंतरिक बिंदु के लिए,  =
=  एक शीर्ष के अलावा एक सीमा बिंदु के लिए, और
एक शीर्ष के अलावा एक सीमा बिंदु के लिए, और  - शीर्ष पर कोण, यदि दिया गया नोड एक शीर्ष है। यह देखना आसान है कि f (M) =
- शीर्ष पर कोण, यदि दिया गया नोड एक शीर्ष है। यह देखना आसान है कि f (M) =  +
+  = बी +
= बी +  - 1. यह जांचना बाकी है कि संख्या f (M) बहुभुज M के क्षेत्रफल के बराबर है।
- 1. यह जांचना बाकी है कि संख्या f (M) बहुभुज M के क्षेत्रफल के बराबर है।
बहुभुज M को बहुभुज M 1 और M 2 में काटा जाता है, जिसमें जाली के नोड्स पर शीर्ष होते हैं। तब f(M) = f(M 1) + f(M 2) क्योंकि प्रत्येक नोड के लिए कोण जुड़ते हैं। इसलिए, यदि दो बहुभुज M, M 1 और M 2 के लिए पिक का सूत्र सत्य है, तो यह तीसरे के लिए भी सत्य है।
यदि M भुजाओं वाला एक आयत है पीऔर क्यू, जाली रेखाओं के साथ निर्देशित, तब
एफ (एम) = (पी -1) (क्यू -1) +  = पीक्यू।
= पीक्यू।
इस मामले में, पिक का सूत्र मान्य है। आयत M को तिरछे त्रिभुज M 1 और M 2 में काटकर और इस तथ्य का उपयोग करके कि f (M) = f (M 1) + f (M 2) और f (M 1) = f (M 2), यह आसान है। जाली की रेखाओं के साथ निर्देशित पैरों के साथ किसी भी समकोण त्रिभुज के लिए पिक के सूत्र की वैधता को साबित करने के लिए। एक आयत से ऐसे कई त्रिभुजों को काटकर कोई भी त्रिभुज प्राप्त किया जा सकता है।

पिक के सूत्र के प्रमाण को पूरा करने के लिए, यह ध्यान रखना बाकी है कि किसी भी बहुभुज को अप्रतिच्छेदी विकर्णों द्वारा त्रिभुजों में काटा जा सकता है।
श्री का प्रमाण।
एक आकृति के क्षेत्र और इस आकृति में आने वाले नोड्स की संख्या के बीच संबंध एक आयत के मामले में विशेष रूप से स्पष्ट है।

रहने दो ऐ बी सी डी- ग्रिड लाइनों के साथ जाने वाले नोड्स और किनारों पर शिखर के साथ एक आयत।
द्वारा निरूपित करें परआयत के अंदर और इसके माध्यम से स्थित नोड्स की संख्या जीइसकी सीमा पर नोड्स की संख्या है। ग्रिड को आधा सेल दाईं ओर और आधा सेल नीचे ले जाएँ।

फिर आयत के क्षेत्र को नोड्स के बीच "वितरित" किया जा सकता है: प्रत्येक परनोड्स शिफ्ट किए गए ग्रिड के पूरे सेल को "नियंत्रित" करते हैं, जिनमें से प्रत्येक जी- 4 बाउंड्री नॉन-कॉर्नर नोड्स - सेल का आधा हिस्सा, और प्रत्येक कॉर्नर पॉइंट - सेल का एक चौथाई। अत: आयत S का क्षेत्रफल है

इसलिए, ग्रिड लाइनों के साथ जाने वाले नोड्स और किनारों पर कोने वाले आयतों के लिए, हमने सूत्र स्थापित किया है 
आइए हम साबित करें कि यह सूत्र न केवल आयतों के लिए, बल्कि ग्रिड नोड्स पर कोने वाले मनमाने बहुभुजों के लिए भी सही है।
द्वारा निरूपित करें एस
एम
बहुभुज क्षेत्रएम
नोड्स पर कोने के साथ, और के माध्यम सेपी
एम
- मूल्य  , कहाँ पेपर
एम
अंदर नोड्स की संख्या हैएम,ए जी
एम
सीमा पर नोड्स की संख्या है। तब पिक फॉर्मूला इस प्रकार लिखा जा सकता है
, कहाँ पेपर
एम
अंदर नोड्स की संख्या हैएम,ए जी
एम
सीमा पर नोड्स की संख्या है। तब पिक फॉर्मूला इस प्रकार लिखा जा सकता है  .
.
हम सूत्र के प्रमाण को कई चरणों में विभाजित करते हैं।
स्टेप 1।
अगर बहुभुजएम
ग्रिड नोड्स पर कोने के साथ 2 बहुभुजों में काटा जाता हैएम
1
और एम
2
,
केवल ग्रिड नोड्स पर भी शिखर होने पर  . चलो बहुभुजएम
बहुभुज में काटेंएम
1
और एम
2
एक खंड द्वारा नोड्स पर शिखर के साथएबी. खंड पर आने वाले को छोड़कर सभी नोड्सएबी,
सूत्र के बाएँ और दाएँ पक्षों को समान योगदान दें। खंड AB पर स्थित नोड्स पर विचार करें।
. चलो बहुभुजएम
बहुभुज में काटेंएम
1
और एम
2
एक खंड द्वारा नोड्स पर शिखर के साथएबी. खंड पर आने वाले को छोड़कर सभी नोड्सएबी,
सूत्र के बाएँ और दाएँ पक्षों को समान योगदान दें। खंड AB पर स्थित नोड्स पर विचार करें।

यदि ऐसा नोड ए और बी (उदाहरण के लिए, सी) के बीच स्थित है, तो बहुभुज के लिएएम
यह आंतरिक है, और बहुभुज के लिएएम
1
और एम
2
- सीमा। इसलिए, उनका योगदानपी
एम
1 के बराबर है, और प्रत्येक भाव में  और
और 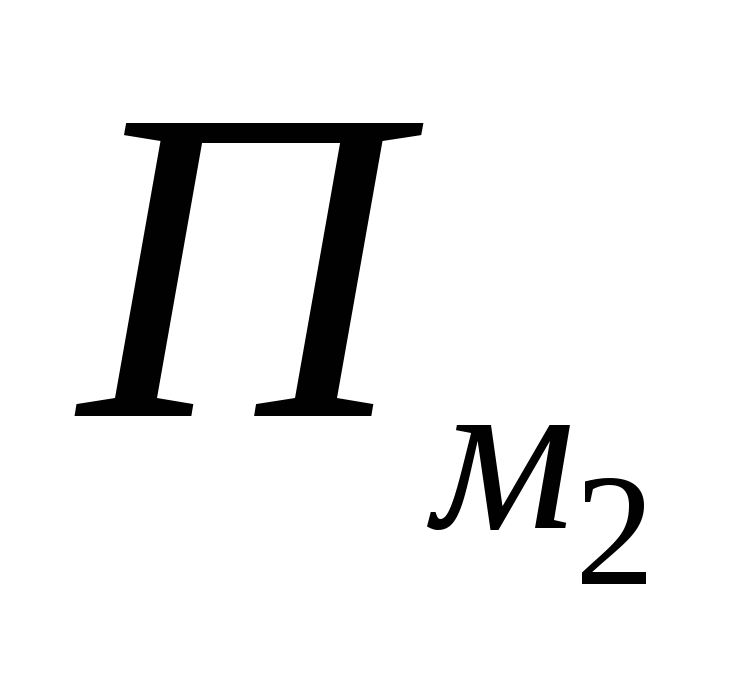 - 0.5 प्रत्येक, यानी ऐसे नोड का योगदानपी
एम
और
- 0.5 प्रत्येक, यानी ऐसे नोड का योगदानपी
एम
और  बराबर हैं।
बराबर हैं।
नोड्स ए और बी पर विचार करें। वे दोनों के लिए सीमा हैं एम, और के लिए एम 1 , एम 2 .
इसलिए, इनमें से प्रत्येक नोड का योगदानपी
एम
0.5 ए . है  -
इकाई। इसका मतलब है कि नोड्स ए और बी का कुल योगदानपी
एम
1 के बराबर है, जो उनके योगदान से 1 कम है
-
इकाई। इसका मतलब है कि नोड्स ए और बी का कुल योगदानपी
एम
1 के बराबर है, जो उनके योगदान से 1 कम है  .
लेकिन
.
लेकिन  , ए ।
, ए ।
सभी नोड्स के कुल "योगदान" से पी एम 1 से घटाया जाता है  2 घटाया जाता है, और यह नोड्स ए और बी के योगदान में अंतर के लिए क्षतिपूर्ति करता है।
2 घटाया जाता है, और यह नोड्स ए और बी के योगदान में अंतर के लिए क्षतिपूर्ति करता है।
इसलिए,  .
.
चरण 2
अगर बहुभुज एमग्रिड नोड्स पर कोने के साथ दो बहुभुजों में काटा जाता है एम 1 और एम 2 (नोड्स पर कोने के साथ भी) और सूत्र कुछ दो बहुभुजों के लिए सही है मिमी 1 , एम 2 , तो यह तीसरे बहुभुज के लिए भी सत्य है।
मान लीजिए, उदाहरण के लिए, यह सत्य हैएम
1
और एम
2
,
अर्थात  . फिर (पहले कदम पर),
लेकिन पर
पहला चरण), अंतिम अभिव्यक्ति बराबर हैपी
एम
,
और समानता
. फिर (पहले कदम पर),
लेकिन पर
पहला चरण), अंतिम अभिव्यक्ति बराबर हैपी
एम
,
और समानता  और पिक फॉर्मूला है।
और पिक फॉर्मूला है।
चरण 3
आइए हम एक समकोण त्रिभुज के लिए पिक सूत्र को सिद्ध करें जिसमें ग्रिड नोड्स और पैर ग्रिड लाइनों पर स्थित हों।
त्रिकोण एबीसीएक आयत बनाने के लिए ऐ बी सी डी .

आयतों के लिए, पिक का सूत्र सही है: एस ऐ बी सी डी = पी ऐ बी सी डी . पहले चरण के अनुसार पी ऐ बी सी डी = पी एबीसी + पी एसीडी , पी एबीसी = पी एसीडी , इसलिए पी ऐ बी सी डी = 2पी एबीसी . लेकिन एस ऐ बी सी डी = 2 एस एबीसी . इसलिए एस एबीसी = पी एबीसी .
चरण 4
ग्रिड नोड्स पर शिखर के साथ एक मनमाना त्रिभुज के लिए पिक का सूत्र सही है।

आकृति की जांच करने के बाद, यह समझना आसान है: इस तरह के किसी भी त्रिकोण को ग्रिड लाइनों के साथ चलने वाले पक्षों के साथ कुछ आयत से "काटकर" प्राप्त किया जा सकता है, कई आयत और ग्रिड लाइनों पर पैरों के साथ समकोण त्रिभुज। और चूँकि पिक का सूत्र आयतों और समकोण त्रिभुजों के लिए सत्य है, तो (चरण 2 याद रखें) यह मूल त्रिभुज के लिए भी सत्य है।
हमने साबित कर दिया है कि यदि बहुभुज को ग्रिड के नोड्स पर शीर्षों वाले त्रिभुजों में काटा जा सकता है, तो इसके लिए पिक का सूत्र सही है।
3. कार्य।
आंकड़ों का क्षेत्रफल ज्ञात कीजिए:
1
.



![]()
बी = 9
जी = 4
![]()



![]()
बी = 9
जी = 5




![]()
एक आकृति के क्षेत्र की गणना।
विधि चुनें
इरकुत्स्क . में कक्षा 5बी एमबीओयू सेकेंडरी स्कूल नंबर 23 के एक छात्र का काम
बालसुकोवा एलेक्जेंड्रा
प्रमुख: खोदरेवा टी.जी.
2014
एक आकृति के क्षेत्र की गणना। विधि चुनें
अध्ययन की वस्तु : चेकर पेपर पर कार्य
अध्ययन का विषय : चेकर पेपर पर बहुभुज के क्षेत्रफल की गणना के लिए समस्याएं, उन्हें हल करने के तरीके और तकनीक।
तलाश पद्दतियाँ कीवर्ड: तुलना, सामान्यीकरण, सादृश्य, साहित्य और इंटरनेट संसाधनों का अध्ययन, सूचना विश्लेषण।
इस अध्ययन का उद्देश्य:
मुख्य, रोचक, समझने योग्य जानकारी चुनें
प्राप्त जानकारी का विश्लेषण और व्यवस्थित करें
चेकर्ड पेपर पर समस्याओं को हल करने के लिए विभिन्न विधियों और तकनीकों का पता लगाएं
पीक फॉर्मूला का उपयोग करके ज्यामितीय आकृतियों के क्षेत्रों की गणना के लिए सूत्रों की जाँच करें
एकत्रित सामग्री को प्रस्तुत करने के लिए कार्य की इलेक्ट्रॉनिक प्रस्तुति बनाएं
ज्यामिति हमारे मानसिक संकायों के शोधन के लिए सबसे शक्तिशाली उपकरण है और हमें सही ढंग से सोचने और तर्क करने में सक्षम बनाती है।
(जी गैलीलियो)
विषय की प्रासंगिकता
गणित के प्रति जुनून की शुरुआत अक्सर किसी समस्या के बारे में सोचने से होती है। इसलिए, "बहुभुज के क्षेत्र" विषय का अध्ययन करते समय, प्रश्न उठता है कि क्या ऐसे कार्य हैं जो पाठ्यपुस्तक में माने गए कार्यों से भिन्न हैं। ऐसे कार्यों में चेकर पेपर पर कार्य शामिल हैं। ऐसी समस्याओं की ख़ासियत क्या है, क्या चेकर्ड पेपर पर समस्याओं को हल करने के लिए विशेष तरीके और तकनीकें हैं। गणित की एक कक्षा में, शिक्षक ने हमें बहुभुजों की गणना के लिए एक दिलचस्प विधि से परिचित कराया। मैंने इस विषय पर साहित्य, इंटरनेट संसाधनों का अध्ययन करना शुरू किया। ऐसा लगता है कि आकर्षक चीजें एक चेकर प्लेन पर पाई जा सकती हैं, यानी कागज के एक अंतहीन टुकड़े पर, समान वर्गों में पंक्तिबद्ध। यह पता चला है कि चेकर पेपर से जुड़े कार्य काफी विविध हैं। मैंने सीखा कि कागज के एक टुकड़े पर खींचे गए बहुभुजों के क्षेत्रों की गणना कैसे की जाती है। एक पिंजरे में कागज पर कई कार्यों के लिए हल करने, विशिष्ट तरीकों और तकनीकों के लिए कोई सामान्य नियम नहीं है। यह उनकी संपत्ति है जो एक विशिष्ट शैक्षिक कौशल या कौशल के विकास के लिए उनके मूल्य को निर्धारित नहीं करती है, लेकिन सामान्य रूप से सोचने, प्रतिबिंबित करने, विश्लेषण करने, समानता की तलाश करने की क्षमता, यानी ये कार्य अपने व्यापक अर्थों में सोच कौशल विकसित करते हैं।
और मैंने यह भी सीखा कि ऐसे कार्यों को जीआईए और एकीकृत राज्य परीक्षा के नियंत्रण और माप सामग्री में माना जाता है। इसलिए, मैं इस सामग्री के अध्ययन को न केवल आगे की शैक्षिक प्रक्रिया में, बल्कि गैर-मानक ओलंपियाड समस्याओं को हल करने के लिए भी उपयोगी मानता हूं।
2.क्षेत्र की अवधारणा
वर्ग- इस आकृति के आकार को दर्शाने वाली द्वि-आयामी ज्यामितीय आकृति की संख्यात्मक विशेषता। ऐतिहासिक रूप से, क्षेत्र गणना को कहा जाता था . वह आकृति जिसका क्षेत्रफल होता है, कहलाती है बराबरी .
ज्यामिति की दृष्टि से समतल आकृति का क्षेत्रफल
1. वर्ग- मानक आकृति के संबंध में एक सपाट आकृति का माप, जो एक वर्ग है जिसकी भुजा एक लंबाई के बराबर है।
2. वर्ग- एक निश्चित वर्ग (उदाहरण के लिए, बहुभुज) के सपाट आंकड़ों के लिए जिम्मेदार एक संख्यात्मक विशेषता। लंबाई की एक इकाई के बराबर भुजा वाले वर्ग का क्षेत्रफल, क्षेत्रफल की एक इकाई के बराबर लिया जाता है
3. वर्ग- एक सकारात्मक मूल्य, जिसके संख्यात्मक मूल्य में निम्नलिखित गुण हैं:
समान आकृतियों के क्षेत्रफल समान होते हैं;
यदि किसी आकृति को ऐसे भागों में विभाजित किया जाता है जो साधारण आकृतियाँ हैं (अर्थात, जिन्हें समतल त्रिभुजों की एक परिमित संख्या में विभाजित किया जा सकता है), तो इस आकृति का क्षेत्रफल इसके क्षेत्रफलों के योग के बराबर है भागों;
माप की इकाई के बराबर भुजा वाले वर्ग का क्षेत्रफल एक के बराबर होता है।
इस प्रकार, हम यह निष्कर्ष निकाल सकते हैं कि क्षेत्र एक विशिष्ट मूल्य नहीं है, लेकिन केवल एक सपाट आकृति की कुछ सशर्त विशेषता देता है। एक मनमाना आकृति का क्षेत्रफल ज्ञात करने के लिए, यह निर्धारित करना आवश्यक है कि लंबाई की एक इकाई के बराबर भुजा वाले कितने वर्ग हैं। उदाहरण के लिए, आइए एक आयत लें जिसमें एक वर्ग सेंटीमीटर ठीक 6 बार फिट बैठता है। इसका अर्थ है कि आयत का क्षेत्रफल 6 सेमी2 है।
सभी क्षेत्रों के लिए माप की न्यूनतम इकाई के रूप में माप की इकाई के बराबर एक वर्ग के क्षेत्र का चुनाव आकस्मिक नहीं है। यह लोगों के बीच एक समझौते का परिणाम है जो "प्राकृतिक" सदियों पुराने चयन के दौरान उत्पन्न हुआ था। इसके अलावा, माप की एक इकाई के लिए अन्य प्रस्ताव भी थे। इसलिए, उदाहरण के लिए, एक समबाहु त्रिभुज के क्षेत्रफल को ऐसी इकाई के रूप में लेने का प्रस्ताव किया गया था (अर्थात, किसी भी समतल आकृति को समबाहु त्रिभुजों की एक निश्चित संख्या के "योग" के रूप में दर्शाया जा सकता है), जिससे एक क्षेत्रों के संख्यात्मक प्रतिनिधित्व में परिवर्तन।
इस प्रकार, क्षेत्रों की गणना के सूत्र गणित में दिखाई दिए और किसी व्यक्ति द्वारा तुरंत महसूस नहीं किए गए - यह विभिन्न युगों और विभिन्न देशों में रहने वाले कई वैज्ञानिक। (गलत सूत्रों को विज्ञान में जगह नहीं मिली और वे गुमनामी में चले गए)। सच्चे फ़ार्मुलों को हज़ारों वर्षों में पूरक, सुधारा और प्रमाणित किया गया, जब तक कि वे अपने आधुनिक रूप में हम तक नहीं पहुँचे।
बेशक क्षेत्र मापमाप की एक इकाई के रूप में ली गई आकृति के क्षेत्रफल के साथ दी गई आकृति के क्षेत्रफल की तुलना करना शामिल है। तुलना के परिणामस्वरूप, एक निश्चित संख्या प्राप्त होती है - दिए गए आंकड़े के क्षेत्र का संख्यात्मक मान। यह संख्या दर्शाती है कि किसी दी गई आकृति का क्षेत्रफल क्षेत्रफल की इकाई के रूप में ली गई आकृति के क्षेत्रफल से कितनी गुना अधिक (या कम) है।
टी  इस प्रकार, हम यह निष्कर्ष निकाल सकते हैं कि क्षेत्र एक कृत्रिम मात्रा है, जिसे ऐतिहासिक रूप से मनुष्य द्वारा एक सपाट आकृति की कुछ संपत्ति को मापने के लिए पेश किया गया था। इस तरह के मूल्य को दर्ज करने की आवश्यकता यह जानने की बढ़ती आवश्यकता के कारण थी कि यह या वह क्षेत्र कितना बड़ा है, किसी खेत को बोने के लिए या सजावटी टाइलों को सजाने के लिए फर्श की सतह के क्षेत्रफल की गणना करने के लिए कितना अनाज चाहिए।
इस प्रकार, हम यह निष्कर्ष निकाल सकते हैं कि क्षेत्र एक कृत्रिम मात्रा है, जिसे ऐतिहासिक रूप से मनुष्य द्वारा एक सपाट आकृति की कुछ संपत्ति को मापने के लिए पेश किया गया था। इस तरह के मूल्य को दर्ज करने की आवश्यकता यह जानने की बढ़ती आवश्यकता के कारण थी कि यह या वह क्षेत्र कितना बड़ा है, किसी खेत को बोने के लिए या सजावटी टाइलों को सजाने के लिए फर्श की सतह के क्षेत्रफल की गणना करने के लिए कितना अनाज चाहिए।
पीक फॉर्मूला
चेकर पेपर पर बहुभुज के क्षेत्र का अनुमान लगाने के लिए, यह गणना करने के लिए पर्याप्त है कि यह बहुभुज कितनी कोशिकाओं को कवर करता है (हम एक इकाई के रूप में सेल के क्षेत्र को लेते हैं)। अधिक सटीक, अगरएस बहुभुज का क्षेत्र है, बी पूरी तरह से बहुभुज के अंदर स्थित कोशिकाओं की संख्या है, और जी उन कोशिकाओं की संख्या है जिनमें एक इंटीरियर है। हम केवल ऐसे बहुभुजों पर विचार करेंगे, जिनके सभी कोने चेकर्ड पेपर के नोड्स पर स्थित हैं - उनमें जहां बहुभुज ग्रिड लाइनें कम से कम एक सामान्य बिंदु को काटती हैं।
 चेकर पेपर पर खींचे गए किसी भी त्रिभुज के क्षेत्रफल को समकोण त्रिभुजों और आयतों के क्षेत्रफलों के योग या अंतर के रूप में प्रदर्शित करके आसानी से परिकलित किया जा सकता है, जिनकी भुजाएँ खींचे गए त्रिभुज के शीर्षों से गुजरने वाली ग्रिड रेखाओं का अनुसरण करती हैं।
चेकर पेपर पर खींचे गए किसी भी त्रिभुज के क्षेत्रफल को समकोण त्रिभुजों और आयतों के क्षेत्रफलों के योग या अंतर के रूप में प्रदर्शित करके आसानी से परिकलित किया जा सकता है, जिनकी भुजाएँ खींचे गए त्रिभुज के शीर्षों से गुजरने वाली ग्रिड रेखाओं का अनुसरण करती हैं।
ऐसे बहुभुज के क्षेत्रफल की गणना करने के लिए, आप निम्नलिखित प्रमेय का उपयोग कर सकते हैं:
प्रमेय . रहने दो - बहुभुज के अंदर पूर्णांक बिंदुओं की संख्या, - इसकी सीमा पर पूर्णांक बिंदुओं की संख्या, - इसका क्षेत्र। फिरचयन सूत्र:
उदाहरण। आकृति में बहुभुज के लिएली = 7 (लाल डॉट्स), 9 (हरे बिंदु), तोएस = 7+ 9/2 -1 = 10,5 वर्ग इकाइयों।

पिक का प्रमेय- क्लासिक परिणाम और .
एक त्रिभुज का क्षेत्रफल जिसमें नोड्स पर कोने होते हैं और जिसमें कोई नोड नहीं होता है या तो अंदर या किनारों पर (कोने को छोड़कर) 1/2 के बराबर होता है। इस तथ्य।
3. इतिहास
पिक के सूत्र की खोज ऑस्ट्रियाई गणितज्ञ जॉर्ज अलेक्जेंडर (1859-1942) ने की थी . 16 साल की उम्र में, जॉर्ज ने स्कूल की पढ़ाई पूरी की और प्रवेश किया. 20 साल की उम्र में उन्हें भौतिकी और गणित पढ़ाने का अधिकार मिला। 1884 में पीक गयाको . वहाँ उसकी मुलाकात क्लेन के एक अन्य छात्र से हुई,. बाद में, 1885 में, वह वापस आ गयाजहां उन्होंने अपना शेष वैज्ञानिक करियर बिताया।
जॉर्ज पिक आइंस्टीन के मित्र थे। पिक और आइंस्टीन ने न केवल वैज्ञानिक हितों को साझा किया, बल्कि संगीत के प्रति भी भावुक थे। पिक, जो एक चौकड़ी में खेलता था जिसमें विश्वविद्यालय के प्रोफेसर शामिल थे, ने आइंस्टीन को प्राग के वैज्ञानिक और संगीत समाजों से परिचित कराया।
पीक के गणितीय हितों का चक्र अत्यंत विस्तृत था। विशेष रूप से, उनके पास 50 से अधिक वैज्ञानिक पत्र हैं। 1899 में उनके द्वारा खोजी गई पिक की प्रमेय, बहुभुज के क्षेत्रफल की गणना के लिए व्यापक रूप से जानी जाती थी। जर्मनी में, यह प्रमेय स्कूली पाठ्यपुस्तकों में शामिल है।
4.पिक फॉर्मूला के अनुप्रयोग
पिक फॉर्मूला का उपयोग न केवल बहुभुज के क्षेत्रों की गणना के लिए किया जाता है, बल्कि ओलंपियाड स्तर की कई समस्याओं को हल करने के लिए भी किया जाता है।
समस्याओं को हल करते समय पिक के सूत्र का उपयोग करने के कुछ उदाहरण:
1) शतरंज के राजा ने 8 × 8 कोशिकाओं के बोर्ड का चक्कर लगाया, प्रत्येक का दौरा किया
होम फील्ड बिल्कुल एक बार और आखिरी चाल के साथ मूल पर लौटने के साथ
खेत। खेतों के केंद्रों को श्रृंखला में जोड़ने वाली एक टूटी हुई रेखा
राजा पारित हो गया, कोई आत्म-चौराहे नहीं है। कौन सा क्षेत्र कर सकते हैं
इस टूटी हुई रेखा को सीमित करें? (कोशिका की भुजा 1 है।)
यह पिक फॉर्मूला से तुरंत अनुसरण करता है कि लो- से घिरा क्षेत्र-
मान 64/2 - 1 = 31 है; यहाँ जाली नोड्स केंद्र हैं 64
क्षेत्र और, धारणा के अनुसार, वे सभी बहुभुज की सीमा पर स्थित हैं। इसलिए
इस प्रकार, हालांकि राजा के ऐसे "प्रक्षेपवक्र" काफी हैं, लेकिन उनमें से सभी
समान क्षेत्रफल वाले बहुभुजों को सीमित करें।
जीआईए और एकीकृत राज्य परीक्षा के नियंत्रण और माप सामग्री से कार्य
टास्क बी3
1 सेमी 1 सेमी के सेल आकार के साथ चेकर पेपर पर चित्रित आकृति का क्षेत्रफल ज्ञात करें (चित्र देखें)। अपना उत्तर वर्ग सेंटीमीटर में दें।

4। निष्कर्ष
शोध की प्रक्रिया में, मैंने संदर्भ, लोकप्रिय विज्ञान साहित्य का अध्ययन किया। मैंने सीखा कि ग्रिड के नोड्स पर कोने के साथ बहुभुज के क्षेत्र को खोजने की समस्या ने 1899 में ऑस्ट्रियाई गणितज्ञ पिक को अद्भुत पिक फॉर्मूला साबित करने के लिए प्रेरित किया।
अपने काम के परिणामस्वरूप, मैंने चेकर पेपर पर समस्याओं को हल करने के अपने ज्ञान का विस्तार किया, अपने लिए अध्ययन के तहत समस्याओं का वर्गीकरण निर्धारित किया, और उनकी विविधता के बारे में आश्वस्त हो गया।
मैंने सीखा कि एक चेकर शीट पर खींचे गए बहुभुजों के क्षेत्रों की गणना कैसे करें। माना कार्यों में कठिनाई का एक अलग स्तर है - सरल से ओलंपियाड तक। हर कोई उनमें से एक संभव स्तर की जटिलता के कार्य ढूंढ सकता है, जिससे शुरू होकर, अधिक कठिन लोगों को हल करने के लिए आगे बढ़ना संभव होगा।
मैं इस निष्कर्ष पर पहुंचा कि जिस विषय में मेरी दिलचस्पी है वह काफी बहुआयामी है, चेकर पेपर पर कार्य विविध हैं, उन्हें हल करने के तरीके और तकनीक भी विविध हैं। इसलिए, हमने इस दिशा में काम करना जारी रखने का फैसला किया।
5. प्रयुक्त साहित्य:
1. एन.बी. वासिलिव, "अराउंड द पिक फॉर्मूला," क्वांट। - 1974. - नंबर 12
2. कोकसे प्रसोलोव वीवी कार्य योजनामिति में। - एम.: एमटीएसएनएमओ, 2006. टी ई आर जी.एस.एम. ज्यामिति का परिचय। - एम.: नौका, 1966
3. रोस्लोवा एल.ओ., शैरगिन आई.एफ. माप। - एम .: एड। "ओपन वर्ल्ड", 2005।
इंटरनेट संसाधन:
:
काम पर प्रतिक्रिया
"विमान के आंकड़ों के क्षेत्रों की गणना। विधि चुनें"
इस विषय पर विचार करने से छात्र की संज्ञानात्मक गतिविधि में वृद्धि होगी, जो बाद में ज्यामिति के पाठों में ड्राइंग के सामंजस्य को देखना शुरू कर देगा और ज्यामिति (और सामान्य रूप से गणित) को एक उबाऊ विज्ञान के रूप में देखना बंद कर देगा।
गणित के शिक्षक द्वारा समीक्षित
खोदरेवा तात्याना जॉर्जीवना
एक अद्भुत सूत्र है जो आपको गिनने की अनुमति देता है बहुभुज क्षेत्रलगभग त्रुटियों के बिना समन्वय ग्रिड पर। यह एक सूत्र भी नहीं है, यह वास्तविक है प्रमेय. पहली नज़र में, यह जटिल लग सकता है। लेकिन यह कुछ कार्यों को हल करने के लिए पर्याप्त है - और आप समझेंगे कि यह सुविधा कितनी अच्छी है। तो आगे बढ़ो!
आइए एक नई परिभाषा के साथ शुरू करें:
एक समन्वय स्टैक नोड कोई भी बिंदु है जो इस ग्रिड की लंबवत और क्षैतिज रेखाओं के चौराहे पर स्थित है।
पद:
पहली तस्वीर में, नोड्स बिल्कुल भी चिह्नित नहीं हैं। दूसरे में 4 नोड होते हैं। अंत में, तीसरी तस्वीर में, सभी 16 नोड्स चिह्नित हैं।
इसका समस्या B5 से क्या लेना-देना है? तथ्य यह है कि ऐसी समस्याओं में बहुभुज के कोने हमेशाग्रिड के नोड्स पर झूठ। परिणामस्वरूप, निम्नलिखित प्रमेय उनके लिए कार्य करता है:
प्रमेय। एक समन्वय ग्रिड पर एक बहुभुज पर विचार करें जिसका शीर्ष इस ग्रिड के नोड्स पर स्थित है। तब बहुभुज का क्षेत्रफल है:
जहां n दिए गए बहुभुज के अंदर नोड्स की संख्या है, k इसकी सीमा (सीमा नोड्स) पर स्थित नोड्स की संख्या है।
एक उदाहरण के रूप में, एक समन्वय ग्रिड पर एक साधारण त्रिकोण पर विचार करें और आंतरिक और सीमा नोड्स को चिह्नित करने का प्रयास करें।

पहली तस्वीर एक साधारण त्रिकोण दिखाती है। दूसरी तस्वीर पर, इसके आंतरिक नोड्स चिह्नित हैं, जिनकी संख्या n = 10 है। तीसरी तस्वीर पर, सीमा पर स्थित नोड्स को चिह्नित किया गया है, उनमें से कुल k = 6 हैं।
शायद कई पाठक यह नहीं समझते हैं कि n और k की संख्या कैसे गिनें। आंतरिक नोड्स से शुरू करें। यहां सब कुछ स्पष्ट है: हम एक पेंसिल के साथ त्रिकोण पर पेंट करते हैं और देखते हैं कि कितने नोड्स छायांकित हैं।
सीमा नोड्स के साथ, यह थोड़ा और जटिल है। बहुभुज सीमा - बंद टूटी लाइन, जो समन्वय ग्रिड को कई बिंदुओं पर प्रतिच्छेद करता है। सबसे आसान तरीका है कि कुछ "शुरुआती" बिंदु को चिह्नित करें, और फिर बाकी के चारों ओर जाएं।
पॉलीलाइन पर केवल वे बिंदु होंगे जिन पर वे एक साथ प्रतिच्छेद करते हैं तीन पंक्तियाँ:
- दरअसल, एक टूटी हुई रेखा;
- क्षैतिज ग्रिड लाइन;
- ऊर्ध्वाधर रेखा।
आइए देखें कि वास्तविक समस्याओं में यह सब कैसे काम करता है।
काम। त्रिभुज का क्षेत्रफल ज्ञात कीजिए यदि कोशिका का आकार 1 x 1 सेमी है:
सबसे पहले, आइए उन नोड्स को चिह्नित करें जो त्रिभुज के अंदर और साथ ही इसकी सीमा पर स्थित हैं:

यह पता चला है कि केवल एक आंतरिक नोड है: n = 1. छह सीमा नोड हैं: तीन संयोग त्रिभुज के शीर्षों के साथ, और तीन और पक्षों पर झूठ बोलते हैं। कुल कश्मीर = 6.
अब हम सूत्र का उपयोग करके क्षेत्रफल की गणना करते हैं:
बस इतना ही! समस्या सुलझ गयी।
काम। 1 सेमी ब 1 सेमी के सेल आकार के साथ चेकर पेपर पर खींचे गए चतुर्भुज का क्षेत्रफल पाएं। अपना उत्तर वर्ग सेंटीमीटर में दें।
फिर से, हम आंतरिक और सीमा नोड्स को चिह्नित करते हैं। n = 2 आंतरिक नोड हैं। सीमा नोड्स: k = 7, जिनमें से 4 हैं चतुर्भुज के शीर्ष, और 3 और पक्षों पर झूठ बोलते हैं।

यह क्षेत्र सूत्र में संख्या n और k को प्रतिस्थापित करने के लिए बनी हुई है:
अंतिम उदाहरण पर ध्यान दें। यह समस्या वास्तव में 2012 में नैदानिक कार्य में प्रस्तावित की गई थी। यदि आप मानक योजना के अनुसार काम करते हैं, तो आपको बहुत सारे अतिरिक्त निर्माण करने होंगे। और गांठों की विधि से सब कुछ लगभग मौखिक रूप से हल हो जाता है।
क्षेत्रों पर महत्वपूर्ण नोट
लेकिन सूत्र ही सब कुछ नहीं है। आइए सूत्र को थोड़ा फिर से लिखते हैं, शब्दों को दाईं ओर लाते हैं एक आम भाजक के लिए. हम पाते हैं:
संख्या n और k नोड्स की संख्या हैं, वे हमेशा पूर्णांक होते हैं। अतः पूर्ण अंश भी एक पूर्णांक होता है। हम इसे 2 से विभाजित करते हैं, जिसका अर्थ है एक महत्वपूर्ण तथ्य:
क्षेत्र हमेशा व्यक्त किया जाता है पूर्ण संख्या या भिन्न. इसके अलावा, भिन्न के अंत में हमेशा "पांच दसवां" होता है: 10.5; 17.5 आदि
इस प्रकार, समस्या B5 में क्षेत्र को हमेशा एक पूर्णांक या ***.5 के रूप के एक अंश के रूप में व्यक्त किया जाता है। अगर उत्तर अलग है, तो इसका मतलब है कि कहीं गलती हुई है। गणित में असली परीक्षा देते समय इस बात का ध्यान रखें!
प्रस्तुतियों के पूर्वावलोकन का उपयोग करने के लिए, एक Google खाता (खाता) बनाएं और साइन इन करें: https://accounts.google.com
स्लाइड कैप्शन:
माध्यमिक विद्यालय नंबर 7 8 "ए" कक्षा के एक छात्र द्वारा पूरा किया गया यूनोशेवा केन्सिया प्रशिक्षक: बबीना नताल्या अलेक्सेवना साल्स्क 2011 "पीक फॉर्मूला"
कार्य के उद्देश्य: विद्यालय के पाठ्यक्रम से भिन्न, किसी अन्य के अस्तित्व का पता लगाना, एक जालक बहुभुज का क्षेत्रफल ज्ञात करने का सूत्र। वांछित सूत्र के आवेदन के क्षेत्र।
परिचय। सामान्य शिक्षा विद्यालयों में प्राप्त गणितीय शिक्षा सामान्य शिक्षा और आधुनिक मनुष्य की सामान्य संस्कृति का एक अनिवार्य घटक है। इस स्तर पर, स्कूल प्रणाली ग्यारह साल की शिक्षा के लिए डिज़ाइन की गई है। ग्यारहवीं कक्षा के अंत में सभी छात्रों को यूनिफाइड स्टेट परीक्षा देनी होगी, जो स्कूल में पढ़ते समय प्राप्त ज्ञान के स्तर को दर्शाएगी। लेकिन स्कूली पाठ्यक्रम हमेशा किसी भी समस्या को हल करने के लिए सबसे तर्कसंगत तरीके प्रदान नहीं करता है। उदाहरण के लिए, 2010 में यूनिफाइड स्टेट परीक्षा के परिणामों को देखते हुए, यह स्पष्ट है कि टास्क बी 6 के कारण कई छात्र अंक खो देते हैं। मैंने यह पता लगाने के लिए निर्धारित किया कि समय कैसे बचाया जाए और इस समस्या को सही तरीके से कैसे हल किया जाए।
टास्क B6. आंकड़े चेकर पेपर पर 1 सेमी गुणा 1 सेमी मापने वाली कोशिकाओं के साथ दर्शाए गए हैं (आंकड़ा देखें)। उनका क्षेत्रफल वर्ग सेंटीमीटर में ज्ञात कीजिए।
इसलिए, इस कार्य को अभी भी हल करने के लिए, मुझे उस क्षेत्र को खोजने के लिए सूत्रों को लागू करने की आवश्यकता है, जिसे हम कक्षा 8 में पढ़ते हैं। लेकिन इसमें बहुत समय लगेगा, और मुझे प्रश्न का उत्तर जल्द से जल्द देना होगा, क्योंकि परीक्षा के लिए समय सख्ती से सीमित है। इसलिए, शोध करने के बाद, मुझे पता चला कि पिक का प्रमेय है, जिसका स्कूली पाठ्यक्रम में अध्ययन नहीं किया जाता है, लेकिन जो मुझे कार्य को तेजी से करने में मदद करेगा।
इतिहास संदर्भ। जॉर्ज अलेक्जेंडर पिक (10 अगस्त, 1859 - 26 जुलाई, 1942) एक ऑस्ट्रियाई गणितज्ञ थे। टेरेज़िन एकाग्रता शिविर में उनकी मृत्यु हो गई। इसे आज बहुभुजों की एक जालक का क्षेत्रफल ज्ञात करने के पिक सूत्र के कारण जाना जाता है। उन्होंने 1899 में एक पेपर में अपना फॉर्मूला प्रकाशित किया, यह तब लोकप्रिय हुआ जब ह्यूगो स्टीनहॉस ने इसे 1969 के मैथमैटिकल पिक्चर्स के संस्करण में शामिल किया। पिक ने वियना विश्वविद्यालय में अध्ययन किया और 1880 में अपनी पीएचडी पूरी की। डॉक्टरेट की उपाधि प्राप्त करने के बाद, उन्हें प्राग में शेर्ल-फर्डिनेंड विश्वविद्यालय में अर्नेस्ट मच का सहायक नियुक्त किया गया। वे 1881 में वहां शिक्षक बने। 1884 में विश्वविद्यालय से अनुपस्थिति की छुट्टी लेते हुए, उन्होंने लीपज़िग विश्वविद्यालय में फेलिक्स क्लेन के साथ काम करना शुरू किया। वह 1927 में अपनी सेवानिवृत्ति तक प्राग में रहे, जब वे वियना लौट आए। पिक ने (तत्कालीन) प्राग के जर्मन विश्वविद्यालय में समिति की अध्यक्षता की जिसने 1911 में अल्बर्ट आइंस्टीन को गणितीय भौतिकी के प्रोफेसर नियुक्त किया। पिक को चेक एकेडमी ऑफ साइंसेज एंड आर्ट्स का सदस्य चुना गया था, लेकिन प्राग के नाजी अधिग्रहण के बाद उन्हें निष्कासित कर दिया गया था। 1927 में सेवानिवृत्त होने के बाद, पिक वियना लौट आए, जिस शहर में उनका जन्म हुआ था। Anschluss के बाद, जब 12 मार्च, 1938 को नाजियों ने ऑस्ट्रिया में प्रवेश किया, तो पाइक प्राग लौट आया। मार्च 1939 में, नाजियों ने चेकोस्लोवाकिया पर आक्रमण किया। जॉर्ज को 13 जुलाई, 1942 को टेरेज़िन एकाग्रता शिविर में भेजा गया था। दो सप्ताह बाद उनकी मृत्यु हो गई।
पिक का प्रमेय। पिक का प्रमेय संयोजक ज्यामिति और संख्याओं की ज्यामिति का शास्त्रीय परिणाम है। पूर्णांक शीर्षों वाले बहुभुज का क्षेत्रफल B + D/2 - 1 के योग के बराबर होता है, जहाँ B बहुभुज के अंदर पूर्णांक बिंदुओं की संख्या है, और D बहुभुज की सीमा पर पूर्णांक बिंदुओं की संख्या है।
पिक के प्रमेय का एक चापलूसी प्रमाण। इस तरह के किसी भी बहुभुज को आसानी से त्रिभुजों में विभाजित किया जा सकता है जिसमें जाली के नोड्स पर शिखर होते हैं, जिसमें अंदर या किनारों पर कोई नोड नहीं होता है। यह दिखाया जा सकता है कि इन सभी त्रिभुजों के क्षेत्रफल समान हैं और 1/2 के बराबर हैं, और इसलिए, बहुभुज का क्षेत्रफल उनकी संख्या T के आधे के बराबर है। इस संख्या को खोजने के लिए, हम n द्वारा निरूपित करते हैं बहुभुज के पक्षों की संख्या, i द्वारा - इसके अंदर नोड्स की संख्या और b द्वारा - किनारों पर नोड्स की संख्या, कोने सहित। सभी त्रिभुजों के कोणों का योग होता है। आइए अब इस राशि को दूसरे तरीके से खोजें। किसी भी आंतरिक नोड पर एक शीर्ष के साथ कोणों का योग 2 है, यानी ऐसे कोणों का कुल योग 2 i है; पक्षों पर नोड्स पर कोणों का कुल योग, लेकिन शिखर पर नहीं, (बी - एन) है, और बहुभुज के शीर्षों पर कोणों का योग (एन - 2) है। इस प्रकार, टी \u003d 2i π + (बी - एन) π + (एन - 2) , जिससे हम बहुभुज के क्षेत्र एस के लिए एक अभिव्यक्ति प्राप्त करते हैं, जिसे पिक के सूत्र के रूप में जाना जाता है। उदाहरण के लिए, आकृति में b = 9, i = 24, और इसलिए बहुभुज का क्षेत्रफल 27.5 है।
आवेदन पत्र। तो, कार्य B6 पर वापस। अब नए सूत्र को जानकर हम इस चतुर्भुज का क्षेत्रफल आसानी से ज्ञात कर सकते हैं। चूंकि बी 5 है; डी - 14, फिर 5 + 14: 2-1 \u003d 11 (सेमी वर्ग) इस चतुर्भुज का क्षेत्रफल 11 सेमी वर्ग है।
उसी सूत्र का उपयोग करके, हम एक त्रिभुज का क्षेत्रफल ज्ञात कर सकते हैं। चूँकि B-14, G-10, तो 14+10:2-1=18 (वर्ग सेमी) इस त्रिभुज का क्षेत्रफल 18 सेमी वर्ग है।
यदि B-9, D-12, तो: 9+12:2-1=14 (वर्ग सेमी) इस चतुर्भुज का क्षेत्रफल 14 सेमी वर्ग है।
सूत्र का दायरा। इस तथ्य के अलावा कि विभिन्न प्रकार की परीक्षाओं, असाइनमेंट आदि में सूत्र का उपयोग किया जाता है, यह हमारे आस-पास की पूरी दुनिया के साथ होता है।
पीक के सूत्र के अनुसार S = B + ½ G-1 1) शरीर B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) पूंछ B=0, G=8, एस= 0 +½ 8 -1= 3 3) एस= 21+3=24
पीक के सूत्र S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10.5-1 \u003d 45.5 के अनुसार
निष्कर्ष। नतीजतन, मैं इस निष्कर्ष पर पहुंचा कि क्षेत्र की समस्याओं को हल करने के कई अलग-अलग तरीके हैं जिनका स्कूली पाठ्यक्रम में अध्ययन नहीं किया गया है, और उदाहरण के रूप में उन्हें चुनें सूत्र का उपयोग करके दिखाया।
निर्देशिका। स्व-चौराहों के बिना बहुभुज को एक जाली बहुभुज कहा जाता है यदि इसके सभी कोने पूर्णांक निर्देशांक (कार्टेशियन समन्वय प्रणाली में) वाले बिंदुओं पर हों। निर्देशांक तल में एक बिंदु पूर्णांक कहलाता है यदि इसके दोनों निर्देशांक पूर्णांक हों।

