द्विघात समीकरण का आलेखीय समाधान विभिन्न कार्यों के ग्राफ़ बनाने की क्षमता को समेकित करना; द्विघात समीकरणों को आलेखीय रूप से हल करने की क्षमता का निर्माण करना। "फ़ंक्शन के ग्राफ़ का परिवर्तन" विषय पर प्रोजेक्ट

द्विघात समीकरण का आलेखीय समाधान विभिन्न कार्यों के ग्राफ़ बनाने की क्षमता को समेकित करना; द्विघात समीकरणों को आलेखीय रूप से हल करने की क्षमता का निर्माण करना। Brdsk 2009 नगर शैक्षणिक संस्थान - आर्थिक लिसेयुम "द्विघात समारोह" विषय पर पाठ का सामान्यीकरण, बीजगणित ग्रेड 8 शिक्षक फेडोसेवा टी.एम.

द्विघात फलन का आलेखन शाखाओं की दिशा निर्धारित करें: a>0 शाखाएं ऊपर; ए 0 शाखाएं ऊपर; ए"> 0 शाखाएं ऊपर; ए"> 0 शाखाएं ऊपर; a" title="(!LANG:एक द्विघात फ़ंक्शन को प्लॉट करना शाखा दिशा निर्धारित करें: a>0 शाखाएं ऊपर; a"> title="द्विघात फलन का आलेखन शाखाओं की दिशा निर्धारित करें: a>0 शाखाएं ऊपर; ए"> !}

0 शाखाएं ऊपर की ओर निर्देशित होती हैं; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। बिंदु "शीर्षक ="(!LANG: आइए एल्गोरिथ्म का उपयोग करके y=x 2 -2x-3 फ़ंक्शन का एक ग्राफ बनाएं: 1) a=1>0 शाखाओं को ऊपर की ओर निर्देशित किया जाता है; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। एक बिंदु ढूँढना" class="link_thumb"> 3 !}आइए एल्गोरिथ्म का उपयोग करके y=x 2 -2x-3 फ़ंक्शन का एक ग्राफ बनाएं: 1) a=1>0 शाखाओं को ऊपर की ओर निर्देशित किया जाता है; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। हम OX अक्ष के साथ प्रतिच्छेदन बिंदु पाते हैं: x 1 \u003d -1; x 2 \u003d 3 1 समीकरण को हल करने का तरीका x 2 -2x-3 \u003d 0 y x समीकरण को हल करें x 2 +2x-3 \u003d 0 0 शाखाएं ऊपर की ओर निर्देशित होती हैं; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। हम बिंदु पाते हैं "\u003e 0 शाखाएं ऊपर की ओर निर्देशित होती हैं; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - अक्ष परवलय के नियंत्रण बिंदु: (0: -3) , (3; 0) और x = 1 अक्ष के बारे में सममित हम एक परवलय का निर्माण करते हैं। OX अक्ष के साथ चौराहे के बिंदु खोजें: x 1 \u003d -1; x 2 \u003d 3 1 समीकरण को हल करने का तरीका x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 समीकरण को हल करें x 2 + 2x-3 \u003d 0 "\u003e 0 शाखाएं ऊपर की ओर निर्देशित हैं; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। बिंदु "शीर्षक ="(!LANG: आइए एल्गोरिथ्म का उपयोग करके y=x 2 -2x-3 फ़ंक्शन का एक ग्राफ बनाएं: 1) a=1>0 शाखाओं को ऊपर की ओर निर्देशित किया जाता है; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। एक बिंदु ढूँढना"> title="आइए एल्गोरिथ्म का उपयोग करके y=x 2 -2x-3 फ़ंक्शन का एक ग्राफ बनाएं: 1) a=1>0 शाखाओं को ऊपर की ओर निर्देशित किया जाता है; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। एक बिंदु ढूँढना"> !}

दूसरा तरीका: ए)। आइए समीकरण x 2 -2x-3=0 को भागों में विभाजित करें x 2 = 2x+3 आइए दो फलन y= x 2 लिखें; y \u003d 2x + 3 हम एक समन्वय प्रणाली में इन कार्यों के रेखांकन बनाते हैं। प्रतिच्छेदन बिंदुओं के भुज समीकरण के मूल हैं। 0 1 x y समीकरण को हल करें x 2 +2x-3=0

तीसरा तरीका: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x हम एक समन्वय प्रणाली में इन कार्यों के ग्राफ बनाते हैं। प्रतिच्छेदन बिंदुओं के भुज समीकरण के मूल हैं। 0 1 x y समीकरण को हल करें x 2 +2x-3=0

समीकरणों का आलेखीय हल

सुनहरे दिन, 2009

परिचय

प्राचीन काल में द्विघात समीकरणों को हल करने की आवश्यकता एक सैन्य प्रकृति के भूमि और भूकंप के क्षेत्रों को खोजने के साथ-साथ खगोल विज्ञान और गणित के विकास से संबंधित समस्याओं को हल करने की आवश्यकता के कारण हुई थी। बेबीलोन के लोग लगभग 2000 ईसा पूर्व के द्विघात समीकरणों को हल करना जानते थे। बेबीलोन के ग्रंथों में वर्णित इन समीकरणों को हल करने का नियम अनिवार्य रूप से आधुनिक लोगों के साथ मेल खाता है, लेकिन यह ज्ञात नहीं है कि बेबीलोन के लोग इस नियम पर कैसे आए।

यूरोप में द्विघात समीकरणों को हल करने के सूत्र सबसे पहले 1202 में इतालवी गणितज्ञ लियोनार्डो फिबोनाची द्वारा लिखी गई पुस्तक अबेकस में निर्धारित किए गए थे। उनकी पुस्तक ने न केवल इटली में, बल्कि जर्मनी, फ्रांस और अन्य यूरोपीय देशों में भी बीजीय ज्ञान के प्रसार में योगदान दिया।

लेकिन गुणांक बी और सी के सभी संभावित संयोजनों के साथ द्विघात समीकरणों को हल करने के लिए सामान्य नियम, यूरोप में केवल 1544 में एम। स्टीफेल द्वारा तैयार किया गया था।

1591 में फ़्राँस्वा वियत द्विघात समीकरणों को हल करने के लिए सूत्र प्रस्तुत किए।

प्राचीन बेबीलोन में कुछ प्रकार के द्विघात समीकरणों को हल किया जा सकता था।

अलेक्जेंड्रिया के डायोफैंटस और यूक्लिड , अल-ख्वारिज्मीऔर उमर खय्यामज्यामितीय और चित्रमय तरीकों से हल किए गए समीकरण।

7वीं कक्षा में हमने कार्यों का अध्ययन किया वाई \u003d सी, वाई = केएक्स , वाई = केएक्स + एम , वाई = एक्स 2 ,वाई = - एक्स 2 , आठवीं कक्षा में - वाई = एक्स , वाई = |एक्स |, वाई = कुल्हाड़ी 2 + बीएक्स + सी , वाई = क / एक्स. 9वीं कक्षा के बीजगणित पाठ्यपुस्तक में, मैंने ऐसे कार्य देखे जो अभी तक मुझे ज्ञात नहीं थे: वाई = एक्स 3 , वाई = एक्स 4 ,वाई = एक्स 2 एन , वाई = एक्स - 2 एन , वाई = 3 √एक्स , ( एक्स – ए ) 2 + (वाई - बी ) 2 = आर 2 और अन्य। इन कार्यों के रेखांकन बनाने के नियम हैं। मैं सोच रहा था कि क्या ऐसे अन्य कार्य हैं जो इन नियमों का पालन करते हैं।

मेरा काम कार्यों के ग्राफ का अध्ययन करना और समीकरणों को ग्राफिक रूप से हल करना है।

1. कार्य क्या हैं

फ़ंक्शन का ग्राफ़ समन्वय विमान के सभी बिंदुओं का समूह है, जिनमें से एब्सिसास तर्कों के मूल्यों के बराबर हैं, और निर्देशांक फ़ंक्शन के संबंधित मानों के बराबर हैं।

रैखिक कार्य समीकरण द्वारा दिया गया है वाई = केएक्स + बी, कहाँ पे कऔर बी- कुछ नंबर। इस फ़ंक्शन का आलेख एक सीधी रेखा है।

उलटा आनुपातिक कार्य वाई = क / एक्स, जहां k¹ 0. इस फलन के ग्राफ को अतिपरवलय कहते हैं।

समारोह ( एक्स – ए ) 2 + (वाई - बी ) 2 = आर 2 , कहाँ पे ए , बीऔर आर- कुछ नंबर। इस फलन का आलेख बिन्दु A पर केन्द्रित त्रिज्या r का एक वृत्त है। ए , बी).

द्विघात फंक्शन आप = कुल्हाड़ी 2 + बीएक्स + सीकहाँ पे ए, बी , साथ- कुछ नंबर और ए 0. इस फलन का आलेख एक परवलय है।

समीकरण वाई 2 ( ए – एक्स ) = एक्स 2 ( ए + एक्स ) . इस समीकरण का ग्राफ एक वक्र होगा जिसे स्ट्रोफॉइड कहा जाता है।

समीकरण ( एक्स 2 + आप 2 ) 2 = ए ( एक्स 2 – आप 2 ) . इस समीकरण के ग्राफ को बर्नौली लेम्निस्केट कहा जाता है।

समीकरण। इस समीकरण के ग्राफ को एस्ट्रोइड कहते हैं।

वक्र (एक्स 2 वाई 2 - 2 ए एक्स) 2 \u003d 4 ए 2 (एक्स 2 + वाई 2). इस वक्र को कार्डियोइड कहा जाता है।

कार्य: वाई = एक्स 3 - घन परवलय, वाई = एक्स 4 , वाई = 1/ एक्स 2 .

2. एक समीकरण की अवधारणा, उसका आलेखीय हल

समीकरणएक चर युक्त अभिव्यक्ति है।

प्रश्न हल करें- इसका अर्थ है इसकी सभी जड़ों को खोजना, या यह साबित करना कि वे मौजूद नहीं हैं।

समीकरण का मूलएक संख्या है, जिसे समीकरण में प्रतिस्थापित करने पर सही संख्यात्मक समानता उत्पन्न होती है।

समीकरणों को आलेखीय रूप से हल करनाआपको जड़ों का सटीक या अनुमानित मूल्य खोजने की अनुमति देता है, आपको समीकरण की जड़ों की संख्या खोजने की अनुमति देता है।

ग्राफ़ बनाते समय और समीकरणों को हल करते समय, फ़ंक्शन के गुणों का उपयोग किया जाता है, इसलिए इस विधि को अक्सर कार्यात्मक-ग्राफ़िक कहा जाता है।

समीकरण को हल करने के लिए, हम इसे दो भागों में "विभाजित" करते हैं, दो कार्यों का परिचय देते हैं, उनके ग्राफ़ बनाते हैं, ग्राफ़ के प्रतिच्छेदन बिंदुओं के निर्देशांक पाते हैं। इन बिंदुओं के भुज समीकरण के मूल हैं।

3. किसी फलन का आलेख बनाने के लिए एल्गोरिथम

फलन का ग्राफ जानना वाई = एफ ( एक्स ) , आप कार्यों की साजिश कर सकते हैं वाई = एफ ( एक्स + एम ) ,वाई = एफ ( एक्स )+ मैंऔर वाई = एफ ( एक्स + एम )+ मैं. ये सभी ग्राफ़ फ़ंक्शन के ग्राफ़ से प्राप्त किए गए हैं वाई = एफ ( एक्स ) समानांतर अनुवाद परिवर्तन का उपयोग करना: on │ एम │ x-अक्ष के अनुदिश दाएँ या बाएँ स्केल इकाइयाँ और on │ मैं │ स्केल इकाइयों को अक्ष के साथ ऊपर या नीचे आप .

4. द्विघात समीकरण का आलेखीय हल

द्विघात फलन के उदाहरण का उपयोग करते हुए, हम द्विघात समीकरण के आलेखीय हल पर विचार करेंगे। द्विघात फलन का आलेख एक परवलय होता है।

प्राचीन यूनानियों को परवलय के बारे में क्या पता था?

आधुनिक गणितीय प्रतीकवाद की उत्पत्ति 16वीं शताब्दी में हुई थी।

प्राचीन यूनानी गणितज्ञों के पास न तो समन्वय विधि थी और न ही किसी फलन की अवधारणा। हालांकि, परवलय के गुणों का उनके द्वारा विस्तार से अध्ययन किया गया था। प्राचीन गणितज्ञों की आविष्कारशीलता बस आश्चर्यजनक है, क्योंकि वे केवल चित्र और निर्भरता के मौखिक विवरण का उपयोग कर सकते थे।

सबसे अधिक पूरी तरह से परवलय, अतिपरवलय और दीर्घवृत्त का पता लगाया पेर्गा का अपोलोनियस, जो तीसरी शताब्दी ईसा पूर्व में रहते थे। उन्होंने इन वक्रों को नाम भी दिए और संकेत दिया कि एक विशेष वक्र पर स्थित बिंदु किन स्थितियों को संतुष्ट करते हैं (आखिरकार, कोई सूत्र नहीं थे!)

एक परवलय के निर्माण के लिए एक एल्गोरिथ्म है:

हम परवलय A (x 0; y 0) के शीर्ष के निर्देशांक पाते हैं: एक्स 0 = - बी /2 ए ;

वाई 0 \u003d कुल्हाड़ी लगभग 2 + 0 + सी में;

हम परवलय की समरूपता की धुरी पाते हैं (सीधी रेखा x \u003d x 0);

नियंत्रण बिंदुओं के निर्माण के लिए मूल्यों की एक तालिका संकलित करना;

हम प्राप्त बिंदुओं का निर्माण करते हैं और सममिति की धुरी के संबंध में उनके सममित बिंदुओं का निर्माण करते हैं।

1. आइए एल्गोरिथम के अनुसार एक परवलय का निर्माण करें आप = एक्स 2 – 2 एक्स – 3 . अक्ष के साथ प्रतिच्छेदन बिंदुओं का भुज एक्सऔर द्विघात समीकरण के मूल हैं एक्स 2 – 2 एक्स – 3 = 0.

इस समीकरण को आलेखीय रूप से हल करने के पाँच तरीके हैं।

2. आइए समीकरण को दो कार्यों में विभाजित करें: आप = एक्स 2 और आप = 2 एक्स + 3

3. आइए समीकरण को दो कार्यों में विभाजित करें: आप = एक्स 2 –3 और आप =2 एक्स. समीकरण की जड़ें रेखा के साथ परवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

4. समीकरण को रूपांतरित करें एक्स 2 – 2 एक्स – 3 = 0 फ़ंक्शन पर पूर्ण वर्ग का चयन करके: आप = ( एक्स –1) 2 और आप =4. समीकरण की जड़ें रेखा के साथ परवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

5. हम पद को समीकरण के दोनों भागों से विभाजित करते हैं एक्स 2 – 2 एक्स – 3 = 0 पर एक्स, हम पाते हैं एक्स – 2 – 3/ एक्स = 0 आइए इस समीकरण को दो कार्यों में विभाजित करें: आप = एक्स – 2, आप = 3/ एक्स . समीकरण की जड़ें रेखा और अतिपरवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

5. डिग्री समीकरणों का आलेखीय समाधान एन

उदाहरण 1प्रश्न हल करें एक्स 5 = 3 – 2 एक्स .

आप = एक्स 5 , आप = 3 – 2 एक्स .

जवाब:एक्स = 1.

उदाहरण 2प्रश्न हल करें 3 √ एक्स = 10 – एक्स .

इस समीकरण की जड़ें दो कार्यों के रेखांकन के प्रतिच्छेदन बिंदु का भुज है: आप = 3 √ एक्स , आप = 10 – एक्स .

जवाब:एक्स = 8।

निष्कर्ष

फ़ंक्शन ग्राफ़ को ध्यान में रखते हुए: वाई = कुल्हाड़ी 2 + बीएक्स + सी , वाई = क / एक्स , वाई = एक्स , वाई = |एक्स |, वाई = एक्स 3 , वाई = एक्स 4 ,वाई = 3 √एक्स , मैंने देखा कि ये सभी ग्राफ अक्षों के सापेक्ष समानांतर अनुवाद के नियम के अनुसार बनाए गए हैं एक्सऔर आप .

द्विघात समीकरण को हल करने के उदाहरण का उपयोग करते हुए, हम यह निष्कर्ष निकाल सकते हैं कि आलेखीय विधि डिग्री n के समीकरणों पर भी लागू होती है।

समीकरणों को हल करने के लिए चित्रमय तरीके सुंदर और समझने योग्य हैं, लेकिन वे किसी भी समीकरण को हल करने की 100% गारंटी नहीं देते हैं। रेखांकन के प्रतिच्छेदन बिंदुओं के भुज अनुमानित हो सकते हैं।

9वीं कक्षा में और वरिष्ठ कक्षाओं में, मैं अभी भी अन्य कार्यों से परिचित होऊंगा। मुझे यह जानने में दिलचस्पी है कि क्या वे कार्य समानांतर अनुवाद के नियमों का पालन करते हैं, जब उनके रेखांकन की साजिश रचते हैं।

अगले साल मैं समीकरणों और असमानताओं की प्रणालियों के ग्राफिकल समाधान के मुद्दों पर भी विचार करना चाहता हूं।

साहित्य

1. बीजगणित। 7 वीं कक्षा। भाग 1. शैक्षणिक संस्थानों के लिए पाठ्यपुस्तक / ए.जी. मोर्दकोविच। मॉस्को: मेनेमोसिन, 2007।

2. बीजगणित। 8 वीं कक्षा। भाग 1. शैक्षणिक संस्थानों के लिए पाठ्यपुस्तक / ए.जी. मोर्दकोविच। मॉस्को: मेनेमोसिन, 2007।

3. बीजगणित। श्रेणी 9 भाग 1. शैक्षणिक संस्थानों के लिए पाठ्यपुस्तक / ए.जी. मोर्दकोविच। मॉस्को: मेनेमोसिन, 2007।

4. ग्लेज़र जी.आई. स्कूल में गणित का इतिहास। सातवीं-आठवीं कक्षा। - एम .: ज्ञानोदय, 1982।

5. जर्नल गणित 5 2009; नंबर 8 2007; नंबर 23 2008।

6. समीकरणों का ग्राफिक समाधान इंटरनेट साइट्स: Tol WIKI; स्टिमुल.बिज़/एन; wiki.iot.ru/images; berdsk.edu; पेग 3–6.htm।

समीकरणों का आलेखीय हल

सुनहरे दिन, 2009

परिचय

प्राचीन बेबीलोन में कुछ प्रकार के द्विघात समीकरणों को हल किया जा सकता था।

अलेक्जेंड्रिया के डायोफैंटस और यूक्लिड, अल-ख्वारिज्मीऔर उमर खय्यामज्यामितीय और चित्रमय तरीकों से हल किए गए समीकरण।

7वीं कक्षा में हमने कार्यों का अध्ययन किया वाई \u003d सी, वाई =केएक्स, वाई =केएक्स+ एम, वाई =एक्स 2,वाई = -एक्स 2, आठवीं कक्षा में - वाई =एक्स, वाई =|एक्स|, वाई =कुल्हाड़ी2 + बीएक्स+ सी, वाई =क/ एक्स. 9वीं कक्षा के बीजगणित पाठ्यपुस्तक में, मैंने ऐसे कार्य देखे जो अभी तक मुझे ज्ञात नहीं थे: वाई =एक्स 3, वाई =एक्स 4,वाई =एक्स 2एन, वाई =एक्स- 2एन, वाई = 3√एक्स, (एक्स– ए) 2 + (वाई -बी) 2 = आर 2 और अन्य। इन कार्यों के रेखांकन बनाने के नियम हैं। मैं सोच रहा था कि क्या ऐसे अन्य कार्य हैं जो इन नियमों का पालन करते हैं।

1. कार्य क्या हैं

रैखिक कार्य समीकरण द्वारा दिया गया है वाई =केएक्स+ बी, कहाँ पे कऔर बी- कुछ नंबर। इस फ़ंक्शन का आलेख एक सीधी रेखा है।

उलटा आनुपातिक कार्य वाई =क/ एक्स, जहाँ k 0. इस फलन के ग्राफ को अतिपरवलय कहते हैं।

समारोह (एक्स– ए) 2 + (वाई -बी) 2 = आर2 , कहाँ पे ए, बीऔर आर- कुछ नंबर। इस फलन का आलेख बिन्दु A पर केन्द्रित त्रिज्या r का एक वृत्त है। ए, बी).

द्विघात फंक्शन आप= कुल्हाड़ी2 + बीएक्स+ सीकहाँ पे ए,बी, साथ- कुछ नंबर और ए 0. इस फलन का आलेख एक परवलय है।

समीकरण पर2 (ए– एक्स) = एक्स2 (ए+ एक्स) . इस समीकरण का ग्राफ एक वक्र होगा जिसे स्ट्रोफॉइड कहा जाता है।

/>समीकरण (एक्स2 + आप2 ) 2 = ए(एक्स2 – आप2 ) . इस समीकरण के ग्राफ को बर्नौली लेम्निस्केट कहा जाता है।

समीकरण। इस समीकरण के ग्राफ को एस्ट्रोइड कहते हैं।

वक्र (एक्स2 आप2 - 2 एक्स)2 =4 ए2 (एक्स2 +y2 ) . इस वक्र को कार्डियोइड कहा जाता है।

कार्य: वाई =एक्स 3 - घन परवलय, वाई =एक्स 4, वाई = 1/एक्स 2.

2. एक समीकरण की अवधारणा, उसका आलेखीय हल

समीकरणएक चर युक्त अभिव्यक्ति है।

3. किसी फलन का आलेख बनाने के लिए एल्गोरिथम

फलन का ग्राफ जानना वाई =एफ(एक्स) , आप कार्यों की साजिश कर सकते हैं वाई =एफ(एक्स+ एम) ,वाई =एफ(एक्स)+ मैंऔर वाई =एफ(एक्स+ एम)+ मैं. ये सभी ग्राफ़ फ़ंक्शन के ग्राफ़ से प्राप्त किए गए हैं वाई =एफ(एक्स) समानांतर अनुवाद परिवर्तन का उपयोग करना: on │ एम│ x-अक्ष के अनुदिश दाएँ या बाएँ स्केल इकाइयाँ और on │ मैं│ स्केल इकाइयों को अक्ष के साथ ऊपर या नीचे आप.

4. द्विघात समीकरण का आलेखीय हल

प्राचीन यूनानियों को परवलय के बारे में क्या पता था?

आधुनिक गणितीय प्रतीकवाद की उत्पत्ति 16वीं शताब्दी में हुई थी।

एक परवलय के निर्माण के लिए एक एल्गोरिथ्म है:

परवलय A (x0; y0) के शीर्ष के निर्देशांक ज्ञात कीजिए: एक्स=- बी/2 ए;

y0=aho2+in0+s;

परवलय की सममिति का अक्ष ज्ञात कीजिए (सीधी रेखा x=x0);

पृष्ठ ब्रेक--

नियंत्रण बिंदुओं के निर्माण के लिए मूल्यों की एक तालिका संकलित करना;

1. आइए एल्गोरिथम के अनुसार एक परवलय का निर्माण करें आप= एक्स2 – 2 एक्स– 3 . अक्ष के साथ प्रतिच्छेदन बिंदुओं का भुज एक्सऔर द्विघात समीकरण के मूल हैं एक्स2 – 2 एक्स– 3 = 0.

इस समीकरण को आलेखीय रूप से हल करने के पाँच तरीके हैं।

2. आइए समीकरण को दो कार्यों में विभाजित करें: आप= एक्स2 और आप= 2 एक्स+ 3

3. आइए समीकरण को दो कार्यों में विभाजित करें: आप= एक्स2 –3 और आप=2 एक्स. समीकरण की जड़ें रेखा के साथ परवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

4. समीकरण को रूपांतरित करें एक्स2 – 2 एक्स– 3 = 0 फ़ंक्शन पर पूर्ण वर्ग का चयन करके: आप= (एक्स–1) 2 और आप=4. समीकरण की जड़ें रेखा के साथ परवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

5. हम पद को समीकरण के दोनों भागों से विभाजित करते हैं एक्स2 – 2 एक्स– 3 = 0 पर एक्स, हम पाते हैं एक्स– 2 – 3/ एक्स= 0 आइए इस समीकरण को दो कार्यों में विभाजित करें: आप= एक्स– 2, आप= 3/ एक्स. समीकरण की जड़ें रेखा और अतिपरवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

5. डिग्री समीकरणों का आलेखीय समाधानएन

उदाहरण 1प्रश्न हल करें एक्स5 = 3 – 2 एक्स.

आप= एक्स5 , आप= 3 – 2 एक्स.

जवाब:एक्स = 1.

उदाहरण 2प्रश्न हल करें 3 √ एक्स= 10 – एक्स.

इस समीकरण की जड़ें दो कार्यों के रेखांकन के प्रतिच्छेदन बिंदु का भुज है: आप= 3 √ एक्स, आप= 10 – एक्स.

जवाब:एक्स = 8।

निष्कर्ष

फ़ंक्शन ग्राफ़ को ध्यान में रखते हुए: वाई =कुल्हाड़ी2 + बीएक्स+ सी, वाई =क/ एक्स, वाई =एक्स, वाई =|एक्स|, वाई =एक्स 3, वाई =एक्स 4,वाई = 3√एक्स, मैंने देखा कि ये सभी ग्राफ अक्षों के सापेक्ष समानांतर अनुवाद के नियम के अनुसार बनाए गए हैं एक्सऔर आप.

साहित्य

5. जर्नल गणित 5 2009; नंबर 8 2007; नंबर 23 2008।

इस वीडियो पाठ में, विषय "फ़ंक्शन y \u003d x 2। समीकरणों का आलेखीय हल। इस पाठ के दौरान, छात्र समीकरणों को हल करने के एक नए तरीके से परिचित हो सकेंगे - ग्राफिकल, जो फ़ंक्शन ग्राफ़ के गुणों के ज्ञान पर आधारित है। शिक्षक आपको दिखाएगा कि y=x 2 फलन को आलेखीय रूप से कैसे हल किया जाए।

विषय:समारोह

पाठ:समारोह. समीकरणों का आलेखीय हल

समीकरणों का आलेखीय समाधान फलन रेखांकन और उनके गुणों के ज्ञान पर आधारित होता है। हम उन कार्यों को सूचीबद्ध करते हैं जिनके ग्राफ हम जानते हैं:

1), ग्राफ x-अक्ष के समानांतर एक सीधी रेखा है, जो y-अक्ष पर एक बिंदु से होकर गुजरती है। एक उदाहरण पर विचार करें: y=1:

विभिन्न मूल्यों के लिए, हमें x-अक्ष के समानांतर सीधी रेखाओं का एक परिवार मिलता है।

2) प्रत्यक्ष आनुपातिकता फलन इस फलन का ग्राफ मूल बिन्दु से गुजरने वाली एक सीधी रेखा है। एक उदाहरण पर विचार करें:

हमने पिछले पाठों में इन ग्राफ़ को पहले ही बना लिया है, याद रखें कि प्रत्येक पंक्ति को बनाने के लिए, आपको एक बिंदु का चयन करना होगा जो इसे संतुष्ट करता है, और मूल को दूसरे बिंदु के रूप में लें।

गुणांक k की भूमिका को याद करें: जैसे-जैसे फलन बढ़ता है, रेखा के बीच का कोण और x-अक्ष की धनात्मक दिशा न्यून होती है; जब फलन घटता है, तो सीधी रेखा और x-अक्ष की धनात्मक दिशा के बीच का कोण अधिक होता है। इसके अलावा, एक ही संकेत के दो मापदंडों k के बीच निम्नलिखित संबंध हैं: सकारात्मक k के लिए, यह जितना बड़ा होता है, उतनी ही तेजी से कार्य बढ़ता है, और नकारात्मक के लिए, k modulo के बड़े मूल्यों के लिए फ़ंक्शन तेजी से घटता है।

3) रैखिक कार्य। कब - हमें y-अक्ष के साथ प्रतिच्छेदन बिंदु मिलता है और इस प्रकार की सभी रेखाएं बिंदु (0; m) से होकर गुजरती हैं। इसके अलावा, जैसे-जैसे फ़ंक्शन बढ़ता है, रेखा और x-अक्ष की धनात्मक दिशा के बीच का कोण न्यून होता है; जब फलन घटता है, तो सीधी रेखा और x-अक्ष की धनात्मक दिशा के बीच का कोण अधिक होता है। और निश्चित रूप से, k का मान फ़ंक्शन के मान के परिवर्तन की दर को प्रभावित करता है।

4))। इस फ़ंक्शन का ग्राफ एक परवलय है।

उदाहरणों पर विचार करें।

उदाहरण 1 - समीकरण को आलेखीय रूप से हल करें:

हम इस प्रकार के कार्यों को नहीं जानते हैं, इसलिए ज्ञात कार्यों के साथ काम करने के लिए हमें दिए गए समीकरण को बदलने की जरूरत है:

हमें समीकरण के दोनों भागों में परिचित फलन मिले हैं:

आइए कार्यों के रेखांकन बनाएं:

ग्राफ़ में दो प्रतिच्छेदन बिंदु होते हैं: (-1; 1); (2; 4)

आइए देखें कि क्या समाधान सही पाया गया है, निर्देशांक को समीकरण में बदलें:

पहला बिंदु सही पाया गया है।

, , , , , ,

दूसरा बिंदु भी सही पाया जाता है।

अत: समीकरण के हल हैं और

हम पिछले उदाहरण के समान कार्य करते हैं: हम दिए गए समीकरण को हमारे लिए ज्ञात कार्यों में बदलते हैं, उनके ग्राफ को प्लॉट करते हैं, चौराहे की धाराएं पाते हैं, और यहां से हम समाधान इंगित करते हैं।

हमें दो कार्य मिलते हैं:

आइए रेखांकन बनाएं:

इन ग्राफ़ में प्रतिच्छेदन बिंदु नहीं हैं, जिसका अर्थ है कि दिए गए समीकरण का कोई हल नहीं है

निष्कर्ष: इस पाठ में, हमने हमें ज्ञात कार्यों और उनके ग्राफ़ की समीक्षा की, उनके गुणों को याद किया और समीकरणों को हल करने के लिए एक चित्रमय तरीका माना।

1. डोरोफीव जी.वी., सुवोरोवा एस.बी., बनिमोविच ई.ए. एट अल। बीजगणित 7. छठा संस्करण। एम.: ज्ञानोदय। 2010

2. मर्ज़लीक ए.जी., पोलोन्स्की वी.बी., याकिर एम.एस. बीजगणित 7. एम .: वेंटाना-ग्राफ

3. कोल्यागिन यू.एम., तकाचेवा एम.वी., फेडोरोवा एन.ई. और अन्य। बीजगणित 7 .M ।: शिक्षा। 2006

टास्क 1: मकरचेव यू.एन., मिंड्युक एन.जी., नेशकोव के.आई. एट अल बीजगणित 7, संख्या 494, पृष्ठ 110;

टास्क 2: मकारिचेव यू.एन., मिंड्युक एन.जी., नेशकोव के.आई. और अन्य बीजगणित 7, संख्या 495, आइटम 110;

टास्क 3: मकरचेव यू.एन., मिंड्युक एन.जी., नेशकोव के.आई. एट अल बीजगणित 7, संख्या 496, पृष्ठ 110;

पेशेवर विकास के लिए दागिस्तान संस्थान

शैक्षणिक कर्मचारी

शारीरिक और गणितीय शिक्षा और आईसीटी विभाग

परियोजना

विषय पर:

« निर्माण और पी सुधारों

फ़ंक्शन ग्राफ़

स्कूल के गणित में »

रबाडानोवा पी.ए.

गणित शिक्षक

MBOU "कोचुबे सेकेंडरी स्कूल"

तारुमोव्स्की जिला

2015

1. परिचय……………………………………………………….3

2. अध्याय मैं. परियोजना के विषय पर साहित्य की समीक्षा……………………….….5

3. अध्याय द्वितीय. अनुभवजन्य भाग:

3.1. फ़ंक्शन ग्राफ़ को परिवर्तित करने के लिए मूल तरीके………..7

3.2. सम प्लॉटिंगऔरविषम कार्य …………….. 10

3.3. व्युत्क्रम फलन प्लॉट करना ………………………… 11

3.4. ग्राफ़ का विरूपण (संपीड़न और तनाव)………………….12

3.5. स्थानांतरण, प्रतिबिंब और विरूपण का संयोजन ………………… 13

4. स्वतंत्र समाधान के लिए कार्य ………………………………14

5.निष्कर्ष………………………………………………………15

6. निष्कर्ष……………………………………………………………………17

परिचय

फ़ंक्शन ग्राफ़ का परिवर्तन सीधे व्यावहारिक गतिविधियों से संबंधित मूलभूत गणितीय अवधारणाओं में से एक है। रेखांकन वास्तविक दुनिया की परिवर्तनशीलता और गतिशीलता, वास्तविक वस्तुओं और घटनाओं के पारस्परिक संबंधों को दर्शाते हैं।

कार्यात्मक रेखा मूल और एकीकृत राज्य परीक्षाओं में शामिल मूल विषय है।साथ ही, कई गणितीय अवधारणाओं को आलेखीय विधियों द्वारा माना जाता है। उदाहरण के लिए, toद्विघातफ़ंक्शन को द्विघात समीकरणों और असमानताओं के साथ निकट संबंध में पेश और अध्ययन किया जाता है।इसलिए यह इस प्रकार है किछात्रों को किसी फ़ंक्शन के ग्राफ़ बनाने और बदलने का तरीका सिखाना स्कूल में गणित पढ़ाने के मुख्य कार्यों में से एक है।

फ़ंक्शन के अध्ययन से इसके बारे में पता लगाना संभव हो जाता हैपरिभाषा का क्षेत्र और कार्य का दायरा, दायराघटती या बढ़ती दरें, स्पर्शोन्मुख, अंतरालस्थिरता, आदि पर हस्ताक्षर करें। हालांकि, एक ग्राफ बनाने के लिएkov कई कार्य हो सकते हैंकई तरीकों का प्रयोग करेंइसे आसान बनाएंइमारत। अतः विद्यार्थियों में पद्धतिगत योजनाओं के अनुसार आलेख बनाने की योग्यता होनी चाहिए।

उपरोक्त परिभाषित करता हैप्रासंगिकता शोध के विषय।

अध्ययन की वस्तु स्कूली गणित में कार्यात्मक रेखा रेखांकन के परिवर्तन का अध्ययन है।

अध्ययन का विषय - माध्यमिक विद्यालय में फंक्शन ग्राफ बनाने और बदलने की प्रक्रिया।

अध्ययन का उद्देश्य: शैक्षिक - किसी फ़ंक्शन के ग्राफ़ के निर्माण और परिवर्तित करने के लिए एक कार्यप्रणाली योजना की पहचान करना शामिल है;विकसित होना - अमूर्त, एल्गोरिथम, तार्किक सोच, स्थानिक कल्पना का विकास;शिक्षात्मक - स्कूली बच्चों की ग्राफिक संस्कृति की शिक्षा, मानसिक कौशल का निर्माण।

लक्ष्यों ने निम्नलिखित के निर्णय का नेतृत्व कियाकार्य:

1. अध्ययन के तहत समस्या पर शैक्षिक और कार्यप्रणाली का विश्लेषण करें।

2. कार्यप्रणाली योजनाओं की पहचान करेंगणित के स्कूल पाठ्यक्रम में फ़ंक्शन ग्राफ़ का परिवर्तन।

3. सबसे प्रभावी तरीकों और साधनों का चयन करेंमाध्यमिक विद्यालय में फ़ंक्शन ग्राफ़ का निर्माण और परिवर्तनइसमें योगदान करना: शैक्षिक सामग्री का अर्थपूर्ण आत्मसात करना; छात्रों की संज्ञानात्मक गतिविधि में वृद्धि; उनकी रचनात्मक क्षमताओं का विकास।

परिकल्पनाअनुसंधान: छात्रों की ग्राफिक संस्कृति के कार्यों और शिक्षा का अध्ययन करने की प्रक्रिया में ग्राफिक कौशल का गठन होगा प्रभावी यदि छात्रों के पास स्कूल गणित पाठ्यक्रम में फ़ंक्शन ग्राफ़ बनाने और बदलने के लिए एक व्यवस्थित योजना है।

अध्याय मैं . परियोजना के विषय पर साहित्य की समीक्षा।

परियोजना की तैयारी में, हमने निम्नलिखित साहित्य का अध्ययन किया:

शिवशिंस्की, आई। ख। बीजगणित में प्रमेय और समस्याएं, प्राथमिक कार्य - एम।, 2002। - 115 पी।

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. कार्य और रेखांकन (मूल तकनीक) - M., 1985. - 120 s

वी.जेड.जैतसेव, वी.वी. रियाज़कोव, एम.आई. स्कैनवी। प्राथमिक गणित - एम।, 2010 (पुनः जारी)। - 590 पी।

कुज़मिन, एम. के. एक समारोह के ग्राफ का निर्माण - जे। स्कूल में गणित। - 2003. - नंबर 5। - एस 61-62।

शिलोव जी.ई. चार्ट कैसे बनाते हैं? - एम।, 1982।

इसहाक तनातार। कार्यों के रेखांकन के ज्यामितीय परिवर्तन - MTsNMO, 2012

परयह ध्यान दिया जाता है कि एक ग्राफ का उपयोग करके एक निश्चित सेट पर फ़ंक्शन के व्यवहार को "पढ़ने" की क्षमता का उपयोग न केवल गणित के पाठ्यक्रम में किया जाता है, बल्कि किसी व्यक्ति की किसी भी व्यावहारिक गतिविधि में भी किया जाता है जिसमें उसे कुछ ग्राफिक से निपटना होता है। निर्भरता का प्रतिनिधित्व। इसलिए, छात्रों को किसी फ़ंक्शन के ग्राफ़ से इसके कुछ गुणों को निर्धारित करने में सक्षम होना चाहिए।

रेखांकन के परिवर्तन के लिए सैद्धांतिक सामग्री में सख्ती से कहा गया है। तकनीक के साथ चित्र के साथ चित्र, अलग-अलग जटिलता के उदाहरण और उनके समाधान हैं, जो ज्ञान को गहरा करना और जटिल कार्यों की साजिश करना संभव बनाता है।

एक इलेक्ट्रॉनिक प्रशिक्षण पाठ्यक्रम का प्रतिनिधित्व करता है, जिसकी मात्रा और सामग्री हाई स्कूल गणित पाठ्यक्रम के लिए आवश्यकताओं को पूरा करती है। सैद्धांतिक सामग्री ग्राफिक एनीमेशन चित्रों द्वारा समर्थित है जो अध्ययन के तहत विषय का एक दृश्य प्रतिनिधित्व देते हैं। पाठ्यक्रम में तीन मॉड्यूल शामिल हैं: एक सैद्धांतिक सामग्री अध्ययन मॉड्यूल, एक आत्म-परीक्षा मॉड्यूल और एक ज्ञान नियंत्रण मॉड्यूल।

परियोजना के अनुभवजन्य भाग के लिए, पद्धतिगत चार्टिंग योजनाओं से, स्वतंत्र कार्य के उदाहरणों का उपयोग किया गया था।

अध्याय 1 के निष्कर्ष

शैक्षिक और पद्धतिगत साहित्य के अध्ययन की अनुमति है:

1. कार्यप्रणाली योजना की पहचान करेंस्कूल गणित पाठ्यक्रम में किसी फ़ंक्शन के ग्राफ़ का अध्ययन, निर्माण और रूपांतरण।

2. सबसे प्रभावी तरीकों और साधनों का चयन करेंस्कूली गणित में फलन ग्राफ का निर्माण और परिवर्तन,योगदान:

शैक्षिक सामग्री का सार्थक आत्मसात;

छात्रों की संज्ञानात्मक गतिविधि में वृद्धि;

उनकी रचनात्मक क्षमताओं का विकास।

3. दिखाओ कि गणित में विभिन्न अवधारणाओं के अध्ययन में कार्यात्मक रेखा का महत्वपूर्ण प्रभाव पड़ता है।

अध्याय 2. अनुभवजन्य भाग

इस अध्याय में, हम फ़ंक्शन ग्राफ़ को बदलने के लिए मुख्य विधियों पर विचार करेंगे, और विभिन्न कार्यों के लिए ग्राफ़ के विभिन्न संयोजनों के निर्माण के लिए पद्धतिगत योजनाएँ देंगे।

2.1. फंक्शन ग्राफ रूपांतरण के लिए बुनियादी तकनीक

y-अक्ष के अनुदिश अनुवाद

एफ ( एक्स ) एफ ( एक्स )+ बी .

के लिएएक समारोह की साजिश रचनेआप = एफ( एक्स) + बीपता लगानाउन्हें:

1. एक फंक्शन ग्राफ बनाएंआप= एफ( एक्स)

2. धुरी ले जाएँएब्सिस्सा ऑन| बी| इकाइयाँ ऊपरबी>0 या कि| बी| खाना खा लोनीचे की ओर झुकनाबी < 0. नई व्यवस्था में प्राप्तदीनाट ग्राफ एक फ़ंक्शन का ग्राफ हैआप = एफ( एक्स) + बी.

2. स्थानांतरण साथ में कुल्हाड़ियों सूच्याकार आकृति का भुज

एफ ( एक्स ) एफ ( एक्स + ए ) .

आप = एफ( एक्स+ ए) पता लगानाउन्हें:

3. फॉर्म का एक फंक्शन प्लॉट करना आप = एफ (- एक्स )

एफ (एक्स ) एफ (- एक्स ).

फ़ंक्शन प्लॉट करने के लिएआप = एफ( - एक्स) इस प्रकार है:

एक फ़ंक्शन प्लॉट करेंआप = एफ( एक्स)

इसे वापस प्रतिबिंबित करेंy-अक्ष के सापेक्ष

परिणामी ग्राफ हैफंक्शन ग्राफआप = एफ( - एक्स)।

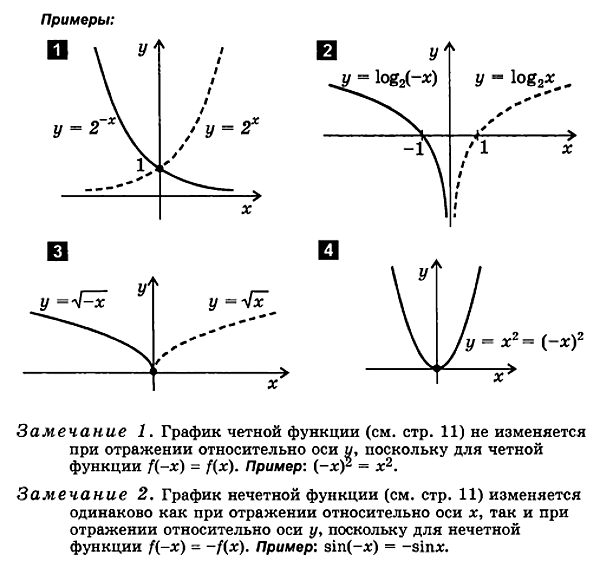
4. फॉर्म का एक फंक्शन प्लॉट करना वाई = - एफ ( एक्स )

एफ ( एक्स ) - एफ ( एक्स )

- एफ( एक्स) इस प्रकार है:

एक फ़ंक्शन प्लॉट करेंआप= एफ( एक्स)

इसे एक्स-अक्ष के बारे में प्रतिबिंबित करें

2.2. सम प्लॉटिंग और अजीब विशेषताएं

साजिश रचते समयसम और विषम कार्यों के लिए, निम्नलिखित गुणों का उपयोग करना सुविधाजनक है:

1. एक सम फलन का ग्राफ simmety-अक्ष के सापेक्ष उबड़-खाबड़।

2. एक विषम फलन का आलेख मूल के परितः सममित होता है।

सम और विषम कार्यों के ग्राफ बनाने के लिए, तर्क के सकारात्मक मूल्यों के लिए ग्राफ की केवल सही शाखा को प्लॉट करना पर्याप्त है। बाईं शाखा विषम फलन के मूल के बारे में और सम फलन के लिए y-अक्ष के बारे में सममित रूप से पूर्ण होती है।

सम फंक्शन प्लॉट करने के लिए आप = एफ ( एक्स ) बाद युगल:

केवल इस फलन के ग्राफ की एक शाखा की रचना करेंतर्क x≥0 के सकारात्मक मूल्यों की सीमा।

हेइस शाखा को y-अक्ष के परितः अनुरेखित कीजिए

एक अजीब समारोह की साजिश रचने के लिए आप = एफ ( एक्स ) इस प्रकार है:

इस फ़ंक्शन की केवल ग्राफ़ शाखा बनाएंतर्क के सकारात्मक मूल्यों का क्षेत्र (х≥0)।

हेमूल के संबंध में इस शाखा का पता लगाएंऋणात्मक x मानों के क्षेत्र में।

2.3. उलटा कार्य प्लॉट करना

जैसा कि पहले ही उल्लेख किया गया है, प्रत्यक्ष और उलटा कार्यचर के बीच समान संबंध दिखाएंx और y, केवल इस अंतर के साथ कि प्रतिलोम फलन में येचर ने भूमिकाएँ बदल दी हैं, जो बदलने के बराबर हैसमन्वय अक्षों का अंकन। इसलिए, ग्राफउलटा कार्य प्रत्यक्ष कार्य के ग्राफ के सममित हैद्विभाजक के बारे मेंमैंऔरतृतीयसमन्वय कोण,यानी अपेक्षाकृत सीधावाई = एक्स। इस प्रकार, हम प्राप्त करते हैंअगला नियम।

फलन y = . को आलेखित करने के लिए (एक्स) समारोह के विपरीतआप = एफ( एक्स), बनाया जाना चाहिएअनुसूचीआप = एफ( एक्स) और इसे सीधी रेखा y = x के सापेक्ष परावर्तित करें।

2.4. ग्राफ़ का विरूपण (संपीड़न और तनाव)

1. y-अक्ष के अनुदिश ग्राफ का संपीडन (विस्तार)

एफ ( एक्स ) ए ∙ एफ ( एक्स ).

फ़ंक्शन प्लॉट करने के लिएआप= ए∙ एफ( एक्स) इस प्रकार है:

8. x-अक्ष के अनुदिश ग्राफ का संपीडन (विस्तार)

एफ( एक्स)

फ़ंक्शन y . को प्लॉट करने के लिए= एफ( एक्स) इस प्रकार है:

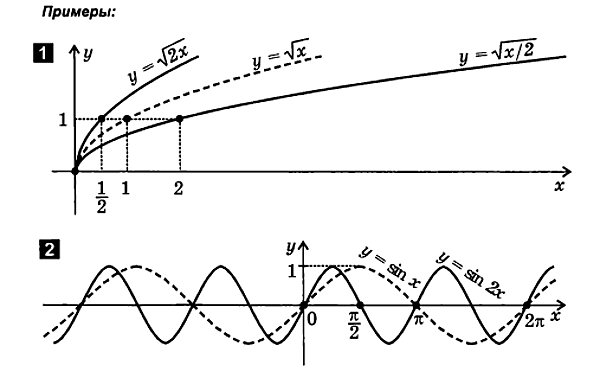
2.5. अनुवाद, प्रतिबिंब और विरूपण का संयोजन

बहुत बार जब के लिए फ़ंक्शन ग्राफ़ प्लॉट करते हैंसंयोजन बदलें.

ऐसी कई आसन तकनीकों का लगातार अनुप्रयोगका उपयोग करके ग्राफ के निर्माण को महत्वपूर्ण रूप से सरल बनाने की अनुमति देता हैचल रहा है और अक्सर इसे अंत में कम कर देता हैसबसे सरल प्राथमिक कार्यों में से एक का निर्माणबातें विचार करें कि, पूर्वगामी को ध्यान में रखते हुए, यह इस प्रकार हैफ़ंक्शन ग्राफ़ बनाएं।

आइए ध्यान दें कि यह समय हैअगले उत्तराधिकारी में सरलीकरण डॉक करना उचित हैनेस।

समता का उपयोग करना orसमारोह विषमता।

अक्ष स्थानांतरण।

प्रतिबिंब और विरूपण।

ग्राफ का निर्माण उल्टे क्रम में किया जाता है।

उदाहरण। एक फ़ंक्शन प्लॉट करें

निर्माण निम्नलिखित चरणों में किया जाएगा:

1. प्राकृतिक लघुगणक की साजिश रचें:

2. निचोड़अक्ष के लिएओए2 बार:;
3. सममित रूप से प्रदर्शित करेंअक्ष के बारे मेंओए: ;
4. अक्ष के अनुदिश गति करेंबैलपर(!!!) दांई ओर::

5. अक्ष के बारे में सममित रूप से प्रदर्शित करेंबैल: ;
6. चालअक्ष के अनुदिशओए3 यूनिट ऊपर::

फंक्शन ग्राफ के निर्माण और रूपांतरण के उदाहरण

उदाहरण 1 एक फ़ंक्शन प्लॉट करें.

सबसे पहले, एक साइन ग्राफ बनाएं, इसकी अवधि बराबर है:

फंक्शन ग्राफग्राफ को संपीड़ित करके प्राप्त किया गयादो बार y-अक्ष के लिए।लॉग .

एक फ़ंक्शन प्लॉट करेंपर = 2 क्योंकिएक्स।

एक फ़ंक्शन प्लॉट करेंआप = पापएक्स .

निष्कर्ष

परियोजना कार्य पर काम के दौरान, इस मुद्दे पर विभिन्न शैक्षिक और पद्धति संबंधी साहित्य का विश्लेषण किया गया। अध्ययन के परिणामों ने अध्ययन के सबसे विशिष्ट सकारात्मक पहलुओं की पहचान करना संभव बना दियास्कूल गणित पाठ्यक्रम में एक समारोह के रेखांकन का निर्माण और परिवर्तन

परियोजना का मुख्य लक्ष्य स्वतंत्र गतिविधि के तर्कसंगत तरीकों के निर्माण में, चित्र पढ़ने और ड्राइंग में छात्रों के कौशल और क्षमताओं को विकसित करना है।

समग्र रूप से ग्राफिक शिक्षा में सुधार की आवश्यकता न केवल आधुनिक उत्पादन आवश्यकताओं से निर्धारित होती है, बल्कि छात्रों की तकनीकी सोच और संज्ञानात्मक क्षमताओं के विकास में ग्राफिक्स की भूमिका से भी निर्धारित होती है। किसी व्यक्ति की ग्राफिक जानकारी को संसाधित करने की क्षमता उसके मानसिक विकास के संकेतकों में से एक है। इसलिए, ग्राफिक प्रशिक्षण सामान्य शैक्षिक प्रशिक्षण का एक अभिन्न अंग बन जाना चाहिए।

जाँच - परिणाम

इस प्रकार, विकसित परियोजना "फ़ंक्शन ग्राफ़ का निर्माण और परिवर्तन", गणित की केंद्रीय अवधारणाओं में से एक को समर्पित है - कार्यात्मक निर्भरता, छात्रों के ज्ञान के व्यवस्थितकरण और विस्तार पर केंद्रित है। फ़ंक्शन ग्राफ़ को बदलने के लिए विशिष्ट तरीकों का अध्ययन सख्त कार्यप्रणाली योजनाओं के अनुसार विश्लेषणात्मक और चित्रमय तरीके से किया जाता है। एकत्रित सामग्री का उपयोग कक्षा में और छात्रों के स्व-प्रशिक्षण के लिए किया जा सकता है। कक्षाओं के संचालन के लिए संगठन और प्रशिक्षण के विभिन्न रूपों और विधियों का उपयोग किया जा सकता है।

छात्र के लिए पोर्टल। आत्म प्रशिक्षण

संबंधित आलेख