Построение двух взаимно перпендикулярных плоскостей. Как известно, плоскости перпендикулярны, если прямая, принадлежащая одной плоскости, перпендикулярна другой плоскости. Поэтому плоскость, перпендикулярную к заданной, можно провести через прямую, перпендикулярную к заданной плоскости, или перпендикулярно прямой, лежащей в заданной плоскости.

Изображенные на рис. 4.12 плоскости (плоскость треугольника АВС и плоскость Р) взаимно перпендикулярны, так как плоскость Р перпендикулярна к прямой А1, лежащей в плоскости треугольника. Проекции плоскости P, проходящей через прямую с проекциями m 2 n 2 , m 1 n 1 и перпендикулярной плоскости, заданной проекциями a 2 b 2 c 2 , a 1 b 1 c 1 треугольника, показано на рис. 4.12.

Построение: 1. Провести главные линии плоскости, С1 - горизонталь, С2 - фронталь.

2. Через произвольную точку Е (расположенную вне треугольника АВС) провести прямую EF перпендикулярно главным линиям плоскости (c 2 f 2 перпендикулярна c 2 2 2 и c 1 f 1 перепендикулярна с 1 1 1).

3. Через точку N провести произвольно прямую ЕМ, пересекающуюся с EF, получим плоскость Р заданную двумя пересекающимися прямыми(ЕМ Х EF).

Таким образом плоскость Р(МЕ Х EF) перепендикулярна плоскости Q(треугольник АВС).

Следует заметить, что у взаимно перпендикулярных плоскостей общего положения их одноименные следы никогда не перпендикулярны. Но если одна из заданных плоскостей (или обе) является плоскостью общего положения, то взаимная перпендикулярность на эпюре одной пары их следов свидетельствует о перпендикулярности плоскостей в пространстве.

18)Прямую линию пересечения двух плоскостей можно определить по двум их общим точкам. Для этого определяют точки пересечения любых двух прямых линий одной плоскости с другой плоскостью или точки пересечения прямой на каждой из плоскостей с другой плоскостью

Последовательность построения:

Линию пересечения двух плоскостей можно найти применяя при решении вспомогательные секущие плоскости. Обычно выбирают проецирующие плоскости (часто горизонтальные или фронтальные)

Выбирают произвольную секущую вспомогательную горизонтальную плоскость Ф1 она пересекает заданные плоскости по прямым линиям (12и34) которые (на п1 пересекаются в точке к)

Вторая секущая горизонтальная плоскость пересекает заданные плоскости так же по горизонталям они в свою очередь пересекаются в точке Е

Прямая КЕ является линией пересечения заданных плоскостей.

Рассмотрим решение этой задачи на плоском чертеже.

1-й этап решения Для построения точки M использована горизонтально проецирующая плоскость - посредник ("), в которую заключена сторона AB треугольника ABC.

2-й этап решения Строим линию пересечения (на чертеже она задана точками 1 и 2) плоскости-посредника (") и плоскости DEK.

3-й этап решения Находим точку M пересечения прямой 1 - 2 с прямой AB.

Найдена одна точка M искомой линии пересечения.

Для построения точки N использована горизонтально проецирующая плоскость  ("), в которую заключена сторона AC треугольника ABC.

Построения аналогичны предыдущим.

Определение видимости на плоскости H выполнено с помощью горизонтально конкурирующих точек 4 и 8

Точка 4 расположена над точкой 8 (4" и 8"), поэтому на плоскости H часть треугольника DEK, расположенная в сторону точки 4, закрывает собой часть треугольника ABC, расположенную от линии пересечения в сторону точки 8. С помощью пары фронтально конкурирующих точек 6 и 7 определена видимость на плоскости V.

Пересечение двух фронтально проецирующих плоскостей (?)

Пересечение двух горизонтально проецурующих плоскостей (?)

19)Разрезом называется изображение предмета, мысленно рассеченного одной или несколькими плоскостями, при этом мысленное рассечение предмета относиться только к данному разрезу и не влечет за собой изменение других изображений того же предмета. На разрезе показывают то, что расположено в секущей плоскости и то, что расположено за ней.

В зависимости от числа секущих плоскостей разрезу подразделяются на:

Простые (при одной секущей плоскости)

Сложные (при нескольких секущих плоскостях)

В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекции разрезы разделяются на:

ГОРИЗОНТАЛЬНЫЕ – секущая плоскость параллельна горизонтальной плоскости проекции

ВЕРТИКАЛЬНЫЕ - секущая плоскость перпендикулярна горизонтальной плоскости проекции

НАКЛОНЫЕ – секущая плоскость некоторый непрямой угол с горизонтальной плоскостью =) ВЕРТИКАЛЬНЫЙ разрез называют фронтальным если секуща плоскость параллельна фронтальной плоскости проекций. И профильным если секущая плоскость параллельна профильной плоскости проекций.

СЛОЖНЫЕ разрезы бывают ПРОДОЛЬНЫМИ, если секущии плоскости направлены вдоль длинны или высоты предмета. И ПОПЕРЕЧНЫМИ ЕСЛИ секущие плоскости направлены ПЕРПЕНДИКУЛЯРНО длинне или высоте предмета.

СТУПЕНЧАТЫМИ – если секущее плоскости параллельны между собой

ЛОМАНЫМИ – если секущие плоскости пересекаются между собой.

МЕСТНЫЕ разрезы служат для выявления внутреннего строения предмета в отдельном ограниченном месте. МЕСТНЫЙ РАЗРЕЗ выделяется на виде сплошной, волнистой, тонкой линией.

Обозначение разрезов – Положение секущей плоскости указывают разомкнутой линией сечения. Начальный и конечный штрихи линии сечения не должны пересекать контур соответствующего изображения. На начальном и конечном штрихе нужно ставить стрелки указывающие направление взгляда Стрелки должны наноситься на расстоянии 2…3 мм от внешнего конца штриха.

ПРИ СЛОЖНОМ РАЗРЕЗЕ штрихи разомкнутой линии сечения проводят так же у перегибов линии сечения.

ОКОЛО стрелок, указывающих направление взгляда, со внешней стороны угла наносят прописные буквы русского алфавита. Буквенные обозначения присваиваются в алфавитном порядке без повторений и без пропусков.

Сам разрез должен быть отмечен надписью по типу А-А

Если секущая плоскость совпадает с плоскостью симметрии предмета, а разрез выполнен на месте соответствующего вида в проекционной связи, то для горизонтальных, фронтальных и профильных разрезов отмечать положение секуще плоскости не нужно и разрез надписью не сопровождается.

Если контурная линия предмета совпадает с осью симметрии то границу между видом и разрезом указывают волнистой линией которую проводят так, чтобы сохранилось изображение ребра.

Две плоскости, которые пересекаются, называются перпендикулярными , если третья плоскость, перпендикулярная прямой пересечения этих двух плоскостей, пересекает их по перпендикулярным прямым (см. рисунок).

Любая плоскость, перпендикулярная к прямой пересечения перпендикулярных плоскостей, пересекает их по перпендикулярным прямым.

Признак перпендикулярности плоскостей

Теорема 1. Если плоскость проходит через прямую, перпендикулярную к другой плоскости, то эти плоскости перпендикулярны (см. рисунок).

Теорема 2. Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна линии их пересечения, то она перпендикулярна и ко второй плоскости (см. рисунок).

Пример применения теоремы 2
Пусть есть две перпендикулярные плоскости и , которые пересекаются по прямой a (см. рисунок). Найти расстояние от точки A , которая лежит в плоскости и не лежит в плоскости , плоскости .

В плоскости строим перпендикуляр к a через точку A . Пусть он пересекает a в точке B . AB - искомое расстояние.
Обратите внимание на такое.
1. Через точку вне плоскости можно провести множество плоскостей, перпендикулярных к этой плоскости (см. рисунок). (Но все они пройдут через перпендикулярную к этой плоскости прямую, которая проходит через данную точку.)

2. Если плоскость перпендикулярна к данной плоскости, то это не значит, что она перпендикулярна и к произвольной прямой, параллельной этой плоскости.
Например, на рисунке ниже , и пересекаются по прямой b , причем a входит в одной из плоскостей и . Следовательно, прямая a в то же время параллельная двум перпендикулярным плоскостям.

Данный урок поможет желающим получить представление о теме «Признак перпендикулярности двух плоскостей». В начале него мы повторим определение двугранного и линейного угла. Затем рассмотрим, какие плоскости называются перпендикулярными, и докажем признак перпендикулярности двух плоскостей.

Тема: Перпендикулярность прямых и плоскостей

Урок: Признак перпендикулярности двух плоскостей

Определение. Двугранным углом называется фигура, образованная двумя полуплоскостями, не принадлежащими одной плоскости, и их общей прямой а (а - ребро).

Рис. 1

Рассмотрим две полуплоскости α и β (рис. 1). Их общая граница - l. Указанная фигура называется двугранным углом. Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.

Двугранный угол измеряется своим линейным углом. На общем ребре l двугранного угла выберем произвольную точку. В полуплоскостях α и β из этой точки проведем перпендикуляры a и b к прямой l и получим линейный угол двугранного угла.

Прямые a и b образуют четыре угла, равных φ, 180° - φ, φ, 180° - φ. Напомним, углом между прямыми называется наименьший из этих углов.

Определение. Углом между плоскостями называется наименьший из двугранных углов, образованных этими плоскостями. φ - угол между плоскостями α и β, если

Определение. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°.

Рис. 2

На ребре l выбрана произвольная точка М (рис. 2). Проведем две перпендикулярные прямые МА = а и МВ = b к ребру l в плоскости α и в плоскости β соответственно. Получили угол АМВ. Угол АМВ - это линейный угол двугранного угла. Если угол АМВ равен 90°, то плоскости α и β называются перпендикулярными.

Прямая b перпендикулярна прямой l по построению. Прямая b перпендикулярна прямой а, так как угол между плоскостями α и β равен 90°. Получаем, что прямая b перпендикулярна двум пересекающимся прямым а и l из плоскости α. Значит, прямая b перпендикулярна плоскости α.

Аналогично можно доказать, что прямая а перпендикулярна плоскости β. Прямая а перпендикулярна прямой l по построению. Прямая а перпендикулярна прямой b, так как угол между плоскостями α и β равен 90°. Получаем, что прямая а перпендикулярна двум пересекающимся прямым b и l из плоскости β. Значит, прямая а перпендикулярна плоскости β.

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Доказать:

Рис. 3

Доказательство:

Пусть плоскости α и β пересекаются по прямой АС (рис. 3). Чтобы доказать, что плоскости взаимно перпендикулярны, нужно построить линейный угол между ними и показать, что этот угол равен 90°.

Прямая АВ перпендикулярна по условию плоскости β, а значит, и прямой АС, лежащей в плоскости β.

Проведем прямую АD перпендикулярно прямой АС в плоскости β. Тогда ВАD -линейный угол двугранного угла.

Прямая АВ перпендикулярна плоскости β, а значит, и прямой АD, лежащей в плоскости β. Значит, линейный угол ВАD равен 90°. Значит, плоскости α и β перпендикулярны, что и требовалось доказать.

Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей (рис. 4).

Доказать:

Рис. 4

Доказательство:

Прямая l перпендикулярна плоскости γ, а плоскость α проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости α и γ перпендикулярны.

Прямая l перпендикулярна плоскости γ, а плоскость β проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости β и γ перпендикулярны.

Понятие перпендикулярных плоскостей

При пересечении двух плоскостей у нас получается $4$ двугранных угла. Два угла равны $\varphi $, а два другие равны ${180}^0-\varphi $.

Определение 1

Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.

Определение 2

Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен $90^\circ$ (рис. 1).

Рисунок 1. Перпендикулярные плоскости

Признак перпендикулярности двух плоскостей

Теорема 1

Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.

Доказательство.

Пусть нам даны плоскости $\alpha $ и $\beta $, которые пересекаются по прямой $AC$. Пусть прямая $AB$, лежащая в плоскости $\alpha $ перпендикулярна плоскости $\beta $ (рис. 2).

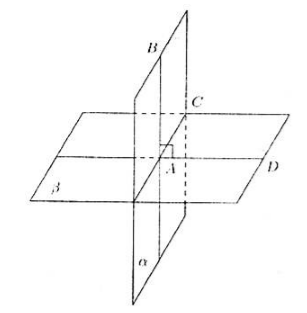
Рисунок 2.

Так как прямая $AB$ перпендикулярна плоскости $\beta $, то она перпендикулярна и прямой $AC$. Проведем дополнительно прямую $AD$ в плоскости $\beta $, перпендикулярно прямой $AC$.

Получаем, что угол $BAD$ - линейный угол двугранного угла, равный $90^\circ$. То есть, по определению 1, угол между плоскостями равен $90^\circ$, значит, данные плоскости перпендикулярны.

Теорема доказана.

Из этой теоремы следует следующая теорема.

Теорема 2

Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.

Доказательство.

Пусть нам даны две плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Плоскость $\gamma $ перпендикулярна прямой $c$ (рис. 3)

Рисунок 3.

Так как прямая $c$ принадлежит плоскости $\alpha $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\alpha $ и $\gamma $ перпендикулярны.

Так как прямая $c$ принадлежит плоскости $\beta $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\beta $ и $\gamma $ перпендикулярны.

Теорема доказана.

Для каждой из этих теорем справедливы и обратные утверждения.

Примеры задач

Пример 1

Пусть нам дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Найти все пары перпендикулярных плоскостей (рис. 5).

Рисунок 4.

Решение.

По определению прямоугольного параллелепипеда и перпендикулярных плоскостей видим следующие восемь пар перпендикулярных между собой плоскостей: $(ABB_1)$ и $(ADD_1)$, $(ABB_1)$ и $(A_1B_1C_1)$, $(ABB_1)$ и $(BCC_1)$, $(ABB_1)$ и $(ABC)$, $(DCC_1)$ и $(ADD_1)$, $(DCC_1)$ и $(A_1B_1C_1)$, $(DCC_1)$ и $(BCC_1)$, $(DCC_1)$ и $(ABC)$.

Пример 2

Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.

Доказательство.

Пусть нам даны перпендикулярные плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Из точки $A$ плоскости $\beta $ проведен перпендикуляр $AC$ к плоскости $\alpha $. Предположим, что $AC$ не лежит в плоскости $\beta $ (рис. 6).

Рисунок 5.

Рассмотрим треугольник $ABC$. Он является прямоугольным с прямым углом $ACB$. Следовательно, $\angle ABC\ne {90}^0$.

Но, с другой стороны, $\angle ABC$ является линейным углом двугранного угла, образованного этими плоскостями. То есть двугранный угол, образованный этими плоскостями не равняется 90 градусам. Получаем, что угол между плоскостями не равен $90^\circ$. Противоречие. Следовательно, $AC$ лежит в плоскости $\beta $.