Ito ay isang medyo kawili-wiling seksyon ng matematika na talagang kinakaharap ng lahat ng nagtapos na mga mag-aaral at mag-aaral. Gayunpaman, hindi lahat ay may gusto sa matan. Nabigo ang ilan na maunawaan kahit ang mga pangunahing bagay tulad ng tila karaniwang pag-aaral ng function. Nilalayon ng artikulong ito na itama ang oversight na ito. Gustong matuto nang higit pa tungkol sa pagsusuri ng function? Gusto mo bang malaman kung ano ang mga extremum point at kung paano hanapin ang mga ito? Kung gayon ang artikulong ito ay para sa iyo.
Pagsisiyasat ng graph ng isang function
Upang magsimula sa, ito ay nagkakahalaga ng pag-unawa kung bakit ito ay kinakailangan upang pag-aralan ang tsart sa lahat. May mga simpleng function na madaling iguhit. Ang isang kapansin-pansing halimbawa ng naturang function ay ang parabola. Hindi mahirap iguhit ang kanyang tsart. Ang kailangan lang ay, gamit ang isang simpleng pagbabago, upang mahanap ang mga numero kung saan ang function ay tumatagal ng halaga 0. At sa prinsipyo, ito lang ang kailangan mong malaman upang gumuhit ng isang parabola graph.
Ngunit paano kung ang function na kailangan nating i-graph ay mas kumplikado? Dahil ang mga katangian ng mga kumplikadong pag-andar ay sa halip ay hindi halata, kinakailangan upang magsagawa ng isang buong pagsusuri. Pagkatapos lamang ay maaaring ipakita ang function na graphical. Paano ito gagawin? Mahahanap mo ang sagot sa tanong na ito sa artikulong ito.
Plano ng pagsusuri ng function
Ang unang bagay na dapat gawin ay magsagawa ng isang mababaw na pag-aaral ng function, kung saan makikita natin ang domain ng kahulugan. Kaya, magsimula tayo sa pagkakasunud-sunod. Ang domain ng kahulugan ay ang hanay ng mga halaga kung saan tinukoy ang function. Sa madaling salita, ito ang mga numero na maaaring gamitin sa function sa halip na x. Upang matukoy ang saklaw, kailangan mo lamang tingnan ang entry. Halimbawa, malinaw na ang function na y (x) \u003d x 3 + x 2 - x + 43 ay may domain ng kahulugan - ang hanay ng mga tunay na numero. Well, sa isang function tulad ng (x 2 - 2x) / x, ang lahat ay medyo naiiba. Dahil ang numero sa denominator ay hindi dapat katumbas ng 0, kung gayon ang domain ng function na ito ay magiging lahat ng tunay na numero, maliban sa zero.
Susunod, kailangan mong hanapin ang tinatawag na mga zero ng function. Ito ang mga halaga ng argumento kung saan ang buong function ay kumukuha ng halagang zero. Upang gawin ito, kinakailangang i-equate ang function sa zero, isaalang-alang ito nang detalyado at magsagawa ng ilang mga pagbabago. Kunin natin ang pamilyar na function na y(x) = (x 2 - 2x)/x. Mula sa kurso sa paaralan, alam natin na ang isang fraction ay 0 kapag ang numerator ay zero. Samakatuwid, itinatapon namin ang denominator at nagsimulang magtrabaho kasama ang numerator, tinutumbasan ito sa zero. Nakukuha namin ang x 2 - 2x \u003d 0 at inaalis namin ang x sa mga bracket. Samakatuwid x (x - 2) \u003d 0. Bilang resulta, nalaman namin na ang aming function ay katumbas ng zero kapag ang x ay katumbas ng 0 o 2.
Sa panahon ng pag-aaral ng graph ng isang function, marami ang nahaharap sa isang problema sa anyo ng mga extremum point. At ito ay kakaiba. Pagkatapos ng lahat, ang mga extremes ay isang medyo simpleng paksa. ayaw maniwala? Tingnan para sa iyong sarili sa pamamagitan ng pagbabasa sa bahaging ito ng artikulo, kung saan pag-uusapan natin ang tungkol sa minimum at maximum na mga puntos.

Upang magsimula sa, ito ay nagkakahalaga ng pag-unawa kung ano ang isang extremum. Ang extremum ay ang limitasyong halaga na naaabot ng isang function sa isang graph. Mula dito lumalabas na mayroong dalawang matinding halaga - isang maximum at isang minimum. Para sa kalinawan, maaari mong tingnan ang larawan sa itaas. Sa lugar na sinisiyasat, ang point -1 ay ang maximum ng function na y (x) \u003d x 5 - 5x, at ang point 1, ayon sa pagkakabanggit, ay ang minimum.
Gayundin, huwag malito ang mga konsepto sa isa't isa. Ang mga extremum point ng isang function ay ang mga argumento kung saan ang ibinigay na function ay nakakakuha ng matinding halaga. Sa turn, ang extremum ay ang halaga ng minima at maxima ng function. Halimbawa, isaalang-alang muli ang figure sa itaas. Ang -1 at 1 ay ang mga extremum point ng function, at ang 4 at -4 ay ang mga extremum mismo.
Paghahanap ng mga extremum point

Ngunit paano mo mahahanap ang mga extremum point ng isang function? Ang lahat ay medyo simple. Ang unang bagay na dapat gawin ay hanapin ang derivative ng equation. Sabihin nating nakuha natin ang gawain: "Hanapin ang mga extremum point ng function na y (x), x ang argumento. Para sa kalinawan, kunin natin ang function na y (x) \u003d x 3 + 2x 2 + x + 54. Ibahin natin ang pagkakaiba at kunin ang sumusunod na equation: 3x 2 + 4x + 1. Bilang resulta, nakakuha kami ng karaniwang quadratic equation. Ang kailangan lang gawin ay i-equate ito sa zero at hanapin ang mga ugat. Dahil mas malaki sa zero ang discriminant (D \u003d 16 - 12 \u003d 4), ang equation na ito ay tinutukoy ng dalawang ugat. Nahanap namin ang mga ito at nakakuha ng dalawang halaga: 1/3 at -1. Ito ang magiging mga extremum point ng function. Gayunpaman, paano mo pa rin matutukoy sino sino? Aling punto ang pinakamataas at alin ang pinakamababa? Upang gawin ito, kailangan mong kumuha ng kalapit na punto at alamin ang halaga nito. Halimbawa, kunin natin ang numero -2, na nasa kaliwa kasama ang coordinate linya mula sa -1. Pinapalitan namin ang halagang ito sa aming equation na y (-2) = 12 - 8 + 1 = 5. Bilang resulta, nakakuha kami ng positibong numero. Nangangahulugan ito na sa pagitan mula 1/3 hanggang -1 ang pagtaas ng function, na, sa turn, ay nangangahulugan na sa mga pagitan mula sa min mula sa infinity hanggang 1/3 at mula -1 hanggang plus infinity, bumababa ang function. Kaya, maaari nating tapusin na ang bilang na 1/3 ay ang pinakamababang punto ng function sa inimbestigahang agwat, at -1 ay ang pinakamataas na punto.

Nararapat din na tandaan na ang pagsusulit ay nangangailangan hindi lamang upang makahanap ng mga extremum na puntos, kundi pati na rin upang magsagawa ng ilang uri ng operasyon sa kanila (magdagdag, magparami, atbp.). Ito ay para sa kadahilanang ito na ito ay nagkakahalaga ng pagbibigay ng espesyal na pansin sa mga kondisyon ng problema. Pagkatapos ng lahat, dahil sa kawalan ng pansin, maaari kang mawalan ng mga puntos.
Mula sa artikulong ito, matututunan ng mambabasa ang tungkol sa kung ano ang isang labis na halaga ng pagganap, pati na rin ang tungkol sa mga tampok ng paggamit nito sa pagsasanay. Ang pag-aaral ng naturang konsepto ay lubhang mahalaga para sa pag-unawa sa mga pundasyon ng mas mataas na matematika. Ang paksang ito ay mahalaga sa isang mas malalim na pag-aaral ng kurso.
Sa pakikipag-ugnayan sa
Ano ang isang matinding?
Sa kurso sa paaralan, maraming mga kahulugan ng konsepto ng "extremum" ang ibinigay. Ang artikulong ito ay naglalayong magbigay ng pinakamalalim at pinakamalinaw na pag-unawa sa termino para sa mga taong walang alam sa isyu. Kaya, ang termino ay nauunawaan kung hanggang saan ang functional interval ay nakakakuha ng isang minimum o maximum na halaga sa isang partikular na hanay.
Ang extremum ay parehong minimum na halaga ng function at ang maximum sa parehong oras. Mayroong pinakamababang punto at pinakamataas na punto, iyon ay, ang matinding halaga ng argumento sa graph. Ang mga pangunahing agham kung saan ginagamit ang konseptong ito:
- mga istatistika;
- kontrol ng makina;
- econometrics.
Ang mga matinding puntos ay may mahalagang papel sa pagtukoy ng pagkakasunud-sunod ng isang naibigay na function. Ang sistema ng coordinate sa graph sa pinakamahusay na nagpapakita ng pagbabago sa matinding posisyon depende sa pagbabago sa functionality.
Extrema ng derivative function
Mayroon ding isang bagay bilang isang "derivative". Ito ay kinakailangan upang matukoy ang extremum point. Mahalagang huwag malito ang pinakamababa o pinakamataas na puntos sa pinakamalaki at pinakamaliit na halaga. Ang mga ito ay magkakaibang mga konsepto, bagaman maaaring sila ay magkatulad.
Ang halaga ng function ay ang pangunahing kadahilanan sa pagtukoy kung paano hanapin ang pinakamataas na punto. Ang derivative ay hindi nabuo mula sa mga halaga, ngunit eksklusibo mula sa matinding posisyon nito sa isang pagkakasunud-sunod o iba pa.
Ang derivative mismo ay tinutukoy batay sa data ng mga extreme point, at hindi ang pinakamalaki o pinakamaliit na halaga. Sa mga paaralang Ruso, ang linya sa pagitan ng dalawang konsepto na ito ay hindi malinaw na iginuhit, na nakakaapekto sa pag-unawa sa paksang ito sa pangkalahatan.
Isaalang-alang natin ngayon ang isang bagay bilang isang "matalim na labis". Sa ngayon, mayroong isang matinding minimum na halaga at isang matinding maximum na halaga. Ang kahulugan ay ibinigay alinsunod sa pag-uuri ng Russia ng mga kritikal na punto ng isang function. Ang konsepto ng isang extremum point ay ang batayan para sa paghahanap ng mga kritikal na punto sa isang tsart.

Upang tukuyin ang gayong konsepto, ginamit ang teorama ni Fermat. Ito ang pinakamahalaga sa pag-aaral ng mga matinding punto at nagbibigay ng isang malinaw na ideya ng kanilang pag-iral sa isang anyo o iba pa. Upang matiyak ang sukdulan, mahalagang lumikha ng ilang mga kundisyon para sa pagbaba o pagtaas sa tsart.
Upang tumpak na masagot ang tanong na "paano mahahanap ang pinakamataas na punto", dapat mong sundin ang mga probisyong ito:
- Paghahanap ng eksaktong lugar ng kahulugan sa tsart.
- Maghanap ng derivative ng isang function at isang extremum point.
- Lutasin ang mga karaniwang hindi pagkakapantay-pantay para sa domain ng argumento.
- Mapatunayan kung aling mga function ang isang punto sa isang graph ay tinukoy at tuloy-tuloy.

Pansin! Ang paghahanap para sa isang kritikal na punto ng isang function ay posible lamang kung mayroong isang derivative ng hindi bababa sa pangalawang order, na sinisiguro ng isang mataas na proporsyon ng pagkakaroon ng isang extremum point.
Kinakailangang kondisyon para sa extremum ng function
Upang magkaroon ng extremum, mahalaga na mayroong parehong minimum na puntos at pinakamataas na puntos. Kung ang panuntunang ito ay sinusunod lamang bahagyang, kung gayon ang kondisyon para sa pagkakaroon ng isang extremum ay nilabag.

Ang bawat pag-andar sa anumang posisyon ay dapat na maiiba upang makilala ang mga bagong kahulugan nito. Mahalagang maunawaan na ang kaso kapag nawala ang isang punto ay hindi ang pangunahing prinsipyo ng paghahanap ng naiba-iba na punto.
Ang isang matalim na extremum, pati na rin ang isang minimum na function, ay isang napakahalagang aspeto ng paglutas ng isang problema sa matematika gamit ang matinding mga halaga. Upang mas maunawaan ang bahaging ito, mahalagang sumangguni sa mga halaga ng tabular para sa pagtatalaga ng functional.
| Isang kumpletong paggalugad ng kahulugan | Pag-plot ng Halaga |
| 1. Pagpapasiya ng mga punto ng pagtaas at pagbaba ng mga halaga. 2. Paghahanap ng mga break point, extremum at intersection na may mga coordinate axes. 3. Ang proseso ng pagtukoy ng mga pagbabago sa posisyon sa tsart. 4. Pagpapasiya ng index at direksyon ng convexity at convexity, na isinasaalang-alang ang pagkakaroon ng mga asymptotes. 5. Paglikha ng isang talahanayan ng buod ng pag-aaral sa mga tuntunin ng pagtukoy ng mga coordinate nito. 6. Paghahanap ng mga pagitan ng pagtaas at pagbaba ng sukdulan at talamak na mga puntos. 7. Pagpapasiya ng convexity at concavity ng curve. 8. Ang pagbuo ng isang graph batay sa pag-aaral ay nagpapahintulot sa iyo na makahanap ng minimum o maximum. |
Ang pangunahing elemento, kapag kinakailangan upang gumana sa mga extremum, ay ang eksaktong pagbuo ng graph nito. Ang mga guro ng paaralan ay hindi madalas na binibigyang pansin ang gayong mahalagang aspeto, na isang matinding paglabag sa proseso ng edukasyon. Ang graph ay binuo lamang batay sa mga resulta ng pag-aaral ng functional data, ang kahulugan ng sharp extrema, pati na rin ang mga puntos sa graph. Ang matalim na extrema ng derivative ng isang function ay ipinapakita sa isang plot ng eksaktong mga halaga gamit ang karaniwang pamamaraan para sa pagtukoy ng mga asymptotes. |
Isaalang-alang ang graph ng isang tuluy-tuloy na function y=f(x) ipinapakita sa figure.
Halaga ng function sa punto x 1 ay magiging mas malaki kaysa sa mga halaga ng function sa lahat ng mga kalapit na punto sa kaliwa at sa kanan ng x isa. Sa kasong ito, ang function ay sinasabing mayroon sa punto x 1 max. Sa punto x Ang 3 function ay malinaw na mayroon ding maximum. Kung isasaalang-alang natin ang punto x 2 , kung gayon ang halaga ng function sa loob nito ay mas mababa kaysa sa lahat ng kalapit na halaga. Sa kasong ito, ang function ay sinasabing mayroon sa punto x 2 pinakamababa. Katulad din para sa punto x 4 .
Function y=f(x) sa punto x 0 ay may maximum, kung ang halaga ng function sa puntong ito ay mas malaki kaysa sa mga halaga nito sa lahat ng mga punto ng ilang pagitan na naglalaman ng punto x 0 , ibig sabihin. kung mayroong ganoong kapitbahayan ng punto x 0 , na para sa lahat x≠x 0 , kabilang sa kapitbahayan na ito, mayroon tayong hindi pagkakapantay-pantay f(x)<f(x 0 ) .
Function y=f(x) Mayroon itong pinakamababa sa punto x 0 , kung mayroong ganoong kapitbahayan ng punto x 0 , kung ano ang para sa lahat x≠x 0 na kabilang sa kapitbahayan na ito, mayroon tayong hindi pagkakapantay-pantay f(x)>f(x0.
Ang mga punto kung saan naabot ng function ang maximum at minimum nito ay tinatawag na extremum point, at ang mga value ng function sa mga puntong ito ay ang extrema ng function.
Bigyang-pansin natin ang katotohanan na ang isang function na tinukoy sa isang segment ay maaaring maabot ang maximum at minimum nito lamang sa mga puntong nasa loob ng segment na isinasaalang-alang.
Tandaan na kung ang isang function ay may maximum sa isang punto, hindi ito nangangahulugan na sa puntong ito ang function ay may pinakamataas na halaga sa buong domain. Sa figure na tinalakay sa itaas, ang function sa punto x 1 ay may maximum, kahit na may mga punto kung saan ang mga halaga ng function ay mas malaki kaysa sa punto x 1 . Sa partikular, f(x 1) < f(x 4) ibig sabihin. ang minimum ng function ay mas malaki kaysa sa maximum. Mula sa kahulugan ng maximum, sumusunod lamang na ito ang pinakamalaking halaga ng function sa mga puntong sapat na malapit sa pinakamataas na punto.
Theorem 1. (Isang kinakailangang kondisyon para sa pagkakaroon ng extremum.) Kung ang differentiable function y=f(x) ay nasa punto x=x 0 extremum, pagkatapos ang derivative nito sa puntong ito ay naglalaho.
Patunay. Hayaan, para sa katiyakan, sa punto x 0 ang function ay may maximum. Pagkatapos ay para sa sapat na maliit na mga palugit Δ x meron kami f(x 0 + Δ x)
Pagpasa sa mga hindi pagkakapantay-pantay na ito sa limitasyon bilang Δ x→ 0 at isinasaalang-alang na ang derivative f "(x 0) ay umiiral, at samakatuwid ang limitasyon sa kaliwa ay hindi nakasalalay sa kung paano Δ x→ 0, nakukuha natin: para sa Δ x → 0 – 0 f"(x 0) ≥ 0 at sa Δ x → 0 + 0 f"(x 0) ≤ 0. Dahil f"(x 0) ay tumutukoy sa isang numero, kung gayon ang dalawang hindi pagkakapantay-pantay na ito ay magkatugma lamang kung f"(x 0) = 0.
Ang napatunayang teorama ay nagsasaad na ang pinakamataas at pinakamababang puntos ay maaari lamang kabilang sa mga halaga ng argumento kung saan nawawala ang hinalaw.
Isinaalang-alang namin ang kaso kapag ang isang function ay may derivative sa lahat ng punto ng isang partikular na segment. Ano ang mangyayari kapag wala ang derivative? Isaalang-alang ang mga halimbawa.
Mga halimbawa.
- y=|x|.
Ang function ay walang derivative sa isang punto x=0 (sa puntong ito, ang graph ng function ay walang tiyak na tangent), ngunit sa puntong ito ang function ay may pinakamababa, dahil y(0)=0, at para sa lahat x≠ 0y > 0.
- Hayaan x< x
0 . Pagkatapos c< x
0 at f "(c)> 0.
Kaya f "(c)(x-x 0)<
0 at, samakatuwid,
f(x) - f(x 0 )< 0, ibig sabihin. f(x)< f(x 0 ).
- Hayaan x > x 0 . Pagkatapos c>x 0 at f"(c)< 0. ibig sabihin f "(c)(x-x 0)< 0. Kaya f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Hanapin ang saklaw ng isang function f(x).
- Hanapin ang unang derivative ng isang function f"(x).
- Tukuyin ang mga kritikal na punto, para dito:
- hanapin ang tunay na mga ugat ng equation f"(x)=0;
- hanapin ang lahat ng mga halaga x sa ilalim kung saan ang derivative f"(x) ay wala.
- Tukuyin ang tanda ng derivative sa kaliwa at kanan ng kritikal na punto. Dahil ang sign ng derivative ay nananatiling pare-pareho sa pagitan ng dalawang kritikal na punto, sapat na upang matukoy ang sign ng derivative sa anumang punto sa kaliwa at sa isang punto sa kanan ng kritikal na punto.
- Kalkulahin ang halaga ng function sa mga extremum point.
- Hanapin ang lahat ng kritikal na punto ng isang function sa pagitan ( a, b) at kalkulahin ang mga halaga ng function sa mga puntong ito.
- Kalkulahin ang mga halaga ng function sa mga dulo ng segment para sa x=a, x=b.
- Sa lahat ng nakuhang halaga, piliin ang pinakamalaki at pinakamaliit.
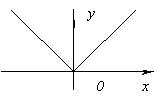
Ang function ay walang derivative sa x=0, dahil napupunta ito sa infinity kung kailan x=0. Ngunit sa puntong ito, ang pag-andar ay may maximum.

Ang function ay walang derivative sa x=0 kasi ![]() sa x→0. Sa puntong ito, ang function ay walang maximum o minimum. Talaga, f(x)=0 at sa x<0f(x)<0, а при x>0f(x)>0.
sa x→0. Sa puntong ito, ang function ay walang maximum o minimum. Talaga, f(x)=0 at sa x<0f(x)<0, а при x>0f(x)>0.

Kaya, mula sa mga ibinigay na halimbawa at ang formulated theorem ay malinaw na ang function ay maaaring magkaroon ng extremum lamang sa dalawang kaso: 1) sa mga punto kung saan ang derivative ay umiiral at katumbas ng zero; 2) sa punto kung saan wala ang derivative.
Gayunpaman, kung sa isang punto x 0 alam natin yan f"(x 0 ) =0, pagkatapos ay hindi ito maaaring concluded mula dito na sa punto x 0 ang function ay may extremum.
Halimbawa. ![]() .
.

Ngunit punto x Ang =0 ay hindi isang extremum point, dahil sa kaliwa ng puntong ito ang mga halaga ng function ay matatagpuan sa ibaba ng axis baka, at sa itaas sa kanan.
Ang mga halaga ng isang argumento mula sa domain ng isang function, kung saan nawawala o wala ang derivative ng function, ay tinatawag kritikal na mga punto.
Ito ay sumusunod mula sa naunang nabanggit na ang extremum point ng isang function ay kabilang sa mga kritikal na punto, at, gayunpaman, hindi lahat ng kritikal na punto ay isang extremum point. Samakatuwid, upang mahanap ang extremum ng function, kailangan mong hanapin ang lahat ng mga kritikal na punto ng function, at pagkatapos ay suriin ang bawat isa sa mga puntong ito nang hiwalay para sa maximum at minimum. Para dito, nagsisilbi ang sumusunod na theorem.
Theorem 2. (Isang sapat na kondisyon para sa pagkakaroon ng extremum.) Hayaang maging tuluy-tuloy ang function sa ilang pagitan na naglalaman ng kritikal na punto x 0 , at naiba sa lahat ng punto ng agwat na ito (maliban, marahil, ang punto mismo x 0). Kung, kapag dumadaan mula kaliwa pakanan sa puntong ito, nagbabago ang derivative sign mula plus hanggang minus, pagkatapos ay sa punto x = x 0 ang function ay may maximum. Kung, kapag dumadaan x 0 mula kaliwa hanggang kanan, ang derivative ay nagbabago ng sign mula minus hanggang plus, pagkatapos ang function ay may pinakamababa sa puntong ito.
Kaya, kung
Patunay. Ipagpalagay muna natin na kapag dumaan x 0, ang derivative ay nagbabago ng sign mula plus hanggang minus, i.e. para sa lahat x malapit sa punto x 0 f "(x)> 0 para sa x< x 0 , f"(x)< 0 para sa x > x 0 . Ilapat natin ang Lagrange theorem sa pagkakaiba f(x) - f(x 0 ) = f "(c)(x- x 0), saan c nasa pagitan ng x at x 0 .
Kaya, para sa lahat ng mga halaga x sapat na malapit sa x 0 f(x)< f(x 0 ) . At ito ay nangangahulugan na sa punto x 0 ang function ay may maximum.
Ang pangalawang bahagi ng pinakamababang teorama ay napatunayang katulad.

Ilarawan natin ang kahulugan ng theorem na ito sa figure. Hayaan f"(x 1 ) =0 at para sa alinman x, sapat na malapit sa x 1, ang hindi pagkakapantay-pantay
f"(x)< 0 sa x< x 1 , f "(x)> 0 sa x > x 1 .
Pagkatapos ay sa kaliwa ng punto x 1 ang function ay tumataas, at bumababa sa kanan, samakatuwid, kapag x = x Ang 1 function ay napupunta mula sa pagtaas hanggang sa pagbaba, iyon ay, mayroon itong maximum.
Katulad nito, maaaring isaalang-alang ng isa ang mga punto x 2 at x 3 .

Sa eskematiko, ang lahat ng nasa itaas ay maaaring ilarawan sa larawan:
Ang panuntunan para sa pag-aaral ng function na y=f(x) para sa isang extremum
Mga halimbawa. I-explore ang mga function para sa minimum at maximum.
ANG PINAKA DAKILANG AT MINIMUM NA MGA VALUE NG PAG-andar SA INTERCEPT
ang pinakadakila ang halaga ng isang function sa isang segment ay ang pinakamalaki sa lahat ng value nito sa segment na ito, at hindi bababa sa ay ang pinakamaliit sa lahat ng mga halaga nito.
Isaalang-alang ang function y=f(x) tuloy-tuloy sa pagitan [ a, b]. Tulad ng nalalaman, ang naturang function ay umabot sa pinakamataas at pinakamababang halaga nito, alinman sa hangganan ng segment, o sa loob nito. Kung ang maximum o minimum na halaga ng function ay naabot sa panloob na punto ng segment, ang halagang ito ay ang maximum o minimum ng function, iyon ay, naabot ito sa mga kritikal na punto.
Kaya, nakukuha namin ang sumusunod ang panuntunan para sa paghahanap ng pinakamalaki at pinakamaliit na halaga ng isang function sa segment [ a, b] :
>> Extremes
Extremum ang pag-andar
Kahulugan ng extremum
Function y = f(x) ay tinatawag dumarami (humihina) sa ilang pagitan kung para sa x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).
Kung ang isang differentiable function na y \u003d f (x) sa isang segment ay tumataas (bumababa), kung gayon ang derivative nito sa segment na ito f " (x)> 0
(f"(x)< 0).
Dot x tungkol sa tinawag lokal na pinakamataas na punto (pinakamababa) ng function na f (x ) kung mayroong kapitbahayan ng punto x o, para sa lahat ng mga punto kung saan ang hindi pagkakapantay-pantay f (x)≤ f (x o) (f (x)≥ f (x o )).
Tinatawag ang pinakamataas at pinakamababang puntos matinding puntos, at ang mga halaga ng function sa mga puntong ito ay nito extrema.
matinding puntos
Mga kinakailangang kondisyon para sa isang extremum . Kung punto x tungkol sa ay isang extremum point ng function na f (x), pagkatapos ay alinman sa f " (x o ) = 0, o f(x o ) ay wala. Ang ganitong mga punto ay tinatawag mapanganib, kung saan ang function mismo ay tinukoy sa kritikal na punto. Ang extrema ng isang function ay dapat hanapin sa mga kritikal na punto nito.
Ang unang sapat na kondisyon. Hayaan x tungkol sa - kritikal na punto. kung f" (x ) kapag dumadaan sa punto x tungkol sa binabago ang plus sign sa minus, pagkatapos ay sa punto x o ang function ay may maximum, kung hindi man ito ay may isang minimum. Kung ang derivative ay hindi nagbabago ng sign kapag dumadaan sa isang kritikal na punto, pagkatapos ay sa punto x tungkol sa walang extremum.
Ang pangalawang sapat na kondisyon.
Hayaang magkaroon ang function na f(x).
f" (x ) sa paligid ng punto x
tungkol sa
at ang pangalawang derivative sa pinakadulo x o. kung f"(x o) = 0, >0 ( <0), то точка x o ay isang lokal na minimum (maximum) na punto ng function na f(x). Kung =0, dapat gamitin ng isa ang unang sapat na kundisyon, o isama ang mas mataas.
Sa isang segment, maaaring maabot ng function na y \u003d f (x) ang pinakamaliit o pinakamalaking halaga alinman sa mga kritikal na punto o sa mga dulo ng segment.
Halimbawa 3.22.
Desisyon. Bilang f " (
Mga gawain para sa paghahanap ng extremum ng isang function
Halimbawa 3.23. a
Desisyon. x at y y
0
≤ x≤
> 0, habang x >a /4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
mga function sq..
mga yunit).
Halimbawa 3.24. p ≈
Desisyon. pp
S"
R = 2, H = 16/4 = 4.
Halimbawa 3.22.Hanapin ang extrema ng function f (x) = 2x 3 - 15x 2 + 36x - 14.
Desisyon. Bilang f " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), pagkatapos ay ang mga kritikal na punto ng function x 1 \u003d 2 at x 2 \u003d 3. Ang mga matinding puntos ay maaari lamang sa mga ito puntos. Dahil kapag dumadaan sa punto x 1 \u003d 2, ang derivative ay nagbabago ng sign mula plus hanggang minus, pagkatapos ay sa puntong ito ang function ay may maximum. Kapag dumadaan sa punto x 2 \u003d 3, ang derivative ay nagbabago ng sign mula minus hanggang plus, samakatuwid, sa punto x 2 \u003d 3, ang function ay may pinakamababa. Pagkalkula ng mga halaga ng function sa mga puntos
x 1 = 2 at x 2 = 3, nakita namin ang extrema ng function: maximum f (2) = 14 at minimum f (3) = 13.
Halimbawa 3.23.Kinakailangan na bumuo ng isang hugis-parihaba na lugar malapit sa pader na bato upang ito ay nabakuran ng wire mesh sa tatlong panig, at magkadugtong sa dingding sa ikaapat na bahagi. Para dito mayroong a mga linear na metro ng grid. Sa anong aspect ratio magkakaroon ang site ng pinakamalaking lugar?
Desisyon.Tukuyin ang mga gilid ng site sa pamamagitan ng x at y. Ang lugar ng site ay katumbas ng S = xy. Hayaan y ay ang haba ng gilid na katabi ng dingding. Pagkatapos, ayon sa kondisyon, ang pagkakapantay-pantay na 2x + y = ay dapat hawakan. Samakatuwid y = a - 2x at S = x (a - 2x), kung saan
0
≤ x≤ a /2 (ang haba at lapad ng pad ay hindi maaaring negatibo). S "= a - 4x, a - 4x = 0 para sa x = a/4, kung saan
y \u003d a - 2 × a / 4 \u003d a / 2. Sa abot ng Ang x = a /4 ay ang tanging kritikal na punto, tingnan natin kung nagbabago ang tanda ng derivative kapag dumadaan sa puntong ito. Para sa x a /4 S "> 0, habang x >a /4 S " < 0, значит, в точке x=a
/4 функция S имеет максимум. Значение
mga function S(a/4) = a/4(a - a/2) = a 2/8 (sq..
mga yunit).
Dahil ang S ay tuloy-tuloy at ang mga halaga nito sa mga dulo ng S(0) at S(a /2) ay katumbas ng zero, kung gayon ang halagang makikita ay ang pinakamalaking halaga ng function. Kaya, ang pinakakanais-nais na aspect ratio ng site sa ilalim ng ibinigay na mga kondisyon ng problema ay y = 2x.
Halimbawa 3.24.Kinakailangang gumawa ng closed cylindrical tank na may kapasidad na V=16 p ≈ 50 m 3. Ano ang dapat na mga sukat ng tangke (radius R at taas H) upang magamit ang hindi bababa sa dami ng materyal para sa paggawa nito?
Desisyon.Ang kabuuang lugar ng ibabaw ng silindro ay S = 2 p R(R+H). Alam namin ang dami ng silindro V = p R 2 N Þ N \u003d V / p R 2 \u003d 16 p / p R 2 \u003d 16 / R 2. Kaya S(R) = 2 p (R2+16/R). Nahanap namin ang derivative ng function na ito:
S"(R) \u003d 2 p (2R- 16 / R 2) \u003d 4 p (R- 8 / R 2). S" (R) = 0 para sa R 3 = 8, samakatuwid,
R = 2, H = 16/4 = 4.
Mga pag-andar, hindi kinakailangang malaman ang tungkol sa pagkakaroon ng una at pangalawang derivatives at maunawaan ang kanilang pisikal na kahulugan. Una kailangan mong maunawaan ang mga sumusunod:
- ang extrema ng function ay nag-maximize o, sa kabaligtaran, i-minimize ang halaga ng function sa isang arbitraryong maliit na kapitbahayan;
- sa extremum point ay hindi dapat magkaroon ng discontinuity ng function.
At ngayon ang parehong bagay, lamang sa mga simpleng termino. Tumingin sa dulo ng ballpen. Kung ang panulat ay inilagay patayo, na may nakasulat na dulo, kung gayon ang pinakagitna ng bola ang magiging matinding punto - ang pinakamataas na punto. Sa kasong ito, pinag-uusapan natin ang maximum. Ngayon, kung ibabaling mo ang panulat na may dulo ng pagsulat pababa, pagkatapos ay sa gitna ng bola magkakaroon na ng isang minimum na function. Sa tulong ng figure na ibinigay dito, maaari mong isipin ang mga nakalistang manipulasyon para sa isang stationery na lapis. Kaya, ang extrema ng isang function ay palaging kritikal na mga punto: ang maxima o minima nito. Ang katabing seksyon ng tsart ay maaaring arbitraryong matalim o makinis, ngunit dapat itong umiiral sa magkabilang panig, tanging sa kasong ito ang punto ay isang extremum. Kung ang tsart ay nasa isang gilid lamang, ang puntong ito ay hindi magiging isang extremum kahit na ang mga extremum na kondisyon ay natutugunan sa isa sa mga gilid nito. Ngayon, pag-aralan natin ang extrema ng function mula sa siyentipikong pananaw. Upang maituring na extremum ang isang punto, kinakailangan at sapat na:
- ang unang derivative ay katumbas ng zero o hindi umiiral sa punto;
- ang unang derivative na pagbabago sign sa puntong ito.

Medyo naiiba ang interpretasyon sa kundisyon mula sa punto de vista ng mga higher-order derivatives: para sa isang function na naiba-iba sa isang punto, sapat na mayroong odd-order derivative na hindi katumbas ng zero, habang ang lahat ng lower-order derivatives ay dapat umiiral at katumbas ng zero. Ito ang pinakasimpleng interpretasyon ng mga teorema mula sa mga aklat-aralin. Ngunit para sa karamihan ng mga ordinaryong tao, ito ay nagkakahalaga ng pagpapaliwanag sa puntong ito na may isang halimbawa. Ang batayan ay isang ordinaryong parabola. Agad na magpareserba, sa zero point ay mayroon itong minimum. Maliit na math lang:
- unang hinalaw (X 2) | = 2X, para sa zero point 2X = 0;
- pangalawang derivative (2X) | = 2, para sa zero point 2 = 2.

Sa simpleng paraan na ito, inilalarawan ang mga kundisyon na tumutukoy sa extrema ng function para sa mga first-order derivatives at para sa higher-order derivatives. Maaari nating idagdag dito na ang pangalawang derivative ay ang parehong derivative ng isang kakaibang order, hindi katumbas ng zero, na tinalakay nang mas mataas ng kaunti. Pagdating sa extrema ng isang function ng dalawang variable, dapat matugunan ang mga kundisyon para sa parehong argumento. Kapag naganap ang paglalahat, pagkatapos ay papasok ang mga partial derivatives. Iyon ay, ito ay kinakailangan para sa pagkakaroon ng isang extremum sa isang punto na ang parehong first-order derivatives ay katumbas ng zero, o hindi bababa sa isa sa mga ito ay wala. Para sa sapat na pagkakaroon ng extremum, sinisiyasat ang isang expression, na siyang pagkakaiba sa pagitan ng produkto ng mga second-order derivatives at ang square ng mixed second-order derivative ng function. Kung ang expression na ito ay mas malaki kaysa sa zero, pagkatapos ay mayroong isang extremum, at kung mayroong isang pagkakapantay-pantay sa zero, kung gayon ang tanong ay nananatiling bukas, at ang karagdagang pananaliksik ay kinakailangan.
