1. The fish is in danger. Swimming at a speed V past a large coral, a small fish felt danger and began to move with a constant (in modulus and direction) acceleration a = 2 m/s 2 . After a time t = 5 s after the start accelerated movement its speed turned out to be directed at an angle of 90 to the initial direction of motion and was twice the initial one. Determine the module of the initial speed V, with which the fish swam past the coral.
Solution 1: Let's use the vector equation
V con \u003d V + a * t. Considering that Vcon = 2V and that
V con V, it can be represented as vector triangle speeds. Using the Pythagorean theorem, we find the answer: V = at= 4.5 m/s.
Complete correct solution
The triangle of speeds is built
Using the Pythagorean theorem, the answer is found
If the problem was solved analytically, the first 5 points are given for the written system of equations (dependence of velocity projections on time)
Correct answer received
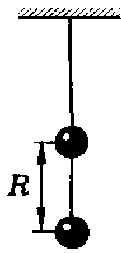
2.
Two identical balls, mass 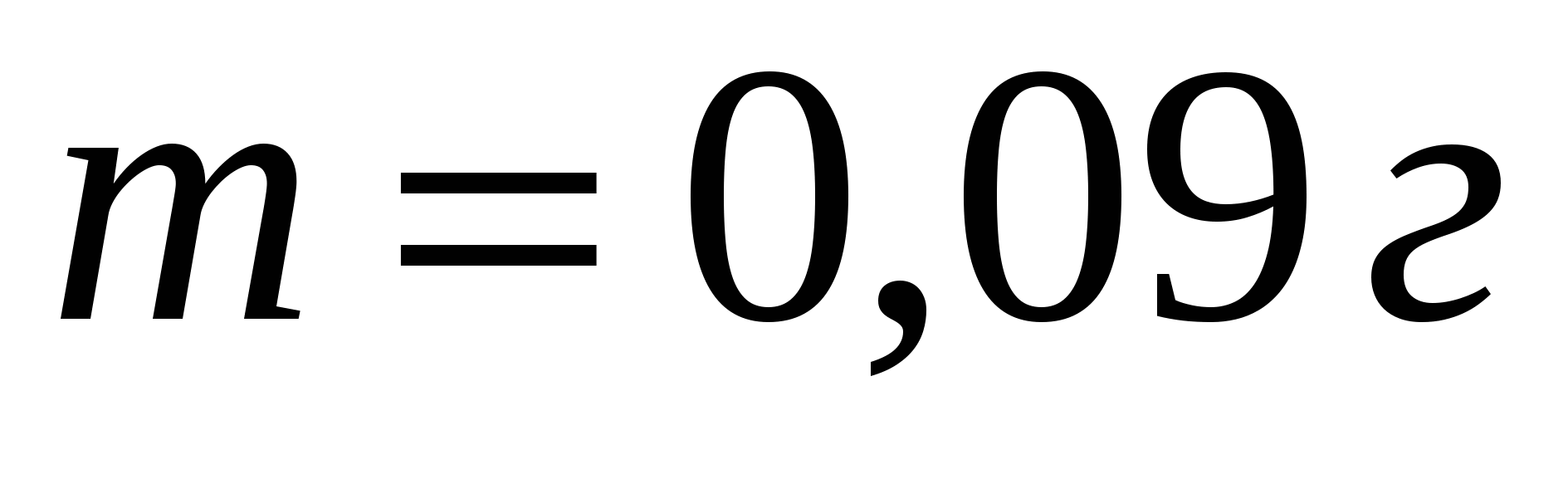 each, charged the same signs, connected by a thread and suspended from the ceiling (Fig.). What charge must each ball have in order for the thread tension to be the same? Distance between ball centers
each, charged the same signs, connected by a thread and suspended from the ceiling (Fig.). What charge must each ball have in order for the thread tension to be the same? Distance between ball centers  . What is the tension of each thread?
. What is the tension of each thread?
The coefficient of proportionality in the Coulomb law k \u003d 9 10 9 Nm 2 /C 2.
Solution 2:
The figure shows the forces acting on both bodies. From it it is clear that
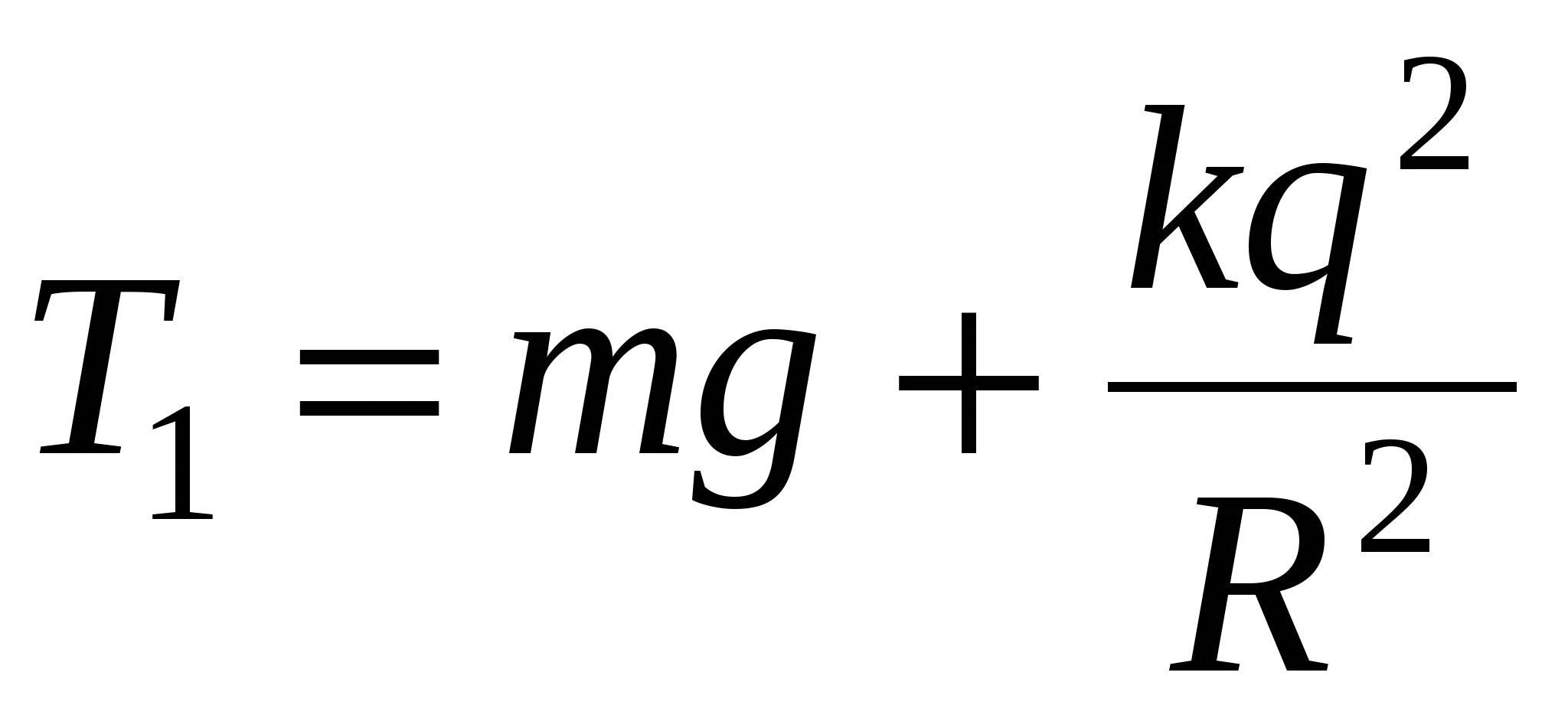
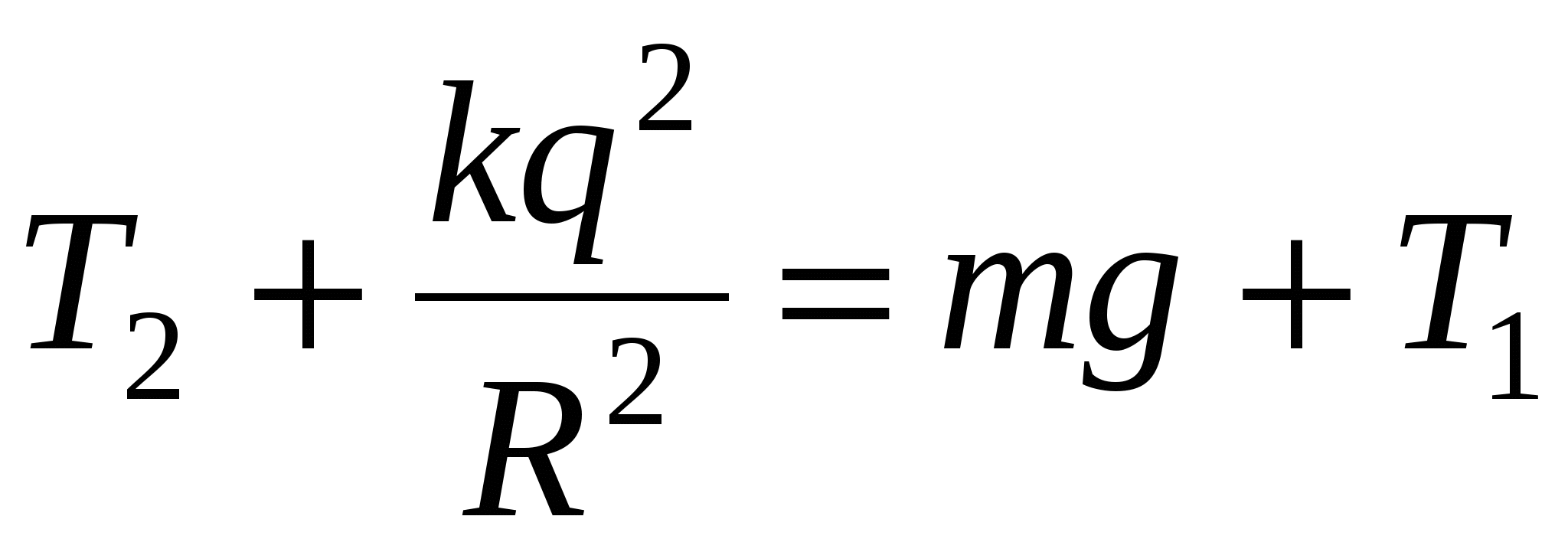
Given that 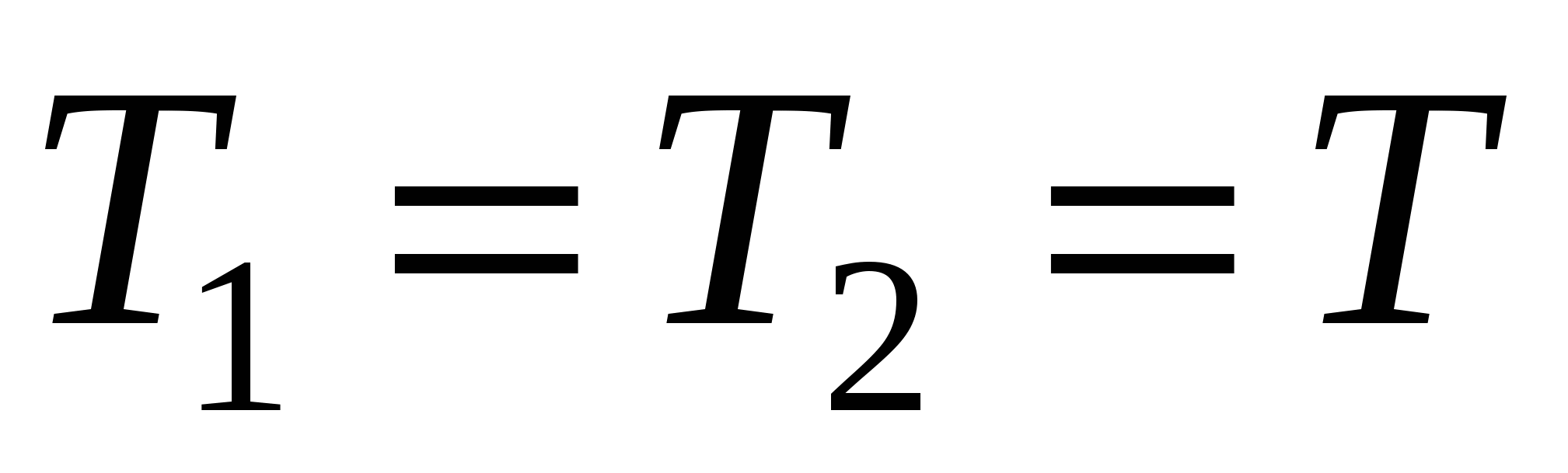 find
find
![]() Cl.
Cl.
Correctness (falseness) of the decision
Complete correct solution
The right decision. There are some minor flaws that do not affect the overall solution.
Made a drawing with active forces, Newton's 2nd law is written for 1 and 2 bodies.
Correct answer received
There are separate equations related to the essence of the problem in the absence of a solution (or in case of an erroneous solution).
The solution is incorrect or missing.
Task 3.
The calorimeter contains water with a mass m in = 0.16 kg and a temperature t in = 30 o C. In order,
to cool the water, ice of mass m l = 80 g was transferred from the refrigerator into a glass.
the refrigerator maintains a temperature t l \u003d -12 o C. Determine the final temperature in
calorimeter. Specific heat capacity of water C in \u003d 4200 J / (kg * o C), specific heat ice
Cl \u003d 2100 J / (kg * o C), specific heat ice melting λ = 334 kJ/kg.
Solution 3:
Since it is not clear what the final content of the calorimeter will be (will all the ice melt?)
Let's solve the problem in numbers.
The amount of heat released when cooling water: Q 1 \u003d 4200 * 0.16 * 30 J \u003d 20160
The amount of heat absorbed when ice is heated: Q 2 \u003d 2100 * 0.08 * 12 J \u003d 2016
The amount of heat absorbed during the melting of ice: Q 3 \u003d 334000 * 0.08 J \u003d 26720 J.
It can be seen that the amount of heat Q 1 is not enough to melt all the ice
(Q 1< Q 2 + Q 3). Это означает, что в конце процесса в сосуде будут находится и лёд, и вода, а
the temperature of the mixture will be equal to t = 0 o C.
Correctness (falseness) of the decision
Complete correct solution
The right decision. There are some minor flaws that do not affect the overall solution.
The solution as a whole is correct, however, it contains significant errors (not physical, but mathematical).
A formula was written for calculating the amount of heat for 1, 2 and 3 processes (2 points for each formula)
Correct answer received
There is an understanding of the physics of the phenomenon, but one of the equations necessary for solving has not been found; as a result, the resulting system of equations is not complete and it is impossible to find a solution.
There are separate equations related to the essence of the problem in the absence of a solution (or in case of an erroneous solution).
The solution is incorrect or missing.
Task 4
The experimenter collected electrical circuit consisting of different batteries with
negligible internal resistances and identical fusible
fuses, and drew a diagram of it (the fuses in the diagram are indicated in black
rectangles). At the same time, he forgot to indicate in the figure part of the EMF of the batteries. However
uh ![]() the experimenter remembers that on that day during the experiment all the fuses remained
the experimenter remembers that on that day during the experiment all the fuses remained
whole. Retrieve the unknown EMF values.
Solution 4:
If, when bypassing any closed circuit algebraic sum EMF was
would not zero, then a very large current would arise in this circuit (due to the smallness
internal resistance batteries) and the fuses would blow. Since this is not
happened, we can write the following equalities:
E1 - E2 - E4 = 0, whence E4 = 4 V,
E3 + E5 - E4 = 0, whence E5 = 1 V,
E5 + E2 - E6 = 0, hence E6 = 6 V.
Correctness (falseness) of the decision
Complete correct solution
The right decision. There are some minor flaws that do not affect the overall solution.
The idea is formulated that the sum of the EMF is equal to zero when bypassing any circuit
Correctly found values of three unknown EMF - 2 points for each
There is an understanding of the physics of the phenomenon, but one of the equations necessary for solving has not been found; as a result, the resulting system of equations is not complete and it is impossible to find a solution.
There are separate equations related to the essence of the problem in the absence of a solution (or in case of an erroneous solution).
The solution is incorrect or missing.
A small bar through a system of blocks is connected by an inextensible thread with a long cart that can roll on a horizontal surface. The bar is placed on a trolley and set in motion with constant speedν = 2 m/s, directed horizontally along the cart (see Fig. 1.1).
What speed relative to the bar will the cart have at the moment when the angle between the inclined thread and the horizon is α = 60°? Consider that at the indicated moment the cart has not reached the wall to which the blocks are attached.
Possible Solution
Due to the inextensibility of the thread, the projection of the speed of the point A of the rope on the direction AB is equal to the projection of the speed of the point D of the rope on the direction DC, i.e. ν∙cosα = u, where u is the speed of the trolley relative to the ground. The speed of the trolley relative to the bar is: ν rel. = u+ ν = ν∙(1+cosα) = 3 m/s.
Answer: v rel. = 3 m/s.
Evaluation criteria
Task 2
An ice floe with a bullet frozen into it hangs on a thread and is partially submerged in water, which is in a thin-walled cylindrical glass standing on a table. The ice does not touch the walls and bottom of the glass. The area of the bottom of the glass S = 100 cm 2. The tension force of the thread is F = 1 N. How much will the water level in the glass change after the ice has melted? Will it rise or fall? The bullet has a mass m = 10 g and a density ρ = 10,000 kg/m 3 . Water density ρ 0 \u003d 1000 kg / m 3
Possible Solution
Consider external forces acting on the contents of a glass, in which we include water, ice and a bullet. Gravity is compensated by two upward external forces- force F and pressure force from the bottom. The latter, according to Newton's third law, is equal in absolute value to the force of pressure on the bottom from the side of the liquid. From the equilibrium condition for the contents of the glass in the initial state, it follows:
F + S∙ρ 0 ∙g∙h 1 = m containing ∙g,
where h 1 is the height of the water level in the initial state.
After the ice melts, the mass of the contents is preserved, but the level changes
water in the glass and hence the pressure of the water near the bottom. In addition, the force F ceases to act, but to the bottom with the force
![]()
the bullet starts to hit. The new equilibrium condition for the contents of the glass has the form:
S∙ρ 0 ∙g∙h2 + N = m containing ∙g,
where h 2 is the height of the water level in the final state.
Subtracting the second equation from the first equation, we obtain an expression for changing the water level in the glass:
![]()
Since this value is positive, the level will rise.
Evaluation criteria
Total no more 10 points for the task!
Task 3
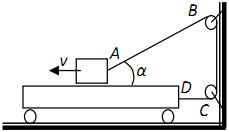
A small ball of mass m, suspended on a light inextensible thread from the ceiling of a room, was released without initial velocity from the state in which the thread was horizontal. Find the work done by the tension on the ball as it moves from the top to the bottom. Give the answer for the frame of reference associated with the room, and for the frame of reference moving horizontally relative to the room in the plane of the picture with a constant speed V. The length of the thread is L. The frame of reference associated with the room can be considered inertial.
Possible Solution
In the frame of reference associated with the room, the tension force of the thread at any moment of motion is directed perpendicular to the speed of the ball, therefore, its work is zero.
The law of conservation of mechanical energy for a ball has the form
m∙g∙L = m∙u 2 /2,
where you can find the speed of the ball in the lower position:
In a moving frame of reference starting speed ball is modulo V, and
the modulus of the final velocity of the ball is |V – u|. Then from the theorem on kinetic energy for a ball:
![]()
From this we obtain that the work of the thread tension force is equal to:
Since in a moving reference frame at any moment the angle between the velocity vectors of the ball and the tension force is obtuse, the work of this force is negative.
Evaluation criteria
Task 4
A board of mass m 1 = 2 kg lies on the table, and a block of mass m 2 = 1 kg lies on the board. A light thread is tied to the bar, the second end of which is thrown over an ideal block fixed on the edge of the board. The coefficients of friction between the board and the table and between the bar and the board are the same and equal to μ = 0.1. The section of the thread between the bar and the block is horizontal. With what modulus accelerations will the bar and the board begin to move if a downward force F = 5 N is applied to the vertical section of the thread? Acceleration free fall can be considered equal to g \u003d 10 m / s 2.
Possible Solution
Three forces act on the board in the horizontal direction: the thread tension force directed to the right and the friction forces directed to the left from the side of the floor and the bar. The horizontal component of the thread tension force acting on the board to the right is 5 N in absolute value. It is greater than the sum of the modules of the maximum possible friction forces that act on the board:
μ[(m 1 + m 2)∙g + F] + μ∙m 2 + μ∙m 2 ∙g = 4.5 H
Therefore, the board will slide across the floor to the right. At the same time, it is obvious that
the block will slide along the board to the left. From Newton's second law,
written for the board and for the bar, we find the modules of their accelerations:
Evaluation criteria
Task 5
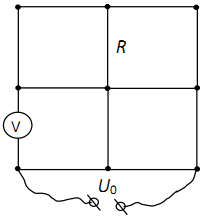
An electrical circuit is a wire mesh consisting of links having the same resistance. R. One link is replaced by a voltmeter, the resistance of which is also equal to R. A voltage source is connected to the grid U 0 = 20 V as shown in Figure 5.1. Find the voltmeter reading.
Possible Solution
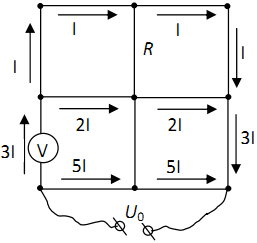
Let us depict schematically the currents flowing in the links of the grid, taking into account its symmetry and Ohm's law for the circuit section. According to this law, the current strengths in parallel links under the same voltage are inversely proportional to the resistances of these links. When depicting currents, one must also take into account the conservation law electric charge for grid nodes, the sum of currents flowing into the node must be equal to the sum of currents flowing out of the node. In addition, note that, due to the symmetry of the circuit, currents do not flow through the middle vertical conductors.
If a current flows through the upper links with a force I, then a current flows through the middle horizontal conductors with a force 2 I(because current I flows through links with a common resistance 4 R, and the current 2 I- through links with a common resistance 2 R). current force 3 I flows through a circuit with a common resistance 10 R/3 - this section includes all elements, except for the two lower horizontal links. This means that through the two lower horizontal links with a total resistance 2 R current flows with force 5 I. The voltage across these two lower links is U 0 = IR. For a voltmeter, you can write: U v = 3∙ I∙ R. From here
U v =3∙ U 0 / 10 = 6 V.
Answer : U v = 6 V
Evaluation criteria
When solving by constructing an equivalent circuit:
- Points for each correct action add up.
- At arithmetic error(including an error in the conversion of units of measurement) score reduced by 1 point.
- Maximum for 1 task - 10 points.
- Total for work - 50 points.
