Lesson content

Adding fractions with the same denominators

Adding fractions is of two types:

1. Adding fractions with the same denominators
2. Adding fractions with different denominators

Let's start with adding fractions with the same denominators. Everything is simple here. To add fractions with the same denominators, you need to add their numerators, and leave the denominator unchanged. For example, let's add the fractions and . We add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into four parts. If you add pizza to pizza, you get pizza:

Example 2 Add fractions and .

The answer is an improper fraction. If the end of the task comes, then it is customary to get rid of improper fractions. To get rid of an improper fraction, you need to select the whole part in it. In our case, the integer part is allocated easily - two divided by two is equal to one:

This example can be easily understood if we think of a pizza that is divided into two parts. If you add more pizzas to the pizza, you get one whole pizza:

Example 3. Add fractions and .

Again, add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you add more pizzas to pizza, you get pizzas:

Example 4 Find the value of an expression

This example is solved in exactly the same way as the previous ones. The numerators must be added and the denominator left unchanged:

Let's try to depict our solution using a picture. If you add pizzas to a pizza and add more pizzas, you get 1 whole pizza and more pizzas.

As you can see, adding fractions with the same denominators is not difficult. It is enough to understand the following rules:

1. To add fractions with the same denominators, you need to add their numerators, and leave the denominator unchanged;

Adding fractions with different denominators

Now we will learn how to add fractions with different denominators. When adding fractions, the denominators of those fractions must be the same. But they are not always the same.

For example, fractions can be added because they have the same denominators.

But fractions cannot be added at once, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

There are several ways to reduce fractions to the same denominator. Today we will consider only one of them, since the rest of the methods may seem complicated for a beginner.

The essence of this method lies in the fact that first (LCM) of the denominators of both fractions is sought. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained. They do the same with the second fraction - the NOC is divided by the denominator of the second fraction and the second additional factor is obtained.

Then the numerators and denominators of the fractions are multiplied by their additional factors. As a result of these actions, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to add such fractions.

Example 1. Add fractions and

First of all, we find the least common multiple of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 2. The least common multiple of these numbers is 6

LCM (2 and 3) = 6

Now back to fractions and . First, we divide the LCM by the denominator of the first fraction and get the first additional factor. LCM is the number 6, and the denominator of the first fraction is the number 3. Divide 6 by 3, we get 2.

The resulting number 2 is the first additional factor. We write it down to the first fraction. To do this, we make a small oblique line above the fraction and write down the found additional factor above it:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction and get the second additional factor. LCM is the number 6, and the denominator of the second fraction is the number 2. Divide 6 by 2, we get 3.

The resulting number 3 is the second additional factor. We write it to the second fraction. Again, we make a small oblique line above the second fraction and write down the found additional factor above it:

Now we are all set to add. It remains to multiply the numerators and denominators of fractions by their additional factors:

Look closely at what we have come to. We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to add such fractions. Let's complete this example to the end:

Thus the example ends. To add it turns out.

Let's try to depict our solution using a picture. If you add pizzas to a pizza, you get one whole pizza and another sixth of a pizza:

Reduction of fractions to the same (common) denominator can also be depicted using a picture. Bringing the fractions and to a common denominator, we get the fractions and . These two fractions will be represented by the same slices of pizzas. The only difference will be that this time they will be divided into equal shares (reduced to the same denominator).

The first drawing shows a fraction (four pieces out of six) and the second picture shows a fraction (three pieces out of six). Putting these pieces together we get (seven pieces out of six). This fraction is incorrect, so we have highlighted the integer part in it. The result was (one whole pizza and another sixth pizza).

Note that we have painted this example in too much detail. In educational institutions it is not customary to write in such a detailed manner. You need to be able to quickly find the LCM of both denominators and additional factors to them, as well as quickly multiply the additional factors found by your numerators and denominators. While at school, we would have to write this example as follows:

But there is also the other side of the coin. If detailed notes are not made at the first stages of studying mathematics, then questions of the kind “Where does that number come from?”, “Why do fractions suddenly turn into completely different fractions? «.

To make it easier to add fractions with different denominators, you can use the following step-by-step instructions:

1. Find the LCM of the denominators of fractions;
2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction;
3. Multiply the numerators and denominators of fractions by their additional factors;
4. Add fractions that have the same denominators;
5. If the answer turned out to be an improper fraction, then select its whole part;

Example 2 Find the value of an expression .

Let's use the instructions above.

Step 1. Find the LCM of the denominators of fractions

Find the LCM of the denominators of both fractions. The denominators of the fractions are the numbers 2, 3 and 4

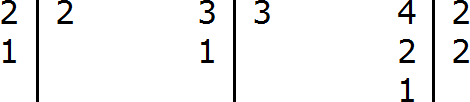
Step 2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction

Divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 2. Divide 12 by 2, we get 6. We got the first additional factor 6. We write it over the first fraction:

Now we divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 3. Divide 12 by 3, we get 4. We got the second additional factor 4. We write it over the second fraction:

Now we divide the LCM by the denominator of the third fraction. LCM is the number 12, and the denominator of the third fraction is the number 4. Divide 12 by 4, we get 3. We got the third additional factor 3. We write it over the third fraction:

Step 3. Multiply the numerators and denominators of fractions by your additional factors

We multiply the numerators and denominators by our additional factors:

Step 4. Add fractions that have the same denominators

We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. It remains to add these fractions. Add up:

The addition didn't fit on one line, so we moved the remaining expression to the next line. This is allowed in mathematics. When an expression does not fit on one line, it is carried over to the next line, and it is necessary to put an equal sign (=) at the end of the first line and at the beginning of a new line. The equal sign on the second line indicates that this is a continuation of the expression that was on the first line.

Step 5. If the answer turned out to be an improper fraction, then select the whole part in it

Our answer is an improper fraction. We must single out the whole part of it. We highlight:

Got an answer

Subtraction of fractions with the same denominators

There are two types of fraction subtraction:

1. Subtraction of fractions with the same denominators
2. Subtraction of fractions with different denominators

First, let's learn how to subtract fractions with the same denominators. Everything is simple here. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator the same.

For example, let's find the value of the expression . To solve this example, it is necessary to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged. Let's do this:

This example can be easily understood if we think of a pizza that is divided into four parts. If you cut pizzas from a pizza, you get pizzas:

Example 2 Find the value of the expression .

Again, from the numerator of the first fraction, subtract the numerator of the second fraction, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you cut pizzas from a pizza, you get pizzas:

Example 3 Find the value of an expression

This example is solved in exactly the same way as the previous ones. From the numerator of the first fraction, you need to subtract the numerators of the remaining fractions:

As you can see, there is nothing complicated in subtracting fractions with the same denominators. It is enough to understand the following rules:

1. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged;
2. If the answer turned out to be an improper fraction, then you need to select the whole part in it.

Subtraction of fractions with different denominators

For example, a fraction can be subtracted from a fraction, since these fractions have the same denominators. But a fraction cannot be subtracted from a fraction, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.

The common denominator is found according to the same principle that we used when adding fractions with different denominators. First of all, find the LCM of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained, which is written over the first fraction. Similarly, the LCM is divided by the denominator of the second fraction and a second additional factor is obtained, which is written over the second fraction.

The fractions are then multiplied by their additional factors. As a result of these operations, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to subtract such fractions.

Example 1 Find the value of an expression:

These fractions have different denominators, so you need to bring them to the same (common) denominator.

First, we find the LCM of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 4. The least common multiple of these numbers is 12

LCM (3 and 4) = 12

Now back to fractions and

Let's find an additional factor for the first fraction. To do this, we divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 3. Divide 12 by 3, we get 4. We write the four over the first fraction:

We do the same with the second fraction. We divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 4. Divide 12 by 4, we get 3. Write a triple over the second fraction:

Now we are all set for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to subtract such fractions. Let's complete this example to the end:

Got an answer

Let's try to depict our solution using a picture. If you cut pizzas from a pizza, you get pizzas.

This is the detailed version of the solution. Being at school, we would have to solve this example in a shorter way. Such a solution would look like this:

Reduction of fractions and to a common denominator can also be depicted using a picture. Bringing these fractions to a common denominator, we get the fractions and . These fractions will be represented by the same pizza slices, but this time they will be divided into the same fractions (reduced to the same denominator):

The first drawing shows a fraction (eight pieces out of twelve), and the second picture shows a fraction (three pieces out of twelve). By cutting off three pieces from eight pieces, we get five pieces out of twelve. The fraction describes these five pieces.

Example 2 Find the value of an expression

These fractions have different denominators, so you first need to bring them to the same (common) denominator.

Find the LCM of the denominators of these fractions.

The denominators of the fractions are the numbers 10, 3 and 5. The least common multiple of these numbers is 30

LCM(10, 3, 5) = 30

Now we find additional factors for each fraction. To do this, we divide the LCM by the denominator of each fraction.

Let's find an additional factor for the first fraction. LCM is the number 30, and the denominator of the first fraction is the number 10. Divide 30 by 10, we get the first additional factor 3. We write it over the first fraction:

Now we find an additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 30, and the denominator of the second fraction is the number 3. Divide 30 by 3, we get the second additional factor 10. We write it over the second fraction:

Now we find an additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is the number 30, and the denominator of the third fraction is the number 5. Divide 30 by 5, we get the third additional factor 6. We write it over the third fraction:

Now everything is ready for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.

The continuation of the example will not fit on one line, so we move the continuation to the next line. Don't forget about the equal sign (=) on the new line:

The answer turned out to be a correct fraction, and everything seems to suit us, but it is too cumbersome and ugly. We should make it easier. What can be done? You can reduce this fraction.

To reduce a fraction, you need to divide its numerator and denominator by (gcd) the numbers 20 and 30.

So, we find the GCD of the numbers 20 and 30:

Now we return to our example and divide the numerator and denominator of the fraction by the found GCD, that is, by 10

Got an answer

Multiplying a fraction by a number

To multiply a fraction by a number, you need to multiply the numerator of the given fraction by this number, and leave the denominator the same.

Example 1. Multiply the fraction by the number 1.

Multiply the numerator of the fraction by the number 1

The entry can be understood as taking half 1 time. For example, if you take pizza 1 time, you get pizza

From the laws of multiplication, we know that if the multiplicand and the multiplier are interchanged, then the product will not change. If the expression is written as , then the product will still be equal to . Again, the rule for multiplying an integer and a fraction works:

This entry can be understood as taking half of the unit. For example, if there is 1 whole pizza and we take half of it, then we will have pizza:

Example 2. Find the value of an expression

Multiply the numerator of the fraction by 4

The answer is an improper fraction. Let's take a whole part of it:

The expression can be understood as taking two quarters 4 times. For example, if you take pizzas 4 times, you get two whole pizzas.

And if we swap the multiplicand and the multiplier in places, we get the expression. It will also be equal to 2. This expression can be understood as taking two pizzas from four whole pizzas:

Multiplication of fractions

To multiply fractions, you need to multiply their numerators and denominators. If the answer is an improper fraction, you need to select the whole part in it.

Example 1 Find the value of the expression .

Got an answer. It is desirable to reduce this fraction. The fraction can be reduced by 2. Then the final solution will take the following form:

The expression can be understood as taking a pizza from half a pizza. Let's say we have half a pizza:

How to take two-thirds from this half? First you need to divide this half into three equal parts:

And take two from these three pieces:

We'll get pizza. Remember what a pizza looks like divided into three parts:

One slice from this pizza and the two slices we took will have the same dimensions:

In other words, we are talking about the same pizza size. Therefore, the value of the expression is

Example 2. Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer is an improper fraction. Let's take a whole part of it:

Example 3 Find the value of an expression

Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer turned out to be a correct fraction, but it will be good if it is reduced. To reduce this fraction, you need to divide the numerator and denominator of this fraction by the greatest common divisor (GCD) of the numbers 105 and 450.

So, let's find the GCD of the numbers 105 and 450:

Now we divide the numerator and denominator of our answer to the GCD that we have now found, that is, by 15

Representing an integer as a fraction

Any whole number can be represented as a fraction. For example, the number 5 can be represented as . From this, the five will not change its meaning, since the expression means “the number five divided by one”, and this, as you know, is equal to five:

Reverse numbers

Now we will get acquainted with a very interesting topic in mathematics. It's called "reverse numbers".

Definition. Reverse to numbera is the number that, when multiplied bya gives a unit.

Let's substitute in this definition instead of a variable a number 5 and try to read the definition:

Reverse to number 5 is the number that, when multiplied by 5 gives a unit.

Is it possible to find a number that, when multiplied by 5, gives one? It turns out you can. Let's represent five as a fraction:

Then multiply this fraction by itself, just swap the numerator and denominator. In other words, let's multiply the fraction by itself, only inverted:

What will be the result of this? If we continue to solve this example, we get one:

This means that the inverse of the number 5 is the number, since when 5 is multiplied by one, one is obtained.

The reciprocal can also be found for any other integer.

You can also find the reciprocal for any other fraction. To do this, it is enough to turn it over.

Division of a fraction by a number

Let's say we have half a pizza:

Let's divide it equally between two. How many pizzas will each get?

It can be seen that after splitting half of the pizza, two equal pieces were obtained, each of which makes up a pizza. So everyone gets a pizza.

Division of fractions is done using reciprocals. Reciprocals allow you to replace division with multiplication.

To divide a fraction by a number, you need to multiply this fraction by the reciprocal of the divisor.

Using this rule, we will write down the division of our half of the pizza into two parts.

So, you need to divide the fraction by the number 2. Here the dividend is a fraction and the divisor is 2.

To divide a fraction by the number 2, you need to multiply this fraction by the reciprocal of the divisor 2. The reciprocal of the divisor 2 is a fraction. So you need to multiply by

One of the most important sciences, the application of which can be seen in disciplines such as chemistry, physics and even biology, is mathematics. The study of this science allows you to develop some mental qualities, improve the ability to concentrate. One of the topics that deserve special attention in the course "Mathematics" is the addition and subtraction of fractions. Many students find it difficult to study. Perhaps our article will help to better understand this topic.

How to subtract fractions whose denominators are the same

Fractions are the same numbers with which you can perform various actions. Their difference from integers lies in the presence of a denominator. That is why when performing actions with fractions, you need to study some of their features and rules. The simplest case is the subtraction of ordinary fractions, the denominators of which are represented as the same number. It will not be difficult to perform this action if you know a simple rule:

• In order to subtract the second from one fraction, it is necessary to subtract the numerator of the fraction to be subtracted from the numerator of the reduced fraction. We write this number into the numerator of the difference, and leave the denominator the same: k / m - b / m = (k-b) / m.

Examples of subtracting fractions whose denominators are the same

7/19 - 3/19 = (7 - 3)/19 = 4/19.

From the numerator of the reduced fraction "7" subtract the numerator of the subtracted fraction "3", we get "4". We write this number in the numerator of the answer, and put in the denominator the same number that was in the denominators of the first and second fractions - "19".

The picture below shows a few more such examples.

Consider a more complex example where fractions with the same denominators are subtracted:

29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7)/47 = 9/47.

From the numerator of the reduced fraction "29" by subtracting in turn the numerators of all subsequent fractions - "3", "8", "2", "7". As a result, we get the result "9", which we write in the numerator of the answer, and in the denominator we write the number that is in the denominators of all these fractions - "47".

Adding fractions with the same denominator

Addition and subtraction of ordinary fractions is carried out according to the same principle.

• To add fractions with the same denominators, you need to add the numerators. The resulting number is the numerator of the sum, and the denominator remains the same: k/m + b/m = (k + b)/m.

Let's see how it looks like in an example:

1/4 + 2/4 = 3/4.

To the numerator of the first term of the fraction - "1" - we add the numerator of the second term of the fraction - "2". The result - "3" - is written in the numerator of the amount, and the denominator is left the same as that was present in the fractions - "4".

Fractions with different denominators and their subtraction

We have already considered the action with fractions that have the same denominator. As you can see, knowing simple rules, solving such examples is quite easy. But what if you need to perform an action with fractions that have different denominators? Many high school students are confused by such examples. But even here, if you know the principle of the solution, the examples will no longer be difficult for you. There is also a rule here, without which the solution of such fractions is simply impossible.

To subtract fractions with different denominators, they must be reduced to the same smallest denominator.



We will talk in more detail about how to do this.

Fraction property

In order to reduce several fractions to the same denominator, you need to use the main property of the fraction in the solution: after dividing or multiplying the numerator and denominator by the same number, you get a fraction equal to the given one.

So, for example, the fraction 2/3 can have denominators such as "6", "9", "12", etc., that is, it can look like any number that is a multiple of "3". After we multiply the numerator and denominator by "2", we get a fraction of 4/6. After we multiply the numerator and denominator of the original fraction by "3", we get 6/9, and if we perform a similar action with the number "4", we get 8/12. In one equation, this can be written as:

2/3 = 4/6 = 6/9 = 8/12…

How to bring multiple fractions to the same denominator

Consider how to reduce several fractions to the same denominator. For example, take the fractions shown in the picture below. First you need to determine what number can become the denominator for all of them. To make it easier, let's decompose the available denominators into factors.

The denominator of the fraction 1/2 and the fraction 2/3 cannot be factored. The denominator of 7/9 has two factors 7/9 = 7/(3 x 3), the denominator of the fraction 5/6 = 5/(2 x 3). Now you need to determine which factors will be the smallest for all these four fractions. Since the first fraction has the number “2” in the denominator, it means that it must be present in all denominators, in the fraction 7/9 there are two triples, which means that they must also be present in the denominator. Given the above, we determine that the denominator consists of three factors: 3, 2, 3 and is equal to 3 x 2 x 3 = 18.



Consider the first fraction - 1/2. Its denominator contains "2", but there is not a single "3", but there should be two. To do this, we multiply the denominator by two triples, but, according to the property of the fraction, we must multiply the numerator by two triples:
1/2 = (1 x 3 x 3)/(2 x 3 x 3) = 9/18.

Similarly, we perform actions with the remaining fractions.

• 2/3 - one three and one two are missing in the denominator:
  2/3 = (2 x 3 x 2)/(3 x 3 x 2) = 12/18.
• 7/9 or 7/(3 x 3) - the denominator is missing two:
  7/9 = (7 x 2)/(9 x 2) = 14/18.
• 5/6 or 5/(2 x 3) - the denominator is missing a triple:
  5/6 = (5 x 3)/(6 x 3) = 15/18.

All together it looks like this:



How to subtract and add fractions with different denominators

As mentioned above, in order to add or subtract fractions with different denominators, they must be reduced to the same denominator, and then use the rules for subtracting fractions with the same denominator, which have already been described.

Consider this with an example: 4/18 - 3/15.

Finding multiples of 18 and 15:

• The number 18 consists of 3 x 2 x 3.
• The number 15 consists of 5 x 3.
• The common multiple will consist of the following factors 5 x 3 x 3 x 2 = 90.

After the denominator is found, it is necessary to calculate a factor that will be different for each fraction, that is, the number by which it will be necessary to multiply not only the denominator, but also the numerator. To do this, we divide the number that we found (common multiple) by the denominator of the fraction for which additional factors need to be determined.

• 90 divided by 15. The resulting number "6" will be a multiplier for 3/15.
• 90 divided by 18. The resulting number "5" will be a multiplier for 4/18.

The next step in our solution is to bring each fraction to the denominator "90".

We have already discussed how this is done. Let's see how this is written in an example:

(4 x 5) / (18 x 5) - (3 x 6) / (15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.

If fractions with small numbers, then you can determine the common denominator, as in the example shown in the picture below.



Similarly produced and having different denominators.

Subtraction and having integer parts

Subtraction of fractions and their addition, we have already analyzed in detail. But how to subtract if the fraction has an integer part? Again, let's use a few rules:

• Convert all fractions that have an integer part to improper ones. In simple words, remove the whole part. To do this, the number of the integer part is multiplied by the denominator of the fraction, the resulting product is added to the numerator. The number that will be obtained after these actions is the numerator of an improper fraction. The denominator remains unchanged.
• If fractions have different denominators, they should be reduced to the same.
• Perform addition or subtraction with the same denominators.
• When receiving an improper fraction, select the whole part.



There is another way by which you can add and subtract fractions with integer parts. For this, actions are performed separately with integer parts, and separately with fractions, and the results are recorded together.



The above example consists of fractions that have the same denominator. In the case when the denominators are different, they must be reduced to the same, and then follow the steps as shown in the example.

Subtracting fractions from a whole number

Another of the varieties of actions with fractions is the case when the fraction must be subtracted from At first glance, such an example seems difficult to solve. However, everything is quite simple here. To solve it, it is necessary to convert an integer into a fraction, and with such a denominator, which is in the fraction to be subtracted. Next, we perform a subtraction similar to subtraction with the same denominators. For example, it looks like this:

7 - 4/9 = (7 x 9)/9 - 4/9 = 53/9 - 4/9 = 49/9.

The subtraction of fractions given in this article (Grade 6) is the basis for solving more complex examples, which are considered in subsequent classes. Knowledge of this topic is used subsequently to solve functions, derivatives, and so on. Therefore, it is very important to understand and understand the actions with fractions discussed above.

Here we will understand how subtraction of common fractions. First, we get the rule for subtracting fractions with the same denominators. Next, consider the subtraction of fractions with different denominators and give examples of subtraction with detailed solutions. After that, we will focus on subtracting a fraction from a natural number and subtracting a number from a fraction. In conclusion, we will show how the subtraction of ordinary fractions is carried out using the properties of this action.

Immediately, we note that in this article we will only talk about subtracting a smaller fraction from a larger fraction. Other cases are discussed in the article subtraction of rational numbers.

Page navigation.

Subtraction of fractions with the same denominators

To begin with, let's give an example that will allow us to understand how the subtraction of fractions with the same denominators.

Suppose there were five eighths of an apple on the plate, that is, 5/8 of the apple, after which two eighths were taken away. According to the meaning of subtraction (see the general idea of ​​subtraction), the specified action is described as follows: . It is clear that in this case 5−2=3 eighths of an apple remains on the plate. That is, .

The considered example illustrates rule for subtracting fractions with the same denominator: when subtracting fractions with the same denominators, the numerator of the subtrahend is subtracted from the numerator of the minuend, and the denominator remains the same.

The voiced rule with the help of letters is written as follows: . We will use this formula when subtracting fractions with the same denominators.

Consider examples of subtracting fractions with the same denominators.

Example.

Subtract the common fraction 17/15 from the common fraction 24/15.

Solution.

The denominators of the subtracted fractions are equal. The numerator of the minuend is 24 , and the numerator of the subtrahend is 17 , their difference is 7 (24−17=7, if necessary, see the subtraction of natural numbers). Therefore, subtracting fractions with the same denominators 24/15 and 17/15 gives a fraction 7/15.

A short version of the solution looks like this: .

Answer:

.

If possible, it is necessary to reduce the fraction and (or) select the whole part from the improper fraction, which is obtained by subtracting fractions with the same denominators.

Example.

Compute the difference.

Solution.

We use the formula for subtracting fractions with the same denominators: .

Obviously, the numerator and denominator of the resulting fraction are divisible by 2 (see), that is, 22/12 is a reduced fraction. By reducing this fraction by 2, we arrive at the fraction 11/6.

Fraction 11/6 is incorrect (see proper and improper fractions). Therefore, it is necessary to select the whole part from it: .

So, the calculated difference of fractions with the same denominators is .

Here is the whole solution: .

Answer:

.

Subtraction of fractions with different denominators

Subtraction of fractions with different denominators is reduced to subtraction of fractions with the same denominators. To do this, it is enough to bring fractions with different denominators to a common denominator.

So to spend subtraction of fractions with different denominators, necessary:

• reduce fractions to a common denominator (usually fractions lead to the lowest common denominator);
• Subtract the resulting fractions with the same denominators.

Consider examples of subtracting fractions with different denominators.

Example.

Subtract from the common fraction 2/9 the common fraction 1/15.

Solution.

Since the denominators of the fractions to be subtracted are different, we first perform the reduction of fractions to the lowest common denominator: since LCM(9, 15)=45, then the additional factor of the fraction 2/9 is the number 45:9=5, and the additional factor of the fraction is 1/15 is the number 45:15=3 , then and .

It remains to subtract the fraction 3/45 from the fraction 10/45, we get , which gives us the required difference of fractions with different denominators.

Briefly, the solution is written as follows: .

Answer:

We should not forget about the reduction of the fraction obtained after subtraction, as well as the selection of the whole part.

Example.

Subtract the fraction 7/36 from the fraction 19/9.

Solution.

After reducing fractions with different denominators to the lowest common denominator 36, we have fractions 76/9 and 7/36. We calculate their difference: .

The resulting fraction is reducible, after its reduction by 3, we get 23/12. And this fraction is incorrect, having separated the integer part from it, we have .

Let's put together all the actions performed when subtracting the original fractions with different denominators:.

Answer:

.

Subtraction of a natural number from an ordinary fraction

Subtracting a natural number from a fraction can be reduced to the subtraction of ordinary fractions. To do this, it is enough to represent a natural number as a fraction with a denominator of 1. Let's take a look at an example solution.

Example.

Subtract the number 3 from the fraction 83/21.

Solution.

Since the number 3 is equal to the fraction 3/1, then.

Answer:

However, it is more convenient to subtract a natural number from an improper fraction by representing the fraction as a mixed number. Let's show the solution of the previous example in this way.

Subtracting a fraction from a natural number

Subtracting a fraction from a natural number can be reduced to the subtraction of ordinary fractions by representing a natural number as a fraction. Let's analyze the solution of an example illustrating this approach.

Example.

Subtract the common fraction 5/3 from the natural number 7.

Solution.

We represent the number 7 as a fraction 7/1, after which we perform the subtraction: .

Having selected the integer part from the resulting fraction, we get the final answer.

Answer:

However, there is a more rational way to subtract a fraction from a natural number. Its advantages are especially noticeable when the natural number to be reduced and the denominator of the fraction to be subtracted are large numbers. All this will be seen from the examples below.

If the subtracted fraction is correct, then the reduced natural number can be replaced by the sum of two numbers, one of which is equal to one, subtract the correct fraction from one, and then complete the calculation.

Example.

Subtract the common fraction 13/62 from the natural number 1065.

Solution.

The subtracted ordinary fraction is correct. Let's replace the number 1065 with the sum 1064+1 and get . It remains to calculate the value of the resulting expression (we will talk more about the calculation of such expressions in).

Due to the properties of subtraction, the resulting expression can be rewritten as . Calculate the value of the difference in brackets, replacing the unit with a fraction 1/1 , we have . In this way, . This completes the subtraction of the fraction 13/62 from the natural number 1065.

Here is the whole solution:

And now, for comparison, let's show what numbers we would have to work with if we decided to reduce the subtraction of the original numbers to the subtraction of fractions:

Answer:

.

If the fraction to be subtracted is incorrect, then it can be replaced by a mixed number, and then subtract the mixed number from a natural number.

Note! Before writing a final answer, see if you can reduce the fraction you received.

Subtraction of fractions with the same denominators examples:

,

,

Subtracting a proper fraction from one.

If it is necessary to subtract from the unit a fraction that is correct, the unit is converted to the form of an improper fraction, its denominator is equal to the denominator of the subtracted fraction.

An example of subtracting a proper fraction from one:

The denominator of the fraction to be subtracted = 7 , i.e., we represent the unit as an improper fraction 7/7 and subtract according to the rule for subtracting fractions with the same denominators.

Subtracting a proper fraction from a whole number.

Rules for subtracting fractions - correct from integer (natural number):

• We translate the given fractions, which contain an integer part, into improper ones. We get normal terms (it does not matter if they have different denominators), which we consider according to the rules given above;
• Next, we calculate the difference of the fractions that we received. As a result, we will almost find the answer;
• We perform the inverse transformation, that is, we get rid of the improper fraction - we select the integer part in the fraction.

Subtract a proper fraction from a whole number: we represent a natural number as a mixed number. Those. we take a unit in a natural number and translate it into the form of an improper fraction, the denominator is the same as that of the subtracted fraction.

Fraction subtraction example:

In the example, we replaced the unit with an improper fraction 7/7 and instead of 3 we wrote down a mixed number and subtracted a fraction from the fractional part.

Subtraction of fractions with different denominators.

Or, to put it another way, subtraction of different fractions.

Rule for subtracting fractions with different denominators. In order to subtract fractions with different denominators, it is necessary, first, to bring these fractions to the lowest common denominator (LCD), and only after that to subtract as with fractions with the same denominators.

The common denominator of several fractions is LCM (least common multiple) natural numbers that are the denominators of the given fractions.

Attention! If in the final fraction the numerator and denominator have common factors, then the fraction must be reduced. An improper fraction is best represented as a mixed fraction. Leaving the result of the subtraction without reducing the fraction where possible is an unfinished solution to the example!

Procedure for subtracting fractions with different denominators.

• find the LCM for all denominators;
• put additional multipliers for all fractions;
• multiply all numerators by an additional factor;
• we write the resulting products in the numerator, signing a common denominator under all fractions;
• subtract the numerators of fractions, signing the common denominator under the difference.

In the same way, addition and subtraction of fractions is carried out in the presence of letters in the numerator.

Subtraction of fractions, examples:

Subtraction of mixed fractions.

At subtraction of mixed fractions (numbers) separately, the integer part is subtracted from the integer part, and the fractional part is subtracted from the fractional part.

The first option is to subtract mixed fractions.

If the fractional parts the same denominators and numerator of the fractional part of the minuend (we subtract from it) ≥ the numerator of the fractional part of the subtrahend (we subtract it).

For example:

The second option is to subtract mixed fractions.

When the fractional parts various denominators. To begin with, we reduce the fractional parts to a common denominator, and then we subtract the integer part from the integer, and the fractional from the fractional.

For example:

The third option is to subtract mixed fractions.

The fractional part of the minuend is less than the fractional part of the subtrahend.

Example:

Because fractional parts have different denominators, which means, as in the second option, we first bring ordinary fractions to a common denominator.

The numerator of the fractional part of the minuend is less than the numerator of the fractional part of the subtrahend.3 < 14. So, we take a unit from the integer part and bring this unit to the form of an improper fraction with the same denominator and numerator = 18.

In the numerator from the right side we write the sum of the numerators, then we open the brackets in the numerator from the right side, that is, we multiply everything and give similar ones. We do not open brackets in the denominator. It is customary to leave the product in the denominators. We get:

Actions with fractions.

Attention!
There are additional
material in Special Section 555.
For those who strongly "not very..."
And for those who "very much...")

So, what are fractions, types of fractions, transformations - we remembered. Let's tackle the main question.

What can you do with fractions? Yes, everything is the same as with ordinary numbers. Add, subtract, multiply, divide.

All these actions with decimal operations with fractions are no different from operations with integers. Actually, this is what they are good for, decimal. The only thing is that you need to put the comma correctly.

mixed numbers, as I said, are of little use for most actions. They still need to be converted to ordinary fractions.

And here are the actions with ordinary fractions will be smarter. And much more important! Let me remind you: all actions with fractional expressions with letters, sines, unknowns, and so on and so forth are no different from actions with ordinary fractions! Operations with ordinary fractions are the basis for all algebra. It is for this reason that we will analyze all this arithmetic in great detail here.

Addition and subtraction of fractions.

Everyone can add (subtract) fractions with the same denominators (I really hope!). Well, let me remind you that I’m completely forgetful: when adding (subtracting), the denominator does not change. The numerators are added (subtracted) to give the numerator of the result. Type:

In short, in general terms:

What if the denominators are different? Then, using the main property of the fraction (here it came in handy again!), We make the denominators the same! For example:

Here we had to make the fraction 4/10 from the fraction 2/5. Solely for the purpose of making the denominators the same. I note, just in case, that 2/5 and 4/10 are the same fraction! Only 2/5 is uncomfortable for us, and 4/10 is even nothing.

By the way, this is the essence of solving any tasks in mathematics. When we're out uncomfortable expressions do the same, but more convenient to solve.

Another example:

The situation is similar. Here we make 48 out of 16. By simple multiplication by 3. This is all clear. But here we come across something like:

How to be?! It's hard to make a nine out of a seven! But we are smart, we know the rules! Let's transform every fraction so that the denominators are the same. This is called "reduce to a common denominator":

How! How did I know about 63? Very simple! 63 is a number that is evenly divisible by 7 and 9 at the same time. Such a number can always be obtained by multiplying the denominators. If we multiply some number by 7, for example, then the result will certainly be divided by 7!

If you need to add (subtract) several fractions, there is no need to do it in pairs, step by step. You just need to find the denominator that is common to all fractions, and bring each fraction to this same denominator. For example:

And what will be the common denominator? You can, of course, multiply 2, 4, 8, and 16. We get 1024. Nightmare. It is easier to estimate that the number 16 is perfectly divisible by 2, 4, and 8. Therefore, it is easy to get 16 from these numbers. This number will be the common denominator. Let's turn 1/2 into 8/16, 3/4 into 12/16, and so on.

By the way, if we take 1024 as a common denominator, everything will work out too, in the end everything will be reduced. Only not everyone will get to this end, because of the calculations ...

Solve the example yourself. Not a logarithm... It should be 29/16.

So, with the addition (subtraction) of fractions is clear, I hope? Of course, it is easier to work in a shortened version, with additional multipliers. But this pleasure is available to those who honestly worked in the lower grades ... And did not forget anything.

And now we will do the same actions, but not with fractions, but with fractional expressions. New rakes will be found here, yes ...

So, we need to add two fractional expressions:

We need to make the denominators the same. And only with the help multiplication! So the main property of the fraction says. Therefore, I cannot add one to x in the first fraction in the denominator. (But that would be nice!). But if you multiply the denominators, you see, everything will grow together! So we write down, the line of the fraction, leave an empty space on top, then add it, and write the product of the denominators below, so as not to forget:

And, of course, we don’t multiply anything on the right side, we don’t open brackets! And now, looking at the common denominator of the right side, we think: in order to get the denominator x (x + 1) in the first fraction, we need to multiply the numerator and denominator of this fraction by (x + 1). And in the second fraction - x. You get this:

Note! Parentheses are here! This is the rake that many step on. Not brackets, of course, but their absence. Parentheses appear because we multiply the whole numerator and the whole denominator! And not their individual pieces ...

In the numerator of the right side, we write the sum of the numerators, everything is as in numerical fractions, then we open the brackets in the numerator of the right side, i.e. multiply everything and give like. You don't need to open the brackets in the denominators, you don't need to multiply something! In general, in denominators (any) the product is always more pleasant! We get:

Here we got the answer. The process seems long and difficult, but it depends on practice. Solve examples, get used to it, everything will become simple. Those who have mastered the fractions in the allotted time, do all these operations with one hand, on the machine!

And one more note. Many famously deal with fractions, but hang on examples with whole numbers. Type: 2 + 1/2 + 3/4= ? Where to fasten a deuce? No need to fasten anywhere, you need to make a fraction out of a deuce. It's not easy, it's very simple! 2=2/1. Like this. Any whole number can be written as a fraction. The numerator is the number itself, the denominator is one. 7 is 7/1, 3 is 3/1 and so on. It's the same with letters. (a + b) \u003d (a + b) / 1, x \u003d x / 1, etc. And then we work with these fractions according to all the rules.

Well, on addition - subtraction of fractions, knowledge was refreshed. Transformations of fractions from one type to another - repeated. You can also check. Shall we settle a little?)

Calculate:

Answers (in disarray):

71/20; 3/5; 17/12; -5/4; 11/6

Multiplication / division of fractions - in the next lesson. There are also tasks for all actions with fractions.

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.