Draw a polygon on checkered paper. For example, such as shown in Figure 1.

Let's try to calculate its area now. How to do it? Probably the easiest way is to break it into right-angled triangles and rectangles, the areas of which are already easy to calculate and add up the results. The method I used is simple, but very cumbersome, and besides, it is not suitable for all polygons.

Consider a non-degenerate simple integer polygon (that is, it is connected - any two of its points can be connected by a continuous curve that is entirely contained in it, and all its vertices have integer coordinates, its boundary is a connected polyline without self-intersections, and it has a non-zero square). To calculate the area of ​​such a polygon, you can use the following theorem:

Pick's theorem. Let be the number of integer points inside the polygon, be the number of integer points on its boundary, and be its area. Then Pick's formula:

Example. For the polygon in Figure 1 (yellow dots), (blue dots, don't forget the vertices!), so square units.

Proof of Pick's theorem. First, note that Pick's formula is true for the unit square. Indeed, in this case we have

Consider a rectangle with sides lying on the lattice lines. Let the lengths of its sides be equal to and. We have in this case and, according to the Pick formula,

Consider now a right triangle with legs lying on the coordinate axes. Such a triangle is obtained from a rectangle with sides and, considered in the previous case, by cutting it diagonally. Let integer points lie on the diagonal. Then for this case we get that

Now consider an arbitrary triangle. It can be obtained by cutting off several right-angled triangles and, possibly, a rectangle from a rectangle (see figures 2 and 3). Since Pick's formula is true for both a rectangle and a right-angled triangle, we get that it will also be true for an arbitrary triangle.

It remains to take the last step: move from triangles to polygons. Any polygon can be divided into triangles (for example, by diagonals). Therefore, we just need to prove that when adding any triangle to an arbitrary polygon, Pick's formula remains true.

Let the polygon and the triangle have a common side. Assume that Pick's formula is valid for, and we will prove that it will also be true for the polygon obtained from the addition. Since and have a common side, all integer points lying on this side, except for two vertices, become interior points of the new polygon. Vertices will be boundary points. Let us denote the number of common points by and get

The number of interior integer points of the new polygon,

The number of boundary points for the new polygon.

From these equalities we get

Since we assumed that the theorem is true for and for separately, then

Thus, the Pick formula is proved.

This formula was discovered by the Austrian mathematician Peak Georg Aleksandrov (1859 - 1943) in 1899. In addition to this formula, Georg Pick discovered the Pick, Pick - Julia, Pick - Nevalina theorems, proved the Schwarz - Pick inequality. AT Appendix 1 you can see the non-standard tasks I have considered for applying the Pick formula.

Peak Formula

1. Introduction

2. Peak formula. Proof I.

Proof II.

The proof of Sh.

3. Tasks.

4. The formula for the area of ​​a polygon in terms of the coordinates of the vertices.

5. Tasks.

6. Literature

Peak formula.

1. Introduction.

We draw wisdom from history,

in poetry - wit,

in mathematics - insight.

F. Bacon

The plot will unfold on a regular piece of checkered paper.

The lines going along the sides of the cells form a grid, and the vertices of the cells are the nodes of this grid. Let's draw a polygon on the sheet with vertices at the nodes and find its area.

You can search for it in different ways. For example, you can cut a polygon into fairly simple shapes, find their areas and add them up.

But here we are in for a lot of trouble. The figure is easily broken into rectangles, trapezoids, and triangles, and its area is calculated effortlessly.

Although the polygon looks simple enough, it will take a lot of work to calculate its area. What if the polygon looked fancier? It turns out that the areas of polygons whose vertices are located at the nodes of the grid can be calculated much more simply: there is a formula that relates their area to the number of nodes lying inside and on the border of the polygon. This wonderful and simple formula is called Pick's formula.

2. Peak formula.

The vertices of a polygon (not necessarily convex) are located at the nodes of an integer lattice. Inside it lies B nodes of the lattice, and on the border of G nodes. Let us prove that its area is B + – 1 (Peak's formula).

Proof I.

Consider a polygon whose vertices are at the nodes of an integer lattice, that is, they have integer coordinates.

We divide the polygon into triangles with vertices at the nodes of the lattice, which do not contain nodes either inside or on the sides.

Denote:

n is the number of sides of the polygon,

m is the number of triangles with vertices at the nodes of the lattice that do not contain nodes either inside or on the sides,

B is the number of nodes inside the polygon,

Г is the number of nodes on the sides, including the vertices.

The areas of all these triangles are the same and equal.

Therefore, the area of ​​the polygon is
.

180 0 m .

Now let's find this sum in a different way.

The sum of angles with a vertex at any internal node is 360 0 .

Then the sum of angles with vertices at all internal nodes is 360 0 V.

The total sum of the angles at the nodes on the sides, but not at the vertices, is 180 0 (G - n).

The sum of the angles at the vertices of the polygon is 180 0 ( n – 2) .

The total sum of the angles of all triangles is 360 0 V + 180 0 (G - n) + 180 0 (n – 2).

So 180 0 m\u003d 360 0 V + 180 0 (G - n) + 180 0 (n – 2),

180 0 m\u003d 360 0 V + 180 0 G - 180 0 n + 180 0 n– 180 0 2,

180 0 m\u003d 360 0 V + 180 0 G– 360 0,

= B + – 1 ,

whence we obtain the expression for the area S of the polygon:

S= B + – 1 ,

known as Pick's formula.

In the figure: V = 24, D = 9, therefore,S = 24 + – 1 = 27,5.

Find the area of ​​the first polygon using the Peak formula:

B = 28 (green dots);

D = 20 (blue dots).

We get, S =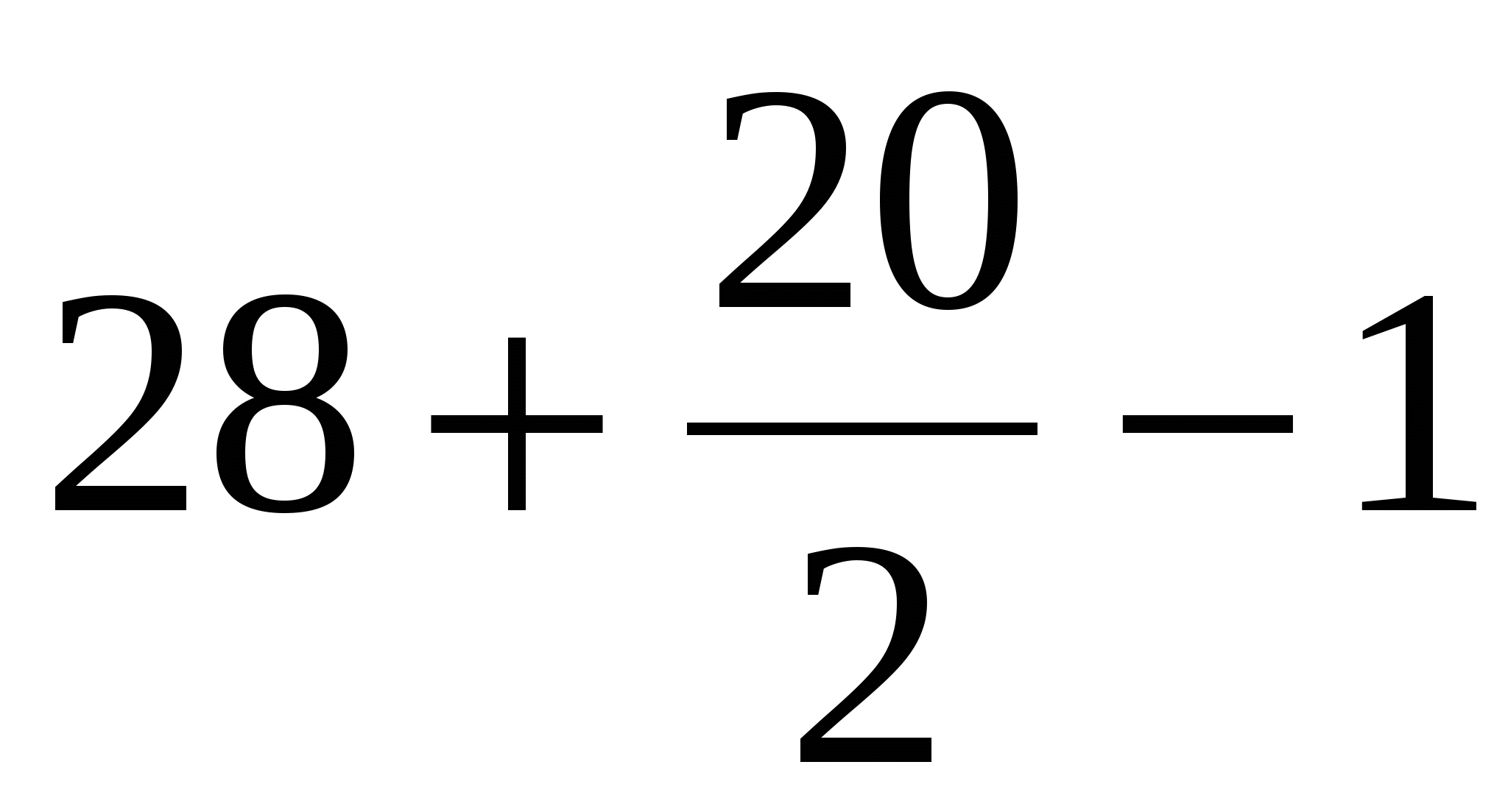
= 37 square units

Proof II.

To each polygon M with vertices at the nodes of an integer lattice we assign the number f (M) =
, where the summation is over all lattice nodes belonging to M, and the angle is defined as follows: =
for an interior point of a polygon, =
for a boundary point other than a vertex, and – angle at the vertex, if the given node is a vertex. It is easy to see that f (M) =
+
= B + – 1. It remains to check that the number f (M) is equal to the area of ​​the polygon M.

Let the polygon M be cut into polygons M 1 and M 2 with vertices at the nodes of the lattice. Then f(M) = f(M 1) + f(M 2) because for each node the angles add up. Therefore, if Pick's formula is true for two of the polygons M, M 1 and M 2, then it is also true for the third.

If M is a rectangle with sides p and q, directed along the lattice lines, then

f (M) = (p – 1)(q – 1) +
= pq.

In this case, Pick's formula is valid. By cutting the rectangle M diagonally into triangles M 1 and M 2 and using the fact that f (M) = f (M 1) + f (M 2) and f (M 1) = f (M 2), it is easy to prove the validity of Pick's formula for any right triangle with legs directed along the lines of the lattice. By cutting off several such triangles from a rectangle, any triangle can be obtained.

To complete the proof of Pick's formula, it remains to note that any polygon can be cut into triangles by non-intersecting diagonals.

The proof of Sh.

The connection between the area of ​​a figure and the number of nodes that fall into this figure is especially clear in the case of a rectangle.

Let be ABCD- a rectangle with vertices at the nodes and sides going along the grid lines.

Denote by AT the number of nodes lying inside the rectangle, and through G is the number of nodes on its boundary. Move the grid half a cell to the right and half a cell down.

Then the territory of the rectangle can be "distributed" between the nodes as follows: each of AT nodes "controls" the whole cell of the shifted grid, each of G- 4 boundary non-corner nodes - half of the cell, and each of the corner points - a quarter of the cell. Therefore, the area of ​​the rectangle S is

So, for rectangles with vertices at nodes and sides going along grid lines, we have established the formula

Let us prove that this formula is true not only for rectangles, but also for arbitrary polygons with vertices at the grid nodes.

Denote by S m polygon areaM with vertices at nodes, and throughP m - value
, whereAT m is the number of nodes insideM, a G m is the number of nodes on the boundary. Then the Pick formula can be written as
.

We divide the proof of the formula into several steps.

Step 1.

If polygonM with vertices at grid nodes cut into 2 polygonsM 1 and M 2 , also having vertices only at the grid nodes, then
. Let the polygonM cut into polygonsM 1 and M 2 with vertices at nodes by a segment AB. All nodes, except those that fall on the segmentAB, give the same contribution to the left and right parts of the formula. Consider the nodes lying on the segment AB.

If such a node lies between A and B (for example, C), then for a polygonM it is internal, and for polygonsM 1 and M 2 - boundary. Therefore, his contribution toP m equals 1, and in each of the expressions
and
– 0.5 each, that is, the contributions of such a node toP m and
are equal.

Consider nodes A and B. They are boundary both for M, and for M 1 , M 2 .

Therefore, the contribution of each of these nodes toP m is 0.5 a
- unit. This means that the total contribution of nodes A and B toP m equals 1, which is 1 less than their contribution to
. But
, a .

From the total "contribution" of all nodes P m 1 is subtracted from
2 is subtracted, and this compensates for the difference in the contributions of nodes A and B.

So,
.

Step 2

If polygon M with vertices at the grid nodes cut into two polygons M 1 and M 2 (also with vertices at nodes) and the formula is true for some two of the polygons MM 1 , M 2 , then it is also true for the third polygon.

Let, for example, it is true forM 1 and M 2 , i.e
. Then (on the first step), but on first step), the last expression is equal toP m , and equality
and there is the Pick formula.

Step 3

Let us prove Pick's formula for a right triangle with vertices at the grid nodes and legs lying on the grid lines.

Triangle ABC build to a rectangle ABCD .

For rectangles, Pick's formula is correct: S ABCD = P ABCD . According to the first step P ABCD = P ABC + P ACD , P ABC = P ACD , so P ABCD = 2P ABC . But S ABCD = 2 S ABC . So S ABC = P ABC .

Step 4

Pick's formula is correct for an arbitrary triangle with vertices at the grid nodes.

Having examined the figure, it is easy to understand: any such triangle can be obtained by “cutting off” from some rectangle with sides running along the grid lines, several rectangles and right-angled triangles with legs on the grid lines. And since Pick's formula is true for rectangles and right-angled triangles, then (remember step 2) it is also true for the original triangle.

We have proved that if a polygon can be cut into triangles with vertices at the nodes of the grid, then Pick's formula is true for it.

3. Tasks.

Find the area of ​​the figures:

1
.

B=9

G = 4

B=9

G = 5

Calculating the area of ​​a figure.

Pick method

The work of a student of class 5B MBOU secondary school No. 23 in Irkutsk

Balsukova Alexandra

Head: Khodyreva T.G.

2014

Calculating the area of ​​a figure. Pick method

Object of study : tasks on checkered paper

Subject of study : problems for calculating the area of ​​a polygon on checkered paper, methods and techniques for solving them.

Research methods Keywords: comparison, generalization, analogy, study of literature and Internet resources, information analysis.

Purpose of the study:

choose the main, interesting, understandable information

Analyze and organize the information received

Find different methods and techniques for solving problems on checkered paper

check the formulas for calculating the areas of geometric shapes using the Peak formula

Create an electronic presentation of the work to present the collected material

Geometry is the most powerful tool for the refinement of our mental faculties and enables us to think and reason correctly.

(G. Galileo)

Relevance of the topic

Passion for mathematics often begins with thinking about a problem. So, when studying the topic "Areas of polygons", the question arises whether there are tasks that are different from the tasks considered in the textbook. Such tasks include tasks on checkered paper. What is the peculiarity of such problems, are there special methods and techniques for solving problems on checkered paper. In a math class, the teacher introduced us to an interesting method for calculating polygons. I began to study the literature, Internet resources on this topic. It would seem that fascinating things can be found on a checkered plane, that is, on an endless piece of paper, lined into identical squares. It turns out that the tasks associated with checkered paper are quite diverse. I learned how to calculate the areas of polygons drawn on a checkered piece of paper. For many tasks on paper in a cage there is no general rule for solving, specific methods and techniques. This is their property that determines their value for the development of not a specific educational skill or skill, but in general the ability to think, reflect, analyze, look for analogies, that is, these tasks develop thinking skills in their broadest sense.

And I also learned that such tasks are considered in the control and measuring materials of the GIA and the Unified State Examination. Therefore, I consider the study of this material useful for its application not only in the further educational process, but also for solving non-standard Olympiad problems.

2.The concept of area

Square- numerical characteristic of a two-dimensional geometric figure, showing the size of this figure. Historically, area calculation was called . A figure that has area is called squaring .

The area of ​​a flat figure in terms of geometry

1. Square- the measure of a flat figure in relation to the standard figure, which is a square with a side equal to one length.

2. Square- a numerical characteristic attributed to flat figures of a certain class (for example, polygons). The area of ​​a square with a side equal to a unit of length, taken equal to a unit of area

3. Square- a positive value, the numerical value of which has the following properties:

 Equal figures have equal areas;

 If a figure is divided into parts that are simple figures (that is, those that can be divided into a finite number of flat triangles), then the area of ​​\u200b\u200bthis figure is equal to the sum of the areas of its parts;

 The area of ​​a square with a side equal to the unit of measurement is equal to one.

Thus, we can conclude that the area is not a specific value, but only gives some conditional characteristic of a flat figure. To find the area of ​​an arbitrary figure, it is necessary to determine how many squares with a side equal to one length, it contains. For example, let's take a rectangle in which a square centimeter fits exactly 6 times. This means that the area of ​​the rectangle is 6 cm2.

The choice of the area of ​​a square with a side equal to the unit of measurement as the minimum unit of measurement for all areas is not accidental. This is the result of an agreement between people that arose in the course of "natural" centuries-old selection. In addition, there were other proposals for a unit of measure. So, for example, it was proposed to take the area of ​​an equilateral triangle as such a unit (i.e., any flat figure could be represented as a “sum” of a certain number of equilateral triangles), which would lead to a change in the numerical representation of areas.

Thus, formulas for calculating areas appeared in mathematics and were not immediately realized by a person - this many scientists living in different eras and different countries. (Wrong formulas did not find a place in science and went into oblivion). The true formulas were supplemented, corrected and substantiated over thousands of years, until they reached us in their modern form.

Of course area measurement consists in comparing the area of ​​a given figure with the area of ​​a figure taken as a unit of measurement. As a result of the comparison, a certain number is obtained - the numerical value of the area of ​​\u200b\u200bthe given figure. This number shows how many times the area of ​​a given figure is greater (or less) than the area of ​​the figure, taken as a unit of area.

T Thus, we can conclude that the area is an artificial quantity, historically introduced by man to measure some property of a flat figure. The need to enter such a value was due to the growing need to know how large this or that territory is, how much grain is needed to sow a field or calculate the floor surface area for decorating ornamental tiles.

Peak Formula

To estimate the area of ​​a polygon on checkered paper, it is enough to calculate how many cells this polygon covers (we take the area of ​​\u200b\u200bthe cell as a unit). More precisely, ifS is the area of ​​the polygon, B is the number of cells that lie entirely inside the polygon, and G is the number of cells that have an interior. We will consider only such polygons, all the vertices of which lie at the nodes of the checkered paper - in those where the grid lines of the polygon intersect at least one common point.

The area of ​​any triangle drawn on checkered paper can be easily calculated by representing it as the sum or difference of the areas of right-angled triangles and rectangles whose sides follow the grid lines passing through the vertices of the drawn triangle.

To calculate the area of ​​such a polygon, you can use the following theorem:

Theorem . Let be - the number of integer points inside the polygon, - the number of integer points on its boundary, - its area. ThenPick's formula:

Example. For the polygon in the figureL = 7 (red dots), 9 (green dots), soS = 7+ 9/2 -1 = 10,5 square units.

Pick's theorem- classic result and .

The area of ​​a triangle with vertices at the nodes and containing no nodes either inside or on the sides (except for the vertices) is equal to 1/2. This fact.

3. History

Pick's formula was discovered by the Austrian mathematician Georg Alexander (1859-1942) in . At the age of 16, Georg finished school and entered. At the age of 20 he received the right to teach physics and mathematics. In 1884 Peak went to to . There he met another student of Klein,. Later, in 1885, he returned towhere he spent the rest of his scientific career.

Georg Pick was friends with Einstein. Pick and Einstein not only shared scientific interests, but were also passionate about music. Pick, who played in a quartet that consisted of university professors, introduced Einstein to the scientific and musical societies of Prague.

The circle of mathematical interests of Peak was extremely wide. In particular, he has more than 50 scientific papers. Pick's theorem, discovered by him in 1899, was widely known for calculating the area of ​​a polygon. In Germany, this theorem is included in school textbooks.

4.Applications of Pick's formula

The Pick formula is used not only to calculate the areas of polygons, but also to solve many problems of the Olympiad level.

Some examples of using Pick's formula when solving problems:

1) The chess king went around the board of 8 × 8 cells, having visited each

home field exactly once and with the last move returning to the original

field. A broken line connecting in series the centers of the fields that

the king passed, has no self-intersections. What area can

limit this broken line? (The side of the cell is 1.)

It immediately follows from the Pick formula that the area bounded by the lo-

mana is 64/2 − 1 = 31; here the lattice nodes are the centers 64

fields and, by assumption, they all lie on the boundary of the polygon. So

Thus, although there are quite a lot of such "trajectories" of the king, but all of them

limit polygons of equal areas.

Tasks from the control and measuring materials of the GIA and the Unified State Examination

Task B3

Find the area of ​​the figure depicted on checkered paper with a cell size of 1 cm 1 cm (see Fig.). Give your answer in square centimeters.

4.Conclusion

In the process of research, I studied reference, popular science literature. I learned that the problem of finding the area of ​​a polygon with vertices at the nodes of the grid inspired the Austrian mathematician Pick in 1899 to prove the wonderful Pick formula.

As a result of my work, I expanded my knowledge of solving problems on checkered paper, determined for myself the classification of the problems under study, and became convinced of their diversity.

I learned how to calculate the areas of polygons drawn on a checkered sheet. The tasks considered have a different level of difficulty - from simple to Olympiad. Everyone can find among them tasks of a feasible level of complexity, starting from which, it will be possible to move on to solving more difficult ones.

I came to the conclusion that the topic that interested me is quite multifaceted, the tasks on checkered paper are diverse, the methods and techniques for solving them are also diverse. Therefore, our I decided to continue working in this direction.

5. Literature used:

1. N. B. Vasil’ev, “Around the Pick formula,” Kvant. - 1974. - No. 12

2. Kokse Prasolov VV Tasks in planimetry. - M.: MTsNMO, 2006.t e r G.S.M. Introduction to geometry. - M.: Nauka, 1966

3. Roslova L.O., Sharygin I.F. Measurements. - M.: Ed. "Open World", 2005.

Internet resources:

:

Feedback on work

“Calculation of the areas of plane figures. Pick Method"

Consideration of this topic will increase the cognitive activity of the student, who later in geometry lessons will begin to see the harmony of the drawing and will cease to perceive geometry (and mathematics in general) as a boring science.

Reviewed by math teacher

Khodyreva Tatyana Georgievna

There is a wonderful formula that allows you to count polygon area on the coordinate grid almost without errors. It's not even a formula, it's real theorem. At first glance, it may seem complicated. But it is enough to solve a couple of tasks - and you will understand how cool this feature is. So go ahead!

Let's start with a new definition:

A coordinate stack node is any point that lies at the intersection of the vertical and horizontal lines of this grid.

Designation:

In the first picture, the nodes are not marked at all. The second one has 4 nodes. Finally, in the third picture, all 16 nodes are marked.

What does this have to do with problem B5? The fact is that the vertices of the polygon in such problems always lie at the nodes of the grid. As a consequence, the following theorem works for them:

Theorem. Consider a polygon on a coordinate grid whose vertices lie at the nodes of this grid. Then the area of ​​the polygon is:

where n is the number of nodes inside the given polygon, k is the number of nodes that lie on its boundary (boundary nodes).

As an example, consider an ordinary triangle on a coordinate grid and try to mark the internal and boundary nodes.

The first picture shows an ordinary triangle. On the second picture, its internal nodes are marked, the number of which is n = 10. On the third picture, the nodes lying on the border are marked, there are k = 6 of them in total.

Perhaps many readers do not understand how to count the numbers n and k. Start with internal nodes. Everything is obvious here: we paint over the triangle with a pencil and see how many nodes are shaded.

With boundary nodes, it's a little more complicated. polygon border - closed broken line, which intersects the coordinate grid at many points. The easiest way is to mark some "starting" point, and then go around the rest.

Boundary nodes will be only those points on the polyline at which they simultaneously intersect three lines:

1. Actually, a broken line;
2. Horizontal grid line;
3. vertical line.

Let's see how it all works in real problems.

Task. Find the area of ​​a triangle if the cell size is 1 x 1 cm:

First, let's mark the nodes that lie inside the triangle, as well as on its border:

It turns out that there is only one internal node: n = 1. There are six boundary nodes: three coincide with triangle vertices, and three more lie on the sides. Total k = 6.

Now we calculate the area using the formula:

That's all! Problem solved.

Task. Find the area of ​​a quadrilateral depicted on checkered paper with a cell size of 1 cm by 1 cm. Give your answer in square centimeters.

Again, we mark the internal and boundary nodes. There are n = 2 internal nodes. Boundary nodes: k = 7, of which 4 are vertices of the quadrilateral, and 3 more lie on the sides.

It remains to substitute the numbers n and k in the area formula:

Pay attention to the last example. This problem was actually proposed at the diagnostic work in 2012. If you work according to the standard scheme, you will have to do a lot of additional constructions. And by the method of knots, everything is solved almost orally.

Important note on areas

But the formula is not everything. Let's rewrite the formula a little, bringing the terms on the right side to a common denominator. We get:

The numbers n and k are the number of nodes, they are always integers. So the whole numerator is also an integer. We divide it by 2, which implies an important fact:

The area is always expressed whole number or fraction. Moreover, at the end of the fraction there is always “five tenths”: 10.5; 17.5 etc.

Thus, the area in problem B5 is always expressed as an integer or a fraction of the form ***.5. If the answer is different, it means that a mistake has been made somewhere. Keep this in mind when you take the real exam in mathematics!

To use the preview of presentations, create a Google account (account) and sign in: https://accounts.google.com

Slides captions:

Completed by a student of secondary school No. 7 8 "A" class Yunosheva Ksenia Instructor: Babina Natalya Alekseevna Salsk 2011 "Peak Formula"

Objectives of the work: Finding out the existence of another, different from the school curriculum, formula for finding the area of ​​a lattice polygon. Areas of application of the desired formula.

Introduction. Mathematical education received in general education schools is an essential component of general education and the general culture of modern man. At this stage, the school system is designed for eleven years of education. All students at the end of the eleventh grade will have to take the Unified State Exam, which will show the level of knowledge gained while studying at school. But the school curriculum does not always provide the most rational ways to solve any problems. For example, looking at the results of the Unified State Examination in 2010, it is clear that many students lose points due to task B6. I set out to figure out how to save time and solve this problem correctly.

Task B6. Figures are depicted on checkered paper with cells measuring 1 cm by 1 cm (see figure). Find their area in square centimeters.

So, in order to still solve this task, I need to apply the formulas for finding the area, which we study in grade 8. But it will take a lot of time, and I need to answer the question as quickly as possible, because the time for the exam is strictly limited. Therefore, after doing research, I found out that there is Pick's theorem, which is not studied in the school curriculum, but which will help me cope with the task faster.

History reference. Georg Alexander Pick (August 10, 1859 – July 26, 1942) was an Austrian mathematician. He died in the Terezin concentration camp. It is known today because of Pick's formula for determining the area of ​​a lattice of polygons. He published his formula in a paper in 1899, it became popular when Hugo Steinhaus included it in a 1969 edition of Mathematical Pictures. Pick studied at the University of Vienna and completed his PhD in 1880. After receiving his doctorate, he was appointed assistant to Ernest Mach at the Scherl-Ferdinand University in Prague. He became a teacher there in 1881. Taking a leave of absence from the university in 1884, he began working with Felix Klein at the University of Leipzig. He remained in Prague until his retirement in 1927, when he returned to Vienna. Pick chaired the committee at the (then) German University of Prague which appointed Albert Einstein professor of mathematical physics in 1911. Pick was elected a member of the Czech Academy of Sciences and Arts, but was expelled after the Nazi takeover of Prague. After retiring in 1927, Pick returned to Vienna, the city where he was born. After the Anschluss, when the Nazis entered Austria on March 12, 1938, Pieck returned to Prague. In March 1939, the Nazis invaded Czechoslovakia. Georg was sent to Terezin concentration camp on July 13, 1942. He died two weeks later.

Pick's theorem. Pick's theorem is a classical result of combinatorial geometry and the geometry of numbers. The area of ​​a polygon with integer vertices is equal to the sum B + D/2 - 1, where B is the number of integer points inside the polygon, and D is the number of integer points on the boundary of the polygon.

A flattering proof of Pick's theorem. Any such polygon can be easily divided into triangles with vertices at the nodes of the lattice, containing no nodes either inside or on the sides. It can be shown that the areas of all these triangles are the same and equal to 1/2, and, therefore, the area of ​​the polygon is equal to half of their number T. To find this number, we denote by n the number of sides of the polygon, by i - the number of nodes inside it and by b - the number of nodes on the sides, including the vertices. The total sum of the angles of all triangles is πТ. Now let's find this sum in a different way. The sum of angles with a vertex at any internal node is 2 π , i.e. the total sum of such angles is 2 π i ; the total sum of the angles at the nodes on the sides, but not at the vertices, is (b - n) π, and the sum of the angles at the vertices of the polygon is (n - 2) π. Thus, π T \u003d 2i π + (b - n) π + (n - 2) π, from which we obtain an expression for the area S of a polygon, known as Pick's formula. For example, in the figure b = 9, i = 24, and therefore the area of ​​the polygon is 27.5.

Application. So, back to task B6. Now, knowing the new formula, we can easily find the area of ​​this quadrilateral. Since B is 5; D - 14, then 5 + 14: 2-1 \u003d 11 (cm squared) The area of ​​\u200b\u200bthis quadrangle is 11 cm squared.

Using the same formula, we can find the area of ​​a triangle. Since B-14, G-10, then 14+10:2-1=18 (square cm) The area of ​​this triangle is 18 cm squared.

If B-9, D-12, then: 9+12:2-1=14 (cm squared) The area of ​​this quadrilateral is 14 cm squared.

Scope of the formula. In addition to the fact that the formula is used in various kinds of exams, assignments, and so on, it accompanies the whole world around us.

According to Peak's formula S = B + ½ G-1 1) body B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) tail B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24

According to Peak's formula S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10.5-1 \u003d 45.5

Conclusion. As a result, I came to the conclusion that there are many different ways to solve area problems that are not studied in the school curriculum, and showed them using the Pick formula as an example.

Directory. A polygon without self-intersections is called a lattice polygon if all its vertices are at points with integer coordinates (in the Cartesian coordinate system). A point in the coordinate plane is called integer if both of its coordinates are integers.