One of the most important sciences, the application of which can be seen in disciplines such as chemistry, physics and even biology, is mathematics. The study of this science allows you to develop some mental qualities, improve the ability to concentrate. One of the topics that deserve special attention in the course "Mathematics" is the addition and subtraction of fractions. Many students find it difficult to study. Perhaps our article will help to better understand this topic.
How to subtract fractions whose denominators are the same
Fractions are the same numbers with which you can perform various actions. Their difference from integers lies in the presence of a denominator. That is why when performing actions with fractions, you need to study some of their features and rules. The simplest case is the subtraction of ordinary fractions, the denominators of which are represented as the same number. It will not be difficult to perform this action if you know a simple rule:
- In order to subtract the second from one fraction, it is necessary to subtract the numerator of the fraction to be subtracted from the numerator of the reduced fraction. We write this number into the numerator of the difference, and leave the denominator the same: k / m - b / m = (k-b) / m.
Examples of subtracting fractions whose denominators are the same
7/19 - 3/19 = (7 - 3)/19 = 4/19.
From the numerator of the reduced fraction "7" subtract the numerator of the subtracted fraction "3", we get "4". We write this number in the numerator of the answer, and put in the denominator the same number that was in the denominators of the first and second fractions - "19".
The picture below shows a few more such examples.

Consider a more complex example where fractions with the same denominators are subtracted:
29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7)/47 = 9/47.
From the numerator of the reduced fraction "29" by subtracting in turn the numerators of all subsequent fractions - "3", "8", "2", "7". As a result, we get the result "9", which we write in the numerator of the answer, and in the denominator we write the number that is in the denominators of all these fractions - "47".
Adding fractions with the same denominator
Addition and subtraction of ordinary fractions is carried out according to the same principle.
- To add fractions with the same denominators, you need to add the numerators. The resulting number is the numerator of the sum, and the denominator remains the same: k/m + b/m = (k + b)/m.
Let's see how it looks like in an example:
1/4 + 2/4 = 3/4.
To the numerator of the first term of the fraction - "1" - we add the numerator of the second term of the fraction - "2". The result - "3" - is written in the numerator of the amount, and the denominator is left the same as that was present in the fractions - "4".

Fractions with different denominators and their subtraction
We have already considered the action with fractions that have the same denominator. As you can see, knowing simple rules, solving such examples is quite easy. But what if you need to perform an action with fractions that have different denominators? Many high school students are confused by such examples. But even here, if you know the principle of the solution, the examples will no longer be difficult for you. There is also a rule here, without which the solution of such fractions is simply impossible.
- 2/3 - one three and one two are missing in the denominator:
2/3 = (2 x 3 x 2)/(3 x 3 x 2) = 12/18. - 7/9 or 7/(3 x 3) - the denominator is missing two:
7/9 = (7 x 2)/(9 x 2) = 14/18. - 5/6 or 5/(2 x 3) - the denominator is missing a triple:
5/6 = (5 x 3)/(6 x 3) = 15/18. - The number 18 consists of 3 x 2 x 3.
- The number 15 consists of 5 x 3.
- The common multiple will consist of the following factors 5 x 3 x 3 x 2 = 90.
- 90 divided by 15. The resulting number "6" will be a multiplier for 3/15.
- 90 divided by 18. The resulting number "5" will be a multiplier for 4/18.
- Convert all fractions that have an integer part to improper ones. In simple words, remove the whole part. To do this, the number of the integer part is multiplied by the denominator of the fraction, the resulting product is added to the numerator. The number that will be obtained after these actions is the numerator of an improper fraction. The denominator remains unchanged.
- If fractions have different denominators, they should be reduced to the same.
- Perform addition or subtraction with the same denominators.
- When receiving an improper fraction, select the whole part.
To subtract fractions with different denominators, they must be reduced to the same smallest denominator.

We will talk in more detail about how to do this.
Fraction property
In order to reduce several fractions to the same denominator, you need to use the main property of the fraction in the solution: after dividing or multiplying the numerator and denominator by the same number, you get a fraction equal to the given one.
So, for example, the fraction 2/3 can have denominators such as "6", "9", "12", etc., that is, it can look like any number that is a multiple of "3". After we multiply the numerator and denominator by "2", we get a fraction of 4/6. After we multiply the numerator and denominator of the original fraction by "3", we get 6/9, and if we perform a similar action with the number "4", we get 8/12. In one equation, this can be written as:
2/3 = 4/6 = 6/9 = 8/12…
How to bring multiple fractions to the same denominator
Consider how to reduce several fractions to the same denominator. For example, take the fractions shown in the picture below. First you need to determine what number can become the denominator for all of them. To make it easier, let's decompose the available denominators into factors.
The denominator of the fraction 1/2 and the fraction 2/3 cannot be factored. The denominator of 7/9 has two factors 7/9 = 7/(3 x 3), the denominator of the fraction 5/6 = 5/(2 x 3). Now you need to determine which factors will be the smallest for all these four fractions. Since the first fraction has the number “2” in the denominator, it means that it must be present in all denominators, in the fraction 7/9 there are two triples, which means that they must also be present in the denominator. Given the above, we determine that the denominator consists of three factors: 3, 2, 3 and is equal to 3 x 2 x 3 = 18.

Consider the first fraction - 1/2. Its denominator contains "2", but there is not a single "3", but there should be two. To do this, we multiply the denominator by two triples, but, according to the property of the fraction, we must multiply the numerator by two triples:
1/2 = (1 x 3 x 3)/(2 x 3 x 3) = 9/18.
Similarly, we perform actions with the remaining fractions.
All together it looks like this:

How to subtract and add fractions with different denominators
As mentioned above, in order to add or subtract fractions with different denominators, they must be reduced to the same denominator, and then use the rules for subtracting fractions with the same denominator, which have already been described.
Consider this with an example: 4/18 - 3/15.
Finding multiples of 18 and 15:
After the denominator is found, it is necessary to calculate a factor that will be different for each fraction, that is, the number by which it will be necessary to multiply not only the denominator, but also the numerator. To do this, we divide the number that we found (common multiple) by the denominator of the fraction for which additional factors need to be determined.
The next step in our solution is to bring each fraction to the denominator "90".
We have already discussed how this is done. Let's see how this is written in an example:
(4 x 5) / (18 x 5) - (3 x 6) / (15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.
If fractions with small numbers, then you can determine the common denominator, as in the example shown in the picture below.

Similarly produced and having different denominators.
Subtraction and having integer parts
Subtraction of fractions and their addition, we have already analyzed in detail. But how to subtract if the fraction has an integer part? Again, let's use a few rules:

There is another way by which you can add and subtract fractions with integer parts. For this, actions are performed separately with integer parts, and separately with fractions, and the results are recorded together.

The above example consists of fractions that have the same denominator. In the case when the denominators are different, they must be reduced to the same, and then follow the steps as shown in the example.
Subtracting fractions from a whole number
Another of the varieties of actions with fractions is the case when the fraction must be subtracted from At first glance, such an example seems difficult to solve. However, everything is quite simple here. To solve it, it is necessary to convert an integer into a fraction, and with such a denominator, which is in the fraction to be subtracted. Next, we perform a subtraction similar to subtraction with the same denominators. For example, it looks like this:
7 - 4/9 = (7 x 9)/9 - 4/9 = 53/9 - 4/9 = 49/9.
The subtraction of fractions given in this article (Grade 6) is the basis for solving more complex examples, which are considered in subsequent classes. Knowledge of this topic is used subsequently to solve functions, derivatives, and so on. Therefore, it is very important to understand and understand the actions with fractions discussed above.
Consider the fraction $\frac63$. Its value is 2, since $\frac63 =6:3 = 2$. What happens if the numerator and denominator are multiplied by 2? $\frac63 \times 2=\frac(12)(6)$. Obviously, the value of the fraction has not changed, so $\frac(12)(6)$ is also equal to 2 as y. multiply the numerator and denominator by 3 and get $\frac(18)(9)$, or by 27 and get $\frac(162)(81)$ or by 101 and get $\frac(606)(303)$. In each of these cases, the value of the fraction that we get by dividing the numerator by the denominator is 2. This means that it has not changed.
The same pattern is observed in the case of other fractions. If the numerator and denominator of the fraction $\frac(120)(60)$ (equal to 2) is divided by 2 (result of $\frac(60)(30)$), or by 3 (result of $\frac(40)(20) $), or by 4 (the result of $\frac(30)(15)$) and so on, then in each case the value of the fraction remains unchanged and equal to 2.
This rule also applies to fractions that are not equal. whole number.
If the numerator and denominator of the fraction $\frac(1)(3)$ are multiplied by 2, we get $\frac(2)(6)$, that is, the value of the fraction has not changed. And in fact, if you divide the cake into 3 parts and take one of them, or divide it into 6 parts and take 2 parts, you will get the same amount of pie in both cases. Therefore, the numbers $\frac(1)(3)$ and $\frac(2)(6)$ are identical. Let's formulate a general rule.
The numerator and denominator of any fraction can be multiplied or divided by the same number, and the value of the fraction does not change.
This rule is very useful. For example, it allows in some cases, but not always, to avoid operations with large numbers.
For example, we can divide the numerator and denominator of the fraction $\frac(126)(189)$ by 63 and get the fraction $\frac(2)(3)$ which is much easier to calculate. One more example. We can divide the numerator and denominator of the fraction $\frac(155)(31)$ by 31 and get the fraction $\frac(5)(1)$ or 5, since 5:1=5.
In this example, we first encountered a fraction whose denominator is 1. Such fractions play an important role in calculations. It should be remembered that any number can be divided by 1 and its value will not change. That is, $\frac(273)(1)$ is equal to 273; $\frac(509993)(1)$ equals 509993 and so on. Therefore, we do not have to divide numbers by , since every integer can be represented as a fraction with a denominator of 1.
With such fractions, the denominator of which is equal to 1, you can perform the same arithmetic operations as with all other fractions: $\frac(15)(1)+\frac(15)(1)=\frac(30)(1) $, $\frac(4)(1) \times \frac(3)(1)=\frac(12)(1)$.
You may ask what is the use of representing an integer as a fraction, which will have a unit under the line, because it is more convenient to work with an integer. But the fact is that the representation of an integer as a fraction gives us the opportunity to perform various actions more efficiently when we are dealing with both integers and fractional numbers at the same time. For example, to learn add fractions with different denominators. Suppose we need to add $\frac(1)(3)$ and $\frac(1)(5)$.
We know that you can only add fractions whose denominators are equal. So, we need to learn how to bring fractions to such a form when their denominators are equal. In this case, we again need the fact that you can multiply the numerator and denominator of a fraction by the same number without changing its value.
First, we multiply the numerator and denominator of the fraction $\frac(1)(3)$ by 5. We get $\frac(5)(15)$, the value of the fraction has not changed. Then we multiply the numerator and denominator of the fraction $\frac(1)(5)$ by 3. We get $\frac(3)(15)$, again the value of the fraction has not changed. Therefore, $\frac(1)(3)+\frac(1)(5)=\frac(5)(15)+\frac(3)(15)=\frac(8)(15)$.
Now let's try to apply this system to the addition of numbers containing both integer and fractional parts.
We need to add $3 + \frac(1)(3)+1\frac(1)(4)$. First, we convert all the terms into fractions and get: $\frac31 + \frac(1)(3)+\frac(5)(4)$. Now we need to bring all the fractions to a common denominator, for this we multiply the numerator and denominator of the first fraction by 12, the second by 4, and the third by 3. As a result, we get $\frac(36)(12) + \frac(4 )(12)+\frac(15)(12)$, which is equal to $\frac(55)(12)$. If you want to get rid of improper fraction, it can be turned into a number consisting of an integer and a fractional part: $\frac(55)(12) = \frac(48)(12)+\frac(7)(12)$ or $4\frac(7)( 12)$.
All the rules that allow operations with fractions, which we have just studied, are also valid in the case of negative numbers. So, -1: 3 can be written as $\frac(-1)(3)$, and 1: (-3) as $\frac(1)(-3)$.
Since both dividing a negative number by a positive number and dividing a positive number by a negative result in negative numbers, in both cases we will get the answer in the form of a negative number. I.e
$(-1) : 3 = \frac(1)(3)$ or $1 : (-3) = \frac(1)(-3)$. The minus sign when written this way refers to the entire fraction as a whole, and not separately to the numerator or denominator.
On the other hand, (-1) : (-3) can be written as $\frac(-1)(-3)$, and since dividing a negative number by a negative number gives a positive number, then $\frac(-1 )(-3)$ can be written as $+\frac(1)(3)$.
Addition and subtraction of negative fractions is carried out in the same way as the addition and subtraction of positive fractions. For example, what is $1- 1\frac13$? Let's represent both numbers as fractions and get $\frac(1)(1)-\frac(4)(3)$. Let's reduce the fractions to a common denominator and get $\frac(1 \times 3)(1 \times 3)-\frac(4)(3)$, i.e. $\frac(3)(3)-\frac(4) (3)$, or $-\frac(1)(3)$.
§ 87. Addition of fractions.
Adding fractions has many similarities to adding integers. Addition of fractions is an action consisting in the fact that several given numbers (terms) are combined into one number (sum), which contains all units and fractions of units of terms.
We will consider three cases in turn:
1. Addition of fractions with the same denominators.
2. Addition of fractions with different denominators.
3. Addition of mixed numbers.
1. Addition of fractions with the same denominators.
Consider an example: 1 / 5 + 2 / 5 .
Take the segment AB (Fig. 17), take it as a unit and divide it into 5 equal parts, then the part AC of this segment will be equal to 1/5 of the segment AB, and the part of the same segment CD will be equal to 2/5 AB.
It can be seen from the drawing that if we take the segment AD, then it will be equal to 3/5 AB; but segment AD is precisely the sum of segments AC and CD. So, we can write:
1 / 5 + 2 / 5 = 3 / 5
Considering these terms and the resulting amount, we see that the numerator of the sum was obtained by adding the numerators of the terms, and the denominator remained unchanged.
From this we get the following rule: To add fractions with the same denominators, you must add their numerators and leave the same denominator.
Consider an example:
2. Addition of fractions with different denominators.
Let's add fractions: 3/4 + 3/8 First they need to be reduced to the lowest common denominator:
The intermediate link 6/8 + 3/8 could not have been written; we have written it here for greater clarity.
Thus, to add fractions with different denominators, you must first bring them to the lowest common denominator, add their numerators and sign the common denominator.
Consider an example (we will write additional factors over the corresponding fractions):
3. Addition of mixed numbers.
Let's add the numbers: 2 3 / 8 + 3 5 / 6.
Let us first bring the fractional parts of our numbers to a common denominator and rewrite them again:
![]()
Now add the integer and fractional parts in sequence:
§ 88. Subtraction of fractions.
Subtraction of fractions is defined in the same way as subtraction of whole numbers. This is an action by which, given the sum of two terms and one of them, another term is found. Let's consider three cases in turn:
1. Subtraction of fractions with the same denominators.
2. Subtraction of fractions with different denominators.
3. Subtraction of mixed numbers.
1. Subtraction of fractions with the same denominators.
Consider an example:
13 / 15 - 4 / 15
Let's take the segment AB (Fig. 18), take it as a unit and divide it into 15 equal parts; then the AC part of this segment will be 1/15 of AB, and the AD part of the same segment will correspond to 13/15 AB. Let's set aside another segment ED, equal to 4/15 AB.
We need to subtract 4/15 from 13/15. In the drawing, this means that the segment ED must be subtracted from the segment AD. As a result, segment AE will remain, which is 9/15 of segment AB. So we can write:

The example we made shows that the numerator of the difference was obtained by subtracting the numerators, and the denominator remained the same.
Therefore, in order to subtract fractions with the same denominators, you need to subtract the numerator of the subtrahend from the numerator of the minuend and leave the same denominator.
2. Subtraction of fractions with different denominators.
Example. 3/4 - 5/8
First, let's reduce these fractions to the smallest common denominator:

The intermediate link 6 / 8 - 5 / 8 is written here for clarity, but it can be skipped in the future.
Thus, in order to subtract a fraction from a fraction, you must first bring them to the smallest common denominator, then subtract the numerator of the subtrahend from the numerator of the minuend and sign the common denominator under their difference.
Consider an example:
![]()
3. Subtraction of mixed numbers.
Example. 10 3 / 4 - 7 2 / 3 .
Let's bring the fractional parts of the minuend and the subtrahend to the lowest common denominator:
We subtracted a whole from a whole and a fraction from a fraction. But there are cases when the fractional part of the subtrahend is greater than the fractional part of the minuend. In such cases, you need to take one unit from the integer part of the reduced, split it into those parts in which the fractional part is expressed, and add to the fractional part of the reduced. And then the subtraction will be performed in the same way as in the previous example:
§ 89. Multiplication of fractions.
When studying the multiplication of fractions, we will consider the following questions:
1. Multiplying a fraction by an integer.
2. Finding a fraction of a given number.
3. Multiplication of a whole number by a fraction.
4. Multiplying a fraction by a fraction.
5. Multiplication of mixed numbers.
6. The concept of interest.
7. Finding percentages of a given number. Let's consider them sequentially.
1. Multiplying a fraction by an integer.
Multiplying a fraction by an integer has the same meaning as multiplying an integer by an integer. Multiplying a fraction (multiplicand) by an integer (multiplier) means composing the sum of identical terms, in which each term is equal to the multiplicand, and the number of terms is equal to the multiplier.
So, if you need to multiply 1/9 by 7, then this can be done like this:
We easily got the result, since the action was reduced to adding fractions with the same denominators. Hence,
Consideration of this action shows that multiplying a fraction by an integer is equivalent to increasing this fraction as many times as there are units in the integer. And since the increase in the fraction is achieved either by increasing its numerator
![]() or by decreasing its denominator
or by decreasing its denominator ![]() , then we can either multiply the numerator by the integer, or divide the denominator by it, if such a division is possible.
, then we can either multiply the numerator by the integer, or divide the denominator by it, if such a division is possible.
From here we get the rule:
To multiply a fraction by an integer, you need to multiply the numerator by this integer and leave the same denominator or, if possible, divide the denominator by this number, leaving the numerator unchanged.
When multiplying, abbreviations are possible, for example:
2. Finding a fraction of a given number. There are many problems in which you have to find, or calculate, a part of a given number. The difference between these tasks and others is that they give the number of some objects or units of measurement and you need to find a part of this number, which is also indicated here by a certain fraction. To facilitate understanding, we will first give examples of such problems, and then introduce the method of solving them.
Task 1. I had 60 rubles; 1 / 3 of this money I spent on the purchase of books. How much did the books cost?
Task 2. The train must cover the distance between cities A and B, equal to 300 km. He has already covered 2/3 of that distance. How many kilometers is this?
Task 3. There are 400 houses in the village, 3/4 of them are brick, the rest are wooden. How many brick houses are there?
Here are some of the many problems that we have to deal with to find a fraction of a given number. They are usually called problems for finding a fraction of a given number.
Solution of problem 1. From 60 rubles. I spent 1 / 3 on books; So, to find the cost of books, you need to divide the number 60 by 3:
Problem 2 solution. The meaning of the problem is that you need to find 2 / 3 of 300 km. Calculate first 1/3 of 300; this is achieved by dividing 300 km by 3:
300: 3 = 100 (that's 1/3 of 300).
To find two-thirds of 300, you need to double the resulting quotient, that is, multiply by 2:
100 x 2 = 200 (that's 2/3 of 300).
Solution of problem 3. Here you need to determine the number of brick houses, which are 3/4 of 400. Let's first find 1/4 of 400,
400: 4 = 100 (that's 1/4 of 400).
To calculate three quarters of 400, the resulting quotient must be tripled, that is, multiplied by 3:
100 x 3 = 300 (that's 3/4 of 400).
Based on the solution of these problems, we can derive the following rule:
To find the value of a fraction from a given number, you need to divide this number by the denominator of the fraction and multiply the resulting quotient by its numerator.
3. Multiplication of a whole number by a fraction.
Earlier (§ 26) it was established that the multiplication of integers should be understood as the addition of identical terms (5 x 4 \u003d 5 + 5 + 5 + 5 \u003d 20). In this paragraph (paragraph 1) it was established that multiplying a fraction by an integer means finding the sum of identical terms equal to this fraction.
In both cases, the multiplication consisted in finding the sum of identical terms.
Now we move on to multiplying a whole number by a fraction. Here we will meet with such, for example, multiplication: 9 2 / 3. It is quite obvious that the previous definition of multiplication does not apply to this case. This is evident from the fact that we cannot replace such multiplication by adding equal numbers.
Because of this, we will have to give a new definition of multiplication, i.e., in other words, to answer the question of what should be understood by multiplication by a fraction, how this action should be understood.
The meaning of multiplying an integer by a fraction is clear from the following definition: to multiply an integer (multiplier) by a fraction (multiplier) means to find this fraction of the multiplier.
Namely, multiplying 9 by 2/3 means finding 2/3 of nine units. In the previous paragraph, such problems were solved; so it's easy to figure out that we end up with 6.
But now an interesting and important question arises: why such seemingly different actions as finding the sum of equal numbers and finding the fraction of a number are called the same word “multiplication” in arithmetic?
This happens because the previous action (repeating the number with terms several times) and the new action (finding the fraction of a number) give an answer to homogeneous questions. This means that we proceed here from the considerations that homogeneous questions or tasks are solved by one and the same action.
To understand this, consider the following problem: “1 m of cloth costs 50 rubles. How much will 4 m of such cloth cost?
This problem is solved by multiplying the number of rubles (50) by the number of meters (4), i.e. 50 x 4 = 200 (rubles).
Let's take the same problem, but in it the amount of cloth will be expressed as a fractional number: “1 m of cloth costs 50 rubles. How much will 3/4 m of such cloth cost?
This problem also needs to be solved by multiplying the number of rubles (50) by the number of meters (3/4).
You can also change the numbers in it several times without changing the meaning of the problem, for example, take 9/10 m or 2 3/10 m, etc.
Since these problems have the same content and differ only in numbers, we call the actions used in solving them the same word - multiplication.
How is a whole number multiplied by a fraction?
Let's take the numbers encountered in the last problem:
According to the definition, we must find 3 / 4 of 50. First we find 1 / 4 of 50, and then 3 / 4.
1/4 of 50 is 50/4;
3/4 of 50 is .
Hence.
Consider another example: 12 5 / 8 = ?
1/8 of 12 is 12/8,
5/8 of the number 12 is .
Hence,
From here we get the rule:
To multiply an integer by a fraction, you need to multiply the integer by the numerator of the fraction and make this product the numerator, and sign the denominator of the given fraction as the denominator.
We write this rule using letters:
To make this rule perfectly clear, it should be remembered that a fraction can be considered as a quotient. Therefore, it is useful to compare the found rule with the rule for multiplying a number by a quotient, which was set out in § 38
It must be remembered that before performing multiplication, you should do (if possible) cuts, For example:
4. Multiplying a fraction by a fraction. Multiplying a fraction by a fraction has the same meaning as multiplying an integer by a fraction, that is, when multiplying a fraction by a fraction, you need to find the fraction in the multiplier from the first fraction (multiplier).
Namely, multiplying 3/4 by 1/2 (half) means finding half of 3/4.
How do you multiply a fraction by a fraction?
Let's take an example: 3/4 times 5/7. This means that you need to find 5 / 7 from 3 / 4 . Find first 1/7 of 3/4 and then 5/7
1/7 of 3/4 would be expressed like this:
5 / 7 numbers 3 / 4 will be expressed as follows:
Thus,
![]()
Another example: 5/8 times 4/9.
1/9 of 5/8 is ,
4/9 numbers 5/8 are .
Thus, ![]()
From these examples, the following rule can be deduced:
To multiply a fraction by a fraction, you need to multiply the numerator by the numerator, and the denominator by the denominator and make the first product the numerator and the second product the denominator of the product.
This is the rule in general view can be written like this:
![]()
When multiplying, it is necessary to make (if possible) reductions. Consider examples:

5. Multiplication of mixed numbers. Since mixed numbers can easily be replaced by improper fractions, this circumstance is usually used when multiplying mixed numbers. This means that in those cases where the multiplicand, or the multiplier, or both factors are expressed as mixed numbers, then they are replaced by improper fractions. Multiply, for example, mixed numbers: 2 1/2 and 3 1/5. We turn each of them into an improper fraction and then we will multiply the resulting fractions according to the rule of multiplying a fraction by a fraction:
Rule. To multiply mixed numbers, you must first convert them to improper fractions and then multiply according to the rule of multiplying a fraction by a fraction.
Note. If one of the factors is an integer, then the multiplication can be performed based on the distribution law as follows:
6. The concept of interest. When solving problems and when performing various practical calculations, we use all kinds of fractions. But one must keep in mind that many quantities admit not any, but natural subdivisions for them. For example, you can take one hundredth (1/100) of a ruble, it will be a penny, two hundredths is 2 kopecks, three hundredths is 3 kopecks. You can take 1/10 of the ruble, it will be "10 kopecks, or a dime. You can take a quarter of the ruble, i.e. 25 kopecks, half a ruble, i.e. 50 kopecks (fifty kopecks). But they practically don’t take, for example , 2/7 rubles because the ruble is not divided into sevenths.
The unit of measurement for weight, i.e., the kilogram, allows, first of all, decimal subdivisions, for example, 1/10 kg, or 100 g. And such fractions of a kilogram as 1/6, 1/11, 1/13 are uncommon.
In general our (metric) measures are decimal and allow decimal subdivisions.
However, it should be noted that it is extremely useful and convenient in a wide variety of cases to use the same (uniform) method of subdividing quantities. Many years of experience have shown that such a well-justified division is the "hundredths" division. Let's consider a few examples related to the most diverse areas of human practice.
1. The price of books has decreased by 12/100 of the previous price.
Example. The previous price of the book is 10 rubles. She went down by 1 ruble. 20 kop.
2. Savings banks pay out during the year to depositors 2/100 of the amount that is put into savings.
Example. 500 rubles are put into the cash desk, the income from this amount for the year is 10 rubles.
3. The number of graduates of one school was 5/100 of the total number of students.
EXAMPLE Only 1,200 students studied at the school, 60 of them graduated from school.
The hundredth of a number is called a percentage..
The word "percent" is borrowed from the Latin language and its root "cent" means one hundred. Together with the preposition (pro centum), this word means "for a hundred." The meaning of this expression follows from the fact that initially in ancient Rome interest was the money that the debtor paid to the lender “for every hundred”. The word "cent" is heard in such familiar words: centner (one hundred kilograms), centimeter (they say centimeter).
For example, instead of saying that the plant produced 1/100 of all the products produced by it during the past month, we will say this: the plant produced one percent of the rejects during the past month. Instead of saying: the plant produced 4/100 more products than the established plan, we will say: the plant exceeded the plan by 4 percent.
The above examples can be expressed differently:
1. The price of books has decreased by 12 percent of the previous price.
2. Savings banks pay depositors 2 percent per year of the amount put into savings.
3. The number of graduates of one school was 5 percent of the number of all students in the school.
To shorten the letter, it is customary to write the% sign instead of the word "percentage".
However, it must be remembered that the % sign is usually not written in calculations, it can be written in the problem statement and in the final result. When performing calculations, you need to write a fraction with a denominator of 100 instead of an integer with this icon.
You need to be able to replace an integer with the specified icon with a fraction with a denominator of 100:
Conversely, you need to get used to writing an integer with the indicated icon instead of a fraction with a denominator of 100:
7. Finding percentages of a given number.
Task 1. The school received 200 cubic meters. m of firewood, with birch firewood accounting for 30%. How much birch wood was there?
The meaning of this problem is that birch firewood was only a part of the firewood that was delivered to the school, and this part is expressed as a fraction of 30 / 100. So, we are faced with the task of finding a fraction of a number. To solve it, we must multiply 200 by 30 / 100 (tasks for finding the fraction of a number are solved by multiplying a number by a fraction.).
So 30% of 200 equals 60.
The fraction 30 / 100 encountered in this problem can be reduced by 10. It would be possible to perform this reduction from the very beginning; the solution to the problem would not change.
Task 2. There were 300 children of various ages in the camp. Children aged 11 were 21%, children aged 12 were 61% and finally 13 year olds were 18%. How many children of each age were in the camp?
In this problem, you need to perform three calculations, that is, successively find the number of children 11 years old, then 12 years old, and finally 13 years old.
So, here it will be necessary to find a fraction of a number three times. Let's do it:
1) How many children were 11 years old?
2) How many children were 12 years old?
3) How many children were 13 years old?
After solving the problem, it is useful to add the numbers found; their sum should be 300:
63 + 183 + 54 = 300
You should also pay attention to the fact that the sum of the percentages given in the condition of the problem is 100:
21% + 61% + 18% = 100%
This suggests that the total number of children in the camp was taken as 100%.
3 a da cha 3. The worker received 1,200 rubles per month. Of these, he spent 65% on food, 6% on an apartment and heating, 4% on gas, electricity and radio, 10% on cultural needs and 15% he saved. How much money was spent on the needs indicated in the task?
To solve this problem, you need to find a fraction of the number 1,200 5 times. Let's do it.
1) How much money is spent on food? The task says that this expense is 65% of all earnings, i.e. 65/100 of the number 1,200. Let's do the calculation:
![]()
2) How much money was paid for an apartment with heating? Arguing like the previous one, we arrive at the following calculation:
3) How much money did you pay for gas, electricity and radio?
4) How much money is spent on cultural needs?
5) How much money did the worker save?
For verification, it is useful to add the numbers found in these 5 questions. The amount should be 1,200 rubles. All earnings are taken as 100%, which is easy to check by adding up the percentages given in the problem statement.
We have solved three problems. Despite the fact that these tasks were about different things (delivery of firewood for the school, the number of children of different ages, the expenses of the worker), they were solved in the same way. This happened because in all tasks it was necessary to find a few percent of the given numbers.
§ 90. Division of fractions.
When studying the division of fractions, we will consider the following questions:
1. Divide an integer by an integer.
2. Division of a fraction by an integer
3. Division of an integer by a fraction.
4. Division of a fraction by a fraction.
5. Division of mixed numbers.
6. Finding a number given its fraction.
7. Finding a number by its percentage.
Let's consider them sequentially.
1. Divide an integer by an integer.
As was indicated in the section on integers, division is the action consisting in the fact that, given the product of two factors (the dividend) and one of these factors (the divisor), another factor is found.
The division of an integer by an integer we considered in the department of integers. We met there two cases of division: division without a remainder, or "entirely" (150: 10 = 15), and division with a remainder (100: 9 = 11 and 1 in the remainder). We can therefore say that in the realm of integers, exact division is not always possible, because the dividend is not always the product of the divisor and the integer. After the introduction of multiplication by a fraction, we can consider any case of division of integers as possible (only division by zero is excluded).
For example, dividing 7 by 12 means finding a number whose product times 12 would be 7. This number is the fraction 7/12 because 7/12 12 = 7. Another example: 14: 25 = 14/25 because 14/25 25 = 14.
Thus, to divide an integer by an integer, you need to make a fraction, the numerator of which is equal to the dividend, and the denominator is the divisor.
2. Division of a fraction by an integer.
Divide the fraction 6 / 7 by 3. According to the definition of division given above, we have here the product (6 / 7) and one of the factors (3); it is required to find such a second factor that, when multiplied by 3, would give the given product 6 / 7. Obviously, it should be three times smaller than this product. This means that the task set before us was to reduce the fraction 6 / 7 by 3 times.
We already know that the reduction of a fraction can be done either by decreasing its numerator or by increasing its denominator. Therefore, you can write:
![]()
In this case, the numerator 6 is divisible by 3, so the numerator should be reduced by 3 times.
Let's take another example: 5 / 8 divided by 2. Here the numerator 5 is not divisible by 2, which means that the denominator will have to be multiplied by this number:
![]()
Based on this, we can state the rule: To divide a fraction by an integer, you need to divide the numerator of the fraction by that integer(if possible), leaving the same denominator, or multiply the denominator of the fraction by this number, leaving the same numerator.
3. Division of an integer by a fraction.
Let it be required to divide 5 by 1 / 2, i.e. find a number that, after multiplying by 1 / 2, will give the product 5. Obviously, this number must be greater than 5, since 1 / 2 is a proper fraction, and when multiplying a number by a proper fraction, the product must be less than the multiplicand. To make it clearer, let's write our actions as follows: 5: 1 / 2 = X , so x 1 / 2 \u003d 5.
We must find such a number X , which, when multiplied by 1/2, would give 5. Since multiplying a certain number by 1/2 means finding 1/2 of this number, then, therefore, 1/2 of the unknown number X is 5, and the whole number X twice as much, i.e. 5 2 \u003d 10.
So 5: 1 / 2 = 5 2 = 10
Let's check: ![]()
Let's consider one more example. Let it be required to divide 6 by 2 / 3 . Let's first try to find the desired result using the drawing (Fig. 19).
Fig.19
Draw a segment AB, equal to 6 of some units, and divide each unit into 3 equal parts. In each unit, three-thirds (3 / 3) in the entire segment AB is 6 times larger, i.e. e. 18/3. We connect with the help of small brackets 18 obtained segments of 2; There will be only 9 segments. This means that the fraction 2/3 is contained in b units 9 times, or, in other words, the fraction 2/3 is 9 times less than 6 integer units. Hence,
How to get this result without a drawing using only calculations? We will argue as follows: it is required to divide 6 by 2 / 3, i.e., it is required to answer the question, how many times 2 / 3 is contained in 6. Let's find out first: how many times is 1 / 3 contained in 6? In a whole unit - 3 thirds, and in 6 units - 6 times more, i.e. 18 thirds; to find this number, we must multiply 6 by 3. Hence, 1/3 is contained in b units 18 times, and 2/3 is contained in b units not 18 times, but half as many times, i.e. 18: 2 = 9. Therefore , when dividing 6 by 2 / 3 we did the following:
![]()
From here we get the rule for dividing an integer by a fraction. To divide an integer by a fraction, you need to multiply this integer by the denominator of the given fraction and, making this product the numerator, divide it by the numerator of the given fraction.
We write the rule using letters:
To make this rule perfectly clear, it should be remembered that a fraction can be considered as a quotient. Therefore, it is useful to compare the found rule with the rule for dividing a number by a quotient, which was set out in § 38. Note that the same formula was obtained there.
When dividing, abbreviations are possible, for example:
4. Division of a fraction by a fraction.
Let it be required to divide 3/4 by 3/8. What will denote the number that will be obtained as a result of division? It will answer the question how many times the fraction 3/8 is contained in the fraction 3/4. To understand this issue, let's make a drawing (Fig. 20).

Take the segment AB, take it as a unit, divide it into 4 equal parts and mark 3 such parts. Segment AC will be equal to 3/4 of segment AB. Let us now divide each of the four initial segments in half, then the segment AB will be divided into 8 equal parts and each such part will be equal to 1/8 of the segment AB. We connect 3 such segments with arcs, then each of the segments AD and DC will be equal to 3/8 of the segment AB. The drawing shows that the segment equal to 3/8 is contained in the segment equal to 3/4 exactly 2 times; So the result of the division can be written like this:
3 / 4: 3 / 8 = 2
Let's consider one more example. Let it be required to divide 15/16 by 3/32:
We can reason like this: we need to find a number that, after being multiplied by 3 / 32, will give a product equal to 15 / 16. Let's write the calculations like this:
15 / 16: 3 / 32 = X
3 / 32 X = 15 / 16
3/32 unknown number X make up 15 / 16
1/32 unknown number X is ,
32 / 32 numbers X make up .
Hence,
![]()
Thus, to divide a fraction by a fraction, you need to multiply the numerator of the first fraction by the denominator of the second, and multiply the denominator of the first fraction by the numerator of the second and make the first product the numerator and the second the denominator.
Let's write the rule using letters:
When dividing, abbreviations are possible, for example:
5. Division of mixed numbers.
When dividing mixed numbers, they must first be converted into improper fractions, and then the resulting fractions should be divided according to the rules for dividing fractional numbers. Consider an example:
Convert mixed numbers to improper fractions:
![]()
Now let's split:
Thus, to divide mixed numbers, you need to convert them to improper fractions and then divide according to the rule for dividing fractions.
6. Finding a number given its fraction.
Among the various tasks on fractions, there are sometimes those in which the value of some fraction of an unknown number is given and it is required to find this number. This type of problem will be inverse to the problem of finding a fraction of a given number; there a number was given and it was required to find some fraction of this number, here a fraction of a number is given and it is required to find this number itself. This idea will become even clearer if we turn to the solution of this type of problem.
Task 1. On the first day, glaziers glazed 50 windows, which is 1 / 3 of all windows of the built house. How many windows are in this house?
Decision. The problem says that 50 glazed windows make up 1/3 of all the windows of the house, which means that there are 3 times more windows in total, i.e.
The house had 150 windows.
Task 2. The shop sold 1,500 kg of flour, which is 3/8 of the total stock of flour in the shop. What was the store's initial supply of flour?
Decision. It can be seen from the condition of the problem that the sold 1,500 kg of flour make up 3/8 of the total stock; this means that 1/8 of this stock will be 3 times less, i.e., to calculate it, you need to reduce 1500 by 3 times:
1,500: 3 = 500 (that's 1/8 of the stock).
Obviously, the entire stock will be 8 times larger. Hence,
500 8 \u003d 4,000 (kg).
The initial supply of flour in the store was 4,000 kg.
From the consideration of this problem, the following rule can be deduced.
To find a number by a given value of its fraction, it is enough to divide this value by the numerator of the fraction and multiply the result by the denominator of the fraction.
We solved two problems on finding a number given its fraction. Such problems, as it is especially well seen from the last one, are solved by two actions: division (when one part is found) and multiplication (when the whole number is found).
However, after we have studied the division of fractions, the above problems can be solved in one action, namely: division by a fraction.
For example, the last task can be solved in one action like this:
In the future, we will solve the problem of finding a number by its fraction in one action - division.
7. Finding a number by its percentage.
In these tasks, you will need to find a number, knowing a few percent of this number.
Task 1. At the beginning of this year, I received 60 rubles from the savings bank. income from the amount I put into savings a year ago. How much money did I put in the savings bank? (Cash offices give depositors 2% of income per year.)
The meaning of the problem is that a certain amount of money was put by me in a savings bank and lay there for a year. After a year, I received 60 rubles from her. income, which is 2/100 of the money I put in. How much money did I deposit?
Therefore, knowing the part of this money, expressed in two ways (in rubles and in fractions), we must find the entire, as yet unknown, amount. This is an ordinary problem of finding a number given its fraction. The following tasks are solved by division:
So, 3,000 rubles were put into the savings bank.
Task 2. In two weeks, fishermen fulfilled the monthly plan by 64%, having prepared 512 tons of fish. What was their plan?
From the condition of the problem, it is known that the fishermen completed part of the plan. This part is equal to 512 tons, which is 64% of the plan. How many tons of fish need to be harvested according to the plan, we do not know. The solution of the problem will consist in finding this number.
Such tasks are solved by dividing:
So, according to the plan, you need to prepare 800 tons of fish.
Task 3. The train went from Riga to Moscow. When he passed the 276th kilometer, one of the passengers asked the passing conductor how much of the journey they had already traveled. To this the conductor replied: “We have already covered 30% of the entire journey.” What is the distance from Riga to Moscow?
It can be seen from the condition of the problem that 30% of the journey from Riga to Moscow is 276 km. We need to find the entire distance between these cities, i.e., for this part, find the whole:
§ 91. Reciprocal numbers. Replacing division with multiplication.
Take the fraction 2/3 and rearrange the numerator to the place of the denominator, we get 3/2. We got a fraction, the reciprocal of this one.
In order to get a fraction reciprocal of a given one, you need to put its numerator in the place of the denominator, and the denominator in the place of the numerator. In this way, we can get a fraction that is the reciprocal of any fraction. For example:
3 / 4 , reverse 4 / 3 ; 5 / 6 , reverse 6 / 5
Two fractions that have the property that the numerator of the first is the denominator of the second and the denominator of the first is the numerator of the second are called mutually inverse.
Now let's think about what fraction will be the reciprocal of 1/2. Obviously, it will be 2 / 1, or just 2. Looking for the reciprocal of this, we got an integer. And this case is not isolated; on the contrary, for all fractions with a numerator of 1 (one), the reciprocals will be integers, for example:
1 / 3, inverse 3; 1 / 5, reverse 5
Since when finding reciprocals we also met with integers, in the future we will not talk about reciprocals, but about reciprocals.
Let's figure out how to write the reciprocal of a whole number. For fractions, this is solved simply: you need to put the denominator in the place of the numerator. In the same way, you can get the reciprocal of an integer, since any integer can have a denominator of 1. So the reciprocal of 7 will be 1 / 7, because 7 \u003d 7 / 1; for the number 10 the reverse is 1 / 10 since 10 = 10 / 1
This idea can be expressed in another way: the reciprocal of a given number is obtained by dividing one by the given number. This statement is true not only for integers, but also for fractions. Indeed, if you want to write a number that is the reciprocal of the fraction 5 / 9, then we can take 1 and divide it by 5 / 9, i.e.

Now let's point out one property mutually reciprocal numbers, which will be useful to us: the product of mutually reciprocal numbers is equal to one. Indeed:
Using this property, we can find reciprocals in the following way. Let's find the reciprocal of 8.
Let's denote it with the letter X , then 8 X = 1, hence X = 1 / 8 . Let's find another number, the inverse of 7/12, denote it by a letter X , then 7 / 12 X = 1, hence X = 1:7 / 12 or X = 12 / 7 .
We introduced here the concept of reciprocal numbers in order to slightly supplement information about the division of fractions.
When we divide the number 6 by 3 / 5, then we do the following:
![]()
Pay special attention to the expression and compare it with the given one: .
If we take the expression separately, without connection with the previous one, then it is impossible to solve the question of where it came from: from dividing 6 by 3/5 or from multiplying 6 by 5/3. In both cases the result is the same. So we can say that dividing one number by another can be replaced by multiplying the dividend by the reciprocal of the divisor.
The examples that we give below fully confirm this conclusion.
Lesson contentAdding fractions with the same denominators
Adding fractions is of two types:
- Adding fractions with the same denominators
- Adding fractions with different denominators
Let's start with adding fractions with the same denominators. Everything is simple here. To add fractions with the same denominators, you need to add their numerators, and leave the denominator unchanged. For example, let's add the fractions and . We add the numerators, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into four parts. If you add pizza to pizza, you get pizza:

Example 2 Add fractions and .

The answer is an improper fraction. If the end of the task comes, then it is customary to get rid of improper fractions. To get rid of an improper fraction, you need to select the whole part in it. In our case, the whole part is easily distinguished - two divided by two is equal to one:

This example can be easily understood if we think of a pizza that is divided into two parts. If you add more pizzas to the pizza, you get one whole pizza:

Example 3. Add fractions and .
Again, add the numerators, and leave the denominator unchanged:
![]()
This example can be easily understood if we think of a pizza that is divided into three parts. If you add more pizzas to pizza, you get pizzas:

Example 4 Find the value of an expression 
This example is solved in exactly the same way as the previous ones. The numerators must be added and the denominator left unchanged:
Let's try to depict our solution using a picture. If you add pizzas to a pizza and add more pizzas, you get 1 whole pizza and more pizzas.

As you can see, adding fractions with the same denominators is not difficult. It is enough to understand the following rules:
- To add fractions with the same denominator, you need to add their numerators, and leave the denominator unchanged;
Adding fractions with different denominators
Now we will learn how to add fractions with different denominators. When adding fractions, the denominators of those fractions must be the same. But they are not always the same.
For example, fractions can be added because they have the same denominators.
But fractions cannot be added at once, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.
There are several ways to reduce fractions to the same denominator. Today we will consider only one of them, since the rest of the methods may seem complicated for a beginner.
The essence of this method lies in the fact that first (LCM) of the denominators of both fractions is sought. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained. They do the same with the second fraction - the LCM is divided by the denominator of the second fraction and the second additional factor is obtained.
Then the numerators and denominators of the fractions are multiplied by their additional factors. As a result of these actions, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to add such fractions.
Example 1. Add fractions and
First of all, we find the least common multiple of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 2. The least common multiple of these numbers is 6
LCM (2 and 3) = 6
Now back to fractions and . First, we divide the LCM by the denominator of the first fraction and get the first additional factor. LCM is the number 6, and the denominator of the first fraction is the number 3. Divide 6 by 3, we get 2.
The resulting number 2 is the first additional factor. We write it down to the first fraction. To do this, we make a small oblique line above the fraction and write down the found additional factor above it:
We do the same with the second fraction. We divide the LCM by the denominator of the second fraction and get the second additional factor. LCM is the number 6, and the denominator of the second fraction is the number 2. Divide 6 by 2, we get 3.
The resulting number 3 is the second additional factor. We write it to the second fraction. Again, we make a small oblique line above the second fraction and write the found additional factor above it:
Now we are all set to add. It remains to multiply the numerators and denominators of fractions by their additional factors:

Look closely at what we have come to. We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to add such fractions. Let's complete this example to the end:

Thus the example ends. To add it turns out.
Let's try to depict our solution using a picture. If you add pizzas to a pizza, you get one whole pizza and another sixth of a pizza:

Reduction of fractions to the same (common) denominator can also be depicted using a picture. Bringing the fractions and to a common denominator, we get the fractions and . These two fractions will be represented by the same slices of pizzas. The only difference will be that this time they will be divided into equal shares (reduced to the same denominator).

The first drawing shows a fraction (four pieces out of six) and the second picture shows a fraction (three pieces out of six). Putting these pieces together we get (seven pieces out of six). This fraction is incorrect, so we have highlighted the integer part in it. The result was (one whole pizza and another sixth pizza).
Note that we have painted this example in too much detail. In educational institutions it is not customary to write in such a detailed manner. You need to be able to quickly find the LCM of both denominators and additional factors to them, as well as quickly multiply the additional factors found by your numerators and denominators. While at school, we would have to write this example as follows:

But there is also the other side of the coin. If detailed notes are not made at the first stages of studying mathematics, then questions of the kind “Where does that number come from?”, “Why do fractions suddenly turn into completely different fractions? «.
To make it easier to add fractions with different denominators, you can use the following step-by-step instructions:
- Find the LCM of the denominators of fractions;
- Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction;
- Multiply the numerators and denominators of fractions by their additional factors;
- Add fractions that have the same denominators;
- If the answer turned out to be an improper fraction, then select its whole part;
Example 2 Find the value of an expression  .
.
Let's use the instructions above.
Step 1. Find the LCM of the denominators of fractions
Find the LCM of the denominators of both fractions. The denominators of the fractions are the numbers 2, 3 and 4
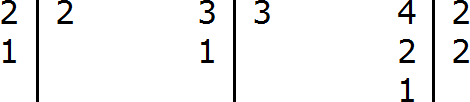
Step 2. Divide the LCM by the denominator of each fraction and get an additional multiplier for each fraction
Divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 2. Divide 12 by 2, we get 6. We got the first additional factor 6. We write it over the first fraction:
Now we divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 3. Divide 12 by 3, we get 4. We got the second additional factor 4. We write it over the second fraction:
Now we divide the LCM by the denominator of the third fraction. LCM is the number 12, and the denominator of the third fraction is the number 4. Divide 12 by 4, we get 3. We got the third additional factor 3. We write it over the third fraction:
Step 3. Multiply the numerators and denominators of fractions by your additional factors
We multiply the numerators and denominators by our additional factors:
Step 4. Add fractions that have the same denominators
We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. It remains to add these fractions. Add up:

The addition didn't fit on one line, so we moved the remaining expression to the next line. This is allowed in mathematics. When an expression does not fit on one line, it is carried over to the next line, and it is necessary to put an equal sign (=) at the end of the first line and at the beginning of a new line. The equal sign on the second line indicates that this is a continuation of the expression that was on the first line.
Step 5. If the answer turned out to be an improper fraction, then select the whole part in it
Our answer is an improper fraction. We must single out the whole part of it. We highlight:

Got an answer
Subtraction of fractions with the same denominators
There are two types of fraction subtraction:
- Subtraction of fractions with the same denominators
- Subtraction of fractions with different denominators
First, let's learn how to subtract fractions with the same denominators. Everything is simple here. To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator the same.
For example, let's find the value of the expression . To solve this example, it is necessary to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged. Let's do this:

This example can be easily understood if we think of a pizza that is divided into four parts. If you cut pizzas from a pizza, you get pizzas:

Example 2 Find the value of the expression .
Again, from the numerator of the first fraction, subtract the numerator of the second fraction, and leave the denominator unchanged:

This example can be easily understood if we think of a pizza that is divided into three parts. If you cut pizzas from a pizza, you get pizzas:

Example 3 Find the value of an expression 
This example is solved in exactly the same way as the previous ones. From the numerator of the first fraction, you need to subtract the numerators of the remaining fractions:

As you can see, there is nothing complicated in subtracting fractions with the same denominators. It is enough to understand the following rules:
- To subtract another from one fraction, you need to subtract the numerator of the second fraction from the numerator of the first fraction, and leave the denominator unchanged;
- If the answer turned out to be an improper fraction, then you need to select the whole part in it.
Subtraction of fractions with different denominators
For example, a fraction can be subtracted from a fraction, since these fractions have the same denominators. But a fraction cannot be subtracted from a fraction, because these fractions have different denominators. In such cases, fractions must be reduced to the same (common) denominator.
The common denominator is found according to the same principle that we used when adding fractions with different denominators. First of all, find the LCM of the denominators of both fractions. Then the LCM is divided by the denominator of the first fraction and the first additional factor is obtained, which is written over the first fraction. Similarly, the LCM is divided by the denominator of the second fraction and a second additional factor is obtained, which is written over the second fraction.
The fractions are then multiplied by their additional factors. As a result of these operations, fractions that had different denominators turn into fractions that have the same denominators. And we already know how to subtract such fractions.
Example 1 Find the value of an expression:
These fractions have different denominators, so you need to bring them to the same (common) denominator.
First, we find the LCM of the denominators of both fractions. The denominator of the first fraction is the number 3, and the denominator of the second fraction is the number 4. The least common multiple of these numbers is 12
LCM (3 and 4) = 12
Now back to fractions and
Let's find an additional factor for the first fraction. To do this, we divide the LCM by the denominator of the first fraction. LCM is the number 12, and the denominator of the first fraction is the number 3. Divide 12 by 3, we get 4. We write the four over the first fraction:
We do the same with the second fraction. We divide the LCM by the denominator of the second fraction. LCM is the number 12, and the denominator of the second fraction is the number 4. Divide 12 by 4, we get 3. Write a triple over the second fraction:
Now we are all set for subtraction. It remains to multiply the fractions by their additional factors:

We came to the conclusion that fractions that had different denominators turned into fractions that had the same denominators. And we already know how to subtract such fractions. Let's complete this example to the end:

Got an answer
Let's try to depict our solution using a picture. If you cut pizzas from a pizza, you get pizzas.

This is the detailed version of the solution. Being at school, we would have to solve this example in a shorter way. Such a solution would look like this:

Reduction of fractions and to a common denominator can also be depicted using a picture. Bringing these fractions to a common denominator, we get the fractions and . These fractions will be represented by the same pizza slices, but this time they will be divided into the same fractions (reduced to the same denominator):

The first drawing shows a fraction (eight pieces out of twelve), and the second picture shows a fraction (three pieces out of twelve). By cutting off three pieces from eight pieces, we get five pieces out of twelve. The fraction describes these five pieces.
Example 2 Find the value of an expression 
These fractions have different denominators, so you first need to bring them to the same (common) denominator.
Find the LCM of the denominators of these fractions.
The denominators of the fractions are the numbers 10, 3 and 5. The least common multiple of these numbers is 30
LCM(10, 3, 5) = 30
Now we find additional factors for each fraction. To do this, we divide the LCM by the denominator of each fraction.
Let's find an additional factor for the first fraction. LCM is the number 30, and the denominator of the first fraction is the number 10. Divide 30 by 10, we get the first additional factor 3. We write it over the first fraction:
Now we find an additional factor for the second fraction. Divide the LCM by the denominator of the second fraction. LCM is the number 30, and the denominator of the second fraction is the number 3. Divide 30 by 3, we get the second additional factor 10. We write it over the second fraction:
Now we find an additional factor for the third fraction. Divide the LCM by the denominator of the third fraction. LCM is the number 30, and the denominator of the third fraction is the number 5. Divide 30 by 5, we get the third additional factor 6. We write it over the third fraction:
Now everything is ready for subtraction. It remains to multiply the fractions by their additional factors:
We came to the conclusion that fractions that had different denominators turned into fractions that have the same (common) denominators. And we already know how to subtract such fractions. Let's finish this example.
The continuation of the example will not fit on one line, so we move the continuation to the next line. Don't forget about the equal sign (=) on the new line:

The answer turned out to be a correct fraction, and everything seems to suit us, but it is too cumbersome and ugly. We should make it easier. What can be done? You can reduce this fraction.
To reduce a fraction, you need to divide its numerator and denominator by (gcd) the numbers 20 and 30.
So, we find the GCD of the numbers 20 and 30:

Now we return to our example and divide the numerator and denominator of the fraction by the found GCD, that is, by 10

Got an answer
Multiplying a fraction by a number
To multiply a fraction by a number, you need to multiply the numerator of the given fraction by this number, and leave the denominator the same.
Example 1. Multiply the fraction by the number 1.
Multiply the numerator of the fraction by the number 1
![]()
The entry can be understood as taking half 1 time. For example, if you take pizza 1 time, you get pizza

From the laws of multiplication, we know that if the multiplicand and the multiplier are interchanged, then the product will not change. If the expression is written as , then the product will still be equal to . Again, the rule for multiplying an integer and a fraction works:
![]()
This entry can be understood as taking half of the unit. For example, if there is 1 whole pizza and we take half of it, then we will have pizza:

Example 2. Find the value of an expression
Multiply the numerator of the fraction by 4
![]()
The answer is an improper fraction. Let's take a whole part of it:
![]()
The expression can be understood as taking two quarters 4 times. For example, if you take pizzas 4 times, you get two whole pizzas.

And if we swap the multiplicand and the multiplier in places, we get the expression. It will also be equal to 2. This expression can be understood as taking two pizzas from four whole pizzas:

Multiplication of fractions
To multiply fractions, you need to multiply their numerators and denominators. If the answer is an improper fraction, you need to select the whole part in it.
Example 1 Find the value of the expression .
![]()
Got an answer. It is desirable to reduce this fraction. The fraction can be reduced by 2. Then the final solution will take the following form:

The expression can be understood as taking a pizza from half a pizza. Let's say we have half a pizza:
How to take two-thirds from this half? First you need to divide this half into three equal parts:

And take two from these three pieces:

We'll get pizza. Remember what a pizza looks like divided into three parts:

One slice from this pizza and the two slices we took will have the same dimensions:

In other words, we are talking about the same pizza size. Therefore, the value of the expression is

Example 2. Find the value of an expression
Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:

The answer is an improper fraction. Let's take a whole part of it:
![]()
Example 3 Find the value of an expression
Multiply the numerator of the first fraction by the numerator of the second fraction, and the denominator of the first fraction by the denominator of the second fraction:
![]()
The answer turned out to be a correct fraction, but it will be good if it is reduced. To reduce this fraction, you need to divide the numerator and denominator of this fraction by the greatest common divisor (GCD) of the numbers 105 and 450.
So, let's find the GCD of the numbers 105 and 450:
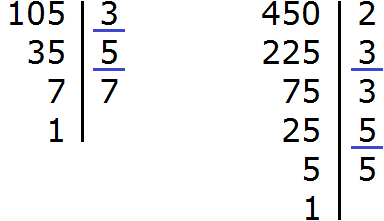
Now we divide the numerator and denominator of our answer to the GCD that we have now found, that is, by 15
Representing an integer as a fraction
Any whole number can be represented as a fraction. For example, the number 5 can be represented as . From this, the five will not change its meaning, since the expression means “the number five divided by one”, and this, as you know, is equal to five:
Reverse numbers
Now we will get acquainted with a very interesting topic in mathematics. It's called "reverse numbers".
Definition. Reverse to numbera is the number that, when multiplied bya gives a unit.
Let's substitute in this definition instead of a variable a number 5 and try to read the definition:
Reverse to number 5 is the number that, when multiplied by 5 gives a unit.
Is it possible to find a number that, when multiplied by 5, gives one? It turns out you can. Let's represent five as a fraction:
Then multiply this fraction by itself, just swap the numerator and denominator. In other words, let's multiply the fraction by itself, only inverted:
What will be the result of this? If we continue to solve this example, we get one:
![]()
This means that the inverse of the number 5 is the number, since when 5 is multiplied by one, one is obtained.
The reciprocal can also be found for any other integer.
You can also find the reciprocal for any other fraction. To do this, it is enough to turn it over.
Division of a fraction by a number
Let's say we have half a pizza:
Let's divide it equally between two. How many pizzas will each get?

It can be seen that after splitting half of the pizza, two equal pieces were obtained, each of which makes up a pizza. So everyone gets a pizza.
Division of fractions is done using reciprocals. Reciprocals allow you to replace division with multiplication.
To divide a fraction by a number, you need to multiply this fraction by the reciprocal of the divisor.
Using this rule, we will write down the division of our half of the pizza into two parts.
So, you need to divide the fraction by the number 2. Here the dividend is a fraction and the divisor is 2.
To divide a fraction by the number 2, you need to multiply this fraction by the reciprocal of the divisor 2. The reciprocal of the divisor 2 is a fraction. So you need to multiply by
In this lesson, we will consider the addition and subtraction of algebraic fractions with the same denominators. We already know how to add and subtract common fractions with the same denominators. It turns out that algebraic fractions follow the same rules. The ability to work with fractions with the same denominators is one of the cornerstones in learning the rules for working with algebraic fractions. In particular, understanding this topic will make it easy to master a more complex topic - addition and subtraction of fractions with different denominators. As part of the lesson, we will study the rules for adding and subtracting algebraic fractions with the same denominators, as well as analyze a number of typical examples
Rule for adding and subtracting algebraic fractions with the same denominators
Sfor-mu-li-ru-em pr-vi-lo slo-zhe-niya (you-chi-ta-niya) al-geb-ra-and-che-dro-bey with one-on-to-you -mi-know-on-te-la-mi (it is co-pa-yes-et with the ana-logic right-of-thumb for ordinary-but-ven-nyh-dr-bay): That is for the addition or you-chi-ta-niya al-geb-ra-and-che-dro-bey with one-to-you-mi-know-me-on-te-la-mi is necessary -ho-di-mo with-stand with-from-vet-stu-u-th al-geb-ra-i-che-sum of the number of-li-te-lei, and the sign-me-on-tel leave without iz-me-no-ny.
We will analyze this right-vi-lo both on the example of ordinary-but-vein-shot-beats, and on the example of al-geb-ra-and-che-dro- bey.
Examples of applying the rule for ordinary fractions
Example 1. Add fractions:.
Decision
Let's add the number-whether-they-whether draw-beat, and let's leave the sign-me-on-tel the same. After that, we divide the numer-li-tel and the sign-me-on-tel into simple multipliers and so-kra-tim. Let's get it: ![]() .
.
Note: standard error, I’ll start up something when resolving in a good kind of example, for -key-cha-et-sya in the following-du-u-sch-so-so-be-so-she-tion: ![]() . This is a gross mistake, since the sign-on-tel remains the same as it was in the original fractions.
. This is a gross mistake, since the sign-on-tel remains the same as it was in the original fractions.
Example 2. Add fractions:.
Decision
This za-da-cha is nothing from-whether-cha-et-sya from the previous one:.
Examples of applying the rule for algebraic fractions
From the usual-but-vein-nyh dro-bay per-rey-dem to al-geb-ra-i-che-skim.
Example 3. Add fractions:.
Solution: as already stated above, the addition of al-geb-ra-and-che-dro-bey is nothing from-is-cha-is-sya from the zhe-niya usually-but-vein-nyh dro-bay. Therefore, the solution method is the same:.
Example 4. You-honor fractions:.
Decision
You-chi-ta-nie al-geb-ra-and-che-dro-bey from-whether-cha-et-sya from the complication only by the fact that in the number of pi-sy-va-et-sya difference in the number of-li-te-lei is-run-nyh-dro-bay. So .
Example 5. You-honor fractions:.
Decision: .
Example 6. Simplify:.
Decision: .
Examples of applying the rule followed by reduction
In a fraction, someone-paradise is in a re-zul-ta-those addition or you-chi-ta-nia, it is possible to co-beautifully niya. In addition, you should not forget about the ODZ al-geb-ra-i-che-dro-bey.
Example 7. Simplify:.
Decision: .
Wherein . In general, if the ODZ of the out-of-hot-drow-bay owls-pa-yes-et with the ODZ of the total-go-howl, then you can not indicate it (after all, a fraction, in a lu-chen- naya in from-ve-those, also will not exist with co-from-vet-stu-u-s-knowing-che-no-yah-re-men-nyh). But if the ODZ is the source of the running dro-bay and from-ve-that does not co-pa-yes-et, then the ODZ indicates the need-ho-di-mo.
Example 8. Simplify:.
Decision: . At the same time, y (ODZ of the outgoing draw-bay does not coincide with the ODZ of re-zul-ta-ta).
Addition and subtraction of ordinary fractions with different denominators
To store and you-chi-tat al-geb-ra-and-che-fractions with different-we-know-me-on-te-la-mi, pro-ve-dem ana-lo -gyu from the usual-but-ven-ny-mi dro-bya-mi and re-re-not-sem it into al-geb-ra-and-che-fractions.
Ras-look at the simplest example for ordinary venous shots.
Example 1. Add fractions:.
Decision:
Let's remember the right-vi-lo-slo-drow-bay. For na-cha-la fractions, it is necessary to add-ve-sti to the common sign-me-to-te-lu. In the role of a general sign-me-on-te-la for ordinary-but-vein-draw-beats, you-stu-pa-et least common multiple(NOK) the source of the signs-me-on-the-lei.
Definition
The smallest-neck-to-tu-ral-number, someone-swarm is de-lit at the same time into numbers and.
To find the NOC, you need to de-lo-live know-me-on-the-whether into simple multipliers, and then choose to take everything pro- there are many, many, some of them are included in the difference between both signs-me-on-the-lei.
; . Then the LCM of numbers should include two twos and two threes:.
After finding the general sign-on-te-la, it is necessary for each of the dro-bays to find an additional multi- zhi-tel (fak-ti-che-ski, in de-pouring a common sign-me-on-tel on sign-me-on-tel co-from-rep-to-th-th fraction).
Then, each fraction is multiplied by a semi-chen-ny to-half-no-tel-ny multiplier. Fractions with the same-on-to-you-know-me-on-te-la-mi, warehouses and you-chi-tat someone we are on - studied in the past lessons.
By-lu-cha-eat: ![]() .
.
Answer:.
Ras-look-rim now the fold of al-geb-ra-and-che-dro-bey with different signs-me-on-te-la-mi. Sleep-cha-la, we-look at the fractions, know-me-on-the-whether some of them are-la-yut-sya number-la-mi.
Addition and subtraction of algebraic fractions with different denominators
Example 2. Add fractions:.
Decision:
Al-go-rhythm of re-she-niya ab-so-lyut-but ana-lo-gi-chen previous-du-sche-mu p-me-ru. It’s easy to take a common denominator on the given fractions: and add-to-full multipliers for each of them.
![]() .
.
Answer:.
So, sfor-mu-li-ru-em al-go-rhythm of complication and you-chi-ta-niya al-geb-ra-and-che-dro-beats with different-we-know-me-on-te-la-mi:
1. Find the smallest common sign-me-on-tel draw-bay.
2. Find additional multipliers for each of the draw-bay fractions).
3. Do-multiply-live numbers-whether-the-whether on the co-ot-vet-stu-u-s-up to-half-no-tel-nye-multiple-those.
4. Add-to-live or you-honor the fractions, use the right-wi-la-mi of the fold and you-chi-ta-niya draw-bay with one-to-you-know -me-on-te-la-mi.
Ras-look-rim now an example with dro-bya-mi, in the know-me-on-the-le-there-are-there-are-there-are-beech-ven-nye you-ra-same -tion.
