Burkovskaya Nina Dmitrievna
Math teacher
Ural Technological College "Service".
Program theme: Bodies of rotation - 10 hours.
Lesson topic: Right circular cone, its elements. Sections of a cone by a plane. Cone development. The surface area of a cone.
The purpose of the lesson: Formation of theoretical knowledge about a cone as a body of revolution, its properties, types of section by a plane and the area of the full surface. Mathematical thinking, spatial representation;
Independence of educational and cognitive activity.
Lesson type: Combined lesson.
Management methods: Lecture-practical lesson.
Lesson equipment: Math environmentGeoGebra.
DURING THE CLASSES:
Organizational moment - 1 - 2 minutes.
Greeting students.
Mark absent.
II . Homework survey
1. The area of the lateral surface of the cylinder;
2. The area of the full surface of the cylinder;
3. A cylinder inscribed in a prism;
4. Cylinder circumscribed near a prism.
III . Explanation of new material. Brief summary.
1. Cone - a body that consists of a circle - the base of the cone, a point that does not lie in the plane of this circle - the top of the cone and all segments connecting the top of the cone with the points of the base.
The cone is obtained by rotating a right triangle around the leg.
2. Now consider how the cone is built. First draw a circle with a centerOand directOSperpendicular to the plane of this circle. We connect each point of the circle by a segment with a pointS. The surface formed by these segments is called the conical surface, and the segments themselves are called the generators of the conical surface.
3. t.S- the top of the cone circle (O, OA) - the base of the cone
SA= SBare cone generators. Line segmentSOis the height of the cone. StraightSO- cone axis
4. a) the axial section of the cone is an isosceles triangle

The axial section of the cone is the section of the cone by a plane that passes through the axis of the cone and
through its top is an isosceles triangle.

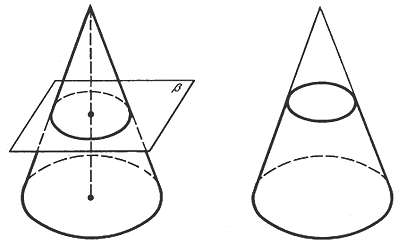
The section of the cone by a plane perpendicular to the axis of symmetry is a circle,
AB - section perpendicular to the axis of symmetry and parallel to the base.
 We express the area of the lateral surface of the cone in terms of its generatrix and the radius of the base.
We express the area of the lateral surface of the cone in terms of its generatrix and the radius of the base.
Degree measure of an arc
The length of the arc of the sector is equal to the length of the circumference of the base of the cone.
express through and, then
, .
How to find the total surface area?
The total surface area is the sum of the lateral surface area and the base area.
, .
The tangent plane to the cone is the plane passing through the generatrix of the cone and perpendicular to the plane of the axial section containing this generatrix..
IV . Fixing new material:
Task: The radius of the base of the cone is 14 cm. Find the area of the section drawn perpendicular to its axis through its middle .
 Decision:
△
BUT
S
O - rectangular (
S
O
basis),
∠
S
AO=30
0
,
S
O (lies against an angle of 30
0
)=, then
AS
=2O
S
\u003d 2 * 12 \u003d 24. According to Pythagorean O;
S
b.
=
Answer:
S
b.
=.
Decision:
△
BUT
S
O - rectangular (
S
O
basis),
∠
S
AO=30
0
,
S
O (lies against an angle of 30
0
)=, then
AS
=2O
S
\u003d 2 * 12 \u003d 24. According to Pythagorean O;
S
b.
=
Answer:
S
b.
=.
Homework §6.1 – 6.2, no.8
Literature
Zh. Kaidasov, V. Gusev, A. Kagazbaeva Geometry 10, 11 grades. Didactic material on geometry for grades 10, 11.
One of the figures that occurs when solving geometric problems in space is a cone. It, unlike polyhedra, belongs to the class of figures of rotation. We will consider in the article what is meant by it in geometry, and we will examine the characteristics of various sections of the cone.
Suppose there is some curve in the plane. It can be a parabola, a circle, an ellipse, and so on. Take a point that does not belong to the specified plane, and connect all points of the curve to it. The resulting surface is called a cone or simply a cone.
If the original curve is closed, then the conical surface can be filled with matter. The figure obtained in this way is a three-dimensional body. It is also called a cone. Several paper cones are shown below.
The conical surface is found in ordinary life. For example, an ice cream cone or a striped traffic cone has this shape, which is designed to attract the attention of drivers and pedestrians.

Types of cones
As you might guess, the figures under consideration differ from each other by the type of curve on which they are formed. For example, there is a round cone or an elliptical one. This curve is called the base of the figure. However, the shape of the base is not the only feature that allows cones to be classified.
Their second important characteristic is the position of the height relative to the base. The height of a cone is a straight line segment, which is lowered from the top of the figure to the plane of the base and is perpendicular to this plane. If the height intersects the base in the geometric center (for example, in the center of the circle), then the cone will be straight, if the perpendicular segment falls to any other point of the base or beyond it, then the figure will be inclined.

Geometric names of cone elements
It was said above that the cone has a base. It is bounded by a circle, which is called the guide of the cone. The segments connecting the guide to a point that does not lie in the plane of the base are called generators. The set of all points of the generators is called the conical or lateral surface of the figure. For a round right cone, all generators have the same length.
The point where the generators intersect is called the vertex of the figure. Unlike polyhedra, a cone has a single vertex and no faces.
The straight line passing through the top of the figure and the center of the circle is called the axis. The axis contains the height of a straight cone, so it forms a right angle with the plane of the base. This information is important when calculating the area of the axial section of the cone.
Round straight cone - rotation figure
The cone under consideration is a fairly symmetrical figure, which can be obtained as a result of the rotation of a triangle. Suppose we have a triangle with a right angle. To get a cone, it is enough to rotate this triangle around one of the legs as shown in the figure below.

It can be seen that the axis of rotation is the axis of the cone. One of the legs will be equal to the height of the figure, and the second leg will become the radius of the base. The hypotenuse of a triangle as a result of rotation will describe a conical surface. It will be the generatrix of the cone.
This method of obtaining a round straight cone is convenient to use to study the mathematical relationship between the linear parameters of the figure: the height h, the radius of the round base r and the guide g. The corresponding formula follows from the properties of a right triangle. It is listed below:
Since we have one equation and three variables, this means that in order to uniquely set the parameters of a round cone, it is necessary to know any two quantities.
Sections of a cone by a plane that does not contain the vertex of the figure
The question of constructing sections of a figure is not trivial. The fact is that the shape of the section of the cone by the surface depends on the relative position of the figure and the secant.
Suppose we intersect the cone with a plane. What will be the result of this geometric operation? Section shape options are shown in the figure below.

The pink section is a circle. It is formed as a result of the intersection of the figure with a plane that is parallel to the base of the cone. These are sections perpendicular to the axis of the figure. The figure formed above the cutting plane is a cone similar to the original one, but having a smaller circle at the base.
The green section is an ellipse. It is obtained if the cutting plane is not parallel to the base, but it only intersects. The figure cut off above the plane is called an elliptical inclined cone.
The blue and orange sections are parabolic and hyperbolic, respectively. As can be seen from the figure, they are obtained if the cutting plane simultaneously intersects the side surface and the base of the figure.
To determine the areas of the sections of the cone that have been considered, it is necessary to use the formulas for the corresponding figure on the plane. For example, for a circle, this is Pi multiplied by the square of the radius, and for an ellipse, this is the product of Pi by the length of the minor and major semiaxes:
circle: S \u003d pi * r 2;
ellipse: S = pi*a*b .
Sections Containing the Top of a Cone
Now consider the options for sections that arise if the cutting plane passes through the top of the cone. Three cases are possible:
- The section is a single point. For example, a plane passing through the vertex and parallel to the base gives just such a section.
- The section is a straight line. This situation occurs when the plane is tangent to a conical surface. The straight line of the section in this case will be the generatrix of the cone.
- Axial section. It is formed when the plane contains not only the top of the figure, but also its entire axis. In this case, the plane will be perpendicular to the round base and will divide the cone into two equal parts.
It is obvious that the areas of the first two types of sections are equal to zero. As for the cross-sectional area of the cone for the 3rd type, this issue is discussed in more detail in the next paragraph.
Axial section
It was noted above that the axial section of a cone is the figure formed when the cone is intersected by a plane passing through its axis. It is easy to guess that this section will represent the figure shown in the figure below.

This is an isosceles triangle. The vertex of the axial section of the cone is the vertex of this triangle, formed by the intersection of identical sides. The latter are equal to the length of the generatrix of the cone. The base of a triangle is the diameter of the base of the cone.
The calculation of the area of the axial section of the cone is reduced to finding the area of the resulting triangle. If the radius of the base r and the height h of the cone are initially known, then the area S of the section under consideration will be equal to:
This expression is a consequence of applying the standard formula for the area of a triangle (half the height multiplied by the base).
Note that if it is equal to the diameter of its round base, then the axial section of the cone is an equilateral triangle.
A triangular section is formed when the cutting plane is perpendicular to the base of the cone and passes through its axis. Any other plane parallel to the named one will give a hyperbola in section. However, if the plane contains the vertex of the cone and intersects its base not through the diameter, then the resulting section will also be an isosceles triangle.
The task of determining the linear parameters of the cone
We will show how to use the formula written for the area of the axial section to solve a geometric problem.
It is known that the area of the axial section of the cone is 100 cm 2 . The resulting triangle is equilateral. What is the height of the cone and the radius of its base?
Since the triangle is equilateral, its height h is related to the length of side a by the following relationship:
Given that the side of the triangle is twice the radius of the base of the cone, and substituting this expression into the formula for the cross-sectional area, we get:
S = h*r = √3/2*2*r*r =>
r = √(S/√3).
Then the height of the cone is:
h = √3/2*2*r = √3*√(S/√3) = √(√3*S).
It remains to substitute the value of the area from the condition of the problem and get the answer:
r = √(100/√3) ≈ 7.60 cm;
h = √(√3*100) ≈ 13.16 cm.
In what areas is it important to know the parameters of the considered sections?
The study of various types of cone sections is not only of theoretical interest, but also has practical applications.
First, it should be noted the area of aerodynamics, where with the help of conic sections it is possible to create ideal smooth shapes of solid bodies.

Secondly, conic sections are trajectories along which space objects move in gravitational fields. What exactly is the trajectory of the movement of the cosmic bodies of the system is determined by the ratio of their masses, absolute velocities and distances between them.
The radius of the base of the cone with the vertex is equal to 6, and the length of its generatrix is equal to 9. Points and are chosen on the circle of the base of the cone, dividing the circle into two arcs, the lengths of which are related as 1:3. Find the area of the section of the cone by the plane.
The solution of the problem

This lesson shows how to correctly construct a section of a cone by a plane and find the area of this section. The main point in solving this problem is the ratio of arcs, which is given by the condition: given that the ratio is 1:3, it can be clearly determined that the degree measure of one arc will be 90 °. And this greatly simplifies the solution of the problem. The formula for the area of a triangle: half the product of the base and the height - makes it possible to determine the segments whose lengths we need to find. To find the length of the base, we use the Pythagorean theorem (the triangle turns out to be not only rectangular, but also isosceles - the legs of the triangle are the radii of the base of the circle). We also find the height of the section using the Pythagorean theorem. We already know the base (we need half of it) and the length of the generatrix is given by condition. It remains to find the product of the obtained segments and divide it into two. Answer received.
The solution of this problem is recommended for students of the 8th grade when studying the topic "Area" ("The Pythagorean theorem", "Area of the triangle"); for 11th grade students when studying the topic "Body of revolution" ("Problem solving. Cone"). In preparation for the exam, the lesson is recommended when repeating the topic “Area”, “Body of revolution”.
You will need
- Cone drawing with specified parameters
- Ruler
- Pencil
- Mathematical formulas and definitions
- Cone height
- The radius of the circle of the base of the cone
- Triangle area formula
Instruction
Draw a cone with the given parameters. Label the center of the circle as O and the vertex as P. You need to know the radius and height of the cone. Remember the heights of the cone. It is a perpendicular, from the top of the cone to its base. The point of intersection of the height of the cone with the base at the right cone coincides with the center of the base circle. Construct an axial section of the cone. It is the diameter of the base and the generators of the cone, which pass through the points of intersection of the diameter with the circle. Label the resulting points as A and B.
The axial section is formed by two right triangles lying in the same plane and having one common leg. There are two ways to calculate the area of the axial section. The first way is to find the areas of the resulting triangles and add them together. This is the most visual way, but in fact it is no different from the classic calculation of a triangle. So, you got 2 right-angled triangles, the common leg of which is the height of the cone h, the second legs are the radii of the circumference of the base R, and the hypotenuses are the generators of the cone. Since all three sides of these triangles are equal to each other, then the triangles themselves also turned out to be equal, according to the third property of the equality of triangles. The area of a right triangle is equal to half the product of its legs, that is, S=1/2Rh. The area of the two triangles, respectively, will be equal to the product of the base and the height, S=Rh.
The axial section is most often considered as, the height of which is the height of the cone. In this case, this is a triangle APV, the base of which is equal to the diameter of the circumference of the base of the cone D, and the height is equal to the height of the cone h. Its area is calculated according to the classical formula for the area of a triangle, that is, as a result, we obtain the same formula S = 1/2Dh = Rh, where S is the area of the triangle, R is the radius of the base circle, and h is the height of the triangle, which is also the height of the cone.
Helpful advice
The area of the axial section of the cone is calculated by the formula for the area of a trapezoid. In this case, you need to know both base radii, height and midline.
Sources:
- Lesson Topic “Sections of a Cone
A cone is a body obtained by the union of all the rays emanating from one point, which is called the top of the cone and passing through a flat surface, which is called the base of the cone. The area of a cone is the area of its lateral surface and the area of the base, which is a circle.

You will need
- Elementary knowledge of stereometry.
Instruction
The final area of a cone is equal to the sum of the areas of its surface and base. That is, S \u003d P * R * R + P * R * l. Well, or after the transformation, S \u003d P * R (R + l).
Related videos
note
Area is a positive value, and if you get a negative value, then you made a mistake somewhere. Check all your calculations carefully.
Helpful advice
Knowing the area of the cone and the radius of its base, you can find the length of its guide, and knowing the area and length of the guide - the radius of its base.
Sources:
- how to find the surface of a cone in 2019
Constructing a section of a cone is not such a difficult task. The main thing is to follow a strict sequence of actions. Then this task will be easy to do and will not require much effort from you.

You will need
- - paper;
- - pen;
- - circle;
- - ruler.
Instruction
When answering this question, you first need to decide what parameters the section is set to.
Let this be the line of intersection of the plane l with the plane and the point O, which is the point of intersection with its section.
The construction is illustrated in Fig.1. The first step in constructing a section is through the center of the section of its diameter, extended to l perpendicular to this line. As a result, point L is obtained. Further, through point O, draw a straight line LW, and build two directing cones lying in the main section O2M and O2C. At the intersection of these guides lie the point Q, as well as the already shown point W. These are the first two points of the required section.

Now draw a perpendicular MC at the base of the cone BB1 and build the generators of the perpendicular section O2B and O2B1. In this section, draw a straight line RG through t.O, parallel to BB1. T.R and t.G - two more points of the desired section. If the cross section of the ball were known, then it could be constructed already at this stage. However, this is not an ellipse at all, but something elliptical, having symmetry with respect to the segment QW. Therefore, you should build as many points of the section as possible in order to connect them in the future with a smooth curve to get the most reliable sketch.
Construct an arbitrary section point. To do this, draw an arbitrary diameter AN at the base of the cone and build the corresponding guides O2A and O2N. Through PO draw a straight line passing through PQ and WG, until it intersects with the newly constructed guides at points P and E. These are two more points of the desired section. Continuing in the same way and further, you can arbitrarily desired points.
True, the procedure for obtaining them can be slightly simplified using symmetry with respect to QW. To do this, it is possible to draw straight lines SS' parallel to RG in the plane of the desired section, parallel to RG until they intersect with the surface of the cone. The construction is completed by rounding the constructed polyline from chords. It suffices to construct half of the required section due to the already mentioned symmetry with respect to QW.
Related videos
Tip 4: How to find the area of the axial section of a truncated cone
To solve this problem, you need to remember what a truncated cone is and what properties it has. Be sure to draw. This will determine which geometric figure is a section. It is quite possible that after this the solution of the problem will no longer be difficult for you.

Instruction
A round cone is a body obtained by rotating a triangle around one of its legs. Straight lines coming from the top cones and intersecting its base are called generators. If all generators are equal, then the cone is straight. At the base of the round cones lies a circle. The perpendicular dropped to the base from the top is the height cones. At the round straight cones height coincides with its axis. The axis is a straight line connecting to the center of the base. If the horizontal cutting plane of the circular cones, then its upper base is a circle.
Since it is not specified in the condition of the problem, it is the cone that is given in this case, we can conclude that this is a straight truncated cone, the horizontal section of which is parallel to the base. Its axial section, i.e. vertical plane, which through the axis of a circular cones, is an isosceles trapezoid. All axial sections round straight cones are equal to each other. Therefore, to find square axial sections, it is required to find square trapezoid, the bases of which are the diameters of the bases of the truncated cones, and the sides are its generators. Truncated Height cones is also the height of the trapezoid.
The area of a trapezoid is determined by the formula: S = ½(a+b) h, where S is square trapezoid; a - the value of the lower base of the trapezoid; b - the value of its upper base; h - the height of the trapezoid.
Sectional area of a cone. Another article with cones is presented for you. At the time of this writing, the blog has solved all examples (prototypes) of tasks with cones that are possible in the exam. The solution process is simple (1-2 actions), with a certain practice they are solved orally. You need to know the concept of a generatrix, information about this in. It is also necessary to understand how sections of a cone are formed.
1. If the plane passes through the vertex of the cone, then the section is a triangle.

*If the plane passes through the axis of the cone, then the section is an isosceles triangle, the height of which is equal to the height of the cone, and the base on which this height is lowered is equal to the diameter of the base of the cone.
2. If the plane passes perpendicular to the axis of the cone, then the section is a circle.
A feature of these tasks is that the triangle area formula is applied,. Repeat formulas periodically. Consider the tasks:
324453. The area of the base of the cone is 16pi, the height is 6. Find the area of the axial section of the cone.

The axial section of the cone is a triangle with a base equal to the diameter of the base of the cone and a height equal to the height of the cone. Let's denote the diameter as D, the height as H, write down the formula for the area of a triangle:

The height is known, we calculate the diameter. We use the formula for the area of a circle:
So the diameter will be equal to 8. Calculate the cross-sectional area:

Answer: 24
324454. The area of the base of the cone is 18. The plane parallel to the plane of the base of the cone divides its height into segments of length 3 and 6, counting from the top. Find the cross-sectional area of the cone by this plane.

The section is a circle. You need to find the area of this circle.
Let's build an axial section:

Consider triangles AKL and AOC - they are similar. It is known that in similar figures the ratios of the corresponding elements are equal. We will consider the relationship of heights and legs (radii):
OC is the radius of the base, it can be found:
Means

Now we can calculate the cross-sectional area:

*This is an algebraic way of calculating without using the area property of similar bodies. It could be argued like this:
Two cones (original and cut off) are similar, which means that spare their bases are similar figures. For the areas of similar figures, there is a dependence:
The similarity coefficient in this case is equal to 1/3 (the height of the original cone is 9, cut off 3), 3/9=1/3.
Thus, the area of \u200b\u200bthe base of the resulting cone is:
Answer: 2
323455. The height of the cone is 8, and the length of the generatrix is 10. Find the area of the axial section of this cone.

Let the generatrix be L, the height be H, and the radius of the base be R.
Find the diameter of the base and use the formula for the area of a triangle to calculate the area. According to the Pythagorean theorem:
Let the generatrix be L, the height be H, the radius of the base be R. That's it. Good luck to you!
Sincerely, Alexander Krutitskikh.
P.S: I would be grateful if you tell about the site in social networks.
