होने देना zq - फ़ंक्शन f(z), t.s का एकवचन बिंदु। एफ (जेड)लेकिन इस बिंदु पर विश्लेषणात्मक है (विशेष रूप से, इसे परिभाषित नहीं किया जा सकता है)। यदि बिंदु का ऐसा पंचर पड़ोस मौजूद है zq (अर्थात, समुच्चय O z - zq f(z) एलियटिक है, तब ज़ोबुलाया पृथक एकवचन बिंदुकार्यों एफ (जेड)।इस परिभाषा को भी मामले में संरक्षित किया गया है जेडएन =ऊ, यदि आयोडीन एक बिंदु का एक पंचर पड़ोस है zq = oo सेट को समझें जेड >मैं - मूल पर केंद्रित किसी वृत्त की उपस्थिति। दूसरे शब्दों में, एकवचन बिंदु zq को अलग-थलग कहा जाता है यदि इस बिंदु का एक पड़ोस मौजूद है जिसमें अन्य एकवचन बिंदु हैं जो से भिन्न हैं zq. नीचे हर जगह, हम एकल-मूल्यवान वर्ण के केवल एकवचन बिंदुओं पर विचार करते हैं (फ़ंक्शन एफ (जेड)अद्वितीय माना जाता है)।

समारोह के व्यवहार के आधार पर एफ (जेड)पर जेड -> zqएकवचन बिंदु तीन प्रकार के होते हैं। पृथक एकवचन बिंदु zq फ़ंक्शन एफ (जेड)बुलाया:

1) हटाने योग्य एकवचन बिंदुअगर कोई सीमित सीमा है

2) खंभासीमा हो तो

3) आवश्यक बिंदु,यदि एफ (जेड) के लिए न तो कोई परिमित है और न ही अनंत सीमा है जेड-> zq.

उदाहरण 26.1. आइए हम दिखाते हैं कि तीनों प्रकार के एकवचन बिंदु साकार होते हैं। विचार करना एफ(जेड)= बिंदु zq = 0 पृथक है

इस समारोह का एकवचन बिंदु। सूत्र (22.12) का उपयोग करके, हम विस्तार प्राप्त करते हैं

जिससे यह इस प्रकार है कि वहाँ मौजूद है lim फाई (जेड)= 1. इसलिए, zq = 0 है

फ़ंक्शन का एक हटाने योग्य एकवचन बिंदु है फाई (जेड)।

समारोह f'j (जेड) =--- एक बिंदु पर एक ध्रुव है ज़ो= 1 क्योंकि

2 आर" एक्स

अब फ़ंक्शन पर विचार करें ) जेड (जेड)= ई 1 ^ आर और दिखाओ कि ज़ो = O इस फलन का एक अनिवार्य एकवचन बिंदु है। प्रयास करते समय जेडवास्तविक अक्ष के अनुदिश शून्य करने के लिए, फलन f . की बाएँ और दाएँ सीमाएँ (जेड)अलग: lim साथ 1 / 1 = 0, लिम 1 /* = . के साथओएस यह संकेत करता है,

x->0-0 x->0+0

क्या च: मैं (जेड) 2 . के लिए न तो कोई परिमित है और न ही अनंत सीमा -> ओह, यानी। zq = 0 इस फलन का अनिवार्य रूप से एकवचन बिंदु है। (ध्यान दें कि जैसे-जैसे बिंदु जाता है z-iyकाल्पनिक अक्ष समारोह पर शून्य करने के लिए

इसकी कोई सीमा नहीं है।)

बेशक, गैर-पृथक एकवचन बिंदु भी हैं। उदाहरण के लिए। फ़ंक्शन में बिंदुओं पर ध्रुव होते हैं जेड एन = -, पी= ±1, ±2,...

फलस्वरूप, Zq = 0 इस फ़ंक्शन का एक गैर-पृथक एकवचन बिंदु है: इस बिंदु के किसी भी (मनमाने ढंग से छोटा) पड़ोस में अन्य एकवचन बिंदु हैं जी पी.

होने देना ज़ो-किसी फ़ंक्शन का अंतिम पृथक एकवचन बिंदु एफ (जेड)।फिर एफ (जेड)कुछ पंचर पड़ोस में समान है 0 बिंदु के ज़ो ज़ोइस पड़ोस को आंतरिक त्रिज्या r = 0 के साथ एक अंगूठी के रूप में माना जा सकता है। प्रमेय 25.1 के अनुसार, पड़ोस में, फ़ंक्शन एफ (जेड)लॉरेंट श्रृंखला (25.2) में विस्तारित किया जा सकता है। हम दिखाएंगे कि फ़ंक्शन का व्यवहार 2 . के लिए -> zq (अर्थात एकवचन बिंदु का प्रकार ज़ो)अपघटन के मुख्य भाग (25.2) के रूप पर निर्भर करता है; यह परिस्थिति "मुख्य भाग" शब्द की उत्पत्ति की व्याख्या करती है।

प्रमेय 2जी.2. एक फ़ंक्शन f(z) का एक पृथक एकवचन बिंदु zo हटाने योग्य है यदि और केवल यदि इस बिंदु के एक पंचर पड़ोस में लोरैप विस्तार में ओड है

वे। केवल सही भाग से मिलकर बनता है, और मुख्य भाग के सभी गुणांक गोली के बराबर हैं।

सबूत। 1. चलो ज़ोहटाने योग्य एकवचन बिंदु है। आइए हम साबित करें कि फ़ंक्शन का लॉरेंट विस्तार एफ (जेड)(26.1) रूप है। एकवचन बिंदु के बाद से ज़ोहटाने योग्य, फिर एक सीमित सीमा होती है एफ (जेड) = ए।फलस्वरूप, एफ (जेड)कुछ पंचर पड़ोस में बंधा हुआ 0 z - बिंदु का zq ज़ो,वे। )(जेड) सभी के लिए जेडइस मोहल्ले से। कोई भी ले जाओ आर।यू р /?|, और लॉरेंट श्रृंखला के गुणांक के लिए सूत्रों (25.3) का उपयोग करें:

विस्तार के मुख्य भाग के गुणांकों के लिए एन =- 1,-2,... ऐसे मूल्यों के लिए पीअपने पास पी~एन-ई 0 एट आर-> 0. मान के बाद से आरमनमाने ढंग से छोटा चुना जा सकता है, फिर श्री ~"मनमाने ढंग से छोटा हो सकता है। चूंकि |सी टी,| ^ श्री~नऔर cn p पर निर्भर नहीं है, तो cn = 0 के लिए तथा= - 1, -2,..., जिसे सिद्ध करना था।

2. आइए अब मान लें कि लॉरेंट प्रसार का रूप (26.1) है। श्रृंखला (26.1) एक शक्ति श्रृंखला है और। इसलिए, न केवल पंचर में, बल्कि पूरे मोहल्ले में अभिसरण होता है जेड-zq डॉट सहित ज़ो;इसका योग एस (जेड)के लिए विश्लेषणात्मक है जेड और एस (जेड) = )(जेड) 0 z . पर - ज़ोआर।इसलिए, एक सीमित सीमा है )(जेड)\u003d अपराह्न 5 (आर) \u003d 5 (आर) - इसलिए, एकवचन बिंदु zq

Z->Zo Z-*Zo

डिस्पोजेबल। प्रमेय सिद्ध हो चुका है।

टिप्पणी। यह प्रमेय के प्रमाण से निम्नानुसार है कि एक पंचर पड़ोस में एक हटाने योग्य एकवचन बिंदु के 0 z - zo, फ़ंक्शन एफ (जेड)समारोह एस (आर) के साथ मेल खाता है, जो पूरे पड़ोस में विश्लेषणात्मक है जेड - क्षेत्र इसलिए, यदि हम /(th) = . डालते हैं एस (जेडक्यू), फिर, फ़ंक्शन के मूल्यों को बदले बिना एफ (जेड)पंचर पड़ोस के किसी भी बिंदु पर, हम इस फ़ंक्शन को r में विश्लेषणात्मक बनाते हैं, अर्थात। सुविधा को "हटाएं"। यह "हटाने योग्य विलक्षणता" शब्द की व्याख्या करता है। ऐसे बिंदुओं पर नियमित रूप से विचार करना स्वाभाविक है, न कि फ़ंक्शन के एकवचन बिंदु के रूप में एफ (जेड)।

उदाहरण के लिए, फ़ंक्शन पर विचार करें

उदाहरण 26.1 में, यह दिखाया गया कि Pm (n) = 1. अर्थात्। एकवचन बिंदु

zq = 0 हटाने योग्य है। सेटिंग /i(0) = 1, हम इस तरह विलक्षणता को समाप्त करते हैं और एक फ़ंक्शन प्राप्त करते हैं जो बिंदु पर विश्लेषणात्मक है zq = 0 (और पूरे तल C में)।

आइए अब हम ध्रुवों को लॉरेंट के प्रसार के संदर्भ में चिह्नित करें।

प्रमेय 26.3. एक फ़ंक्शन f(z) का एक पृथक विलक्षण बिंदु Zo एक ध्रुव है यदि और केवल यदि, जब केंद्र Zq के साथ लॉरेंट विस्तार के प्रमुख भाग में केवल विशिष्ट संख्या की सीमित संख्या होती है

n के साथ शून्य गुणांक से:

सबूत। 1. चलो zq - पोल, यानी। लिम /( जेड) = ऊ

आइए हम साबित करें कि फ़ंक्शन का लॉरेंट विस्तार एफ (जेड)फॉर्म (2G.2) है। चूंकि लि एफ (जेड)= ऊ। तब बिंदु का एक पंचर पड़ोस मौजूद है

किओ zq. जिसमें एफ (जेड)विश्लेषणात्मक है और इसमें कोई शून्य नहीं है। फिर समारोह जी (जेड) = 1 /एफ (जेड)इस पंचर पड़ोस में भी विश्लेषणात्मक होगा, और सीमित जी (जेड)= 0. इसलिए, ज़ोडिस्पोजेबल है *-? *0

समारोह का एकवचन बिंदु जी (जेड)।आइए फिर से परिभाषित करें जी (जेड)बिंदु पर ज़ो, डालना जी (जो)= 0. तब जी (जेड)(पंचर नहीं) बिंदु के पूरे पड़ोस में विश्लेषणात्मक हो जाता है जेड 0,तथा र् 0इसका पृथक शून्य होगा। द्वारा निरूपित करें एनइस शून्य की बहुलता (क्रम)। जैसा कि 23 में दिखाया गया था, बिंदु के पड़ोस में zq समारोह जी (जेड)रूप में प्रस्तुत करने योग्य (देखें (23.2))

तथा (जेड$) एफ 0 और वाई> (जेड)बिंदु के कुछ पड़ोस में विश्लेषणात्मक है ज़ो-इसलिये आईपी ​​(जेड)बिंदु पर निरंतर ज़ोतथा जी>(जो) एफ 0" तो आईपी ​​(जेड)इस बिंदु के कुछ पड़ोस में भी कोई शून्य नहीं है। इसलिए फ़ंक्शन 1 /-पी(जेड)इस पड़ोस में भी विश्लेषणात्मक होगा और इसलिए, टेलर श्रृंखला में इसका विस्तार करता है:

कोष्ठकों को खोलना और गुणांकों के पदनामों को बदलते हुए, हम अंतिम विस्तार को फॉर्म में लिखते हैं

जहाँ c_jv = 1>ओ एफ 0. इस प्रकार, f(r) के लॉरेंट प्रसार के मुख्य भाग में केवल सीमित संख्या में पद होते हैं; हम आवश्यक समानता (26.2) पर पहुंच गए हैं।

2. चलो एक बिंदु के एक छिद्रित पड़ोस में वांसमारोह )(जेड)लॉरेंट विस्तार (26.2) (अधिक विस्तारित रूप में, देखें (26.3)) द्वारा दर्शाया गया है, जिसके मुख्य भाग में केवल सीमित संख्या में शब्द हैं, और साथ-डी" एफ 0. हमें यह सिद्ध करना होगा कि Zq - फंक्शन पोल एफ (जेड)।समानता (26.3) को से गुणा करना (जी - जीओ) आईवी, हमें फ़ंक्शन मिलता है

(26.4) में श्रृंखला एक शक्ति श्रृंखला है जो न केवल पंचर में, बल्कि बिंदु के पूरे पड़ोस में एक विश्लेषणात्मक कार्य में परिवर्तित होती है। Zq. इसलिए, समारोह एच (जेड)इस पड़ोस में विश्लेषणात्मक बन जाता है यदि हम इसे सेटिंग द्वारा वें में विस्तारित करते हैं एच (जो)= s_dg एफ 0. तब

इस प्रकार बिंदु o एक ध्रुव है, और प्रमेय 26.3 सिद्ध हो जाता है।

ज़ीरोथ फ़ंक्शन की बहुलता (क्रम) जी (जेड)= 1//(आर) कहा जाता है ध्रुव आदेशसमारोह / (आर)। यदि एक एन-ध्रुव का क्रम वें है, तो जी (जेड)= (आर - ज़ो)एन आईपी(जेड),और जाओ) एफ 0, और, जैसा कि प्रमेय 26.3 के प्रमाण के पहले भाग में दिखाया गया है, f(r) के विस्तार का रूप (26.3) है, जहाँ c_/v एफ 0. इसके विपरीत, यदि f(r) श्रृंखला (26.3) में फैलता है और ई-जेड एफ 0, तब

टी.एस. एन-फलन f(r) के ध्रुव का क्रम। इस तरह, समारोह के zq ध्रुव का क्रम/(जी) बिंदु zq के पंचर पड़ोस में लॉरेंट विस्तार के मुख्य भाग के प्रमुख गैर-शून्य गुणांक की संख्या के बराबर है(अर्थात ऐसी संख्या के बराबर एन,क्या s_dg एफ 0 और एसपी= 0 पर पी > एन)।

आइए हम निम्नलिखित अभिकथन को सिद्ध करें, जो सुविधाजनक है) अनुप्रयोगों के लिए।

परिणाम 26.4. बिंदु zq कल्पना के क्रम N का एक ध्रुव है/(जी) अगर और केवल अगर/(जी) रूप में प्रतिनिधित्व करते हैं

जहाँ h(z) एक बिंदु के पड़ोस में एक विश्लेषणात्मक कार्य हैवां और एच(जो) एफ 0.

सबूत। समारोह सीपी (जेड) = एल / एच (जेड)बिंदु r के कुछ पड़ोस में विश्लेषणात्मक है। कोरोलरी 26.4 की स्थिति निम्नलिखित के बराबर है:

इसीलिए zq - बहुलता शून्य एनकार्यों जी (जेड)।और इसलिए बहुलता ध्रुव एनफ़ंक्शन / (2)।

द्वितीय उदाहरण 26.5. किसी फ़ंक्शन के पृथक एकवचन बिंदु खोजें और उनके प्रकार का निर्धारण करें।

D e u c tio n. वे बिंदु जिन पर (जेड .) 2 + 1 )(z+ एच) 2 = 0. अगर जेड 2 एल 1 = 0 तो 2 = ±आरयदि (जेड .) 4- एच) 2 = 0, तो जेड= -3। इसलिए, फ़ंक्शन के तीन एकवचन बिंदु हैं जेड= आर, 22 = -आर, जेड3 = - 3. विचार करें जेड:

जी -प्रथम-क्रम ध्रुव (हमने कोरोलरी 26.4 का उपयोग किया)। इसी प्रकार सिद्ध किया जा सकता है कि 22 = -मैंपहले क्रम का एक ध्रुव भी। 2h के लिए हमारे पास है:

आइए हम अनिवार्य रूप से एकवचन बिंदुओं पर विचार करें।

प्रमेय 26.6. एक फ़ंक्शन f(z) का एक पृथक एकवचन बिंदु zq अनिवार्य रूप से एकवचन होता है यदि और केवल यदि zq पर केंद्रित लॉरेंट विस्तार का मुख्य भाग अनंत रूप से कई भिन्न होता है। शून्य, पी के साथ गुणांक।

सबूत। प्रमेय 26.6 प्रमेय 26.2 और 26.3 से सीधे अनुसरण करता है। दरअसल, अगर बिंदु zq अनिवार्य रूप से एकवचन है, तो लॉरेंट विस्तार का मुख्य भाग अनुपस्थित नहीं हो सकता है या इसमें सीमित संख्या में शब्द शामिल नहीं हो सकते हैं (अन्यथा बिंदु Zq या तो हटाने योग्य या एक पोल होगा)। इसलिए, मुख्य भाग में पदों की संख्या अनंत होनी चाहिए।

इसके विपरीत, यदि मुख्य भाग में अपरिमित रूप से अनेक सदस्य हों, तो Zq न तो हटाने योग्य बिंदु हो सकता है और न ही ध्रुव। नतीजतन, यह बिंदु अनिवार्य रूप से एकवचन है।

परिभाषा के अनुसार, एक अनिवार्य रूप से एकवचन बिंदु की विशेषता इस तथ्य से होती है कि फलन f(2) के लिए न तो कोई परिमित है और न ही अनंत सीमा है। जेड ->zq. एक अनिवार्य रूप से एकवचन बिंदु के पड़ोस में किसी फ़ंक्शन का व्यवहार कितना अनियमित है, इसका अधिक संपूर्ण विचार निम्नलिखित प्रमेय द्वारा दिया गया है।

प्रमेय 26.7 (सोचोकी का प्रमेय)। यदि zq अनिवार्य रूप से एकवचन है, तो फलन f(z .) का बिंदु), तब किसी सम्मिश्र संख्या के लिएएल, ए = सहितऊ, अंक z n का एक क्रम इस प्रकार है कि z n -> zo andलिम एफ (जेडएन) = लेकिन।

n->ओएस

सबूत। पहले मामले पर विचार करें ए =ऊ प्रमेय 2G.2 के प्रमाण के पहले भाग में, हमने स्थापित किया कि यदि एफ (जेड)बिंदु r0 के कुछ पंचर पड़ोस में घिरा है, तो सभी गुणांक c, एन = - 1, - 2,... मुख्य भाग के शून्य के बराबर हैं (और, फलस्वरूप, वें में विलक्षणता हटाने योग्य है)। चूंकि धारणा के अनुसार r0 एक अनिवार्य रूप से एकवचन बिंदु है, फ़ंक्शन f(r) बिंदु r0 के किसी भी छिद्रित पड़ोस में असीम है। आइए हम कुछ संकीर्ण पड़ोस 0 Z इस प्रकार लें कि च (जी) > 1 (यदि |/(r)| z - zo R/2 एक बिंदु है जेड-2 , जहां |/(डीडी)| > 2, आदि: पंक्चर पड़ोस में O 71. यह स्पष्ट है कि rn -e go और lim /(r«) = oo. इस प्रकार, स्थिति A = oo में, प्रमेय 26.7

सिद्ध किया हुआ।

चलो अब ए एफऊ पहले मान लें कि एक पंचर पड़ोस है 0

= -Y y---- इस छिद्रित पड़ोस में विश्लेषणात्मक होगा और इसके परिणामस्वरूप,

/(जी) - लेकिन

फलस्वरूप, r फलन (r) का एक पृथक एकवचन बिंदु है। आइए दिखाते हैं। कि r0 (r) का अनिवार्य रूप से एकवचन बिंदु है। यह गलत हो जाने दो। तब एक सीमा होती है (r), या तो परिमित या अनंत। इसलिये

/(r) = A + , तो Hsh /(r) भी मौजूद है, जो स्थिति के विपरीत है

एफ (जी) ~ :-*जेड 0

प्रमेय का दृश्य। इस प्रकार r0 फलन (r) का अनिवार्य रूप से एकवचन बिंदु है। ऊपर जो सिद्ध किया गया था, उसके अनुसार r n बिंदुओं का एक क्रम इस प्रकार है कि r n o और lim (r n) = oo। यहाँ से

हमने इस धारणा के तहत आवश्यक अभिकथन को सिद्ध कर दिया है कि f(r) एफ एबिंदु r के कुछ छिद्रित पड़ोस में आइए अब मान लें कि यह सत्य नहीं है, अर्थात। बिंदु वें के किसी भी मनमाने ढंग से छोटे पंचर पड़ोस में ऐसा बिंदु है जी",कि f(r") = A. फिर किसी के लिए पीपंचर पड़ोस में 0 f(z u) = L. इस प्रकार, अभीष्ट अभिकथन सत्य है पी-युओ

सभी मामलों में, और प्रमेय 26.7 सिद्ध होता है।

(सोखोट्स्की के) प्रमेय 26.7 के अनुसार, अनिवार्य रूप से एकवचन बिंदु के किसी भी (मनमाने ढंग से छोटे) पंचर पड़ोस में, फ़ंक्शन f(r) विस्तारित जटिल विमान C में किसी भी संख्या के करीब मान लेता है।

अलग-अलग एकवचन बिंदुओं का अध्ययन करने के लिए, बुनियादी प्राथमिक कार्यों के प्रसिद्ध टेलर विस्तार अक्सर उपयोगी होते हैं।

उदाहरण 2जी.8. फ़ंक्शन के लिए एकवचन बिंदु zq = 0 का प्रकार निर्धारित करें

हल और ई। हम टेलर श्रृंखला में आर की शक्तियों में अंश और हर का विस्तार करते हैं। (22.11) 3 में प्रतिस्थापित करना जेड r के बजाय और 1 घटाकर, हम प्राप्त करते हैं

(22.12) का उपयोग करके, हम हर का विस्तार प्राप्त करते हैं:

इन विस्तारों में श्रृंखला पूरे जटिल विमान € में परिवर्तित होती है। हमारे पास है

और /2(2) बिंदु के पड़ोस में समान हैं ज़ो = 0 (और पूरे तल में भी) और /2(20) एफ 0, तब एच (जेड)बिंदु gF 0 के कुछ पड़ोस में भी विश्लेषणात्मक है। कोरोलरी 26.4 के अनुसार, बिंदु ज़ो = 0 आदेश का ध्रुव है एन = 4.

द्वितीय उदाहरण 26.9. फ़ंक्शन के एकवचन बिंदु खोजें एफ (जेड)= पाप जे - और उनके प्रकार का निर्धारण करें।

ई और ई में पी ई। फ़ंक्शन का एक अंतिम एकवचन बिंदु है zq = 1. C से अन्य बिंदुओं पर, फलन डब्ल्यू =--- विश्लेषणात्मक; इसलिए पाप कार्य वूविश्लेषणात्मक होगा।

ज्या के प्रसार में प्रतिस्थापित करने पर (22.12) - r के स्थान पर, हम प्राप्त करते हैं

हमने बिंदु 20 = 1 के एक पंचर पड़ोस में लॉरेंट श्रृंखला में पाप फ़ंक्शन का विस्तार प्राप्त किया है। चूंकि परिणामी विस्तार में नकारात्मक शक्तियों (आर -1) के साथ असीम रूप से कई शब्द हैं, फिर zq = 1 एक अनिवार्य एकवचन बिंदु है (इस मामले में, लॉरेंट विस्तार में केवल मुख्य भाग होता है, और सही भाग गायब होता है)।

ध्यान दें कि इस मामले में श्रृंखला विस्तार का सहारा लिए बिना, परिभाषा से सीधे विलक्षणता की प्रकृति को स्थापित करना भी संभव था। वास्तव में, अनुक्रम (r") और (2") में परिवर्तित होते हैं ज़ो= 1, और ऐसा कि एफ (जेड "एन)= 1,/(2") = 0 (ऐसे क्रमों को स्वयं निर्दिष्ट करें)। तो, एफ (जेड)कोई सीमा नहीं है जब जेड -> 1 और इसलिए बिंदु zq-1 अनिवार्य रूप से एकवचन है।

आइए हम एक बिंदु के पड़ोस में एक समारोह के लॉरेंट विस्तार की अवधारणा का परिचय दें Zq = 00 और इस बिंदु पर विस्तार और विलक्षणता की प्रकृति के बीच संबंध पर विचार करें। ध्यान दें कि एक पृथक एकवचन बिंदु और उसके प्रकार (हटाने योग्य, ध्रुव, या अनिवार्य रूप से एकवचन) की परिभाषा मामले पर लागू होती है zq = महासागर अपरिवर्तित। लेकिन प्रमेय 26.2. 26.3 और 26.6, लॉरेंट विस्तार की प्रकृति से संबंधित, को बदलने की आवश्यकता है। बात यह है कि सदस्य सी एन (जेड - 2ओ) पी. पी= -1,-2,..., मुख्य भाग, अंतिम बिंदु के पास फ़ंक्शन की "अनियमितता" को परिभाषित करता है Zq, जैसा कि 2 ऊ की ओर प्रवृत्त होता है, वे "सही ढंग से" व्यवहार करेंगे (0 की प्रवृत्ति)। इसके विपरीत, नियमित भाग के सदस्यों के साथ पी= 1,2,... ऊ की ओर प्रवृत्त होगा; वे विलक्षणता की प्रकृति को निर्धारित करते हैं ज़क = ऊ। इसलिए, ऊ के पड़ोस में विस्तार का मुख्य हिस्सा सकारात्मक शक्तियों वाले शब्द होंगे पी,और सही - नकारात्मक के साथ।

आइए एक नया वेरिएबल पेश करें डब्ल्यू = 12. समारोह टीवी = 1/2, विस्तारित ताकि u(oo) = 0, वन-टू-वन और अनुरूप रूप से आस-पड़ोस का मानचित्रण करें जेड > आरअंक zq = 00 |w| . के पड़ोस में wq = 0. यदि फलन एफ (जेड)एक छिद्रित पड़ोस में विश्लेषिकी आर z Zq = oc, तब फलन जी (डब्ल्यू) = एफ (एल / डब्ल्यू)पीले पड़ोस में विश्लेषणात्मक होगा 0 wo = 0. चूंकि 2 -> oo के लिए होगा वू-> 0, तब

इसीलिए जी (डब्ल्यू)बिंदु पर है wq = 0 उसी प्रकार की विलक्षणता है जैसे एफ (जेड)बिंदु पर Zq = 00। आइए हम बिंदु wo = 0 के एक पंचर पड़ोस में लॉरेंट श्रृंखला में फ़ंक्शन G(w) का विस्तार करें:

(26.5) के दाईं ओर का योग क्रमशः विस्तार के सही और मुख्य भागों का प्रतिनिधित्व करता है। चलिए वेरिएबल पर चलते हैं जेड,प्रतिस्थापन डब्ल्यू = 1/जेड:

दर्शाने पी\u003d -ए *, 6 * \u003d 6_ " \u003d पी के साथऔर यह देखते हुए जी (एल / जेड) = एफ (जेड), हम पाते हैं

अपघटन (2G.G) कहलाता है बिंदु zq . के एक पंचर पड़ोस में फ़ंक्शन f(z) का लॉरेंट विस्तार= ऊ। (2G.6) में पहला योग कहलाता है दाहिना भाग, और दूसरा योग है मुख्य हिस्सायह अपघटन। चूंकि ये योग विस्तार (26.5) के सही और प्रमुख भागों के अनुरूप हैं, इसलिए विस्तार (26.6) प्रमेय 26.2, 26.3 और 26.6 के अनुरूपों को संतुष्ट करता है। इस प्रकार, निम्नलिखित प्रमेय प्रमेय 26.2 का एक एनालॉग है।

प्रमेय 26.10. पृथक एकवचन बिंदुZq - ओएस (कार्य/(जी) हटाने योग्य है अगर और केवल अगर इस बिंदु के एक छिद्रित पड़ोस में लॉरेंट विस्तार का रूप है

टी.एस. केवल सही भाग से मिलकर बनता है।

हम डालते हैं /(oo) = कंश्रृंखला (26.7) द्वारा परिभाषित फ़ंक्शन पड़ोस में परिवर्तित होता है जेड > आरअंक 2o \u003d महासागर, कहा जाता है बिंदु z . पर विश्लेषणात्मकओ = ऊ। (ध्यान दें कि यह परिभाषा फ़ंक्शन की विश्लेषणात्मकता के बराबर है जी (डब्ल्यू) बिंदु पर वाह = 0.)

उदाहरण 26.11. फ़ंक्शन के एकवचन बिंदु zq = oo की जाँच करें

चूँकि सीमा परिमित है, तो ज़ो = oo फ़ंक्शन f(r) का एक हटाने योग्य एकवचन बिंदु है। अगर हम /(oo) = lim . डालते हैं जे (जेड)= 0, तब एफ (जेड)हो जाएगा

बिंदु पर टिक ज़ो= ओएस आइए हम दिखाते हैं कि संगत प्रसार कैसे ज्ञात करें (26.7)। चलिए वेरिएबल पर चलते हैं वू = 1 एफजेड.स्थानापन्न जेड= 1 /?ई, हमें मिलता है

(अंतिम समानता बिंदु ww = 0 के पंचर पड़ोस में मान्य है, लेकिन हम परिभाषा का विस्तार करेंगे (7(0) = 0)। परिणामी फ़ंक्शन में एकवचन बिंदु हैं डब्ल्यू =±मैं, डब्ल्यू =-1/3, और बिंदु पर Wq = 0 विश्लेषणात्मक है। विस्तार समारोह जी (डब्ल्यू)डिग्री के अनुसार वू(जैसा कि उदाहरण 25.7 में किया गया था) और परिणामी घात श्रृंखला में प्रतिस्थापित करना डब्ल्यू = 1/जेडकोई फ़ंक्शन का विस्तार (26.7) प्राप्त कर सकता है एफ (जेड)।

प्रमेय 26.3 मामले के लिए ज़ो= oo निम्नलिखित रूप में फिर से लिखा जाएगा।

प्रमेय 26.12. पृथक एकवचन बिंदुजाओ = ओसी फलन f(z) एक ध्रुव है यदि और केवल यदि लॉरेंट विस्तार का मुख्य भाग है (26.6) गैर-शून्य गुणांक की केवल एक सीमित संख्या हैसाथ":

यहां श्रृंखला नियमित हिस्सा है, और कोष्ठक बहुपद विस्तार का मुख्य भाग है। महासागर में ध्रुव की बहुलता को ध्रुव की बहुलता के रूप में परिभाषित किया जाता है डब्ल्यूक्यू = 0 कार्य जी (जेड)।यह देखना आसान है कि ध्रुव की बहुलता संख्या के साथ मेल खाती है एनमें (26.8)।

क्यू पी | (i 2 + 1) (z + 3) 2

एक कार्य। दिखाएँ कि समारोह एफ (जेड) =-- -- में है

बिंदु ज़ो =ऊ पोल ऑर्डर 3.

प्रमेय 26.6 एक आवश्यक एकवचन बिंदु पर मामले के लिए फिर से लिखा गया है ज़ो= ओएस लगभग शब्दशः, और हम इस पर विस्तार से ध्यान नहीं देते हैं।

एकवचन बिंदु

गणित में।

1) समीकरण F द्वारा दिए गए वक्र का एकवचन बिंदु ( एक्स, वाई) = 0, - बिंदु एम 0 ( एक्स 0, वाई 0), जिसमें फलन F के दोनों आंशिक अवकलज ( एक्स, वाई) गायब होना:

यदि, इसके अतिरिक्त, फलन F के सभी द्वितीय आंशिक अवकलज नहीं हैं ( एक्स, वाई) बिंदु पर M 0 शून्य के बराबर है, तो O. t. को दोहरा कहा जाता है। यदि, बिंदु M 0 पर पहले डेरिवेटिव के गायब होने के साथ, सभी दूसरे डेरिवेटिव गायब हो जाते हैं, लेकिन सभी तीसरे डेरिवेटिव शून्य के बराबर नहीं होते हैं, तो O. t को ट्रिपल कहा जाता है, और इसी तरह। डबल ओ टी के पास वक्र की संरचना का अध्ययन करते समय, अभिव्यक्ति के संकेत द्वारा एक महत्वपूर्ण भूमिका निभाई जाती है

यदि > 0, तो O. t. को पृथक्कृत कहा जाता है; उदाहरण के लिए, वक्र वाई 2 - एक्स 4 + 4x 2= 0 मूल एक पृथक O. t. है (देखें चावल। एक ) यदि x 2 + y 2 + a 2) 2 - 4ए 2 एक्स 2 - ए 4= 0 निर्देशांक की उत्पत्ति नोडल O. t. है (देखें चावल। 2 ) यदि = 0, तो O. t. वक्र या तो अलग-थलग है या इस तथ्य की विशेषता है कि वक्र की विभिन्न शाखाओं में इस बिंदु पर एक सामान्य स्पर्शरेखा होती है, उदाहरण के लिए: स्पर्शरेखा और एक वक्र की तरह एक बिंदु बनाते हैं वाई 2 - एक्स 3= 0 (देखें चावल। 3 , एक); बी) दूसरी तरह की पुच्छल - वक्र की विभिन्न शाखाएं एक वक्र की तरह सामान्य स्पर्शरेखा के एक ही तरफ स्थित होती हैं (वाई - एक्स 2)2 - एक्स 5= 0 (देखें चावल। 3 , बी); सी) आत्म-संपर्क का बिंदु (वक्र के लिए वाई 2 - एक्स 4= 0 मूल आत्म-संपर्क का एक बिंदु है; (सेमी। चावल। 3 , में)। निर्दिष्ट ओ. टी. के साथ कई अन्य ओ. टी. विशेष नामों के साथ हैं; उदाहरण के लिए, एक स्पर्शोन्मुख बिंदु एक सर्पिल का शीर्ष होता है जिसमें अनंत संख्या में घुमाव होते हैं (चित्र देखें। चावल। चार ), विराम बिंदु, कोने बिंदु, आदि।

2) अवकल समीकरण का एकवचन बिंदु वह बिंदु होता है जिस पर अवकल समीकरण के दाईं ओर के अंश और हर दोनों एक साथ गायब हो जाते हैं (देखें। विभेदक समीकरण)

जहां पी और क्यू लगातार अलग-अलग कार्य हैं। ओ. टी. को मूल स्थान पर स्थित मानते हुए और टेलर सूत्र का उपयोग करते हुए (देखें। टेलर सूत्र), हम समीकरण (1) को इस रूप में निरूपित कर सकते हैं

जहां पी 1 ( एक्स, वाई) और क्यू 1 ( एक्स, वाई) के संबंध में अपरिमित हैं

अर्थात्, यदि 1 2 और 1 λ 2 > 0 या 1 = 2, तो O. t. एक नोड है; नोड के पर्याप्त रूप से छोटे पड़ोस के बिंदुओं से गुजरने वाले सभी अभिन्न वक्र इसमें प्रवेश करते हैं। यदि 1 ≠ λ 2 और λ 1 λ 2 i β, α 0 और β 0, तो O. t. एक फोकस है; फोकस के पर्याप्त रूप से छोटे पड़ोस में बिंदुओं से गुजरने वाले सभी अभिन्न वक्र सर्पिल होते हैं जिनमें फोकस के किसी भी मनमाने ढंग से छोटे पड़ोस में अनंत संख्या में घुमाव होते हैं। अगर, अंत में, 1,2 = ± मैंβ, β 0, तो O. t का वर्ण P के प्रसार में रैखिक पदों द्वारा निर्धारित नहीं होता है ( एक्स, वाई) और क्यू ( एक्स, वाई), जैसा कि उपरोक्त सभी मामलों में हुआ था; यहाँ O. t. एक फोकस या केंद्र हो सकता है, या इसका एक अधिक जटिल चरित्र हो सकता है। केंद्र के पड़ोस में, सभी अभिन्न वक्र बंद होते हैं और उनके अंदर केंद्र होता है। तो, उदाहरण के लिए, बिंदु (0, 0) समीकरणों के लिए एक नोड है पर" = 2यू/एक्स(λ 1 = 1, 2 = 2; देखें चावल। 5 , ए) और आप" = यू/एक्स(λ 1 = 2 = 1; देखें चावल। 5 , बी), समीकरण के लिए एक सैडल y" = -y/x(λ 1 = -1, 2 = 1 ; सेमी। चावल। 6 ), समीकरण के लिए फोकस वाई" =(एक्स + वाई) / (एक्स - वाई) (λ 1 = 1 - मैं, 2 = 1 + मैं; सेमी। चावल। 7 ) और समीकरण के लिए केंद्र वाई" = -एक्स / वाई(λ 1 = -मैं, 2 = मैं; सेमी। चावल। आठ ).

अगर एक्स, वाई) और क्यू ( एक्स, वाई) विश्लेषणात्मक हैं, उच्च क्रम के ओ टी के पड़ोस को क्षेत्रों में विभाजित किया जा सकता है: डी 1 - इंटीग्रल कर्व्स से भरा, दोनों सिरों ओ. टी। (अण्डाकार क्षेत्रों) में प्रवेश करते हैं, डी 2 - इंटीग्रल कर्व्स से भरा होता है, एक छोर ओ. टी. (परवलयिक क्षेत्र) में प्रवेश करता है, और डी 3 - ओ. टी. में शामिल दो अभिन्न वक्रों से घिरा क्षेत्र, जिसके बीच अतिपरवलय (हाइपरबोलिक क्षेत्र) के प्रकार के अभिन्न वक्र होते हैं (देखें। चावल। 9 ) यदि O. बिंदु में प्रवेश करने वाले कोई अभिन्न वक्र नहीं हैं, तो O. बिंदु को स्थिर प्रकार का बिंदु कहा जाता है। एक स्थिर ओ टी के पड़ोस में ओ टी युक्त बंद अभिन्न वक्र होते हैं, जिनके बीच सर्पिल स्थित होते हैं (चित्र 1 देखें)। चावल। दस ).

O. t. अंतर समीकरणों का अध्ययन, अर्थात, संक्षेप में, O. t. M के पड़ोस में अभिन्न वक्रों के परिवारों के व्यवहार का अध्ययन। लाइपुनोवए, ए. पोंकारेऔर आदि।)।

3) एकल-मूल्यवान विश्लेषणात्मक फ़ंक्शन का एकवचन बिंदु - एक बिंदु जिस पर फ़ंक्शन की विश्लेषणात्मकता का उल्लंघन होता है (देखें। विश्लेषणात्मक कार्य) यदि O. t का कोई पड़ोस है। एक, अन्य O. t. से मुक्त, फिर बिंदु एकपृथक O. t. if . कहा जाता है एकएक पृथक ओ.टी. है और एक परिमित ओ.टी. मौजूद है, जिसे हटाने योग्य ओ.टी. कहा जाता है। बिंदु ए पर फ़ंक्शन की परिभाषा को उचित रूप से बदलकर (या इस बिंदु पर इसे फिर से परिभाषित करना, यदि फ़ंक्शन बिल्कुल परिभाषित नहीं है), अर्थात्, सेटिंग एफ(एक)= बी, हासिल करना संभव है एकसंशोधित कार्य का एक सामान्य बिंदु बन जाएगा। उदाहरण के लिए, डॉट जेड= 0 फलन f 1 के लिए हटाने योग्य O.T. है ( जेड) = एफ(जेड), यदि जेड 0, और एफ 1(0),=1, बिंदु जेड= 0 एक सामान्य बिंदु है [ एफ 1 (जेड) बिंदु पर विश्लेषणात्मक है जेड= 0]। यदि एक एक- पृथक O. t. और a को फ़ंक्शन का ध्रुव या अनिवार्य रूप से एकवचन बिंदु कहा जाता है एफ(जेड), अगर लॉरेंट श्रृंखला) कार्य करता है एफ(जेड) एक पृथक ओ.टी. के पड़ोस में नकारात्मक शक्तियां नहीं होती हैं जेड - ए, यदि एक- हटाने योग्य O. t., में सीमित संख्या में नकारात्मक शक्तियां होती हैं जेड - ए, यदि एक- पोल (इस मामले में, पोल का क्रम आरएक अनिवार्य रूप से एकवचन बिंदु - की उच्चतम शक्ति के रूप में परिभाषित किया गया है। उदाहरण के लिए, फ़ंक्शन के लिए

पी = 2, 3,…)

दूरसंचार विभाग जेड= 0 क्रम का ध्रुव है आर, समारोह के लिए

दूरसंचार विभाग जेड= 0 एक अनिवार्य एकवचन बिंदु है।

एक शक्ति श्रृंखला के अभिसरण के चक्र की सीमा पर इस सर्कल के अंदर दी गई शक्ति श्रृंखला द्वारा दर्शाए गए फ़ंक्शन का कम से कम एक ओ.टी. होना चाहिए। एकल-मूल्यवान विश्लेषणात्मक फ़ंक्शन (प्राकृतिक सीमा) के अस्तित्व के क्षेत्र के सभी सीमा बिंदु इस फ़ंक्शन के सीमा बिंदु हैं। इस प्रकार, इकाई वृत्त के सभी बिंदु | जेड| = 1 फ़ंक्शन के लिए विशेष हैं

एक बहु-मूल्यवान विश्लेषणात्मक कार्य के लिए, "O. टी।" अधिक मुश्किल। O. t के अलावा, किसी फ़ंक्शन की रीमैन सतह की अलग-अलग शीट में (अर्थात, एकल-मूल्यवान विश्लेषणात्मक तत्वों का O. t.), कोई भी शाखा बिंदु फ़ंक्शन का O. t भी होता है। रीमैन सतह के पृथक शाखा बिंदु (यानी, शाखा बिंदु जैसे कि उनके कुछ पड़ोस में किसी भी पत्ते में कोई अन्य ओ.टी. कार्य नहीं होते हैं) को निम्नानुसार वर्गीकृत किया जाता है। यदि a परिमित क्रम का एक पृथक शाखा बिंदु है और एक परिमित a मौजूद है, तो इसे एक महत्वपूर्ण ध्रुव कहा जाता है। यदि एक एकअनंत क्रम का एक पृथक शाखा बिंदु है, और ए को एक अनुवांशिक ओ टी कहा जाता है। अन्य सभी पृथक शाखा बिंदुओं को महत्वपूर्ण अनिवार्य रूप से एकवचन बिंदु कहा जाता है। उदाहरण: डॉट जेड= 0 फलन f का एक सामान्य क्रांतिक बिंदु है ( जेड) = लॉग जेडऔर फ़ंक्शन का एक महत्वपूर्ण आवश्यक एकवचन बिंदु एफ (जेड) = पाप लॉग जेड.

हटाने योग्य को छोड़कर कोई भी ओ टी, विश्लेषणात्मक निरंतरता के लिए एक बाधा है, यानी, एक अपरिवर्तनीय ओ टी के माध्यम से गुजरने वाले वक्र के साथ विश्लेषणात्मक निरंतरता असंभव है।

महान सोवियत विश्वकोश। - एम .: सोवियत विश्वकोश. 1969-1978 .

देखें कि "विशेष बिंदु" अन्य शब्दकोशों में क्या है:

यहाँ अंक। एकवचन बिंदु (अंतर समीकरण) भी देखें। गणित में एक विशेषता या विलक्षणता एक ऐसा बिंदु है जिस पर गणितीय वस्तु (आमतौर पर एक फ़ंक्शन) परिभाषित नहीं होती है या अनियमित व्यवहार होता है (उदाहरण के लिए, एक बिंदु जिस पर ... विकिपीडिया

एक विश्लेषणात्मक कार्य एक ऐसा बिंदु है जिस पर विश्लेषणात्मकता की शर्तों का उल्लंघन होता है। यदि एक विश्लेषणात्मक कार्य f(z) को बिंदु z0 के कुछ पड़ोस में हर जगह परिभाषित किया गया है ... भौतिक विश्वकोश

एक विश्लेषणात्मक कार्य वह बिंदु है जिस पर किसी फ़ंक्शन की विश्लेषणात्मकता का उल्लंघन होता है ... बड़ा विश्वकोश शब्दकोश

एकवचन बिंदु- - [हां। एन। लुगिंस्की, एम.एस. फ़ज़ी ज़िलिंस्काया, यू.एस. कबीरोव। इलेक्ट्रिकल इंजीनियरिंग और पावर इंडस्ट्री का अंग्रेजी रूसी शब्दकोश, मॉस्को, 1999] इलेक्ट्रिकल इंजीनियरिंग विषय, बुनियादी अवधारणाएं एन एकवचन बिंदु ... तकनीकी अनुवादक की हैंडबुक

1) एक विश्लेषणात्मक फलन f(z) का एक OT एक जटिल चर z के फलन f(z) के एक अवयव के विश्लेषणात्मक निरंतरता में इस चर के तल पर किसी पथ के साथ एक बाधा है। विश्लेषणात्मक कार्य f(z) को कुछ द्वारा परिभाषित किया जाए ... ... गणितीय विश्वकोश

एक विश्लेषणात्मक कार्य, वह बिंदु जिस पर फ़ंक्शन की विश्लेषणात्मकता का उल्लंघन होता है। * * * एकवचन बिंदु एक विश्लेषणात्मक फ़ंक्शन का एक एकल बिंदु, एक बिंदु जिस पर फ़ंक्शन की विश्लेषणात्मकता का उल्लंघन होता है ... विश्वकोश शब्दकोश

एकवचन बिंदु- यपेटिंगेसिस टास्क स्टेटसस टी sritis automatika atitikmenys: engl। एकवचन बिंदु वोक। विलक्षण पंकट, एम रस। एकवचन बिंदु, fpranc। बिंदु कण, एम; पॉइंट सिंगुलियर, मी ... ऑटोमेटिकोस टर्मिन, odynas

टेलर श्रृंखला उन कार्यों का अध्ययन करने के लिए एक प्रभावी उपकरण के रूप में कार्य करती है जो सर्कल ज़ोल में विश्लेषणात्मक होते हैं एक कुंडलाकार क्षेत्र में विश्लेषणात्मक कार्यों का अध्ययन करने के लिए, यह पता चला है कि सकारात्मक और नकारात्मक शक्तियों (z - zq) में विस्तार का निर्माण संभव है। टेलर के विस्तार का सामान्यीकरण करने वाला रूप। श्रृंखला (1), जिसे दो श्रृंखलाओं के योग के रूप में समझा जाता है, लॉरेंट श्रृंखला कहलाती है। यह स्पष्ट है कि श्रृंखला के अभिसरण का क्षेत्र (1) प्रत्येक श्रृंखला (2) के अभिसरण के क्षेत्रों का सामान्य हिस्सा है। चलो उसे ढूंढते हैं। पहली श्रृंखला के अभिसरण का क्षेत्र एक वृत्त है जिसकी त्रिज्या कॉची-हैडमर्ड सूत्र द्वारा निर्धारित की जाती है अभिसरण के चक्र के अंदर, श्रृंखला (3) एक विश्लेषणात्मक कार्य में परिवर्तित होती है, और छोटे त्रिज्या के किसी भी चक्र में, यह बिल्कुल अभिसरण करती है और समान रूप से। दूसरी श्रृंखला चर के संबंध में एक शक्ति श्रृंखला है। श्रृंखला (5) अपने अभिसरण के चक्र के भीतर जटिल चर m-*oo के विश्लेषणात्मक कार्य में परिवर्तित होती है, और छोटे त्रिज्या के किसी भी सर्कल में यह बिल्कुल और समान रूप से परिवर्तित होती है, जिसका अर्थ है कि श्रृंखला (4) का अभिसरण क्षेत्र वृत्त का रूप है - यदि फिर श्रृंखला (3) और (4) के अभिसरण का एक सामान्य क्षेत्र है - एक गोलाकार वलय जिसमें श्रृंखला (1) अभिसरण करती है एक विश्लेषणात्मक समारोह के लिए। इसके अलावा, किसी भी रिंग में, यह बिल्कुल और समान रूप से परिवर्तित होता है। उदाहरण 1. रेड लॉरेंट श्रृंखला के अभिसरण के क्षेत्र का निर्धारण करें पृथक एकवचन बिंदु और उनका वर्गीकरण (जेड), जो एक गोलाकार अंगूठी में एकल-मूल्यवान और राजनीतिक है, इस अंगूठी में एक अभिसरण श्रृंखला के योग के रूप में दर्शाया जा सकता है जिसका गुणांक है Cn विशिष्ट रूप से उन सूत्रों द्वारा निर्धारित और परिकलित होते हैं जहां 7p त्रिज्या m का एक वृत्त है आइए हम रिंग R के अंदर एक मनमाना बिंदु z तय करें। हम बिंदु r0 पर केंद्रों के साथ वृत्त बनाते हैं जिनकी त्रिज्या असमानताओं को संतुष्ट करती है और एक नई अंगूठी पर विचार करती है। एक गुणा जुड़े डोमेन के लिए कॉची इंटीग्रल प्रमेय के अनुसार, हमने प्रत्येक इंटीग्रल को योग (8) में अलग से बदल दिया है। सर्कल 7d* के साथ सभी बिंदुओं के लिए, एक समान रूप से अभिसरण श्रृंखला 1 1 का संबंध डी संतुष्ट है। इसलिए, अंश ^ को vi- /" / सर्कल पर सभी बिंदुओं के लिए £ ir> संबंध में दर्शाया जा सकता है इसलिए, अंश ^ को सूत्रों (10) और (12) में एक समान रूप से अभिसरण श्रृंखला के योग के रूप में दर्शाया जा सकता है, जो एक गोलाकार वलय में विश्लेषणात्मक कार्य हैं। इसलिए, कॉची के प्रमेय के अनुसार, यदि वृत्त 7/r और 7r/ को किसी वृत्त द्वारा प्रतिस्थापित किया जाता है, तो संगत समाकलों के मान नहीं बदलते हैं। यह हमें सूत्रों (10) और (12) को संयोजित करने की अनुमति देता है। सूत्र (8) के दाईं ओर के समाकलों को क्रमशः उनके व्यंजकों (9) और (11) के साथ बदलने पर, हमें वांछित विस्तार प्राप्त होता है। चूंकि z एक मनमाना है रिंग का बिंदु, यह इस प्रकार है कि श्रृंखला (14) इस रिंग में हर जगह फ़ंक्शन f (z) में परिवर्तित हो जाती है, और किसी भी रिंग में श्रृंखला इस फ़ंक्शन में बिल्कुल और समान रूप से परिवर्तित हो जाती है। आइए अब हम सिद्ध करें कि रूप (6) का अपघटन अद्वितीय है। मान लें कि एक और अपघटन होता है। फिर, रिंग R के अंदर हर जगह, हमारे पास परिधि पर, श्रृंखला (15) समान रूप से अभिसरण होती है। समानता के दोनों पक्षों को गुणा करें (जहाँ m एक निश्चित पूर्णांक है, और दोनों श्रृंखला शब्द को पद से एकीकृत करें। परिणामस्वरूप, हम बाईं ओर, और दाईं ओर - Csh। इस प्रकार, (4, \u003d सेंट) प्राप्त करते हैं। चूँकि m एक मनमाना संख्या है, तो अंतिम समानता श्रृंखला (6), जिसके गुणांकों की गणना सूत्र (7) द्वारा की जाती है, को रिंग 7 में फ़ंक्शन f(z) की लॉरेंट श्रृंखला कहा जाता है। लॉरेंट श्रृंखला शायद ही कभी व्यवहार में उपयोग की जाती है, क्योंकि, एक नियम के रूप में, उन्हें बोझिल गणना की आवश्यकता होती है। आमतौर पर, यदि संभव हो तो, प्राथमिक कार्यों के तैयार टेलर विस्तार का उपयोग किया जाता है। विस्तार की विशिष्टता के आधार पर, कोई भी वैध विधि उसी की ओर ले जाती है परिणाम। उदाहरण 2 विभिन्न डोमेन के कार्यों के लॉरेंट श्रृंखला विस्तार पर विचार करें, यह मानते हुए कि फ्यूसिजा / (जेड) में दो एकवचन बिंदु हैं: इसलिए, तीन रिंग डोमेन हैं और, बिंदु r = 0 पर केंद्रित है। जिनमें से प्रत्येक में फलन f(r) विश्लेषणात्मक है: a) वृत्त वृत्त का बाहरी भाग है (चित्र 27)। आइए हम इनमें से प्रत्येक क्षेत्र में फ़ंक्शन /(z) के लॉरेंट विस्तारों को खोजें। हम /(z) को प्राथमिक भिन्नों के योग के रूप में निरूपित करते हैं a) वृत्त परिवर्तन संबंध (16) निम्नानुसार है। b) फंक्शन -z के लिए वलय इस वलय में अभिसारी रहता है, क्योंकि फंक्शन j^j के लिए |z| > 1 विचलन। इसलिए, हम फ़ंक्शन /(z) को निम्नानुसार रूपांतरित करते हैं: सूत्र (19) को फिर से लागू करने पर, हम प्राप्त करते हैं कि यह श्रृंखला इसके लिए अभिसरण करती है। विस्तारों (18) और (21) को संबंध (20) में प्रतिस्थापित करने पर, हम प्राप्त करते हैं c) फ़ंक्शन -z के लिए वृत्त की बाहरीता |z| > 2 डाइवर्ज, और फंक्शन के लिए सीरीज (21) आइए हम फंक्शन /(z) को निम्नलिखित रूप में निरूपित करें: /<*> सूत्रों (18) और (19) का उपयोग करते हुए, हम OR 1 प्राप्त करते हैं। उदाहरण 3. फंक्शन लॉरेंट श्रृंखला के 8 लॉरेंट श्रृंखला के अपघटन का पता लगाएं पृथक एकवचन बिंदु और कुंडलाकार क्षेत्र ए में उनका वर्गीकरण हम निम्नलिखित रूप में फ़ंक्शन f (z) के प्रतिनिधित्व का उपयोग करते हैं: और दूसरे शब्द का उपयोग करके रूपांतरित करते हैं ज्यामितीय प्रगति की शर्तों के योग के लिए सूत्र, हम प्राप्त अभिव्यक्तियों को सूत्र (22) में प्रतिस्थापित करते हैं, हमारे पास उदाहरण 4 है। पतले zq = 0 के पड़ोस में लॉरेंट श्रृंखला में फ़ंक्शन का विस्तार करें। किसी भी जटिल के लिए , हमने माना है कि यह विस्तार किसी भी बिंदु z 0 के लिए मान्य है। इस मामले में, कुंडलाकार क्षेत्र एक बिंदु z के साथ पूरा जटिल विमान है - 0। इस क्षेत्र को निम्नलिखित संबंधों द्वारा परिभाषित किया जा सकता है: यह फ़ंक्शन विश्लेषणात्मक है क्षेत्र में लॉरेंट श्रृंखला के गुणांकों के लिए सूत्रों (13) से, पिछले पैराग्राफ के समान तर्क से, कोई कोइव असमानताओं को प्राप्त कर सकता है। यदि फलन f(z) एक वृत्त पर परिबद्ध है, जहाँ M एक स्थिरांक है), तो पृथक एकवचन बिंदु A बिंदु zo को फलन f(z) का एक पृथक एकवचन बिंदु कहा जाता है, यदि बिंदु का एक कुंडलाकार पड़ोस मौजूद है ( इस सेट को कभी-कभी बिंदु 2o का एक छेदा हुआ पड़ोस भी कहा जाता है, जहां फ़ंक्शन f(z) एकल-मूल्यवान और विश्लेषणात्मक होता है। बिंदु zo पर ही, फ़ंक्शन या तो परिभाषित नहीं है या एकल-मूल्यवान और विश्लेषणात्मक नहीं है। बिंदु zo के निकट आने पर फ़ंक्शन /(z) के व्यवहार के आधार पर तीन प्रकार के एकवचन बिंदुओं को प्रतिष्ठित किया जाता है। एक पृथक एकवचन बिंदु को कहा जाता है: 1) हटाने योग्य यदि कोई परिमित है 2) pmusach यदि 3) एक अनिवार्य रूप से एकवचन बिंदु यदि फ़ंक्शन f(z) की कोई सीमा नहीं है प्रमेय 16. फ़ंक्शन f(z) का एक पृथक एकवचन बिंदु z0 एक हटाने योग्य एकवचन बिंदु है यदि और केवल यदि बिंदु zo के पड़ोस में फ़ंक्शन f(z) के लॉरेंट विस्तार में एक प्रमुख भाग शामिल नहीं है, अर्थात, लेट ज़ो - हटाने योग्य एकवचन बिंदु का रूप है। फिर एक परिमित मौजूद होता है, और इसलिए फ़ंक्शन f(z) बिंदु r के एक प्रोकोलॉजिकल पड़ोस में घिरा होता है। हम कॉची असमानताओं के आधार पर सेट करते हैं क्योंकि p को मनमाने ढंग से छोटा चुनना संभव है, फिर सभी गुणांक नकारात्मक पर घात (z - 20) शून्य के बराबर हैं: इसके विपरीत, लॉरेंट को बिंदु zq के पड़ोस में फ़ंक्शन /(r) के विस्तार में केवल सही भाग शामिल है, अर्थात, इसका रूप (23) है और, इसलिए , टेलर है। यह देखना आसान है कि z -* z0 के लिए फ़ंक्शन /(r) का एक सीमा मान है: प्रमेय 17. फ़ंक्शन f(z) का एक पृथक एकवचन बिंदु zq हटाने योग्य है यदि और केवल यदि फ़ंक्शन J(z) है बिंदु zq के कुछ पंचर पड़ोस में बंधे, Zgmchai नहीं। मान लीजिए r0 f(r) का एक हटाने योग्य एकवचन बिंदु है। यह मानते हुए कि फलन f(r) बिंदु th पर केन्द्रित किसी वृत्त में विश्लेषणात्मक है। यह बिंदु के नाम को परिभाषित करता है - डिस्पोजेबल। प्रमेय 18. फ़ंक्शन f(z) का एक पृथक एकवचन बिंदु zq एक ध्रुव है यदि और केवल यदि बिंदु के पड़ोस में फ़ंक्शन f(z) के लॉरेंट विस्तार के मुख्य भाग में एक परिमित (और सकारात्मक) संख्या है शून्येतर पदों का, अर्थात्, 4 का रूप है मान लीजिए z0 एक ध्रुव है। तब से बिंदु z0 का एक पंचर पड़ोस मौजूद है जिसमें फ़ंक्शन f(z) विश्लेषणात्मक और गैर-शून्य है। फिर इस पड़ोस में एक विश्लेषणात्मक कार्य परिभाषित किया गया है, और इसलिए, बिंदु zq फ़ंक्शन का एक हटाने योग्य एकवचन बिंदु (शून्य) है या जहां h(z) एक विश्लेषणात्मक फ़ंक्शन है, h(z0) 0. पड़ोस में विश्लेषणात्मक है बिंदु zq का, और इसलिए, जहां से हम प्राप्त करते हैं, आइए अब मान लें कि फ़ंक्शन f(z) में बिंदु zo के एक पंचर पड़ोस में रूप (24) का अपघटन है। इसका मतलब है कि इस पड़ोस में फ़ंक्शन f(z) फ़ंक्शन के साथ विश्लेषणात्मक है। फ़ंक्शन g(z) के लिए, विस्तार मान्य है जिससे यह स्पष्ट है कि zq फ़ंक्शन g(z) का एक हटाने योग्य एकवचन बिंदु है और मौजूद है फिर फ़ंक्शन 0 पर जाता है - फ़ंक्शन का ध्रुव एक और सरल है तथ्य। बिंदु Zq फलन f(z) का एक ध्रुव है यदि और केवल यदि फलन g(z) = y को बिंदु zq के पड़ोस में एक विश्लेषणात्मक फलन के लिए g(z0) = 0 सेट करके बढ़ाया जा सकता है। क्रम फलन f(z) के ध्रुव की कोटि, फलन jfa के शून्य की कोटि कहलाती है। प्रमेय 16 और 18 निम्नलिखित अभिकथन का संकेत देते हैं। प्रमेय 19. एक पृथक एकवचन पतला अनिवार्य रूप से एकवचन होता है यदि और केवल यदि इस बिंदु के एक पंचर पड़ोस में लॉरेंट विस्तार के मुख्य भाग में असीम रूप से कई गैर-शून्य शब्द होते हैं। उदाहरण 5. फलन का एकवचन बिंदु zo = 0 है। हमारे पास लॉरेंट श्रृंखला पृथक एकवचन बिंदु हैं और उनका वर्गीकरण इसलिए, zo = 0 एक हटाने योग्य एकवचन बिंदु है। शून्य बिंदु के आसपास लॉरेंट श्रृंखला में फ़ंक्शन /(z) के विस्तार में केवल सही भाग होता है: उदाहरण 7। f(z) = फलन f(z) का एकवचन बिंदु zq = 0 है। वास्तविक और काल्पनिक अक्षों पर इस फलन के व्यवहार पर विचार करें: वास्तविक अक्ष पर x 0 पर, काल्पनिक अक्ष पर इसलिए, न तो परिमित और न ही z -* 0 पर अनंत सीमा f(z) मौजूद नहीं है। अतः बिंदु r0 = 0 फलन f(z) का अनिवार्य रूप से एकवचन बिंदु है। आइए हम शून्य बिंदु के पड़ोस में फ़ंक्शन f(z) के लॉरेंट विस्तार को खोजें। किसी भी जटिल सी के लिए हमने सेट किया है। फिर लॉरेंट के विस्तार में z की नकारात्मक शक्तियों के साथ अनंत संख्या में शब्द हैं।

दो स्वायत्त अंतर समीकरणों की प्रणालियों द्वारा वर्णित मॉडल।

चरण विमान। चरण चित्र। आइसोक्लाइन विधि। मुख्य समद्विबाहु. स्थिर राज्य स्थिरता। रैखिक प्रणाली। मुख्य बिंदु प्रकार: नोड, सैडल, फोकस, केंद्र। उदाहरण: प्रथम कोटि की रासायनिक अभिक्रियाएँ।

जैविक प्रणालियों के गुणों के गुणात्मक मॉडलिंग पर सबसे दिलचस्प परिणाम दो अंतर समीकरणों के मॉडल पर प्राप्त किए गए थे, जो विधि का उपयोग करके गुणात्मक अध्ययन की अनुमति देते हैं। चरण विमान. सामान्य रूप के दो स्वायत्त साधारण अंतर समीकरणों की एक प्रणाली पर विचार करें

(4.1)

पी (एक्स, वाई), क्यू (एक्स, वाई)- कुछ डोमेन में परिभाषित निरंतर कार्य जीयूक्लिडियन विमान ( एक्स, वाई- कार्टेशियन निर्देशांक) और इस क्षेत्र में क्रम के निरंतर व्युत्पन्न पहले से कम नहीं हैं।

क्षेत्र जीअसीमित या सीमित हो सकता है। यदि चर एक्स, वाईएक विशिष्ट जैविक अर्थ है (पदार्थों की सांद्रता, प्रजातियों की बहुतायत), सबसे अधिक बार क्षेत्र जीदाहिने आधे तल का धनात्मक चतुर्थांश है:

0 £ एक्स< ¥ ,0 £ आप< ¥ .

पदार्थों की सांद्रता या प्रजातियों की बहुतायत भी ऊपर से पोत की मात्रा या निवास के क्षेत्र से सीमित हो सकती है। फिर चर की श्रेणी का रूप है:

0 £ एक्स< x 0 , 0 £ आप< y 0 .

चर एक्स, वाईसमीकरणों की प्रणाली (4.1) के अनुसार समय में परिवर्तन, ताकि सिस्टम की प्रत्येक स्थिति चर के मूल्यों की एक जोड़ी से मेल खाती हो ( एक्स, वाई).

इसके विपरीत, चर के प्रत्येक जोड़े के लिए ( एक्स, वाई) प्रणाली की एक निश्चित स्थिति से मेल खाती है।

समन्वय अक्षों वाले एक विमान पर विचार करें, जिस पर चर के मान प्लॉट किए गए हैं एक्स, वाई. हर बिंदु एमयह विमान प्रणाली की एक निश्चित स्थिति से मेल खाता है। इस तरह के एक विमान को चरण विमान कहा जाता है और सिस्टम के सभी राज्यों की समग्रता को दर्शाता है। बिंदु M(x, y) को दर्शित करने वाला या निरूपित करने वाला बिंदु कहा जाता है।

चलो शुरुआती समय में टी = टी 0 बिंदु निर्देशांक का प्रतिनिधित्व करता है एम 0 (एक्स(टी 0), यू(टी 0)). समय के हर अगले पल में टीचित्रण बिंदु चर के मूल्यों में परिवर्तन के अनुसार आगे बढ़ेगा एक्स(टी), यू(टी). अंक का सेट एम(एक्स(टी), वाई (टी)) चरण तल पर, जिसकी स्थिति समय के साथ चर बदलने की प्रक्रिया में सिस्टम की स्थिति से मेल खाती है एक्स (टी), वाई (टी)समीकरणों (4.1) के अनुसार कहा जाता है चरण प्रक्षेपवक्र।

चर के विभिन्न प्रारंभिक मूल्यों के लिए चरण प्रक्षेपवक्र का सेट सिस्टम का आसानी से दिखाई देने वाला "चित्र" देता है। इमारत चरण चित्रआपको चरों में परिवर्तन की प्रकृति के बारे में निष्कर्ष निकालने की अनुमति देता है एक्स, वाईसमीकरणों की मूल प्रणाली के विश्लेषणात्मक समाधानों को जाने बिना(4.1).

एक चरण चित्र को चित्रित करने के लिए, चरण विमान के प्रत्येक बिंदु पर सिस्टम प्रक्षेपवक्र के लिए दिशाओं के वेक्टर क्षेत्र का निर्माण करना आवश्यक है। एक वेतन वृद्धि निर्दिष्ट करकेडी टी> 0,हमें संबंधित वेतन वृद्धि मिलती है डी एक्सतथा डी आपभावों से:

डी एक्स = पी (एक्स, वाई)डी टी,

डी वाई = क्यू (एक्स, वाई)डी टी।

वेक्टर दिशा डाई/डीएक्सबिंदु पर ( एक्स, वाई) कार्यों के संकेत पर निर्भर करता है पी (एक्स, वाई), क्यू (एक्स, वाई)और एक तालिका द्वारा दिया जा सकता है:

पी (एक्स, वाई)> 0, क्यू (एक्स, वाई)> 0
पी (एक्स, वाई)<0,Q(x,y)<0
पी (एक्स, वाई)> 0, क्यू (एक्स, वाई)<0
पी (एक्स, वाई)<0,Q(x,y)>0

.(4.2)

इस समीकरण का हल वाई = वाई(एक्स, सी), या परोक्ष रूप से एफ(एक्स, वाई)= सी,कहाँ पे साथसमाकलन का स्थिरांक है, समीकरण के समाकल वक्रों का परिवार देता है (4.2) - चरण प्रक्षेपवक्रप्रणाली (4.1) विमान पर एक्स, वाई.

आइसोक्लाइन विधि

एक चरण चित्र बनाने के लिए, एक का उपयोग करता है आइसोक्लाइन विधि -चरण तल पर रेखाएँ खींची जाती हैं जो एक विशिष्ट कोण पर अभिन्न वक्रों को काटती हैं। समद्विबाहु समीकरण (4.2) से प्राप्त करना आसान है। चलो रखो

कहाँ पे लेकिन– एक निश्चित स्थिरांक। अर्थ लेकिनचरण प्रक्षेपवक्र के स्पर्शरेखा के ढलान के स्पर्शरेखा का प्रतिनिधित्व करता है और इससे मान ले सकता है -¥ करने के लिए + ¥ . के बजाय प्रतिस्थापन डाई/डीएक्समें (4.2) मात्रा लेकिनहम समद्विबाहु समीकरण प्राप्त करते हैं:

.(4.3)

समीकरण (4.3) विमान के प्रत्येक बिंदु पर संबंधित अभिन्न वक्र के लिए एकमात्र स्पर्शरेखा निर्धारित करता है, उस बिंदु को छोड़कर जहां पी (एक्स, वाई)= 0, क्यू (एक्स, वाई) = 0 , जिसमें स्पर्शरेखा की दिशा अनिश्चित हो जाती है, क्योंकि व्युत्पन्न का मान अनिश्चित हो जाता है:

.

यह बिंदु सभी समद्विबाहुओं का प्रतिच्छेदन बिंदु है - विशेष बिंदु।यह एक साथ चर के समय व्युत्पन्न गायब हो जाता है एक्सतथा आप.

इस प्रकार, एकवचन बिंदु पर, चर के परिवर्तन की दर शून्य के बराबर होती है। इसलिए, चरण प्रक्षेपवक्र (4.2) के अंतर समीकरणों का एकवचन बिंदु से मेल खाता है प्रणाली की स्थिर स्थिति(4.1), और इसके निर्देशांक चर के स्थिर मान हैं एक्स, वाई।

विशेष रुचि के हैं मुख्य समद्विबाहु:

डाई/डीएक्स = 0, पी(एक्स, वाई)=0 – क्षैतिज स्पर्शरेखा की समद्विबाहु और

डाई/डीएक्स=¥ , क्यू(एक्स, वाई)=0 – ऊर्ध्वाधर स्पर्शरेखाओं की समद्विबाहु रेखा।

मुख्य समद्विबाहुओं का निर्माण करके और उनके प्रतिच्छेदन का बिंदु ज्ञात करके (एक्स, वाई), जिसके निर्देशांक शर्तों को पूरा करते हैं:

इस प्रकार हम चरण तल के सभी समद्विबाहुओं के प्रतिच्छेदन बिंदु का पता लगाएंगे, जिस पर चरण प्रक्षेपवक्र के स्पर्शरेखा की दिशा अनिश्चित है। यह - एकवचन बिंदु, जो मेल खाती है प्रणाली की स्थिर स्थिति(चित्र। 4.2)।

सिस्टम (4.1) में उतने ही स्थिर राज्य हैं जितने कि चरण तल पर मुख्य समद्विबाहुओं के प्रतिच्छेदन बिंदु हैं।

प्रत्येक चरण प्रक्षेपवक्र एक ही अवस्था से गुजरने वाली एक गतिशील प्रणाली की गतियों के एक समूह से मेल खाती है और केवल समय संदर्भ की शुरुआत से एक दूसरे से भिन्न होती है।

यदि कॉची प्रमेय की शर्तें संतुष्ट हैं, तो अंतरिक्ष के प्रत्येक बिंदु के माध्यम से एक्स, वाई, टीएकल अभिन्न वक्र से होकर गुजरता है। वही सच है, स्वायत्तता के लिए धन्यवाद, चरण प्रक्षेपवक्र के लिए: एक अद्वितीय चरण प्रक्षेपवक्र चरण विमान के प्रत्येक बिंदु से होकर गुजरता है।

स्थिर राज्य स्थिरता

सिस्टम को संतुलन में रहने दें।

तब प्रतिनिधि बिंदु प्रणाली के एकवचन बिंदु पर स्थित होता है, जिसमें परिभाषा के अनुसार:

.

एक विलक्षण बिंदु स्थिर है या नहीं यह इस बात से निर्धारित होता है कि प्रतिनिधि बिंदु स्थिर अवस्था से एक छोटे से विचलन के साथ निकलता है या नहीं। जैसा कि दो समीकरणों की प्रणाली पर लागू होता है, भाषा में स्थिरता की परिभाषाइ, डीनिम्नलिखित नुसार।

संतुलन राज्य स्थिर है यदि संतुलन राज्य से विचलन के किसी दिए गए क्षेत्र के लिए (इ )क्षेत्र निर्दिष्ट किया जा सकता है डी (इ ), संतुलन की स्थिति के आसपास और संपत्ति होने के कारण कोई भी प्रक्षेपवक्र जो क्षेत्र के अंदर शुरू नहीं होता है डी , सीमा पर कभी नहीं पहुंचेंगे इ . (चित्र 4.4)

सिस्टम के एक बड़े वर्ग के लिए - रफ सिस्टम – जिस व्यवहार की प्रकृति समीकरणों के प्रकार में एक छोटे से परिवर्तन के साथ नहीं बदलती है, स्थिर अवस्था के आसपास के व्यवहार के प्रकार के बारे में जानकारी मूल नहीं, बल्कि सरलीकृत अध्ययन करके प्राप्त की जा सकती है। रेखीयकृतव्यवस्था।

रैखिक प्रणाली।

दो रैखिक समीकरणों की एक प्रणाली पर विचार करें:

.(4.4)

यहां ए बी सी डी- स्थिरांक, एक्स, वाई- कार्टेशियन चरण तल पर निर्देशांक करता है।

सामान्य समाधान फॉर्म में मांगा जाएगा:

.(4.5)

इन व्यंजकों को (4.4) में रखिए और से घटाइए इ मैं टी:

(4.6)

अज्ञात के साथ समीकरणों की बीजगणितीय प्रणाली (4.6) ए, बीएक गैर-शून्य समाधान केवल तभी होता है जब इसका निर्धारक, अज्ञात के गुणांक से बना होता है, शून्य के बराबर होता है:

.

इस सारणिक का विस्तार करते हुए, हमें निकाय का अभिलक्षणिक समीकरण प्राप्त होता है:

.(4.7)

इस समीकरण का हल सूचक का मान देता हैमैं 1,2 , जिसके तहत गैर-शून्य मान संभव हैं एतथा बीसमीकरण के हल (4.6)। ये मान हैं

.(4.8)

यदि मूलक व्यंजक ऋणात्मक है, तोमैं 1,2 जटिल संयुग्म संख्याएँ। मान लें कि समीकरण (4.7) के दोनों मूलों में अशून्य वास्तविक भाग हैं और कोई बहुमूल नहीं हैं। तब प्रणाली के सामान्य समाधान (4.4) को घातांक के साथ घातांक के एक रैखिक संयोजन के रूप में दर्शाया जा सकता हैमैं 1 , मैं 2 :

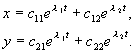(4.9)

चरण तल पर प्रणाली के संभावित प्रक्षेपवक्र की प्रकृति का विश्लेषण करने के लिए, हम उपयोग करते हैं रैखिक सजातीय समन्वय परिवर्तन,जो सिस्टम को लाएगा कानूनी फॉर्म:

,(4.10)

जो मूल प्रणाली (4.4) की तुलना में चरण तल पर अधिक सुविधाजनक प्रतिनिधित्व की अनुमति देता है। आइए नए निर्देशांक पेश करेंξ , η सूत्रों के अनुसार:

(4.1)

रैखिक बीजगणित के पाठ्यक्रम से ज्ञात होता है कि यदि वास्तविक भाग शून्य के बराबर नहीं हैंमैं 1 , मैं 2 मूल प्रणाली (4.4) को परिवर्तनों की सहायता से (4.11) हमेशा विहित रूप (4.10) में बदला जा सकता है और चरण तल पर इसके व्यवहार का अध्ययन किया जा सकता हैξ , η . उन विभिन्न मामलों पर विचार करें जो स्वयं को यहां प्रस्तुत कर सकते हैं।

जड़ें 1 , λ 2 - वैध और एक ही चिन्ह का

इस मामले में, परिवर्तन गुणांक वास्तविक हैं, हम वास्तविक विमान से आगे बढ़ते हैंएक्स, वाईवास्तविक विमान , के लिए। समीकरणों के दूसरे (4.10) को पहले से भाग देने पर, हम प्राप्त करते हैं:

.(4.12)

इस समीकरण को एकीकृत करते हुए, हम पाते हैं:

कहाँ .(4.13)

आइए हम λ . द्वारा समझने के लिए सहमत हों 2 एक बड़े मापांक के साथ विशेषता समीकरण की जड़, जो हमारे तर्क की व्यापकता का उल्लंघन नहीं करती है। फिर, चूंकि विचाराधीन मामले में जड़ें 1 , 2 - वैध और एक ही चिन्ह के,एक>1 , और हम परवलयिक प्रकार के अभिन्न वक्रों के साथ काम कर रहे हैं।

सभी अभिन्न वक्र (अक्ष को छोड़कर η , जो से मेल खाती है ) अक्ष के मूल पर स्पर्श करें ξ, जो समीकरण का एक अभिन्न वक्र भी है (4.11)। निर्देशांक की उत्पत्ति एक विलक्षण बिंदु है।

आइए अब हम चरण प्रक्षेप पथ के साथ प्रतिनिधि बिंदु की गति की दिशा का पता लगाएं। अगर 1, 2 ऋणात्मक हैं, तो, जैसा कि समीकरणों (4.10), |ξ|, |η| . से देखा जा सकता है समय के साथ कमी। प्रतिनिधित्व बिंदु मूल के करीब पहुंचता है, लेकिन उस तक कभी नहीं पहुंचता है। अन्यथा, यह कॉची के प्रमेय का खंडन करेगा, जिसमें कहा गया है कि केवल एक चरण प्रक्षेपवक्र चरण विमान के प्रत्येक बिंदु से होकर गुजरता है।

ऐसा एकवचन बिंदु जिसके माध्यम से अभिन्न वक्र गुजरते हैं, जैसे कि परवलय का परिवार मूल बिन्दु से होकर गुजरता है, इसे नोड कहते हैं (चित्र। 4.5)

. पर गाँठ-प्रकार संतुलन अवस्था 1, 2 < 0 लाइपुनोव के अनुसार स्थिर है, क्योंकि प्रतिनिधित्व बिंदु सभी अभिन्न वक्रों के साथ निर्देशांक की उत्पत्ति की ओर बढ़ता है। यह स्थिर गाँठ. अगर 1, 2 > 0, तब |ξ|, |η| समय के साथ बढ़ता है और प्रतिनिधि बिंदु मूल बिंदु से दूर चला जाता है। इस मामले में, एकवचन बिंदु– अस्थिर गाँठ .

चरण विमान पर एक्स, वाई समाकलन वक्रों के व्यवहार का सामान्य गुणात्मक स्वरूप बना रहेगा, लेकिन समाकलन वक्रों की स्पर्श रेखाएँ निर्देशांक अक्षों से मेल नहीं खाएँगी। इन स्पर्शरेखाओं के झुकाव का कोण गुणांकों के अनुपात द्वारा निर्धारित किया जाएगा α , β , γ , δ समीकरणों (4.11) में।

जड़ें 1 , λ 2 मान्य हैं और उनके अलग-अलग संकेत हैं।

से कनवर्ट करें COORDINATES एक्स, वाई निर्देशांक करने के लिए ξ, η फिर से असली। विहित चर के समीकरणों में फिर से रूप (4.10) होता है, लेकिन अब संकेत 1, 2 को अलग। चरण प्रक्षेपवक्र समीकरण का रूप है:

कहाँ ,(4.14)

समाकलन (4.14), हम पाते हैं

(4.15)

यह समीकरण अतिपरवलयिक प्रकार के वक्रों के परिवार को परिभाषित करता है, जहां दोनों अक्षों का समन्वय करते हैंस्पर्शोन्मुख हैं (at एक=1 हमारे पास समद्विबाहु अतिपरवलय का परिवार होगा). इस मामले में निर्देशांक अक्ष भी अभिन्न वक्र हैं– ये मूल से गुजरने वाले एकमात्र अभिन्न वक्र होंगे। प्रत्येकजिनमें से तीन चरण प्रक्षेपवक्र शामिल हैं: संतुलन की स्थिति (या संतुलन की स्थिति से दूर) और संतुलन की स्थिति से दो आंदोलनों की। अन्य सभी अभिन्न वक्र– अतिपरवलय हैं जो मूल बिन्दु से नहीं गुजरते हैं (चित्र। 4.6) इस एकवचन बिंदु को कहा जाता है "काठी ». पहाड़ की काठी के पास की स्तर रेखाएँ काठी के आसपास के चरण प्रक्षेपवक्र की तरह व्यवहार करती हैं।

आइए हम संतुलन की स्थिति के पास चरण प्रक्षेपवक्र के साथ प्रतिनिधि बिंदु की गति की प्रकृति पर विचार करें। चलो, उदाहरण के लिए, 1 >0 , 2<0 . तब प्रतिनिधि बिंदु अक्ष पर रखा गया ξ , मूल स्थान से दूर चला जाएगा, और अक्ष पर रखा जाएगा η – निर्देशांक की उत्पत्ति के लिए अनिश्चित काल तक पहुंचेंगे, सीमित समय में उस तक पहुंचे बिना. जहां भी प्रतिनिधित्व बिंदु प्रारंभिक क्षण में होता है (एकवचन बिंदु और स्पर्शोन्मुख बिंदुओं के अपवाद के साथ) η =0), यह अंततः संतुलन की स्थिति से दूर चला जाएगा, भले ही शुरुआत में यह एक अभिन्न वक्र के साथ एक विलक्षण बिंदु की ओर बढ़ता हो.

जाहिर सी बात है सैडल-प्रकार का एकवचन बिंदु हमेशा अस्थिर होता है . स्पर्शोन्मुख पर केवल विशेष रूप से चुनी गई प्रारंभिक शर्तों के तहतη =0 प्रणाली संतुलन की स्थिति में पहुंच जाएगी। हालांकि, यह इस दावे का खंडन नहीं करता है कि सिस्टम अस्थिर है। यदि आप गिनते हैं, कि चरण तल पर सिस्टम की सभी प्रारंभिक अवस्थाएँ समान रूप से संभावित हैं, तो ऐसी प्रारंभिक अवस्था की संभावना जो दिशा में गति से मेल खाती हैप्रति एकवचन बिंदु शून्य के बराबर है। इसलिए, कोई भी वास्तविक आंदोलन प्रणाली को संतुलन की स्थिति से हटा देगा।निर्देशांक पर वापस जा रहे हैंएक्स, वाई,हमें मूल के चारों ओर प्रक्षेप पथों की गति की प्रकृति का समान गुणात्मक चित्र मिलता है।

नोड और सैडल के माने गए मामलों के बीच की सीमा मामला हैजब विशिष्ट संकेतकों में से एक, उदाहरण के लिए λ 1 , गायब हो जाता है, जो तब होता है जब सिस्टम का निर्धारक- अभिव्यक्ति एडीबी = 0(देखें सूत्र 4.8 ). इस मामले में, समीकरणों (4.4) के दाहिने हाथ के गुणांक एक दूसरे के समानुपाती होते हैं:

और प्रणाली अपने संतुलन के लिए रेखा के सभी बिंदुओं को बताती है:

शेष अभिन्न वक्र ढलान के साथ समानांतर रेखाओं का एक परिवार है , जिसके साथ प्रतिनिधि बिंदु या तो संतुलन की स्थिति में पहुंचते हैं या इससे दूर चले जाते हैं, जो कि विशेषता समीकरण की दूसरी जड़ के संकेत पर निर्भर करता है 2 = ए + डी।(चित्र 4. 7 ) इस मामले में, संतुलन राज्य के निर्देशांक चर के प्रारंभिक मूल्य पर निर्भर करते हैं।

जड़ें 1 , λ 2 – जटिलसंयुग्म

इस मामले में, वास्तव मेंएक्सतथा आपहम करेंगे जटिल संयुग्म हैं ξ , η (4.10) . हालांकि, एक और मध्यवर्ती परिवर्तन की शुरुआत करके, इस मामले में वास्तविक रैखिक सजातीय परिवर्तन के विचार को कम करना भी संभव है। चलो रखो:

(4.16)

कहाँ पे ए, बी,तथा यू, वी – वास्तविक मूल्य। यह दिखाया जा सकता है कि से परिवर्तनएक्स, वाईप्रति यू, वी हमारी मान्यताओं के तहत, वास्तविक, रैखिक, एक गैर-शून्य निर्धारक के साथ सजातीय है। समीकरणों के कारण(4.10, 4.16) हमारे पास है :

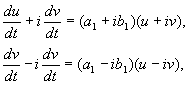
कहाँ पे

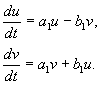(4.17)

समीकरण के दूसरे को पहले से विभाजित करना, हम पाते हैं:

जिसे एकीकृत करना आसान है, अगर हम ध्रुवीय समन्वय प्रणाली पर स्विच करते हैं (आर, φ ) . प्रतिस्थापन के बादहम कहाँ से प्राप्त करते हैं:

.(4.18)

इस प्रकार, चरण तल परआप, वोहम लघुगणकीय सर्पिलों के परिवार के साथ काम कर रहे हैं, जिनमें से प्रत्येक के पास हैमूल में स्पर्शोन्मुख बिंदु।एकवचन बिंदु जो सर्पिल के रूप वाले सभी अभिन्न वक्रों का स्पर्शोन्मुख बिंदु है, नेस्टेड फ्रेंड इनदोस्त, बुलाया केंद्र ( अंजीर.4.8 ) .

आइए हम चरण प्रक्षेपवक्र के साथ प्रतिनिधित्व बिंदु के आंदोलन की प्रकृति पर विचार करें। पहले समीकरण (4.17) को से गुणा करनातुम, और दूसरा to वीऔर जोड़ने पर, हमें मिलता है:

कहाँ पे

होने देना एक 1 < 0 (एक 1 = पुनःλ ) . प्रतिनिधित्व बिंदु तब एक सीमित समय में उस तक पहुंचे बिना लगातार मूल तक पहुंचता है। इसका मतलब है कि चरण प्रक्षेपवक्र घुमावदार सर्पिल हैं और नम दोलनों के अनुरूप हैंचर। यह - स्थिर फोकस .

स्थिर फोकस के मामले में, जैसा कि एक स्थिर नोड के मामले में होता है, न केवल लाइपुनोव की स्थिति संतुष्ट होती है, बल्कि अधिक कठोर आवश्यकता भी होती है। अर्थात्, किसी भी प्रारंभिक विचलन के लिए, सिस्टम अंततः संतुलन की स्थिति के लिए वांछित के रूप में वापस आ जाएगा। ऐसी स्थिरता, जिसमें प्रारंभिक विचलन न केवल बढ़ता है, बल्कि क्षय, शून्य की ओर प्रवृत्त होता है, कहलाता है पूर्ण स्थिरता .

यदि सूत्र में (4.18) एक 1 >0 , तो प्रतिनिधित्व बिंदु मूल से दूर चला जाता है, और हम इसके साथ काम कर रहे हैं अस्थिर फोकस . विमान से चलते समययू, वीचरण विमान के लिएएक्स, आपसर्पिल भी सर्पिल बने रहेंगे, लेकिन विकृत हो जाएंगे।

अब उस मामले पर विचार करें जबएक 1 =0 . विमान पर चरण प्रक्षेपवक्रआप, वोमंडलियां होंगी जो विमान मेंएक्स, वाईफिट दीर्घवृत्त:

इस प्रकार, अतएक 1=0 एक विशेष बिंदु के माध्यम सेएक्स = 0, वाई = 0 कोई अभिन्न वक्र गुजरता नहीं है। ऐसा पृथक एकवचन बिंदु, जिसके निकट समाकलन वक्र बंद वक्र होते हैं, विशेष रूप से, एक दूसरे में एम्बेडेड और एकवचन बिंदु को घेरने वाले दीर्घवृत्त, केंद्र कहलाते हैं।

इस प्रकार, विशेषता समीकरण (4.7) की जड़ों की प्रकृति के आधार पर छह प्रकार के संतुलन संभव हैं। विमान पर चरण प्रक्षेपवक्र का दृश्य एक्स, वाईइन छह मामलों के लिए अंजीर में दिखाया गया है। 4.9.

चावल। 4.9.रैखिक समीकरणों (4.4) की प्रणाली के लिए एक स्थिर राज्य के पड़ोस में चरण चित्रों के प्रकार।

पांच प्रकार की संतुलन अवस्थाएँ खुरदरी होती हैं, समीकरणों (4.4) के दाहिने हाथ में पर्याप्त रूप से छोटे बदलावों के साथ उनकी प्रकृति नहीं बदलती है। इस मामले में, परिवर्तन न केवल दाहिने हाथ में, बल्कि उनके पहले क्रम के डेरिवेटिव में भी छोटे होने चाहिए। संतुलन की छठी अवस्था - केंद्र - स्थूल नहीं है। समीकरणों के दाईं ओर के मापदंडों में छोटे बदलावों के साथ, यह स्थिर या अस्थिर फोकस में चला जाता है।

द्विभाजन आरेख

आइए हम संकेतन का परिचय दें:

. (4.11)

तब अभिलक्षणिक समीकरण को रूप में लिखा जा सकता है:

. (4.12)

आयताकार कार्टेशियन निर्देशांक वाले एक विमान पर विचार करें एस , डी और उस पर एक या दूसरे प्रकार के संतुलन राज्य के अनुरूप क्षेत्रों को चिह्नित करें, जो कि विशेषता समीकरण की जड़ों की प्रकृति से निर्धारित होता है

.(4.13)

संतुलन अवस्था के स्थायित्व की शर्त y . के ऋणात्मक वास्तविक भाग की उपस्थिति होगीमैं 1 और मैं 2 . इसके लिए एक आवश्यक और पर्याप्त शर्त है असमानताओं की पूर्तिएस > 0, डी > 0 . आरेख (4.15) पर, यह स्थिति पैरामीटर विमान की पहली तिमाही में स्थित बिंदुओं से मेल खाती है। एकवचन बिंदु फोकस होगा यदिमैं 1 और मैं 2 जटिल। यह स्थिति विमान के उन बिंदुओं से मेल खाती है जिनके लिए , वे। एक परवलय की दो शाखाओं के बीच के बिंदुएस 2 = 4 डी. अर्ध-अक्षीय बिंदु एस = 0, डी>0, केंद्र प्रकार के संतुलन राज्यों के अनुरूप है। वैसे ही,मैं 1 और मैं 2 - मान्य, लेकिन अलग-अलग संकेत, यानी। एक विलक्षण बिंदु एक सैडल होगा यदि डी<0, आदि। नतीजतन, हमें पैरामीटर विमान का एक विभाजन आरेख मिलता है एस, डी, विभिन्न प्रकार के संतुलन राज्यों के अनुरूप क्षेत्रों में।

चावल। 4.10.द्विभाजन आरेख

रैखिक समीकरणों की प्रणाली के लिए 4.4

यदि रैखिक प्रणाली के गुणांक ए बी सी डीकुछ पैरामीटर पर निर्भर करते हैं, तो जब यह पैरामीटर बदल जाता है, तो मान भी बदल जाएंगेएस , डी . सीमाओं से गुजरते समय, चरण चित्र की प्रकृति गुणात्मक रूप से बदल जाती है। इसलिए, ऐसी सीमाओं को द्विभाजन सीमाएँ कहा जाता है - सीमा के विपरीत किनारों पर, सिस्टम में दो टोपोलॉजिकल रूप से भिन्न चरण चित्र होते हैं और, तदनुसार, दो अलग-अलग प्रकार के व्यवहार होते हैं।

आरेख दिखाता है कि ऐसे परिवर्तन कैसे हो सकते हैं। यदि हम विशेष मामलों को बाहर करते हैं - निर्देशांक की उत्पत्ति - तो यह देखना आसान है कि सैडल y-अक्ष को पार करते समय स्थिर या अस्थिर नोड में जा सकता है। एक स्थिर नोड या तो एक सैडल या स्थिर फोकस में जा सकता है, और इसी तरह। ध्यान दें कि स्थिर नोड-स्थिर फोकस और अस्थिर नोड-अस्थिर फोकस संक्रमण द्विभाजित नहीं हैं, क्योंकि इस मामले में चरण स्थान की टोपोलॉजी नहीं बदलती है। हम व्याख्यान 6 में चरण स्थान और द्विभाजन संक्रमणों की टोपोलॉजी के बारे में अधिक विस्तार से बात करेंगे।

द्विभाजन संक्रमणों के तहत, एकवचन बिंदु की स्थिरता की प्रकृति बदल जाती है। उदाहरण के लिए, केंद्र के माध्यम से एक स्थिर फोकस अस्थिर फोकस में बदल सकता है। इस विभाजन को कहा जाता है एंड्रोनोव-हॉप का द्विभाजनइसका अध्ययन करने वाले वैज्ञानिकों के नाम से। गैर-रेखीय प्रणालियों में इस द्विभाजन के साथ, एक सीमा चक्र का जन्म होता है, और सिस्टम स्व-दोलन बन जाता है (व्याख्यान 8 देखें)।

उदाहरण। रैखिक रासायनिक प्रतिक्रियाओं की प्रणाली

पदार्थ एक्सबाहर से एक स्थिर दर से बहता है, पदार्थ Y में बदल जाता है और पदार्थ की सांद्रता के समानुपाती दर पर होता है यू, प्रतिक्रिया क्षेत्र से बाहर ले जाया जाता है। सभी प्रतिक्रियाएं पहले क्रम की हैं, बाहर से पदार्थ की आमद को छोड़कर, जिसमें शून्य क्रम है। प्रतिक्रिया योजना इस तरह दिखती है:

(4.14)

और समीकरणों की प्रणाली द्वारा वर्णित है:

(4.15)

हम दाहिने हाथ के पक्षों को शून्य के बराबर करके स्थिर सांद्रता प्राप्त करते हैं:

.(4.16)

सिस्टम के चरण चित्र पर विचार करें। आइए प्रणाली के दूसरे समीकरण (4.16) को पहले समीकरण से भाग दें। हम पाते हैं:

.(4.17)

समीकरण (4.17) चरण तल पर चरों के व्यवहार को निर्धारित करता है। आइए हम इस प्रणाली के एक चरण चित्र का निर्माण करें। सबसे पहले, हम चरण तल पर मुख्य समद्विबाहु रेखाएँ खींचते हैं। ऊर्ध्वाधर स्पर्शरेखा के समद्विबाहु का समीकरण:

क्षैतिज स्पर्शरेखा के समद्विबाहु के लिए समीकरण:

एकवचन बिंदु (स्थिर अवस्था) मुख्य समद्विबाहु रेखा के चौराहे पर स्थित है।

आइए अब हम यह निर्धारित करें कि निर्देशांक अक्ष किस कोण पर समाकलन वक्रों को प्रतिच्छेद करते हैं।

यदि एक एक्स = 0, फिर।

इस प्रकार, समाकलन वक्रों की स्पर्शरेखा की प्रवणता की स्पर्शरेखा वाई = वाई (एक्स), y-अक्ष को पार करना एक्स = 0, ऊपरी आधे तल में ऋणात्मक है (याद रखें कि चर एक्स, वाईएकाग्रता मान हैं, और इसलिए हम केवल चरण तल के ऊपरी दाएं चतुर्थांश में रुचि रखते हैं)। इस मामले में, स्पर्शरेखा के झुकाव के कोण के स्पर्शरेखा का मान मूल बिंदु से दूरी के साथ बढ़ता है।

अक्ष पर विचार करें वाई = 0. इस अक्ष के प्रतिच्छेदन पर, समाकल वक्रों का वर्णन समीकरण द्वारा किया जाता है

पर एब्सिस्सा अक्ष को पार करने वाले अभिन्न वक्रों की ढलान की स्पर्शरेखा धनात्मक होती है और शून्य से अनंत तक बढ़ती जाती है एक्स.

पर ।

फिर, एक और वृद्धि के साथ, ढलान की स्पर्शरेखा निरपेक्ष मान में घट जाती है, शेष ऋणात्मक और -1 पर तक जाती है एक्स ® ¥ . मुख्य समद्विबाहु रेखाओं और निर्देशांक अक्षों पर अभिन्न वक्रों की स्पर्शरेखाओं की दिशा जानने के बाद, चरण प्रक्षेपवक्र की पूरी तस्वीर बनाना आसान है।

लापुनोव विधि का उपयोग करके एकवचन बिंदु की स्थिरता की प्रकृति को स्थापित किया जाएगा। प्रणाली के विशेषता निर्धारक का रूप है:

.

सारणिक का विस्तार करते हुए, हम सिस्टम की विशेषता समीकरण प्राप्त करते हैं: , अर्थात। अभिलक्षणिक समीकरण के मूल दोनों ऋणात्मक हैं। इसलिए, सिस्टम की स्थिर स्थिति एक स्थिर नोड है। उसी समय, पदार्थ की एकाग्रता एक्सएक स्थिर अवस्था में हमेशा नीरस रूप से जाता है, पदार्थ Y की सांद्रता न्यूनतम या अधिकतम से गुजर सकती है। ऐसी प्रणाली में दोलन शासन असंभव है।