გაკვეთილის მიზნები:

უწყვეტი ფუნქციების თვისებებზე დაყრდნობით ინტერვალების განზოგადებული მეთოდის ეფექტური გამოყენების ცოდნის, უნარებისა და შესაძლებლობების ჩამოყალიბება;

ეკვივალენტური გარდაქმნებისკენ მიმავალი მოქმედებების ალგორითმის ფორმულირება;

ასწავლეთ საკუთარ თავს მისი გამოყენება უტოლობების ამოხსნისას;

განახორციელოს ცოდნის, უნარებისა და შესაძლებლობების ახალ პირობებში გადატანა.

საგანმანათლებლო: სისტემატიზაცია, კონსოლიდაცია, ცოდნის, უნარებისა და შესაძლებლობების განზოგადება.

საგანმანათლებლო: განათლება სრულფასოვანი თანმიმდევრული არგუმენტაციის, სიზუსტის, დამოუკიდებლობის საჭიროების შესახებ.

განმავითარებელი: მათემატიკური ლოგიკის განვითარება, აზროვნების მათემატიკური სტილის ფორმირება (მსჯელობის კურსის მკაფიო გაკვეთა), კოგნიტური ინტერესი.

1) შესავალი, გაკვეთილის მიზნისა და ამოცანების დასახვა - 2 წთ.

2) საშინაო დავალების შემოწმება - 2 წთ. (ფრონტალური მუშაობა, თვითკონტროლი).

3) უტოლობების ამოხსნის ეტაპების მათემატიკური დასაბუთება ინტერვალის მეთოდით - 4 წთ (მომზადებული მოსწავლის პასუხები).

4) უტოლობათა თვისებების გამეორება - 2 წთ.

5) ახალი სასწავლო მასალის ასიმილაციის (შესწავლისთვის) მომზადება საბაზისო ცოდნის გამეორებით და განახლებით - 5 წთ. (ფრონტალური მუშაობა, კითხვებზე პასუხები, პრობლემური სიტუაციები).

6) განზოგადებული ინტერვალის მეთოდი უტოლობათა ამოხსნის, საწყისი გაგება - 13 წთ. (უტოლობების კოლექტიური ამოხსნა ინტერვალების მეთოდით: დაფაზე და რვეულებში).

7) ინფორმაცია საშინაო დავალების შესახებ, მისი შესრულების ინსტრუქცია - 1 წთ.

8) ახალი ცოდნის კონსოლიდაცია - 15 წთ. (დამოუკიდებელი სამუშაო - ვარიანტი 1).

9) გაკვეთილის შეჯამება, რეფლექსია - 1 წთ.

1) შესავალი, გაკვეთილის მიზანი და ამოცანები. (მასწავლებლის ამბავი)

1) სკოლაში ინტერვალების მეთოდის უფრო ფართო გამოყენების აუცილებლობა ნაკარნახევია მათემატიკის სწავლების მთელი პროცესის იდეოლოგიით. საქმე იმაშია, რომ ფუნქციური ხაზი (ერთ-ერთი მთავარი მათემატიკის საფუძვლების შესწავლაში) იღებს ძლიერ ტექნოლოგიურ მხარდაჭერას. ინტერვალების მეთოდი ემყარება ფუნქციური დამოკიდებულების ისეთ მნიშვნელოვან მახასიათებლებს, როგორიცაა ფუნქციის ნულები, მისი მუდმივი ნიშნის ინტერვალები და ერთფეროვნება. შემდეგ უფრო ნათელი ხდება განტოლებებისა და უტოლობების ფუნქციური წარმოშობა, ასევე მათი ამოხსნის მეთოდები. უფრო ვიზუალური ხდება ფუნქციის უწყვეტობის კატეგორიები, მისი გრაფიკის ქცევა უსასრულო უწყვეტობის წერტილების სიახლოვეს, თეორემები ფესვზე, ნიშნის მუდმივობა, უკიდურესი წერტილები და მათი ტიპები. და ეს ყველაფერი ორგანულად არის დაკავშირებული ერთ ფუნქციურ მთლიანობაში.

მეორე მხრივ, ფასდაუდებელია გამოყენებული სასწავლო ობიექტების გეომეტრიზაციაც, ე.ი. ვიზუალურად, ფიგურალურად წარმოადგინოს ფუნქციონალური დამოკიდებულების ყველა გამოყენებული მათემატიკური ინსტრუმენტი.

ძირითადი პრინციპები, რომლებიც ემყარება ინტერვალის მეთოდს:

• ფუნქციური (განზოგადებული) მიდგომა;
• ფუნქციონალური თვისებების გეომეტრიზაციაზე დამოკიდებულება;
• კვლევის ვიზუალიზაცია.

ეს იწვევს მეთოდის შემდეგ უპირატესობას იმავე ტიპის ამოცანებში გამოყენებულ სხვა მეთოდებთან შედარებით: მიზნის მიღწევის სიმარტივე და სიჩქარე; ხილვადობა (და კონტროლის ან ორმაგი შემოწმების შესაძლებლობა); ეკონომია გამოთვლით რესურსებსა და დროს; მთელი სიტუაციის გაშუქების სიგანე, განზოგადებული აზროვნების და ანალიზის უნარების ჩამოყალიბება და განვითარება, ასევე ლოგიკური დასკვნების გამოტანის შესაბამისი უნარები.

2) საშინაო დავალების შემოწმება.(სლაიდი ნომერი 4)

3) მოთხრობა უტოლობების ამოხსნის ინტერვალების მეთოდის შესახებ. (პასუხობს მოსწავლე).

უტოლობების ამოხსნის მათემატიკური დასაბუთება ინტერვალების მეთოდით.

1) განვიხილოთ უტოლობა: (x-2)(x-3)>0. (სლაიდი ნომერი 5)

თქვენ შეგიძლიათ ამოხსნათ ასე: ორი ფაქტორის ნამრავლი (რაოდენობა) დადებითია, თუ და მხოლოდ იმ შემთხვევაში, თუ ორივე ფაქტორს აქვს ერთი და იგივე ნიშანი, ე.ი. უტოლობა უდრის ორი სისტემის კომბინაციას: (სლაიდი ნომერი 6)

პირველი სისტემიდან ვიღებთ x >3, მეორედან x< 2.

გამოსავალი არის ორი სისტემის ამონახსნების გაერთიანება.

პასუხი:

გრაფიკული მეთოდი (სლაიდი ნომერი 7)

კიდევ ერთი მეთოდია ინტერვალის მეთოდი(სლაიდი ნომერი 8).

მისი იდეა ასეთია.

რეალურ ხაზზე მონიშნეთ (x-2)(x-3) მრავალწევრის ნულები (ფესვები) მდგომი

უტოლობის მარცხენა მხარეს, ე.ი. ნომრები 2 და 3.

როდესაც x >3 (უფრო დიდი ფესვის მარჯვნივ), მაშინ (x-2)(x-3)>0, რადგან თითოეული ფაქტორი დადებითია.

თუ ღერძის გასწვრივ მოძრაობთ უარყოფითი მიმართულებით, მაშინ x=3 წერტილის გავლისას ფაქტორი (x-3) იცვლის ნიშანს. ნამრავლში (x-2) (x-3) გამოჩნდება ერთი უარყოფითი ფაქტორი, შედეგად (x-2) (x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

ახლა ადვილია უტოლობის ამოხსნის დაწერა:

დასკვნა: პროდუქტს შეუძლია შეცვალოს ნიშანი მხოლოდ x=2 და x=3 წერტილებში გავლისას

და, შესაბამისად, ინარჩუნებს ნიშანს თითოეულ მიღებულ ინტერვალზე.

ამ მარტივ მაგალითში ადვილია ინტერვალის მეთოდის იდეის გაგება, მაგრამ ის არ აჩვენებს რაიმე შესამჩნევ უპირატესობას.

ინტერვალის მეთოდის რაციონალურობა, მისი სიმძლავრე, განვიხილავთ შემდეგ მაგალითს (სლაიდი No9, 10,11, 12))

2) ამოხსენით უტოლობა (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) (x-10)>0.

ამ უტოლობის გადასაჭრელად სისტემების სიმრავლის გამოყენებით, უნდა გავითვალისწინოთ 512 სისტემის ნაკრები 10 უტოლობით თითოეულ სისტემაში.

მოდით გამოვიყენოთ ინტერვალის მეთოდი. ნამდვილ წრფეზე ვნიშნავთ მრავალწევრის ნულებს. x>10 ინტერვალზე პოლინომი დადებითი იქნება, რადგან თითოეული ფაქტორი დადებითია. ყოველი მომდევნო ფესვის გავლისას პოლინომი შეიცვლება ნიშანს, ვინაიდან პროდუქტში გამოჩნდება დამატებითი უარყოფითი ფაქტორი. ახლა ადვილია უტოლობის ამოხსნის დაწერა ნიშნების მონაცვლეობის გამოყენებით.

ინტერვალის მეთოდის უპირატესობები.

• მიზნის მიღწევის სიმარტივე და სიჩქარე;
• ხილვადობა (და კონტროლის ან ორმაგი შემოწმების შესაძლებლობა);
• გამოთვლითი სამუშაოს და დროის მნიშვნელოვანი შემცირება;
• მთელი სიტუაციის გაშუქების სიგანე;
• განზოგადებული აზროვნებისა და ანალიზის უნარ-ჩვევების ჩამოყალიბება და განვითარება, ასევე ლოგიკური დასკვნების გამოტანის შესაბამისი უნარები.

კომენტარი. ძალიან მოსახერხებელია უტოლობების ამოხსნა, რომელთა მარცხენა მხარე ფაქტორიზირებულია, ვინაიდან ნულების (ფესვების) პოვნა რთული არ არის.

ამოცანა: ამოხსენით უტოლობა ინტერვალის მეთოდით (x+3) 3 (x-4) 2 (x-5)>0(სლაიდი 13)

4) უტოლობების თვისებების გამეორება.

ა) კითხვა: რომელ უტოლობას ეწოდება ეკვივალენტი?

(ორ უტოლობას ექვივალენტური ეწოდება, თუ პირველი უტოლობის ნებისმიერი ამონახსნი არის მეორის ამოხსნა და, პირიქით, მეორის ნებისმიერი ამონახსნი არის პირველის ამონახსნი).

ან: ორ უტოლობას ეკვივალენტად ეძახიან, თუ მათი ამონახსნების სიმრავლეები ერთნაირია.

სლაიდი 14. უტოლობების თვისებების გამეორება.

სლაიდი 15. უპასუხე კითხვას და ახსენი.

უტოლობები თანაბარია?

1) 4x-5<0 и 4х<5

2) -2x+5>0 და 2x-5<0

3) -3x 2 +5x-7>0 და 3x 2 -5x+7<0

4) (x+1)>0 და (x 2 +5x+10)(x+1)>0

5) ზეპირი ფრონტალური მუშაობა ახალი სასწავლო მასალის ათვისებისთვის (შესწავლისთვის) მომზადებაში საბაზისო ცოდნის გამეორებითა და განახლებით.

სლაიდი 16. უწყვეტი ფუნქციის განსაზღვრა წერტილში.

სლაიდი 17. უწყვეტი ფუნქციების თვისება.

სლაიდი 18. იპოვეთ უწყვეტობის ხარვეზები.

სლაიდი 19. იპოვე შეცდომა.

სლაიდი 20. ამოხსენი უტოლობა სიტყვიერად,
სქემის გამოყენებით.

სლაიდი 21, 22. უტოლობის ჩანაცვლება ეკვივალენტური პირობით.

უტოლობის ამოხსნა

ეს უტოლობა უდრის f(x) პირობას < 0 ითვლიან

ამიტომ, ჩვენ უნდა ვიპოვოთ x-ის ყველა მნიშვნელობა, რომლისთვისაც არის პირობა f(x) < 0.

6) განზოგადებული ინტერვალის მეთოდი უტოლობათა ამოხსნის, საწყისი გაგება - 10 წთ. (უტოლობების კოლექტიური ამოხსნა ინტერვალების მეთოდით: დაფაზე და რვეულებში).

სლაიდი 23. ალგორითმი. უტოლობების ამოხსნის განზოგადებული მეთოდი.

უტოლობების ამოხსნა f(x)>0, f(x) > 0, f(x)<0, f(x)< 0 ინტერვალის მეთოდით. (სქემა)

სლაიდი 24 და 25. უტოლობის ამოხსნა ალგორითმით. (ალგორითმის ყველა პუნქტის კომენტარები).

სლაიდი 26. ამ უთანასწორობის ამოხსნის გრაფიკული ილუსტრაცია.

სლაიდი 27. ამოხსენით უტოლობა დაფაზე და რვეულებში .

სლაიდი 28. ამ უტოლობის ამოხსნის გრაფიკული ილუსტრაცია.

სლაიდი 29. ამოხსენით უტოლობა დაფაზე და რვეულებში

სლაიდი 30. ამ უტოლობის ამოხსნის გრაფიკული ილუსტრაცია.

სლაიდი 31, 32. ამოიღეთ უტოლობა სიტყვიერად, სურათის მიხედვით

7) ინფორმაცია საშინაო დავალების შესახებ.(გადაწყვეტა ინტერვალის მეთოდით ვარიანტი ნომერი 2)

8) ახალი ცოდნის კონსოლიდაცია (დამოუკიდებელი სამუშაო, ვარიანტი No1).

9) გაკვეთილის შეჯამება, თვითკონტროლი მზა გადაწყვეტილებებზე (სლაიდები 33, 34, 35), ინტერვალების განზოგადებული მეთოდის ალგორითმის გამეორება და მისი გამოყენება.

10) მასალის ათვისების ანალიზი და მოსწავლეთა ინტერესი თემით.ეს მეთოდი უნივერსალურია ნებისმიერი უტოლობის გადაჭრისას, მათ შორის რაციონალური, მოდულური, ირაციონალური, ექსპონენციალური, ლოგარითმული, რადგან ინტერვალის მეთოდი ამცირებს უტოლობების ამოხსნას განტოლებების ამოხსნამდე, ფუნქციის დომენისა და მნიშვნელობის პოვნა წერტილში არ იწვევს სირთულეებს. მაგრამ მე მომიწია უტოლობების მაგალითების მოყვანა, სადაც ამ მეთოდის გამოყენება არ არის გამართლებული, სადაც უფრო რაციონალურია უტოლობების ამოხსნის სხვა მეთოდების გამოყენება.

პრეზენტაცია „განგრძობითობის გამოყენება უტოლობების ამოხსნაში“. (35 სლაიდი)

განმარტება 4. ფუნქციას სეგმენტზე უწყვეტი ეწოდება, თუ ის უწყვეტია ამ სეგმენტის ყველა წერტილში (a წერტილში ის მარჯვნიდან უწყვეტია, ე.ი. და b წერტილში მარცხნივ უწყვეტია, ე.ი.).

ყველა ძირითადი ელემენტარული ფუნქცია უწყვეტია მათი განმარტების სფეროში.

უწყვეტი ფუნქციების თვისებები სეგმენტზე:

• 1) თუ ფუნქცია უწყვეტია სეგმენტზე, მაშინ ის შემოსაზღვრულია ამ სეგმენტზე (ვაიერშტრასის პირველი თეორემა).
• 2) თუ ფუნქცია უწყვეტია სეგმენტზე, მაშინ ამ სეგმენტზე ის აღწევს თავის მინიმალურ მნიშვნელობას და მაქსიმალურ მნიშვნელობას (ვაიერშტრასის მეორე თეორემა) (იხ. ნახ. 2).
• 3) თუ ფუნქცია უწყვეტია სეგმენტზე და იღებს სხვადასხვა ნიშნის მნიშვნელობებს მის ბოლოებში, მაშინ სეგმენტის შიგნით არის მინიმუმ ერთი წერტილი ისეთი (ბოლცანო-კოშის თეორემა).

ფუნქციების წყვეტის წერტილები და მათი კლასიფიკაცია

ფუნქციის უწყვეტობის წერტილის სეგმენტი

წერტილებს, რომლებზეც უწყვეტობის პირობა არ არის დაკმაყოფილებული, ამ ფუნქციის შეწყვეტის წერტილებს უწოდებენ. თუ არის ფუნქციის შეწყვეტის წერტილი, მაშინ მასში არ არის დაკმაყოფილებული 1, 2 განმარტებებში მითითებული ფუნქციის უწყვეტობის სამი პირობა მაინც, კერძოდ:

1) ფუნქცია განისაზღვრება წერტილის სიახლოვეს, მაგრამ არ არის განსაზღვრული თავად წერტილში. ასე რომ, მაგალითში 2 ა) განხილულ ფუნქციას აქვს შესვენება წერტილში, რადგან ის ამ ეტაპზე არ არის განსაზღვრული.

2) ფუნქცია განსაზღვრულია წერტილში და მის სამეზობლოში, არის ცალმხრივი საზღვრები და, მაგრამ ისინი ერთმანეთის ტოლი არ არიან: . მაგალითად, ფუნქცია 2 ბ) მაგალითიდან არის განსაზღვრული წერტილისა და მის სამეზობლოში, მაგრამ, ვინაიდან, a.

3) ფუნქცია განსაზღვრულია წერტილში და მის შემოგარენში, არის ცალმხრივი საზღვრები და, ისინი ერთმანეთის ტოლია, მაგრამ არ უდრის ფუნქციის მნიშვნელობას წერტილში: . მაგალითად, ფუნქცია. აქ არის შესვენების წერტილი: ამ დროს ფუნქცია არის განსაზღვრული, არის ცალმხრივი საზღვრები და ერთმანეთის ტოლი, მაგრამ, ე.ი.

ფუნქციის წყვეტის წერტილები კლასიფიცირდება შემდეგნაირად.

განმარტება 5. წერტილს ეწოდება პირველი სახის ფუნქციის უწყვეტობის წერტილი, თუ არსებობს სასრული საზღვრები და ამ წერტილში, მაგრამ ისინი არ არიან ერთმანეთის ტოლები: . რაოდენობას მაშინ უწოდებენ ფუნქციის ნახტომს წერტილში.

განმარტება 6 . წერტილს ეწოდება ფუნქციის მოხსნადი შეწყვეტის წერტილი, თუ ამ წერტილში არის სასრული ზღვრები და, ისინი ერთმანეთის ტოლია: , მაგრამ თავად ფუნქცია არ არის განსაზღვრული წერტილში, ან არის განსაზღვრული, მაგრამ.

განმარტება 7. წერტილს ეწოდება მეორე სახის ფუნქციის უწყვეტობის წერტილი, თუ ამ მომენტში ცალმხრივი ზღვრებიდან (ან) მაინც არ არსებობს ან უდრის უსასრულობას.

მაგალითი 3. იპოვეთ შემდეგი ფუნქციების წყვეტის წერტილები და დაადგინეთ მათი ტიპი: ა) ბ)

გადაწყვეტილება. ა) ფუნქცია განსაზღვრულია და უწყვეტია u ინტერვალებზე, ვინაიდან თითოეულ ამ ინტერვალზე იგი მოცემულია უწყვეტი ელემენტარული ფუნქციებით. მაშასადამე, მოცემული ფუნქციის წყვეტის წერტილები შეიძლება იყოს მხოლოდ ის წერტილები, რომლებზეც ფუნქცია ცვლის თავის ანალიტიკურ მინიჭებას, ე.ი. წერტილები ი. ვიპოვოთ ფუნქციის ცალმხრივი საზღვრები წერტილში:

ვინაიდან ცალმხრივი საზღვრები არსებობს და სასრულია, მაგრამ ერთმანეთის ტოლი არ არის, წერტილი არის პირველი ტიპის უწყვეტობის წერტილი. ფუნქციის ნახტომი:

ერთი წერტილისთვის ვპოულობთ.

ფუნქციის უწყვეტობა ინტერვალზე

პარამეტრის სახელი	მნიშვნელობა
სტატიის თემა:	ფუნქციის უწყვეტობა ინტერვალზე
რუბრიკა (თემატური კატეგორია)	მათემატიკა

განმარტება.ფუნქციას ეწოდება უწყვეტი ინტერვალზე, თუ ის უწყვეტია ამ ინტერვალის ყველა წერტილში.

თუ ფუნქცია განსაზღვრულია X=ადა სადაც ვ(X) = ვ(ა),

მერე ამას ამბობენ ვ(X) წერტილში და უწყვეტი მარჯვნივ. ანალოგიურად, თუ ვ(X) = ვ(ბ), მაშინ ჩვენ ამას ვამბობთ წერტილში ბამ ფუნქციას დარჩა უწყვეტი.

განმარტება.ფუნქციას ჩვეულებრივ უწოდებენ უწყვეტს სეგმენტზე [ ა, ბ], თუ ის უწყვეტია მის თითოეულ წერტილში (წერტილში აუწყვეტი მარჯვნივ, წერტილში ბუწყვეტია მარცხნივ).

უმაღლესი ღირებულებაფუნქციები ზე = ვ(x) სეგმენტზე [ ა, ბ ვ(x 1) რომ ვ(x) £ ვ(x 1) ყველასთვის X Î [ ა, ბ].

ყველაზე დაბალი ღირებულებაფუნქციები ზე = ვ(x) სეგმენტზე [ ა, ბ] ჩვეულებრივად არის დავარქვათ ასეთი მისი ღირებულება ვ(x 2) რომ ვ(x) ³ ვ(x 2) ყველასთვის X Î [ ა, ბ].

ფუნქციებს, რომლებიც უწყვეტია ინტერვალზე, აქვთ მთელი რიგი მნიშვნელოვანი თვისებები, რომლებიც გამოიხატება შემდეგი თეორემებით.

თეორემა 3.3.1.უწყვეტი ფუნქცია სეგმენტზე [ ა, ბ], აღწევს მასზე მინიმალურ მნიშვნელობას მდა ყველაზე დიდი ღირებულება მ, ანუ არის ასეთი პუნქტები x 1 და xამ სეგმენტის 2, რომელიც ვ(x 1) = მ, ვ(x 2) = მ.

თეორემას აქვს მარტივი გეომეტრიული მნიშვნელობა (იხ. სურ. 2).

თეორემა 3.3.2.ფუნქციის შემთხვევაში ზე = ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ] და იღებს არათანაბარ მნიშვნელობებს მის ბოლოებში ვ(ა) = A, ვ(ბ) = B, A ¹ B, მაშინ როგორიც არ უნდა იყოს რიცხვი C A-სა და B-ს შორის, არის წერტილი თან Î [ ა, ბ] ისეთივე როგორც ვ(თან) = C.

თეორემის გეომეტრიული მნიშვნელობა ილუსტრირებულია ნახ.3-ში. ნებისმიერი სწორი ხაზი ზე= C, სადაც A< C < B (или A >C > B), კვეთს ფუნქციის გრაფიკს ზე = ვ(x).

შედეგი.თუ ფუნქცია უწყვეტია სეგმენტზე და იღებს სხვადასხვა ნიშნის მნიშვნელობებს მის ბოლოებზე, მაშინ ამ სეგმენტზე არის მინიმუმ ერთი წერტილი, სადაც ფუნქცია ქრება.

შედეგის გეომეტრიული მნიშვნელობა ილუსტრირებულია ნახ.4-ში.

კითხვები თვითკონტროლისთვის

1. რა ფუნქციას ეწოდება უწყვეტი წერტილი?

2. მიეცით კიდევ ერთი ეკვივალენტური განმარტება ფუნქციისა და არგუმენტების გაზრდის გზით.

3. რა შეიძლება ითქვას ორი უწყვეტი ფუნქციის ჯამს, განსხვავებას, ნამრავლსა და კოეფიციენტზე?

4. არგუმენტის რა მნიშვნელობებისთვის არის მთელი რაციონალური და წილად-რაციონალური ფუნქციები უწყვეტი?

5. როდის არის კომპლექსური ფუნქცია წერტილში უწყვეტი?

6. რას უწოდებენ ჩვეულებრივ ფუნქციების წყვეტის წერტილს?

7. რომელ წერტილებს უწოდებენ პირველი სახის შეწყვეტის წერტილებს?

8. რა მნიშვნელობას უწოდებენ ჩვეულებრივ ფუნქციის ნახტომს?

9. განმარტეთ „მოხსნადი წყვეტის წერტილის“ ცნებები. მიეცით მაგალითები.

10. რა წერტილებს უწოდებენ მეორე სახის შეწყვეტის წერტილებს? მიეცით მაგალითები.

11. განმარტეთ ცნებები: „„განგრძობა ინტერვალზე““, „განგრძობა მარჯვნივ““, „განგრძობა მარცხნივ“, „განგრძობა სეგმენტზე““.

12. განსაზღვრეთ ფუნქციების უდიდესი და უმცირესი მნიშვნელობები.

13. ჩამოაყალიბეთ თეორემა უწყვეტობის ურთიერთობის შესახებ ფუნქციის უდიდესი და უმცირესი მნიშვნელობების მქონე სეგმენტზე. ახსენი სურათით.

14. ჩამოაყალიბეთ თეორემა სეგმენტზე ფუნქციების უწყვეტობისა და ფუნქციის სიდიდეების სეგმენტის კავშირის შესახებ. აჩვენეთ მისი გეომეტრიული მნიშვნელობა ფიგურაში.

15. მიეცით ზემოაღნიშნული თეორემის შედეგი და მისი გეომეტრიული ინტერპრეტაცია.

ლექცია №4

ლექციის თემა: ფუნქციის წარმოებული

ლექციის გეგმა:წარმოებულის ცნება, მისი გეომეტრიული და ფიზიკური მნიშვნელობა. დიფერენცირების ძირითადი წესები. რთული ფუნქციის წარმოებული. წარმოებულის ზოგიერთი გამოყენება.

4.1. წარმოებულის ცნება, მისი გეომეტრიული და ფიზიკური მნიშვნელობა

განიხილეთ ფუნქცია ზე = ვ(x) მითითებულია ინტერვალში] ა, ბ[. დაე იყოს XÎ ] ა, ბ[და X Î ] ა, ბ[, შემდეგ ფუნქცია იზრდება წერტილში X 0 გამოიხატება ფორმულით D ზე = ვ(x 0+D X) – ვ(x 0).

განმარტება. y ფუნქციის წარმოებული = ვ(x) წერტილში X 0-ს ჩვეულებრივ უწოდებენ ამ ფუნქციის გაზრდის შეფარდების ზღვარს არგუმენტის ზრდასთან, როდესაც ეს უკანასკნელი ნულისკენ მიისწრაფვის:

ვ(x 0) = ან y"(x 0) =.

წარმოებულის გეომეტრიული მნიშვნელობა: ამ ფუნქციის წარმოებული წერტილში უდრის Ox ღერძს შორის კუთხის ტანგენტს და შესაბამის წერტილში ამ ფუნქციის გრაფიკის ტანგენტს (იხ. სურ. 1):

ვ"(x 0) = თან ა.

განმარტება. თუ ფუნქცია ვ(x) განისაზღვრება ინტერვალზე [ ა, ბ], არის უწყვეტი ინტერვალის ყველა წერტილში ( ა, ბ), წერტილში აუწყვეტი მარჯვნივ, წერტილში ბარის უწყვეტი მარცხნივ, მაშინ ვამბობთ, რომ ფუნქცია ვ(x) უწყვეტი სეგმენტზე [ა, ბ].

სხვა სიტყვებით რომ ვთქვათ, ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ] თუ დაკმაყოფილებულია სამი პირობა:

1) "x 0 Î( ა, ბ): ვ(x) = ვ(x 0);

2) ვ(x) = ვ(ა);

3) ვ(x) = ვ(ბ).

ინტერვალზე უწყვეტი ფუნქციებისთვის განვიხილავთ რამდენიმე თვისებას, რომელსაც ჩამოვაყალიბებთ შემდეგი თეორემების სახით დამტკიცების გარეშე.

თეორემა 1. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], შემდეგ ის აღწევს თავის უმცირეს და უდიდეს მნიშვნელობას ამ სეგმენტზე.

ეს თეორემა აცხადებს (ნახ. 1.15), რომ სეგმენტზე [ ა, ბ] არის ასეთი წერტილი x 1 რომ ვ(x 1) £ ვ(x) ნებისმიერისთვის x[ ა, ბ] და რომ არსებობს წერტილი x 2 (x 2 О[ ა, ბ]) ისეთივე როგორც " xÎ[ ა, ბ] (ვ(x 2) ³ ვ(x)).

მნიშვნელობა ვ(x 1) არის ყველაზე დიდი მოცემული ფუნქციისთვის [ ა, ბ], ა ვ(x 2) - ყველაზე პატარა. აღნიშნე: ვ(x 1) = მ, ვ(x 2) =მ. ვინაიდან ამისთვის ვ(x) მოქმედებს შემდეგი უტოლობა: xÎ[ ა, ბ] მ£ ვ(x) £ მ, შემდეგ მივიღებთ შემდეგ დასკვნას თეორემა 1-დან.

შედეგი. თუ ფუნქცია ვ(x) არის უწყვეტი სეგმენტზე, შემდეგ შემოსაზღვრულია ამ სეგმენტზე.

თეორემა 2. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ] და იღებს სხვადასხვა ნიშნების მნიშვნელობებს სეგმენტის ბოლოებში, მაშინ არის ასეთი შიდა წერტილი x 0 სეგმენტი [ ა, ბ], რომელშიც ფუნქცია გადადის 0-ზე, ე.ი. $ x 0 Î ( ა, ბ) (ვ(x 0) = 0).

ეს თეორემა ამბობს, რომ ფუნქციის გრაფიკი y=f(x), უწყვეტი სეგმენტზე [ ა, ბ], კვეთს ღერძს ოქსიერთხელ მაინც თუ ღირებულებები ვ(ა) და ვ(ბ) აქვს საპირისპირო ნიშნები. ასე რომ, (ნახ. 1.16) ვ(ა) > 0, ვ(ბ) < 0 и функция ვ(x) ქრება წერტილებში x 1 , x 2 , x 3 .

თეორემა 3. დაუშვით ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], ვ(ა) = ა, ვ(ბ) = ბდა ა¹ ბ. (სურ. 1.17). შემდეგ ნებისმიერი ნომრისთვის C, დადებული რიცხვებს შორის ადა ბ, არის ასეთი შინაგანი წერტილი x 0 სეგმენტი [ ა, ბ], რა ვ(x 0) = C.

შედეგი. თუ ფუნქცია ვ(x) არის უწყვეტი ინტერვალზე [ ა, ბ], მ- ყველაზე პატარა ღირებულება ვ(x), მ- ფუნქციის უდიდესი მნიშვნელობა ვ(x) სეგმენტზე [ ა, ბ], მაშინ ფუნქცია იღებს (ერთხელ მაინც) ნებისმიერ მნიშვნელობას მშორის მდა მდა, შესაბამისად, სეგმენტი [ მ, მ] არის ფუნქციის ყველა მნიშვნელობის ნაკრები ვ(x) სეგმენტზე [ ა, ბ].

გაითვალისწინეთ, რომ თუ ფუნქცია უწყვეტია ინტერვალზე ( ა, ბ) ან აქვს სეგმენტზე [ ა, ბ] შეწყვეტის წერტილის, მაშინ 1, 2, 3 თეორემები წყვეტენ ჭეშმარიტებას ასეთი ფუნქციისთვის.

დასასრულს, განიხილეთ თეორემა შებრუნებული ფუნქციის არსებობის შესახებ.

შეგახსენებთ, რომ ინტერვალი არის სეგმენტი, ინტერვალი, ან სასრული ან უსასრულო ნახევარინტერვალი.

თეორემა 4. დაე იყოს ვ(x) არის უწყვეტი ინტერვალზე X, იზრდება (ან მცირდება) მიერ Xდა აქვს მნიშვნელობების სპექტრი ი. შემდეგ ფუნქციისთვის y=f(x) არის შებრუნებული ფუნქცია x= ჯ(წ) განსაზღვრულია ინტერვალზე ი, უწყვეტი და მზარდი (ან კლებადი) on იმრავალი მნიშვნელობით X.

კომენტარი. დაუშვით ფუნქცია x= ჯ(წ) არის შებრუნებული ფუნქციისთვის ვ(x). ვინაიდან არგუმენტი ჩვეულებრივ აღინიშნება x, და ფუნქცია მეშვეობით წ, შემდეგ შებრუნებულ ფუნქციას ვწერთ როგორც y=ჯ(x).

მაგალითი 1. ფუნქცია y=x 2 (სურ. 1.8, ა) კომპლექტზე X= თუ ის უწყვეტია ამ სეგმენტის ყველა შიდა წერტილში და მის ბოლოებზე, ე.ი. წერტილებში ადა ბ, უწყვეტია მარჯვნივ და მარცხნივ, შესაბამისად.

თეორემა 1.უწყვეტი ფუნქცია სეგმენტზე [ ა, ბ], ამ სეგმენტის ერთ წერტილში მაინც იღებს უდიდეს მნიშვნელობას და ერთ წერტილში მაინც - უმცირესს.

თეორემა ამბობს, რომ თუ ფუნქცია y = f(x)უწყვეტი სეგმენტზე [ ა, ბ], მაშინ არის მინიმუმ ერთი წერტილი x 1 Î [ ა, ბ] ისეთი, რომ ფუნქციის მნიშვნელობა f(x)ამ მომენტში იქნება ყველაზე დიდი მისი ყველა მნიშვნელობიდან ამ სეგმენტზე: f(x1) ≥ f(x). ანალოგიურად, არსებობს ასეთი წერტილი x2, რომელშიც ფუნქციის მნიშვნელობა იქნება სეგმენტის ყველა მნიშვნელობიდან ყველაზე პატარა: f(x 1) ≤ f(x).

ნათელია, რომ შეიძლება იყოს რამდენიმე ასეთი წერტილი, მაგალითად, ფიგურა აჩვენებს, რომ ფუნქცია f(x)იღებს უმცირეს მნიშვნელობას ორ წერტილში x2და x 2 ".

კომენტარი. თეორემის განცხადება შეიძლება მცდარი გახდეს, თუ გავითვალისწინებთ ფუნქციის მნიშვნელობას ინტერვალზე ( ა, ბ). მართლაც, თუ გავითვალისწინებთ ფუნქციას y=x(0, 2), შემდეგ ის უწყვეტია ამ ინტერვალზე, მაგრამ არ აღწევს მასში მაქსიმალურ ან მინიმალურ მნიშვნელობებს: ის აღწევს ამ მნიშვნელობებს ინტერვალის ბოლოებში, მაგრამ ბოლოები არ ეკუთვნის ჩვენს რეგიონი.

ასევე, თეორემა წყვეტს ჭეშმარიტებას უწყვეტი ფუნქციებისთვის. მიეცი მაგალითი.

შედეგი.თუ ფუნქცია f(x)უწყვეტი [ ა, ბ], მაშინ ის შემოიფარგლება ამ სეგმენტზე.

თეორემა 2.დაუშვით ფუნქცია y = f(x)უწყვეტი ინტერვალით [ ა, ბ] და იღებს სხვადასხვა ნიშნის მნიშვნელობებს ამ სეგმენტის ბოლოებში, მაშინ არის მინიმუმ ერთი წერტილი სეგმენტის შიგნით x=C, სადაც ფუნქცია ქრება: f(C)= 0, სადაც a< C< b

ამ თეორემას აქვს მარტივი გეომეტრიული მნიშვნელობა: თუ უწყვეტი ფუნქციის გრაფიკის წერტილები y = f(x)სეგმენტის ბოლოების შესაბამისი [ ა, ბ] დაწექი ღერძის მოპირდაპირე მხარეს ოქსი, მაშინ ეს გრაფიკი სეგმენტის ერთ წერტილში მაინც კვეთს ღერძს ოქსი. უწყვეტ ფუნქციებს შეიძლება არ ჰქონდეს ეს თვისება.

ეს თეორემა აღიარებს შემდეგ განზოგადებას.

თეორემა 3 (თეორემა შუალედური სიდიდეების შესახებ).დაუშვით ფუნქცია y = f(x)უწყვეტი ინტერვალით [ ა, ბ] და f(a) = A, f(b) = B. შემდეგ ნებისმიერი ნომრისთვის Cშორის ადა ბამ სეგმენტის შიგნით არის ასეთი წერტილი CÎ [ ა, ბ], რა f(c) = C.

ეს თეორემა გეომეტრიულად აშკარაა. განვიხილოთ ფუნქციის გრაფიკი y = f(x). დაე იყოს f(a) = A, f(b) = B. შემდეგ ნებისმიერი ხაზი y=C, სად C- ნებისმიერი რიცხვი შორის ადა ბ, ერთ წერტილში მაინც კვეთს ფუნქციის გრაფიკს. გადაკვეთის წერტილის აბსცისა იქნება ეს მნიშვნელობა x=C, რომელიც f(c) = C.

ამრიგად, უწყვეტი ფუნქცია, რომელიც გადადის მისი ერთი მნიშვნელობიდან მეორეზე, აუცილებლად გადის ყველა შუალედურ მნიშვნელობას. Კერძოდ:

შედეგი.თუ ფუნქცია y = f(x)არის უწყვეტი რაღაც ინტერვალზე და იღებს უდიდეს და უმცირეს მნიშვნელობებს, შემდეგ ამ ინტერვალზე იღებს, ერთხელ მაინც, ნებისმიერ მნიშვნელობას მის უმცირეს და უდიდეს მნიშვნელობებს შორის.

წარმოებული და მისი აპლიკაციები. წარმოებული განმარტება

მოდით რაიმე ფუნქცია y=f(x),განსაზღვრულია გარკვეული ინტერვალით. თითოეული არგუმენტის მნიშვნელობისთვის xამ ინტერვალიდან ფუნქცია y=f(x)აქვს გარკვეული მნიშვნელობა.

განვიხილოთ ორი არგუმენტის მნიშვნელობა: საწყისი x 0 და ახალი x.

განსხვავება x–x 0 ეწოდება x არგუმენტის ზრდაწერტილში x 0 და აღინიშნება Δx. ამრიგად, ∆x = x – x 0 (არგუმენტის ზრდა შეიძლება იყოს დადებითი ან უარყოფითი). ამ თანასწორობიდან გამომდინარეობს, რომ x=x 0 +Δx, ე.ი. ცვლადის საწყისმა მნიშვნელობამ მიიღო გარკვეული ზრდა. მაშინ, თუ წერტილში x 0 ფუნქციის მნიშვნელობა იყო f(x 0 ), შემდეგ ახალ წერტილში xფუნქცია მიიღებს მნიშვნელობას f(x) = f(x 0 +∆x).

განსხვავება წ-წ 0 = f(x) – f(x 0 ) დაურეკა ფუნქციის გაზრდა y = f(x)წერტილში x 0 და აღინიშნება სიმბოლოთი Δy. ამრიგად,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

როგორც წესი, არგუმენტის საწყისი მნიშვნელობა x 0 ითვლება ფიქსირებულ და ახალ მნიშვნელობად x- ცვლადი. მერე წ 0 = f(x 0 ) მუდმივი გამოდის და y = f(x)- ცვლადი. ნამატები Δyდა Δxასევე იქნება ცვლადები და ფორმულა (1) აჩვენებს, რომ Dyარის ცვლადის ფუნქცია Δx.

შეადგინეთ ფუნქციის ზრდის შეფარდება არგუმენტის ზრდასთან

მოდი ვიპოვოთ ამ ურთიერთობის ზღვარი აქ Δx→0. თუ ეს ზღვარი არსებობს, მაშინ მას ამ ფუნქციის წარმოებული ეწოდება. f(x)წერტილში x 0 და აღნიშნეთ ვ "(x 0). Ისე,

წარმოებულიამ ფუნქციას y = f(x)წერტილში x 0 ეწოდება Δ ფუნქციის ნამატის შეფარდების ზღვარს წΔ არგუმენტის ნამატამდე xროდესაც ეს უკანასკნელი თვითნებურად იხრება ნულისკენ.

გაითვალისწინეთ, რომ ერთი და იგივე ფუნქციისთვის წარმოებული სხვადასხვა წერტილში xშეუძლია მიიღოს სხვადასხვა ღირებულებები, ე.ი. წარმოებული შეიძლება ჩაითვალოს არგუმენტის ფუნქციად x. ეს ფუნქცია აღინიშნება ვ "(x)

წარმოებული აღინიშნება სიმბოლოებით ვ "(x), y", . წარმოებულის სპეციფიკური მნიშვნელობა ზე x = aაღინიშნა ვ "(ა) ან წ "| x=a.

ფუნქციის წარმოებულის პოვნის ოპერაცია f(x)ეწოდება ამ ფუნქციის დიფერენციაცია.

წარმოებულის განსაზღვრებით პირდაპირ მოსაძებნად, შეგიძლიათ გამოიყენოთ შემდეგი ემპირიული წესი:

მაგალითები.

წარმოებულის მექანიკური მნიშვნელობა

ფიზიკიდან ცნობილია, რომ ერთგვაროვანი მოძრაობის კანონს აქვს ფორმა s = v t, სად ს- გზა გაიარა დროის მომენტამდე ტ, ვარის ერთგვაროვანი მოძრაობის სიჩქარე.

თუმცა, მას შემდეგ ბუნებაში მიმდინარე მოძრაობების უმეტესობა არათანაბარია, შემდეგ, ზოგადად, სიჩქარე და, შესაბამისად, მანძილი სდროზე იქნება დამოკიდებული ტ, ე.ი. დროის ფუნქცია იქნება.

ასე რომ, მატერიალური წერტილი კანონის მიხედვით ერთი მიმართულებით მოძრაობდეს სწორი ხაზით s=s(t).

გაითვალისწინეთ დროში მომენტი ტ 0 . ამ დროისთვის პუნქტმა გზა გაიარა s=s(t 0 ). მოდით განვსაზღვროთ სიჩქარე ვმატერიალური მომენტი ტ 0 .

ამისათვის განიხილეთ დროის სხვა მომენტი ტ 0 + Δ ტ. იგი შეესაბამება გავლილ მანძილს ს =s(ტ 0 + Δ ტ). შემდეგ დროის ინტერვალისთვის Δ ტწერტილმა გაიარა Δs გზა =s(ტ 0 + Δ უ)–s(t).

განვიხილოთ ურთიერთობა. მას ეწოდება საშუალო სიჩქარე Δ დროის ინტერვალში ტ. საშუალო სიჩქარე ზუსტად ვერ ახასიათებს წერტილის მოძრაობის სიჩქარეს მომენტში ტ 0 (რადგან მოძრაობა არათანაბარია). იმისათვის, რომ უფრო ზუსტად გამოხატოთ ეს ნამდვილი სიჩქარე საშუალო სიჩქარის გამოყენებით, თქვენ უნდა აიღოთ უფრო მცირე დროის ინტერვალი Δ ტ.

ასე რომ, მოძრაობის სიჩქარე მოცემულ დროს ტ 0 (მყისიერი სიჩქარე) არის საშუალო სიჩქარის ზღვარი დან ტ 0-მდე ტ 0 +Δ ტროდესაც Δ ტ→0:

,

იმათ. არათანაბარი მოძრაობის სიჩქარეარის გავლილი მანძილის წარმოებული დროის მიმართ.

წარმოებულის გეომეტრიული მნიშვნელობა

ჯერ შემოვიღოთ მრუდის ტანგენტის განმარტება მოცემულ წერტილში.

მოდით გვქონდეს მრუდი და მასზე ფიქსირებული წერტილი M 0(იხ. სურათი) განვიხილოთ კიდევ ერთი წერტილი მეს მრუდი და დახაზეთ სეკანტი M 0 M. თუ წერტილი მიწყებს მოძრაობას მრუდის გასწვრივ და წერტილი M 0რჩება სტაციონარული, სეკანტი იცვლის თავის პოზიციას. თუ წერტილის შეუზღუდავი მიახლოებით მმრუდი წერტილამდე M 0ნებისმიერ მხარეს, სეკანტი მიდრეკილია გარკვეული სწორი ხაზის პოზიციაზე M 0 T, შემდეგ სწორი ხაზი M 0 Tმოცემულ წერტილში მრუდის ტანგენსი ეწოდება M 0.

რომ., ტანგენსიმრუდამდე მოცემულ წერტილში M 0სეკანტის ზღვრულ პოზიციას უწოდებენ M 0 Mროდესაც წერტილი მმიდრეკილია მრუდის გასწვრივ წერტილამდე M 0.

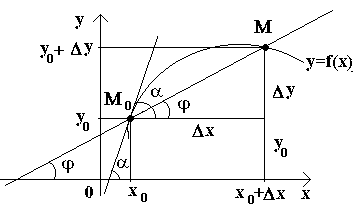
ახლა განვიხილოთ უწყვეტი ფუნქცია y=f(x)და ამ ფუნქციის შესაბამისი მრუდი. გარკვეული ღირებულებისთვის X 0 ფუნქცია იღებს მნიშვნელობას y0=f(x0).ეს ღირებულებები x 0 და წმრუდზე 0 შეესაბამება წერტილს M 0 (x 0; y 0).მოდი მოვიყვანოთ არგუმენტი x0ნამატი Δ X. არგუმენტის ახალი მნიშვნელობა შეესაბამება ფუნქციის გაზრდილ მნიშვნელობას წ 0 +Δ y=f(x 0 –Δ x). ჩვენ მივიღებთ ქულას M(x 0+Δ x; y 0+Δ y).დავხატოთ სეკანტი M 0 Mდა ფ-ით აღვნიშნოთ ღერძის დადებითი მიმართულების სეკანტის მიერ წარმოქმნილი კუთხე ოქსი. დავამყაროთ კავშირი და აღვნიშნოთ, რომ.

თუ ახლა Δ x→0, მაშინ, Δ ფუნქციის უწყვეტობის გამო ზე→0 და, შესაბამისად, წერტილი მმრუდის გასწვრივ მოძრაობს, განუსაზღვრელი ვადით უახლოვდება წერტილს M 0. შემდეგ სეკანტი M 0 Mმიდრეკილია დაიკავოს მრუდის ტანგენტის პოზიცია წერტილში M 0, და კუთხე φ→α Δ-ზე x→0, სადაც α აღნიშნავს კუთხეს ღერძის ტანგენტსა და დადებით მიმართულებას შორის ოქსი. ვინაიდან tg φ ფუნქცია განუწყვეტლივ დამოკიდებულია φ-ზე φ≠π/2, შემდეგ φ→α tg φ → tg α და, შესაბამისად, ტანგენსის დახრილობა იქნება:

იმათ. f"(x)= tgα.

ამრიგად, გეომეტრიულად y" (x 0)წარმოადგენს ამ ფუნქციის გრაფიკის ტანგენტის დახრილობას წერტილში x0, ე.ი. არგუმენტის მოცემული მნიშვნელობისთვის x, წარმოებული უდრის ფუნქციის გრაფიკზე ტანგენტის მიერ წარმოქმნილი კუთხის ტანგენტს f(x)შესაბამის წერტილში M 0 (x; y)დადებითი ღერძის მიმართულებით ოქსი.

მაგალითი.იპოვეთ მრუდის ტანგენსის დახრილობა y = x 2 წერტილში მ(-1; 1).

ჩვენ უკვე ვნახეთ, რომ ( x 2)" = 2X. მაგრამ მრუდის ტანგენსის დახრილობა არის tg α = წ"| x=-1 = - 2.

ფუნქციების განსხვავებულობა. განსხვავებული ფუნქციის უწყვეტობა

ფუნქცია y=f(x)დაურეკა დიფერენცირებადირაღაც მომენტში x 0 თუ მას აქვს გარკვეული წარმოებული ამ ეტაპზე, ე.ი. თუ მიმართების ზღვარი არსებობს და სასრულია.

თუ ფუნქცია დიფერენცირებადია რომელიმე სეგმენტის ყველა წერტილში [ ა; ბ] ან ინტერვალი ( ა; ბ), შემდეგ ამბობენ, რომ ეს დიფერენცირებადისეგმენტზე [ ა; ბ] ან, შესაბამისად, ინტერვალში ( ა; ბ).

მოქმედებს შემდეგი თეორემა, რომელიც ამყარებს კავშირს დიფერენცირებად და უწყვეტ ფუნქციებს შორის.

თეორემა.თუ ფუნქცია y=f(x)რაღაც მომენტში დიფერენცირებადია x0, მაშინ ის ამ ეტაპზე უწყვეტია.

ამრიგად, ფუნქციის დიფერენცირებადობა გულისხმობს მის უწყვეტობას.

მტკიცებულება. Თუ , მაშინ

,

სადაც α არის უსასრულოდ მცირე მნიშვნელობა, ე.ი. რაოდენობა, რომელიც მიდრეკილია ნულისკენ Δ-ზე x→0. Მაგრამ შემდეგ

Δ წ=ვ "(x0) Δ x+αΔ x=> Δ წ→0 Δ-ზე x→0, ე.ი. f(x) – f(x0)→0 საათზე x→x 0, რაც ნიშნავს, რომ ფუნქცია f(x)უწყვეტი წერტილში x 0 . ქ.ე.დ.

ამრიგად, შეწყვეტის წერტილებში ფუნქციას არ შეიძლება ჰქონდეს წარმოებული. საპირისპირო დებულება არ არის ჭეშმარიტი: არის უწყვეტი ფუნქციები, რომლებიც არ არის დიფერენცირებადი ზოგიერთ წერტილში (ანუ მათ არ აქვთ წარმოებული ამ წერტილებში).

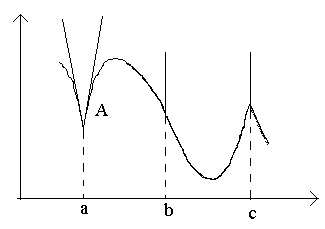
განვიხილოთ ფიგურაში მოცემული პუნქტები ა, ბ, გ.

წერტილში აΔ-ზე x→0 მიმართებას არ აქვს ლიმიტი (რადგან ცალმხრივი ზღვრები განსხვავებულია Δ-სთვის x→0–0 და Δ x→0+0). წერტილში აგრაფიკს არ აქვს განსაზღვრული ტანგენსი, მაგრამ არსებობს ორი განსხვავებული ცალმხრივი ტანგენსი დახრილებით რომ 1 და რომ 2. ამ ტიპის წერტილს კუთხის წერტილი ეწოდება.

წერტილში ბΔ-ზე x→0 თანაფარდობა არის მუდმივი ნიშნის უსასრულოდ დიდი მნიშვნელობა. ფუნქციას აქვს უსასრულო წარმოებული. ამ ეტაპზე, გრაფიკს აქვს ვერტიკალური ტანგენსი. წერტილის ტიპი - „შემოქცევის წერტილი“ ვერტიკალური ტანგენტით.

წერტილში გცალმხრივი წარმოებულები არის სხვადასხვა ნიშნის უსასრულოდ დიდი რაოდენობა. ამ ეტაპზე, გრაფიკს აქვს ორი შერწყმული ვერტიკალური ტანგენსი. ტიპი - "კუსპი" ვერტიკალური ტანგენტით - კუთხის წერტილის განსაკუთრებული შემთხვევა.