Definição 9.3. Vetor X chamado próprio vetor matrizes MAS se existe esse número λ, que a igualdade vale: MAS X= λ X, ou seja, o resultado da aplicação a X transformação linear dada pela matriz MAS, é a multiplicação desse vetor pelo número λ . O próprio número λ chamado próprio número matrizes MAS.

Substituindo em fórmulas (9.3) x`j = λxj, obtemos um sistema de equações para determinar as coordenadas do autovetor:

. (9.5)

Este sistema linear homogêneo terá uma solução não trivial somente se seu determinante principal for 0 (regra de Cramer). Escrevendo esta condição no formulário:

obtemos uma equação para determinar os autovalores λ chamado equação característica. Resumidamente, pode ser representado da seguinte forma:

| A-λE | = 0, (9.6)

já que seu lado esquerdo é o determinante da matriz A-λE. Polinômio em relação a λ | A-λE| chamado polinômio característico matrizes A.

Propriedades do polinômio característico:

1) O polinômio característico de uma transformação linear não depende da escolha da base. Prova. (ver (9.4)), mas Consequentemente, . Assim, não depende da escolha da base. Portanto, e | A-λE| não muda na transição para uma nova base.

2) Se a matriz MAS transformação linear é simétrico(Essa. um ij = um ji), então todas as raízes da equação característica (9.6) são números reais.

Propriedades de autovalores e autovetores:

1) Se escolhermos uma base de autovetores x 1, x 2, x 3 correspondente aos autovalores λ 1 , λ 2 , λ 3 matrizes MAS, então nesta base a transformação linear A tem uma matriz diagonal:

(9.7) A prova desta propriedade segue da definição de autovetores.

2) Se a transformação autovalores MAS são diferentes, então os autovetores correspondentes a eles são linearmente independentes.

3) Se o polinômio característico da matriz MAS tem três raízes diferentes, então em alguma base a matriz MAS tem uma forma diagonal.

Vamos encontrar os autovalores e autovetores da matriz Vamos fazer a equação característica: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Encontre as coordenadas dos autovetores correspondentes a cada valor encontrado λ. De (9.5) segue que se X (1) ={x 1 , x 2 , x 3) é o autovetor correspondente a λ 1 = -2, então

é um sistema colaborativo, mas indeterminado. Sua solução pode ser escrita como X (1) ={uma,0,-uma), onde a é qualquer número. Em particular, se você precisar que | x (1) |=1, X (1) =

Substituindo no sistema (9.5) λ 2 = 3, obtemos um sistema para determinar as coordenadas do segundo autovetor - x (2) ={y1, y2, y3}:

, Onde X (2) ={b,-b,b) ou, desde | x (2) |=1, x (2) =

Por λ 3 = 6 encontre o autovetor x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) ou na versão normalizada

x (3) = Pode ser visto que X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = bc- 2bc + bc= 0. Assim, os autovetores desta matriz são ortogonais aos pares.

Aula 10

Formas quadráticas e sua ligação com matrizes simétricas. Propriedades de autovetores e autovalores de uma matriz simétrica. Redução de uma forma quadrática a uma forma canônica.

Definição 10.1.forma quadrática variáveis ​​reais x 1, x 2,…, xné chamado um polinômio de segundo grau com relação a essas variáveis, que não contém um termo livre e termos de primeiro grau.

Exemplos de formas quadráticas:

(n = 2),

(n = 3). (10.1)

Lembre-se da definição de uma matriz simétrica dada na última aula:

Definição 10.2. A matriz quadrada é chamada simétrico, se , ou seja, se os elementos da matriz simétricos em relação à diagonal principal são iguais.

Propriedades de autovalores e autovetores de uma matriz simétrica:

1) Todos os autovalores de uma matriz simétrica são reais.

Prova (para n = 2).

Deixe a matriz MAS parece: . Vamos fazer a equação característica:

(10.2) Encontre o discriminante:

Portanto, a equação tem apenas raízes reais.

2) Os autovetores de uma matriz simétrica são ortogonais.

Prova (para n= 2).

As coordenadas dos autovetores e devem satisfazer as equações.

Matrizes do tipo diagonal são arranjadas de maneira mais simples. Surge a questão de saber se é possível encontrar uma base na qual a matriz de um operador linear tenha uma forma diagonal. Essa base existe.
Seja dado um espaço linear R n e um operador linear A atuando nele; neste caso, o operador A toma R n em si, ou seja, A:R n → R n .

Definição. Um vetor diferente de zero é chamado de autovetor do operador A se o operador A se traduz em um vetor colinear a ele, ou seja, . O número λ é chamado de autovalor ou autovalor do operador A correspondente ao autovetor.
Observamos algumas propriedades de autovalores e autovetores.
1. Qualquer combinação linear de autovetores do operador A correspondente ao mesmo autovalor λ é um autovetor com o mesmo autovalor.
2. Autovetores operador A com autovalores distintos aos pares λ 1 , λ 2 , …, λ m são linearmente independentes.
3. Se os autovalores λ 1 =λ 2 = λ m = λ, então o autovalor λ corresponde a não mais que m autovetores linearmente independentes.

Então, se existem n autovetores linearmente independentes correspondendo a diferentes autovalores λ 1 , λ 2 , …, λ n , então eles são linearmente independentes, portanto, podem ser tomados como base do espaço R n . Vamos encontrar a forma da matriz do operador linear A na base de seus autovetores, para os quais atuamos com o operador A nos vetores de base: então .
Assim, a matriz do operador linear A na base de seus autovetores tem uma forma diagonal, e os autovalores do operador A estão na diagonal.
Existe outra base em que a matriz tem uma forma diagonal? A resposta a esta questão é dada pelo seguinte teorema.

Teorema. A matriz de um operador linear A na base (i = 1..n) tem uma forma diagonal se e somente se todos os vetores da base são autovetores do operador A.

Regra para encontrar autovalores e autovetores

Deixe o vetor , onde x 1 , x 2 , …, x n - coordenadas do vetor em relação à base e é o autovetor do operador linear A correspondente ao autovalor λ , ou seja . Esta relação pode ser escrita na forma matricial

. (*)

A equação (*) pode ser considerada como uma equação para encontrar , e , ou seja, estamos interessados ​​em soluções não triviais, pois o autovetor não pode ser zero. Sabe-se que soluções não triviais de um sistema homogêneo de equações lineares existem se e somente se det(A - λE) = 0. Assim, para que λ seja um autovalor do operador A é necessário e suficiente que det(A - λE ) = 0.
Se a equação (*) for escrita em detalhes na forma de coordenadas, obtemos um sistema de equações homogêneas lineares:

(1)
Onde é a matriz do operador linear.

O sistema (1) tem uma solução diferente de zero se seu determinante D for igual a zero

Temos uma equação para encontrar autovalores.
Essa equação é chamada de equação característica, e seu lado esquerdo é chamado de polinômio característico da matriz (operador) A. Se o polinômio característico não tem raízes reais, então a matriz A não tem vetores próprios e não pode ser reduzida a uma forma diagonal.
Sejam λ 1 , λ 2 , …, λ n as raízes reais da equação característica, podendo haver múltiplos entre elas. Substituindo esses valores por sua vez no sistema (1), encontramos os autovetores.

Exemplo 12. O operador linear A atua em R 3 de acordo com a lei , onde x 1 , x 2 , .., x n são as coordenadas do vetor na base , , . Encontre os autovalores e autovetores desse operador.
Solução. Construímos a matriz deste operador:
.
Compomos um sistema para determinar as coordenadas de autovetores:

Compomos a equação característica e a resolvemos:

.
λ 1,2 = -1, λ 3 = 3.
Substituindo λ = -1 no sistema, temos:
ou
Porque , então existem duas variáveis ​​dependentes e uma variável livre.
Seja x 1 uma incógnita livre, então Resolvemos este sistema de qualquer maneira e encontramos a solução geral deste sistema: O sistema fundamental de soluções consiste em uma solução, pois n - r = 3 - 2 = 1.
O conjunto de autovetores correspondentes ao autovalor λ = -1 tem a forma: , onde x 1 é qualquer número diferente de zero. Vamos escolher um vetor deste conjunto, por exemplo, definindo x 1 = 1: .
Argumentando de forma semelhante, encontramos o autovetor correspondente ao autovalor λ = 3: .
No espaço R 3 a base consiste em três vetores linearmente independentes, mas obtivemos apenas dois autovetores linearmente independentes, a partir dos quais a base em R 3 não pode ser formada. Consequentemente, a matriz A de um operador linear não pode ser reduzida a uma forma diagonal.

Exemplo 13 Dada uma matriz .
1. Prove que o vetor é um autovetor da matriz A. Encontre o autovalor correspondente a este autovetor.
2. Encontre uma base na qual a matriz A tenha uma forma diagonal.
Solução.
1. Se , então é um autovetor

.
Vetor (1, 8, -1) é um autovetor. Autovalor λ = -1.
A matriz tem uma forma diagonal na base composta por autovetores. Um deles é famoso. Vamos encontrar o resto.
Estamos procurando por autovetores do sistema:

Equação característica: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Encontre o autovetor correspondente ao autovalor λ = -3:

O posto da matriz deste sistema é igual a dois e é igual ao número de incógnitas, portanto, este sistema tem apenas uma solução zero x 1 = x 3 = 0. x 2 aqui pode ser qualquer coisa diferente de zero, por exemplo, x 2 = 1. Assim, o vetor (0 ,1,0) é um autovetor correspondente a λ = -3. Vamos checar:
.
Se λ = 1, obtemos o sistema
O posto da matriz é dois. Risque a última equação.
Seja x 3 a incógnita livre. Então x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Assumindo x 3 = 1, temos (-3,-9,1) - um autovetor correspondente ao autovalor λ = 1. Verifique:

.
Como os autovalores são reais e diferentes, os vetores correspondentes a eles são linearmente independentes, de modo que podem ser tomados como base em R 3 . Assim, na base , , A matriz A tem a forma:
.
Nem toda matriz de um operador linear A:R n → R n pode ser reduzida a uma forma diagonal, pois para alguns operadores lineares pode haver menos de n autovetores linearmente independentes. No entanto, se a matriz for simétrica, exatamente m vetores linearmente independentes correspondem à raiz da equação característica da multiplicidade m.

Definição. Uma matriz simétrica é uma matriz quadrada na qual os elementos simétricos em relação à diagonal principal são iguais, ou seja, na qual .
Observações. 1. Todos os autovalores de uma matriz simétrica são reais.
2. Autovetores de uma matriz simétrica correspondente a diferentes autovalores aos pares são ortogonais.
Como uma das inúmeras aplicações do aparato estudado, consideramos o problema de determinar a forma de uma curva de segunda ordem.

Com a matriz A, se existe um número l tal que AX = lX.

Neste caso, o número l é chamado autovalor operador (matriz A) correspondente ao vetor X.

Em outras palavras, um autovetor é um vetor que, sob a ação de um operador linear, se transforma em um vetor colinear, ou seja, basta multiplicar por algum número. Em contraste, vetores impróprios são mais difíceis de transformar.

Escrevemos a definição do autovetor como um sistema de equações:

Vamos mover todos os termos para o lado esquerdo:

O último sistema pode ser escrito na forma matricial da seguinte forma:

(A - lE)X \u003d O

O sistema resultante sempre tem uma solução zero X = O. Tais sistemas em que todos os termos livres são iguais a zero são chamados homogêneo. Se a matriz de tal sistema for quadrada e seu determinante não for igual a zero, de acordo com as fórmulas de Cramer, sempre obteremos uma solução única - zero. Pode-se provar que o sistema tem soluções não nulas se e somente se o determinante desta matriz for igual a zero, ou seja,

|A - lE| = = 0

Esta equação com incógnita l é chamada equação característica (polinômio característico) matriz A (operador linear).

Pode-se provar que o polinômio característico de um operador linear não depende da escolha da base.

Por exemplo, vamos encontrar os autovalores e autovetores do operador linear dado pela matriz A = .

Para isso, compomos a equação característica |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; autovalores l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

Para encontrar os autovetores, resolvemos dois sistemas de equações

(A + 5E) X = O

(A - 7E) X = O

Para o primeiro deles, a matriz expandida terá a forma

,

de onde x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, ou seja X (1) \u003d (- (2/3) s; s).

Para o segundo deles, a matriz expandida terá a forma

,

de onde x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, ou seja X (2) \u003d ((2/3) s 1; s 1).

Assim, os autovetores deste operador linear são todos os vetores da forma (-(2/3)c; c) com autovalor (-5) e todos os vetores da forma ((2/3)c 1 ; c 1) com autovalor 7 .

Pode-se provar que a matriz do operador A na base composta por seus autovetores é diagonal e tem a forma:

,

onde l i são os autovalores dessa matriz.

A recíproca também é verdadeira: se a matriz A em alguma base for diagonal, então todos os vetores dessa base serão autovetores dessa matriz.

Também pode ser provado que se um operador linear tem n autovalores distintos aos pares, então os autovetores correspondentes são linearmente independentes, e a matriz deste operador na base correspondente tem uma forma diagonal.

Vamos explicar isso com o exemplo anterior. Tomemos valores arbitrários diferentes de zero c e c 1 , mas tais que os vetores X (1) e X (2) sejam linearmente independentes, ou seja, formaria uma base. Por exemplo, seja c \u003d c 1 \u003d 3, depois X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Vamos verificar a independência linear desses vetores:

12 ≠ 0. Nesta nova base, a matriz A terá a forma A * = .

Para verificar isso, usamos a fórmula A * = C -1 AC. Vamos encontrar C -1 primeiro.

C-1 = ;

Formas quadráticas

forma quadrática f (x 1, x 2, x n) de n variáveis ​​é chamado de soma, cada termo do qual é o quadrado de uma das variáveis, ou o produto de duas variáveis ​​diferentes, tomadas com um certo coeficiente: f (x 1 , x 2, x n) = (aij = aji).

A matriz A, composta por esses coeficientes, é chamada matriz forma quadrática. É sempre simétrico matriz (ou seja, uma matriz simétrica em torno da diagonal principal, a ij = a ji).

Na notação matricial, a forma quadrática tem a forma f(X) = X T AX, onde

De fato

Por exemplo, vamos escrever a forma quadrática na forma matricial.

Para fazer isso, encontramos uma matriz de forma quadrática. Seus elementos diagonais são iguais aos coeficientes nos quadrados das variáveis, e os demais elementos são iguais à metade dos coeficientes correspondentes da forma quadrática. É por isso

Seja a coluna-matriz de variáveis ​​X obtida por uma transformação linear não degenerada da coluna-matriz Y, ou seja. X = CY, onde C é uma matriz não degenerada de ordem n. Então a forma quadrática f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Assim, sob uma transformação linear não degenerada C, a matriz da forma quadrática toma a forma: A * = C T AC.

Por exemplo, vamos encontrar a forma quadrática f(y 1, y 2) obtida da forma quadrática f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 por uma transformação linear.

A forma quadrática é chamada canônico(Tem visão canônica) se todos os seus coeficientes a ij = 0 para i ≠ j, ou seja.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Sua matriz é diagonal.

Teorema(a prova não é dada aqui). Qualquer forma quadrática pode ser reduzida a uma forma canônica usando uma transformação linear não degenerada.

Por exemplo, vamos reduzir à forma canônica a forma quadrática
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Para fazer isso, primeiro selecione o quadrado completo para a variável x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5 x 2 2 - x 2 x 3.

Agora selecionamos o quadrado completo para a variável x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Em seguida, a transformação linear não degenerada y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 e y 3 \u003d x 3 traz essa forma quadrática para a forma canônica f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Observe que a forma canônica de uma forma quadrática é definida de forma ambígua (a mesma forma quadrática pode ser reduzida à forma canônica de diferentes maneiras). No entanto, as formas canônicas obtidas por vários métodos têm várias propriedades comuns. Em particular, o número de termos com coeficientes positivos (negativos) de uma forma quadrática não depende de como a forma é reduzida a essa forma (por exemplo, no exemplo considerado sempre haverá dois coeficientes negativos e um positivo). Essa propriedade é chamada de lei da inércia das formas quadráticas.

Vamos verificar isso reduzindo a mesma forma quadrática à forma canônica de uma maneira diferente. Vamos iniciar a transformação com a variável x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, onde y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) ) x 3 e y 3 = x 1 . Aqui, um coeficiente negativo -3 em y 1 e dois coeficientes positivos 3 e 2 em y 2 e y 3 (e usando outro método, obtivemos um coeficiente negativo (-5) em y 2 e dois coeficientes positivos: 2 em y 1 e 1/20 para y 3).

Deve-se notar também que o posto de uma matriz de forma quadrática, chamado o posto da forma quadrática, é igual ao número de coeficientes diferentes de zero da forma canônica e não muda sob transformações lineares.

A forma quadrática f(X) é chamada positivamente (negativo) certo, se para todos os valores das variáveis ​​que não são simultaneamente iguais a zero, é positivo, ou seja. f(X) > 0 (negativo, ou seja,
f(X)< 0).

Por exemplo, a forma quadrática f 1 (X) \u003d x 1 2 + x 2 2 é definida positiva, porque é a soma dos quadrados, e a forma quadrática f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 é definida negativa, porque representa pode ser representado como f 2 (X) \u003d - (x 1 - x 2) 2.

Na maioria das situações práticas, é um pouco mais difícil estabelecer a definição de sinal de uma forma quadrática, então um dos seguintes teoremas é usado para isso (nós os formulamos sem provas).

Teorema. Uma forma quadrática é positiva (negativa) definida se e somente se todos os autovalores de sua matriz são positivos (negativos).

Teorema(critério de Sylvester). Uma forma quadrática é definida positiva se e somente se todos os menores principais da matriz desta forma são positivos.

Maior (canto) menor A k-ésima ordem da matriz A de n-ésima ordem é chamada de determinante da matriz, composta pelas k primeiras linhas e colunas da matriz A().

Observe que para formas quadráticas negativas-definidas, os sinais dos menores principais se alternam e os menores de primeira ordem devem ser negativos.

Por exemplo, examinamos a forma quadrática f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 para definição de sinal.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Portanto, a forma quadrática é definida positiva.

Método 2. O menor principal de primeira ordem da matriz A D 1 = a 11 = 2 > 0. O menor principal de segunda ordem D 2 = = 6 - 4 = 2 > 0. Portanto, de acordo com o critério de Sylvester, a forma quadrática é positiva definida.

Examinamos outra forma quadrática para definição de sinal, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Método 1. Vamos construir uma matriz de forma quadrática А = . A equação característica terá a forma = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Portanto, a forma quadrática é definida negativa.

Método 2. O menor principal de primeira ordem da matriz A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Portanto, de acordo com o critério de Sylvester, a forma quadrática é definida negativa (os sinais dos menores principais se alternam, a partir de menos).

E como outro exemplo, examinamos a forma quadrática f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 para definição de sinal.

Método 1. Vamos construir uma matriz de forma quadrática А = . A equação característica terá a forma = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Um desses números é negativo e o outro é positivo. Os sinais dos autovalores são diferentes. Portanto, uma forma quadrática não pode ser definida negativa ou positiva, ou seja, esta forma quadrática não é definida por sinal (pode assumir valores de qualquer sinal).

Método 2. O menor principal de primeira ordem da matriz A D 1 = a 11 = 2 > 0. O menor principal de segunda ordem D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

SISTEMA DE EQUAÇÕES LINEARES HOMOGÊNEAS

Um sistema de equações lineares homogêneas é um sistema da forma

É claro que neste caso , Porque todos os elementos de uma das colunas nesses determinantes são iguais a zero.

Como as incógnitas são encontradas pelas fórmulas , então no caso em que Δ ≠ 0, o sistema tem uma única solução zero x = y = z= 0. No entanto, em muitos problemas, a questão de saber se um sistema homogêneo tem soluções diferentes de zero é de interesse.

Teorema. Para que um sistema de equações lineares homogêneas tenha uma solução diferente de zero, é necessário e suficiente que Δ ≠ 0.

Então, se o determinante for Δ ≠ 0, então o sistema tem uma solução única. Se Δ ≠ 0, então o sistema de equações lineares homogêneas tem um número infinito de soluções.

Exemplos.

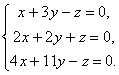
Autovetores e Autovalores de Matriz

Seja uma matriz quadrada , Xé alguma coluna-matriz cuja altura coincide com a ordem da matriz UMA. .

Em muitos problemas, deve-se considerar a equação para X

onde λ é algum número. É claro que para qualquer λ esta equação tem solução zero.

O número λ para o qual esta equação tem soluções diferentes de zero é chamado autovalor matrizes UMA, uma X para tal λ é chamado próprio vetor matrizes UMA.

Vamos encontrar o autovetor da matriz UMA. Porque o E∙X=X, então a equação matricial pode ser reescrita como ou . Na forma expandida, esta equação pode ser reescrita como um sistema de equações lineares. Sério .

E portanto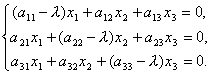

Então, temos um sistema de equações lineares homogêneas para determinar as coordenadas x 1, x2, x 3 vetor X. Para que o sistema tenha soluções diferentes de zero, é necessário e suficiente que o determinante do sistema seja igual a zero, ou seja,

Esta é uma equação de 3º grau em relação a λ. É chamado equação característica matrizes UMA e serve para determinar os autovalores λ.

Cada autovalor λ corresponde a um autovetor X, cujas coordenadas são determinadas a partir do sistema no valor correspondente de λ.

Exemplos.

ÁLGEBRA VETORIAL. CONCEITO VETORIAL

Ao estudar vários ramos da física, existem quantidades que são completamente determinadas definindo seus valores numéricos, por exemplo, comprimento, área, massa, temperatura etc. Tais valores são chamados escalares. No entanto, além deles, também existem quantidades, para a determinação das quais, além do valor numérico, também é necessário conhecer sua direção no espaço, por exemplo, a força que atua sobre o corpo, a velocidade e a aceleração do corpo quando ele se move no espaço, a força do campo magnético em um determinado ponto no espaço e etc. Tais quantidades são chamadas de quantidades vetoriais.

Vamos introduzir uma definição rigorosa.

Segmento direcional Vamos chamar um segmento, em relação às extremidades do qual se sabe qual deles é o primeiro e qual é o segundo.

Vetor um segmento direcionado é chamado, tendo um certo comprimento, ou seja, Este é um segmento de um determinado comprimento, no qual um dos pontos que o limitam é considerado o início e o segundo - o fim. Se um UMAé o início do vetor, Bé o seu fim, então o vetor é denotado pelo símbolo, além disso, o vetor é frequentemente denotado por uma única letra . Na figura, o vetor é indicado por um segmento e sua direção por uma seta.

módulo ou grandes vetor é chamado de comprimento do segmento direcionado que o define. Indicado por || ou ||.

O chamado vetor zero, cujo início e fim coincidem, também será referido como vetores. Está marcado. O vetor zero não tem direção definida e seu módulo é igual a zero ||=0.

Vetores e são chamados colinear se estiverem localizados na mesma linha ou em linhas paralelas. Neste caso, se os vetores e forem igualmente direcionados, escreveremos , opostamente.

Vetores localizados em linhas retas paralelas ao mesmo plano são chamados coplanar.

Dois vetores e são chamados igual se eles são colineares, têm a mesma direção e são iguais em comprimento. Neste caso, escreva .

Segue-se da definição de igualdade de vetores que um vetor pode ser movido paralelamente a si mesmo colocando sua origem em qualquer ponto do espaço.

Por exemplo.

OPERAÇÕES LINEARES EM VETORES

1. Multiplicando um vetor por um número.

   O produto de um vetor por um número λ é um novo vetor tal que:

   O produto de um vetor e um número λ é denotado por .

   

   Por exemplo,é um vetor apontando na mesma direção do vetor e tendo um comprimento metade do vetor .

   A operação inserida tem o seguinte propriedades:

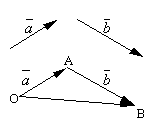
2. Adição de vetores.

   Sejam e dois vetores arbitrários. Pegue um ponto arbitrário O e construir um vetor . Depois disso, do ponto UMA deixe de lado o vetor. O vetor que conecta o início do primeiro vetor com o final do segundo é chamado soma desses vetores e é denotado .

   

   A definição formulada de adição vetorial é chamada regra do paralelogramo, uma vez que a mesma soma de vetores pode ser obtida como segue. Afaste-se do ponto O vetores e . Construa um paralelogramo sobre esses vetores OABC. Como os vetores , então o vetor , que é a diagonal do paralelogramo desenhado a partir do vértice O, obviamente será a soma dos vetores .

   

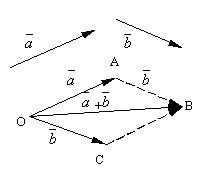
   É fácil verificar o seguinte propriedades de adição de vetor.

3. Diferença de vetores.

   Um vetor colinear a um dado vetor , igual em comprimento e direção oposta, é chamado oposto vetor para um vetor e é denotado por . O vetor oposto pode ser considerado como resultado da multiplicação do vetor pelo número λ = –1: .