Formulação do problema

A tarefa envolve familiarizar o usuário com os conceitos básicos de métodos numéricos, como determinante e matriz inversa, e várias formas de calculá-los. Neste relatório teórico, numa linguagem simples e acessível, introduzem-se inicialmente os conceitos e definições básicos, com base nos quais se procede a uma investigação mais aprofundada. O usuário pode não ter conhecimentos especiais na área de métodos numéricos e álgebra linear, mas poderá facilmente utilizar os resultados deste trabalho. Para maior clareza, é fornecido um programa para calcular o determinante da matriz por vários métodos, escrito na linguagem de programação C ++. O programa é utilizado como um suporte de laboratório para a criação de ilustrações para o relatório. E também está sendo realizado um estudo de métodos para resolução de sistemas de equações algébricas lineares. A inutilidade de calcular a matriz inversa é comprovada, portanto, o artigo fornece maneiras mais otimizadas de resolver equações sem calculá-la. É explicado por que existem tantos métodos diferentes para calcular determinantes e matrizes inversas e suas deficiências são analisadas. Erros no cálculo do determinante também são considerados e a precisão alcançada é estimada. Além dos termos russos, seus equivalentes em inglês também são usados ​​​​no trabalho para entender sob quais nomes procurar procedimentos numéricos em bibliotecas e o que significam seus parâmetros.

Definições básicas e propriedades simples

Determinante

Vamos introduzir a definição do determinante de uma matriz quadrada de qualquer ordem. Esta definição irá recorrente, ou seja, para estabelecer qual é o determinante da matriz de ordem, você precisa já saber qual é o determinante da matriz de ordem. Observe também que o determinante existe apenas para matrizes quadradas.

O determinante de uma matriz quadrada será denotado por ou det .

Definição 1. determinante matriz quadrada número de segunda ordem é chamado .

determinante matriz quadrada de ordem , é chamada de número

onde é o determinante da matriz de ordem obtido da matriz excluindo a primeira linha e a coluna com o número .

Para maior clareza, escrevemos como você pode calcular o determinante de uma matriz de quarta ordem:

Comente. O cálculo real de determinantes para matrizes acima da terceira ordem com base na definição é usado em casos excepcionais. Via de regra, o cálculo é feito de acordo com outros algoritmos, que serão discutidos posteriormente e que exigem menos trabalho computacional.

Comente. Na Definição 1, seria mais correto dizer que o determinante é uma função definida no conjunto das matrizes de ordem quadrada e que assume valores no conjunto dos números.

Comente. Na literatura, ao invés do termo "determinante", também é utilizado o termo "determinante", que tem o mesmo significado. Da palavra "determinante" surgiu a designação det.

Consideremos algumas propriedades dos determinantes, que formulamos na forma de afirmações.

Declaração 1. Ao transpor uma matriz, o determinante não muda, ou seja, .

Declaração 2. O determinante do produto das matrizes quadradas é igual ao produto dos determinantes dos fatores, ou seja, .

Declaração 3. Se duas linhas de uma matriz forem trocadas, seu determinante mudará de sinal.

Declaração 4. Se uma matriz tem duas linhas idênticas, então seu determinante é zero.

No futuro, precisaremos adicionar strings e multiplicar uma string por um número. Faremos essas operações sobre linhas (colunas) da mesma forma que as operações sobre matrizes linha (matrizes coluna), ou seja, elemento por elemento. O resultado será uma linha (coluna), que, via de regra, não coincide com as linhas da matriz original. Na presença de operações de somar linhas (colunas) e multiplicá-las por um número, também podemos falar de combinações lineares de linhas (colunas), ou seja, somas com coeficientes numéricos.

Declaração 5. Se uma linha de uma matriz for multiplicada por um número, seu determinante será multiplicado por esse número.

Declaração 6. Se a matriz contém uma linha zero, então seu determinante é zero.

Declaração 7. Se uma das linhas da matriz for igual à outra multiplicada por um número (as linhas são proporcionais), o determinante da matriz é zero.

Declaração 8. Deixe a i-ésima linha da matriz parecer . Então , onde a matriz é obtida da matriz substituindo a i-ésima linha pela linha , e a matriz é obtida substituindo a i-ésima linha pela linha .

Declaração 9. Se uma das linhas da matriz for adicionada a outra, multiplicada por um número, o determinante da matriz não será alterado.

Declaração 10. Se uma das linhas de uma matriz é uma combinação linear de suas outras linhas, o determinante da matriz é zero.

Definição 2. adição algébrica a um elemento da matriz é chamado um número igual a , onde é o determinante da matriz obtido da matriz deletando a i-ésima linha e a j-ésima coluna. O complemento algébrico para um elemento de matriz é denotado por .

Exemplo. Deixar . Então

Comente. Usando adições algébricas, a definição de 1 determinante pode ser escrita da seguinte forma:

Declaração 11. Decomposição do determinante em uma string arbitrária.

O determinante da matriz satisfaz a fórmula

Exemplo. Calcular .

Solução. Vamos usar a expansão na terceira linha, é mais rentável, porque na terceira linha dois números de três são zeros. Pegue

Declaração 12. Para uma matriz quadrada de ordem em , temos a relação .

Declaração 13. Todas as propriedades do determinante formuladas para linhas (declarações 1 - 11) também são válidas para colunas, em particular, a decomposição do determinante na j-ésima coluna é válida e igualdade no .

Declaração 14. O determinante de uma matriz triangular é igual ao produto dos elementos de sua diagonal principal.

Consequência. O determinante da matriz identidade é igual a um, .

Conclusão. As propriedades listadas acima permitem encontrar determinantes de matrizes de ordens suficientemente altas com uma quantidade relativamente pequena de cálculos. O algoritmo de cálculo é o seguinte.

Algoritmo para criar zeros em uma coluna. Seja necessário calcular o determinante de ordem. Se , troque a primeira linha e qualquer outra linha na qual o primeiro elemento não seja zero. Com isso, o determinante , será igual ao determinante da nova matriz de sinal oposto. Se o primeiro elemento de cada linha for igual a zero, então a matriz tem coluna zero e, pelas Afirmações 1, 13, seu determinante é igual a zero.

Então, consideramos isso já na matriz original. Deixe a primeira linha inalterada. Vamos adicionar à segunda linha a primeira linha, multiplicada pelo número . Então o primeiro elemento da segunda linha será igual a .

Os elementos restantes da nova segunda linha serão denotados por , . O determinante da nova matriz de acordo com a Declaração 9 é igual a . Multiplique a primeira linha pelo número e adicione-a à terceira. O primeiro elemento da nova terceira linha será igual a

Os elementos restantes da nova terceira linha serão denotados por , . O determinante da nova matriz de acordo com a Declaração 9 é igual a .

Continuaremos o processo de obtenção de zeros em vez dos primeiros elementos de strings. Finalmente, multiplicamos a primeira linha por um número e o adicionamos à última linha. O resultado é uma matriz, denotada por , que tem a forma

e . Para calcular o determinante da matriz, usamos a expansão na primeira coluna

Desde então

O determinante da matriz de ordem está no lado direito. Aplicamos o mesmo algoritmo a ele, e o cálculo do determinante da matriz será reduzido ao cálculo do determinante da matriz de ordem. O processo é repetido até chegarmos ao determinante de segunda ordem, que é calculado por definição.

Se a matriz não tiver nenhuma propriedade específica, não é possível reduzir significativamente a quantidade de cálculos em comparação com o algoritmo proposto. Outro lado bom desse algoritmo é que é fácil escrever um programa para um computador calcular os determinantes de matrizes de grandes ordens. Em programas padrão para calcular determinantes, esse algoritmo é usado com pequenas alterações associadas à minimização da influência de erros de arredondamento e erros de dados de entrada em cálculos de computador.

Exemplo. Determinante da Matriz de Cálculo .

Solução. A primeira linha permanece inalterada. À segunda linha somamos a primeira, multiplicada pelo número:

O determinante não muda. À terceira linha somamos a primeira, multiplicada pelo número:

O determinante não muda. Na quarta linha adicionamos a primeira, multiplicada pelo número:

O determinante não muda. Como resultado, obtemos

Usando o mesmo algoritmo, calculamos o determinante de uma matriz de ordem 3, que está à direita. Deixamos a primeira linha inalterada, na segunda linha adicionamos a primeira, multiplicada pelo número :

À terceira linha somamos a primeira, multiplicada pelo número :

Como resultado, obtemos

Responda. .

Comente. Embora frações tenham sido usadas nos cálculos, o resultado foi um número inteiro. De fato, usando as propriedades dos determinantes e o fato de que os números originais são inteiros, as operações com frações poderiam ser evitadas. Mas na prática da engenharia, os números raramente são inteiros. Portanto, via de regra, os elementos do determinante serão frações decimais e não é aconselhável usar truques para simplificar os cálculos.

matriz inversa

Definição 3. A matriz é chamada matriz inversa para uma matriz quadrada se .

Segue-se da definição que a matriz inversa será uma matriz quadrada da mesma ordem que a matriz (caso contrário, um dos produtos ou não seria definido).

A matriz inversa de uma matriz é denotada por . Assim, se existe, então .

Da definição de uma matriz inversa, segue-se que a matriz é a inversa da matriz, ou seja, . Matrizes e podem ser consideradas inversas entre si ou mutuamente inversas.

Se o determinante de uma matriz for zero, então sua inversa não existe.

Como para encontrar a matriz inversa é importante se o determinante da matriz é igual a zero ou não, apresentamos as seguintes definições.

Definição 4. Vamos chamar a matriz quadrada degenerar ou matriz especial, se e não degenerado ou matriz não singular, E se .

Declaração. Se existe uma matriz inversa, então ela é única.

Declaração. Se uma matriz quadrada é não degenerada, então sua inversa existe e (1) onde são adições algébricas aos elementos .

Teorema. Uma matriz inversa para uma matriz quadrada existe se e somente se a matriz for não singular, a matriz inversa for única e a fórmula (1) for válida.

Comente. Atenção especial deve ser dada aos lugares ocupados pelas adições algébricas na fórmula da matriz inversa: o primeiro índice mostra o número coluna, e o segundo é o número linhas, no qual o complemento algébrico calculado deve ser escrito.

Exemplo. .

Solução. Encontrando o determinante

Desde , então a matriz é não degenerada, e o inverso para ela existe. Encontrando adições algébricas:

Compomos a matriz inversa colocando as adições algébricas encontradas de forma que o primeiro índice corresponda à coluna e o segundo à linha: (2)

A matriz resultante (2) é a resposta para o problema.

Comente. No exemplo anterior, seria mais preciso escrever a resposta assim:
(3)

No entanto, a notação (2) é mais compacta e é mais conveniente realizar cálculos adicionais, se houver, com ela. Portanto, escrever a resposta na forma (2) é preferível se os elementos das matrizes forem inteiros. E vice-versa, se os elementos da matriz forem frações decimais, é melhor escrever a matriz inversa sem um fator na frente.

Comente. Ao encontrar a matriz inversa, você deve realizar muitos cálculos e uma regra incomum para organizar as adições algébricas na matriz final. Portanto, há uma grande chance de erro. Para evitar erros, você deve fazer uma verificação: calcule o produto da matriz original pela final em uma ordem ou outra. Se o resultado for uma matriz identidade, então a matriz inversa foi encontrada corretamente. Caso contrário, você precisa procurar por um erro.

Exemplo. Encontrar a inversa de uma matriz .

Solução. - existe.

Responda: .

Conclusão. Encontrar a matriz inversa pela fórmula (1) requer muitos cálculos. Para matrizes de quarta ordem e superiores, isso é inaceitável. O algoritmo real para encontrar a matriz inversa será dado mais tarde.

Calculando o determinante e a matriz inversa usando o método de Gauss

O método de Gauss pode ser usado para encontrar o determinante e a matriz inversa.

Ou seja, o determinante da matriz é igual a det .

A matriz inversa é encontrada resolvendo sistemas de equações lineares usando o método de eliminação gaussiana:

Onde é a j-ésima coluna da matriz identidade , é o vetor desejado.

Os vetores solução resultantes - formam, obviamente, as colunas da matriz, pois .

Fórmulas para o determinante

1. Se a matriz for não singular, então e (o produto dos elementos principais).

Como para encontrar a matriz inversa é importante se o determinante da matriz é igual a zero ou não, apresentamos as seguintes definições.

Definição 14.9 Vamos chamar a matriz quadrada degenerar ou matriz especial, se e não degenerado ou matriz não singular, E se .

Oferta 14.21 Se existe uma matriz inversa, então ela é única.

Prova. Let Duas matrizes E Ser o inverso da matriz . Então

Consequentemente, .

regra de Cramer.

Deixe a equação matricial AX=B

Onde ; é o determinante obtido do determinante D substituição eu-ésima coluna pela coluna de membros livres da matriz B:

Prova O teorema é dividido em três partes:

1. A solução do sistema (1) existe e é única.

2. As igualdades (2) são consequência da equação matricial (1).

3. As igualdades (2) implicam a equação matricial (1).

Como , também existe uma única matriz inversa .
Multiplicando ambas as partes da equação matricial (1) à esquerda por , obtemos a solução desta equação:

singularidade matriz inversa prova a primeira parte do teorema.

Vamos à prova correspondência um a um entre as fórmulas (1) e (2).

Usando a fórmula (4), obtemos uma expressão para eu-º elemento. Para isso você precisa multiplicar eu-ésima linha da matriz

por coluna B.

Dado que eu-ésima linha da matriz associada é composta por adições algébricas, obtemos o seguinte resultado:

A derivação das fórmulas de Cramer está completa. Vamos agora mostrar que as expressões

Vamos mudar a ordem do somatório no lado direito da expressão resultante:

onde é o símbolo delta Kronecker.

Dado que o símbolo delta remove o somatório sobre um dos índices, obtemos o resultado desejado:

Números complexos: A ideia é definir novos objetos com a ajuda dos já conhecidos. Os números reais estão localizados em uma linha reta. Ao passar para o plano, obtemos números complexos. Definição: Um número complexo é um par de números reais z = (a,b). O número a = Re z é chamado de parte real e b = Im z a parte imaginária do número complexo z .

Operações com números complexos: Os números complexos z1 z2 são Z1 = z2 ⇔ Re z1 = Re z2 & Im z1 = Im z2. Adição: Z=z1+z2. ⇔Rez=Rez1+Rez2 & Imz1+ Imz2. O número (0,0) é denotado por 0. Este é o elemento neutro. Verifica-se que a adição de números complexos tem propriedades semelhantes às da adição de números reais. (1. Z1+ z2 = z2 + z1 – comutatividade; 2. Z1 + (z2 + z3) = (z1 + z2) + z3 – associatividade; 3. Z1 + 0 = z1 - existência de zero (elemento neutro); 4. z + (−z) = 0 - a existência do elemento oposto). Multiplicação: z= z1 z2⇔Re z=Re z1 Re z2-Im z1 Im z2 & Im z1=Im z1 Re z2+Im z2 Re z1. Um número complexo z está no eixo real se Imz = 0 . Os resultados das operações sobre tais números coincidem com os resultados das operações sobre números reais comuns. A multiplicação de números complexos tem as propriedades de fechamento, comutatividade e associatividade. O número (1,0) é denotado por 1. É um elemento neutro por multiplicação.Se a∈ R, z ∈C , então Re(az) = aRe z, Im(az) = a Imz . Definição O número (0,1) é denotado por eu e é chamada de unidade imaginária. Nesta notação, obtemos a representação de um número complexo na forma algébrica: z = a + ib, a,b∈ R. i=-1.(a,b)=(a,0)+(0,b) ;(a,0)+b(0,1)=a+ib=z; (a1+ib)(a2+ib2)=a1a2+i(a1b2+1-a2b1)-b1b2; (a+ib)(1+0i)=a+ib; z(a,b), z(0+i0)=0; z!=0; a 2 + b 2 > 0 (a + ib) (a-ib / a 2 + b 2) = 1. O número é chamado conjugado para z se Re =Re z ; Eu estou =- Eu sou z.

= + ; = ; z =(a+ib)(a-ib)=a 2 +b 2 O módulo de um número z é um número real| z |= . Fórmula justa| z| 2 = z Segue da definição que z ≠ 0⇔| z|≠ 0. z -1 = /|z| 2 (1)

Forma trigonométrica de um número complexo: a=rcos(t); b=r sen(t). Z=a+ib=r(cos(t)+isin(t))(2) t-argumento de um número complexo. Z1=z2 =>|z1|=|z2|

arg(z1)-arg(z2)=2pk.

Z1=r1(cos(t1)+isin(t1), Z2=r2(cos(t2)+isin(t2)), Z3=z1 z2=T1T2(cos(t1+t2)+isin(t1+t2)( 1)

Arg(z1z2)=arg(z1)+arg(z2) (2)

Z!=0 z -1 = /|z| 2 =1/r(cos(-t)+i(sin(-t)) Z=r(cos(t)+istn(t))

R(cos(t)-isin(t))

Definição: A raiz do grau n da unidade é a solução da equação z n =1 Proposta. Existem n raízes n-ésimas distintas da unidade. Eles são escritos como z = cos(2 π k / n) + isin(2 π k / n), k = 0,..., n −1 . Teorema. No conjunto dos números complexos, a equação sempre tem n soluções: Z=r(cos(t)+isin(t)); z n =r n (cos(nt)+isin(nt))=1(cos(0)+isin(0))=>z n =1 .Z-inteiros. K pertence a Z. k=2=E 2 =E n-1 E n ; En =1; E n+p =E p . Assim, está provado que as soluções da equação são os vértices de um n-gon regular, e um dos vértices coincide com 1.

n-ésima raiz de z 0. Z k \u003d Z 0; Z0 =0=>Z=0; Z 0 !=0;Z=r(cos(t)-isin(t)); Z 0 \u003d r 0 (cos (t0) + isin (t0)); r0!=0; Z n \u003d r n (cos (nt) + isin (nt))

r n \u003d r 0, nt-t 0 \u003d 2pk; r=; t=(2пk+t0)/n; z= (cos((2pk+t0)/n)+isin((2pk+t0)/n)= (cos t0/n+isin t0/n)(cos(2pk/n)+isin(2pk/n) )=Z 1 E k ;z=z 1 E k ;Z 1 n =z 0, k=0, n=1

Matrizes. Definição: Uma matriz m × n é uma tabela retangular contendo m linhas e n colunas, cujos elementos são números reais ou complexos. Os elementos da matriz têm índices duplos.

Se m = n, então é uma matriz quadrada de ordem m, e os elementos com o mesmo índice formam a diagonal principal da matriz.

Operações de Matriz: Definição: Duas matrizes A,B são chamadas

iguais se seus tamanhos forem iguais e A = B,1≤ i ≤ m,1≤ j ≤ n

Adição. Matrizes de mesmo tamanho são consideradas. Definição:C = A + B ⇔ C = A + B, ∀i, j Frase. A adição de matrizes é comutativa, associativa, existe um elemento neutro e para cada matriz existe um elemento oposto.

O elemento neutro é a matriz zero, cujos elementos são todos iguais a 0. É denotado por Θ.

Multiplicação. Uma matriz A m × n é denotada por Amn . Definição: C mk =A mn Bnkó

C= Observe que, em geral, a multiplicação não é comutativa. O fechamento é válido para uma matriz quadrada de tamanho fixo. Sejam dadas três matrizes Amn , Bnk , Ckr. Então (AB)C = A(BC). Se existe um produto de 3 matrizes, então é associativo.

O símbolo Kronecker δij . É 1 se os índices coincidem e 0 caso contrário. Definição. A matriz identidade In é uma matriz quadrada de ordem n para a qual as igualdades n I n [ i | j] = δij Frase. Igualdades I m A mn =A mn I n =A mn

A adição e a multiplicação de matrizes estão ligadas pelas leis da distributividade. A(B+C)=AB+AC; (A+B)C=AC+BC;(A(B+C)= = = +

Transposição de matrizes. Uma matriz transposta é uma matriz obtida a partir da original substituindo linhas por colunas.

(A+B) T = A T + B T

(AB) T \u003d B T A T; (AB) T \u003d (AB) \u003d \u003d (B T A T)

Multiplicando uma matriz por um número. O produto do número a pela matriz A mn é chamado de nova matriz B=aA

1*A=A;a(A+B)=aA+aB;(a+b)A=aA+bA;

A(BC)=(aB)C=B(aC); (ab)A=a(bA)=b(aA)

espaço linear(L) sobre o campo F é chamado de conjunto de vetores L=(α,β..)

1.α+β=β+α(comutatividade) 2.α+(β+γ)= (α+β)+γ, (ab)α=a(bα)(associatividade) 3.α+θ=α, α∙1=α(existência de neutro) 4.α+(-α)=θ (existência de oposto)

a(α+β)=aα+aβ, (a+b)α=aα+bα. Documentação (|(a+b)α|=|a+b||α|, |aα|=|a||α|,|bα|=|b||α|, a e b>0, |a +b|=a+b,|a|=a,|b|=b.) aα+(-a)α=θ, (a+0)α=aα

Um exemplo de espaço linear é um conjunto de matrizes de tamanho fixo com operações de adição e multiplicação por um número.

O sistema de vetores lineares é chamado linearmente dependente, se 1.a 1 ,a 2 ..a n ≠0 2. a 1 α 1 ,a 2 α 2 ..a n α n =θ Se o sistema não é linearmente dependente, então é linearmente independente. Considere 1. n=1 α 1 depende. a 1 ≠0, a 1 α 1 =θ, a 1 -1 (a 1 α 1)= a 1 -1∙ θ=θ, (a 1 -1 a 1)α 1 =1∙α 1 =α 1 ; 2. n=2 α 1 ,α 2 dependem. a 1 ≠0, a 1 α 1 + a 2 α 2 =θ, α 1 = -a 1 -1 a 2 α 2 = b 2 α 2; 3.n≥2 α 1 ..α n dependente. a 1 ≠0, α 1 =Σ k =2 n b k α k , 1α 1 - Σ k =2 n b k α k =θ, (1,b 2 ..b n)≠0

Frase: Um sistema de vetores contendo mais de 1 vetor é linearmente dependente, então algum vetor do sistema é uma combinação linear dos outros.

Se um sistema de vetores contém um subsistema linearmente dependente, então todo o sistema é linearmente dependente. Documentação: (α 1 ..α n dependente. Sistema: α 1 ..α n ;α n +1 ..α m , a 1 α 1 +..+a n α n +0α n +1 +.. +0α m =θ, a 1 ..a n ,0..0≠0.) Se o sistema contém um vetor nulo, então ele é linearmente dependente. Teorema dos espaços lineares: (Seja dado 2 sistemas de vetores α 1 ..α m , β 1 ..β n. O sistema de vetores α é expresso em termos de β se cada vetor α for uma combinação linear β α i = Σ k =1 n a ik β k , (α ) ( (β), (β) ( (γ)→ (α) ( (γ)) Teorema: Dados 2 sistemas de vetores, α é independente e, (α) ( (β)→m≤n Provemos que α 1 ..α m +1 β 1 ..β m (α) ( (β)→(α ) depende (Vamos provar por indução. m=1: α 1 =a 11 β 1 , α 2 =a 21 β 1. a 11 =0→ α 1 =θ. a 11 α 2 – a 21 α 1 = a 11 a 21 β 1 - a 21 a 11 β 1 =θ. α 1 = a 11 β 1 +.. a 1 n -1 β n -1 .. α n = a n 1 β 1 + .. a nn -1 β n - 1 Se todos os coeficientes =0 a 11 =a 12 =..=a 1 n -1 =0→ α 1 =θ→ todo o sistema é linearmente dependente a 1 n -1 ≠0 α 2 ′= α 2 – с 2 α 1 =b 21 β 1 +..+b 2 n -2 β n -2 , c 2 =a 2 n -1 / a 1 n -1 , α 3 ′= α 3 –с 3 α 1 . . α n ′= α n –с n α 1. Por pré-indução, existe um conjunto diferente de zero de números d 2 ..d n: d 2 α 2 ′+d 3 α 3 ′+.. d n α n ′=θ , d 2 ( α 2 –с 2 α 1)+d 3 (α 3 –с 3 α 1)+.. d n (α n –с n α 1)=θ , (α) ( (β) , m>n →(α )depende se (α) independente →m≤n)

MLNP-max.line.independent.subsystem. Seja dado um sistema de vetores α 1 ..α n de algum subsistema. α i 1 ..α in é chamado de MLIS se 1. α 1 ..α n é independente2. α i 1 ..α ir , α ij depende. Cada vetor do sistema é uma combinação linear de vetores MLLM. ( α i 1 ..α ir , α ij dependente a i 1 α i 1 +.. a ir α ir +a ij α ij =θ

a i 1 ..a ir , a ij ≠0 se a ij =0 → a i 1 α i 1 +.. a ir α ir =θ a i 1 ..a ir =0 contradição a ij ≠0 α ij = a ij - 1 (-a i 1 α i 1 -.. a ir α ir) (α 1 ..α n) ( (α i 1 ..α ir)

Consequência: Qualquer 2 MLIS de um sistema de vetores contém o mesmo número de vetores (α i 1 ..α ir) ( (α j 1 ..α jk) , (α j 1 ..α jk) ( (α i 1 . .α ir ) k≤r, r≤k →r=k O número de vetores MLLM é chamado classificação sistema original. No caso de um espaço linear (um sistema de vetores consiste em todos os vetores no espaço), o MLLM mb é finito ou infinito. Consideramos o caso final. O número de vetores (rank) é a dimensão do espaço linear. base MLNP. O espaço dos segmentos direcionados. Dois vetores não colineares formam base no espaço de vetores no plano. α 3 = α 1 ′+ α 2 ′ = a 1 α 1 + a 2 α 2 . 3 vetores linearmente dependentes α 3 =a 1 α 1 + a 2 α 2 . Complanaridade - 3 vetores são paralelos ao mesmo plano α 4 = α 4 ′+ α 5 ′ , α 4 ′=a 1 α 1 + a 2 α 2 , α 5 ′= a 3 α 3 , α 4 = a 1 α 1 + a 2 α 2 + a 3 α 3 . Espaço de strings de comprimento n. α= Frase: O espaço de strings de comprimento n tem dimensão n. (ξ 1 =<1…0>ξ2 =<0,1…0>.. n =<0…1>,a 1 ξ 1 + a 2 ξ 2 +.. a n ξ n =θ=<0,..0> → a 1 =a 2 =..a n =0 (independência linear) β= β= b 1 ξ 1 + b 2 ξ 2 +.. b n ξ n →o espaço de strings de comprimento n tem dimensão e n.

Classificação da matriz.

Dois sistemas de vetores α e β são chamados equivalentes se cada vetor

α( β(expresso) e β( α.

Frase. As fileiras dos sistemas equivalentes coincidem.

α i 1 , α i 2 ,…, α ir – MLLM α , β i 1 , β i 2 ,…, β ik – MLLM β , α i 1 , α i 2 ,…, α ir< β < β i 1 , β i 2 ,…, β ik → r<=k

Trocando as posições de α e β → r>=k >>> Portanto, r=k.

Definição. Seja a matriz A=

α i =

Classificação da matriz A é chamado de posto do sistema de vetores α1, α2,…, αm, composto por esta matriz >>rank(A)-rank

A partir da definição, é óbvio que, quando as colunas são reorganizadas, a classificação não muda. Vamos mostrar que, quando as colunas são reorganizadas, a classificação também não muda.

A'=

α'i=

Dependente linear:

b 1 α 1 + b 2 α 2 +…+ b m α m =θ, b 1 a 11 +b 2 a 21 +…+b m a m 1=0, b 1 α' 1 + b 2 α' 2 +…+ b m α' m , b 1 a 11 +b 2 a 21 +…+b m a m 1=0

É igual à soma dos produtos dos elementos de alguma linha ou coluna e seus complementos algébricos, ou seja, , onde i 0 é fixo.
A expressão (*) é chamada de decomposição do determinante D em termos dos elementos da linha com o número i 0 .

Atribuição de serviço. Este serviço destina-se a encontrar o determinante da matriz online com a execução de toda a solução em formato Word. Além disso, um modelo de solução é criado no Excel.

Instrução. Selecione a dimensão da matriz, clique em Avançar.

Dimensão da matriz 2 3 4 5 6 7 8 9 10

Existem duas maneiras de calcular o determinante: por definição e decomposição por linha ou coluna. Se você deseja encontrar o determinante criando zeros em uma das linhas ou colunas, pode usar esta calculadora.

Algoritmo para encontrar o determinante

1. Para matrizes de ordem n=2, o determinante é calculado pela fórmula: Δ=a 11 *a 22 -a 12 *a 21
2. Para matrizes de ordem n=3, o determinante é calculado por meio de adições algébricas ou método Sarrus.
3. Uma matriz com dimensão maior que três é decomposta em adições algébricas, para as quais são calculados seus determinantes (menores). Por exemplo, Determinante da matriz de 4ª ordemé encontrado através da expansão em linhas ou colunas (ver exemplo).

Para calcular o determinante contendo funções na matriz, métodos padrão são usados. Por exemplo, calcule o determinante de uma matriz de 3ª ordem:

Vamos usar a expansão da primeira linha.
Δ = sin(x)× + 1× = 2sin(x)cos(x)-2cos(x) = sin(2x)-2cos(x)

Métodos para calcular determinantes

Encontrando o determinante por meio de adições algébricasé um método comum. Sua versão simplificada é o cálculo do determinante pela regra de Sarrus. No entanto, com uma grande dimensão de matriz, os seguintes métodos são usados:

1. cálculo do determinante por redução de ordem
2. cálculo do determinante pelo método gaussiano (reduzindo a matriz a uma forma triangular).

No Excel, para calcular o determinante, utiliza-se a função = MOPRED (intervalo de células).

Uso aplicado de determinantes

Os determinantes são calculados, via de regra, para um sistema específico, dados na forma de uma matriz quadrada. Considere alguns tipos de tarefas em encontrando o determinante da matriz. Às vezes é necessário encontrar um parâmetro desconhecido a para o qual o determinante seria igual a zero. Para fazer isso, é necessário elaborar uma equação para o determinante (por exemplo, de acordo com regra do triângulo) e, igualando a 0 , calcule o parâmetro a .
decomposição por colunas (pela primeira coluna):
Menor para (1,1): Exclua a primeira linha e a primeira coluna da matriz.
Vamos encontrar o determinante para este menor. ∆ 1,1 \u003d (2 (-2) -2 1) \u003d -6.

Vamos determinar o menor para (2,1): para fazer isso, excluímos a segunda linha e a primeira coluna da matriz.

Vamos encontrar o determinante para este menor. ∆ 2,1 = (0 (-2)-2 (-2)) = 4 . Menor para (3,1): Exclua a 3ª linha e a 1ª coluna da matriz.
Vamos encontrar o determinante para este menor. ∆ 3,1 = (0 1-2 (-2)) = 4
O determinante principal é: ∆ = (1 (-6)-3 4+1 4) = -14

Vamos encontrar o determinante usando expansão por linhas (pela primeira linha):
Menor para (1,1): Exclua a primeira linha e a primeira coluna da matriz.

Vamos encontrar o determinante para este menor. ∆ 1,1 \u003d (2 (-2) -2 1) \u003d -6. Menor para (1,2): Exclua a 1ª linha e a 2ª coluna da matriz. Vamos calcular o determinante para este menor. ∆ 1,2 \u003d (3 (-2) -1 1) \u003d -7. E para encontrar o menor para (1,3) excluímos a primeira linha e a terceira coluna da matriz. Vamos encontrar o determinante para este menor. ∆ 1,3 = (3 2-1 2) = 4
Encontramos o determinante principal: ∆ \u003d (1 (-6) -0 (-7) + (-2 4)) \u003d -14

Sistema de m equações lineares com n incógnitas chamado de sistema da forma

Onde aij e b eu (eu=1,…,m; b=1,…,n) são alguns números conhecidos, e x 1 ,…,x n- desconhecido. Na notação dos coeficientes aij primeiro índice eu denota o número da equação, e o segundo jé o número da incógnita em que esse coeficiente se encontra.

Os coeficientes para as incógnitas serão escritos na forma de uma matriz , que chamaremos matriz do sistema.

Os números do lado direito das equações b 1 ,…, b m chamado membros livres.

Agregar n números c 1 ,…,c n chamado decisão deste sistema, se cada equação do sistema se tornar uma igualdade após a substituição de números nela c 1 ,…,c n em vez das incógnitas correspondentes x 1 ,…,x n.

Nossa tarefa será encontrar soluções para o sistema. Neste caso, podem surgir três situações:

Um sistema de equações lineares que tem pelo menos uma solução é chamado articulação. Caso contrário, ou seja se o sistema não tem soluções, então ele é chamado incompatível.

Considere maneiras de encontrar soluções para o sistema.

MÉTODO DE MATRIZ PARA RESOLUÇÃO DE SISTEMAS DE EQUAÇÕES LINEARES

As matrizes permitem escrever brevemente um sistema de equações lineares. Seja dado um sistema de 3 equações com três incógnitas:

Considere a matriz do sistema 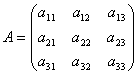e colunas de matrizes de membros desconhecidos e livres

Vamos encontrar o produto

Essa. como resultado do produto, obtemos os lados esquerdos das equações desse sistema. Então, usando a definição de igualdade de matrizes, esse sistema pode ser escrito como

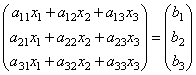ou mais curto UMA∙X=B.

Aqui matrizes UMA e B são conhecidos, e a matriz x desconhecido. Ela precisa ser encontrada, porque. seus elementos são a solução desse sistema. Esta equação é chamada equação matricial.

Seja o determinante da matriz diferente de zero | UMA| ≠ 0. Então a equação da matriz é resolvida como segue. Multiplique ambos os lados da equação à esquerda pela matriz A-1, a inversa da matriz UMA: . Porque o A -1 A = E e E∙X=X, então obtemos a solução da equação matricial na forma X = A -1 B .

Observe que, como a matriz inversa só pode ser encontrada para matrizes quadradas, o método da matriz só pode resolver os sistemas em que o número de equações é igual ao número de incógnitas. No entanto, a notação matricial do sistema também é possível no caso em que o número de equações não é igual ao número de incógnitas, então a matriz UMA não é quadrado e, portanto, é impossível encontrar uma solução para o sistema na forma X = A -1 B.

Exemplos. Resolver sistemas de equações.

REGRA DE CRAMER

Considere um sistema de 3 equações lineares com três incógnitas:

Determinante de terceira ordem correspondente à matriz do sistema, ou seja, composto de coeficientes em incógnitas,

chamado determinante do sistema.

Compomos mais três determinantes da seguinte forma: substituímos sucessivamente 1, 2 e 3 colunas no determinante D por uma coluna de membros livres

Então podemos provar o seguinte resultado.

Teorema (regra de Cramer). Se o determinante do sistema for Δ ≠ 0, então o sistema em questão tem uma e apenas uma solução, e

Prova. Então, considere um sistema de 3 equações com três incógnitas. Multiplique a 1ª equação do sistema pelo complemento algébrico A 11 elemento um 11, 2ª equação - em A21 e 3º - em A 31:

Vamos somar estas equações:

Considere cada um dos colchetes e o lado direito desta equação. Pelo teorema da expansão do determinante em termos dos elementos da 1ª coluna

Da mesma forma, pode-se mostrar que e .

Finalmente, é fácil ver que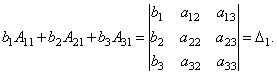

Assim, obtemos a igualdade: .

Consequentemente, .

As igualdades e são derivadas de forma semelhante, de onde segue a afirmação do teorema.

Assim, notamos que se o determinante do sistema for Δ ≠ 0, então o sistema tem solução única e vice-versa. Se o determinante do sistema for igual a zero, então o sistema tem um conjunto infinito de soluções ou não tem soluções, ou seja, incompatível.

Exemplos. Resolver um sistema de equações

MÉTODO GAUSS

Os métodos considerados anteriormente podem ser usados ​​​​para resolver apenas os sistemas nos quais o número de equações coincide com o número de incógnitas e o determinante do sistema deve ser diferente de zero. O método gaussiano é mais universal e adequado para sistemas com qualquer número de equações. Consiste na eliminação sucessiva de incógnitas das equações do sistema.

Considere novamente um sistema de três equações com três incógnitas:

.

Deixamos a primeira equação inalterada e da 2ª e 3ª excluímos os termos que contêm x 1. Para fazer isso, dividimos a segunda equação por uma 21 e multiplique por - uma 11 e depois some com a 1ª equação. Da mesma forma, dividimos a terceira equação em uma 31 e multiplique por - uma 11 e, em seguida, adicioná-lo ao primeiro. Como resultado, o sistema original terá a forma:

Agora, da última equação, eliminamos o termo que contém x2. Para fazer isso, divida a terceira equação por , multiplique por e some à segunda. Teremos então um sistema de equações:

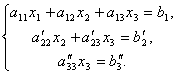
Portanto, a partir da última equação, é fácil encontrar x 3, então da 2ª equação x2 e finalmente a partir do dia 1 - x 1.

Ao usar o método gaussiano, as equações podem ser trocadas, se necessário.

Freqüentemente, em vez de escrever um novo sistema de equações, eles se limitam a escrever a matriz estendida do sistema:

e depois trazê-lo para uma forma triangular ou diagonal usando transformações elementares.

Para transformações elementares matrizes incluem as seguintes transformações:

1. permutação de linhas ou colunas;
2. multiplicar uma string por um número diferente de zero;
3. adicionando a uma linha outras linhas.

Exemplos: Resolver sistemas de equações usando o método de Gauss.

Assim, o sistema tem um número infinito de soluções.

2.Se │A│=0, então a matriz A é degenerada e a matriz inversa A -1 não existe.

Se o determinante da matriz A não for igual a zero, então a matriz inversa existe.

3. Encontre A T transposto para A.

4. Encontre os complementos algébricos dos elementos da matriz transposta e componha a matriz adjunta a partir deles. 5. Calculamos a matriz inversa de acordo com a fórmula: 6. Verifique a exatidão do cálculo da matriz inversa, com base em sua definição A -1 ∙A = A ∙A -1 = E.

· №28

· Em uma matriz m x n, excluindo quaisquer linhas e colunas, pode-se selecionar submatrizes quadradas de ordem k, onde k≤min(m; n). Os determinantes de tais submatrizes são chamados de menores de ordem k da matriz A.

· O posto de uma matriz A é a ordem mais alta dos menores não nulos dessa matriz.

· O posto de uma matriz A é denotado por rang A ou r(A).

· Da definição segue:

· 1) o posto de uma matriz de tamanho m x n não excede o menor de seus tamanhos, ou seja, r(A) ≤ min (m; n).

· 2) r(A)=0 se e somente se todos os elementos da matriz forem iguais a zero, ou seja, A=0.

· 3) Para uma matriz quadrada de ordem n, r(A) = n se e somente se a matriz A é não singular.

· No caso geral, determinar o posto de uma matriz pela enumeração de todos os menores é bastante trabalhoso. Para facilitar esta tarefa, são utilizadas transformações elementares que preservam o posto da matriz:

· 1) Rejeição da linha (coluna) zero.

· 2) Multiplicação de todos os elementos de uma linha (coluna) de uma matriz por um número diferente de zero.

· 3) Alteração da ordem das linhas (colunas) da matriz.

· 4) Somar a cada elemento de uma linha (coluna) os elementos correspondentes de outra linha (coluna), multiplicado por qualquer número.

· 5) Transposição de matrizes.

· Teorema. O posto de uma matriz não mudará sob transformações elementares da matriz.

№31

— Deixe o número de equações no sistema (1) ser igual ao número de variáveis, ou seja, m=n. Então a matriz do sistema é quadrada, e seu determinante Δ=│А│ é chamado de determinante do sistema.

— Suponha que │А│ não seja igual a zero, então existe uma matriz inversa A -1 .

— Multiplicando ambas as partes da igualdade da matriz à esquerda pela matriz inversa A -1, obtemos:

— A -1 (AX) \u003d A -1 B.

A solução do sistema de equações pelo método da matriz inversa será a matriz coluna:

X \u003d A -1 B.

(A -1 A)X \u003d EX \u003d X

— Teorema de Cramer. Seja Δ o determinante da matriz do sistema A, e Δj seja o determinante da matriz obtida da matriz substituindo a j-ésima coluna por uma coluna de termos livres. Então, se Δ não for igual a zero, então o sistema tem uma solução única definida pelas fórmulas de Cramer:

onde j=1..n.

№33

—
O método de Gauss - o método de eliminação sucessiva de variáveis ​​- consiste no fato de que, com a ajuda de transformações elementares, o sistema de equações é reduzido a um sistema equivalente de forma escalonada ou triangular.

— Considere a matriz:

— esta matriz é chamada de matriz estendida do sistema (1), porque além da matriz do sistema A, inclui adicionalmente uma coluna de membros livres.

№26

— Um vetor N-dimensional é um conjunto ordenado de n números reais escritos como X=(x 1,x 2,...x n) , onde x i é a i-ésima componente do vetor X.

— Dois vetores n-dimensionais são iguais se e somente se seus respectivos componentes são iguais, ou seja, X=Y se x i =y i , i=1…n.

O conjunto de vetores com componentes reais, no qual são definidas as operações de adição de vetores e multiplicação de um vetor por um número que satisfaça as propriedades acima, é chamado de espaço vetorial.

— Um espaço vetorial R é chamado de n-dimensional se houver n vetores linearmente independentes nele e quaisquer n + 1 vetores já forem dependentes. O número n é chamado de dimensão do espaço vetorial R e é denotado por dim(R).

№29

Operadores lineares

— Definição. Se for dada uma lei (regra), segundo a qual cada vetor x do espaço está associado a um único vetor y do espaço

então eles dizem: que o operador (transformação, mapeamento) A(x) é dado, agindo de a e

escreva y=A(x).

— Um operador é chamado linear se para qualquer vetor x e y do espaço

e qualquer número λ, valem as seguintes relações:

№37

— Seja A um conjunto formado por um número finito de elementos a 1 , a 2 , a 3 …a n . Grupos podem ser formados a partir de vários elementos do conjunto A. Se cada grupo inclui o mesmo número de elementos m (m de n), diz-se que eles formam compostos de n elementos com m cada. Existem três tipos de conexões: posicionamentos, combinações e permutações.

— conexões, cada uma das quais inclui todos os n elementos do conjunto A e que, portanto, diferem umas das outras apenas na ordem dos elementos são chamadas de permutações de n elementos. O número de tais permutações é denotado pelo símbolo Р n .

№35

A definição clássica de probabilidade é baseada no conceito de equiprobabilidade dos eventos.

Equivalência de eventos significa que não há razão para preferir qualquer um deles em detrimento de outros.

Vamos considerar um teste, como resultado do qual pode ocorrer o evento A. Cada resultado, no qual ocorre o evento A, é chamado de evento favorável A.

A probabilidade de um evento A (denotado por P(A)) é a razão entre o número de resultados favoráveis ​​ao evento A (denotado por k) e o número de todos os resultados do teste - N, ou seja, P(A)=k/N.

— As seguintes propriedades decorrem da definição clássica de probabilidade:

— A probabilidade de qualquer evento situa-se entre zero e um.

— A probabilidade de um determinado evento é igual a um.

— A probabilidade de um evento impossível é zero

№39, 40

— Teorema da adição. Se A e B são inconsistentes, então P(A + B) = P(A) + P(B)