critério de Fisher

O critério de Fisher é usado para testar a hipótese sobre a igualdade das variâncias de duas populações gerais distribuídas de acordo com a lei normal. É um critério paramétrico.

O teste F de Fisher é chamado de razão de variância, uma vez que é formado como a razão de duas estimativas de variâncias não viesadas comparadas.

Sejam obtidas duas amostras como resultado das observações. Com base neles, as variações e tendo e graus de liberdade. Vamos supor que a primeira amostra seja retirada da população geral com uma variância , e o segundo - da população geral com uma variância . A hipótese nula é apresentada sobre a igualdade das duas variâncias, ou seja, H0:
ou . Para rejeitar esta hipótese, é necessário provar a significância da diferença em um dado nível de significância.
.

O valor do critério é calculado pela fórmula:

Obviamente, se as variâncias forem iguais, o valor do critério será igual a um. Em outros casos, será maior (menos) que um.

O critério tem uma distribuição de Fisher
. O teste de Fisher é um teste bicaudal, e a hipótese nula
rejeitado em favor da alternativa
E se . Aqui onde
são os volumes da primeira e segunda amostras, respectivamente.

O sistema STATISTICA implementa um teste de Fisher unicaudal, ou seja, como sempre tomar a dispersão máxima. Nesse caso, a hipótese nula é rejeitada em favor da alternativa se .

Exemplo

Deixe a tarefa ser definida para comparar a eficácia do treinamento de dois grupos de alunos. O nível de progresso caracteriza o nível de gestão do processo de aprendizagem, e a dispersão caracteriza a qualidade da gestão da aprendizagem, o grau de organização do processo de aprendizagem. Ambos os indicadores são independentes e geralmente devem ser considerados em conjunto. O nível de progresso (expectativa matemática) de cada grupo de alunos é caracterizado pela média aritmética e , e a qualidade é caracterizada pelas variâncias amostrais correspondentes das estimativas: e . Ao avaliar o nível de desempenho atual, verificou-se que é o mesmo para ambos os alunos: == 4,0. Variações de amostra:
e
. O número de graus de liberdade correspondentes a essas estimativas:
e
. Assim, para estabelecer diferenças na eficácia do treinamento, podemos usar a estabilidade do desempenho acadêmico, ou seja, vamos testar a hipótese.

Calcular
(o numerador deve ter uma grande variância), . De acordo com as tabelas ( ESTATISTICAS – Probabilidadedistribuiçãocalculadora) encontramos , que é menor que o calculado, portanto, a hipótese nula deve ser rejeitada em favor da alternativa . Essa conclusão pode não satisfazer o pesquisador, pois ele está interessado no verdadeiro valor da razão
(sempre temos uma grande variância no numerador). Ao verificar um critério unilateral, obtemos , que é menor que o valor calculado acima. Assim, a hipótese nula deve ser rejeitada em favor da alternativa.

Teste de Fisher no programa STATISTICA no ambiente Windows

Para um exemplo de teste de uma hipótese (critério de Fisher), usamos (criamos) um arquivo com duas variáveis ​​(fisher.sta):

Arroz. 1. Tabela com duas variáveis ​​independentes

Para testar a hipótese, é necessário nas estatísticas básicas ( BásicoEstatisticasemesas) escolha o teste de Student para variáveis ​​independentes. ( teste t, independente, por variáveis).

Arroz. 2. Testando hipóteses paramétricas

Após selecionar as variáveis ​​e pressionar a tecla Resumo os valores dos desvios padrão e o teste de Fisher são calculados. Além disso, o nível de significância é determinado p, onde a diferença é insignificante.

Arroz. 3. Resultados do teste da hipótese (teste F)

Usando Probabilidadecalculadora e definindo o valor dos parâmetros, você pode plotar a distribuição de Fisher com uma marca do valor calculado.

Arroz. 4. Área de aceitação (rejeição) da hipótese (critério F)

Fontes.

Testando hipóteses sobre a relação de duas variâncias

URL: /tryphonov3/terms3/testdi.htm

Aula 6. :8080/resources/math/mop/lections/lection_6.htm

F - Critério Fisher

URL: /home/portal/applications/Multivariatadvisor/F-Fisheer/F-Fisheer.htm

Teoria e prática da pesquisa probabilística e estatística.

URL: /active/referats/read/doc-3663-1.html

F - Critério Fisher

Neste exemplo, vamos considerar como a confiabilidade da equação de regressão obtida é estimada. O mesmo teste é usado para testar a hipótese de que os coeficientes de regressão são ambos zero, a=0 , b=0 . Em outras palavras, a essência dos cálculos é responder à pergunta: ele pode ser usado para análises e previsões posteriores?

Use este teste t para determinar a semelhança ou diferença entre as variâncias em duas amostras.

Assim, o objetivo da análise é obter alguma estimativa, com a ajuda da qual seria possível afirmar que, em um determinado nível de α, a equação de regressão resultante é estatisticamente confiável. Por esta o coeficiente de determinação R 2 é usado.
A significância do modelo de regressão é verificada por meio do teste F de Fisher, cujo valor calculado é encontrado como a razão da variância da série inicial de observações do indicador estudado e a estimativa imparcial da variância da sequência residual para este modelo.
Se o valor calculado com k 1 =(m) ek 2 =(n-m-1) graus de liberdade for maior que o valor tabular em um determinado nível de significância, então o modelo é considerado significativo.

onde m é o número de fatores no modelo.
A avaliação da significância estatística da regressão linear pareada é realizada de acordo com o seguinte algoritmo:
1. É apresentada uma hipótese nula de que a equação como um todo é estatisticamente insignificante: H 0: R 2 =0 ao nível de significância α.
2. Em seguida, determine o valor real do critério F:


onde m=1 para regressão aos pares.
3. O valor da tabela é determinado a partir das tabelas de distribuição de Fisher para um determinado nível de significância, levando em consideração que o número de graus de liberdade para a soma total dos quadrados (variância maior) é 1 e o número de graus de liberdade para a soma residual de quadrados (variância menor) na regressão linear é n-2 (ou através da função Excel FDISP(probabilidade, 1, n-2)).
A tabela F é o valor máximo possível do critério sob a influência de fatores aleatórios para determinados graus de liberdade e nível de significância α. Nível de significância α - a probabilidade de rejeitar a hipótese correta, desde que seja verdadeira. Normalmente α é considerado igual a 0,05 ou 0,01.
4. Se o valor real do critério F for menor que o valor da tabela, eles dizem que não há razão para rejeitar a hipótese nula.
Caso contrário, a hipótese nula é rejeitada e a hipótese alternativa sobre a significância estatística da equação como um todo é aceita com probabilidade (1-α).
Valor da tabela do critério com graus de liberdade k 1 =1 ek 2 =48, tabela F = 4

conclusões: Uma vez que o valor real da tabela F > F, o coeficiente de determinação é estatisticamente significativo ( a estimativa encontrada da equação de regressão é estatisticamente confiável) .

Análise de variação

.

Indicadores de qualidade da equação de regressão

Exemplo. Com base em um total de 25 empresas comerciais, a relação entre os sinais é estudada: X - o preço das mercadorias A, mil rublos; Y - lucro de uma empresa comercial, milhões de rublos. Ao avaliar o modelo de regressão, obtiveram-se os seguintes resultados intermediários: ∑(y i -y x) 2 = 46000; ∑(y i -y sr) 2 = 138000. Que indicador de correlação pode ser determinado a partir desses dados? Calcule o valor deste indicador, com base neste resultado e usando Teste F de Fisher tirar uma conclusão sobre a qualidade do modelo de regressão.
Solução. Com base nesses dados, uma correlação empírica pode ser determinada: , onde ∑(y cf -y x) 2 = ∑(y i -y cf) 2 - ∑(y i -y x) 2 = 138.000 - 46.000 = 92.000.
η 2 = 92.000/138.000 = 0,67, η = 0,816 (0,7< η < 0.9 - связь между X и Y высокая).

Teste F de Fisher: n = 25, m = 1.
R 2 \u003d 1 - 46000 / 138000 \u003d 0,67, F \u003d 0,67 / (1-0,67)x (25 - 1 - 1) \u003d 46. F tabela (1; 23) \u003d 4,27
Como o valor real de F > Ftabl, a estimativa encontrada da equação de regressão é estatisticamente confiável.

Pergunta: Que estatística é usada para testar a significância de um modelo de regressão?
Resposta: Para a significância de todo o modelo como um todo, são usadas estatísticas F (critério de Fisher).

Para comparar duas populações normalmente distribuídas que não têm diferenças nas médias amostrais, mas há uma diferença nas variâncias, use critério de Fisher. O critério real é calculado pela fórmula:

onde o numerador é o maior valor da variância da amostra e o denominador é o menor valor. Para inferir a significância das diferenças entre as amostras, usamos O PRINCÍPIO BÁSICO teste de hipóteses estatísticas. Pontos críticos para
estão contidos na tabela. A hipótese nula é rejeitada se o valor real
excederá ou será igual ao valor crítico (padrão)
este valor para o nível de significância aceito  e número de graus de liberdade k 1 = n grande -1 ; k 2 = n menor -1 .

Exemplo: ao estudar o efeito de uma determinada droga na taxa de germinação de sementes, verificou-se que no lote experimental de sementes e controle, a taxa média de germinação é a mesma, mas há diferença na dispersão.
=1250,
=417. Os tamanhos amostrais são os mesmos e iguais a 20.

=2,12. Portanto, a hipótese nula é rejeitada.

dependência de correlação. Coeficiente de correlação e suas propriedades. Equações de regressão.

UMA TAREFA a análise de correlação é reduzida para:

Estabelecer a direção e a forma de comunicação entre os signos;

medindo sua estanqueidade.

funcional uma relação um-para-um entre variáveis ​​é chamada quando um certo valor de uma variável (independente) X , chamado de argumento, corresponde a um valor específico de outra variável (dependente) no chamado de função. ( Exemplo: dependência da velocidade de uma reação química com a temperatura; dependência da força de atração nas massas dos corpos atraídos e a distância entre eles).

correlação chama-se uma relação entre variáveis ​​de natureza estatística, quando um determinado valor de um recurso (considerado como variável independente) corresponde a toda uma série de valores numéricos de outro recurso. ( Exemplo: relação entre produtividade e precipitação; entre altura e peso, etc.).

Campo de correlação é um conjunto de pontos cujas coordenadas são iguais aos pares de valores de variáveis ​​obtidos experimentalmente X e no .

Pela forma do campo de correlação, pode-se julgar a presença ou ausência de uma conexão e seu tipo.

A ligação é chamada positivo se aumentar uma variável aumenta outra variável.

A ligação é chamada negativo quando um aumento em uma variável diminui outra variável.

A ligação é chamada linear , se puder ser representado analiticamente como
.

Um indicador do aperto da conexão é coeficiente de correlação . O coeficiente de correlação empírica é dado por:

O coeficiente de correlação está na faixa de -1 antes da 1 e caracteriza o grau de proximidade entre as quantidades x e y . Se um:

A dependência de correlação entre as características pode ser descrita de diferentes maneiras. Em particular, qualquer forma de conexão pode ser expressa por uma equação geral
. Tipo de equação
e
chamado regressão . Equação de regressão direta no no X em geral pode ser escrito na forma

Equação de regressão direta X no no geralmente parece

Os valores mais prováveis ​​dos coeficientes uma e dentro, Com e d pode ser calculado, por exemplo, usando o método dos mínimos quadrados.

critério de Fisher permite comparar os valores das variâncias da amostra de duas amostras independentes. Para calcular F emp, você precisa encontrar a razão das variâncias de duas amostras, de modo que a maior variância fique no numerador e a menor no denominador. A fórmula para calcular o critério de Fisher é a seguinte:

onde são as variâncias da primeira e segunda amostras, respectivamente.

Como, conforme a condição do critério, o valor do numerador deve ser maior ou igual ao valor do denominador, o valor de Femp será sempre maior ou igual a um.

O número de graus de liberdade também é simplesmente definido:

k 1 =n eu - 1 para a primeira amostra (ou seja, para a amostra cuja variância é maior) e k 2 = n 2 - 1 para a segunda amostra.

No Anexo 1, os valores críticos do critério de Fisher são encontrados pelos valores k 1 (linha superior da tabela) e k 2 (coluna esquerda da tabela).

Se t emp >t crit, então a hipótese nula é aceita, caso contrário a alternativa é aceita.

Exemplo 3 Nas duas terceiras séries, dez alunos foram testados quanto ao desenvolvimento mental de acordo com o teste TURMS. Os valores médios obtidos não diferiram significativamente, no entanto, o psicólogo está interessado em saber se existem diferenças no grau de homogeneidade dos indicadores de desenvolvimento mental entre as classes.

Solução. Para o critério de Fisher, é necessário comparar as variâncias dos escores dos testes em ambas as classes. Os resultados do teste são apresentados na tabela:

Tabela 3

Nº de alunos	Primeira série	Segunda classe

Tendo calculado as variâncias para as variáveis ​​X e Y, temos:

s x 2 =572,83; s y 2 =174,04

Então, de acordo com a fórmula (8) para o cálculo de acordo com o critério de F Fisher, encontramos:

De acordo com a tabela do Apêndice 1 para o critério F com graus de liberdade em ambos os casos iguais a k=10 - 1 = 9 encontramos F crit = 3,18 (<3.29), следовательно, в терминах статистических гипотез можно утвер­ждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

6.2 Testes não paramétricos

Comparando a olho (por porcentagem) os resultados antes e depois de qualquer exposição, o pesquisador chega à conclusão de que, se forem observadas diferenças, haverá diferença nas amostras comparadas. Tal abordagem é categoricamente inaceitável, pois é impossível determinar o nível de confiança nas diferenças para percentuais. As porcentagens tomadas por si só não permitem tirar conclusões estatisticamente confiáveis. Para comprovar a eficácia de qualquer impacto, é necessário identificar uma tendência estatisticamente significativa no deslocamento (shift) dos indicadores. Para resolver tais problemas, o pesquisador pode utilizar uma série de critérios de diferença. A seguir, serão considerados os testes não paramétricos: o teste do sinal e o teste do qui-quadrado.

A função FISHER retorna a transformação Fisher dos argumentos X . Essa transformação cria uma função que tem uma distribuição normal em vez de assimétrica. A função FISHER é usada para testar a hipótese usando o coeficiente de correlação.

Descrição da função FISHER no Excel

Ao trabalhar com esta função, você deve definir o valor da variável. Deve-se notar imediatamente que existem algumas situações em que esta função não produzirá resultados. Isso é possível se a variável:

• não é um número. Em tal situação, a função FISHER retornará o valor de erro #VALUE!;
• é menor que -1 ou maior que 1. Nesse caso, a função FISHER retornará o valor de erro #NUM!.

A equação que é usada para descrever matematicamente a função FISHER é:

Z"=1/2*ln(1+x)/(1-x)

Vamos considerar a aplicação desta função em 3 exemplos específicos.



Avaliação da relação entre lucro e custos usando a função FISHER

Exemplo 1. Usando dados sobre a atividade das organizações comerciais, é necessário fazer uma avaliação da relação entre o lucro Y (milhões de rublos) e os custos X (milhões de rublos) usados ​​para desenvolver produtos (dado na tabela 1).

Tabela 1 - Dados iniciais:

№	X	S
1	RUB 210.000.000,00	$ 95.000.000,00
2	RUB 1.068.000.000,00	RUB 76.000.000,00
3	RUB 1.005.000.000,00	RUB 78.000.000,00
4	RUB 610.000.000,00	RUB 89.000.000,00
5	RUB 768.000.000,00	RUB 77.000.000,00
6	RUB 799.000.000,00	RUB 85.000.000,00

O esquema para resolver tais problemas é o seguinte:

1. O coeficiente de correlação linear r xy é calculado;
2. A significância do coeficiente de correlação linear é verificada com base no teste t de Student. Ao mesmo tempo, a hipótese sobre a igualdade do coeficiente de correlação a zero é apresentada e testada. Ao testar essa hipótese, a estatística t é usada. Se a hipótese for confirmada, a estatística t tem distribuição de Student. Se o valor calculado t p > t cr, então a hipótese é rejeitada, o que indica a significância do coeficiente de correlação linear e, consequentemente, a significância estatística da relação entre X e Y;
3. Uma estimativa de intervalo para um coeficiente de correlação linear estatisticamente significativo é determinada.
4. Uma estimativa de intervalo para o coeficiente de correlação linear é determinada com base na transformada z de Fisher inversa;
5. O erro padrão do coeficiente de correlação linear é calculado.

Os resultados da solução desse problema com as funções usadas no pacote Excel são mostrados na Figura 1.

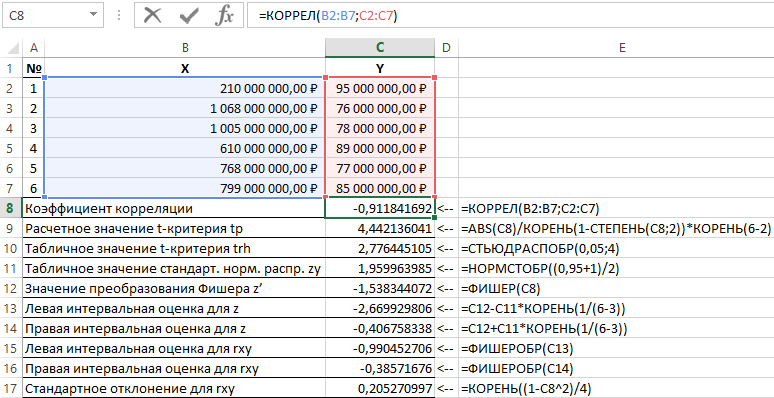
Figura 1 - Exemplo de cálculos.

Nº p/p	Nome do indicador	Fórmula de cálculo
1	Coeficiente de correlação	=CORREL(B2:B7,C2:C7)
2	Valor estimado do critério t tp	=ABS(C8)/RAIZ(1-POWER(C8,2))*RAIZ(6-2)
3	Valor da tabela do teste t trh	=ESTUDAR(0,05,4)
4	Valor de tabela da distribuição normal padrão zy	=NORMINV((0,95+1)/2)
5	Valor da transformada de Fischer z'	=PESCADOR(C8)
6	Estimativa do intervalo esquerdo para z	=C12-C11*RAIZ(1/(6-3))
7	Estimativa de intervalo certo para z	=C12+C11*RAIZ(1/(6-3))
8	Estimativa de intervalo esquerdo para rxy	=FISCHEROBR(C13)
9	Estimativa de intervalo certo para rxy	=FISCHEROBR(C14)
10	Desvio padrão para rxy	=RAIZ((1-C8^2)/4)

Assim, com uma probabilidade de 0,95, o coeficiente de correlação linear encontra-se na faixa de (–0,386) a (–0,990) com um erro padrão de 0,205.

Verificando a significância estatística da regressão na função FDISP

Exemplo 2. Verifique a significância estatística da equação de regressão múltipla usando o teste F de Fisher, tire conclusões.

Para testar a significância da equação como um todo, apresentamos a hipótese H 0 sobre a insignificância estatística do coeficiente de determinação e a hipótese oposta H 1 sobre a significância estatística do coeficiente de determinação:

H 1: R 2 ≠ 0.

Vamos testar as hipóteses usando o teste F de Fisher. Os indicadores são mostrados na tabela 2.

Tabela 2 - Dados iniciais

Para fazer isso, usamos a seguinte função no pacote Excel:

FDISP(α;p;n-p-1)

• α é a probabilidade associada à distribuição dada;
• p e n são o numerador e o denominador dos graus de liberdade, respectivamente.

Sabendo que α = 0,05, p = 2 e n = 53, obtemos o seguinte valor para F crit (ver Figura 2).

Figura 2 - Exemplo de cálculos.

Assim, podemos dizer que F calc > F crit. Como resultado, aceita-se a hipótese H 1 sobre a significância estatística do coeficiente de determinação.

Cálculo do valor do indicador de correlação no Excel

Exemplo 3. Usando os dados de 23 empresas sobre: ​​X - o preço do produto A, mil rublos; Y - lucro de uma empresa comercial, milhões de rublos, sua dependência está sendo estudada. A avaliação do modelo de regressão deu o seguinte: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Que indicador de correlação pode ser determinado a partir desses dados? Calcule o valor do índice de correlação e, usando o critério de Fisher, tire uma conclusão sobre a qualidade do modelo de regressão.

Vamos definir F crit a partir da expressão:

F calc \u003d R 2 / 23 * (1-R 2)

onde R é o coeficiente de determinação igual a 0,67.

Assim, o valor calculado F calc = 46.

Para determinar F crit, usamos a distribuição de Fisher (veja a Figura 3).

Figura 3 - Exemplo de cálculos.

Assim, a estimativa obtida da equação de regressão é confiável.