Valor esperado. expectativa matemática variável aleatória discreta X, que assume um número finito de valores Xeu com probabilidades Reu, é chamado de soma:

expectativa matemática variável aleatória contínua Xé chamado de integral do produto de seus valores X na densidade de distribuição de probabilidade f(x):

(6b)

Integral impróprio (6 b) é assumido como absolutamente convergente (caso contrário, dizemos que a expectativa M(X) não existe). A expectativa matemática caracteriza significa variável aleatória X. Sua dimensão coincide com a dimensão de uma variável aleatória.

Propriedades da esperança matemática:

Dispersão. dispersão variável aleatória X número é chamado:

A dispersão é característica de dispersão valores de uma variável aleatória X em relação ao seu valor médio M(X). A dimensão da variância é igual à dimensão da variável aleatória ao quadrado. Com base nas definições de variância (8) e expectativa matemática (5) para uma variável aleatória discreta e (6) para uma variável aleatória contínua, obtemos expressões semelhantes para a variância:

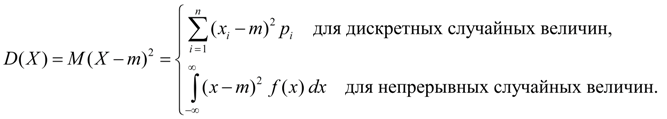(9)

Aqui m = M(X).

Propriedades de dispersão:

Desvio padrão:

(11)

Como a dimensão do desvio padrão é a mesma de uma variável aleatória, é mais frequente que a variância usada como medida de dispersão.

momentos de distribuição. Os conceitos de expectativa matemática e variância são casos especiais de um conceito mais geral para as características numéricas de variáveis ​​aleatórias - momentos de distribuição. Os momentos de distribuição de uma variável aleatória são apresentados como expectativas matemáticas de algumas funções simples de uma variável aleatória. Assim, o momento da ordem k em relação ao ponto X 0 é chamado de expectativa M(X–X 0 )k. Momentos relativos à origem X= 0 são chamados momentos iniciais e estão marcados:

(12)

O momento inicial de primeira ordem é o centro de distribuição da variável aleatória considerada:

(13)

Momentos relativos ao centro de distribuição X= m chamado momentos centrais e estão marcados:

(14)

De (7) segue que o momento central de primeira ordem é sempre igual a zero:

Os momentos centrais não dependem da origem dos valores da variável aleatória, pois com um deslocamento por um valor constante A PARTIR DE seu centro de distribuição é deslocado pelo mesmo valor A PARTIR DE, e o desvio do centro não muda: X – m = (X – A PARTIR DE) – (m – A PARTIR DE).
Agora é óbvio que dispersão- isto é momento central de segunda ordem:

Assimetria. Momento central de terceira ordem:

(17)

serve para avaliar assimetria de distribuição. Se a distribuição é simétrica em relação ao ponto X= m, então o momento central da terceira ordem será igual a zero (assim como todos os momentos centrais das ordens ímpares). Portanto, se o momento central de terceira ordem for diferente de zero, então a distribuição não pode ser simétrica. A magnitude da assimetria é estimada usando um coeficiente de assimetria:

(18)

O sinal do coeficiente de assimetria (18) indica assimetria do lado direito ou do lado esquerdo (Fig. 2).

Arroz. 2. Tipos de assimetria de distribuições.

Excesso. Momento central da quarta ordem:

(19)

serve para avaliar os chamados curtose, que determina o grau de inclinação (pontuação) da curva de distribuição próxima ao centro de distribuição em relação à curva de distribuição normal. Uma vez que para uma distribuição normal, a quantidade tomada como curtose é:

(20)

Na fig. 3 mostra exemplos de curvas de distribuição com diferentes valores de curtose. Para uma distribuição normal E= 0. As curvas mais pontiagudas do que o normal têm curtose positiva e curvas com picos mais planos têm curtose negativa.

Arroz. 3. Curvas de distribuição com diferentes graus de inclinação (curtose).

Momentos de ordem superior em aplicações de engenharia de estatística matemática geralmente não são usados.

Moda discreto variável aleatória é seu valor mais provável. Moda contínuo uma variável aleatória é seu valor no qual a densidade de probabilidade é máxima (Fig. 2). Se a curva de distribuição tem um máximo, então a distribuição é chamada unimodal. Se a curva de distribuição tem mais de um máximo, então a distribuição é chamada de polimodal. Às vezes, existem distribuições cujas curvas não têm um máximo, mas um mínimo. Essas distribuições são chamadas antimodal. No caso geral, a moda e a expectativa matemática de uma variável aleatória não coincidem. Em um caso particular, por modal, ou seja tendo uma moda, uma distribuição simétrica, e desde que haja uma esperança matemática, esta coincide com a moda e o centro de simetria da distribuição.

Mediana variável aleatória Xé o seu significado Eu, para o qual a igualdade vale: i.e. é igualmente provável que a variável aleatória X será menos ou mais Eu. Geometricamente medianaé a abcissa do ponto em que a área sob a curva de distribuição é dividida ao meio (Fig. 2). No caso de uma distribuição modal simétrica, a mediana, a moda e a média são as mesmas.

A moda é o valor mais provável de uma variável aleatória. Com uma distribuição simétrica em relação à média, a moda coincide com a expectativa matemática. Se os valores da variável aleatória não se repetirem, não há moda.

O ponto no eixo x correspondente ao máximo da curva de densidade de distribuição é chamado de moda, ou seja, a moda é o valor mais provável da variável aleatória. No entanto, o modo não existe para todas as distribuições. Um exemplo é a distribuição uniforme. Nesse caso, a definição do centro de distribuição como modalidade é impossível. A moda é geralmente referida como Mo.

Existem conceitos de moda e mediana de uma variável aleatória.

É óbvio que no caso de uma mediana simétrica coincide com a moda e a esperança matemática.

Com base no fato de que a moda não é baseada em medições únicas, mas em um grande volume de observações, ela não pode ser considerada uma variável aleatória. A magnitude do modo não é afetada por vários tipos de atrasos no trabalho e pela perda de suas taxas normais.

Algumas vezes, na análise de distribuições empíricas, são utilizados os conceitos de moda e mediana da distribuição, “... A moda é o valor mais provável de uma variável aleatória,

Uma interpretação probabilística estendida do fenômeno da loteria é o conceito de distribuição probabilística de uma variável aleatória. Ele é usado para determinar as probabilidades de uma variável aleatória assumir um ou outro de seus valores possíveis. Denote por y a variável aleatória e por y seus valores possíveis. Em seguida, para uma variável aleatória discreta, que pode assumir valores possíveis Y, y2, US,. .., yn uma forma conveniente de distribuição de probabilidade deve ser considerada a dependência P(y = y), que normalmente é chamada de série de probabilidade, n série de distribuição. Na prática, para uma avaliação operacional generalizada da distribuição de probabilidade dos valores de risco, as chamadas características numéricas e outras da distribuição de resultados aleatórios são frequentemente usadas: expectativa matemática, variância, desvio padrão, coeficiente de variação, moda, mediana, etc (ver, por exemplo, e outros .). Ou seja, para uma percepção rápida e holística, o empreendedor busca (ou simplesmente você

Com base nos dados do Comitê Estadual de Estatísticas da URSS sobre a distribuição da população pela renda per capita total, tentaremos comparar os indicadores de renda média, mediana e modal (Tabela 1). A tabela mostra que a renda média em termos absolutos supera as rendas mediana e modal, e seu crescimento ocorre principalmente devido ao aumento da proporção de pessoas com renda alta, ou seja, a utilização do indicador de renda média leva a uma superestimação significativa do nível de renda do grosso da população e, em grande medida, oculta o processo de sua diferenciação. Os valores da renda modal gravitam em direção aos grupos de distribuição mais baixos e se desviam da renda mediana para baixo. No entanto, o acerto de uma moda em um ou outro intervalo geralmente é de natureza aleatória, uma mudança bastante pequena na distribuição - e a moda já estará no intervalo vizinho. Por exemplo, em 1989, o nível de renda mais comum era de 100 a 125 rublos (16,1% da população recebia essa renda), mas devido a pequenas mudanças na renda que ocorreram em 1989-1990, o intervalo mais comum acabou sendo o seguinte intervalo (125-150 rublos): , e o valor da própria moda aumentou 15,6 rublos. Além disso, a parcela da população no intervalo modal de renda pode exceder muito ligeiramente outras parcelas.

Para caracterizar o centro de distribuição de uma variável aleatória logaritmicamente normal a, pode-se usar, juntamente com a expectativa matemática Ma já calculada, a moda

Modo - moda. O valor mais provável de uma variável aleatória.

MODA - conceito

Além da expectativa matemática e da dispersão, várias características numéricas são usadas na teoria da probabilidade, refletindo certas características da distribuição.

Definição. O modo Mo(X) de uma variável aleatória X é seu valor mais provável(para o qual a probabilidade r r ou densidade de probabilidade

Se a probabilidade ou densidade de probabilidade atinge um máximo não em um, mas em vários pontos, a distribuição é chamada polimodal(Fig. 3.13).

Moda Musgo), em que a probabilidade R ( ou a densidade de probabilidade (p(x) atinge um máximo global, é chamado valor mais provável variável aleatória (na Fig. 3.13 este Mo(X) 2).

Definição. A mediana Me(X) de uma variável aleatória contínua X é o seu valor, para qual

Essa. a probabilidade de que a variável aleatória X assume um valor menor que a mediana Pelagem) ou maior que ele, igual e igual a 1/2. Linha geometricamente vertical X = Pelagem) passando por um ponto de abcissa igual a Pelagem), divide a área da figura da curva de distribuição em duas partes iguais (Fig. 3.14). Obviamente, no ponto X = Pelagem) a função de distribuição é igual a 1/2, ou seja. P(Eu(X))= 1/2 (Fig. 3.15).

Observe uma propriedade importante da mediana de uma variável aleatória: a expectativa matemática do valor absoluto do desvio da variável aleatória X do valor constante C é mínima então, quando esta constante C é igual à mediana Me(X) = m, ou seja

(a propriedade é semelhante à propriedade (3,10") da minimalidade do quadrado médio do desvio de uma variável aleatória de sua expectativa matemática).

O Exemplo 3.15. Encontre a moda, a mediana e a média de uma variável aleatória Xs densidade de probabilidade φ(x) = 3x 2 para xx.

Solução. A curva de distribuição é mostrada na fig. 3.16. Obviamente, a densidade de probabilidade φ(x) é máxima em X= Mo(X) = 1.

Mediana Pelagem) = b encontramos da condição (3.28):

Onde

A expectativa matemática é calculada pela fórmula (3.25):

Disposição mútua de pontos M(X) > Eu(X) e Musgo) em ordem crescente de abcissa é mostrado na fig. 3.16. ?

Juntamente com as características numéricas mencionadas acima, o conceito de quantis e pontos percentuais é usado para descrever uma variável aleatória.

Definição. Quantil de nível y-quantil )

é chamado tal valor x q de uma variável aleatória , em que sua função de distribuição assume um valor igual a d, ou seja

Alguns quantis receberam um nome especial. Obviamente, o acima mediana variável aleatória é o quantil de nível 0,5, ou seja, Eu (X) \u003d x 05. Os quantis dg 0 2 5 e x 075 são nomeados respectivamente mais baixo e quartil superior K

Intimamente relacionado com o conceito de um quantil é o conceito ponto percentual. Debaixo Ponto YuOuHo-noi quantil implícito x x (( , Essa. tal valor de uma variável aleatória x, sob as quais

0 Exemplo 3.16. De acordo com o exemplo 3.15 encontre o quantil x 03 e 30% de ponto variável aleatório x.

Solução. De acordo com a fórmula (3.23), a função de distribuição

Encontramos o quantil r 0 z da equação (3.29), i.e. x$ 3 \u003d 0,3, de onde L "oz -0,67. Encontre o ponto de 30% da variável aleatória x, ou quantil x 0 7, da equação x$ 7 = 0,7, de onde x 0 7 "0,89. ?

Dentre as características numéricas de uma variável aleatória, os momentos - inicial e central - são de particular importância.

Definição. Momento inicialk-ésima ordem de uma variável aleatória X é a expectativa matemática da k-ésima potência dessa variável :

Definição. Ponto centrala k-ésima ordem de uma variável aleatória X é a expectativa matemática do k-ésimo grau de desvio da variável aleatória X de sua expectativa matemática:

Fórmulas para calcular os momentos para variáveis ​​aleatórias discretas (tomando os valores x 1 com probabilidades p,) e contínua (com densidade de probabilidade cp(x)) são dadas na Tabela. 3.1.

Tabela 3.1

É fácil ver que quando k = 1 primeiro momento inicial da variável aleatória Xé a sua esperança matemática, ou seja, h x \u003d M [X) \u003d a, no para= 2 o segundo momento central é a dispersão, ou seja p 2 = T)(X).

Os momentos centrais p A podem ser expressos em termos dos momentos iniciais usando as fórmulas:

etc.

Por exemplo, c 3 \u003d M (X-a) * \u003d M (X * -ZaX 2 + Za 2 X-a-\u003e) \u003d M (X *) ~ -ZaM (X 2) + Za 2 M (X) ~ a3 \u003d y 3 -Zy ^ + Zy (y, -y ^ \u003d y 3 - Zy ^ + 2y ^ (ao derivar, levamos em consideração que uma = M(X)= V, - valor não aleatório). ?

Como observado acima, a expectativa matemática M(X), ou o primeiro momento inicial, caracteriza o valor médio ou posição, o centro de distribuição de uma variável aleatória X na reta numérica; dispersão OH), ou o segundo momento central p 2 , - s t s - espalhamento de distribuição X relativamente M(X). Momentos de ordem superior servem para uma descrição mais detalhada da distribuição.

Terceiro momento central p 3 serve para caracterizar a assimetria da distribuição (assimetria). Tem a dimensão de um cubo de uma variável aleatória. Para obter um valor adimensional, ele é dividido por cerca de 3, onde a é o desvio padrão da variável aleatória x. Valor recebido MAS chamado coeficiente de assimetria de uma variável aleatória.

Se a distribuição é simétrica em relação à expectativa matemática, então o coeficiente de assimetria é A = 0.

Na fig. 3.17 mostra duas curvas de distribuição: I e II. A curva I tem uma assimetria positiva (lado direito) (L > 0), e a curva II tem uma assimetria negativa (lado esquerdo) (L

Quarto momento central p 4 serve para caracterizar a inclinação (pico do topo ou topo plano - poste) da distribuição.

Moda- o valor no conjunto de observações que ocorre com mais frequência

Mo \u003d X Mo + h Mo * (f Mo - f Mo-1): ((f Mo - f Mo-1) + (f Mo - f Mo + 1)),

aqui X Mo é a borda esquerda do intervalo modal, h Mo é o comprimento do intervalo modal, f Mo-1 é a frequência do intervalo pré-modal, f Mo é a frequência do intervalo modal, f Mo+1 é a frequência do intervalo pós-modal.

A moda de uma distribuição absolutamente contínua é qualquer ponto do máximo local da densidade de distribuição. Para distribuições discretas, uma moda é qualquer valor a i cuja probabilidade pi é maior que as probabilidades de valores vizinhos

mediana variável aleatória contínua X seu valor Me é chamado tal, para o qual é igualmente provável que a variável aleatória venha a ser menor ou maior Eu, ou seja

M e \u003d (n + 1) / 2 P(X < Eu) = P(X > Eu)

Distribuído uniformemente NOVO

Distribuição uniforme. Uma variável aleatória contínua é chamada uniformemente distribuída no segmento () se sua função densidade de distribuição (Fig. 1.6, uma) parece:

Designação: - SW é distribuído uniformemente em .

Assim, a função de distribuição no segmento (Fig. 1.6, b):

Arroz. 1.6. Funções de uma variável aleatória distribuída uniformemente em [ uma,b]: uma– densidades de probabilidade f(x); b– distribuições F(x)

A expectativa matemática e a variância deste RV são determinadas pelas expressões:

Devido à simetria da função densidade, ela coincide com a mediana. A moda não tem distribuição uniforme

Exemplo 4 O tempo de espera para atendimento de uma chamada telefônica é uma variável aleatória que obedece a uma lei de distribuição uniforme no intervalo de 0 a 2 minutos. Encontre as funções de distribuição integral e diferencial desta variável aleatória.

27. Lei normal da distribuição de probabilidade

Uma variável aleatória contínua x tem uma distribuição normal com parâmetros: m,s > 0, se a densidade de distribuição de probabilidade tem a forma:

onde: m é a esperança matemática, s é o desvio padrão.

A distribuição normal também é chamada de gaussiana em homenagem ao matemático alemão Gauss. O fato de uma variável aleatória ter distribuição normal com parâmetros: m, , é denotado da seguinte forma: N (m, s), onde: m=a=M[X];

Muitas vezes, em fórmulas, a expectativa matemática é denotada por uma . Se uma variável aleatória é distribuída de acordo com a lei N(0,1), então ela é chamada de valor normal normalizado ou padronizado. A função de distribuição para ele tem a forma:

O gráfico da densidade da distribuição normal, que é chamada de curva normal ou curva gaussiana, é mostrado na Fig. 5.4.

Arroz. 5.4. Densidade de distribuição normal

propriedades uma variável aleatória com uma lei de distribuição normal.

1. Se , então para encontrar a probabilidade de que esse valor caia em um determinado intervalo ( x 1; x 2) a fórmula é usada:

2. A probabilidade de que o desvio de uma variável aleatória de sua expectativa matemática não exceda o valor (em valor absoluto) é igual a:

3. "Regra de Três Sigma". Se uma variável aleatória , é praticamente certo que seus valores estão contidos no intervalo (). (A probabilidade de ultrapassar esses limites é de 0,0027.) A regra permite, conhecendo os parâmetros ( e ), determinar aproximadamente o intervalo de valores práticos de uma variável aleatória.

distribuição exponencial

Uma variável aleatória X tem uma distribuição exponencial com um parâmetro se sua densidade tem a forma

Integrando a densidade, obtemos a função de distribuição exponencial:

Principais características da distribuição exponencial:

Gráficos de densidade e funções da distribuição exponencial resultante