A função MEDIAN no Excel é utilizada para analisar um intervalo de valores numéricos e retorna um número que é o meio do conjunto em estudo (mediana). Ou seja, esta função divide condicionalmente o conjunto de números em dois subconjuntos, o primeiro dos quais contém números menores que a mediana e o segundo - mais. A mediana é um dos vários métodos para determinar a tendência central de uma faixa em estudo.

Exemplos de uso da função MEDIAN no Excel

Ao estudar as faixas etárias dos alunos, foram utilizados dados de um grupo de alunos selecionados aleatoriamente na universidade. A tarefa é determinar a idade média dos alunos.

Dados iniciais:

Fórmula para cálculo:

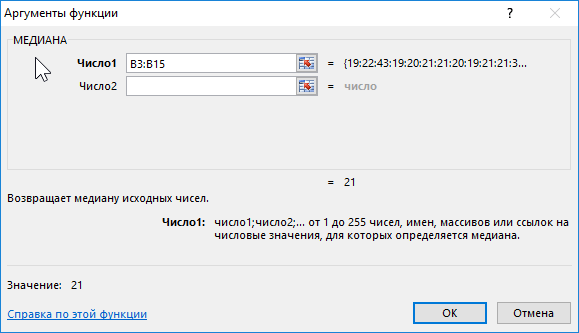
Descrição do argumento:

• B3:B15 - o intervalo das idades estudadas.

Resultado:

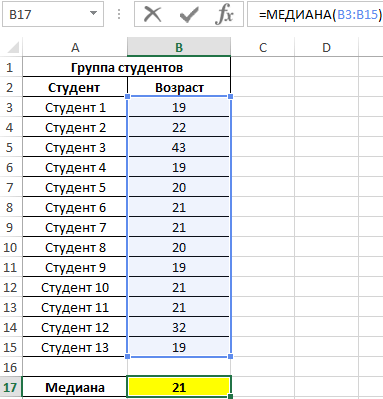
Ou seja, há alunos no grupo com idade inferior a 21 anos e superior a esse valor.



Comparando as funções MEDIAN e AVERAGE para calcular o valor médio

Durante a ronda da noite no hospital, a temperatura corporal de cada paciente foi medida. Demonstrar a viabilidade de usar o parâmetro mediano em vez do valor médio para explorar uma série de valores obtidos.

Dados iniciais:

Fórmula para encontrar o valor médio:

Fórmula para encontrar a mediana:

Como pode ser visto a partir do valor médio, a temperatura média dos pacientes está acima do normal, mas isso não é verdade. A mediana mostra que pelo menos metade dos pacientes apresenta temperatura corporal normal, não superior a 36,6.

Atenção! Outro método para determinar a tendência central é a moda (o valor mais comum na faixa em estudo). Para determinar a tendência central no Excel, use a função MODA. Observe que neste exemplo, os valores de mediana e moda são os mesmos:

Ou seja, o valor mediano que divide um conjunto em subconjuntos de valores menores e maiores também é o valor que ocorre com mais frequência no conjunto. Como você pode ver, a maioria dos pacientes tem uma temperatura de 36,6.

Um exemplo de cálculo da mediana em análise estatística no Excel

Exemplo 3. Há 3 vendedores trabalhando em uma loja. Com base nos resultados dos últimos 10 dias, é necessário determinar o funcionário para quem o bônus será emitido. Ao escolher o melhor trabalhador, leva-se em consideração o grau de eficiência de seu trabalho, e não o número de mercadorias vendidas.

Tabela de dados de origem:

Para caracterizar a eficiência, usaremos três indicadores ao mesmo tempo: o valor médio, a mediana e a moda. Vamos defini-los para cada funcionário usando as fórmulas AVERAGE, MEDIAN e FASHION, respectivamente:

Para determinar o grau de dispersão dos dados, utilizamos um valor que é o valor total do módulo da diferença entre a média e moda, média e mediana, respectivamente. Ou seja, o coeficiente x=|av-med|+|av-mod|, onde:

• av – valor médio;
• med é a mediana;
• mod - moda.

Calcule o valor do coeficiente x para o primeiro vendedor:

Da mesma forma, realizaremos cálculos para outros vendedores. Resultados:

Vamos definir o vendedor a quem o bônus será dado:

Nota: A função SMALL retorna o primeiro valor mínimo do intervalo considerado de valores do fator x.

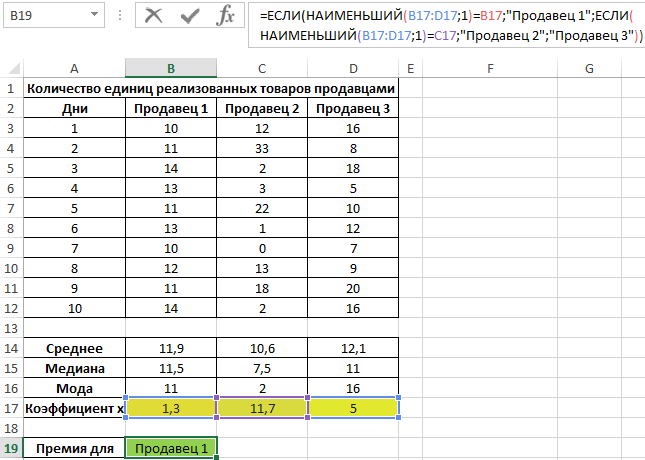
O coeficiente x é alguma característica quantitativa da estabilidade do trabalho dos vendedores, que foi introduzido pelo economista da loja. Com sua ajuda, foi possível determinar a faixa com os menores desvios de valores. Este método demonstra como três métodos de determinação da tendência central podem ser usados ​​ao mesmo tempo para obter os resultados mais confiáveis.

Recursos do uso da função MEDIAN no Excel

A função tem a seguinte sintaxe:

MEDIANA(número1, [número2],...)

Descrição dos argumentos:

• number1 é um argumento obrigatório que caracteriza o primeiro valor numérico contido no intervalo em estudo;
• [number2] – segundo opcional (e argumentos subsequentes, até 255 argumentos no total) caracterizando o segundo e os valores subsequentes do intervalo em estudo.

Notas 1:

1. Ao calcular, é mais conveniente transferir todo o intervalo dos valores estudados de uma só vez, em vez de inserir os argumentos sequencialmente.
2. Os argumentos são dados numéricos, nomes contendo números, dados de referência e matrizes (por exemplo, =MEDIAN((1;2;3;5;7;10))).
3. Ao calcular a mediana, são levadas em consideração células contendo valores vazios ou lógicos TRUE, FALSE, que serão interpretados como valores numéricos 1 e 0, respectivamente. Por exemplo, o resultado da execução de uma função com valores lógicos nos argumentos (TRUE; FALSE) é equivalente ao resultado da execução com argumentos (1; 0) e é igual a 0,5.
4. Se um ou mais argumentos de função receberem valores de texto que não podem ser convertidos em valores numéricos ou contiverem códigos de erro, a função retornará o código de erro #VALUE!.
5. Outras funções do Excel podem ser usadas para determinar a mediana da amostra: PERCENTILE.INC, QUARTILE.INC, GREAT Exemplos de uso:

• =PERCENTIL.ON(A1:A10,0.5) porque por definição a mediana é o percentil 50.
• =QUARTIL.ON(A1:A10,2) porque a mediana é o 2º quartil.
• =GRANDE(A1:A9;COUNT(A1:A9)/2), mas somente se o número de números no intervalo for um número ímpar.

Notas 2:

1. Se no intervalo em estudo todos os números estiverem distribuídos simetricamente em torno da média, a média aritmética e a mediana para este intervalo serão equivalentes.
2. Com grandes desvios de dados no intervalo (“dispersão” de valores), a mediana reflete melhor a tendência na distribuição dos valores do que a média aritmética. Um excelente exemplo é o uso da mediana para determinar o nível real de salários da população de um estado em que os funcionários recebem uma ordem de grandeza a mais do que os cidadãos comuns.
3. A faixa de valores investigados pode conter:

• Número ímpar de números. Nesse caso, a mediana será um único número dividindo o intervalo em dois subconjuntos de valores maiores e menores, respectivamente;
• Um número par de números. Em seguida, a mediana é calculada como a média aritmética de dois valores numéricos dividindo o conjunto nos dois subconjuntos indicados acima.

TESTE

No tópico: "Moda. Mediana. Métodos para calculá-los"

Introdução

Os valores médios e os indicadores de variação relacionados desempenham um papel muito importante nas estatísticas, o que se deve ao assunto de seu estudo. Portanto, este tópico é um dos centrais do curso.

A média é um indicador generalizador muito comum nas estatísticas. Isso se explica pelo fato de que somente com a ajuda da média é possível caracterizar a população de acordo com um atributo quantitativamente variável. Um valor médio em estatística é uma característica generalizante de um conjunto de fenômenos do mesmo tipo de acordo com algum atributo quantitativamente variável. A média mostra o nível desse atributo, relacionado à unidade da população.

Estudando fenômenos sociais e buscando identificar suas características, características típicas em condições específicas de lugar e tempo, os estatísticos fazem uso extensivo de valores médios. Com a ajuda de médias, diferentes populações podem ser comparadas entre si de acordo com características variadas.

As médias usadas em estatística pertencem à classe das médias de poder. Das médias de potência, a média aritmética é a mais utilizada, menos frequentemente a média harmônica; a média harmônica é usada apenas no cálculo das taxas médias da dinâmica e a média quadrada - apenas no cálculo dos indicadores de variação.

A média aritmética é o quociente da divisão da soma das opções pelo seu número. É usado nos casos em que o volume de um atributo variável para toda a população é formado pela soma dos valores dos atributos para suas unidades individuais. A média aritmética é o tipo mais comum de média, pois corresponde à natureza dos fenômenos sociais, onde o volume de sinais variáveis ​​no agregado é mais frequentemente formado precisamente como a soma dos valores do atributo em unidades individuais de a população.

De acordo com sua propriedade definidora, a média harmônica deve ser utilizada quando o volume total do atributo é formado pela soma dos valores recíprocos da variante. É utilizado quando, dependendo do material disponível, os pesos não precisam ser multiplicados, mas divididos em opções ou, o que dá no mesmo, multiplicados pelo seu valor inverso. A média harmônica nesses casos é a recíproca da média aritmética dos valores recíprocos do atributo.

A média harmônica deve ser usada naqueles casos em que não são usadas as unidades da população - os portadores do atributo, mas os produtos dessas unidades e o valor do atributo são usados ​​como pesos.

1. Definição de moda e mediana em estatísticas

As médias aritméticas e harmônicas são as características generalizantes da população de acordo com um ou outro atributo variável. As características descritivas auxiliares da distribuição de um atributo variável são a moda e a mediana.

Em estatística, moda é o valor de uma característica (variante) que é mais frequentemente encontrada em uma determinada população. Na série de variação, esta será a variante com maior frequência.

A mediana em estatística é chamada de variante, que está no meio da série de variação. A mediana divide a série ao meio, em ambos os lados (para cima e para baixo) há o mesmo número de unidades populacionais.

A moda e a mediana, ao contrário das médias exponenciais, são características específicas, seu valor é qualquer variante particular na série de variação.

A moda é usada nos casos em que é necessário caracterizar o valor que ocorre com mais frequência de um recurso. Se for necessário, por exemplo, saber qual é o salário mais comum na empresa, o preço de mercado pelo qual foi vendido o maior número de mercadorias, o tamanho dos sapatos mais procurados pelos consumidores etc., nesses casos recorrem à moda.

A mediana é interessante por mostrar o limite quantitativo do valor da variável característica, que foi atingido por metade dos membros da população. Deixe o salário médio dos funcionários do banco chegar a 650.000 rublos. por mês. Essa característica pode ser complementada se dissermos que metade dos trabalhadores recebeu um salário de 700.000 rublos. e superior, ou seja vamos pegar a mediana. A moda e a mediana são características típicas nos casos em que as populações são homogêneas e em grande número.

2. Encontrando a moda e a mediana em uma série de variação discreta

Encontrar a moda e a mediana em uma série variacional, onde os valores dos atributos são dados por determinados números, não é muito difícil. Considere a tabela 1. com a distribuição das famílias pelo número de filhos.

Tabela 1. Distribuição das famílias por número de filhos

Obviamente, neste exemplo, a moda será uma família com dois filhos, pois este valor de opções corresponde ao maior número de famílias. Pode haver distribuições onde todas as variantes são igualmente frequentes, caso em que não há moda, ou, em outras palavras, todas as variantes podem ser ditas igualmente modais. Em outros casos, não uma, mas duas opções podem ser a frequência mais alta. Então haverá dois modais, a distribuição será bimodal. As distribuições bimodais podem indicar a heterogeneidade qualitativa da população de acordo com a característica em estudo.

Para encontrar a mediana em uma série de variação discreta, você precisa dividir a soma das frequências pela metade e adicionar ½ ao resultado. Assim, na distribuição de 185 famílias pelo número de filhos, a mediana será: 185/2 + ½ = 93, ou seja. A 93ª opção, que divide a linha ordenada ao meio. Qual é o significado da opção 93? Para descobrir, você precisa acumular frequências, começando pelas menores opções. A soma das frequências da 1ª e 2ª opção é 40. É claro que não há 93 opções aqui. Se somarmos a frequência da 3ª opção a 40, obtemos a soma igual a 40 + 75 = 115. Portanto, a 93ª opção corresponde ao terceiro valor do atributo variável, e a mediana será uma família com dois filhos .

A moda e a mediana neste exemplo coincidiram. Se tivéssemos uma soma par de frequências (por exemplo, 184), aplicando a fórmula acima, obtemos o número de opções medianas, 184/2 + ½ = 92,5. Como não há opções fracionárias, o resultado indica que a mediana está no meio entre 92 e 93 opções.

3. Cálculo da moda e mediana na série de variação do intervalo

A natureza descritiva da moda e da mediana se deve ao fato de não compensarem os desvios individuais. Eles sempre correspondem a uma determinada variante. Portanto, a moda e a mediana não requerem cálculos para encontrá-los se todos os valores do recurso forem conhecidos. No entanto, na série de variação de intervalo, os cálculos são usados ​​para encontrar o valor aproximado da moda e da mediana dentro de um determinado intervalo.

Para calcular um determinado valor do valor modal de um sinal incluído em um intervalo, a seguinte fórmula é usada:

M o \u003d X Mo + i Mo * (f Mo - f Mo-1) / ((f Mo - f Mo-1) + (f Mo - f Mo + 1)),

Onde X Mo é o limite mínimo do intervalo modal;

i Mo é o valor do intervalo modal;

fMo é a frequência do intervalo modal;

f Mo-1 - a frequência do intervalo anterior ao modal;

f Mo+1 é a frequência do intervalo que segue o modal.

Vamos mostrar o cálculo da moda usando o exemplo dado na Tabela 2.

Tabela 2. Distribuição dos trabalhadores do empreendimento de acordo com a implantação dos padrões de produção

Para encontrar a moda, primeiro determinamos o intervalo modal da série dada. Pode-se ver pelo exemplo que a frequência mais alta corresponde ao intervalo onde a variante se encontra na faixa de 100 a 105. Este é o intervalo modal. O valor do intervalo modal é 5.

Substituindo os valores numéricos da tabela 2. na fórmula acima, obtemos:

M o \u003d 100 + 5 * (104 -12) / ((104 - 12) + (104 - 98)) \u003d 108,8

O significado desta fórmula é o seguinte: o valor daquela parte do intervalo modal, que deve ser adicionado ao seu limite mínimo, é determinado dependendo da magnitude das frequências dos intervalos anteriores e subsequentes. Neste caso, adicionamos 8,8 a 100, ou seja, mais da metade do intervalo, porque a frequência do intervalo anterior é menor que a frequência do intervalo subsequente.

Vamos calcular a mediana agora. Para encontrar a mediana na série de variação do intervalo, primeiro determinamos o intervalo em que ela está localizada (o intervalo da mediana). Tal intervalo será aquele cuja frequência acumulada é igual ou maior que a metade da soma das frequências. As frequências cumulativas são formadas pela soma gradual das frequências, a partir do intervalo com o menor valor de característica. Metade da soma das frequências que temos é 250 (500:2). Portanto, de acordo com a tabela 3, o intervalo mediano será o intervalo com o valor dos salários de 350.000 rublos. até 400.000 rublos.

Tabela 3. Cálculo da mediana na série de variação do intervalo

Antes desse intervalo, a soma das frequências acumuladas era de 160. Portanto, para obter o valor da mediana, é necessário somar mais 90 unidades (250 - 160).

Eu mediano eles chamam tal valor do recurso que cai no meio da série classificada e o divide em duas partes iguais em número de unidades. Assim, na série de distribuição ranqueada, metade da série apresenta valores de características que ultrapassam a mediana, enquanto a outra metade apresenta valores inferiores à mediana.

A mediana é usada em vez da média aritmética quando as variantes extremas da série classificada (menor e maior) em comparação com o resto se tornam excessivamente grandes ou excessivamente pequenas.

NO discreto em uma série variacional contendo um número ímpar de unidades, a mediana é igual à variante característica com o número:
,
onde N é o número de unidades populacionais.
Em uma série discreta composta por um número par de unidades populacionais, a mediana é definida como a média das opções com números e :
.
Na distribuição dos trabalhadores por tempo de serviço, a mediana é igual à média das opções que possuem números 10: 2 = 5 e 10: 2 + 1 = 6 na série ranqueada. As opções para o quinto e sexto recurso são 4 anos, assim
Do ano
Ao calcular a mediana em intervalo primeira linha encontrar intervalo mediano, (ou seja, contendo a mediana), para a qual as frequências ou frequências acumuladas são usadas. A mediana é o intervalo cuja frequência acumulada é igual ou maior que a metade da população total. O valor mediano é então calculado usando a fórmula:
,
onde é o limite inferior do intervalo mediano;
é a largura do intervalo mediano;
é a frequência acumulada do intervalo anterior à mediana;
é a frequência do intervalo mediano.
Vamos calcular a mediana da série de distribuição dos trabalhadores por salário (veja a palestra "Resumo e agrupamento de dados estatísticos").
O intervalo salarial mediano é UAH 800-900, pois sua frequência acumulada é 17, que é mais da metade da soma de todas as frequências (). Então
Eu = 800+100 UAH.
O valor obtido indica que metade dos trabalhadores tem salários abaixo de UAH 875, mas isso é superior ao seu tamanho médio.
Para determinar a mediana, você pode usar frequências cumulativas em vez de frequências cumulativas.
A mediana, como a moda, não depende dos valores extremos da variante, portanto também é usada para caracterizar o centro em séries de distribuição com limites indefinidos.
propriedade mediana : a soma dos valores absolutos dos desvios da variante da mediana é menor do que de qualquer outro valor (incluindo a média aritmética):

Esta propriedade da mediana é usada no transporte ao projetar a localização de paradas de bonde e trólebus, postos de gasolina, pontos de montagem, etc.
Exemplo. Há 10 garagens em uma rodovia de 100 km de extensão. Para projetar a construção de um posto de gasolina, foram coletados dados sobre o número de viagens esperadas para cada posto de gasolina.
Tabela 2 - Dados sobre o número de idas a postos de gasolina para cada garagem.

É necessário colocar um posto de gasolina para que a quilometragem total dos carros para reabastecimento seja a menor.
Opção 1. Se o posto de gasolina estiver localizado no meio da rodovia, ou seja, no quilômetro 50 (o centro da faixa de mudança do sinal), as corridas, levando em consideração o número de passageiros, serão:
a) em uma direção:
;
b) ao contrário:
;
c) quilometragem total em ambos os sentidos: .

Opção 2. Se o posto de gasolina estiver localizado no trecho médio da rodovia, determinado pela fórmula da média aritmética, levando em consideração o número de passageiros:

A mediana pode ser determinada graficamente, por cumulado (veja a palestra "Resumo e agrupamento de dados estatísticos"). Para fazer isso, a última ordenada, igual à soma de todas as frequências ou frequências, é dividida ao meio. A partir do ponto obtido, a perpendicular é restaurada à interseção com o cumulado. A abcissa do ponto de interseção dá o valor da mediana.

4. Moda. Mediana. Média geral e amostral

A moda está na tela, a mediana está no triângulo e as médias são a temperatura no hospital e na enfermaria. Continuamos nosso curso prático estatísticas divertidas (Lição 1) estudo das características centrais população estatística, cujos nomes você vê no cabeçalho. E vamos começar do seu fim, porque Valores médios discurso veio quase desde os primeiros parágrafos do tópico. Para leitores avançados índice:

• Média geral e amostral– cálculo segundo dados primários e para a série variacional discreta gerada;
• Moda– definição e achado para um caso discreto;
• Mediana– uma definição geral de como encontrar a mediana;
• Média, moda e mediana da série de variação do intervalo– cálculo a partir de dados primários e da série finalizada. Fórmulas de moda e mediana,
• Quartis, decis, percentis - brevemente sobre o principal.

Bem, é melhor que os “dummies” se familiarizem com o material na ordem:

Então vamos explorar alguns população volume, ou seja, sua característica numérica, não importa discreto ou contínuo (Lições 2, 3).

Secundário geral chamado média todos os valores deste conjunto:

Se os números forem iguais (o que é típico para série discreta) , então a fórmula pode ser escrita de uma forma mais compacta:
, Onde
opção vezes repetidas;
opção - vezes;
opção - vezes;
…
opção - vezes.

Exemplo de cálculo ao vivo Secundário geral conheceu em exemplo 2, mas para não ser chato, nem vou lembrar seu conteúdo.

Mais longe. Como lembramos, o processamento de toda a população em geral é muitas vezes difícil ou impossível e, portanto, eles organizam representante amostragem volume, e com base no estudo desta amostra, é feita uma conclusão sobre toda a população.

Média da amostra chamado média todos os valores de amostra:

e na presença das mesmas opções, a fórmula será escrita de forma mais compacta:
- como a soma dos produtos da variante no correspondente frequências .

A média amostral permite estimar com precisão o verdadeiro valor de , o que é suficiente para muitos estudos. Quanto maior a amostra, mais precisa será essa estimativa.

Vamos começar a prática, ou melhor continuar, com série de variação discreta e a condição familiar:

Exemplo 8

Com base nos resultados de um estudo seletivo dos trabalhadores da oficina, foram estabelecidas suas categorias de qualificação: 4, 5, 6, 4, 4, 2, 3, 5, 4, 4, 5, 2, 3, 3, 4, 5 , 5, 2, 3, 6, 5, 4, 6, 4, 3.

Quão decidir tarefa? Se nos for dado dados primários(valores brutos originais), então eles podem ser estupidamente resumidos e divididos pelo tamanho da amostra:
- a categoria média de qualificação dos trabalhadores da loja.

Mas em muitos problemas é necessário compor uma série variacional (cm. Exemplo 4) :

- ou esta série foi originalmente proposta (o que acontece com mais frequência). E então, claro, usamos a fórmula "civilizada":

Moda . A moda de uma série variacional discreta é opção com frequência máxima. Nesse caso . A moda é fácil de encontrar na mesa e ainda mais fácil alcance de frequênciaé a abcissa do ponto mais alto:


Às vezes, existem vários desses valores (com a mesma frequência máxima) e, em seguida, cada um deles é considerado uma moda.

Se tudo ou quase tudo opções diferente (o que é típico para série de intervalo), então o valor modal é determinado de uma maneira ligeiramente diferente, que é discutida na 2ª parte da lição.

Mediana . Mediana da série de variação * - este é o valor que o divide em duas partes iguais (de acordo com o número de opções).

Mas agora precisamos encontrar a média, moda e mediana.

Solução: encontrar meio de acordo com os dados primários, é melhor somar todas as opções e dividir o resultado pelo volume da população:
antro unidades

Esses cálculos, a propósito, não levarão muito tempo, mesmo usando uma calculadora offline. Mas se houver Excel, então, é claro, pontuação em qualquer célula livre =SOMA(, selecione todos os números com o mouse, feche o colchete ) , coloque um sinal de divisão / , digite o número 30 e pressione Digitar. Preparar.

Quanto à moda, sua avaliação com base em dados iniciais torna-se inutilizável. Embora vejamos os mesmos números entre eles, mas entre eles pode facilmente haver cinco ou seis ou sete opções com a mesma frequência máxima, por exemplo, frequência 2. Além disso, os preços podem ser arredondados. Portanto, o valor modal é calculado de acordo com a série intervalar gerada (mais sobre isso depois).

O que você pode dizer sobre a mediana: conectando no excel =MEDIA(, selecione todos os números com o mouse, feche o colchete ) e clique Digitar: . Além disso, aqui você nem precisa classificar nada.

Mas em Exemplo 6 ordenado em ordem crescente (lembre-se e classifique - link acima), e esta é uma boa oportunidade para repetir o algoritmo formal para encontrar a mediana. Dividimos a amostra ao meio:

E por ser composto por um número par de opções, a mediana é igual à média aritmética da 15ª e 16ª opções ordenadamente(!) série de variação:

antro unidades

Situação dois. Quando uma série de intervalo pronta é fornecida (uma tarefa de aprendizado típica).

Continuamos a analisar o mesmo exemplo com botas, onde, de acordo com os dados iniciais foi compilado por IVR. Calcular meio os pontos médios dos intervalos são necessários:

– para usar a fórmula de caso discreto familiar:

- excelente resultado! A discrepância com o valor mais preciso () calculado a partir dos dados primários é de apenas 0,04.

De fato, aqui aproximamos a série intervalar por uma discreta, e essa aproximação se mostrou muito eficaz. No entanto, não há nenhum benefício particular aqui, porque. com software moderno, não é difícil calcular o valor exato mesmo para uma grande variedade de dados primários. Mas isso com a condição de que sejam conhecidos por nós :)

Com outros indicadores centrais, tudo fica mais interessante.

Para encontrar moda, você precisa encontrar espaçamento modal (com frequência máxima)- neste problema, este é um intervalo com uma frequência de 11, e use a seguinte fórmula feia:
, Onde:

é o limite inferior do intervalo modal;
é o comprimento do intervalo modal;
é a frequência do intervalo modal;
– frequência do intervalo anterior;
– frequência do próximo intervalo.

Nesse caminho:
antro unidades - como você pode ver, o preço "na moda" dos sapatos é visivelmente diferente da média aritmética.

Sem entrar na geometria da fórmula, vou simplesmente dar histograma de frequências relativas e observe:


de onde se vê claramente que o modo é deslocado em relação ao centro do intervalo modal em direção ao intervalo esquerdo com maior frequência. Logicamente.

Para referência, analisarei casos raros:

– se o intervalo modal for extremo, então ;

- se forem encontrados 2 intervalos modais próximos, por exemplo, e , então consideramos o intervalo modal , enquanto intervalos próximos (esquerda e direita), se possível, também são ampliados em 2 vezes.

- se houver uma distância entre os intervalos modais, aplicar a fórmula a cada intervalo, obtendo assim 2 ou mais modas.

Aqui está um mod de despacho :)

E a mediana. Se uma série de intervalo pronta é fornecida, a mediana é calculada usando uma fórmula um pouco menos terrível, mas a princípio é tedioso (um erro de digitação freudiano :)) encontrar intervalo mediano - este é um intervalo contendo uma variante (ou 2 variantes), que divide a série de variação em duas partes iguais.

Acima, descrevi como determinar a mediana, focando em frequências cumulativas relativas, aqui é mais conveniente calcular as frequências acumuladas "comuns". O algoritmo computacional é exatamente o mesmo - o primeiro valor é demolido à esquerda (flecha Vermelha), e cada seguinte é obtido como a soma do anterior com a frequência atual da coluna da esquerda (marcas verdes como exemplo):

Todos entendem o significado dos números na coluna da direita? - este é o número de opções que conseguiram "acumular" em todos os intervalos "passados", incluindo o atual.

Como temos um número par de opções (30 peças), a mediana será o intervalo que contém 30/2 = 15ª e 16ª opções. E focando nas frequências acumuladas, é fácil chegar à conclusão de que essas opções estão contidas no intervalo.

Fórmula mediana:
, Onde:
- o volume da população estatística;
é o limite inferior do intervalo mediano;
é o comprimento do intervalo mediano;
– frequência intervalo mediano;
– Frequência acumulativa anterior intervalo.

Nesse caminho:
antro unidades – observe que o valor da mediana, ao contrário, acabou sendo deslocado para a direita, porque à direita há um número significativo de opções:


E para casos especiais de referência.

Devido ao fato de o pesquisador não possuir dados sobre o volume de vendas em cada casa de câmbio, o cálculo da média aritmética para determinar o preço médio por dólar é inadequado.

Mediana de uma série de números

No entanto, é possível determinar o valor do atributo, que é chamado de mediana (Me). Mediana

Número mediano: NoMe = ;

Moda

Tabela 3.6.

fé a soma das frequências da série;

S frequências cumulativas

S são frequências acumuladas.

Na fig. 3.2. Um histograma de uma série de distribuição de bancos por lucro é mostrado (conforme Tabela 3.6.).

x é a quantidade de lucro, milhões de rublos,

f é o número de bancos.

"MEDIA DA SÉRIE ORDENADA"

Versão HTML de texto da publicação

Resumo da lição de álgebra na 7ª série

Tema da aula: "MEDIA DA SÉRIE ORDENADA".

professor da filial da Lake School da escola secundária MKOU Burkovskaya Eremenko Tatyana Alekseevna
Metas:
o conceito de mediana como característica estatística de uma série ordenada; formar a capacidade de encontrar a mediana para séries ordenadas com número par e ímpar de membros; formar a capacidade de interpretar os valores da mediana dependendo da situação prática, consolidar o conceito do conjunto de números da média aritmética. Desenvolver habilidades de trabalho independentes. Desperte o interesse pela matemática.
Durante as aulas

trabalho oral.
As linhas são dadas: 1) 4; 1; oito; 5; 1; 2); 9; 3; 0,5; ; 3) 6; 0,2; ; quatro; 6; 7,3; 6. Encontre: a) os maiores e menores valores de cada linha; b) o intervalo de cada linha; c) a moda de cada linha.
II. Explicação do novo material.
Trabalho de livro didático. 1. Considere o problema do parágrafo 10 do livro. O que significa linha ordenada? Ressalto que antes de encontrar a mediana, deve-se sempre ordenar as séries de dados. 2. No quadro, conhecemos as regras para encontrar a mediana para séries com número par e ímpar de membros:
Mediana

ordenadamente

fileira
números
Com

ímpar

número

membros
chamou o número escrito no meio, e
mediana

linha ordenada
números
com número par de membros
é chamado de média aritmética de dois números escritos no meio.
Mediana

arbitrário

fileira
é chamado de mediana 1 3 1 7 5 4 da série ordenada correspondente.
Observo que os indicadores são a média aritmética, moda e mediana para

diferentemente

caracterizar

dados,

recebido

resultado

observações.

III. Formação de competências e habilidades.
1º grupo. Exercícios de aplicação de fórmulas para encontrar a mediana de uma série ordenada e não ordenada. 1.
№ 186.
Solução: a) Número de membros da série P= 9; mediana Eu= 41; b) P= 7, a linha é ordenada, Eu= 207; dentro) P= 6, a linha é ordenada, Eu== 21; G) P= 8, a linha é ordenada, Eu== 2,9. Resposta: a) 41; b) 207; aos 21; e) 2.9. Os alunos comentam sobre como a mediana é encontrada. 2. Encontre a média aritmética e a mediana de uma série de números: a) 27, 29, 23, 31, 21, 34; dentro) ; 1. b) 56, 58, 64, 66, 62, 74. Solução: Para encontrar a mediana, é necessário ordenar cada linha: a) 21, 23, 27, 29, 31, 34. P = 6; X = = 27,5; Eu== 28; 20 22 2 + 2, 6 3, 2 2 + 1125; ; ; 3636 21 23 27 29 31 34 165 66 +++++ = 27 29 2 + b) 56, 58, 62, 64, 66, 74.

Como encontrar a mediana nas estatísticas

P = 6; X = 63,3; Eu== 63; dentro) ; 1. P = 5; X = : 5 = 3: 5 = 0,6; Eu = . 3.
№ 188
(oralmente). Resposta: sim; b) não; c) não; e) sim. 4. Sabendo que a série ordenada contém t números, onde té um número ímpar, indique o número do termo que é a mediana se té igual a: a) 5; b) 17; c) 47; d) 201. Resposta: a) 3; b) 9; c) 24; d) 101. 2º grupo. Tarefas práticas para encontrar a mediana da série correspondente e interpretar o resultado. 1.
№ 189.
Solução: Número de membros da linha P= 12. Para encontrar a mediana, as séries devem ser ordenadas: 136, 149, 156, 158, 168, 174, 178, 179, 185, 185, 185, 194. Mediana da série Eu= = 176. A produção mensal foi superior à mediana para os seguintes membros do artel: 56 58 62 64 66 74 380 66 +++++ =≈ 62 64 2 + 1125; ; ; 3636 1125 12456 18 1:5:5 6336 6 6 ++++ ⎛⎞ ++++ = = ⎜⎟ ⎝⎠ 2 3 67 174 178 22 xx++ = 1) Kvitko; 4) Bobkov; 2) Baranov; 5) Rylov; 3) Antonov; 6) Astafiev. Resposta: 176. 2.
№ 192.
Solução: Vamos organizar a série de dados: 30, 31, 32, 32, 32, 32, 32, 32, 33, 35, 35, 36, 36, 36, 38, 38, 38, 40, 40, 42; número de membros da linha P= 20. Deslize UMA = x max- x min = 42 - 30 = 12. Modo Mo= 32 (este valor ocorre 6 vezes - com mais frequência do que outros). Mediana Eu= = 35. Nesse caso, o intervalo mostra a maior dispersão de tempo para processamento da peça; a moda mostra o valor mais típico do tempo de processamento; mediana é o tempo de processamento que metade dos torneiros não ultrapassou. Resposta: 12; 32; 35.
4. Resumo da lição.
Qual é a mediana de uma série de números? – A mediana de uma série de números pode não coincidir com nenhum dos números da série? – Que número é a mediana de uma série ordenada contendo 2 P números? 2 P– 1 números? Como encontrar a mediana de uma série não ordenada?
Trabalho de casa:
№ 187, № 190, № 191, № 254. 10 11 35 35 22 xx + + =

Na seção educação geral básica

Moda e mediana

Os valores médios também incluem a moda e a mediana.

A mediana e a moda são frequentemente usadas como uma característica média naquelas populações onde o cálculo da média (aritmética, harmônica, etc.) é impossível ou impraticável.

Por exemplo, uma pesquisa amostral na cidade de Omsk de 12 casas de câmbio comerciais tornou possível fixar vários preços para o dólar quando foi vendido (dados de 10 de outubro de 1995 à taxa de câmbio do dólar -4493 rublos) .

Devido ao fato de o pesquisador não possuir dados sobre o volume de vendas em cada casa de câmbio, o cálculo da média aritmética para determinar o preço médio por dólar é inadequado. No entanto, é possível determinar o valor do atributo, que é chamado de mediana (Me). Mediana fica no meio da linha classificada e a divide.

O cálculo da mediana para dados desagrupados é feito da seguinte forma:

a) organize os valores individuais do recurso em ordem crescente:

4500 4500 4535 4540 4550 4560 4560 4560 4560 4570 4570 4570

b) determine o número de série da mediana pela fórmula:

em nosso exemplo, isso significa que a mediana neste caso está localizada entre o sexto e o sétimo valores de característica na série classificada, pois a série possui um número par de valores individuais. Assim, Me é igual à média aritmética dos valores vizinhos: 4550, 4560.

c) considerar o procedimento de cálculo da mediana no caso de número ímpar de valores individuais.

Suponha que observemos não 12, mas 11 pontos de câmbio, então a série classificada ficará assim (descartamos o 12º ponto):

4500 4500 4535 4540 4550 4560 4560 4560 4560 4570 4570

Número mediano: NoMe = ;

em sexto lugar está = 4560, que é a mediana: Me = 4560. Em ambos os lados é o mesmo número de pontos.

Moda- este é o valor mais comum do atributo em unidades desta população. Corresponde a um determinado valor característico.

No nosso caso, o preço modal por dólar pode ser chamado de 4560 rublos: esse valor é repetido 4 vezes, com mais frequência do que todos os outros.

Na prática, a moda e a mediana geralmente são encontradas a partir de dados agrupados. Como resultado do agrupamento, obteve-se uma série de distribuição dos bancos de acordo com o valor do lucro recebido no exercício (Tabela 3.6.).

Tabela 3.6.

Agrupamento de bancos pelo valor do lucro recebido no exercício

Para determinar a mediana, é necessário calcular a soma das frequências acumuladas. O aumento no total continua até que a soma acumulada das frequências exceda a metade da soma das frequências. No nosso exemplo, a soma das frequências acumuladas (12) ultrapassa metade de todos os valores (20:2). Este valor corresponde ao intervalo da mediana, que contém a mediana (5,5 - 6,4). Vamos determinar seu valor pela fórmula:

onde é o valor inicial do intervalo que contém a mediana;

- o valor do intervalo mediano;

fé a soma das frequências da série;

é a soma das frequências acumuladas que precedem o intervalo mediano;

é a frequência do intervalo mediano.

Assim, 50% dos bancos têm um lucro de 6,1 milhões de rublos e 50% dos bancos - mais de 6,1 milhões de rublos.

A frequência mais alta também corresponde ao intervalo 5,5 - 6,4, ou seja, a moda deve estar neste intervalo. Seu valor é determinado pela fórmula:

onde é o valor inicial do intervalo que contém a moda;

- o valor do intervalo modal;

é a frequência do intervalo modal;

- a frequência do intervalo anterior ao modal;

- a frequência do intervalo que segue o modal.

A fórmula de moda dada pode ser usada em séries variacionais com intervalos iguais.

Assim, neste agregado, o lucro mais comum é de 6,10 milhões de rublos.

A mediana e o modo podem ser determinados graficamente. A mediana é determinada pelo cumulado (Fig. 3.1.). Para construí-lo, é necessário calcular as frequências e frequências acumuladas. As frequências cumulativas mostram quantas unidades da população possuem valores de características não superiores ao valor considerado, e é determinado pela soma sucessiva das frequências do intervalo. Ao construir a série de distribuição de intervalos cumulativos, o limite inferior do primeiro intervalo corresponde a uma frequência igual a zero, e o limite superior corresponde a toda a frequência do intervalo dado. O limite superior do segundo intervalo corresponde à frequência acumulada igual à soma das frequências dos dois primeiros intervalos, e assim sucessivamente.

Vamos construir uma curva cumulativa de acordo com a Tabela. 6 sobre a distribuição dos bancos pelo lucro.

S frequências cumulativas

3,7-4,6 4,6-5,5 5,5-6,4 6,4-7,3 7,3-8,2 Х lucro

Arroz. 3.1. A distribuição acumulada dos bancos por lucro:

x é a quantidade de lucro, milhões de rublos,

S são frequências acumuladas.

Para determinar a mediana, a altura da maior ordenada, que corresponde à população total, é dividida pela metade. Traça-se uma linha reta passando pelo ponto obtido, paralela ao eixo das abcissas, até cruzar com o cumulado. A abcissa do ponto de interseção é a mediana.

A moda é determinada a partir do histograma da distribuição. O histograma é construído assim:

segmentos iguais são plotados no eixo das abcissas, que, na escala aceita, correspondem ao tamanho dos intervalos da série de variação. Os retângulos são construídos nos segmentos, cujas áreas são proporcionais às frequências (ou frequências) do intervalo.

Mediana nas estatísticas

3.2. Um histograma de uma série de distribuição de bancos por lucro é mostrado (conforme Tabela 3.6.).

3,7-4,6 4,6-5,5 5,5-6,4 6,4-7,3 7,3-8,2 Х

Arroz. 3.2. Distribuição dos bancos comerciais por lucro:

x é a quantidade de lucro, milhões de rublos,

f é o número de bancos.

Para determinar a moda, conectamos o vértice direito do retângulo modal com o canto superior direito do retângulo anterior e o vértice esquerdo do retângulo modal com o canto superior esquerdo do próximo retângulo. A abcissa do ponto de intersecção dessas linhas será o modo de distribuição.

Mediana (estatística)

Mediana (estatística), em estatística matemática, um número que caracteriza uma amostra (por exemplo, um conjunto de números). Se todos os elementos da amostra são diferentes, então a mediana é o número da amostra tal que exatamente metade dos elementos da amostra são maiores que ela e a outra metade é menor que ela. Em um caso mais geral, a mediana pode ser encontrada ordenando os elementos da amostra em ordem crescente ou decrescente e tomando o elemento do meio. Por exemplo, a amostra (11, 9, 3, 5, 5) após o pedido se transforma em (3, 5, 5, 9, 11) e sua mediana é o número 5. Se a amostra tiver um número par de elementos, o a mediana pode não ser determinada exclusivamente: para dados numéricos, a meia-soma de dois valores adjacentes é mais frequentemente usada (ou seja, a mediana do conjunto (1, 3, 5, 7) é considerada igual a 4).

Em outras palavras, a mediana em estatística é o valor que divide a série ao meio de tal forma que em ambos os lados dela (para cima ou para baixo) se encontra o mesmo número de unidades de uma dada população.

Tarefa número 1. Cálculo da média aritmética, valor modal e mediano

Devido a esta propriedade, este indicador tem vários outros nomes: o percentil 50 ou o quantil 0,5.

• Significa
  
• Mediana
  
• Moda
  

Mediana (estatística)

Mediana (estatística), em estatística matemática, um número que caracteriza uma amostra (por exemplo, um conjunto de números). Se todos os elementos da amostra são diferentes, então a mediana é o número da amostra tal que exatamente metade dos elementos da amostra são maiores que ela e a outra metade é menor que ela. Em um caso mais geral, a mediana pode ser encontrada ordenando os elementos da amostra em ordem crescente ou decrescente e tomando o elemento do meio. Por exemplo, a amostra (11, 9, 3, 5, 5) após o pedido se transforma em (3, 5, 5, 9, 11) e sua mediana é o número 5.

5.5 Moda e mediana. Seu cálculo em séries variacionais discretas e intervalares

Se a amostra tiver um número par de elementos, a mediana pode não ser determinada exclusivamente: para dados numéricos, a meia-soma de dois valores adjacentes é mais frequentemente usada (ou seja, a mediana do conjunto (1, 3, 5, 7) é considerado igual a 4).

Em outras palavras, a mediana em estatística é o valor que divide a série ao meio de tal forma que em ambos os lados dela (para cima ou para baixo) se encontra o mesmo número de unidades de uma dada população. Devido a esta propriedade, este indicador tem vários outros nomes: o percentil 50 ou o quantil 0,5.

A mediana é usada em vez da média aritmética quando as variantes extremas da série classificada (menor e maior) em comparação com o resto se tornam excessivamente grandes ou excessivamente pequenas.

A função MEDIAN mede a tendência central, que é o centro de um conjunto de números em uma distribuição estatística. Existem três maneiras mais comuns de determinar a tendência central:

• Significa- a média aritmética, que é calculada somando um conjunto de números, seguido pela divisão da soma resultante pelo seu número.
  Por exemplo, a média dos números 2, 3, 3, 5, 7 e 10 é 5, que é o resultado da divisão da soma, que é 30, pelo número, que é 6.
• Mediana- um número que está no meio de um conjunto de números: metade dos números tem valores maiores que a mediana e metade dos números são menores.
  Por exemplo, a mediana para os números 2, 3, 3, 5, 7 e 10 é 4.
• Modaé o número que ocorre com mais frequência no conjunto de números dado.
  Por exemplo, a moda para os números 2, 3, 3, 5, 7 e 10 seria 3.

Aula de álgebra no 7º ano.

Tópico "Media como característica estatística".

Professora Egorova N.I.

O objetivo da aula: formar a compreensão dos alunos sobre a mediana de um conjunto de números e a capacidade de calculá-la para conjuntos numéricos simples, fixando o conceito de conjunto de média aritmética de números.

Tipo de lição: explicação do novo material.

Durante as aulas

1. Momento organizacional.

Informar o tema da lição e formular seus objetivos.

2. Actualização de conhecimentos prévios.

Perguntas para os alunos:

Qual é a média aritmética de um conjunto de números?

Onde está localizada a média aritmética dentro de um conjunto de números?

O que caracteriza a média aritmética de um conjunto de números?

Onde a média aritmética de um conjunto de números é frequentemente usada?

Tarefas orais:

Encontre a média aritmética de um conjunto de números:

Verificando a lição de casa.

Livro didático: Nº 169, Nº 172.

3. Aprendendo novos materiais.

Na lição anterior, conhecemos uma característica estatística como a média aritmética de um conjunto de números. Hoje vamos dedicar uma aula a outra característica estatística - a mediana.

Não apenas a média aritmética mostra onde na reta numérica os números de qualquer conjunto estão localizados e onde está seu centro. Outro indicador é a mediana.

A mediana de um conjunto de números é o número que divide o conjunto em duas partes iguais. Em vez de "mediano" pode-se dizer "meio".

Primeiro, usando exemplos, analisaremos como encontrar a mediana e, em seguida, daremos uma definição estrita.

Considere o seguinte exemplo verbal usando um projetor

No final do ano letivo, 11 alunos da 7ª série passaram o padrão de corrida de 100 metros. Os seguintes resultados foram registrados:

Depois que os caras correram a distância, Petya se aproximou do professor e perguntou qual foi o resultado dele.

“Mais média: 16,9 segundos”, respondeu o professor

"Por que?" Petya ficou surpreso. - Afinal, a média aritmética de todos os resultados é de cerca de 18,3 segundos, e eu corri um segundo ou mais melhor. E, em geral, o resultado de Katya (18,4) está muito mais próximo da média do que o meu.”

“Seu resultado é médio porque cinco pessoas correram melhor que você e cinco pior. Então você está bem no meio”, disse o professor.

Escreva um algoritmo para encontrar a mediana de um conjunto de números:

Ordene o conjunto numérico (componha uma série classificada).

Ao mesmo tempo, riscamos os números “maiores” e “menores” desse conjunto de números até restar um ou dois números.

Se houver apenas um número, então é a mediana.

Se houver dois números restantes, a mediana será a média aritmética dos dois números restantes.

Peça aos alunos que formulem independentemente a definição da mediana de um conjunto de números, depois leiam a definição da mediana no livro didático (p. 40) e resolvam o número 186 (a, b), o número 187 (a) de o livro didático (p. 41).

Comente:

Chame a atenção dos alunos para uma circunstância importante: a mediana é praticamente insensível a desvios significativos de valores extremos individuais de conjuntos de números. Em estatística, essa propriedade é chamada de estabilidade. A estabilidade de um indicador estatístico é uma propriedade muito importante, pois nos protege contra erros aleatórios e dados individuais não confiáveis.

4. Consolidação do material estudado.

Solução de problemas.

Denote x-média aritmética, Me-mediana.

Conjunto de números: 1,3,5,7,9.

x=(1+3+5+7+9):5=25:5=5,

Conjunto de números: 1,3,5,7,14.

x=(1+3+5+7+14):5=30:5=6.

a) Conjunto de números: 3,4,11,17,21

b) Conjunto de números: 17,18,19,25,28

c) Conjunto de números: 25, 25, 27, 28, 29, 40, 50

Conclusão: a mediana de um conjunto de números constituído por um número ímpar de membros é igual ao número do meio.

a) Um conjunto de números: 2, 4, 8, 9.

Eu = (4+8):2=12:2=6

b) Um conjunto de números: 1,3,5,7,8,9.

Eu = (5+7):2=12:2=6

A mediana de um conjunto de números contendo um número par de membros é metade da soma dos dois números do meio.

O aluno recebeu as seguintes notas em álgebra durante o trimestre:

5, 4, 2, 5, 5, 4, 4, 5, 5, 5.

Encontre a pontuação média e a mediana desse conjunto.

Vamos encontrar a pontuação média, ou seja, a média aritmética:

x= (5+4+2+5+5+4+4+5+5+5): 10=44:10 = 4,4

Encontre a mediana deste conjunto de números:

Vamos ordenar um conjunto de números: 2,4,4,4,5,5,5,5,5,5

Apenas 10 números, para encontrar a mediana você precisa pegar dois números do meio e encontrar sua meia soma.

Eu = (5+5):2 = 5

Pergunta aos alunos: Se você fosse um professor, que nota você daria a esse aluno por um trimestre? Justifique a resposta.

O presidente da empresa recebe um salário de 300.000 rublos. três de seus deputados recebem 150.000 rublos cada, quarenta funcionários - 50.000 rublos cada. e o salário de um faxineiro é de 10.000 rublos. Encontre a média aritmética e a mediana dos salários da empresa. Qual dessas características é mais lucrativa para o presidente usar para fins publicitários?

x \u003d (300000 + 3 150000 + 40 50000 + 10000): (1 + 3 + 40 + 1) \u003d 2760000: 45 \u003d 61333,33 (rublos)

Não. 6. Oralmente.

A) Quantos números há no conjunto se sua mediana for seu nono membro?

B) Quantos números existem no conjunto se sua mediana for a média aritmética dos 7º e 8º membros?

C) Em um conjunto de sete números, o maior número foi aumentado em 14. Isso mudará tanto a média aritmética quanto a mediana?

D) Cada um dos números do conjunto foi aumentado em 3. O que acontecerá com a média aritmética e a mediana?

Doces na loja são vendidos por peso. Para descobrir quantos doces estão contidos em um quilo, Masha decidiu encontrar o peso de um doce. Ela pesou vários doces e obteve os seguintes resultados:

12, 13, 14, 12, 15, 16, 14, 13, 11.

Ambas as características são adequadas para estimar o peso de um doce, pois eles não são muito diferentes um do outro.

Assim, para caracterizar a informação estatística, utiliza-se a média aritmética e a mediana. Em muitos casos, algumas das características podem não ter nenhum significado significativo (por exemplo, tendo informações sobre o tempo dos acidentes de trânsito, dificilmente faz sentido falar sobre a média aritmética desses dados).

Dever de casa: parágrafo 10, nº 186 (c, d), nº 190.

5. Os resultados da lição. Reflexão.

1. "Pesquisa estatística: coleta e agrupamento de dados estatísticos"

   Lição

   … Tópicos proposto para o sétimo classe. PLANEJAMENTO TEMÁTICO. § 1. Estatísticacaracterísticas. P 1. Média aritmética, amplitude e moda 1h. P 2. MedianaComo asestatísticacaracterística …

2. O programa de trabalho do curso de formação "álgebra" no 7º ano (nível básico) nota explicativa

   Programa de trabalho

   ... item 10 MedianaComo asestatísticacaracterística 23 p.9 Média aritmética, intervalo e modo 24 Exame nº 2 em tema …

3. Programa de trabalho. Matemáticas. 5º ano pág. Kanashi. 2011

   Programa de trabalho

   ... equações. Média aritmética, amplitude e moda. MedianaComo asestatísticacaracterística. O objetivo é sistematizar e resumir informações sobre ... e habilidades adquiridas na lições de acordo com tópicos(Nós vamos álgebra 10 classe). 11 Classe(4 horas por semana...

4. Ordem nº 51 de 30 de agosto de 2012 Programa de Trabalho de Álgebra Grau 7

   Programa de trabalho

   … material didático MedianaComo asestatísticacaracterística Conhecer a definição de média aritmética, amplitude, moda e medianasComo asestatísticacaracterísticas Frontal e individual...

5. Programa de trabalho em matemática 7º ano ii nível nível básico (1)

   Programa de trabalho

   Como encontrar a mediana de uma série

   mesmo, Como asàs 6 Sala de aula. O estudo Tópicos termina apresentando aos alunos o mais simples estatísticacaracterísticas: médio ... M.: Editora "Genzher", 2009. 3. Zhokhov, V.I. Liçõesálgebraàs 7 Sala de aula: livro. para o professor / V. I. Zhokhov ...

Outros documentos relacionados..