Dovada

Lăsa ABC" este un triunghi arbitrar. Să trecem peste vârf B linie dreaptă paralelă cu linia dreaptă AC (o astfel de linie dreaptă se numește linie dreaptă euclidiană). Marcați un punct pe el D astfel încât punctele A și D stați pe părțile opuse ale unei linii drepte î.Hr.Unghiuri DBCși ACB egală ca culcare interioară în cruce, formată dintr-o secantă î.Hr cu linii paralele ACși BD. Prin urmare, suma unghiurilor unui triunghi la vârfuri Bși DIN egal cu unghiul ABD.Suma tuturor celor trei unghiuri ale unui triunghi este egală cu suma unghiurilor ABDși BAC. Deoarece aceste unghiuri sunt interne unilaterale pentru paralel ACși BD la secant AB, atunci suma lor este 180°. Teorema a fost demonstrată.

Consecințe

Din teoremă rezultă că orice triunghi are două unghiuri ascuțite. Într-adevăr, aplicând demonstrația prin contradicție, să presupunem că triunghiul are un singur unghi ascuțit sau nu are deloc unghiuri ascuțite. Atunci acest triunghi are cel puțin două unghiuri, fiecare dintre ele fiind de cel puțin 90°. Suma acestor unghiuri nu este mai mică de 180°. Dar acest lucru este imposibil, deoarece suma tuturor unghiurilor unui triunghi este de 180°. Q.E.D.

Generalizare la teoria simplex

Unde este unghiul dintre fețele i și j ale simplexului.

Note

• Pe o sferă, suma unghiurilor unui triunghi depășește întotdeauna 180 °, diferența se numește exces sferic și este proporțională cu aria triunghiului.
• În planul Lobachevsky, suma unghiurilor unui triunghi este întotdeauna mai mică de 180°. Diferența este, de asemenea, proporțională cu aria triunghiului.

Vezi si

Fundația Wikimedia. 2010 .

• Taylor
• Podul de jos al lebedelor

Vedeți ce este „Teorema despre suma unghiurilor unui triunghi” în alte dicționare:

Teorema sumei unghiului poligonului- Proprietatea poligoanelor în geometria euclidiană: Suma unghiurilor n ale unui poligon este 180°(n 2). Cuprins 1 Dovada 2 Observație ... Wikipedia

teorema lui Pitagora- Teorema lui Pitagora este una dintre teoremele fundamentale ale geometriei euclidiene, stabilind relatia dintre laturile unui triunghi dreptunghic. Cuprins 1 ... Wikipedia

Aria unui triunghi

teorema lui Pitagora- Teorema lui Pitagora este una dintre teoremele fundamentale ale geometriei euclidiene, stabilind relatia dintre laturile unui triunghi dreptunghic. Cuprins 1 Afirmații 2 Dovezi ... Wikipedia

Teorema cosinusului- Teorema cosinusului este o generalizare a teoremei lui Pitagora. Pătratul unei laturi a unui triunghi este egal cu suma pătratelor celorlalte două laturi ale sale fără a dubla produsul acestor laturi cu cosinusul unghiului dintre ele. Pentru un triunghi plat cu laturile a, b, c și unghiul α ... ... Wikipedia

Triunghi- Acest termen are alte semnificații, vezi Triunghi (sensuri). Un triunghi (în spațiul euclidian) este o figură geometrică formată din trei segmente de linie care leagă trei puncte neliniare. Trei puncte, ...... Wikipedia

Semne de egalitate a triunghiurilor- Notație standard Triunghiul este cel mai simplu poligon având 3 vârfuri (colțuri) și 3 laturi; o parte a unui plan delimitată de trei puncte care nu se află pe aceeași linie dreaptă și trei segmente de linie care leagă aceste puncte în perechi. Vârfurile unui triunghi... Wikipedia

Euclid- Matematician grec antic. A lucrat la Alexandria în secolul al III-lea. î.Hr e. Lucrarea principală „Începuturi” (15 cărți), care conține bazele matematicii antice, geometria elementară, teoria numerelor, teoria generală a relațiilor și o metodă pentru determinarea ariilor și volumelor, ... ... Dicţionar enciclopedic

EUCLID- (a murit între 275 și 270 î.Hr.) matematician antic grec. Informațiile despre momentul și locul nașterii sale nu au ajuns la noi, dar se știe că Euclid a trăit în Alexandria, iar perioada de glorie a activității sale cade în timpul domniei lui Ptolemeu I în Egipt ... ... Dicţionar enciclopedic mare

GEOMETRIE NEEUCLIDANĂ- geometrie asemănătoare cu geometria lui Euclid prin faptul că definește mișcarea figurilor, dar diferă de geometria euclidiană prin faptul că unul dintre cele cinci postulate ale sale (al doilea sau al cincilea) este înlocuit de negația sa. Negarea unuia dintre postulatele euclidiene ...... Enciclopedia Collier

Ținte și obiective:

Educational:

• repeta și generalizează cunoștințele despre triunghi;
• demonstrați teorema sumei triunghiului;
• verifica practic corectitudinea formulării teoremei;
• invata sa aplice cunostintele dobandite in rezolvarea problemelor.

În curs de dezvoltare:

• să dezvolte gândirea geometrică, interesul pentru subiect, activitatea cognitivă și creativă a elevilor, vorbirea matematică, capacitatea de a dobândi în mod independent cunoștințe.

Educational:

• să dezvolte calitățile personale ale elevilor, precum determinarea, perseverența, acuratețea, capacitatea de a lucra în echipă.

Echipament: proiector multimedia, triunghiuri din hârtie colorată, materiale didactice „Live Mathematics”, calculator, ecran.

Etapa pregătitoare: profesorul dă elevului sarcina de a pregăti un context istoric asupra teoremei „Suma unghiurilor unui triunghi”.

Tipul de lecție: învățarea de material nou.

În timpul orelor

I. Moment organizatoric

Salutari. Atitudinea psihologică a elevilor față de muncă.

II. Încălzire

Ne-am întâlnit cu figura geometrică „triunghi” în lecțiile anterioare. Să repetăm ​​ce știm despre triunghi?

Elevii lucrează în grupuri. Li se oferă posibilitatea de a comunica între ei, fiecare pentru a construi independent procesul de cunoaștere.

Ce s-a întâmplat? Fiecare grup își face sugestiile și profesorul le scrie pe tablă. Se discută rezultatele:

Poza 1

III. Noi formulăm sarcina lecției

Deci, știm deja multe despre triunghi. Dar nu tot. Fiecare dintre voi are triunghiuri și raportoare pe birou. Ce crezi, ce sarcină ne putem formula?

Elevii formulează sarcina lecției - să găsească suma unghiurilor unui triunghi.

IV. Explicarea noului material

Partea practică(contribuie la actualizarea cunoștințelor și a abilităților de autocunoaștere) Măsurați unghiurile cu un raportor și găsiți suma lor. Notează rezultatele într-un caiet (ascultă răspunsurile primite). Aflăm că suma unghiurilor pentru fiecare s-a dovedit a fi diferită (acest lucru se poate întâmpla deoarece raportorul a fost aplicat incorect, calculul a fost efectuat cu neglijență etc.).

Îndoiți de-a lungul liniilor punctate și aflați cu ce altceva este egală suma unghiurilor triunghiului:

A)
Figura 2

b)
Figura 3

în)
Figura 4

G)
Figura 5

e)
Figura 6

După finalizarea lucrării practice, elevii formulează răspunsul: Suma unghiurilor unui triunghi este egală cu gradul de măsură a unghiului extins, adică 180°.

Profesor: În matematică, munca practică face posibilă doar un fel de afirmație, dar trebuie dovedită. O afirmație a cărei validitate este stabilită prin demonstrație se numește teoremă. Ce teoremă putem formula și demonstra?

Elevi: Suma unghiurilor unui triunghi este de 180 de grade.

Referință istorică: Proprietatea sumei unghiurilor unui triunghi a fost stabilită în Egiptul antic. Dovada dată în manualele moderne se găsește în comentariile lui Proclu la Elementele lui Euclid. Proclus susține că această dovadă (Fig. 8) a fost descoperită de pitagoreeni (secolul al V-lea î.Hr.). În prima carte a Elementelor, Euclid prezintă o altă demonstrație a teoremei despre suma unghiurilor unui triunghi, care este ușor de înțeles cu ajutorul unui desen (Fig. 7):

Figura 7

Figura 8

Desenele sunt afișate pe ecran printr-un proiector.

Profesorul se oferă să demonstreze teorema cu ajutorul desenelor.

Apoi demonstrația este efectuată folosind CMD „Live Mathematics”. Profesorul la calculator proiectează demonstrația teoremei.

Teorema sumei unghiurilor triunghiulare: „Suma unghiurilor unui triunghi este 180°”

Figura 9

Dovada:

A)

Figura 10

b)

Figura 11

în)

Figura 12

Elevii în caiet fac o scurtă înregistrare a demonstrației teoremei:

Teorema: Suma unghiurilor unui triunghi este 180°.

Figura 13

Dat:Δ ABC

Dovedi: A + B + C = 180°.

Dovada:

Ce trebuia dovedit.

V. Fiz. minut.

VI. Explicația materialului nou (continuare)

Consecința teoremei asupra sumei unghiurilor unui triunghi este derivată de către elevi pe cont propriu, aceasta contribuind la dezvoltarea capacității de a-și formula propriul punct de vedere, de a-l exprima și de a-l argumenta:

În orice triunghi, fie toate unghiurile sunt ascuțite, fie două unghiuri ascuțite, iar al treilea obtuz sau drept.

Dacă toate unghiurile dintr-un triunghi sunt acute, atunci se numește unghiular acut.

Dacă unul dintre unghiurile unui triunghi este obtuz, atunci se numește obtuz.

Dacă unul dintre unghiurile unui triunghi este drept, atunci se numește dreptunghiular.

Teorema sumei triunghiurilor ne permite să clasificăm triunghiurile nu numai după laturi, ci și după unghiuri. (În cursul introducerii tipurilor de triunghiuri, elevii completează un tabel)

tabelul 1

Vedere triunghiulară	Isoscel	Echilateral	Versatil
Dreptunghiular
obtuz
unghiular acut

VII. Consolidarea materialului studiat.

1. Rezolva probleme oral:

(Desenele sunt afișate pe ecran prin proiector)

(rezumat de bază)

Geometrie vizuală Clasa 7. Rezumat de referință Nr. 4 Suma unghiurilor unui triunghi.

Mare om de știință francez al secolului al XVII-lea Blaise Pascal în copilărie, îi plăcea să joace cu forme geometrice. Era familiarizat cu raportorul și știa să măsoare unghiurile. Tânărul cercetător a observat că pentru toate triunghiurile suma a trei unghiuri este aceeași - 180 °. „Cum poți dovedi asta? gândi Pascal. „La urma urmei, nu poți verifica suma unghiurilor tuturor triunghiurilor - există un număr infinit de ele.” Apoi a tăiat două colțuri ale triunghiului cu foarfecele și le-a atașat la al treilea colț. S-a dovedit un unghi dezvoltat, care, după cum știți, este egal cu 180 °. A fost prima descoperire proprie. Soarta ulterioară a băiatului era deja predeterminată.

În acest subiect, veți învăța cinci caracteristici ale egalității triunghiului dreptunghic și poate cea mai populară proprietate a unui triunghi dreptunghic de 30°. Sună așa: piciorul situat opus unui unghi de 30 ° este egal cu jumătate din ipotenuză. Împărțind un triunghi echilateral cu o înălțime, obținem imediat o dovadă a acestei proprietăți.

TEOREMA. Suma unghiurilor unui triunghi este 180°. Pentru a demonstra acest lucru, trasăm o linie prin vârf paralel cu baza. Unghiurile întunecate sunt egale, iar unghiurile gri sunt egale deoarece se află pe linii paralele. Colțul întunecat, colțul gri și colțul de la vârf formează un colț drept, suma lor este de 180°. Din teoremă rezultă că unghiurile unui triunghi echilateral sunt de 60° fiecare și că suma unghiurilor acute ale unui triunghi dreptunghic este de 90°.

colțul exterior triunghiul se numește unghi adiacent unghiului triunghiului. Prin urmare, uneori unghiurile triunghiului însuși sunt numite unghiuri interne.

TEOREMA asupra unghiului exterior al unui triunghi. Unghiul exterior al unui triunghi este egal cu suma a două unghiuri interne care nu sunt adiacente acestuia. Într-adevăr, un colț exterior și două interioare care nu sunt adiacente acestuia completează colțul umplut până la 180°. Din teoremă rezultă că un unghi exterior este mai mare decât orice unghi interior care nu este adiacent acestuia.

TEOREMA privind relațiile dintre laturile și unghiurile unui triunghi. Într-un triunghi, latura mai mare este opusă unghiului mai mare, iar latura mai mare este opusă unghiului mai mare. Din aceasta rezultă: 1) catetul este mai mic decât ipotenuza. 2) Perpendiculara este mai mică decât panta.

Distanța de la punct la linie . Deoarece perpendiculara este mai mică decât orice oblic trasat din același punct, lungimea ei este luată ca distanță de la punct la linie.

inegalitatea triunghiulară . Lungimea oricărei laturi a unui triunghi este mai mică decât suma celorlalte două laturi ale sale, adică A< b + с , b< а + с , Cu< а + b . Consecinţă. Lungimea poliliniei este mai mare decât segmentul care îi leagă capetele.

SEMNELE DE EGALITATE
TRIANGURI DREPTUNGULARE

Pe două picioare. Dacă două catete ale unui triunghi dreptunghic sunt, respectiv, egale cu două catete ale altui triunghi, atunci astfel de triunghiuri sunt congruente.

De-a lungul piciorului și unghiului acut adiacent. Dacă cateta și unghiul ascuțit adiacent acestuia al unui triunghi dreptunghic sunt, respectiv, egale cu cateta și unghiul ascuțit adiacent altui triunghi, atunci astfel de triunghiuri sunt congruente.

De-a lungul piciorului și unghi ascuțit opus. Dacă cateta și unghiul acut opus al unui triunghi dreptunghic sunt egale cu cateta și, respectiv, unghiul ascuțit opus al altui triunghi, atunci astfel de triunghiuri sunt congruente.

Prin ipotenuză și unghi ascuțit. Dacă ipotenuza și unghiul ascuțit al unui triunghi dreptunghic sunt, respectiv, egale cu ipotenuza și unghiul ascuțit al altui triunghi, atunci astfel de triunghiuri sunt congruente.

Dovada acestor criterii se reduce imediat la unul dintre criteriile pentru egalitatea triunghiurilor.

Prin catenă și ipotenuză. Dacă cateta și ipotenuza unui triunghi dreptunghic sunt, respectiv, egale cu cateta și ipotenuza altui triunghi dreptunghic, atunci astfel de triunghiuri sunt congruente.

Dovada. Aplicam triunghiuri cu catete egale. Obținem un triunghi isoscel. Înălțimea sa desenată din vârf va fi și mediana. Apoi, cele doua catete ale triunghiurilor sunt egale, iar triunghiurile sunt egale pe trei laturi.

TEOREMA pe proprietatea unui picior situat opus unui unghi de 30°. Pitul opus unghiului de 30° este egal cu jumătate din ipotenuză. Se demonstrează completând triunghiul la unul echilateral.

TEOREMA asupra proprietății punctelor bisectoare unghiulare. Orice punct de pe bisectoarea unui unghi este echidistant de laturile sale. Dacă un punct este echidistant de laturile unui unghi, atunci se află pe bisectoarea unghiului. Demonstrat desenând două perpendiculare pe laturile unghiului și luând în considerare triunghiuri dreptunghiulare.

Al doilea punct grozav . Bisectoarele unui triunghi se intersectează într-un punct.

Distanța dintre liniile paralele. TEOREMA. Toate punctele fiecăreia dintre cele două drepte paralele sunt la aceeași distanță de cealaltă dreaptă. Definiția distanței dintre liniile paralele rezultă din teoremă.

Definiție. Distanța dintre două drepte paralele este distanța de la orice punct de pe una dintre liniile paralele la cealaltă dreaptă.

Demonstrații detaliate ale teoremelor

Acesta este rezumatul de referință nr. 4 la geometrie în clasa a 7-a. Alegeți următorii pași:

Triunghi . Triunghiuri acute, obtuze și dreptunghiulare.

Picioarele și ipotenuza. Triunghi isoscel și echilateral.

Suma unghiurilor unui triunghi.

Colțul exterior al triunghiului. Semne de egalitate a triunghiurilor.

Liniile și punctele minunate într-un triunghi: înălțimi, mediane,

bisectoare, mediană e perpendiculare, ortocentre,

centrul de greutate, centrul cercului circumscris, centrul cercului înscris.

Teorema lui Pitagora. Raportul de aspect al unui triunghi arbitrar.

Triunghi este un poligon cu trei laturi (sau trei colțuri). Laturile unui triunghi sunt adesea notate cu litere mici, care corespund majusculelor care denotă vârfuri opuse.

Dacă toate cele trei unghiuri sunt acute ( fig. 20), atunci aceasta triunghi acut . Dacă unul dintre colțuri este corect(C, fig.21), acesta este triunghi dreptunghic; laturia, bformând un unghi drept se numesc picioare; laturăcopus unghiului drept se numeste ipotenuză. Dacă unul dintre unghiuri obtuze ( B, fig.22), acesta este triunghi obtuz.


Triunghiul ABC (Fig. 23) - isoscel, dacă Două laturile sale sunt egaleA= c); aceste laturi egale se numesc lateral, este sunat terțul bază triunghi. Triunghi ABC (Fig. 24) - echilateral, dacă toate laturile sale sunt egaleA = b = c). În general ( A ≠ b ≠ c) avem scalen triunghi .

Proprietățile de bază ale triunghiurilor. În orice triunghi:

1. Există un unghi mai mare opus laturii mai mari și invers.

2. Unghiurile egale sunt opuse laturi egale și invers.

În special, toate unghiurile în echilateral triunghiul sunt egale.

3. Suma unghiurilor unui triunghi este 180 º .

Din ultimele două proprietăți rezultă că fiecare unghi într-un echilateral

triunghiul este 60 º.

4. Continuând una dintre laturile triunghiului (AC, fig. 25), primim extern

unghiul BCD . Unghiul exterior al unui triunghi este egal cu suma unghiurilor interioare,

nu are legătură cu acesta :BCD=A+B.

5. Orice latura unui triunghi este mai mică decât suma celorlalte două laturi și mai mult

diferențele lor (A < b + c, A > b – c;b < A + c, b > A – c;c < A + b,c > A – b).

Semne de egalitate a triunghiurilor.

Triunghiurile sunt congruente dacă sunt, respectiv, egale:

A ) două laturi și unghiul dintre ele;

b ) două colțuri și latura adiacentă acestora;

c) trei laturi.

Semne de egalitate ale triunghiurilor dreptunghiulare.

Două dreptunghiular Triunghiurile sunt congruente dacă una dintre următoarele condiții este adevărată:

1) picioarele lor sunt egale;

2) catetul și ipotenuza unui triunghi sunt egale cu catetul și ipotenuza celuilalt;

3) ipotenuza și unghiul ascuțit al unui triunghi sunt egale cu ipotenuza și unghiul ascuțit al celuilalt;

4) cateta și unghiul ascuțit adiacent al unui triunghi sunt egale cu cateta și unghiul ascuțit adiacent al celuilalt;

5) catetul și unghiul ascuțit opus al unui triunghi sunt egale cu cateta și opus unghiului ascutit al celuilalt.

Linii și puncte minunate într-un triunghi.

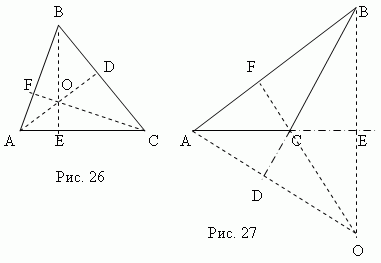
Înălţime triunghiul esteperpendicular,scăpat de la orice vârf în partea opusă ( sau continuarea ei). Această parte se numeștebaza triunghiului . Cele trei altitudini ale unui triunghi se intersectează întotdeaunala un moment datnumit ortocentru triunghi. Ortocentrul unui triunghi acut (punctul O , Fig. 26) este situat în interiorul triunghiului șiortocentrul unui triunghi obtuz (punctul O , Fig.27) – in afara; Ortocentrul unui triunghi dreptunghic coincide cu vârful unghiului drept.

Median - aceasta este segment de linie , legând orice vârf al unui triunghi cu punctul de mijloc al laturii opuse. Trei mediane ale unui triunghi (AD , BE , CF , fig.28) se intersectează la un punct O , care se află întotdeauna în interiorul triunghiului si fiind al lui centrul de greutate. Acest punct împarte fiecare mediană 2:1 din partea de sus.

Bisectoare - aceasta este segment bisectoare colț de sus în punct intersecție cu partea opusă. Trei bisectoare ale unui triunghi (AD , BE , CF , fig.29) se intersectează la un punct Oh, mereu întins în interiorul unui triunghiși fiind centrul cercului înscris(vezi secțiunea „Inscrisși poligoane circumscrise).

Bisectoarea împarte partea opusă în părți proporționale cu laturile adiacente ; de exemplu, în Fig.29 AE : CE = AB : BC .

Perpendiculară mediană este o perpendiculară trasă din medie puncte de segment (laturi). Trei bisectoare perpendiculare ale triunghiului ABC(KO , MO , NU , fig.30 ) se intersectează într-un punct O, adică centru cerc circumscris (punctele K , M , N punctele mijlocii ale laturilor unui triunghi ABC).

Într-un triunghi ascuțit, acest punct se află în interiorul triunghiului; în obtuz - în exterior; într-un dreptunghiular - în mijlocul ipotenuzei. Ortocentrul, centrul de greutate, centrul circumscrisului și centrul cercului înscris coincid doar într-un triunghi echilateral.

Teorema lui Pitagora. Într-un triunghi dreptunghic, pătratul lungimiiIpotenuza este egală cu suma pătratelor lungimilor catetelor.

Dovada teoremei lui Pitagora rezultă în mod evident din Fig.31. Luați în considerare un triunghi dreptunghic ABC cu picioare a, b si ipotenuza c.

Să construim un pătrat AKMB folosind ipotenuza AB ca o parte. Apoiextinde laturile unui triunghi dreptunghic ABC deci pentru a obține un pătrat CDEF , a cărui latură este egală cua + b .Acum este clar că aria unui pătrat CDEF este ( a+b) 2 . Pe de altă parte, aceasta aria este egală cu suma zone patru triunghiuri dreptunghiulareși pătratul AKMB , adică

c 2 + 4 (ab / 2) = c 2 + 2 ab,

de aici,

c 2 + 2 ab= (a+b) 2 ,

si in final avem:

c 2 =A 2 +b 2 .

Raportul de aspect al unui triunghi arbitrar.

În cazul general (pentru un triunghi arbitrar) avem:

c 2 =A 2 +b 2 – 2ab· cos c,

unde C - unghiul dintre laturiAși b .

>>Geometrie: suma unghiurilor unui triunghi. Lecții complete

TEMA LECȚIEI: Suma unghiurilor unui triunghi.

Obiectivele lecției:

• Consolidarea și testarea cunoștințelor elevilor pe tema: „Suma unghiurilor unui triunghi”;
• Dovada proprietăților unghiurilor unui triunghi;
• Utilizarea acestei proprietăți în rezolvarea celor mai simple probleme;
• Utilizarea materialului istoric pentru dezvoltarea activității cognitive a elevilor;
• Insuflarea abilității de precizie în construcția desenelor.

Obiectivele lecției:

• Verificați capacitatea elevilor de a rezolva probleme.

Planul lecției:

1. Triunghi;
2. Teoremă asupra sumei unghiurilor unui triunghi;
3. Exemplu de sarcină.

Triunghi.

Fișier:O.gif Triunghi- cel mai simplu poligon având 3 vârfuri (colțuri) și 3 laturi; o parte a unui plan mărginită de trei puncte și trei segmente de dreaptă care leagă aceste puncte în perechi.
Trei puncte din spațiu care nu se află pe o singură dreaptă corespund unui singur plan.
Orice poligon poate fi împărțit în triunghiuri - acest proces se numește triangulaţie.
Există o secțiune de matematică dedicată în întregime studiului modelelor de triunghiuri - Trigonometrie.

Teoremă asupra sumei unghiurilor unui triunghi.

Fișier:T.gif Teorema sumei unghiurilor triunghiulare este o teoremă clasică în geometria euclidiană care afirmă că suma unghiurilor unui triunghi este de 180°.

dovada" :

Fie dat Δ ABC. Să trasăm o dreaptă paralelă cu (AC) prin vârful B și să marchem punctul D pe acesta, astfel încât punctele A și D să se afle pe laturile opuse ale dreptei BC. Atunci unghiul (DBC) și unghiul (ACB) sunt egale ca cruci interne situate la liniile paralele BD și AC și secanta (BC). Atunci suma unghiurilor triunghiului de la vârfurile B și C este egală cu unghiul (ABD). Dar unghiul (ABD) și unghiul (BAC) la vârful A al triunghiului ABC sunt interioare unilaterale cu drepte paralele BD și AC și secante (AB), iar suma lor este de 180°. Prin urmare, suma unghiurilor unui triunghi este 180°. Teorema a fost demonstrată.

Consecințe.

Unghiul exterior al unui triunghi este egal cu suma celor două unghiuri ale triunghiului care nu sunt adiacente acestuia.

Dovada:

Fie dat Δ ABC. Punctul D se află pe dreapta AC astfel încât A se află între C și D. Atunci BAD este extern unghiului triunghiului la vârful A și A + BAD = 180°. Dar A + B + C = 180°, și deci B + C = 180° – A. Prin urmare BAD = B + C. Corolarul este demonstrat.

Consecințe.

Un unghi exterior al unui triunghi este mai mare decât orice unghi al triunghiului care nu este adiacent acestuia.

O sarcină.

Unghiul exterior al unui triunghi este unghiul adiacent oricărui unghi al acestui triunghi. Demonstrați că un unghi exterior al unui triunghi este egal cu suma a două unghiuri ale triunghiului care nu sunt adiacente acestuia.
(Fig.1)

Soluţie:

Fie în Δ ABC ∠DAC extern (Fig.1). Atunci ∠DAC=180°-∠BAC (după proprietatea unghiurilor adiacente), conform teoremei privind suma unghiurilor unui triunghi ∠B+∠C =180°-∠BAC. Din aceste egalități obținem ∠DAC=∠B+∠C

Fapt interesant:

Suma unghiurilor unui triunghi :

În geometria lui Lobaciovski, suma unghiurilor unui triunghi este întotdeauna mai mică de 180. În geometria lui Euclid, este întotdeauna egală cu 180. În geometria riemanniană, suma unghiurilor unui triunghi este întotdeauna mai mare decât 180.

Din istoria matematicii:

Euclid (secolul al III-lea î.Hr.) în lucrarea „Începuturi” dă următoarea definiție: „Paralele sunt drepte care se află în același plan și, fiind prelungite la nesfârșit de ambele părți, nu se întâlnesc una cu cealaltă de nicio parte”.
Posidonius (secolul I î.Hr.) „Două linii drepte situate în același plan, echidistante una de cealaltă”
Omul de știință grec antic Pappus (sec. III î.Hr.) a introdus simbolul liniilor paralele - semnul =. Ulterior, economistul englez Ricardo (1720-1823) a folosit acest simbol ca semn egal.
Abia în secolul al XVIII-lea au început să folosească simbolul liniilor paralele - semnul ||.
Legătura live dintre generații nu se întrerupe nicio clipă, în fiecare zi învățăm experiența acumulată de strămoșii noștri. Grecii antici, pe baza observațiilor și a experienței practice, au tras concluzii, au exprimat ipoteze, iar apoi, la întâlnirile oamenilor de știință - simpozioane (literalmente „sărbătoare”) - au încercat să fundamenteze și să demonstreze aceste ipoteze. În acel moment, s-a format declarația: „Adevărul se naște într-o dispută”.

Întrebări:

1. Ce este un triunghi?
2. Ce spune teorema sumei triunghiului?
3. Care este unghiul exterior al triunghiului?