Grafické riešenie kvadratickej rovnice Upevniť schopnosť vytvárať grafy rôznych funkcií; Formovať schopnosť graficky riešiť kvadratické rovnice. Projekt na tému "Transformácia grafov funkcie"

Grafické riešenie kvadratickej rovnice Upevniť schopnosť vytvárať grafy rôznych funkcií; Formovať schopnosť graficky riešiť kvadratické rovnice. Brdsk 2009 Mestská vzdelávacia inštitúcia - Ekonomické lýceum Zovšeobecňujúca hodina na tému "Kvadratická funkcia", učiteľ algebry 8. ročník Fedoseeva T.M.

Vykreslenie kvadratickej funkcie Určte smer vetiev: a>0 vetví nahor; a 0 vetví hore; a"> 0 vetví nahor; a"> 0 vetví nahor; a" title="(!LANG:Vykreslenie kvadratickej funkcie Určte smer vetvenia: a>0 vetví nahor; a"> title="Vykreslenie kvadratickej funkcie Určte smer vetiev: a>0 vetví nahor; a"> !}

0 vetví smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Nájdeme bod" title="(!JAZYK: Nakreslíme funkciu y=x 2 -2x-3 pomocou algoritmu: 1) a=1>0 vetvy smerujú nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Hľadanie bodu" class="link_thumb"> 3 !} Zostavme graf funkcie y=x 2 -2x-3 pomocou algoritmu: 1) a=1>0 vetví smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Nájdeme priesečníky s osou OX: x 1 \u003d -1; x 2 \u003d 3 1 spôsob, ako vyriešiť rovnicu x 2 -2x-3 \u003d 0 y x Vyriešiť rovnicu x 2 +2x-3 \u003d 0 0 vetví smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Nájdeme bod "\u003e 0, vetvy sú nasmerované nahor; 2) horné y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3) , (3; 0) a symetrické okolo osi x = 1 Zostavíme parabolu. Nájdite priesečníky s osou OX: x 1 \u003d -1; x 2 \u003d 3 1 spôsob riešenia rovnice x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Vyriešte rovnicu x 2 + 2x-3 \u003d 0 "\u003e 0 vetvy smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Nájdeme bod" title="(!JAZYK: Nakreslíme funkciu y=x 2 -2x-3 pomocou algoritmu: 1) a=1>0 vetvy smerujú nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Hľadanie bodu"> title="Zostavme graf funkcie y=x 2 -2x-3 pomocou algoritmu: 1) a=1>0 vetví smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Hľadanie bodu"> !}

Druhý spôsob: a). Rozdeľme rovnicu x 2 -2x-3=0 na časti x 2 = 2x+3 Napíšme dve funkcie y= x 2 ; y \u003d 2x + 3 Vytvárame grafy týchto funkcií v jednom súradnicovom systéme. Úsečky priesečníkov sú koreňmi rovnice. 0 1 x y Riešte rovnicu x 2 +2x-3=0

Tretí spôsob: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Grafy týchto funkcií zostavujeme v jednom súradnicovom systéme. Úsečky priesečníkov sú koreňmi rovnice. 0 1 x y Riešte rovnicu x 2 +2x-3=0

Grafické riešenie rovníc

Rozkvet, 2009

Úvod

Potreba riešiť kvadratické rovnice v dávnych dobách bola spôsobená potrebou riešenia problémov súvisiacich s hľadaním oblastí pôdy a zemných prác vojenského charakteru, ako aj s rozvojom astronómie a samotnej matematiky. Babylončania vedeli riešiť kvadratické rovnice asi 2000 rokov pred Kristom. Pravidlo na riešenie týchto rovníc uvedené v babylonských textoch sa v podstate zhoduje s modernými, ale nie je známe, ako Babylončania k tomuto pravidlu prišli.

Vzorce na riešenie kvadratických rovníc v Európe boli prvýkrát uvedené v knihe Abacus, ktorú v roku 1202 napísal taliansky matematik Leonardo Fibonacci. Jeho kniha prispela k šíreniu algebraických poznatkov nielen v Taliansku, ale aj v Nemecku, Francúzsku a ďalších európskych krajinách.

Ale všeobecné pravidlo na riešenie kvadratických rovníc so všetkými možnými kombináciami koeficientov b a c sformuloval v Európe až v roku 1544 M. Stiefel.

V roku 1591 François Viet zaviedol vzorce na riešenie kvadratických rovníc.

Niektoré druhy kvadratických rovníc sa dali vyriešiť v starovekom Babylone.

Diophantus Alexandrijský a Euklides , Al-Khwarizmi a Omar Khayyam riešili rovnice geometrickým a grafickým spôsobom.

V 7. ročníku sme študovali funkcie y \u003d C, y= kx , y = kx + m , y = X 2 ,y = - X 2 , v 8. ročníku - y = √ X , y = |X |, y= sekera 2 + bx + c , y = k / X. V učebnici algebry pre 9. ročník som videl funkcie, ktoré mi ešte neboli známe: y= X 3 , y= X 4 ,y= X 2 n , y= X - 2 n , y= 3 √X , ( X – a ) 2 + (y - b ) 2 = r 2 a ďalšie. Existujú pravidlá na vytváranie grafov týchto funkcií. Zaujímalo by ma, či existujú aj iné funkcie, ktoré sa riadia týmito pravidlami.

Mojou úlohou je študovať grafy funkcií a graficky riešiť rovnice.

1. Aké sú funkcie

Graf funkcie je množina všetkých bodov súradnicovej roviny, ktorých úsečky sa rovnajú hodnotám argumentov a súradnice sa rovnajú zodpovedajúcim hodnotám funkcie.

Lineárna funkcia je daná rovnicou y= kx + b, kde k a b- nejaké čísla. Graf tejto funkcie je priamka.

Inverzná proporcionálna funkcia y= k / X, kde k¹ 0. Graf tejto funkcie sa nazýva hyperbola.

Funkcia ( X – a ) 2 + (y – b ) 2 = r 2 , kde a , b a r- nejaké čísla. Grafom tejto funkcie je kružnica s polomerom r so stredom v bode A ( a , b).

kvadratickej funkcie r = sekera 2 + bx + c kde a, b , s- niektoré čísla a a¹ 0. Graf tejto funkcie je parabola.

Rovnica y 2 ( a – X ) = X 2 ( a + X ) . Grafom tejto rovnice bude krivka nazývaná strofoid.

Rovnica ( X 2 + r 2 ) 2 = a ( X 2 – r 2 ) . Graf tejto rovnice sa nazýva Bernoulliho lemniskát.

Rovnica. Graf tejto rovnice sa nazýva astroid.

Krivka (x 2 y 2 - 2 a x) 2 \u003d 4 a 2 (x 2 + y 2). Táto krivka sa nazýva kardioidná.

Funkcie: y= X 3 - kubická parabola, y= X 4 , y = 1/ X 2 .

2. Pojem rovnice, jej grafické riešenie

Rovnica je výraz obsahujúci premennú.

vyriešiť rovnicu- to znamená nájsť všetky jeho korene, alebo dokázať, že neexistujú.

Koreň rovnice je číslo, ktoré po dosadení do rovnice vytvorí správnu číselnú rovnosť.

Grafické riešenie rovníc umožňuje nájsť presnú alebo približnú hodnotu koreňov, umožňuje nájsť počet koreňov rovnice.

Pri vykresľovaní grafov a riešení rovníc sa využívajú vlastnosti funkcie, preto sa metóda často nazýva funkčno-grafická.

Aby sme rovnicu vyriešili, „rozdelíme“ ju na dve časti, zavedieme dve funkcie, zostavíme ich grafy, nájdeme súradnice priesečníkov grafov. Úsečky týchto bodov sú koreňmi rovnice.

3. Algoritmus na zostavenie grafu funkcie

Poznanie grafu funkcie y= f ( X ) , môžete vykresľovať funkcie y= f ( X + m ) ,y= f ( X )+ l a y= f ( X + m )+ l. Všetky tieto grafy sú získané z grafu funkcie y= f ( X ) pomocou paralelnej translačnej transformácie: on │ m │ jednotky mierky doprava alebo doľava pozdĺž osi x a ďalej │ l │ jednotky mierky nahor alebo nadol pozdĺž osi r .

4. Grafické riešenie kvadratickej rovnice

Na príklade kvadratickej funkcie budeme uvažovať o grafickom riešení kvadratickej rovnice. Graf kvadratickej funkcie je parabola.

Čo vedeli starí Gréci o parabole?

Moderná matematická symbolika vznikla v 16. storočí.

Starovekí grécki matematici nemali ani súradnicovú metódu, ani pojem funkcie. Vlastnosti paraboly však podrobne skúmali. Vynaliezavosť starovekých matematikov je jednoducho úžasná, pretože vedeli používať iba kresby a slovné opisy závislostí.

Najviac plne preskúmaná parabola, hyperbola a elipsa Apollonius z Pergy, ktorý žil v 3. storočí pred Kristom. Tieto krivky pomenoval a naznačil, aké podmienky spĺňajú body ležiace na konkrétnej krivke (napokon neexistovali žiadne vzorce!).

Existuje algoritmus na zostavenie paraboly:

Nájdeme súradnice vrcholu paraboly A (x 0; y 0): x 0 =- b /2 a ;

Y 0 \u003d os približne 2 + v 0 + c;

Nájdeme os symetrie paraboly (priamka x \u003d x 0);

Zostavenie tabuľky hodnôt pre stavebné kontrolné body;

Získané body zostrojíme a zostrojíme k nim body symetrické vzhľadom na os súmernosti.

1. Zostavme parabolu podľa algoritmu r = X 2 – 2 X – 3 . Úsečky priesečníkov s osou X a sú koreňmi kvadratickej rovnice X 2 – 2 X – 3 = 0.

Existuje päť spôsobov, ako túto rovnicu graficky vyriešiť.

2. Rozdeľme rovnicu na dve funkcie: r = X 2 a r = 2 X + 3

3. Rozdeľme rovnicu na dve funkcie: r = X 2 –3 a r =2 X. Korene rovnice sú úsečky priesečníkov paraboly s priamkou.

4. Transformujte rovnicu X 2 – 2 X – 3 = 0 výberom celého štvorca na funkcii: r = ( X –1) 2 a r =4. Korene rovnice sú úsečky priesečníkov paraboly s priamkou.

5. Člen po člene obe časti rovnice rozdelíme X 2 – 2 X – 3 = 0 na X, dostaneme X – 2 – 3/ X = 0 Rozdeľme túto rovnicu na dve funkcie: r = X – 2, r = 3/ X . Korene rovnice sú úsečky priesečníkov priamky a hyperboly.

5. Grafické riešenie stupňových rovníc n

Príklad 1 vyriešiť rovnicu X 5 = 3 – 2 X .

r = X 5 , r = 3 – 2 X .

odpoveď: x = 1.

Príklad 2 vyriešiť rovnicu 3 √ X = 10 – X .

Korene tejto rovnice sú úsečkou priesečníka grafov dvoch funkcií: r = 3 √ X , r = 10 – X .

odpoveď: x=8.

Záver

Vzhľadom na funkčné grafy: y= sekera 2 + bx + c , y = k / X , y = √ X , y = |X |, y= X 3 , y= X 4 ,y= 3 √X , Všimol som si, že všetky tieto grafy sú zostavené podľa pravidla paralelného prekladu vzhľadom na osi X a r .

Na príklade riešenia kvadratickej rovnice môžeme konštatovať, že grafická metóda je použiteľná aj pre rovnice stupňa n.

Grafické metódy riešenia rovníc sú krásne a zrozumiteľné, no nedávajú 100% záruku vyriešenia akejkoľvek rovnice. Úsečky priesečníkov grafov môžu byť približné.

V 9. ročníku a vo vyšších ročníkoch sa ešte zoznámim s ďalšími funkciami. Zaujíma ma, či tieto funkcie dodržiavajú pravidlá paralelného prekladu pri vykresľovaní svojich grafov.

Budúci rok sa chcem venovať aj problematike grafického riešenia sústav rovníc a nerovníc.

Literatúra

1. Algebra. 7. trieda. Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

2. Algebra. 8. trieda. Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

3. Algebra. 9. ročník Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

4. Glazer G.I. História matematiky v škole. VII-VIII triedy. – M.: Osveta, 1982.

5. Časopis Matematika №5 2009; č. 8 2007; č. 23 2008.

6. Grafické riešenie rovníc Internetové stránky: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

Grafické riešenie rovníc

Rozkvet, 2009

Úvod

Ale všeobecné pravidlo na riešenie kvadratických rovníc so všetkými možnými kombináciami koeficientov b a c sformuloval v Európe až v roku 1544 M. Stiefel.

V roku 1591 François Viet zaviedol vzorce na riešenie kvadratických rovníc.

Niektoré druhy kvadratických rovníc sa dali vyriešiť v starovekom Babylone.

Diophantus Alexandrijský a Euklides, Al-Khwarizmi a Omar Khayyam riešili rovnice geometrickým a grafickým spôsobom.

V 7. ročníku sme študovali funkcie y \u003d C, y=kx, y =kx+ m, y =X 2,y = -X 2, v 8. ročníku - y = √X, y =|X|, y=sekera2 + bx+ c, y =k/ X. V učebnici algebry pre 9. ročník som videl funkcie, ktoré mi ešte neboli známe: y=X 3, y=X 4,y=X 2n, y=X- 2n, y= 3√X, (X– a) 2 + (y -b) 2 = r 2 a ďalšie. Existujú pravidlá na vytváranie grafov týchto funkcií. Zaujímalo by ma, či existujú aj iné funkcie, ktoré sa riadia týmito pravidlami.

Mojou úlohou je študovať grafy funkcií a graficky riešiť rovnice.

1. Aké sú funkcie

Graf funkcie je množina všetkých bodov súradnicovej roviny, ktorých úsečky sa rovnajú hodnotám argumentov a súradnice sa rovnajú zodpovedajúcim hodnotám funkcie.

Lineárna funkcia je daná rovnicou y=kx+ b, kde k a b- nejaké čísla. Graf tejto funkcie je priamka.

Inverzná proporcionálna funkcia y=k/ X, kde k ¹ 0. Graf tejto funkcie sa nazýva hyperbola.

Funkcia (X– a) 2 + (y -b) 2 = r2 , kde a, b a r- nejaké čísla. Grafom tejto funkcie je kružnica s polomerom r so stredom v bode A ( a, b).

kvadratickej funkcie r= sekera2 + bx+ c kde a,b, s- niektoré čísla a a¹ 0. Graf tejto funkcie je parabola.

Rovnica pri2 (a– X) = X2 (a+ X) . Grafom tejto rovnice bude krivka nazývaná strofoid.

/>Rovnica (X2 + r2 ) 2 = a(X2 – r2 ) . Graf tejto rovnice sa nazýva Bernoulliho lemniskát.

Rovnica. Graf tejto rovnice sa nazýva astroid.

Krivka (X2 r2 – 2 a x)2 = 4 a2 (X2 +y2 ) . Táto krivka sa nazýva kardioidná.

Funkcie: y=X 3 - kubická parabola, y=X 4, y = 1/X 2.

2. Pojem rovnice, jej grafické riešenie

Rovnica je výraz obsahujúci premennú.

vyriešiť rovnicu- to znamená nájsť všetky jeho korene, alebo dokázať, že neexistujú.

Koreň rovnice je číslo, ktoré po dosadení do rovnice vytvorí správnu číselnú rovnosť.

Grafické riešenie rovníc umožňuje nájsť presnú alebo približnú hodnotu koreňov, umožňuje nájsť počet koreňov rovnice.

Pri vykresľovaní grafov a riešení rovníc sa využívajú vlastnosti funkcie, preto sa metóda často nazýva funkčno-grafická.

Aby sme rovnicu vyriešili, „rozdelíme“ ju na dve časti, zavedieme dve funkcie, zostavíme ich grafy, nájdeme súradnice priesečníkov grafov. Úsečky týchto bodov sú koreňmi rovnice.

3. Algoritmus na zostavenie grafu funkcie

Poznanie grafu funkcie y=f(X) , môžete vykresľovať funkcie y=f(X+ m) ,y=f(X)+ l a y=f(X+ m)+ l. Všetky tieto grafy sú získané z grafu funkcie y=f(X) pomocou paralelnej translačnej transformácie: on │ m│ jednotky mierky doprava alebo doľava pozdĺž osi x a ďalej │ l│ jednotky mierky nahor alebo nadol pozdĺž osi r.

4. Grafické riešenie kvadratickej rovnice

Na príklade kvadratickej funkcie budeme uvažovať o grafickom riešení kvadratickej rovnice. Graf kvadratickej funkcie je parabola.

Čo vedeli starí Gréci o parabole?

Moderná matematická symbolika vznikla v 16. storočí.

Existuje algoritmus na zostavenie paraboly:

Nájdite súradnice vrcholu paraboly A (x0; y0): X=- b/2 a;

y0=aho2+in0+s;

Nájdite os súmernosti paraboly (priamka x=x0);

ZLOM STRANY--

Zostavenie tabuľky hodnôt pre stavebné kontrolné body;

Získané body zostrojíme a zostrojíme k nim body symetrické vzhľadom na os súmernosti.

1. Zostavme parabolu podľa algoritmu r= X2 – 2 X– 3 . Úsečky priesečníkov s osou X a sú koreňmi kvadratickej rovnice X2 – 2 X– 3 = 0.

Existuje päť spôsobov, ako túto rovnicu graficky vyriešiť.

2. Rozdeľme rovnicu na dve funkcie: r= X2 a r= 2 X+ 3

3. Rozdeľme rovnicu na dve funkcie: r= X2 –3 a r=2 X. Korene rovnice sú úsečky priesečníkov paraboly s priamkou.

4. Transformujte rovnicu X2 – 2 X– 3 = 0 výberom celého štvorca na funkcii: r= (X–1) 2 a r=4. Korene rovnice sú úsečky priesečníkov paraboly s priamkou.

5. Člen po člene obe časti rovnice rozdelíme X2 – 2 X– 3 = 0 na X, dostaneme X– 2 – 3/ X= 0 Rozdeľme túto rovnicu na dve funkcie: r= X– 2, r= 3/ X. Korene rovnice sú úsečky priesečníkov priamky a hyperboly.

5. Grafické riešenie stupňových rovnícn

Príklad 1 vyriešiť rovnicu X5 = 3 – 2 X.

r= X5 , r= 3 – 2 X.

odpoveď: x = 1.

Príklad 2 vyriešiť rovnicu 3 √ X= 10 – X.

Korene tejto rovnice sú úsečkou priesečníka grafov dvoch funkcií: r= 3 √ X, r= 10 – X.

odpoveď: x=8.

Záver

Vzhľadom na funkčné grafy: y=sekera2 + bx+ c, y =k/ X, y = √X, y =|X|, y=X 3, y=X 4,y= 3√X, Všimol som si, že všetky tieto grafy sú zostavené podľa pravidla paralelného prekladu vzhľadom na osi X a r.

Na príklade riešenia kvadratickej rovnice môžeme konštatovať, že grafická metóda je použiteľná aj pre rovnice stupňa n.

Grafické metódy riešenia rovníc sú krásne a zrozumiteľné, no nedávajú 100% záruku vyriešenia akejkoľvek rovnice. Úsečky priesečníkov grafov môžu byť približné.

V 9. ročníku a vo vyšších ročníkoch sa ešte zoznámim s ďalšími funkciami. Zaujíma ma, či tieto funkcie dodržiavajú pravidlá paralelného prekladu pri vykresľovaní svojich grafov.

Budúci rok sa chcem venovať aj problematike grafického riešenia sústav rovníc a nerovníc.

Literatúra

1. Algebra. 7. trieda. Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

2. Algebra. 8. trieda. Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

3. Algebra. 9. ročník Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

4. Glazer G.I. História matematiky v škole. VII-VIII triedy. – M.: Osveta, 1982.

5. Časopis Matematika №5 2009; č. 8 2007; č. 23 2008.

6. Grafické riešenie rovníc Internetové stránky: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

V tejto video lekcii je téma „Funkcia y \u003d x 2. Grafické riešenie rovníc. Počas tejto hodiny sa žiaci budú môcť zoznámiť s novým spôsobom riešenia rovníc – grafickým, ktorý je založený na znalostiach vlastností funkčných grafov. Učiteľ vám ukáže, ako graficky vyriešiť funkciu y=x 2 .

Predmet:Funkcia

lekcia:Funkcia. Grafické riešenie rovníc

Grafické riešenie rovníc vychádza zo znalosti funkčných grafov a ich vlastností. Uvádzame funkcie, ktorých grafy poznáme:

1), graf je priamka rovnobežná s osou x, prechádzajúca bodom na osi y. Zvážte príklad: y=1:

Pre rôzne hodnoty dostaneme rodinu priamych čiar rovnobežných s osou x.

2) Funkcia priamej úmernosti grafom tejto funkcie je priamka prechádzajúca počiatkom. Zvážte príklad:

Tieto grafy sme už vytvorili v predchádzajúcich lekciách, nezabudnite, že na zostavenie každej čiary musíte vybrať bod, ktorý jej vyhovuje, a ako druhý bod vziať počiatok.

Pripomeňme si úlohu koeficientu k: ako sa funkcia zvyšuje, uhol medzi priamkou a kladným smerom osi x je ostrý; keď funkcia klesá, uhol medzi priamkou a kladným smerom osi x je tupý. Okrem toho existuje nasledujúci vzťah medzi dvoma parametrami k rovnakého znamienka: pre kladné k, čím je väčšie, tým rýchlejšie funkcia rastie, a pre záporné, funkcia klesá rýchlejšie pre veľké hodnoty k modulo.

3) Lineárna funkcia. Keď - dostaneme priesečník s osou y a všetky priamky tohto druhu prechádzajú bodom (0; m). Okrem toho, keď sa funkcia zvyšuje, uhol medzi čiarou a kladným smerom osi x je ostrý; keď funkcia klesá, uhol medzi priamkou a kladným smerom osi x je tupý. A samozrejme, hodnota k ovplyvňuje rýchlosť zmeny hodnoty funkcie.

4). Graf tejto funkcie je parabola.

Zvážte príklady.

Príklad 1 - graficky vyriešte rovnicu:

Funkcie tohto typu nepoznáme, preto musíme danú rovnicu transformovať, aby sme mohli pracovať so známymi funkciami:

V oboch častiach rovnice máme známe funkcie:

Zostavme si grafy funkcií:

Grafy majú dva priesečníky: (-1; 1); (2; 4)

Skontrolujeme, či je riešenie nájdené správne, dosadíme súradnice do rovnice:

Prvý bod je nájdený správne.

, , , , , ,

Druhý bod je tiež nájdený správne.

Riešeniami rovnice sú teda a

Postupujeme podobne ako v predchádzajúcom príklade: danú rovnicu transformujeme na nám známe funkcie, nakreslíme ich grafy, nájdeme priesečníkové prúdy a odtiaľ naznačíme riešenia.

Dostávame dve funkcie:

Poďme zostaviť grafy:

Tieto grafy nemajú priesečníky, čo znamená, že daná rovnica nemá žiadne riešenia

Záver: v tejto lekcii sme si zopakovali funkcie, ktoré sú nám známe, a ich grafy, zapamätali sme si ich vlastnosti a zvážili grafický spôsob riešenia rovníc.

1. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. a kol., Algebra 7. 6. vydanie. M.: Osveta. 2010

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. a iné Algebra 7 .M .: Vzdelávanie. 2006

Úloha 1: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. a kol., Algebra 7, číslo 494, strana 110;

Úloha 2: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. a ďalšie Algebra 7, č. 495, položka 110;

Úloha 3: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. a kol., Algebra 7, číslo 496, strana 110;

DAGESTANSKÝ INŠTITÚT PRE ODBORNÝ ROZVOJ

PEDAGOGICKÍ ZAMESTNANCI

KATEDRA TELESNEJ A MATEMATICKEJ VÝCHOVY A IKT

Projekt

k téme:

« Stavebníctvo a str reformy

funkčné grafy

v školskej matematike »

Rabadanova P.A.

učiteľ matematiky

MBOU "Stredná škola Kochubey"

Tarumovský okres

2015

1. Úvod……………………………………………………………………….….3

2. Kapitola ja. Prehľad literatúry k téme projektu……………………………….….5

3. Kapitola II. Empirická časť:

3.1. Základné metódy na prevod funkčných grafov……….….7

3.2. Vykreslenie párnehoanepárne funkcie ………………… 10

3.3. Vykreslenie inverznej funkcie ………………………… 11

3.4. Deformácia (stlačenie a napätie) grafov………………….12

3.5 Kombinácia prenosu, odrazu a deformácie………………………13

4. Úlohy na samostatné riešenie………………………..…...14

5. Záver……………………………………………………………………………… 15

6. Závery……………………………………………………………….. 17

ÚVOD

Transformácia funkčných grafov je jedným zo základných matematických pojmov priamo súvisiacich s praktickými činnosťami. Grafy odrážajú premenlivosť a dynamiku reálneho sveta, vzájomné vzťahy reálnych predmetov a javov.

Funkčná línia je základnou témou Základnej a Jednotnej štátnej skúšky.Mnohé matematické pojmy sa tiež zvažujú pomocou grafických metód. Napríklad dokvadratickýfunkcia je predstavená a študovaná v úzkej súvislosti s kvadratickými rovnicami a nerovnicami.Z toho teda vyplývanaučiť žiakov zostavovať a transformovať grafy funkcie je jednou z hlavných úloh vyučovania matematiky v škole.

Štúdium funkcie umožňuje zistiť odoména definície a rozsah funkcie, rozsahZníženie alebo zvýšenie frekvencie, asymptoty, intervalystálosť znamienka atď. Avšak na zostavenie grafukov môže byť veľa funkciípoužiť množstvo metóduľahčiťbudova. Preto by študenti mali mať kompetenciu zostavovať grafy podľa metodických schém.

Vyššie uvedené definujerelevantnosť výskumné témy.

Predmet štúdia je náuka o transformácii funkčných čiarových grafov v školskej matematike.

Predmet štúdia - proces konštrukcie a transformácie funkčných grafov na strednej škole.

Účel štúdia: vzdelávací - spočíva v identifikácii metodickej schémy na zostavovanie a konverziu grafov funkcie;rozvíjanie - rozvoj abstraktného, algoritmického, logického myslenia, priestorovej predstavivosti;vzdelávacie - výchova grafickej kultúry školákov, formovanie duševných zručností.

Ciele viedli k rozhodnutiu nasledovnéhoúlohy:

1. Analyzujte pedagogické a metodické zameranie na skúmaný problém.

2. Identifikujte metodologické schémytransformácia funkčných grafov v školskom kurze matematiky.

3. Vyberte najefektívnejšie metódy a prostriedkykonštrukcia a transformácia funkčných grafov na strednej školeprispievanie k: zmysluplnej asimilácii vzdelávacieho materiálu; zvýšenie kognitívnej aktivity študentov; rozvoj ich tvorivých schopností.

HYPOTÉZA výskum: formovanie grafických zručností v procese štúdia funkcií a výchovy grafickej kultúry študentov efektívne, ak študenti majú metodickú schému na vytváranie a transformáciu grafov funkcií v školskom kurze matematiky.

KAPITOLA ja . RECENZIA LITERATÚRY K TÉME PROJEKTU.

Pri príprave projektu sme študovali nasledujúcu literatúru:

Sivashinsky, I. Kh. Vety a problémy v algebre, elementárne funkcie - M., 2002. - 115 s.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Funkcie a grafy (základné techniky) - M., 1985. - 120 s.

V.Z.Zaitsev, V.V. Ryžkov, M.I. Scanavi. Elementárna matematika - M., 2010 (reedícia). - 590 str.

Kuzmin, M. K. Konštrukcia grafu funkcie - J. Matematika v škole. - 2003. - č.5. - S. 61-62.

Shilov G.E. Ako zostaviť grafy? - M., 1982.

Izák Tanatar. Geometrické transformácie grafov funkcií - MTsNMO, 2012

ATJe potrebné poznamenať, že schopnosť „čítať“ správanie funkcie na určitej množine pomocou grafu sa využíva nielen v kurze matematiky, ale aj pri akejkoľvek praktickej činnosti človeka, pri ktorej sa musí zaoberať určitým grafickým reprezentácie závislostí. Preto by žiaci mali vedieť určiť niektoré jej vlastnosti z grafu funkcie.

Teoretický materiál na transformáciu grafov je striktne uvedený v. Technika je doplnená ilustráciami s kresbami, príkladmi rôznej zložitosti a ich riešení, čo umožňuje prehĺbiť vedomosti a vykresliť zložité funkcie.

Predstavuje elektronický vzdelávací kurz, ktorý svojím objemom a obsahom zodpovedá požiadavkám na stredoškolský kurz matematiky. Teoretický materiál je podporený grafickými animačnými ilustráciami, ktoré poskytujú vizuálnu reprezentáciu skúmanej témy. Kurz obsahuje tri moduly: modul teoretického materiálového štúdia, modul samoskúšky a modul ovládania vedomostí.

Z , , boli pre empirickú časť projektu použité metodické diagramové schémy, príklady pre samostatnú prácu.

Závery ku kapitole 1

Štúdium vzdelávacej a metodickej literatúry umožnilo:

1. Identifikujte metodickú schémuštúdium, vytváranie a transformovanie grafov funkcie v kurze školskej matematiky.

2. Vyberte najefektívnejšie metódy a prostriedkykonštrukcia a transformácia funkčných grafov v školskej matematike,prispievanie:

zmysluplná asimilácia vzdelávacieho materiálu;

zvýšenie kognitívnej aktivity študentov;

rozvoj ich tvorivých schopností.

3. ukázať, že funkčná línia má významný vplyv pri štúdiu rôznych pojmov v matematike.

Kapitola 2. EMPIRICKÁ ČASŤ

V tejto kapitole sa budeme zaoberať hlavnými metódami transformácie grafov funkcií a poskytneme metodické schémy na vytváranie rôznych kombinácií grafov pre rôzne funkcie.

2.1. ZÁKLADNÉ TECHNIKY KONVERZIE GRAFOV FUNKCIÍ

Posun pozdĺž osi y

f ( X ) f ( X )+ b .

Prevykreslenie funkcier = f( X) + bstopaem:

1. zostavte funkčný grafr= f( X)

2. pohyb osiúsečka na| b| jednotky až nab>0 alebo pri| b| jesťklaňať sa prib < 0. Získané v novom systémedinat graf je graf funkcier = f( X) + b.

2. Prestup pozdĺž osi úsečka

f ( X ) f ( X + a ) .

r = f( X+ a) sledovaťem:

3. Vykreslenie funkcie formulára r = f (- X )

f (X ) f (- X ).

Na vykreslenie funkcier = f( - x) nasleduje:

vykresliť funkciur = f( X)

odrážať to späťvzhľadom na os y

výsledný graf jefunkčný grafr = f( - X).

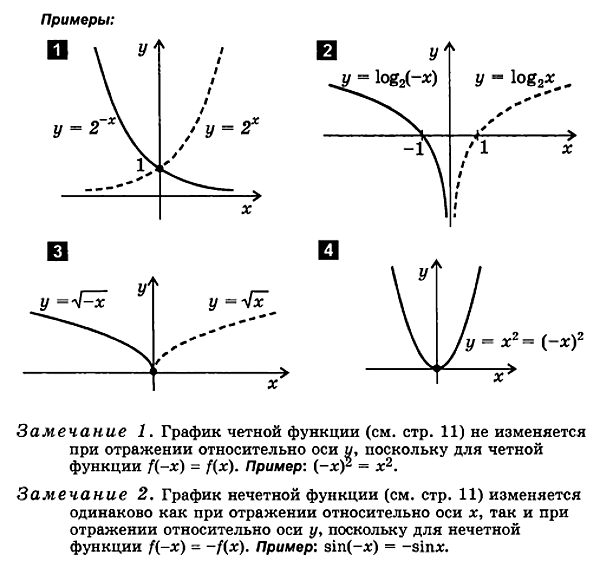
4. Vykreslenie funkcie formulára y= - f ( X )

f ( X ) - f ( X )

- f( X) nasleduje:

vykresliť funkciur= f( X)

odrážať ho okolo osi x

2.2. Vykreslenie párneho a nepárne vlastnosti

Pri kresleníPre párne a nepárne funkcie je vhodné použiť nasledujúce vlastnosti:

1. Graf párnej funkcie simmetricen vzhľadom na os y.

2. Graf nepárnej funkcie je symetrický podľa pôvodu.

Na zostavenie grafov párnej a nepárnej funkcie stačí nakresliť iba pravú vetvu grafu pre kladné hodnoty argumentu. Ľavá vetva je dokončená symetricky okolo začiatku pre nepárnu funkciu a okolo osi y pre párnu funkciu.

Na vykreslenie párnej funkcie r = f ( X ) po duet:

zostrojte vetvu grafu tejto funkcie len vrozsah kladných hodnôt argumentu x≥0.

Osledovať túto vetvu okolo osi y

Na vykreslenie nepárnej funkcie r = f ( X ) nasleduje:

zostavte grafovú vetvu tejto funkcie iba voblasť kladných hodnôt argumentu (х≥0).

Osledovať túto vetvu vzhľadom na pôvoddo oblasti záporných hodnôt x.

2.3. Vykreslenie inverznej funkcie

Ako už bolo uvedené, priame a inverzné funkcieukazujú rovnaký vzťah medzi premennýmix a y, len s tým rozdielom, že v inverznej funkcii tietopremenné zmenili roly, čo je ekvivalentné zmenezápis súradnicových osí. Preto ten grafinverzná funkcia je symetrická ku grafu priamej funkcieo osijaaIIIsúradnicové uhly,teda relatívne rovnéy = x. Tak dostanemeďalšie pravidlo.

Na vykreslenie funkcie y = (x) inverzná k funkciir = f( X), treba postaviťharmonogramr = f( X) a odrážať ju vzhľadom na priamku y = x.

2.4. Deformácia (stlačenie a napätie) grafov

1. Stlačenie (rozšírenie) grafu pozdĺž osi y

f ( X ) A ∙ f ( X ).

Na vykreslenie funkcier= A∙ f( X) nasleduje:

8. Stlačenie (roztiahnutie) grafu pozdĺž osi x

f( X)

Na vykreslenie funkcie y= f( X) nasleduje:

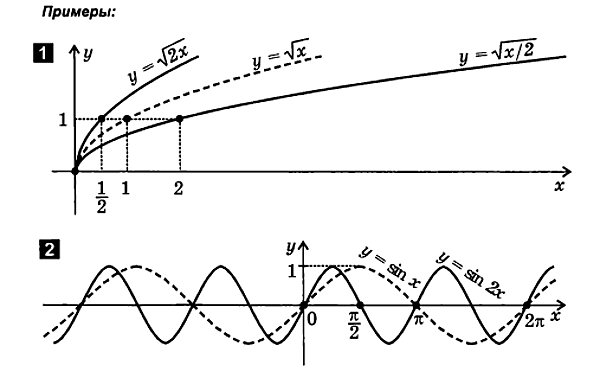
2.5. Kombinácia translácie, odrazu a deformácie

Veľmi často pri vykresľovaní funkčných grafov prezmeniť kombináciu.

Dôsledná aplikácia množstva takýchto techník držania telaumožňuje výrazne zjednodušiť konštrukciu grafu pomocoufunkciu chodu a často ju v závere znížime nakonštrukcia jednej z najjednoduchších elementárnych funkciície. Zvážte, ako z toho vyplýva, vzhľadom na vyššie uvedenévytváranie funkčných grafov.

Všimnime si, že je časodporúča sa vykonať dok na zjednodušenie v ďalšom nástupcoviness.

Pomocou parity respzvláštnosť funkcie.

Prenos osí.

Odraz a deformácia.

Konštrukcia grafu sa vykonáva v opačnom poradí.

Príklad. Nakreslite funkciu

Stavba bude realizovaná v nasledujúcich krokoch:

1. Nakreslite prirodzený logaritmus:

2. stlačiťdo osiOY2 krát:;
3. zobrazovať symetrickyokolo osiOY: ;
4. pohyb po osiVÔLna(!!!) doprava::

5. zobrazenie symetricky okolo osiVÔL: ;
6. pohybovať sapozdĺž osiOY3 jednotky vyššie::

PRÍKLADY KONŠTRUKCIE A KONVERZIE GRAFOV FUNKCIÍ

Príklad 1 Nakreslite funkciu.

Najprv nakreslite sínusový graf, jeho perióda sa rovná:

funkčný grafzískaná kompresiou grafudvakrát na os y. log .

Nakreslite funkciupri = 2 cosX.

Nakreslite funkciur = hriechX .

ZÁVER

Počas práce na projekte bola analyzovaná rôzna náučná a metodologická literatúra k tejto problematike. Výsledky štúdie umožnili identifikovať najcharakteristickejšie pozitívne aspekty štúdie, konštrukcia a transformácia grafov funkcie v kurze školskej matematiky

Hlavným cieľom projektu je rozvíjať zručnosti a schopnosti žiakov v čítaní a kreslení výkresov, pri formovaní racionálnych metód samostatnej činnosti.

Potreba skvalitňovania grafického vzdelávania ako celku je diktovaná nielen modernými výrobnými požiadavkami, ale aj úlohou grafiky v rozvoji technického myslenia a kognitívnych schopností žiakov. Schopnosť človeka spracovávať grafické informácie je jedným z ukazovateľov jeho duševného vývoja. Grafické školenie by sa preto malo stať integrálnou súčasťou všeobecného vzdelávania.

zistenia

Rozpracovaný projekt „Konštrukcia a transformácia funkčných grafov“, venovaný jednému z ústredných pojmov matematiky – funkčnej závislosti, je teda zameraný na systematizáciu a rozšírenie vedomostí žiakov. Štúdium špecifických metód transformácie funkčných grafov sa uskutočňuje analytickým a grafickým spôsobom podľa prísnych metodických schém. Zozbieraný materiál je možné využiť v triede a na samovzdelávanie žiakov. Na vedenie tried možno použiť rôzne formy a metódy organizácie a školenia.

Portál pre študenta. Samotréning

SÚVISIACE ČLÁNKY