Wie man Gleichungen mit einem Variablenwechsel löst. Gleichungen mit Substitution lösen

Einführung

Die mathematische Bildung an einer allgemeinbildenden Schule ist ein wesentlicher Bestandteil der Allgemeinbildung und der allgemeinen Kultur des modernen Menschen. Fast alles, was einen modernen Menschen umgibt, ist auf die eine oder andere Weise mit Mathematik verbunden. Und die neuesten Fortschritte in Physik, Technik und Informationstechnologie lassen keinen Zweifel daran, dass dies auch in Zukunft so bleiben wird. Daher wird die Lösung vieler praktischer Probleme auf das Lösen verschiedener Arten von Gleichungen reduziert, deren Lösung erlernt werden muss.

In der Elementarmathematik werden zwei Arten von Gleichungen unterschieden: algebraische und transzendente.Algebraische Gleichungen umfassen:

linear;

Quadrat; kubisch; Biquad; Gleichung vierten Grades einer allgemeinen Form; zweigliedrige algebraische Gleichung n-ten Grades; Potenz algebraisch; - Rückkehr (algebraisch); – algebraische Gleichung 1. Grades einer allgemeinen Form;

10. gebrochene algebraische Gleichungen, d.h. Gleichungen mit Polynomen und algebraischen Brüchen (Brüche der Form

, wobei und Polynome sind);

11. irrationale Gleichungen, d.h. Gleichungen, die Radikale enthalten, unter denen sich Polynome und algebraische Brüche befinden;

12. Gleichungen, die einen Modul enthalten, unter dessen Modul Polynome und algebraische Brüche enthalten sind.

Gleichungen, die transzendente Funktionen enthalten, wie z. B. logarithmische, exponentielle oder trigonometrische Funktionen, werden als transzendente bezeichnet. In unserer Arbeit betrachten wir algebraische Gleichungen genauer.

In der pädagogischen und methodischen Literatur werden traditionell spezielle Verfahren zum Lösen von Gleichungen betrachtet. Dabei sind die Einzelheiten der Lösung der Gleichungen jedes Abschnitts zweitrangig. Grundsätzlich gibt es vier Hauptmethoden:

Ersetzen der Gleichung h (f(x))=h(g(x)) durch die Gleichung f(x)=g(x);

Variablenersetzungsmethode;

Factoring-Methode;

Funktionsgraphische Methode und ihre verschiedenen Modifikationen.

Die gebräuchlichste davon ist die Variablensubstitutionsmethode.

Darauf aufbauend formulieren wir das Ziel unserer Arbeit: die Möglichkeiten der Methode des Ersetzens der Unbekannten beim Lösen algebraischer Gleichungen zu untersuchen und ihre Anwendung in Standard- und Nichtstandardsituationen zu demonstrieren. Um dieses Ziel zu erreichen, müssen folgende Aufgaben gelöst werden:

1. Erweitern Sie den Inhalt der wichtigsten Konzepte und Aussagen zur Theorie des Lösens von Gleichungen: Lösen einer Gleichung, Äquivalenz und Konsequenz, allgemeine Methoden zum Lösen von Gleichungen.

2. Identifizierung der Möglichkeiten zur Verwendung der Methode zum Ersetzen des Unbekannten beim Lösen algebraischer Gleichungen in Standard- und Nicht-Standardsituationen.

3. Typisierung von Methoden zur Einführung neuer Unbekannter bei der Lösung algebraischer Gleichungen durchzuführen und Kriterien für ihre Anwendbarkeit zu identifizieren

4. Stellen Sie eine Reihe typischer Probleme zusammen, die auf die Verwendung der Ersetzungsmethode beim Lösen von Gleichungen hinauslaufen, und demonstrieren Sie deren Lösung.

1. Grundlegende Konzepte und Aussagen zur Theorie des Lösens von Gleichungen

Im ersten Kapitel unserer Arbeit werden wir den Inhalt der wichtigsten Konzepte und Aussagen zur Theorie des Lösens von Gleichungen enthüllen.

Den Begriff „Gleichung“ lernen wir im Mathematikunterricht bereits in der Grundschule kennen, wobei die Aufgabe „Gleichung lösen“ wohl die häufigste Aufgabe ist. Trotzdem können wir den Begriff "Gleichung" nicht genau definieren, genau definieren, was es bedeutet, "eine Gleichung zu lösen", ohne den Rahmen des Studiums der Elementarmathematik weit zu sprengen. Dazu ist es notwendig, sehr ernsthafte logische und sogar philosophische Kategorien einzubeziehen. Es reicht völlig aus, sich mit diesen Konzepten auf der Ebene des "gesunden Menschenverstandes" vertraut zu machen.

Betrachten Sie zwei Gleichungen A und B mit derselben Unbekannten. Wir werden sagen, dass Gleichung B ist Folge Gleichung A, falls irgendeine Wurzel von Gleichung A eine Wurzel von Gleichung B ist.

Die Gleichungen werden aufgerufen gleichwertig wenn eine Wurzel des einen eine Wurzel des anderen ist und umgekehrt. Gleichungen sind also äquivalent, wenn jede von ihnen eine Folge der anderen ist.

Aus diesen Definitionen folgt zum Beispiel, dass zwei Gleichungen, die keine Lösung haben, äquivalent sind. Wenn A keine Lösungen hat, dann B Folge A, egal welche Gleichung B.

Lassen Sie uns das Konzept des „Lösens einer Gleichung“ definieren. löse die Gleichung- bedeutet, alle solchen Werte der darin enthaltenen Unbekannten zu finden, die die Gleichung in eine Identität verwandeln. Diese Werte werden die Wurzeln der Gleichung genannt.

Der Prozess des Lösens von Gleichungen besteht hauptsächlich darin, eine gegebene Gleichung durch eine andere zu ersetzen, die ihr entspricht.

Wie bereits erwähnt, gibt es vier gebräuchlichste Methoden, die zum Lösen von Gleichungen jeglicher Art verwendet werden. Schauen wir uns jede Methode genauer an.

Die Methode, die Gleichung h (f(x))=h(g(x)) durch die Gleichung f(x)=g(x) zu ersetzen, kann nur angewendet werden, wenn

ist eine monotone Funktion, die jeden ihrer Werte einmal annimmt. Wenn diese Funktion nicht monoton ist, kann das angegebene Verfahren nicht angewendet werden, da Wurzelverluste möglich sind.

Die Essenz der Faktorisierungsmethode ist wie folgt: die Gleichung

kann ersetzt werden:

Nachdem Sie die Gleichungen dieses Satzes gelöst haben, müssen Sie die Wurzeln nehmen, die zum Definitionsbereich der ursprünglichen Gleichung gehören, und den Rest als irrelevant verwerfen.Die Idee einer grafischen Methode zum Lösen der Gleichung

ist wie folgt: Sie müssen Graphen von Funktionen erstellen und ihre Schnittpunkte finden. Die Wurzeln der Gleichung sind die Abszissen dieser Punkte. Mit dieser Methode können Sie die Anzahl der Wurzeln der Gleichung bestimmen, den Wert der Wurzel erraten, ungefähre und manchmal genaue Werte der Wurzeln finden. In einigen Fällen kann die Konstruktion von Funktionsgraphen durch einen Verweis auf einige Eigenschaften von Funktionen ersetzt werden (deshalb sprechen wir nicht von einem grafischen, sondern von einem funktional-grafischen Verfahren zum Lösen von Gleichungen). Wenn zum Beispiel eine der Funktionen

steigt, und der andere sinkt, dann hat die Gleichung entweder keine Wurzeln oder hat eine Wurzel.Lassen Sie uns eine andere ziemlich schöne Variante der funktional-grafischen Methode erwähnen: Wenn auf dem Intervall der größte Wert einer der Funktionen gleich und ist kleinste Wert der anderen Funktion ebenfalls gleich ist, dann ist die Gleichung auf dem Intervall äquivalent zu einem Gleichungssystem.

Lassen Sie uns die Essenz der Variablenänderungsmethode enthüllen: Wenn die Gleichung

Lösen von Gleichungen durch Änderung von Variablen

Die meisten Aufgaben des Lebens

werden als algebraische Gleichungen gelöst:

reduzieren sie auf ihre einfachste Form.

L. N. Tolstoi.

Der Zweck des Unterrichts: Organisation der Bildungsaktivitäten von Studenten zur Beherrschung der Methoden zur Lösung ganzer Gleichungen höheren Grades durch die Methode der Änderung einer Variablen; Einführung in die Konzepte und Methoden zur Lösung reziproker und symmetrischer Gleichungen.

Aufgaben:lehrreich: die Fähigkeit zur Anwendung der Ersatzmethode weiter entwickeln

Variable beim Lösen von Gleichungen; Bildung der Fähigkeit, die gleiche Methode zum Lösen von Gleichungen in verschiedenen Situationen zu sehen; machen Sie sich eine Vorstellung von den Methoden und Wegen zur Lösung von nicht standardmäßigen Problemen und algebraischen Gleichungen auf einem Niveau, das über das Niveau der staatlichen Bildungsstandards hinausgeht;

Entwicklung: Entwicklung des Denkens der Schüler; Gedächtnisentwicklung; Entwicklung

logisches Denken, die Fähigkeit, ihre Gedanken klar zu artikulieren; Entwicklung der Vorstellungskraft der Schüler; Entwicklung der mündlichen Rede.

lehrreich: Erziehung zur Beobachtung; Erziehung zur Genauigkeit

beim Anfertigen von Notizen an der Tafel und in einem Notizbuch; Erziehung zur Selbständigkeit in der Ausübung praktischer Tätigkeiten.

Während des Unterrichts

Zeit organisieren.

Aktualisierung und Systematisierung von Wissen.

Aufgabe Nummer 1. Löse das Kreuzworträtsel. Schreiben Sie Ihre Antworten nur im Nominativ.

Waagerecht:

4. Wie lautet der Ausdruck für eine quadratische Gleichung? (diskriminierend)

6. Der Wert der Variablen, bei dem die Gleichung in eine wahre Gleichheit übergeht. (Wurzel)

8. Gleichung der Form
, wo
. (zweieckig)

9. Französischer Mathematiker mit Bezug zu quadratischen Gleichungen. (Vietnam)

10. Eine Gleichung, in der der linke und der rechte Teil ganzzahlige Ausdrücke sind. (ganz)

11. Gleichungen mit einer Variablen, die denselben Wurzelsatz hat. (äquivalent)

Vertikal:

1. Die Menge der Wurzeln der Gleichung. (Lösung)

2. Lösung der Gleichung
. (Null)

3.Gleichheit, die eine Variable enthält. (Die gleichung)

5. Eine quadratische Gleichung, in der einer der Koeffizienten b oder c gleich 0 ist. (unvollständig)

7. Eine quadratische Gleichung, in der der erste Koeffizient gleich eins ist. (reduziert)

Womit widmen wir unsere Lektion heute? ( Gleichungen lösen )

Aufgabe Nummer 2. Wie würden Sie die Gleichungen für jede Gruppe lösen?

ANTWORTEN: Beispiele der Gruppe 1) löst man am besten durch Faktorisieren, indem man den gemeinsamen Teiler aus Klammern herausnimmt oder abgekürzte Multiplikationsformeln verwendet.

Beispiele der Gruppe 2) werden besser durch Gruppieren und Faktorisieren gelöst.

Beispiele der Gruppe 3) werden besser gelöst, indem man eine neue Variable einführt und zu einer quadratischen Gleichung übergeht.

1 Welchen Multiplikator würden Sie in den Beispielen der Gruppe 1 aus Klammern nehmen?

ANTWORTEN:

Wie würden Sie die Begriffe in den Beispielen der Gruppe 2 gruppieren?

ANTWORTEN:

Was würden Sie in den Beispielen der Gruppe 3 mit einer neuen Variablen bezeichnen?

ANTWORTEN:

Wie kann man ein Polynom faktorisieren?
?

ANTWORTEN: .

Heute zeigst du in der Lektion dein Wissen zum Thema "Gleichungen lösen durch Veränderung der Variablen"

Notieren Sie das Thema der Lektion in Ihren Heften.

Heute werden wir in der Lektion eine der Möglichkeiten zum Lösen von Gleichungen höheren Grades betrachten - die Methode zum Ändern einer Variablen; Wir werden uns mit den Konzepten und Methoden zur Lösung reziproker und symmetrischer Gleichungen vertraut machen.

Die Kunst beim Ersetzen von Variablen besteht darin, herauszufinden, welche Substitution rationaler ist und eher zum Erfolg führt.

Aufgabe Nummer 3.

Löse die Gleichung.(Die Aufgabe an der Tafel wird gleichzeitig von 2 Schülern gelöst.)

a) (Der erste Schüler entscheidet an der Tafel mit Begründung.)

b) (Der zweite Schüler löst die Gleichung im Stillen, erklärt dann die Lösung, die Klasse hört zu und stellt Fragen, wenn etwas nicht klar ist.)

1 Schüler Ersatz:
.

2 Schüler Ersatz:
.

(Zusätzlich für diejenigen, die sich zuvor mit den vorherigen Gleichungen befasst haben).

. .

3 Schüler

(Die Schüler kommentieren den Fortschritt der Entscheidung vor Ort.)

LÖSUNG: Nehmen Sie den gemeinsamen Teiler heraus: ,

wo
oder
, d.h.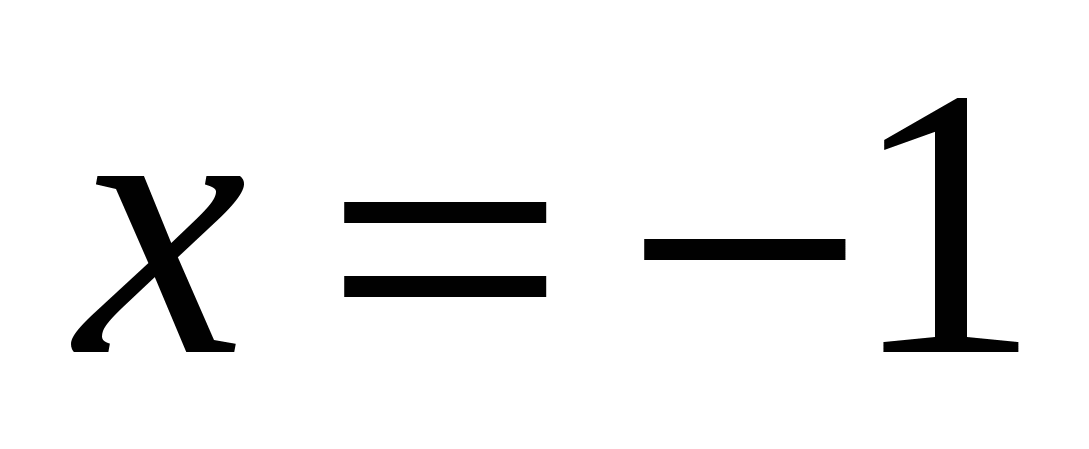

Antworten:

Wissen vertiefen und erweitern

Wir arbeiten weiter. Sie sehen die Gleichung auf der Folie: x 4 -5x 3 +6x 2 -5x + 1 = 0.

Wie würden Sie vorschlagen, es zu lösen? Wie können wir sein?

Ist es möglich, es im Rahmen von Schulprogrammen in Mathematik zu lösen? Sie können mit Nein antworten. Schließlich sehen Standardmethoden zum Lösen von Gleichungen in der Schule vor, Gleichungen nicht höher als den zweiten Grad zu lösen. Aber wir können uns erinnern, dass einzelne Gleichungen höherer Grade noch in der Schule gelöst wurden. Die Methoden ihrer Lösung sind zwar die schöpferische Anwendung bekannter Methoden, ihre Reduktion auf die Lösung einer oder mehrerer Gradgleichungen nicht höher als die zweite.

Sehen Sie sich diese Gleichung genau an? Was haben Sie bemerkt ?(in dieser Gleichung sind die von den Enden äquidistanten Koeffizienten gleich)

Leute, eine Gleichung dieser Art, wenn die von den Enden gleich weit entfernten Koeffizienten gleich sind, wird aufgerufen rückgabefähig. Diese Gleichung wird durch Substitution auf eine quadratische reduziert.

Ich biete Ihnen den folgenden Algorithmus an, um sie zu lösen:

Algorithmus zum Lösen reziproker Gleichungen.

1. Teilen Sie beide Seiten der Gleichung durch x 2.

2. Gruppieren Sie die Begriffe (der erste mit dem letzten, der zweite mit dem vierten).

Bringen Sie die Gleichung in die Form a + c = 0

3.Führen Sie eine neue Variable t = ein , dann t 2 = , d.h. \u003d t 2 - 2.

4. Führen Sie eine Substitution durch und lösen Sie eine quadratische Gleichung.

5. Kehren Sie zur Ersetzung zurück und lösen Sie die resultierenden Gleichungen.

6. Schreiben Sie die Antwort auf.

Die Jungs lernen den Algorithmus.

Der Schüler an der Tafel nach dem Algorithmus und mit Hilfe des Lehrers löst die Gleichung, der Rest schreibt in Notizbücher.

6x 4 – 5x 3 – 38x 2 – 5x + 6 = 0.

Lösung.

6x 2 - 5x - 38 - 5 / x + 6 / x 2 \u003d 0.

6 (x 2 + 1 / x 2) - 5 (x + 1 / x) - 38 \u003d 0.

Geben Sie t ein: Substitution (x + 1/x) = t. Ersatz: (x 2 + 1 / x 2) \u003d t 2 - 2, wir haben:

6t 2 – 5t – 50 = 0.

t = -5/2 oder t = 10/3.

Gehen wir zurück zu x. Nach der umgekehrten Substitution lösen wir die beiden resultierenden Gleichungen:

1) x + 1/x = -5/2;

x 2 + 5/2 x +1 = 0;

x = -2 oder x = -1/2.

2) x + 1/x = 10/3;

x 2 - 10/3 x + 1 = 0;

x = 3 oder x = 1/3.

Antwort: -2; -1/2; 1/3; 3.

Einen großen Beitrag zum Problem der Gleichungen 3. und 4. Grades leisteten die italienischen Mathematiker des 16. Jahrhunderts N. Tartaglia, A. Fiore, D. Cardano u.a. 1535 fand ein wissenschaftliches Duell zwischen A. Fiore und N Tartaglia, bei dem letzterer gewann. In 2 Stunden löste er 30 von Fiore vorgeschlagene Probleme, und Fiore selbst konnte kein einziges lösen, das ihm von Tartaglia gegeben wurde.

Leute, und ich möchte euch heute noch eine Gleichung anbieten, ich habe sie aus der Sammlung von Aufgaben zur Vorbereitung auf die OGE genommen.

. ((x + 1)(x + 4))((x + 2)(x + 3)) = 24,

(x 2 + 5x + 4) (x 2 + 5x + 6) = 24.

Wenn wir die Änderung x 2 + 5x + 4 = t vornehmen, haben wir die Gleichung

t(t + 2) = 24, es ist quadratisch:

t2 + 2t – 24 = 0.

t = -6 oder t = 4.

Nachdem wir die umgekehrte Substitution durchgeführt haben, können wir leicht die Wurzeln der ursprünglichen Gleichung finden.

Antwort: -5; 0.

Kreativer Transfer von Wissen und Können auf neue Bedingungen.

Zu Beginn der Lektion haben wir darüber gesprochen, dass bei wiederholten Elementen in der Gleichung die Variablenersetzungsmethode verwendet werden kann. Wir wissen immer noch nicht, wie man trigonometrische und irrationale Gleichungen löst. Mal sehen, ob wir diese Methode auf sie anwenden können, wenn wir wissen, wie man die einfachsten trigonometrischen und irrationalen Gleichungen löst.

Übung 1: Benennen Sie die Änderung der Variablen in den folgenden Gleichungen.

Aufgabe 2: Schreiben Sie mehrere Gleichungen basierend auf der Methode der Variablenänderung.

Zusammenfassend.

So, Leute, unsere Lektion ist zu Ende. Fassen wir unsere Lektion zusammen.

Welche Ziele haben wir uns zu Beginn des Unterrichts gesetzt?

Wurden unsere Ziele erreicht?

Was haben wir im Unterricht Neues gelernt?

Hausaufgaben.

4x 4 - 8x 3 + 3x 2 - 8x + 4 = 0

(x+1)(x+2)(x+4)(x+5) = 40

. (eine Gleichung italienischer Mathematiker)

Und ich möchte die Lektion mit den Worten des großen Wissenschaftlers Einstein A. beenden:

„Ich muss meine Zeit zwischen Politik und Gleichungen aufteilen. Die Gleichung ist meiner Meinung nach jedoch viel wichtiger, da die Politik nur für diesen Moment existiert und die Gleichung für immer bestehen wird.

Vielen Dank für die Lektion! Auf Wiedersehen!

Variablenänderung im unbestimmten Integral. Formel zur Transformation von Differentialen. Integrationsbeispiele. Beispiele für lineare Substitutionen.

Variablenersetzungsmethode

Mit Hilfe eines Variablenwechsels können Sie einfache Integrale berechnen und in einigen Fällen die Berechnung komplexerer vereinfachen.

Die Variablenersetzungsmethode besteht darin, dass wir von der ursprünglichen Integrationsvariablen, sei es x , zu einer anderen Variablen gehen, die wir als t bezeichnen. Gleichzeitig nehmen wir an, dass die Variablen x und t durch eine Beziehung x = x in Beziehung stehen (t), oder t = t (x). Zum Beispiel x = Protokoll t, x = Sünde t, t = 2 x + 1, usw. Unsere Aufgabe ist es, eine solche Beziehung zwischen x und t so zu wählen, dass sich das ursprüngliche Integral entweder auf ein tabellarisches reduziert oder einfacher wird.

Grundlegende Variablenänderungsformel

Betrachten Sie den Ausdruck, der unter dem Integralzeichen steht. Es besteht aus dem Produkt des Integranden, das wir als f bezeichnen werden (x) und Differential dx : . Gehen wir zu einer neuen Variablen t über, indem wir eine Beziehung x = x wählen (t). Dann müssen wir die Funktion f ausdrücken (x) und das Differential dx bezüglich der Variablen t .

Um den Integranden f auszudrücken (x) durch die Variable t , müssen Sie nur das gewählte Verhältnis x = x anstelle der Variablen x einsetzen (t).

Die Differentialtransformation wird wie folgt durchgeführt:
.
Das heißt, das Differential dx ist gleich dem Produkt der Ableitung von x nach t und dem Differential dt.

Dann
.

In der Praxis ist der häufigste Fall, dass wir eine Ersetzung vornehmen, indem wir eine neue Variable als Funktion der alten wählen: t = t (x). Wenn wir erraten haben, dass der Integrand dargestellt werden kann als
,
wo t′ (x) die Ableitung von t nach x ist
.

Die grundlegende Variablenänderungsformel kann also in zwei Formen dargestellt werden.
(1) ,
wobei x eine Funktion von t ist.
(2) ,
wobei t eine Funktion von x ist.

Wichtiger Hinweis

In Integraltabellen wird die Integrationsvariable meistens als x bezeichnet. Es ist jedoch zu beachten, dass die Integrationsvariable mit einem beliebigen Buchstaben bezeichnet werden kann. Darüber hinaus kann jeder Ausdruck als Integrationsvariable verwendet werden.

Betrachten Sie als Beispiel das Tabellenintegral
.

Dabei kann x durch eine beliebige andere Variable oder eine Funktion einer Variablen ersetzt werden. Hier sind Beispiele für mögliche Optionen:
;
;
.

Beim letzten Beispiel ist zu beachten, dass bei der Übergabe an die Integrationsvariable x das Differential wie folgt transformiert wird:
.
Dann
.

Dieses Beispiel ist die Essenz der Substitutionsintegration. Das heißt, wir müssen das erraten
.
Danach wird das Integral auf ein tabellarisches reduziert.
.

Sie können dieses Integral mit einer Variablenänderung berechnen, indem Sie die Formel anwenden (2) . Sei t = x 2+x. Dann
;
;

.

Beispiele für die Integration durch Variablenänderung

1) Wir berechnen das Integral
.
Das merken wir (sin x)′ = cos x. Dann

.
Hier haben wir die Substitution t = angewendet Sünde x.

2) Wir berechnen das Integral
.
Das merken wir. Dann

.
Hier haben wir die Integration durchgeführt, indem wir die Variable t = geändert haben arctg x.

3) Lassen Sie uns integrieren
.
Das merken wir. Dann

. Hier ist während der Integration die Änderung der Variablen t = x 2 + 1 .

Lineare Substitutionen

Am gebräuchlichsten sind vielleicht lineare Substitutionen. Dies ist eine Substitution einer Variablen des Formulars
t = ax + b
wobei a und b Konstanten sind. Bei einer solchen Änderung sind die Differentiale durch die Beziehung verknüpft
.

Beispiele für die Integration durch lineare Substitutionen

EIN) Integral berechnen
.
Lösung.
.

b) Finde das Integral
.
Lösung.
Lassen Sie uns die Eigenschaften der Exponentialfunktion verwenden.
.
In 2- ist eine Konstante. Wir berechnen das Integral.

.

c) Integral berechnen
.
Lösung.
Wir bringen das quadratische Polynom im Nenner eines Bruchs auf die Summe der Quadrate.
.
Wir berechnen das Integral.

.

D) Finde das Integral
.
Lösung.
Wir transformieren das Polynom unter die Wurzel.

.
Wir integrieren mit der Methode der Variablenänderung.

.
Wir haben zuvor die Formel erhalten
.
Von hier
.
Wenn wir diesen Ausdruck ersetzen, erhalten wir die endgültige Antwort.

Die Mathematik ist ein Bohrloch, durch das der logische Verstand die ideale Welt ausspionieren kann.

Krotov Viktor

In der Schule nehmen rationale Gleichungen den führenden Platz im Algebra-Kurs ein. Ihrem Studium wird mehr Zeit gewidmet als allen anderen Themen. Dies liegt vor allem daran, dass die Gleichungen nicht nur von großer theoretischer Bedeutung sind, sondern auch vielen praktischen Zwecken dienen. Eine große Anzahl von Problemen in der realen Welt läuft darauf hinaus, verschiedene Gleichungen zu lösen, und erst nachdem Sie die Methoden zu ihrer Lösung gemeistert haben, werden Sie Antworten auf verschiedene Fragen der Wissenschaft und Technologie finden.

Für die Herausbildung der Fähigkeit, rationale Gleichungen zu lösen, ist das selbstständige Arbeiten der Studierenden von großer Bedeutung. Bevor es jedoch an die selbstständige Arbeit geht, ist es notwendig, alle möglichen Methoden zur Lösung rationaler Gleichungen genau zu kennen und in der Praxis anwenden zu können.

Schauen wir uns Beispiele im Detail an Variablenänderungsmethode zum Lösen rationaler Gleichungen.

Beispiel 1

Lösen Sie die Gleichung (2x 2 - 3x + 1) 2 = 22x 2 - 33x + 1.

Lösung.

Wir schreiben die Gleichung in die Form um

(2x 2 - 3x + 1) 2 = 11(2x 2 - 3x) + 1. Nehmen wir eine Änderung vor. Sei 2x 2 - 3x \u003d t, dann nimmt die Gleichung die Form an:

(t + 1) 2 = 11t + 1.

Jetzt öffnen wir die Klammern und geben ähnliche ein, wir erhalten:

t2 + 2t + 1 = 11t + 1;

In der resultierenden unvollständigen quadratischen Gleichung entfernen wir den gemeinsamen Faktor aus Klammern, wir haben:

t = 0 oder t = 9.

Jetzt müssen Sie eine inverse Ersetzung vornehmen und jede der resultierenden Gleichungen lösen:

2x 2 - 3x = 0 oder 2x 2 - 3x = 9

x(2x - 3) = 0 2x 2 - 3x - 9 = 0

x = 0 oder x = 3/2 x = 3 oder x = -3/2

Antwort: -1,5; 0; 1,5; 3.

Beispiel 2

Lösen Sie die Gleichung (x 2 - 6x) 2 - 2(x - 3) 2 = 81.

Lösung.

Wenden wir die Differenzquadratformel (a - b) 2 = a 2 - 2ab + b 2 an. Wir schreiben die ursprüngliche Gleichung in die Form

(x 2 - 6x) 2 - 2(x 2 - 6x + 9) = 81. Jetzt können Sie einen Ersatz machen.

Sei x 2 - 6x \u003d t, dann sieht die Gleichung so aus:

t 2 - 2 (t + 9) \u003d 81.

t2 – 2t – 18 – 81 = 0;

t2 – 2t – 99 = 0.

Nach dem Vieta-Theorem sind die Wurzeln der resultierenden Gleichung die Zahlen -9 und 11.

Machen wir die umgekehrte Substitution:

x 2 - 6x = -9 oder x 2 - 6x = 11

x 2 - 6x + 9 = 0 x 2 - 6x - 11 = 0

(x - 3) 2 = 0 D = 80

x = 3 x 1 = 3 + 2√5; x 2 \u003d 3 - 2√5.

Antwort: 3 - 2√5; 3; 3 + 2√5.

Beispiel 3

Löse die Gleichung (x - 1)(x - 3)(x + 5)(x + 7) = 297 und finde das Produkt ihrer Wurzeln.

Lösung.

Lassen Sie uns einen "profitablen" Weg finden, die Faktoren zu gruppieren und die Klammerpaare zu öffnen:

((x - 1)(x + 5))((x - 3)(x + 7)) = 297;

(x 2 + 5x - x - 5) (x 2 + 7x - 3x - 21) = 297;

(x 2 + 4x - 5) (x 2 + 4x - 21) = 297.

Nehmen wir die Änderung x 2 + 4x = t vor, dann sieht die Gleichung so aus:

(t - 5)(t - 21) = 297.

Lassen Sie uns die Klammern öffnen und ähnliche Begriffe angeben:

t2 – 21t – 5t + 105 = 297;

t 2 - 26 t - 192 = 0.

Gemäß dem Vieta-Theorem bestimmen wir, dass die Wurzeln der resultierenden Gleichung die Zahlen -6 und 32 sind.

Nach der umgekehrten Substitution erhalten wir:

x 2 + 4x = -6 oder x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x - 32 = 0

D = 16 - 24< 0 D = 16 + 128 > 0

Keine Wurzeln x 1 = -8; x 2 = 4

Lassen Sie uns das Produkt der Wurzeln finden: -8 4 = -32.

Antwort: -32.

Beispiel 4

Finden Sie die Summe der Wurzeln der Gleichung (x 2 - 2x + 2) 2 + 3x(x 2 - 2x + 2) = 10x 2.

Lösung.

Sei x 2 - 2x + 2 \u003d t, dann nimmt die Gleichung die Form an:

t 2 + 3xt - 10x 2 \u003d 0.

Betrachten Sie die resultierende Gleichung als quadratisch bezüglich t.

D \u003d (3x) 2 - 4 (-10x 2) \u003d 9x 2 + 40x 2 \u003d 49x 2; ≥≤

t 1 = (–3x – 7x) / 2 und t 2 = (–3x + 7x) / 2;

t 1 = –5x und t 2 = 2x.

Seit t \u003d x 2 - 2x + 2 also

x 2 - 2x + 2 = -5x oder x 2 - 2x + 2 = 2x. Lassen Sie uns jede der erhaltenen Gleichungen lösen.

x 2 + 3x + 2 = 0 oder x 2 - 4x + 2 = 0.

Beide Gleichungen haben Wurzeln, weil D > 0.

Unter Verwendung des Vieta-Theorems können wir schließen, dass die Summe der Wurzeln der ersten Gleichung -3 und die der zweiten Gleichung 4 ist. Wir erhalten, dass die Summe der Wurzeln der ursprünglichen Gleichung -3 + 4 = 1 ist

Antwort 1.

Beispiel 5

Finden Sie die Wurzel der Gleichung (x + 1) 4 + (x + 5) 4 = 32, die zum Intervall [-5; zehn].

Lösung.

Sei x = t - 3, dann x + 1 = t - 2; x + 5 = t + 2 und die ursprüngliche Gleichung wird zu:

(t - 2) 4 + (t + 2) 4 \u003d 32. Um Ausdrücke in die vierte Potenz zu erheben, können Sie das Pascal-Dreieck verwenden (Abb. 1);

(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4 ;

(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4 .

Nach Reduktion gleicher Terme erhalten wir:

2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;

t 4 + 6 t 2 2 2 + 2 4 = 16;

t 4 + 24 t 2 + 16 = 16;

t4 + 24t2 = 0;

t 2 (t 2 + 24) = 0;

t \u003d 0 oder t 2 \u003d -24.

Die zweite Gleichung hat keine Wurzeln, was bedeutet, dass t = 0 und nach der umgekehrten Substitution

x \u003d t - 3 \u003d 0 - 3 \u003d -3. Die Wurzel der Gleichung -3 gehört zum Intervall [-5; zehn].

Antwort: -3.

Wie Sie sehen können, müssen Sie beim Lösen rationaler Gleichungen die obigen Formeln kennen und richtig zählen können. Fehler treten am häufigsten bei der Ersatzwahl und beim Rücktausch auf. Um dies zu vermeiden, müssen Sie jede Aktion im Detail beschreiben, dann gibt es keine Fehler in Ihren Entscheidungen.

Site, mit vollständigem oder teilweisem Kopieren des Materials, ist ein Link zur Quelle erforderlich.

Die Mathematik ist ein Bohrloch, durch das der logische Verstand die ideale Welt ausspionieren kann.

Krotov Viktor

Schauen wir uns Beispiele im Detail an Variablenänderungsmethode zum Lösen rationaler Gleichungen.

Beispiel 1

Lösen Sie die Gleichung (2x 2 - 3x + 1) 2 = 22x 2 - 33x + 1.

Lösung.

Wir schreiben die Gleichung in die Form um

(2x 2 - 3x + 1) 2 = 11(2x 2 - 3x) + 1. Nehmen wir eine Änderung vor. Sei 2x 2 - 3x \u003d t, dann nimmt die Gleichung die Form an:

(t + 1) 2 = 11t + 1.

Jetzt öffnen wir die Klammern und geben ähnliche ein, wir erhalten:

t2 + 2t + 1 = 11t + 1;

In der resultierenden unvollständigen quadratischen Gleichung entfernen wir den gemeinsamen Faktor aus Klammern, wir haben:

t = 0 oder t = 9.

Jetzt müssen Sie eine inverse Ersetzung vornehmen und jede der resultierenden Gleichungen lösen:

2x 2 - 3x = 0 oder 2x 2 - 3x = 9

x(2x - 3) = 0 2x 2 - 3x - 9 = 0

x = 0 oder x = 3/2 x = 3 oder x = -3/2

Antwort: -1,5; 0; 1,5; 3.

Beispiel 2

Lösen Sie die Gleichung (x 2 - 6x) 2 - 2(x - 3) 2 = 81.

Lösung.

Wenden wir die Differenzquadratformel (a - b) 2 = a 2 - 2ab + b 2 an. Wir schreiben die ursprüngliche Gleichung in die Form

(x 2 - 6x) 2 - 2(x 2 - 6x + 9) = 81. Jetzt können Sie einen Ersatz machen.

Sei x 2 - 6x \u003d t, dann sieht die Gleichung so aus:

t 2 - 2 (t + 9) \u003d 81.

t2 – 2t – 18 – 81 = 0;

t2 – 2t – 99 = 0.

Nach dem Vieta-Theorem sind die Wurzeln der resultierenden Gleichung die Zahlen -9 und 11.

Machen wir die umgekehrte Substitution:

x 2 - 6x = -9 oder x 2 - 6x = 11

x 2 - 6x + 9 = 0 x 2 - 6x - 11 = 0

(x - 3) 2 = 0 D = 80

x = 3 x 1 = 3 + 2√5; x 2 \u003d 3 - 2√5.

Antwort: 3 - 2√5; 3; 3 + 2√5.

Beispiel 3

Löse die Gleichung (x - 1)(x - 3)(x + 5)(x + 7) = 297 und finde das Produkt ihrer Wurzeln.

Lösung.

Lassen Sie uns einen "profitablen" Weg finden, die Faktoren zu gruppieren und die Klammerpaare zu öffnen:

((x - 1)(x + 5))((x - 3)(x + 7)) = 297;

(x 2 + 5x - x - 5) (x 2 + 7x - 3x - 21) = 297;

(x 2 + 4x - 5) (x 2 + 4x - 21) = 297.

Nehmen wir die Änderung x 2 + 4x = t vor, dann sieht die Gleichung so aus:

(t - 5)(t - 21) = 297.

Lassen Sie uns die Klammern öffnen und ähnliche Begriffe angeben:

t2 – 21t – 5t + 105 = 297;

t 2 - 26 t - 192 = 0.

Gemäß dem Vieta-Theorem bestimmen wir, dass die Wurzeln der resultierenden Gleichung die Zahlen -6 und 32 sind.

Nach der umgekehrten Substitution erhalten wir:

x 2 + 4x = -6 oder x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x - 32 = 0

D = 16 - 24< 0 D = 16 + 128 > 0

Keine Wurzeln x 1 = -8; x 2 = 4

Lassen Sie uns das Produkt der Wurzeln finden: -8 4 = -32.

Antwort: -32.

Beispiel 4

Finden Sie die Summe der Wurzeln der Gleichung (x 2 - 2x + 2) 2 + 3x(x 2 - 2x + 2) = 10x 2.

Lösung.

Sei x 2 - 2x + 2 \u003d t, dann nimmt die Gleichung die Form an:

t 2 + 3xt - 10x 2 \u003d 0.

Betrachten Sie die resultierende Gleichung als quadratisch bezüglich t.

D \u003d (3x) 2 - 4 (-10x 2) \u003d 9x 2 + 40x 2 \u003d 49x 2; ≥≤

t 1 = (–3x – 7x) / 2 und t 2 = (–3x + 7x) / 2;

t 1 = –5x und t 2 = 2x.

Seit t \u003d x 2 - 2x + 2 also

x 2 - 2x + 2 = -5x oder x 2 - 2x + 2 = 2x. Lassen Sie uns jede der erhaltenen Gleichungen lösen.

x 2 + 3x + 2 = 0 oder x 2 - 4x + 2 = 0.

Beide Gleichungen haben Wurzeln, weil D > 0.

Antwort 1.

Beispiel 5

Finden Sie die Wurzel der Gleichung (x + 1) 4 + (x + 5) 4 = 32, die zum Intervall [-5; zehn].

Lösung.

Sei x = t - 3, dann x + 1 = t - 2; x + 5 = t + 2 und die ursprüngliche Gleichung wird zu:

(t - 2) 4 + (t + 2) 4 \u003d 32. Um Ausdrücke in die vierte Potenz zu erheben, können Sie das Pascal-Dreieck verwenden (Abb. 1);

(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4 ;

(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4 .

Nach Reduktion gleicher Terme erhalten wir:

2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;

t 4 + 6 t 2 2 2 + 2 4 = 16;

t 4 + 24 t 2 + 16 = 16;

t4 + 24t2 = 0;

t 2 (t 2 + 24) = 0;

t \u003d 0 oder t 2 \u003d -24.

Die zweite Gleichung hat keine Wurzeln, was bedeutet, dass t = 0 und nach der umgekehrten Substitution

x \u003d t - 3 \u003d 0 - 3 \u003d -3. Die Wurzel der Gleichung -3 gehört zum Intervall [-5; zehn].

Antwort: -3.

blog.site, mit vollständigem oder teilweisem Kopieren des Materials, ist ein Link zur Quelle erforderlich.

Portal für den Studenten. Selbsttraining

Variablenersetzungsmethode

Grundlegende Variablenänderungsformel

Wichtiger Hinweis

Beispiele für die Integration durch Variablenänderung

Lineare Substitutionen

Beispiele für die Integration durch lineare Substitutionen

IN VERBINDUNG STEHENDE ARTIKEL