Suche nach Extrempunkten. Lektion zum Thema: "Ermitteln der Extrema von Funktionen

Dies ist ein ziemlich interessanter Abschnitt der Mathematik, mit dem absolut alle Doktoranden und Studenten konfrontiert sind. Allerdings mag nicht jeder Matan. Einige verstehen nicht einmal grundlegende Dinge wie die scheinbar standardmäßige Funktionsstudie. Dieser Artikel zielt darauf ab, dieses Versehen zu korrigieren. Möchten Sie mehr über die Funktionsanalyse erfahren? Möchten Sie wissen, was Extrempunkte sind und wie man sie findet? Dann ist dieser Artikel für Sie.

Untersuchung des Graphen einer Funktion

Zunächst lohnt es sich zu verstehen, warum es überhaupt notwendig ist, das Diagramm zu analysieren. Es gibt einfache Funktionen, die leicht zu zeichnen sind. Ein markantes Beispiel für eine solche Funktion ist die Parabel. Es ist nicht schwer, ihr Diagramm zu zeichnen. Man muss nur mit einer einfachen Transformation die Zahlen finden, bei denen die Funktion den Wert 0 annimmt. Und das ist im Prinzip alles, was man wissen muss, um eine Parabel zu zeichnen.

Aber was ist, wenn die Funktion, die wir graphisch darstellen müssen, viel komplizierter ist? Da die Eigenschaften komplexer Funktionen eher nicht offensichtlich sind, ist es notwendig, eine vollständige Analyse durchzuführen. Erst dann kann die Funktion grafisch dargestellt werden. Wie es geht? Die Antwort auf diese Frage finden Sie in diesem Artikel.

Funktionsanalyseplan

Das erste, was zu tun ist, ist eine oberflächliche Untersuchung der Funktion durchzuführen, während der wir den Definitionsbereich finden werden. Fangen wir also der Reihe nach an. Der Definitionsbereich ist die Menge jener Werte, durch die die Funktion definiert ist. Einfach ausgedrückt sind dies die Zahlen, die in der Funktion anstelle von x verwendet werden können. Um den Umfang zu bestimmen, genügt ein Blick auf den Eintrag. Zum Beispiel ist es offensichtlich, dass die Funktion y (x) \u003d x 3 + x 2 - x + 43 einen Definitionsbereich hat - die Menge der reellen Zahlen. Nun, bei einer Funktion wie (x 2 - 2x) / x ist alles etwas anders. Da die Zahl im Nenner nicht gleich 0 sein sollte, sind alle reellen Zahlen außer Null der Definitionsbereich dieser Funktion.

Als nächstes müssen Sie die sogenannten Nullstellen der Funktion finden. Dies sind die Werte des Arguments, für die die gesamte Funktion den Wert Null annimmt. Dazu ist es notwendig, die Funktion mit Null gleichzusetzen, sie im Detail zu betrachten und einige Transformationen durchzuführen. Nehmen wir die bereits bekannte Funktion y(x) = (x 2 - 2x)/x. Aus dem Schulunterricht wissen wir, dass ein Bruch 0 ist, wenn der Zähler null ist. Deshalb verwerfen wir den Nenner und beginnen mit dem Zähler, indem wir ihn mit Null gleichsetzen. Wir erhalten x 2 - 2x \u003d 0 und nehmen x aus Klammern. Daher x (x - 2) \u003d 0. Als Ergebnis stellen wir fest, dass unsere Funktion gleich Null ist, wenn x gleich 0 oder 2 ist.

Beim Studium des Graphen einer Funktion stehen viele vor einem Problem in Form von Extrempunkten. Und es ist seltsam. Schließlich sind Extreme ein eher einfaches Thema. Glauben Sie nicht? Überzeugen Sie sich selbst, indem Sie diesen Teil des Artikels lesen, in dem wir über die Mindest- und Höchstpunktzahl sprechen.

Zunächst lohnt es sich zu verstehen, was ein Extremum ist. Ein Extremum ist der Grenzwert, den eine Funktion auf einem Graphen erreicht. Daraus ergibt sich, dass es zwei Extremwerte gibt - ein Maximum und ein Minimum. Zur Verdeutlichung können Sie sich das Bild oben ansehen. Auf dem untersuchten Gebiet ist Punkt -1 das Maximum der Funktion y (x) \u003d x 5 - 5x und Punkt 1 ist das Minimum.

Verwechseln Sie Konzepte auch nicht miteinander. Die Extrempunkte einer Funktion sind diejenigen Argumente, an denen die gegebene Funktion Extremwerte annimmt. Das Extremum wiederum ist der Wert der Minima und Maxima der Funktion. Betrachten Sie zum Beispiel noch einmal die obige Abbildung. -1 und 1 sind die Extremwerte der Funktion, und 4 und -4 sind die Extremwerte selbst.

Extrempunkte finden

Aber wie findet man die Extrempunkte einer Funktion? Alles ist ziemlich einfach. Das erste, was zu tun ist, ist die Ableitung der Gleichung zu finden. Nehmen wir an, wir haben die Aufgabe: „Finde die Extrempunkte der Funktion y (x), x ist das Argument. Nehmen wir zur Verdeutlichung die Funktion y (x) \u003d x 3 + 2x 2 + x + 54. Differenzieren wir und erhalten die folgende Gleichung: 3x 2 + 4x + 1. Als Ergebnis erhalten wir die quadratische Standardgleichung. Alles, was getan werden muss, ist, sie mit Null gleichzusetzen und die Wurzeln zu finden. Da die Diskriminante größer als Null ist (D \u003d 16 - 12 \u003d 4), diese Gleichung wird durch zwei Wurzeln bestimmt. Wir finden sie und erhalten zwei Werte: 1/3 und -1. Dies sind die Extrempunkte der Funktion. Wie können Sie jedoch noch bestimmen? Wer ist wer? Welcher Punkt ist das Maximum und welcher das Minimum? Dazu müssen Sie einen benachbarten Punkt nehmen und seinen Wert herausfinden. Nehmen wir zum Beispiel die Zahl -2, die links von der Koordinate steht Linie von -1. Wir ersetzen diesen Wert in unserer Gleichung y (-2) = 12 - 8 + 1 = 5. Als Ergebnis erhalten wir eine positive Zahl. Das bedeutet, dass auf dem Intervall von 1/3 bis -1 die Funktion zunimmt, was wiederum bedeutet, dass in den Intervallen von min von unendlich bis 1/3 und von -1 bis plus unendlich nimmt die Funktion ab. Daraus können wir schließen, dass die Zahl 1/3 der Minimalpunkt der Funktion auf dem untersuchten Intervall ist und -1 der Maximalpunkt ist.

Es ist auch erwähnenswert, dass die Prüfung nicht nur das Finden von Extrempunkten erfordert, sondern auch eine Art Operation mit ihnen durchzuführen (Addieren, Multiplizieren usw.). Aus diesem Grund lohnt es sich, den Bedingungen des Problems besondere Aufmerksamkeit zu schenken. Schließlich können Sie durch Unachtsamkeit Punkte verlieren.

Aus diesem Artikel erfährt der Leser, was ein Extremum des funktionalen Werts ist, sowie über die Merkmale seiner Verwendung in der Praxis. Das Studium eines solchen Konzepts ist äußerst wichtig für das Verständnis der Grundlagen der höheren Mathematik. Dieses Thema ist grundlegend für ein tieferes Studium des Kurses.

In Kontakt mit

Was ist ein Extrem?

Im Schulunterricht werden viele Definitionen des Begriffs „extremum“ gegeben. Dieser Artikel soll das tiefste und klarste Verständnis des Begriffs für diejenigen vermitteln, die sich mit dem Thema nicht auskennen. Unter dem Begriff wird also verstanden, inwieweit das Funktionsintervall auf einer bestimmten Menge einen minimalen oder maximalen Wert annimmt.

Das Extremum ist gleichzeitig der Minimalwert der Funktion und das Maximum. Es gibt einen Minimalpunkt und einen Maximalpunkt, dh die Extremwerte des Arguments in der Grafik. Die wichtigsten Wissenschaften, in denen dieses Konzept verwendet wird:

  • Statistiken;
  • Maschinensteuerung;
  • Ökonometrie.

Extrempunkte spielen eine wichtige Rolle bei der Bestimmung der Sequenz einer gegebenen Funktion. Das Koordinatensystem in der Grafik zeigt am besten die Änderung der Extremposition in Abhängigkeit von der Änderung der Funktionalität.

Extrema der Ableitungsfunktion

Es gibt auch so etwas wie ein "Derivat". Es ist notwendig, den Extremumpunkt zu bestimmen. Es ist wichtig, die minimalen oder maximalen Punkte nicht mit den größten und kleinsten Werten zu verwechseln. Dies sind unterschiedliche Konzepte, obwohl sie ähnlich erscheinen mögen.

Der Wert der Funktion ist der Hauptfaktor bei der Bestimmung, wie der Maximalpunkt zu finden ist. Die Ableitung wird nicht aus den Werten gebildet, sondern ausschließlich aus ihrer Extremlage in der einen oder anderen Ordnung.

Die Ableitung selbst wird auf der Grundlage der Daten der Extrempunkte bestimmt und nicht des größten oder kleinsten Werts. In russischen Schulen ist die Grenze zwischen diesen beiden Konzepten nicht klar gezogen, was sich auf das Verständnis dieses Themas im Allgemeinen auswirkt.

Betrachten wir nun so etwas wie ein "scharfes Extremum". Bis heute gibt es einen akuten Minimalwert und einen akuten Maximalwert. Die Definition erfolgt gemäß der russischen Klassifikation der kritischen Punkte einer Funktion. Das Konzept eines Extrempunkts ist die Grundlage für das Auffinden kritischer Punkte in einem Diagramm.

Um ein solches Konzept zu definieren, wird der Satz von Fermat verwendet. Es ist das wichtigste bei der Untersuchung von Extrempunkten und gibt eine klare Vorstellung von ihrer Existenz in der einen oder anderen Form. Um Extreme zu gewährleisten, ist es wichtig, bestimmte Bedingungen für das Verringern oder Erhöhen auf dem Diagramm zu schaffen.

Um die Frage "wie finde ich den maximalen Punkt" genau zu beantworten, müssen Sie diese Bestimmungen befolgen:

  1. Den genauen Definitionsbereich auf der Karte finden.
  2. Suche nach der Ableitung einer Funktion und einem Extremum.
  3. Lösen Sie Standardungleichungen für den Definitionsbereich des Arguments.
  4. Beweisen können, in welchen Funktionen ein Punkt auf einem Graphen definiert und stetig ist.

Aufmerksamkeit! Die Suche nach einem kritischen Punkt einer Funktion ist nur möglich, wenn es eine Ableitung mindestens zweiter Ordnung gibt, was durch einen hohen Anteil des Vorhandenseins eines Extremums gewährleistet ist.

Notwendige Bedingung für das Extremum der Funktion

Damit ein Extremum existiert, ist es wichtig, dass es sowohl Minimalpunkte als auch Maximalpunkte gibt. Wird diese Regel nur teilweise eingehalten, so ist die Bedingung für das Vorliegen eines Extremums verletzt.

Jede Funktion in jeder Position muss differenziert werden, um ihre neuen Bedeutungen zu identifizieren. Es ist wichtig zu verstehen, dass der Fall, dass ein Punkt verschwindet, nicht das Hauptprinzip ist, um einen differenzierbaren Punkt zu finden.

Ein scharfes Extremum sowie ein Funktionsminimum sind ein äußerst wichtiger Aspekt beim Lösen eines mathematischen Problems unter Verwendung von Extremwerten. Um diese Komponente besser zu verstehen, ist es wichtig, sich auf die Tabellenwerte für die Zuordnung des Funktionales zu beziehen.

Eine vollständige Erforschung der Bedeutung Plotten eines Wertes
1. Bestimmung von Anstiegs- und Abfallpunkten von Werten.

2. Auffinden von Bruchpunkten, Extremum und Schnittpunkt mit Koordinatenachsen.

3. Der Prozess der Bestimmung von Positionsänderungen auf dem Chart.

4. Bestimmung des Index und der Richtung der Konvexität und Konvexität unter Berücksichtigung des Vorhandenseins von Asymptoten.

5. Erstellung einer zusammenfassenden Tabelle der Studie im Hinblick auf die Bestimmung ihrer Koordinaten.

6. Intervalle der Zunahme und Abnahme von Extrem- und Spitzenpunkten finden.

7. Bestimmung der Konvexität und Konkavität der Kurve.

8. Das Erstellen eines Diagramms basierend auf der Studie ermöglicht es Ihnen, ein Minimum oder Maximum zu finden.

 Das Hauptelement, wenn es notwendig ist, mit Extrema zu arbeiten, ist die genaue Konstruktion seines Graphen.

Schullehrer schenken einem so wichtigen Aspekt oft nicht die volle Aufmerksamkeit, was eine grobe Verletzung des Bildungsprozesses darstellt.

Das Diagramm wird nur auf der Grundlage der Ergebnisse der Untersuchung von Funktionsdaten, der Definition scharfer Extrema sowie von Punkten auf dem Diagramm erstellt.

Scharfe Extrema der Ableitung einer Funktion werden in einem Diagramm mit genauen Werten unter Verwendung des Standardverfahrens zur Bestimmung von Asymptoten angezeigt.

Betrachten Sie den Graphen einer stetigen Funktion y=f(x) in der Abbildung gezeigt.

Funktionswert am Punkt x 1 wird größer sein als die Werte der Funktion an allen benachbarten Punkten sowohl links als auch rechts davon x eines . In diesem Fall soll die Funktion an der Stelle stehen x 1 max. Am Punkt x Die 3-Funktion hat offensichtlich auch ein Maximum. Wenn wir den Punkt bedenken x 2 , dann ist der Wert der darin enthaltenen Funktion kleiner als alle benachbarten Werte. In diesem Fall soll die Funktion an der Stelle stehen x 2 mindestens. Ähnlich für den Punkt x 4 .

Funktion y=f(x) am Punkt x 0 hat maximal, wenn der Wert der Funktion an diesem Punkt größer ist als ihre Werte an allen Punkten eines Intervalls, das den Punkt enthält x 0, d. h. wenn es eine solche Umgebung des Punktes gibt x 0 , was für alle gilt x≠x 0 , Zu dieser Nachbarschaft gehörend, haben wir die Ungleichheit f(x)<f(x 0 ) .

Funktion y=f(x) Es hat Minimum am Punkt x 0 , wenn es eine solche Umgebung des Punktes gibt x 0 , was für alle ist x≠x 0 Zugehörigkeit zu dieser Nachbarschaft haben wir die Ungleichung f(x)>f(x0.

Die Punkte, an denen die Funktion ihr Maximum und Minimum erreicht, werden als Extrempunkte bezeichnet, und die Werte der Funktion an diesen Punkten sind die Extrema der Funktion.

Beachten wir, dass eine auf einem Segment definierte Funktion ihr Maximum und Minimum nur an Punkten erreichen kann, die innerhalb des betrachteten Segments liegen.

Beachten Sie, dass wenn eine Funktion an einem Punkt ein Maximum hat, dies nicht bedeutet, dass die Funktion an diesem Punkt den maximalen Wert im gesamten Definitionsbereich hat. In der oben diskutierten Abbildung ist die Funktion an dem Punkt x 1 hat ein Maximum, obwohl es Punkte gibt, an denen die Werte der Funktion größer sind als an dem Punkt x 1 . Insbesondere, f(x 1) < f(x 4) d.h. das Minimum der Funktion ist größer als das Maximum. Aus der Definition des Maximums folgt nur, dass dies der größte Wert der Funktion an Punkten ist, die ausreichend nahe am Maximumpunkt liegen.

Satz 1. (Eine notwendige Bedingung für die Existenz eines Extremums.) Wenn die differenzierbare Funktion y=f(x) an dem Punkt hat x=x 0 Extremum, dann verschwindet seine Ableitung an diesem Punkt.

Nachweisen. Lassen Sie, für die Bestimmtheit, an der Stelle x 0 hat die Funktion ein Maximum. Dann für hinreichend kleine Inkremente Δ x wir haben f(x 0 + Δ x) 0 ) , d.h. Aber dann

Übergeben Sie diese Ungleichungen an den Grenzwert als Δ x→ 0 und unter Berücksichtigung der Ableitung f "(x 0) existiert, und daher hängt die linke Grenze nicht davon ab, wie Δ x→ 0 erhalten wir: für Δ x → 0 – 0 f"(x 0) ≥ 0 und bei Δ x → 0 + 0 f"(x 0) ≤ 0. Da f"(x 0) eine Zahl definiert, dann sind diese beiden Ungleichungen nur kompatibel, wenn f"(x 0) = 0.

Der bewiesene Satz besagt, dass die Maximal- und Minimalpunkte nur unter den Werten des Arguments liegen können, für die die Ableitung verschwindet.

Wir haben den Fall betrachtet, dass eine Funktion an allen Punkten eines bestimmten Segments eine Ableitung hat. Was passiert, wenn das Derivat nicht existiert? Betrachten Sie Beispiele.

Beispiele.

  1. j=|x|.

    Die Funktion hat an einem Punkt keine Ableitung x=0 (an diesem Punkt hat der Graph der Funktion keine bestimmte Tangente), aber an diesem Punkt hat die Funktion ein Minimum, da j(0)=0, und für alle x≠ 0j > 0.

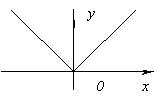
    2. Die Funktion hat keine Ableitung at x=0, da es bei unendlich geht x=0. Aber an diesem Punkt hat die Funktion ein Maximum.

    Die Funktion hat keine Ableitung at x=0 weil bei x→0. An dieser Stelle hat die Funktion weder ein Maximum noch ein Minimum. Wirklich, f(x)=0 und bei x<0f(x)<0, а при x>0f(x)>0.

    Aus den gegebenen Beispielen und dem formulierten Theorem geht also hervor, dass die Funktion nur in zwei Fällen ein Extremum haben kann: 1) an den Punkten, an denen die Ableitung existiert und gleich Null ist; 2) an dem Punkt, an dem das Derivat nicht existiert.

    Allerdings, wenn irgendwann x 0 das wissen wir f"(x 0 ) =0, dann kann daraus nicht geschlossen werden, dass an der Stelle x 0 hat die Funktion ein Extremum.

    Zum Beispiel. .

    Aber Punkt x=0 ist kein Extremumpunkt, da sich links von diesem Punkt die Funktionswerte unterhalb der Achse befinden Ochse, und oben rechts.

    Werte eines Arguments aus dem Definitionsbereich einer Funktion, für die die Ableitung der Funktion verschwindet oder nicht existiert, werden aufgerufen kritische Punkte.


    Aus dem Vorstehenden folgt, dass die Extrempunkte einer Funktion zu den kritischen Punkten gehören, aber nicht jeder kritische Punkt ein Extrempunkt ist. Um das Extremum der Funktion zu finden, müssen Sie daher alle kritischen Punkte der Funktion finden und dann jeden dieser Punkte separat auf Maximum und Minimum untersuchen. Dazu dient der folgende Satz.

    Satz 2. (Eine hinreichende Bedingung für die Existenz eines Extremums.) Die Funktion sei stetig auf einem Intervall, das den kritischen Punkt enthält x 0 und ist an allen Punkten dieses Intervalls differenzierbar (außer vielleicht dem Punkt selbst x 0). Wenn beim Durchgang von links nach rechts durch diesen Punkt die Ableitung das Vorzeichen von Plus nach Minus ändert, dann an diesem Punkt x = x 0 hat die Funktion ein Maximum. Wenn, bei der Durchreise x 0 von links nach rechts, die Ableitung wechselt das Vorzeichen von minus nach plus, dann hat die Funktion an dieser Stelle ein Minimum.

    Also wenn

    Nachweisen. Nehmen wir das zunächst einmal bei der Durchreise an x 0 ändert die Ableitung das Vorzeichen von Plus nach Minus, d.h. für alle x nah dran x 0 f "(x)> 0 für x< x 0 , f"(x)< 0 für x > x 0 . Wenden wir den Satz von Lagrange auf die Differenz an f(x) - f(x 0 ) = f "(c)(x-x 0), wo c liegt zwischen x und x 0 .

    1. Lassen x< x 0 . Dann c< x 0 und f "(c)> 0. Deshalb f "(c)(x-x 0)< 0 und somit

      f(x) - f(x 0 )< 0, d.h. f(x)< f(x 0 ).

    2. Lassen x > x 0 . Dann c>x 0 und f"(c)< 0. Meint f "(c)(x-x 0)< 0. Deshalb f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

    Also für alle Werte x nah genug dran x 0 f(x)< f(x 0 ) . Und das bedeutet das an dem Punkt x 0 hat die Funktion ein Maximum.

    Der zweite Teil des Minimumsatzes wird ähnlich bewiesen.

    Lassen Sie uns die Bedeutung dieses Theorems in der Abbildung veranschaulichen. Lassen f"(x 1 ) =0 und für alle x, nah genug dran x 1 , die Ungleichungen

    f"(x)< 0 bei x< x 1 , f "(x)> 0 bei x > x 1 .

    Dann links vom Punkt x 1 Die Funktion steigt und fällt rechts ab, also wann x = x 1 Funktion geht von steigend nach fallend, d.h. sie hat ein Maximum.

    Ebenso kann man die Punkte betrachten x 2 und x 3 .


    Schematisch lässt sich das alles im Bild darstellen:

    Die Regel zum Studium der Funktion y=f(x) für ein Extremum

    1. Ermitteln Sie den Gültigkeitsbereich einer Funktion f(x).
    2. Finden Sie die erste Ableitung einer Funktion f"(x).
    3. Kritische Punkte bestimmen, dazu:
      1. Finden Sie die wahren Wurzeln der Gleichung f"(x)=0;
      2. alle Werte finden x unter denen die Ableitung f"(x) existiert nicht.
    4. Bestimmen Sie das Vorzeichen der Ableitung links und rechts vom kritischen Punkt. Da das Vorzeichen der Ableitung zwischen zwei kritischen Punkten konstant bleibt, genügt es, das Vorzeichen der Ableitung an einem beliebigen Punkt links und rechts vom kritischen Punkt zu bestimmen.
    5. Berechnen Sie den Wert der Funktion an den Extrempunkten.

    Beispiele. Entdecken Sie Funktionen für Minimum und Maximum.


    DIE GRÖSSTEN UND MINDESTEN FUNKTIONSWERTE AUF DEM ABSCHNITT

    das größte der Wert einer Funktion auf einem Segment ist der größte aller seiner Werte auf diesem Segment, und am wenigsten ist der kleinste aller seiner Werte.

    Betrachten Sie die Funktion y=f(x) kontinuierlich auf dem Segment [ ein, b]. Bekanntermaßen erreicht eine solche Funktion ihren maximalen und minimalen Wert entweder an der Grenze des Segments oder innerhalb desselben. Wird der maximale oder minimale Wert der Funktion am internen Punkt des Segments erreicht, so ist dieser Wert das Maximum oder Minimum der Funktion, dh er wird an kritischen Stellen erreicht.

    Somit erhalten wir folgendes die Regel zum Finden der größten und kleinsten Werte einer Funktion auf dem Segment [ ein, b] :

    1. Finden Sie alle kritischen Punkte einer Funktion im Intervall ( ein, b) und berechnen Sie die Funktionswerte an diesen Stellen.
    2. Berechnen Sie die Werte der Funktion an den Enden des Segments für x=a, x=b.
    3. Wählen Sie von allen erhaltenen Werten den größten und den kleinsten aus.

>> Extreme

Funktionsextremum

Definition von Extremum

Funktion y = f(x) wird aufgerufen zunehmend (abnehmend) in irgendeinem Intervall, wenn für x 1< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).

Wenn eine differenzierbare Funktion y \u003d f (x) auf einem Segment zunimmt (abnimmt), dann ihre Ableitung auf diesem Segment f " (x )> 0

(f"(x)< 0).

Punkt x um genannt lokaler Maximumpunkt (Minimum) der Funktion f (x ), falls es eine Umgebung des Punktes gibt x o, für alle Punkte, deren Ungleichung f (x)≤ f (x o) (f (x)≥ f (xo)).

Die maximalen und minimalen Punkte werden aufgerufen Extrempunkte, und die Werte der Funktion an diesen Punkten sind seine extrem.

Extrempunkte

Notwendige Bedingungen für ein Extremum . Wenn Punkt x um ein Extremum der Funktion f (x) ist, dann ist entweder f " (x o ) = 0 oder f(x o ) existiert nicht. Solche Punkte werden aufgerufen kritisch, wo die Funktion selbst am kritischen Punkt definiert ist. Die Extrema einer Funktion sollten unter ihren kritischen Punkten gesucht werden.

Die erste hinreichende Bedingung. Lassen x um - kritischer Punkt. Wenn f" (x ) beim Durchgang durch den Punkt x um ändert das Pluszeichen in Minus, dann am Punkt x o Die Funktion hat ein Maximum, ansonsten ein Minimum. Ändert die Ableitung beim Durchlaufen eines kritischen Punktes nicht das Vorzeichen, dann am Punkt x um es gibt kein Extremum.

Die zweite hinreichende Bedingung. Die Funktion f(x) habe
f" (x ) in der Nähe des Punktes x um und die zweite Ableitung genau an der Stelle x o. Wenn f"(x o) = 0, >0 ( <0), то точка x o ist ein lokaler minimaler (maximaler) Punkt der Funktion f(x). Wenn =0, dann muss man entweder die erste hinreichende Bedingung verwenden oder höhere einbeziehen.

Auf einem Segment kann die Funktion y \u003d f (x) entweder an kritischen Punkten oder an den Enden des Segments den kleinsten oder größten Wert erreichen.

Beispiel 3.22.

Lösung. Als f " (

Aufgaben zum Finden des Extremums einer Funktion

Beispiel 3.23. a

Lösung. x und j j
0 ≤ x≤
> 0, während x > a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение Funktionen sq.. Einheiten).

Beispiel 3.24. p ≈

Lösung. pp
S"
R = 2, H = 16/4 = 4.

Beispiel 3.22.Finden Sie die Extrema der Funktion f (x) = 2x 3 - 15x 2 + 36x - 14.

Lösung. Als f " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), dann die kritischen Punkte der Funktion x 1 \u003d 2 und x 2 \u003d 3. Extreme Punkte können nur an diesen sein Punkte. Da beim Durchgang durch den Punkt x 1 \u003d 2 die Ableitung das Vorzeichen von Plus nach Minus ändert, hat die Funktion an dieser Stelle ein Maximum. Beim Durchgang durch den Punkt x 2 \u003d 3 ändert die Ableitung das Vorzeichen von Minus nach Plus, daher hat die Funktion am Punkt x 2 \u003d 3 ein Minimum. Berechnung der Werte der Funktion in Punkten
x 1 = 2 und x 2 = 3 finden wir die Extrema der Funktion: Maximum f (2) = 14 und Minimum f (3) = 13.

Beispiel 3.23.Es ist notwendig, in der Nähe der Steinmauer einen rechteckigen Bereich zu bauen, der auf drei Seiten mit Maschendraht eingezäunt ist und auf der vierten Seite an die Mauer angrenzt. Dafür gibt es a laufende Meter des Gitters. Bei welchem ​​Seitenverhältnis hat die Site die größte Fläche?

Lösung.Bezeichnen Sie die Seiten der Website durch x und j. Die Fläche des Standorts ist gleich S = xy. Lassen j ist die Länge der an die Wand angrenzenden Seite. Dann muss per Bedingung die Gleichheit 2x + y = a gelten. Daher y = a - 2x und S = x (a - 2x), wobei
0 ≤ x≤ a /2 (die Länge und Breite des Pads dürfen nicht negativ sein). S "= a - 4x, a - 4x = 0 für x = a/4, woraus
y \u003d a - 2 × a / 4 \u003d a / 2. Weil die x = a /4 ist der einzige kritische Punkt, prüfen wir, ob sich das Vorzeichen der Ableitung beim Durchgang durch diesen Punkt ändert. Für x a /4 S "> 0, während x > a /4 S " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение Funktionen S(a/4) = a/4(a - a/2) = a 2 /8 (sq.. Einheiten). Da S kontinuierlich ist und seine Werte an den Enden von S(0) und S(a /2) gleich Null sind, ist der gefundene Wert der größte Wert der Funktion. Somit ist das günstigste Aspektverhältnis des Standorts unter den gegebenen Bedingungen des Problems y = 2x.

Beispiel 3.24.Es ist erforderlich, einen geschlossenen zylindrischen Tank mit einem Fassungsvermögen von V=16 herzustellen p ≈ 50m 3. Welche Abmessungen sollte der Tank haben (Radius R und Höhe H), um möglichst wenig Material für seine Herstellung zu verwenden?

Lösung.Die Gesamtfläche des Zylinders ist S = 2 p R(R+H). Wir kennen das Volumen des Zylinders V = p R 2 N Þ N \u003d V / p R 2 \u003d 16 p / p R 2 \u003d 16 / R 2. Also S(R) = 2 p (R2+16/R). Wir finden die Ableitung dieser Funktion:
S"(R) \u003d 2 p (2R- 16 / R 2) \u003d 4 p (R- 8 / R 2). S" (R) = 0 für R 3 = 8, also
R = 2, H = 16/4 = 4.

Funktionen ist es überhaupt nicht erforderlich, das Vorhandensein der ersten und zweiten Ableitung zu kennen und ihre physikalische Bedeutung zu verstehen. Zuerst müssen Sie Folgendes verstehen:

  • die Extrema der Funktion maximieren oder minimieren umgekehrt den Wert der Funktion in einer beliebig kleinen Umgebung;
  • am Extremum darf es keinen Sprung in der Funktion geben.

Und jetzt dasselbe, nur in einfachen Worten. Sehen Sie sich die Spitze eines Kugelschreibers an. Wenn der Stift vertikal mit der Schrift nach oben platziert wird, ist die Mitte der Kugel der äußerste Punkt – der höchste Punkt. In diesem Fall sprechen wir vom Maximum. Dreht man nun den Stift mit der Schreibspitze nach unten, so ist in der Mitte der Kugel bereits ein Minimum der Funktion vorhanden. Mit Hilfe der hier angegebenen Abbildung können Sie sich die aufgeführten Manipulationen für einen Briefpapierbleistift vorstellen. Die Extrema einer Funktion sind also immer kritische Punkte: ihre Maxima oder Minima. Der angrenzende Abschnitt des Diagramms kann beliebig scharf oder glatt sein, muss aber auf beiden Seiten vorhanden sein, nur in diesem Fall ist der Punkt ein Extremum. Wenn das Diagramm nur auf einer Seite vorhanden ist, ist dieser Punkt kein Extremum, selbst wenn die Extremumsbedingungen auf einer seiner Seiten erfüllt sind. Lassen Sie uns nun die Extrema der Funktion aus wissenschaftlicher Sicht untersuchen. Damit ein Punkt als Extremum betrachtet werden kann, ist es notwendig und ausreichend, dass:

  • die erste Ableitung war gleich Null oder existierte an der Stelle nicht;
  • die erste Ableitung ändert an dieser Stelle das Vorzeichen.

Aus Sicht der Ableitungen höherer Ordnung wird die Bedingung etwas anders interpretiert: Für eine an einem Punkt differenzierbare Funktion genügt es, dass es eine Ableitung ungerader Ordnung ungleich Null gibt, während alle Ableitungen niedrigerer Ordnung existieren und existieren müssen gleich Null. Dies ist die einfachste Interpretation von Sätzen aus Lehrbüchern, aber für die gewöhnlichsten Menschen lohnt es sich, diesen Punkt anhand eines Beispiels zu erläutern. Die Basis ist eine gewöhnliche Parabel. Reservieren Sie sofort, am Nullpunkt hat es ein Minimum. Nur ein bisschen Mathematik:

  • erste Ableitung (X 2) | = 2X, für Nullpunkt 2X = 0;
  • zweite Ableitung (2X) | = 2, für Nullpunkt 2 = 2.

Auf solch einfache Weise werden die Bedingungen, die die Extrema der Funktion sowohl für Ableitungen erster Ordnung als auch für Ableitungen höherer Ordnung bestimmen, veranschaulicht. Hinzuzufügen ist, dass die zweite Ableitung eben dieselbe Ableitung ungerader Ordnung ungleich Null ist, die etwas weiter oben erwähnt wurde. Wenn es um Extrema einer Funktion zweier Variablen geht, müssen die Bedingungen für beide Argumente erfüllt sein. Bei der Verallgemeinerung kommen partielle Ableitungen ins Spiel. Das heißt, für das Vorhandensein eines Extremums an einem Punkt ist es erforderlich, dass beide Ableitungen erster Ordnung gleich Null sind oder mindestens eine davon nicht existiert. Für das Hinreichen des Vorhandenseins eines Extremums wird ein Ausdruck untersucht, der die Differenz zwischen dem Produkt der Ableitungen zweiter Ordnung und dem Quadrat der gemischten Ableitung zweiter Ordnung der Funktion ist. Wenn dieser Ausdruck größer als Null ist, dann liegt ein Extremum vor, und wenn es eine Gleichheit mit Null gibt, dann bleibt die Frage offen und es bedarf weiterer Forschung.

IN VERBINDUNG STEHENDE ARTIKEL