Eine Funktion y=f(x) heißt an einem Punkt x 0 differenzierbar, wenn sie an diesem Punkt eine bestimmte Ableitung hat, d. h. wenn der Grenzwert der Beziehung existiert und endlich ist.

Wenn die Funktion an jedem Punkt eines Segments [a; b] oder das Intervall (a; b), dann heißt es auf der Strecke [a; b] differenzierbar. b] bzw. im Intervall (a; b).

Es gilt der folgende Satz, der einen Zusammenhang zwischen differenzierbaren und stetigen Funktionen herstellt.

Satz. Wenn die Funktion y=f(x) an einem Punkt x 0 differenzierbar ist, dann ist sie an diesem Punkt stetig.

Somit impliziert die Differenzierbarkeit einer Funktion ihre Stetigkeit.

Nachweisen. Wenn, dann

wobei b ein unendlich kleiner Wert ist, d. h. Größe, die bei Ax>0 gegen Null geht. Aber dann

Dy=f "(x 0) Dx+bDx=> Dy>0 für Dx>0, d. h. f(x) - f(x 0)>0 für x>x 0,

und das bedeutet, dass die Funktion f(x) im Punkt x 0 stetig ist. Q.E.D.

Daher kann die Funktion an Unstetigkeitspunkten keine Ableitung haben. Die umgekehrte Aussage ist nicht wahr: Es gibt stetige Funktionen, die an manchen Punkten nicht differenzierbar sind (das heißt, sie haben an diesen Punkten keine Ableitung).

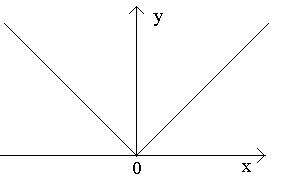
Betrachten Sie die Punkte a, b, c in der Abbildung.

Am Punkt a, wenn Dx>0, hat die Beziehung keine Grenze (da einseitige Grenzen für Dx>0-0 und Dx>0+0 unterschiedlich sind). Es gibt keine definierte Tangente am Punkt A im Diagramm, aber es gibt zwei verschiedene einseitige Tangenten mit Steigungen von 1 und 2 . Diese Art von Punkt wird Eckpunkt genannt.

Am Punkt b ist für Dx>0 das Verhältnis ein vorzeichenkonstanter unendlich großer Wert. Die Funktion hat eine unendliche Ableitung. An diesem Punkt hat der Graph eine vertikale Tangente. Punkttyp – „Wendepunkt“ mit vertikaler Tangente.

Im Punkt c sind die einseitigen Ableitungen unendlich große Mengen unterschiedlicher Vorzeichen. An diesem Punkt weist der Graph zwei verschmolzene vertikale Tangenten auf. Typ - „Spitze“ mit vertikaler Tangente – ein Sonderfall eines Eckpunkts.

1. Betrachten Sie die Funktion y=|x|. Diese Funktion ist im Punkt stetig

Zeigen wir, dass es zu diesem Zeitpunkt keine Ableitung gibt.

f(0+Dx) = f(Dx) = |Dx|. Daher ist Dy = f(Dx) - f(0) = |Dx|

Aber dann für Dx< 0 (т.е. при Дx стремящемся к 0 слева)

Und wenn Dx > 0

Somit hat die Beziehung für Dx > 0 rechts und links unterschiedliche Grenzen, was bedeutet, dass die Beziehung keine Grenze hat, d. h. Ableitung der Funktion y=|x| am Punkt x= 0 existiert nicht. Geometrisch bedeutet dies, dass diese „Kurve“ am Punkt x= 0 keine bestimmte Tangente hat (an diesem Punkt gibt es zwei davon).

2. Die Funktion ist auf der gesamten reellen Geraden definiert und stetig. Lassen Sie uns herausfinden, ob diese Funktion eine Ableitung bei x= 0 hat.

Daher ist die betrachtete Funktion am Punkt x= 0 nicht differenzierbar. Die Tangente an die Kurve an diesem Punkt bildet mit der x-Achse einen Winkel p/2, d.h. fällt mit der y-Achse zusammen.

3 Definition der Ableitung einer Funktion an einem Punkt Die Funktion f(x) sei in einer Umgebung des Punktes x 0 definiert. DEFINITION. Wenn es einen (endlichen) Grenzwert der Beziehung gibt, dann heißt f (x) ein differenzierbarer Punkt x 0, und der Grenzwert selbst heißt Ableitung der Funktion f (x) im Punkt x 0 und wird mit f bezeichnet „(x 0), das heißt, wir bezeichnen x = x – x 0 ist das Inkrement des Arguments beim Übergang von Punkt x 0 zu Punkt x und y = f (x 0 + x) – f (x 0 ) ist das entsprechende Inkrement der Funktion. Dann ist die Ableitung der Funktion f (x) am Punkt x 0 die Grenze des Verhältnisses des Inkrements der Funktion zum Inkrement des Arguments, das sie verursacht hat, wenn das Inkrement von das Argument tendiert gegen Null.

4 Beispiel 1. Lassen Sie uns Beispiele für die Berechnung der Ableitungen einiger einfacher Elementarfunktionen geben, basierend auf der Definition einer Ableitung. y = a x (0 0. Wenn man bedenkt, dass | x | 0 ein beliebiger Punkt ist, dann 0. In Anbetracht dessen | x | 0 ist ein beliebiger Punkt, dann ist „>

0. In Anbetracht dessen | x | 0 ein beliebiger Punkt ist, dann Beispiel 4. y = sinx, x R. Nehmen Sie x 0 R und berechnen Sie das Inkrement der Funktion an diesem Punkt: Also (sinx) = cosx, x R.“ title=" 5 Beispiel 3. Nehmen wir x 0 > 0. Wenn man bedenkt, dass | x | 0 ein beliebiger Punkt ist, dann Beispiel 4. y = sinx, x R. Nehmen wir x 0 R und berechnen das Inkrement der Funktion an diesem Punkt: Also (sinx) = cosx, x R." class="link_thumb"> 5 !} 5 Beispiel 3. Nehmen Sie x 0 > 0. Bedenkt man, dass | x | 0 ist ein beliebiger Punkt, dann Beispiel 4. y = sinx, x R. Nehmen wir x 0 R und berechnen wir das Inkrement der Funktion an diesem Punkt: Also (sinx) = cosx, x R. 0. In Anbetracht dessen | x | 0 ist ein beliebiger Punkt, dann Beispiel 4. y = sinx, x R. Nehmen Sie x 0 R und berechnen Sie das Inkrement der Funktion an diesem Punkt: Also (sinx) = cosx, x R. "> 0. Wenn man bedenkt, dass | x | 0 - beliebiger Punkt, dann Beispiel 4. y \u003d sinx, x R. Nehmen Sie x 0 R und berechnen Sie das Inkrement der Funktion an diesem Punkt: Also (sinx) \u003d cosx, x R. "> 0. In Anbetracht dessen | x | 0 ein beliebiger Punkt ist, dann Beispiel 4. y = sinx, x R. Nehmen Sie x 0 R und berechnen Sie das Inkrement der Funktion an diesem Punkt: Also (sinx) = cosx, x R.“ title=" 5 Beispiel 3. Nehmen wir x 0 > 0. Wenn man bedenkt, dass | x | 0 ein beliebiger Punkt ist, dann Beispiel 4. y = sinx, x R. Nehmen wir x 0 R und berechnen das Inkrement der Funktion an diesem Punkt: Also (sinx) = cosx, x R."> title="5 Beispiel 3. Nehmen Sie x 0 > 0. Bedenkt man, dass | x | 0 ist ein beliebiger Punkt, dann Beispiel 4. y = sinx, x R. Nehmen wir x 0 R und berechnen wir das Inkrement der Funktion an diesem Punkt: Also (sinx) = cosx, x R."> !}

6 SATZ. Wenn eine Funktion f(x) an einem Punkt x 0 differenzierbar ist, dann ist sie an diesem Punkt stetig. Nachweisen. Lassen Sie es dann existieren. Von hier aus erhalten wir, dass f (x) - f (x 0) \u003d f "(x 0) (x - x 0) + (x - x 0) α (x) für x x 0. Das heißt , f ( x) ist im Punkt x 0 stetig. Stetigkeit der differenzierbaren Funktion (1)

7 HINWEIS. Die Stetigkeit einer Funktion an einem Punkt ist keine ausreichende Bedingung für die Existenz einer Ableitung an diesem Punkt. Beispiel 5. f (x) \u003d x. Wir untersuchen das Verhalten von f (x) in der Nähe von x 0 = 0. Hier gilt f (x) f (0) = 0 für x 0. Das heißt, Die Funktion ist am Punkt x 0 \u003d 0 stetig. Betrachten Sie x y 0. Der Grenzwert existiert nicht, da die Funktion f (x) \u003d x also am Punkt x \u003d 0 keine Ableitung hat, obwohl dies der Fall ist an dieser Stelle kontinuierlich

8 Beispiel x y 0 bei x 0. bei x 0. D.h. f(x) ist bei x = 0 stetig. Das heißt, f(x) hat bei x = 0 keine Ableitung und ist daher zu diesem Zeitpunkt nicht differenzierbar. Wir untersuchen das Verhalten von f (x) in der Nähe des Punktes x = 0.

9 Die Funktion y \u003d f (x) sei am Punkt x 0 differenzierbar. Dann kann ihr Inkrement am Punkt x 0 gemäß (1) als y \u003d f (x 0 + x) - f geschrieben werden (x 0) \u003d f ( x 0) x + o(x) bei x. Das Differential der Funktion f (x 0) x - der Hauptlinearteil in Bezug auf x des Inkrements der Funktion y \u003d f (x) am Punkt mit dem Inkrement x und wird mit df (x 0; x) oder df (x 0 ) oder df oder dó bezeichnet. y \u003d f (x 0 + x) - f (x 0) \u003d df (x 0; x) + o (x) bei x. DEFINITION. Der Hauptteil des Inkrements, linear in x. Eine unendlich kleine höhere Ordnung als x. Nun kann das Funktionsinkrement wie folgt geschrieben werden:

10 HINWEIS. Das Inkrement x wird oft mit dem Symbol dx bezeichnet und als Differential der unabhängigen Variablen bezeichnet. Somit kann das Differential einer Funktion an einem Punkt x 0 als df (x 0) \u003d f "(x 0) dx geschrieben werden. Wenn eine Funktion an jedem Punkt eines bestimmten Intervalls differenzierbar ist, dann ist ihr Differential dy a Funktion von x und dx: dy \u003d f "(x)dx. Hieraus ergibt sich insbesondere der Ausdruck für die Ableitung. Das heißt, die Ableitung kann als Verhältnis des Differentials der Funktion zum Differential der unabhängigen Variablen betrachtet werden.

11 Geometrische Bedeutung der Ableitung und des Differentials Die Funktion y \u003d f (x) sei in U (x 0) definiert und am Punkt x 0 differenzierbar. M0M0 M x0x0 x 0 + x y x y = f (x) y0y0 y 0 + y 0 L ist der Sekante von L 0 - Tangente x y \u003d f (x 0 + x) - f (x 0) bei x aufgrund der Kontinuität der Funktion. Die Tangente an den Graphen der Funktion y \u003d f (x) am Punkt M 0 ist die Grenzposition der Sekante L bei x. y Wenn die Funktion am Punkt x 0 differenzierbar ist, dann hat in der Sekantengleichung y / x f (x 0) an x ​​und die Tangentengleichung die Form y \u003d y 0 + f (x 0) (x - x 0) .

12 M0M0 M x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) bei x 0 L0L0 tg \u003d f (x 0) Wenn y / x bei x, dann wird die Gerade x \u003d x 0, die sich aus der Sekantengleichung ergibt, als vertikale Tangente an den Graphen der Funktion at bezeichnet der Punkt M 0. Aus der Tangentengleichung erhalten wir y - y 0 \u003d f (x 0) (x - x 0) \u003d df (x 0) - Inkrement der Tangenten-Ordinate beim Bewegen von Punkt x 0 zu Punkt x . Die Normale zum Funktionsgraphen am Punkt M 0 ist die Gerade senkrecht zur Tangente, die durch den Punkt M 0 verläuft. Seine Gleichung hat die Form y \u003d y 0 - 1 / f (x 0) (x - x 0). L 1 - normal

13 Physikalische Anwendungen der Ableitung und des Differentials Wenn S (t) der Weg ist, den ein materieller Punkt zum Zeitpunkt t zurücklegt, dann ist S "(t) die Momentangeschwindigkeit des materiellen Punktes und dS \u003d S "(t) dt ist die Entfernung, die der materielle Punkt über einen Zeitraum von t bis t + dt zurücklegen würde, wenn er sich mit einer Geschwindigkeit bewegen würde, die der Momentangeschwindigkeit zum Zeitpunkt t entspricht. Wenn Q (t) die Strommenge ist, die zum Zeitpunkt t durch den Querschnitt des Leiters fließt, dann ist Q "(t) \u003d I die Stromstärke. Wenn N (t) die zum Zeitpunkt t gebildete Stoffmenge ist während einer chemischen Reaktion, dann N "(t) - die Geschwindigkeit einer chemischen Reaktion.

Wenn die Funktion j = F(X) ist irgendwann differenzierbar X = X 0, dann ist es an dieser Stelle stetig.

Daher kann die Funktion an Unstetigkeitspunkten keine Ableitung haben. Die umgekehrte Schlussfolgerung ist falsch, d. h. aus der Tatsache, dass irgendwann X = X 0 Funktion j = F(X) stetig ist, folgt daraus nicht, dass es an dieser Stelle differenzierbar ist. Zum Beispiel die Funktion j = |X| kontinuierlich für alle X (–< X < ), но в точке X= 0 hat keine Ableitung. Zu diesem Zeitpunkt gibt es keine Tangente an den Graphen. Es gibt eine rechte Tangente und eine linke Tangente, aber sie stimmen nicht überein.

21 Regeln finden. Produktion Beträge

Regel 1 Wenn die Funktionen y \u003d f (x) und y \u003d g (x) eine Ableitung am Punkt x haben, dann hat ihre Summe auch eine Ableitung am Punkt x und die Ableitung der Summe ist gleich der Summe von die Derivate:
(f (x) + 8 (x))" = f (x) + (x).
In der Praxis wird diese Regel kürzer formuliert: Die Ableitung der Summe ist gleich der Summe der Ableitungen.
Zum Beispiel,
Regel 2 Wenn die Funktion y \u003d f (x) eine Ableitung am Punkt x hat, dann hat die Funktion y \u003d kf (x) eine Ableitung am Punkt x und:

In der Praxis wird diese Regel kürzer formuliert: Der konstante Faktor kann aus dem Vorzeichen der Ableitung entnommen werden. Zum Beispiel,

Regel 3 Wenn die Funktionen y \u003d f (x) und y \u003d g (x) eine Ableitung am Punkt x haben, dann hat ihr Produkt auch eine Ableitung am Punkt x und:

In der Praxis wird diese Regel wie folgt formuliert: Die Ableitung des Produkts zweier Funktionen ist gleich der Summe zweier Terme. Der erste Term ist das Produkt der Ableitung der ersten Funktion und der zweiten Funktion, und der zweite Term ist das Produkt der ersten Funktion und der Ableitung der zweiten Funktion.
Zum Beispiel:
Regel 4 Wenn die Funktionen y \u003d f (x) und y \u003d g (x) dann eine Ableitung haben und der Quotient eine Ableitung am Punkt x hat, gilt außerdem:

Tabelle komplexer Derivate

22 Diffir. funkt. am Punkt

Funktion j=F(X) heißt an einem Punkt differenzierbar X 0, wenn sein Inkrement Δ ist j(X 0,Δ X) kann dargestellt werden als

Δ j(X 0,Δ X)=AΔ X+Ö(Δ X).

Hauptlinearteil AΔ X erhöht Δ j heißt das Differential dieser Funktion im Punkt X 0 entspricht dem Inkrement Δ X, und wird durch das Symbol gekennzeichnet dy(X 0,Δ X).

Damit die Funktion gewährleistet ist j=F(X) war zu diesem Zeitpunkt differenzierbar X 0 ist es notwendig und ausreichend, dass die Ableitung F′( X 0), während die Gleichheit A=F′( X 0).

Der Ausdruck für das Differential hat die Form

dy(X 0,dx)=F′( X 0)dx,

Wo dx=Δ X.

23 Prod. Diff. Funktionen

Ableitung einer komplexen Funktion. Ableitung einer parametrisch definierten Funktion

Lassen j - komplexe Funktion X, d.h. j = F(u), u = G(X), oder

Wenn G(X) Und F(u) sind jeweils differenzierbare Funktionen ihrer Argumente an den Punkten X Und u = G(X), dann ist die komplexe Funktion im Punkt auch differenzierbar X und wird durch die Formel gefunden

Ableitung einer parametrisch gegebenen Funktion.

24 Prod. und Diff. Auftrag von oben

Nun sei die Ableitung th-Ordnung in einer Umgebung des Punktes definiert und differenzierbar. Dann

Wenn eine Funktion eine partielle Ableitung in Bezug auf eine der Variablen in einem Bereich D hat, kann die benannte Ableitung, die selbst eine Funktion von ist, irgendwann partielle Ableitungen in Bezug auf dieselbe oder eine andere Variable haben. Für die ursprüngliche Funktion sind diese Ableitungen partielle Ableitungen zweiter Ordnung (oder zweite partielle Ableitungen).

Eine partielle Ableitung zweiter oder höherer Ordnung nach verschiedenen Variablen wird als gemischte partielle Ableitung bezeichnet. Zum Beispiel,

Ordnungsdifferenz N, Wo n > 1, einer Funktion an einem bestimmten Punkt heißt Differential an diesem Punkt der Ordnung Differential (n - 1), also

Für eine Funktion, die von einer Variablen abhängt, sehen das zweite und dritte Differential wie folgt aus:

Daraus können wir die allgemeine Form des Differentials ableiten N-te Ordnung aus der Funktion:

25 Sätze von Fermat, Rolle, Langrage

v Satz von Fermat: Lassen Sie eine Funktion definiert sein und ihre Maximal- und Minimalwerte erreichen ( M Und M) in einigen von . Wenn es eine Ableitung in gibt, dann ist diese notwendigerweise gleich 0.

Beweis: Es gibt. Zwei Fälle sind möglich:

1) , => , => .

2) , => , => .

Aus 1) und 2) folgt das

v Satz von Rolle (über die Wurzeln der Ableitung): Die Funktion sei stetig am und differenzierbar am und nehme an den Enden des Segments die gleichen Werte an: . Dann gibt es mindestens einen Punkt in , dessen Ableitung ist.

v Beweis: Kontinuierliche Reichweiten M Und M. Dann sind zwei Fälle möglich:

2) Der größte Wert wird innerhalb des Intervalls nach dem Satz von Fermat erreicht.

v Satz von Langrage (über endliche Inkremente): Die Funktion sei stetig auf und differenzierbar auf . Dann gibt es mindestens eine davon, für die die folgende Gleichheit gilt: .

Beweis: Lassen Sie uns die Funktion einführen. (stetig auf und differenzierbar auf ).

Die Funktion erfüllt den Satz von Rolle, für den gilt: , , , .

Die Funktion wird aufgerufen streng ansteigend auf wenn

Die Funktion wird aufgerufen abnehmend auf wenn

Die Funktion wird aufgerufen streng abnehmend auf wenn

Definition: Die Ableitung einer Funktion an einem Punkt ist die Grenze, bis zu der das Verhältnis ihres Inkrements an diesem Punkt zum entsprechenden Inkrement des Arguments tendiert, wenn dieses gegen Null tendiert:

Das heißt, wenn es in definiert ist, dann

Satz 1:

Der Graph einer Funktion hat genau dann eine nichtvertikale Tangente, wenn es an einem bestimmten Punkt einen endlichen Wert der Ableitung dieser Funktion gibt.

Nachweisen:

Es gebe dann einen f'()-endlichen Wert

Es gebe eine nichtvertikale Tangente => existiert - endlich.

Die Sekante tendiert zur Tangente.

Der Satz ist bewiesen.

Ticket 2 Stetigkeit einer Funktion, die eine Ableitung hat.

Eine Funktion f (x), die in einer Umgebung eines Punktes a definiert ist, heißt an diesem Punkt stetig, wenn

Satz: (eine notwendige Bedingung für die Existenz eines Derivats)

Wenn die Funktion einen endlichen Punkt hat, ist sie an diesem Punkt stetig.

Nachweisen:

Daher ist - an einem Punkt stetig.

Der Satz ist bewiesen.

Kommentar : Das Gegenteil ist nicht der Fall. Wenn eine Funktion an einem Punkt stetig ist, folgt daraus nicht, dass sie an diesem Punkt eine Ableitung hat.

Stellungnahme : Wenn eine Funktion in einem Punkt eine rechte und eine linke Ableitung hat, dann ist sie sowohl rechts als auch links stetig.

Ticket 3

Ableitung von Summe, Produkt, Quotient.

Ableitung der Umkehrfunktion.

Definition einer differenzierbaren Funktion. Notwendige und hinreichende Bedingung für Differenzierbarkeit.

Die Funktion soll an einem Punkt (endgültig) eine Ableitung haben: .

Dann kann man für hinreichend kleine Werte als Summe einer Funktion schreiben, die wir mit bezeichnen und die gegen Null tendiert, zusammen mit:

und das Inkrement an einem Punkt kann wie folgt geschrieben werden:

oder (1) ,

Denn unter einem Ausdruck versteht man eine Funktion, deren Verhältnis mit gegen Null geht.

Erläuterung:

Definition .

Eine Funktion heißt an einem Punkt differenzierbar, wenn ihr Inkrement wie folgt dargestellt werden kann: (2),

wobei A nicht von abhängt, aber im Allgemeinen von abhängt.

Satz 1:

Damit eine Funktion an einem Punkt differenzierbar ist, ist es notwendig und ausreichend, dass sie an diesem Punkt eine endliche Ableitung hat.

Nachweisen:

Angemessenheit der Bedingung oben bewiesen: Die Existenz einer endlichen Ableitung impliziert die Möglichkeit der Darstellung in der Form (1), wo man setzen kann

Notwendigkeitsbedingung . Die Funktion sei an einem Punkt differenzierbar. Dann erhalten wir aus (2) unter der Annahme.

Der Grenzwert der rechten Seite für existiert und ist gleich A:.

Dies bedeutet, dass es eine Ableitung gibt. Der Satz ist bewiesen.

Ticket 6 Differential einer Funktion, ihre geometrische Bedeutung.

Wenn die Funktion F hat eine Ableitung f΄(x Ö ) am Punkt X Ö, dann gibt es einen Grenzwert, wobei Δ f=f(x Ö + Δ x)-f(x Ö ) ,, oder wo A=f΄(x Ö ) .

Definition:

Funktion F an einem Punkt differenzierbar X Ö, wenn sein Inkrement wie folgt dargestellt werden kann:

Wo AΔ x=df. (*)

Das Differential ist der wichtigste lineare Teil des Inkrements der Funktion.

Wenn es eine endliche Ableitung gibt f΄(x Ö ) am Punkt X Ö, dann die Funktion f(x) ist an dieser Stelle differenzierbar.

Das Umgekehrte gilt auch: wenn die Funktion F an einem Punkt differenzierbar X Ö, d.h. sein Inkrement kann als (*) dargestellt werden, dann hat es eine Ableitung an dem Punkt X Ö gleich A:

Die geometrische Bedeutung des Differentials:

A Und B– Diagrammpunkte f(x), entsprechend den Werten X Ö Und (X Ö + Δ X) unabhängige Variable. Punktkoordinaten A Und B jeweils gleich f(x Ö ) Und f(x Ö + Δ X). Funktionsinkrement Δ f=f(x Ö + Δ x)-f(x Ö ) am Punkt X Ö gleich der Länge des Segments BD und kann als Summe Δ dargestellt werden f=BD=DC+CB, Wo DC=tgaΔ x=f΄(x Ö ) Δ X Und α ist der Winkel zwischen der Tangente am Punkt A zum Diagramm und die positive Richtung der Achse X. Von hier aus ist das klar Gleichstrom ist das Differential der Funktion F am Punkt X Ö :

DC=df=f΄(x Ö ) Δ X.

Gleichzeitig der Anteil des zweiten Mitglieds CB erhöht Δ F entfielen auf die Größe. Dieser Wert beträgt im Großen und Ganzen Δ X, vielleicht sogar mehr als der Hauptterm, aber es ist eine unendlich kleine höhere Ordnung als Δ X wenn Δ x→0.

EIGENSCHAFTEN VON FUNKTIONEN, DIE IN EINEM INTERVALL KONTINUIERLICH SIND

Betrachten wir einige Eigenschaften von Funktionen, die in einem Intervall stetig sind. Wir präsentieren diese Eigenschaften ohne Beweis.

Funktion y = f(x) angerufen kontinuierlich auf dem Segment [A, B], wenn es an allen inneren Punkten dieses Segments und an seinen Enden stetig ist, d.h. an Punkten A Und B, ist rechts bzw. links stetig.

Satz 1. Eine auf dem Segment stetige Funktion [ A, B] nimmt mindestens an einem Punkt dieses Segments den größten Wert und an mindestens einem Punkt den kleinsten an.

Der Satz besagt, dass wenn die Funktion y = f(x) kontinuierlich auf dem Segment [ A, B], dann gibt es mindestens einen Punkt x 1 Î [ A, B], so dass der Wert der Funktion f(x) Zu diesem Zeitpunkt wird der größte aller Werte in diesem Segment sein: f(x1) ≥ f(x). Ebenso gibt es einen solchen Punkt x2, wobei der Wert der Funktion der kleinste aller Werte im Segment ist: f(x 1) ≤ f(x).

Es ist klar, dass es mehrere solcher Punkte geben kann, zum Beispiel zeigt die Abbildung, dass die Funktion f(x) nimmt an zwei Punkten den kleinsten Wert an x2 Und X 2 ".

Kommentar. Die Aussage des Theorems kann falsch werden, wenn wir den Wert der Funktion auf dem Intervall ( A, B). In der Tat, wenn wir die Funktion betrachten y=x auf (0, 2), dann ist es in diesem Intervall stetig, erreicht darin aber nicht seine Maximal- oder Minimalwerte: Es erreicht diese Werte an den Enden des Intervalls, aber die Enden gehören nicht zu unserem Region.

Außerdem gilt der Satz nicht mehr für diskontinuierliche Funktionen. Gib ein Beispiel.

Folge. Wenn die Funktion f(x) kontinuierlich auf [ A, B], dann ist es auf dieses Intervall beschränkt.

Satz 2. Lassen Sie die Funktion y = f(x) kontinuierlich auf dem Segment [ A, B] und an den Enden dieses Segments Werte unterschiedlichen Vorzeichens annimmt, dann befindet sich mindestens ein Punkt innerhalb des Segments x=C, wobei die Funktion verschwindet: f(C)= 0, wobei a< C< b

Dieser Satz hat eine einfache geometrische Bedeutung: wenn die Punkte des Graphen einer stetigen Funktion y = f(x), entsprechend den Enden des Segments [ A, B] liegen auf gegenüberliegenden Seiten der Achse Ochse, dann schneidet dieser Graph mindestens an einem Punkt des Segments die Achse Ochse. Diskontinuierliche Funktionen verfügen möglicherweise nicht über diese Eigenschaft.

Dieser Satz lässt die folgende Verallgemeinerung zu.

Satz 3 (Satz über Zwischenwerte). Lassen Sie die Funktion y = f(x) kontinuierlich auf dem Segment [ A, B] Und f(a) = A, f(b) = B. Dann für eine beliebige Zahl C zwischen A Und B, es gibt einen solchen Punkt innerhalb dieses Segments CÎ [ A, B], Was f(c) = C.

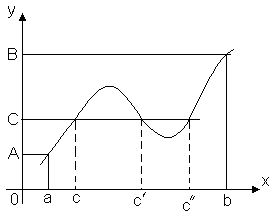
Dieser Satz ist geometrisch offensichtlich. Betrachten Sie den Graphen der Funktion y = f(x). Lassen f(a) = A, f(b) = B. Dann irgendeine Zeile y=C, Wo C- eine beliebige Zahl dazwischen A Und B, schneidet den Graphen der Funktion mindestens in einem Punkt. Die Abszisse des Schnittpunkts ist dieser Wert x=C, bei welchem f(c) = C.

Somit durchläuft eine stetige Funktion, die von einem ihrer Werte zu einem anderen übergeht, notwendigerweise alle Zwischenwerte. Insbesondere:

Folge. Wenn die Funktion y = f(x) in einem Intervall stetig ist und den größten und kleinsten Wert annimmt, dann nimmt es in diesem Intervall mindestens einmal jeden Wert zwischen seinem kleinsten und seinem größten Wert an.

Derivat und seine Anwendungen. Derivative Definition

Lassen Sie uns eine Funktion haben y=f(x), in einem bestimmten Intervall definiert. Für jeden Argumentwert X aus diesem Intervall die Funktion y=f(x) hat eine bestimmte Bedeutung.

Betrachten Sie zwei Argumentwerte: initial X 0 und neu X.

Unterschied x–x 0 heißt Inkrement des Arguments x am Punkt X 0 und bezeichnet Δx. Auf diese Weise, ∆x = x – x 0 (Argumentinkrement kann entweder positiv oder negativ sein). Aus dieser Gleichheit folgt das x=x 0 +Δx, d.h. Der Anfangswert der Variablen wurde etwas erhöht. Dann, wenn an der Stelle X 0 Funktionswert war f(x 0 ), dann am neuen Punkt X Die Funktion übernimmt den Wert f(x) = f(x 0 +∆x).

Unterschied j-j 0 = f(x) – f(x 0 ) angerufen Funktionsinkrement y = f(x) am Punkt X 0 und wird durch das Symbol gekennzeichnet Δy. Auf diese Weise,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Normalerweise der Anfangswert des Arguments X 0 gilt als fest und als neuer Wert X- variabel. Dann j 0 = f(x 0 ) stellt sich als konstant heraus und y = f(x)- variabel. Schritte Δy Und Δx werden auch Variablen sein und Formel (1) zeigt das Dy ist eine Funktion der Variablen Δx.

Stellen Sie das Verhältnis des Inkrements der Funktion zum Inkrement des Arguments zusammen

Finden wir die Grenze dieser Beziehung bei Δx→0. Wenn dieser Grenzwert existiert, wird er als Ableitung dieser Funktion bezeichnet. f(x) am Punkt X 0 und bezeichnen F "(X 0). Also,

Derivat diese Funktion y = f(x) am Punkt X 0 wird als Grenze des Inkrementverhältnisses der Funktion Δ bezeichnet j zum Inkrement des Arguments Δ X wenn dieser willkürlich gegen Null tendiert.

Beachten Sie, dass für dieselbe Funktion die Ableitung an verschiedenen Punkten erfolgt X kann unterschiedliche Werte annehmen, d.h. Die Ableitung kann als Funktion des Arguments betrachtet werden X. Diese Funktion wird bezeichnet F "(X)

Die Ableitung wird durch die Symbole bezeichnet F "(x),y", . Der spezifische Wert der Ableitung bei x = ein bezeichnet F "(A) oder j "| x=a.

Die Operation, die Ableitung einer Funktion zu finden f(x) heißt Differenzierung dieser Funktion.

Um die Ableitung per Definition direkt zu finden, können Sie Folgendes anwenden Faustregel:

Beispiele.

MECHANISCHE BEDEUTUNG DES Derivats

Aus der Physik ist bekannt, dass das Gesetz der gleichförmigen Bewegung die Form hat s = v t, Wo S- bis zu diesem Zeitpunkt zurückgelegter Weg T, v ist die Geschwindigkeit der gleichförmigen Bewegung.

Allerdings seitdem Die meisten in der Natur vorkommenden Bewegungen sind ungleichmäßig, dann im Allgemeinen die Geschwindigkeit und folglich die Entfernung S wird von der Zeit abhängen T, d.h. wird eine Funktion der Zeit sein.

Lassen Sie also den materiellen Punkt gemäß dem Gesetz geradlinig in eine Richtung bewegen s=s(t).

Merken Sie sich einen Moment T 0 . Zu diesem Zeitpunkt hat der Punkt den Pfad überschritten s=s(t 0 ). Bestimmen wir die Geschwindigkeit v materieller Zeitpunkt T 0 .

Denken Sie dazu an einen anderen Zeitpunkt T 0 + Δ T. Sie entspricht der zurückgelegten Strecke s =s(t 0 + Δ T). Dann für das Zeitintervall Δ T der Punkt hat den Weg Δs zurückgelegt =s(t 0 + Δ T)–s(t).

Betrachten wir die Beziehung. Sie wird als Durchschnittsgeschwindigkeit im Zeitintervall Δ bezeichnet T. Die Durchschnittsgeschwindigkeit kann die aktuelle Bewegungsgeschwindigkeit eines Punktes nicht genau charakterisieren T 0 (weil die Bewegung ungleichmäßig ist). Um diese wahre Geschwindigkeit anhand der Durchschnittsgeschwindigkeit genauer auszudrücken, müssen Sie ein kleineres Zeitintervall Δ verwenden T.

Also die Bewegungsgeschwindigkeit zu einem bestimmten Zeitpunkt T 0 (Momentangeschwindigkeit) ist die Grenze der Durchschnittsgeschwindigkeit im Intervall von T 0 bis T 0 +Δ T wenn Δ T→0:

,

diese. Geschwindigkeit ungleichmäßiger Bewegung ist die Ableitung der zurückgelegten Strecke nach der Zeit.

GEOMETRISCHE BEDEUTUNG DES Derivats

Lassen Sie uns zunächst die Definition einer Tangente an eine Kurve an einem bestimmten Punkt einführen.

Nehmen wir an, wir hätten eine Kurve und einen festen Punkt darauf M 0(siehe Abbildung). Betrachten Sie einen anderen Punkt M diese Kurve und zeichne eine Sekante M 0 M. Wenn Punkt M beginnt sich entlang der Kurve und des Punktes zu bewegen M 0 bleibt stationär, die Sekante ändert ihre Position. Wenn, mit unbegrenzter Annäherung an den Punkt M Kurve zu Punkt M 0 Auf jeder Seite nimmt die Sekante tendenziell die Position einer bestimmten Geraden ein M 0 T, dann die Gerade M 0 T heißt Tangente an die Kurve am gegebenen Punkt M 0.

Das., Tangente zur Kurve an einem bestimmten Punkt M 0 wird als Grenzposition der Sekante bezeichnet M 0 M wenn der Punkt M tendiert entlang der Kurve zu einem Punkt M 0.

Betrachten Sie nun die stetige Funktion y=f(x) und die dieser Funktion entsprechende Kurve. Für einen gewissen Wert X 0-Funktion nimmt einen Wert an y0=f(x0). Diese Werte X 0 und j 0 auf der Kurve entspricht einem Punkt M 0 (x 0; y 0). Lassen Sie uns ein Argument vorbringen x0 Inkrement Δ X. Der neue Wert des Arguments entspricht dem inkrementierten Wert der Funktion j 0 +Δ y=f(x 0 –Δ X). Wir bekommen einen Punkt M(x 0+Δ X; y 0+Δ y). Zeichnen wir eine Sekante M 0 M und bezeichnen mit φ den Winkel, den die Sekante mit der positiven Richtung der Achse bildet Ochse. Stellen wir eine Beziehung her und notieren wir das.

Wenn nun Δ X→0 also aufgrund der Stetigkeit der Funktion Δ bei→0 und damit der Punkt M, bewegt sich entlang der Kurve und nähert sich dem Punkt auf unbestimmte Zeit M 0. Dann die Sekante M 0 M neigt dazu, die Position einer Tangente an die Kurve an dem Punkt einzunehmen M 0, und der Winkel φ→α bei Δ X→0, wobei α den Winkel zwischen der Tangente und der positiven Richtung der Achse bezeichnet Ochse. Da die Funktion tg φ bei φ≠π/2 kontinuierlich von φ abhängt, ist bei φ→α tg φ → tg α und daher ist die Steigung der Tangente:

diese. f"(x)= tgα .

Also geometrisch y "(x 0) stellt die Steigung der Tangente an den Graphen dieser Funktion am Punkt dar x0, d.h. für einen gegebenen Wert des Arguments X, die Ableitung ist gleich dem Tangens des Winkels, den die Tangente an den Funktionsgraphen bildet f(x) an der entsprechenden Stelle M 0 (x; y) mit positiver Achsrichtung Ochse.

Beispiel. Finden Sie die Steigung der Tangente an die Kurve y = x 2 am Punkt M(-1; 1).

Das haben wir schon gesehen ( X 2)" = 2X. Aber die Steigung der Tangente an die Kurve beträgt tg α = j"| x=-1 = - 2.

DIFFERENZIERBARKEIT DER FUNKTIONEN. Kontinuität einer differenzierbaren Funktion

Funktion y=f(x) angerufen differenzierbar Irgendwann X 0, wenn es an dieser Stelle eine bestimmte Ableitung hat, d.h. wenn der Grenzwert der Beziehung existiert und endlich ist.

Wenn eine Funktion an jedem Punkt eines Segments differenzierbar ist [ A; B] oder Intervall ( A; B), dann sagen sie es differenzierbar auf dem Segment [ A; B] bzw. im Intervall ( A; B).

Es gilt der folgende Satz, der einen Zusammenhang zwischen differenzierbaren und stetigen Funktionen herstellt.

Satz. Wenn die Funktion y=f(x) irgendwann differenzierbar x0, dann ist es an dieser Stelle stetig.

Somit impliziert die Differenzierbarkeit einer Funktion ihre Stetigkeit.

Nachweisen. Wenn , Das

,

wobei α ein unendlich kleiner Wert ist, d. h. Größe, die bei Δ gegen Null geht X→0. Aber dann

Δ j=F "(x0) Δ X+αΔ X=> Δ j→0 bei Δ X→0, d.h. f(x) – f(x0)→0 um X→X 0 , was bedeutet, dass die Funktion f(x) kontinuierlich am Punkt X 0 . Q.E.D.

Daher kann die Funktion an Unstetigkeitspunkten keine Ableitung haben. Die umgekehrte Aussage ist nicht wahr: Es gibt stetige Funktionen, die an manchen Punkten nicht differenzierbar sind (das heißt, sie haben an diesen Punkten keine Ableitung).

Betrachten Sie die Punkte in der Abbildung a, b, c.

Am Punkt A bei Δ X→0 hat die Beziehung keinen Grenzwert (da die einseitigen Grenzwerte für Δ unterschiedlich sind). X→0–0 und Δ X→0+0). Am Punkt A Der Graph hat keine definierte Tangente, aber es gibt zwei verschiedene einseitige Tangenten mit Steigungen Zu 1 und Zu 2. Diese Art von Punkt wird Eckpunkt genannt.

Am Punkt B bei Δ X→0 Das Verhältnis hat ein konstantes Vorzeichen und einen unendlich großen Wert. Die Funktion hat eine unendliche Ableitung. An diesem Punkt hat der Graph eine vertikale Tangente. Punkttyp – „Wendepunkt“ mit vertikaler Tangente.

Am Punkt C einseitige Ableitungen sind unendlich große Mengen unterschiedlicher Vorzeichen. An diesem Punkt weist der Graph zwei verschmolzene vertikale Tangenten auf. Typ - „Spitze“ mit vertikaler Tangente – ein Sonderfall eines Eckpunkts.